Abstract
Characterisation of the spatial peak intensity at the focus of high intensity focused ultrasound (HIFU) transducers is difficult because of the risk of damage to hydrophone sensors at the high focal pressures generated. Hill et al (1994) provided a simple equation for estimating spatial-peak intensity for solid spherical bowl transducers using measured acoustic power and focal beamwidth. This paper demonstrates theoretically and experimentally that this expression is only strictly valid for spherical bowl transducers without a central (imaging) aperture. A hole in the centre of the transducer results in over-estimation of the peak intensity. Improved strategies for determining focal peak intensity from a measurement of total acoustic power are proposed. Four methods are compared: (i) a solid spherical bowl approximation (after Hill et al 1994), (ii) a numerical method derived from theory, (iii) a method using measured sidelobe to focal peak pressure, and (iv) a method for measuring the focal power fraction (FPF) experimentally. Spatial-peak intensities were estimated for 8 transducers at three drive powers levels: low (approximately 1W), moderate (~10W) and high (20 - 70W). The calculated intensities were compared with those derived from focal peak pressure measurements made using a calibrated hydrophone. The FPF measurement method was found to provide focal peak intensity estimates that agreed most closely (within 15%) with the hydrophone measurements, followed by the pressure ratio method (within 20%). The numerical method was found to consistently over-estimate focal peak intensity (+40% on average), however, for transducers with a central hole it was more accurate than using the solid bowl assumption (+70% overestimation). In conclusion, the ability to make use of an automated beam plotting system, and a hydrophone with good spatial resolution, greatly facilitates characterisation of the FPF, and consequently gives improved confidence in estimating spatial peak intensity from measurement of acoustic power.
Introduction
High intensity focused ultrasound (HIFU) is gaining more widespread use as a non-ionising, non-invasive ablative treatment for soft tissue tumours (Orsi et al 2010). Target organs include the kidney (Ritchie et al 2010), liver (Chen et al 2016), pancreas (Marinova et al 2016, Hwang et al 2009) and prostate (van Velthoven et al 2016, Alkhorayef et al 2015, Crouzet et al 2010). Palliative treatments of painful bone metastasis are also under investigation (Huisman et al 2014). Other applications include the treatment of uterine fibroids (Yoon et al 2013). For tissue ablation, the primary damage mechanism is heating, with the focal intensity being sufficient to ensure coagulative necrosis during exposure. Mechanical damage caused by inertial cavitation may also occur at the HIFU focus (Farny et al 2009). We are primarily interested in clinical applications of HIFU, where there are two options for treatment guidance and monitoring, namely magnetic resonance (MR) (e.g. Bradley et al 2009, Rabinovici et al 2007) and ultrasound imaging (e.g. Orgera et al 2011, Illing et al 2005). MR guided HIFU (MRgHIFU) offers excellent tissue contrast and the ability to monitor temperature using proton resonance frequency shift sequences (Ishihara et al 1995, Roujol et al 2010). Ultrasound guided HIFU (USgHIFU) is inexpensive and more portable, and offers greater inherent temporal and spatial resolution. It therefore provides an attractive alternative to MRgHIFU, although adequate treatment monitoring techniques require further development.
The acoustic pressure or intensity at the focal peak is almost always the preferred parameter for quantifying the output of HIFU transducers when relating exposure to therapeutic effect (ter Haar et al 2011). This is not surprising since the clinical aim is usually to optimise the thermal therapeutic effect in the focal region whilst avoiding damage elsewhere in the field. The pressures generated by tightly focused HIFU transducers often render measurement at the focal site problematic, due to sensor damage. Studies in our laboratory suggest that at low MHz frequencies hydrophones are best suited to the measurement of acoustic pressures below 5 MPa using pulsed exposures (e.g. 20 to 80 cycles long), to avoid acoustic cavitation damage. As a consequence, characterisation at higher power levels is usually achieved by measurement of the total acoustic power in the whole ultrasound beam using devices such as radiation force (Beissner 1993) or buoyancy balances (Shaw 2008). Intensity values are often reported in the literature with little, or no, indication of how these values are obtained, with intensity information being omitted or only the total acoustic power being reported. For proper scientific comparison of data, it is important therefore that methods of quantifying focal peak pressures and intensity be clearly defined and adopted throughout the HIFU community.
As HIFU technology becomes more widespread, there is an increasing need to minimise calibration uncertainties, and to standardise characterisation techniques for the wide range of clinical and research devices available. Single element spherical bowl transducers were commonly used in early clinical HIFU research, (e.g. Visioli et al 1999). The spherical bowl remains the favoured geometry for achieving a high intensity focal point, however improved treatment delivery and monitoring requires use of more complex arrangements. For example, in USgHIFU, a co-axial alignment of therapy and imaging beams allows B-mode visualisation of the tissue between the transducer and the focus (e.g. Wu et al 2004, Pernot et al 2007). To accommodate this co-axial alignment, an imaging aperture, normally a central circular hole, in the HIFU transducer is required. Treatment monitoring and delivery may also be improved by placing detectors in the central aperture for cavitation monitoring (Coussios et al 2007, Gyöngy and Coussios 2010, Jensen et al 2012, Farny et al 2010). In both MRgHIFU and USgHIFU there is growing interest in the use of phased array transducers consisting of a large (≥ 256) number of elements arranged over a spherical shell (Pernot et al 2003, Hand et al 2009, Auboiroux et al 2011). Here we begin by investigating the effect of a central imaging aperture in single element spherical bowl transducers on spatial peak intensity. An expression was formulated by Hill et al (1994) for deriving the temporal average focal peak intensity (referred from here as Isp) from a transducer power output measurement. This expression only provides a very rough approximation of Isp, particularly for transducers with a central imaging aperture (or hole). One of the aims of this paper is to investigate novel ways of estimating Isp from measurements of a transducer’s acoustic power output. Whilst this approach is generally not considered ideal due to the large number of assumptions involved, there may be situations for which it is the only option when a suitable calibrated hydrophone is not available.
The results of the analytical solution of O’Neil (1949) have been extended here to give evidence for a loss of efficiency in depositing the ultrasound energy within the focal region when there is a central aperture in the transducer are described below. We introduce the concept of the focal power fraction (FPF), defined as the fraction of the total power in the ultrasound beam which propagates within the 6dB intensity limits of the focus. Furthermore, the simulations provide data for a range of acoustic field parameters which are then compared to experiment. Four different methods of estimating Isp using acoustic power have been tested. These include: i) the existing expression as derived by Hill et al (1994) referred to here as the solid spherical bowl approximation (SSBA); ii) a numerical method derived from theory which accounts for a central hole in transducer geometry; iii) a variation of the SSBA method in which the ratio of the acoustic pressure amplitudes at the sidelobe and focal peak are measured (pressure ratio method); and (iv) a second variation of the SSBA method in which a detailed measurement of the acoustic field in the focal plane results in a direct estimate of the FPF. Solid bowl transducers (spherically focused, single element transducers without a hole), ‘annular’ transducers (spherically focused, single element transducers with a central hole) and one example of a non-axisymmetric device have been tested experimentally. Experimental verification of the relative accuracy of the four methods was achieved by comparing the computed Isp with that obtained directly from acoustic pressure measurements at the focal peak using a calibrated hydrophone.
Theory
O’Neil (1949) formulated a description of the linear acoustic field near the focal plane for spherical bowl transducers. The velocity potential ψ close to the focal peak was approximated by the sum of a series of Bessel functions J:
| (1) |
| (2) |
| (3) |
| (4) |
where κ is the wavenumber, R is the path length, a is the transducer radius, α is the half angle subtended by the transducer diameter, S is the surface area, u is the velocity potential at the source, θ is the angle between the sound axis and the vector between the centre of the transducer and the field position, and z represents a dimensionless radial position parameter. The first summation term in Equation 2 gives a good approximation for F, a dimensionless focusing function, as the higher order terms provide increasingly smaller contributions. The expression can be considered valid when θ is small (<30°), and the extent of the radiating surface and the radius of curvature are both greater than the wavelength. The acoustic pressure field can then be derived by taking the temporal derivative of the velocity potential which can be shown to be directly proportional to the velocity potential when these conditions are satisfied. This expression was used to quantify the fraction of the total acoustic power incident within a circle defined by the dimensionless parameter ze at the focal plane, i.e. the fractional power function (G):
| (5) |
O’Neil’s expression predicts that, for a solid spherical bowl transducer, ~68% of the total power is contained within the circle defined by the 6 dB limits (ze = 2.215) in the focal plane Hill et al (1994) used this result to derive an equation relating Isp, total acoustic power (W) and the 6 dB beam width (D):
| (6) |
O’Neil’s expression is generally valid for spherical bowl transducers without a central imaging aperture. However, this approach can be expanded to annular transducers (i.e. those with a central circular hole). For a transducer with outer radius r2 and a central hole of radius r1, the velocity potential in the focal plane can be calculated by the subtraction of the velocity potential of a solid bowl transducer with radius r1 from that of one with radius r2, giving:
| (7) |
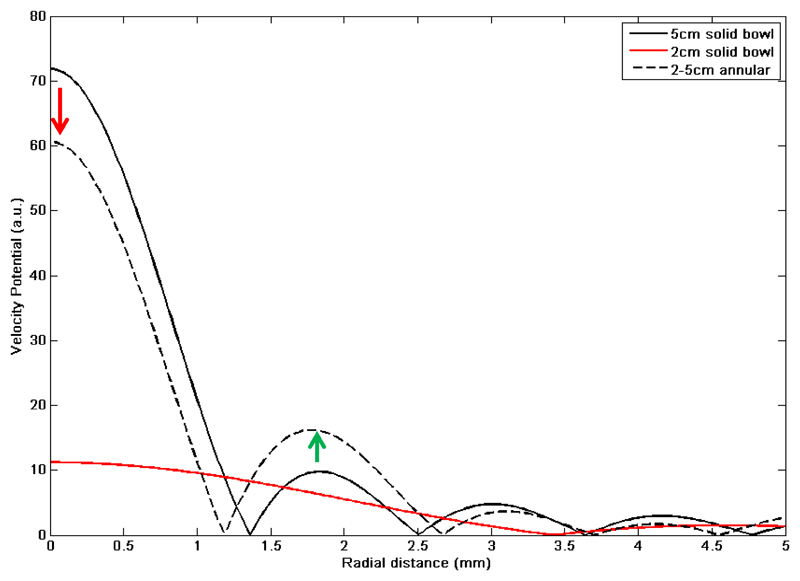
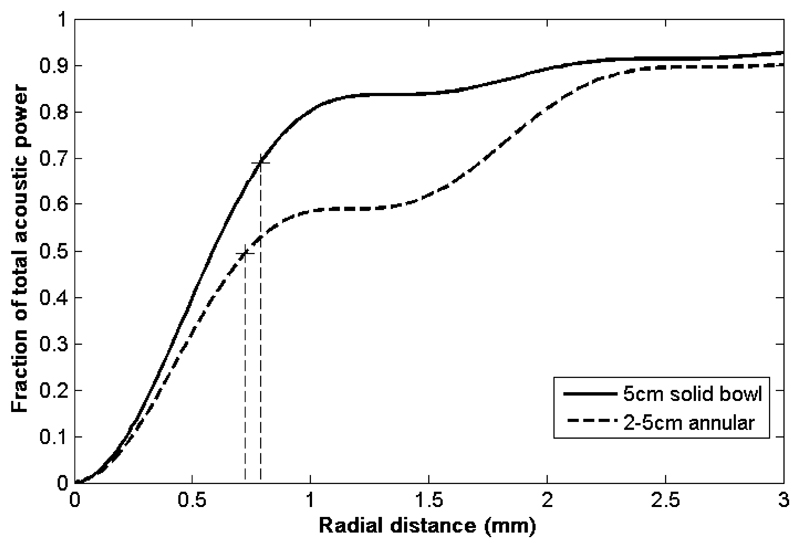
where Fr1 and Fr2 represent the normalised velocity potential profiles for the two solid bowls, and Sr1 and Sr2 represent the respective surface area. Figure 1 shows examples of velocity potentials for 2 MHz spherical bowl transducers with focal length of 15 cm and radii 2 and 5 cm. The velocity potential from an annular transducer (5 cm radius with 2 cm radius imaging hole), computed using the subtraction method in equation 7, is also shown. In this example it is apparent that the first radial sidelobe of the annulus is higher compared to the focal peak than for the 5 cm radius solid bowl transducer. This reduces the fraction of the total power contained within the focus (i.e. the focal power fraction) from ~70% to ~53%, as shown in Figure 2.
Figure 1.
Analytical velocity potential solutions for transducers with a focal length of 15 cm, operating at 2 MHz with radii of 5 cm (black) and 2 cm (red). A complex pressure subtraction of the small radius (2 cm) transducer from the large one (5 cm radius) provides an estimate of the profile for a third annular transducer (dashed line) with 5 cm outer radius and 2 cm inner hole radius. The focal peak is lower, (red arrow) and the amplitude of the first sidelobe is raised (green arrow).
Figure 2.
The fraction of total acoustic power (G curve as described in Equation 5) passing through a circle in the focal plane for a 5 cm radius spherical bowl transducer (solid line) and an annular transducer with 5 cm outer radius and 2 cm hole inner radius (dashed line) transducer are shown. The dashed vertical lines represent the respective 6 dB positions and corresponding G values at those positions for both transducers, demonstrating the lower fractional power that passes through the focal region for the annular transducer.
Using this theoretical framework it is possible to explore the interplay between transducer properties (radius, focal length, imaging hole radius and frequency), and experimentally quantifiable acoustic field parameters such as the focal 6 dB beam width D, the ratio between sidelobe and focal peak pressure, and the focal power fraction (FPF).
Methods
Numerical methods
The velocity potentials of transducers were calculated in Matlab using equations 1-4 and 7. Transducer diameters (2 - 15 cm), central imaging hole diameters (0 - 10 cm) and focal lengths (5 - 20 cm) were varied in 0.5 cm increments to produce a 3D parameter space. Each physically achievable permutation of the above variables was simulated, giving a total of 12,079 transducer configurations. The acoustic frequency was 2.0 MHz and the speed of sound 1500 m/s. For computational precision, calculations were performed in the focal plane with a lateral step size of 0.01 cm with the outer limit set to either a z parameter value (from equation 3) of 65, approximately equivalent to the position of the 20th sidelobe, or to a value of θ equivalent to 0.6 radians, whichever was smallest. This limit was considered sufficient to include the vast majority of the available acoustic power. The first 11 terms of equation 2 were calculated for each transducer; with the velocity potentials computed using Equation 7 for both solid bowl and annular devices. The fractional power function G (Eqn. 5) was calculated by numerical integration of the square of the velocity potential, assuming radial symmetry, and by normalising the result of the integral to a value of 1 at the final z value. The normalised G value at the 6dB focal width was estimated by interpolation function to give a theoretical FPF estimate. The velocity potential amplitudes at the focal peak and first lateral sidelobe for each transducer were recorded to derive the sidelobe to focal peak ratio (SPr). A polynomial fit was applied to the FPF vs SPr data, thus providing a means of predicting the FPF from experimentally derived measurement of SPr. In addition to the calculations described above, a further 8 were performed for the experimental transducer configurations described in this paper.
Experimental measurements
Methods of determining Isp from measurement of acoustic power output were compared directly with intensities inferred from calibrated hydrophone (Onda HGL-0200, Onda Corporation, CA, USA) measurements of focal peak pressure. These hydrophone measurements were considered to be the gold standard against which to assess the accuracy of Isp estimation methods, since they provided a localised measurement of focal peak pressure. This hydrophone’s sensor size complies with the IEC Standard 62127 specification. The accuracy of the hydrophone measurement itself is mostly determined by knowledge of the sensitivity from its calibration (estimated uncertainty of 4.2% in pressure sensitivity at 68% confidence level).
Measurements were performed on 7 transducers, each of which was driven at three peak-peak signal generator drive voltage amplitudes (mVp-p), giving three separate acoustic power levels, which are here referred to as ‘low’, ‘moderate’ and ‘high’. The drive voltage settings were 50 mVp-p for the ‘low’ setting (giving ~1W acoustic power following signal amplification), 150mVp-p for the moderate setting (~12W), with the value for the ‘high’ setting being determined independently for each transducer. The ‘low’ setting allowed measurement under conditions which were approximately linear, as assumed in the theory. The ‘moderate’ power level allowed measurements at a higher level that was still within the safe limits of hydrophone operation. For the ‘high’ power setting, an acoustic attenuator was inserted between the transducer and the hydrophone with approximately 1 cm clearance between the rear (exit) surface of the attenuator and the hydrophone. The aim was to investigate whether a further increase in power and the inclusion of the attenuating medium would result in detectable changes in the measured acoustic field parameters due to the combined effects of non-linear propagation, attenuation and changes in sound speed between the water and phantom materials. The approach here was to achieve approximately the same Isp with the ‘high’ setting as with the ’moderate’ setting, thus enabling a further increase in transducer drive power. In practice this was achieved by performing an insertion loss attenuation measurement at the ‘moderate’ drive level and then using the total attenuation estimate to adjust the drive setting. Because the insertion-loss due to the attenuator is frequency dependent, the exact value of the ‘high’ drive setting was dependent on the drive frequency for each transducer. The use of three power levels allowed an assessment of whether acoustic field parameters determined at a ‘low’ power level (nominally under linear propagation conditions) were a useful surrogate for higher power measurements, i.e. whether it is still possible to predict Isp at higher drive levels with an acceptable level of accuracy.
Transducers and drive system
One of the 7 transducers (number 4) could be operated at two frequencies, giving a total of 8 transducer geometry and frequency combinations, as summarised in Table 1. Transducers 1 to 3 were solid bowls, transducers 4 to 6 were annular devices, transducer 7 was an annular design consisting of an array of 10 closely-spaced (0.5 mm gap) parallel strip elements (Civale et al 2006) where only the 6 more centrally located elements were connected to the electrical drive. The purpose of this was to test the FPF estimation techniques with a non-axisymmetric ultrasound source.
Table 1.
Details of the 8 test transducers. Transducers 4a and 4b are the same device and differ only in operating frequency. Nominal inner and outer diameter dimensions and focal lengths are given, together with the estimated active surface area, transducer f number (all transducer have f number greater than 0.9) and drive frequency.
| Number | 1 | 2 | 3 | 4a | 4b | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Manufacturer / supplier | ICR “Mauve” | Siemens A2-2 | Université de Lyon | Sonic Concepts H148MRA | Sonic Concepts H102MRB | Imasonic SA cdc6282a | Imasonic SA cdc3521 | |
| Piezoelecric Type | Ceramic, air backed | Ceramic, water backed | Ceramic, air backed | Piezo-composite, air backed | Piezo-composite, air backed | Piezo-composite, air backed | Piezo-composite, air backed | |
| f number | 1.79 | 1.29 | 1.00 | 0.98 | 0.98 | 1.36 | 1.36 | |
| Transducer type | Solid Bowl | Solid Bowl | Solid Bowl | Annular | Annular | Annular | Non-axisymmetric | |
| Frequency (MHz) | 1.693 | 1.7 | 1.07 | 2.4 | 1.7 | 1.08 | 1.7 | 1.7 |
| Diameter | 8.4 | 5.6 | 5.0 | 6.4 | 6.4 | 11.0 | 11.0 | |
| Hole diameter | 0.0 | 0.0 | 0.0 | 2.2 | 2.2 | 5.4 | 5.0 | |
| Focal length | 15.0 | 7.2 | 5.0 | 6.3 | 6.3 | 15.0 | 15.0 | |
| Active Area (cm2) | 56.5 | 25.6 | 21.0 | 30.7 | 30.7 | 75.4 | 47.2 | |
 |
 |
 |
 |
 |
 |
 |
 |
|
Each transducer was driven using a 55 dB 300 W amplifier (E&I A300, Acquitek, France) connected to a signal generator (HP 33120A, Agilent Technologies, UK). Electrical power delivered to the transducer was monitored by means of an in-house built pick-off box, providing voltage and current signals, positioned between the amplifier output and the impedance matching circuitry for each transducer. For acoustic field measurements, and power calibrations at the “medium” and ”high” power settings, pulsed excitations were used. For continuous wave sonications, such as those used for calibration of acoustic power at the ‘low’ power setting, the exposure duration was controlled by a timer box accurate to 10 ms.
Hydrophones and beamplotting system
Two hydrophones were used. A Fabry-Perot fibreoptic hydrophone system (Precision Acoustics, UK) was used for relative measurements of acoustic pressure (ie. for beam plotting where absolute values were not required) at the previously defined ‘low’ power. A robust needle hydrophone (HGL-0200, Onda Corporation, CA, USA) was used for focal peak measurements at all three drive power levels, the frequency dependent sensitivity of this device was provided by the manufacturer and verified in house against a reference membrane hydrophone (UC1604, Precision Acoustics, UK) which had previously been calibrated at the National Physical Laboratory (NPL, UK). The Onda hydrophone was preferred for accurate focal peak pressure quantification over the membrane hydrophone because its smaller sensor size reduces errors due to spatial averaging effects (0.2 vs. 0.4 mm diameter).
The hydrophones were mounted on a holder attached to a motorised mechanical gantry which allowed automated positioning in three orthogonal axes, with a precision of 20 μm. The position of the hydrophone was controlled by software written in Labview™ (UMS software, Precision Acoustics, UK) on a personal computer.
The transducer and hydrophone were immersed in a large (50 x 50 x 100 cm) tank filled with de-ionised, filtered (5 μm), UV treated and de-gassed water (<2 mg/l dissolved O2). The HIFU transducers were driven in burst mode using either 40 (transducers 2 to 7) or 80 (transducer 1) cycle bursts. The pulse repetition frequency was set to give a duty cycle of 5%. The hydrophone was connected to a Waverunner 64Xi oscilloscope (Lecroy, US) using a 50 Ω termination impedance. The hydrophone signal was sampled at 250 MHz. During scanned measurements, 100 waveforms were acquired and averaged on the oscilloscope, to improve signal to noise ratio. The averaged waveform data was transferred to a PC and segmented to obtain a small whole number (~5) of cycles. The voltage signal was deconvolved with the Onda hydrophone’s frequency dependent sensitivity data by performing a fast Fourier transform on the segmented signal, dividing the resulting voltage spectrum by the hydrophone’s frequency dependent sensitivity, and finally by performing an inverse Fourier transform to obtain a time dependent pressure waveform. The root mean square focal peak pressure (prms) was then computed and converted to spatial-peak temporal-average intensity using the following expression:
| (8) |
where ρ is the density (1000 kg/m3) and c is the sound speed (1500 m/s).
Acoustic power measurement system
The acoustic power output of each transducer was measured using a buoyancy system based on that published by Shaw (2008). The target was a sealed perspex cylinder filled with castor oil (product number 259853, Sigma Aldrich, UK) with the top surface being an acoustically transparent membrane. The flexible membrane allowed the oil to expand when heated. The buoyancy target was submerged in a cylindrical water tank and attached to a digital balance (LA230S, Sartorius Mechatronics, Germany) by fine nylon wire (Figure 3). Each HIFU transducer was placed above the buoyancy target, firing downwards through the membrane. The target was wide enough (12 cm) to intercept the entire width of the ultrasound beam generated by all the test transducers, its length (18.5 cm) and an acoustic reflector placed at the bottom of the cylinder ensured that all the ultrasound energy was effectively absorbed by the castor oil for frequencies above 1 MHz (total attenuation >30dB). Measurement of the rate of change of target weight during electrical heating gave a sensitivity of 0.33 mgJ-1 with a standard deviation of ±0.01 mgJ-1. Use of the buoyancy method of measuring acoustic power was preferred over the radiation force method for two reasons: the HIFU beam does not have to be aligned perfectly normal to the target’s membrane, and correction for the converging nature of the acoustic beam is not necessary.
Figure 3.
Buoyancy balance used for measurement of total acoustic power. The absorbing castor oil target is positioned in a cylindrical water tank by nylon wire holding the target at four positions, the wires attach to a hook on the underpan weighing mount of a digital balance. The HIFU transducer is attached so that no air is trapped on its surface and no contact is made between it and the wires supporting the target. The HIFU beam propagates into the castor oil target, in the direction shown, through an acoustically transparent membrane (not shown).
Acoustic power calibrations were performed using the 5% duty cycle used with the hydrophone measurements. For these acoustic power measurements the burst length was set to 64 times that used in hydrophone scans and the pulse repetition frequency was reduced by the same factor. The power and uncertainty measured using the 5% duty cycle pulsed mode was then converted to a CW equivalent using a multiplication factor of 20. The increased burst length was used to reduce the drive signal bandwidth and hence power transfer losses. The above procedure was performed for the ‘moderate’ and ‘high’ acoustic power measurements. At the ‘low’ power level the pulsed mode was expected to give very low acoustic power readings (<0.1W) with relatively large percentage errors. CW conditions were therefore used for the ‘low’ setting because the improvement in signal to noise ratio was considered more advantageous than maintaining the 5% duty cycle condition in this instance. For the tone burst calibration mode (5% duty cycle) three 100 second exposures were performed at the moderate and high drive power levels. For the CW exposure mode, four 20 second exposures were performed.
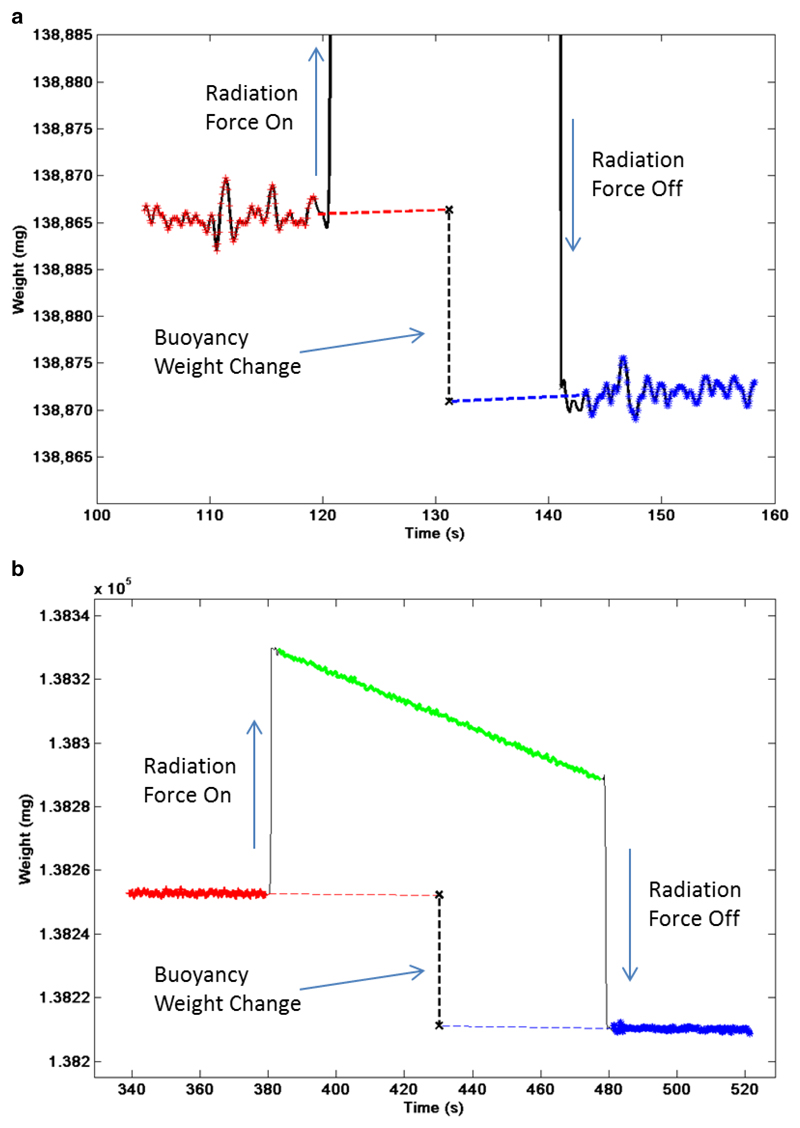
Acoustic power was estimated from the net change in force measured by the balance following each exposure. This was achieved in practice by computing the linear trends from the recorded weight data prior to, and after, exposure and extrapolating these to the temporal mid-point of the exposure, as shown in Figure 4. The net difference in recorded weight was taken to represent the total energy absorbed by the target. For the CW and pulsed mode calibrations 15 and 40 seconds of data were used respectively for calculation of the linear trends. This removes any underlying gradient in the recorded weight change due to thermal exchange of energy between the phantom and the water bath. Power was computed by dividing the total weight change by the buoyancy sensitivity and the exposure time. During acoustic power measurement, the electrical power delivered to the HIFU transducer was monitored using the pick-off box so that the average electrical drive power was known.
Figure 4.
Example of acoustic power measurement from transducer 5. The weight data measured by a digital balance as a function of time is shown for the (a) ‘low’ power setting (constant wave 20 s exposure), and (b) ‘high’ power setting (100 s burst tone exposure at 5% duty cycle). The radiation force on (start of exposure), radiation force off (end of exposure) are indicated together with the net weight change induced by the buoyancy effect. The net weight change is determine by extrapolation using a linear trend from data points before (red) and after (blue) the exposure, the vertical offset between these trends is calculated at the temporal midpoint of the exposure. For clarity the weight scale in the top graph has been expanded, but as a result the full effect of the radiation force at the onset and end of exposure cannot be seen.
Acoustic attenuator
An acoustic attenuator was built in-house using a 10 cm diameter, 4 cm thick Perspex cylinder filled with castor oil (product number 259853, Sigma Aldrich, UK), the front and back windows were acoustically transparent 19 μm thick Melinex windows. The attenuator allowed an increase in the transducer drive power level to allow operation at closer to clinically relevant values, while maintaining pressures and intensities at the focus that could be measured experimentally without risk of damage to the hydrophone.
Intensity estimation methods
i) Solid Spherical Bowl Approximation (SSBA) – this method computes spatial peak intensity using Equation 6. Here the D2 value was measured experimentally with the fibre-optic hydrophone in the trans-axial plane in the orthogonal X (horizontal) and Y (vertical) axes, with D2 being the product of the two measured values. The width was measured at the ‘low’ power setting.
ii) Numerical Approximation –For the special case of the geometrical focal point of a spherically focused, equation 7 may be used to derive a simple expression for the acoustic pressure amplitude pf at the geometrical focus:
| (9) |
where p0 represents the acoustic pressure amplitude at the source (transducer) and S is the total active surface area of the transducer. Equation 9 can then be used to estimate the intensity at the geometrical focal peak by multiplication with its complex conjugate and dividing by the acoustic impedance (pfpf*/2ρc) giving an expression in terms of total acoustic power (W), the surface area (S), wavelength (λ), and focal length (R):
| (10) |
Due to diffraction, however the intensity at the geometrical centre of curvature is not strictly equivalent to the Isp, for HIFU transducers the spatial separation between these two points is typically very small (~1-2 mm) and hence the exact numerical value also differs only by a small amount (<5%). For highly focused transducers the expression in equation 10 can be used as a valid approximation of Isp. Thus the main benefit of this technique is that intensity may be estimated from a measurement of acoustic power using nothing more than the transducer geometry (transducer surface area, focal length) and drive frequency (wavelength) with no other measurement being necessary.
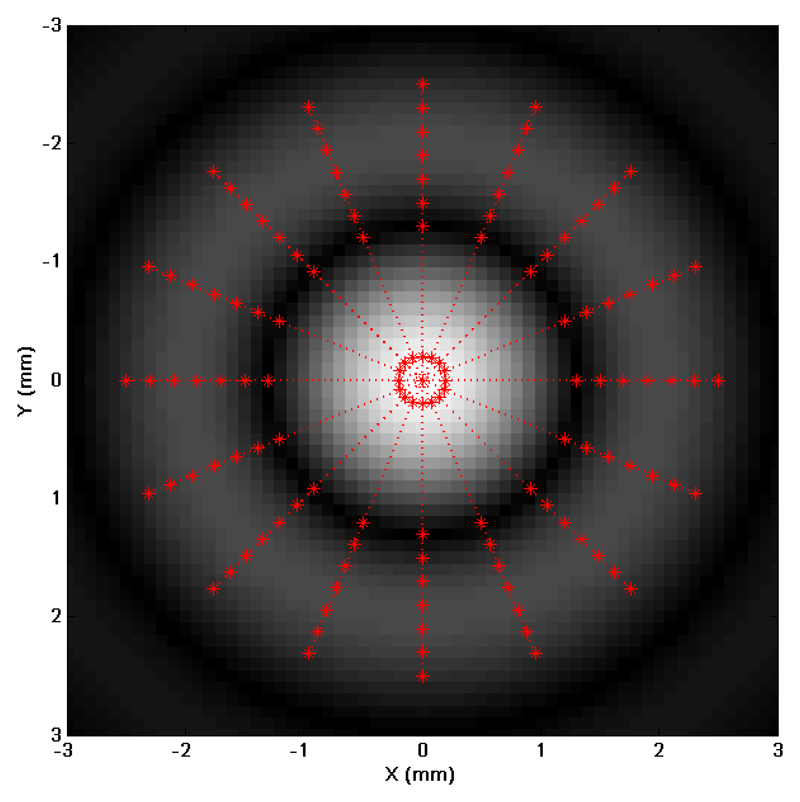
iii) Pressure Ratio – this method requires the use of a hydrophone in order to measure the acoustic pressure amplitudes at the first sidelobe and the focal peak, to give the SPr ratio, thus providing some indication of how effectively the power output of the transducer is brought to a focus. The SPr ratio is computed using the rms pressure (voltage) signal measured by the fibre-optic hydrophone. A dedicated scan routine was used to sample the pressure amplitude at a number of locations around the first sidelobe ring which encircles the main focus in the X-Y plane. This routine consisted of a series of linear scans in the focal plane, all centred on the focal peak (analogous to the spokes of a wheel). For each of these linear scans a small number (7) of measurements were made at radial positions approximately centred on the sidelobe (eg. X = +2 mm, Y = 0 mm), three measurements were then made across the focal peak before a new set of 7 measurements centred on the opposite sidelobe (eg. X = -2 mm, Y= 0 mm) was obtained. A step size of 0.2 mm was used for each of the three sections of these linear scans. This procedure was repeated 8 times at angular intervals of 22.5º in the focal plane. An example of the complete set of measurement positions is shown in Figure 5. A cubic interpolation was used to provide the local maximum pressure at the sidelobe and focal peak, giving a total of 16 sidelobe pressure peak measurements and 8 repeat measurements at the focal peak.
Figure 5.
A representation of the scan positions used for estimating the mean sidelobe to focal peak pressure ratio. The background greyscale distribution represents a simulated acoustic pressure field in the focal plane. The (red) points represent measurement positions along linear scans in the focal plane, each scan includes two opposing sidelobe positions, eg. (x = +2 and -2 mm), and the focal peak. The measurements consisted of 8 linear scans arranged at equal angular separation (22.5°), thus this measurement yielded 16 sidelobe pressure values.
The mean sidelobe and focal peak pressure measurements were used to calculate the SPr ratio and this was used as input to the polynomial expression derived from the numerical simulations described previously to obtain an FPF estimate. Equation 6 was then recomputed with the new FPF replacing the solid bowl assumption value (0.68). A value for D2 identical to those used in the SSBA method was used. The advantage of this method over theoretical method (ii) is that a real, albeit simple, acoustic field measurement is actually made. In principle this might be expected to give Isp estimates with improved accuracy.
iv) FPF estimation – In this method a more detailed scan is performed in the X and Y axis directions by performing 4 cm long linear scans in an orthogonal cross centred at the focal peak with a resolution of 0.25 mm, giving a total of 161 measurement positions for each scan. The rms pressure (voltage) amplitude measured with the hydrophone was interpolated up to 1000 points. The cumulative sum of acoustic power as a function of radial distance for each of the four branches of the orthogonal cross scan was calculated numerically by computing the square of the rms voltage and integrating, assuming radial symmetry over the full 360° in the X-Y plane. The four cumulative curves were then averaged, and normalised to a value of 1 at the final position. The FPF value was finally determined by measuring the average G value at the location of D/2, the 6 dB beam width position. The experimentally measured FPF was inserted into equation 6, replacing the 0.68 in a similar way to the pressure ratio method. This method therefore does not require any input from theory or simulation other than the factors listed in equation 6. The advantage of this method over the pressure ratio method is that a more comprehensive sampling of the acoustic field is undertaken. This would be expected to give a more accurate estimate of the FPF.
Experimental procedure
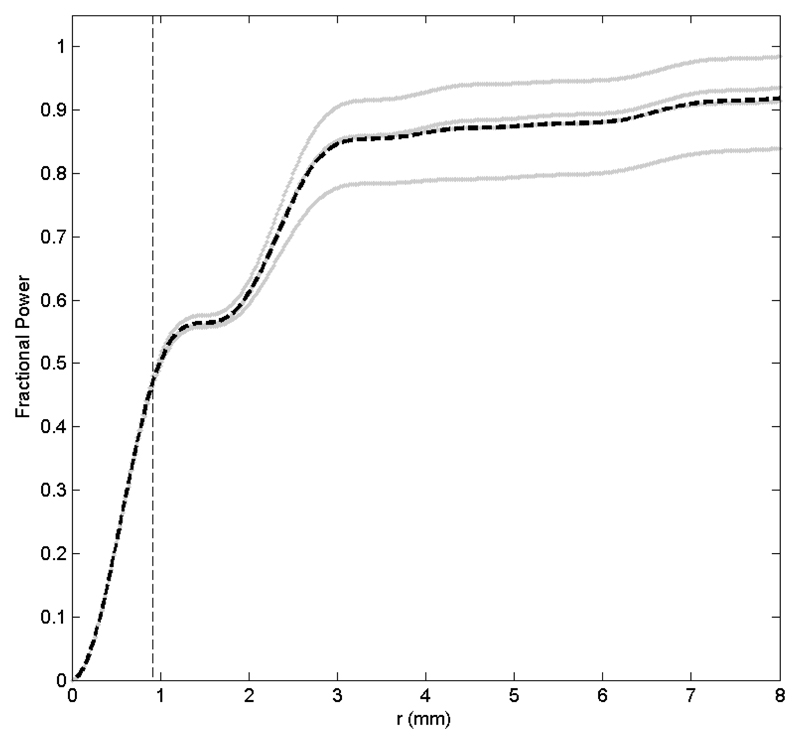
All hydrophone measurements were performed prior to acoustic power calibrations, with each type of scan and measurement repeated three times. The fibre-optic hydrophone was localised on the focal peak at the ‘low’ drive setting. This was achieved with an accuracy of ±50 μm in the focal plane and ±500 μm in the axial direction. Next, the orthogonal-cross scan was performed in the focal plane to give estimates of D and the position of the first sidelobe, and to allow computation of the experimental value of FPF. An example of the type of fractional power curves obtained experimentally is shown in Figure 6. The orthogonal cross scan also provided the position of the sidelobe, and thus coordinates for the sidelobe to focal peak pressure ratio measurement were determined and the scan carried out.
Figure 6.
An example of the experimental measurement of the G curve (Equation 5) for transducer 5. The grey lines show datasets from each of the 4 branches of the orthogonal-cross scan, the dashed black line represents the average of the four datasets. The dashed vertical line indicates the D/2 (-6dB) position which is also determined from the same orthogonal cross scans. At this position the focal power parameter which quantifies the amount of power passing through the focus delineated by the -6dB limit is determined.
The fibreoptic hydrophone was then replaced with the calibrated Onda HGL-0200 hydrophone. Localisation at the focal peak and measurement of the acoustic pressure were performed, at the ‘low’ and ‘moderate’ drive levels. The attenuator was then carefully placed in the ultrasound beam, the hydrophone position was checked, and a measurement of the attenuated focal peak pressure was made. The total attenuation of the absorber was computed and the drive setting was adjusted accordingly to determine the transducer specific ‘high’ drive setting. Finally, the hydrophone localisation was checked once more, and a measurement of the focal peak pressure was made.
Acoustic power measurements with the buoyancy system completed the set of measurements for each transducer.
Analysis of Isp estimates
The Isp computed indirectly from acoustic power measurement were evaluated in terms of percentage differences (d) from those computed using the hydrophone pressure estimates:
| (11) |
where Im and Ir represent the measured (power based) and reference (hydrophone based) Isp estimates respectively. The uncertainties in Isp estimates were calculated for all methods. Sources of error for both power and hydrophone measurements were quantified at the level of one standard deviation (coverage factor k=1 or 68% confidence). Systematic uncertainties for prms measurements at the focal peak with the ONDA HGL-0200 hydrophone arise from pressure sensitivity (4.2%) and oscilloscope bias (as specified by the manufacturer, ±1.5%); random errors included hydrophone localisation error (0.5%), spatial averaging (1%) and a measurement error which was calculated for each transducer and drive level from three repeat measurements. The latter can be thought of as representing the error in the acquisition and digitisation of the hydrophone signal (including electronic noise and any amplifier drift), and this was typically found to be very low (<0.2%). The overall percentage error for prms measurements was calculated by adding the above uncertainties in quadrature, giving a value of ~4.6%, equivalent to an uncertainty in the intensity estimate of ~9.3%.
The uncertainty in the buoyancy sensitivity factor, estimated at 3%, represents the largest source of systematic error in the acoustic power measurements. The random error associated with the power measurement was computed through repeat measurements. The percentage errors for low, moderate and high drive levels were found to be on average ~10%, ~5% and ~1.5% respectively. With the exception of the numerical approximation, all methods used to determine Isp from acoustic power relied on a measurement of D2. The uncertainty in this parameter was calculated for each transducer from three repeat scans in the X and Y axes across the focus, and was found to be ~0.2% on average. Finally, for the last two methods (pressure ratio and FPF estimation methods), the FPF value was estimated from acoustic field measurements are subject to the accuracy in the initial localisation of the hydrophone at the focal peak, and mechanical backlash in the positioning system. We estimate that we are able to localise the hydrophone at the focal peak to <5% of the 6 dB focal width. We estimate the uncertainty in both these FPS estimates to be less than 1%. Adding the uncertainties in quadrature, as appropriate for each method, gave an overall uncertainty for all Isp estimates of 10%, 6% and 4% for the ‘low’, ‘moderate’ and ‘high’ drive settings respectively.
The uncertainty in the calculated percentage differences (δd) between estimates was determined based on the uncertainty in the Isp estimates and was calculated as follows:
| (12) |
where δIm and δIr are the uncertainties, in W/cm2, for the indirect and hydrophone (reference) Isp estimates respectively. This value represents the uncertainty in the calculated percentage difference that might be expected due to the uncertainties listed above. Isp differences (d) for a given method were therefore compared with their associated uncertainty in percentage difference (δd). When the percentage difference was larger than the associated uncertainty the Isp estimate was classified as not being in agreement with the hydrophone measurement, indicating that it was likely that some other source of error had not been considered, or for example the Isp estimate was inaccurate due to invalid assumptions.
Results
Simulations
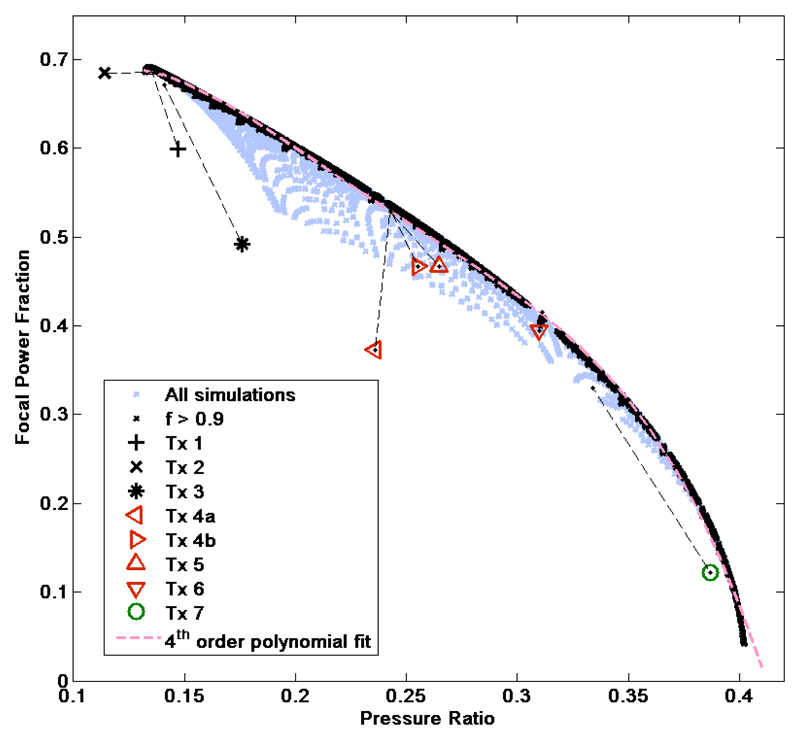
Numerical computations of the pressure fields provided the SPr and allowed calculation of the FPF, which represents the focusing efficiency. These data, plotted in Figure 7, indicate that a loss in the FPF occurs as more power is distributed to the sidelobe rings surrounding the focus. If only focused transducers with an f number >0.9 are considered (n=9219), a clear trend with low data spread is observed. A 4th order polynomial was found to give a satisfactory agreement with the data, the fit coefficients are given in Table 2. The range of the sidelobe to focal peak pressure ratio was 0.15 (efficient focusing) to 0.4 (poor focusing), corresponding to FPF values from 0.68 to 0.1. The deviation of the computed data from the fitted polynomial trend-line for highly focused transducers (f number < 0.9) is thought to be, at least partially, due to approximations which become invalid when highly focused transducers are considered i.e. when the velocity potential must be estimated at large angles from the sound axis (O’Neil 1949).
Figure 7.
The focal power fraction vs. sidelobe to focal peak pressure ratio for 12,079 simulated transducers (purple crosses), of which 9,219 had an f number >0.9 (black crosses), a fourth order polynomial fit is applied to the latter set (pink dashed line). The experimentally measured parameters for the eight test transducers are included as detailed in the legend (solid bowl – black markers, annular – red markers, non-rotationally symmetric – green marker), with dashed lines indicating the deviation from the respective simulated values.
Table 2.
The 4th order polynomial coefficients determined from the simulated focal power parameter vs. sidelobe to focal peak pressure ratio. These data are used to derive a FPP estimate for method iii from and experimental measurement of the sidelobe to focal peak pressure ratio.
| Order | Coefficient |
|---|---|
| 4th | -297.05 |
| 3rd | 281.29 |
| 2nd | -98.87 |
| 1st | 13.63 |
| 0th (constant) | 0.055 |
Acoustic field measurements
The experimentally measured D2, SPr value, and the FPF derived from the pressure ratio and direct estimation methods for each transducer are summarised in Table 3. Values for all these parameters determined from simulation are also included for comparison. For most experimental cases (transducers 3, 4a, 4b, 5 and 6), the measured D2 values agreed with the simulation results to within 5%. For transducers 1, 2 and 7 the measured values were more than 10% greater than the simulated values. The experimentally measured sidelobe to focal peak pressure ratios and FPFs are included in Figure 7, where it is possible to compare them with their simulated values. The discrepancy between measurement and theory was more than 10% for transducers 2, 3 and 7, peaking for transducer 3 at a value of 24%. Overall the hydrophone measurement of the FPF using orthogonal linear scans (FPF estimation method) showed the greatest discrepancies with the simulation results: transducers 1, 4b, 5 and 6 showed discrepancies between 10 and 15%, transducers 3 and 4a of ~30%, transducer 7 of >60%.
Table 3.
The measured acoustic field parameters D2, the sidelobe to focal peak pressure ratio and the focal power parameter as determined by methods iii (derived from the measurement of sidelobe to focal peak pressure ratio) and method iv (direct measurement). Values as determined from the theoretical simulations are included for comparison. The uncertainties represent the precision of the measurement and are given by the standard deviation from three repeat measurements.
| Transducer | 1 | 2 | 3 | 4a | 4b | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|---|
| D2 (mm2) | Theory | 4.94 | 2.521 | 3.81 | 0.673 | 1.46 | 3.373 | 2.29 | 2.951 |
| Measurement | 5.516±0.018 | 2.781±0.007 | 3.831±0.006 | 0.653±0.002 | 1.394±0.005 | 3.359±0.005 | 2.176±0.003 | 3.381±0.004 | |
| Sidelobe to focal peak pressure ratio | Theory | 0.135 | 0.138 | 0.141 | 0.243 | 0.243 | 0.243 | 0.311 | 0.334 |
| Measurement | 0.147±0.0084 | 0.1144±0.0003 | 0.1755±0.0001 | 0.2364±0.0001 | 0.2550±0.0001 | 0.2652±0.0002 | 0.3104±0.0037 | 0.3870±0.0007 | |
| Focal power fraction | Theory | 0.6896 | 0.6858 | 0.6724 | 0.5375 | 0.5298 | 0.5281 | 0.4472 | 0.3296 |
| Method iii | 0.6762±0.0083 | 0.6903±0.0001 | 0.6401±0.0001 | 0.5398±0.0002 | 0.5092±0.0001 | 0.4927±0.0003 | 0.4142±0.0074 | 0.1622±0.0035 | |
| Method iv | 0.5995±0.0021 | 0.685±0.0026 | 0.4922±0.0003 | 0.3727±0.0064 | 0.4667±0.0011 | 0.4669±0.0064 | 0.3946±0.010 | 0.1221±0.0001 | |
Estimation of Isp
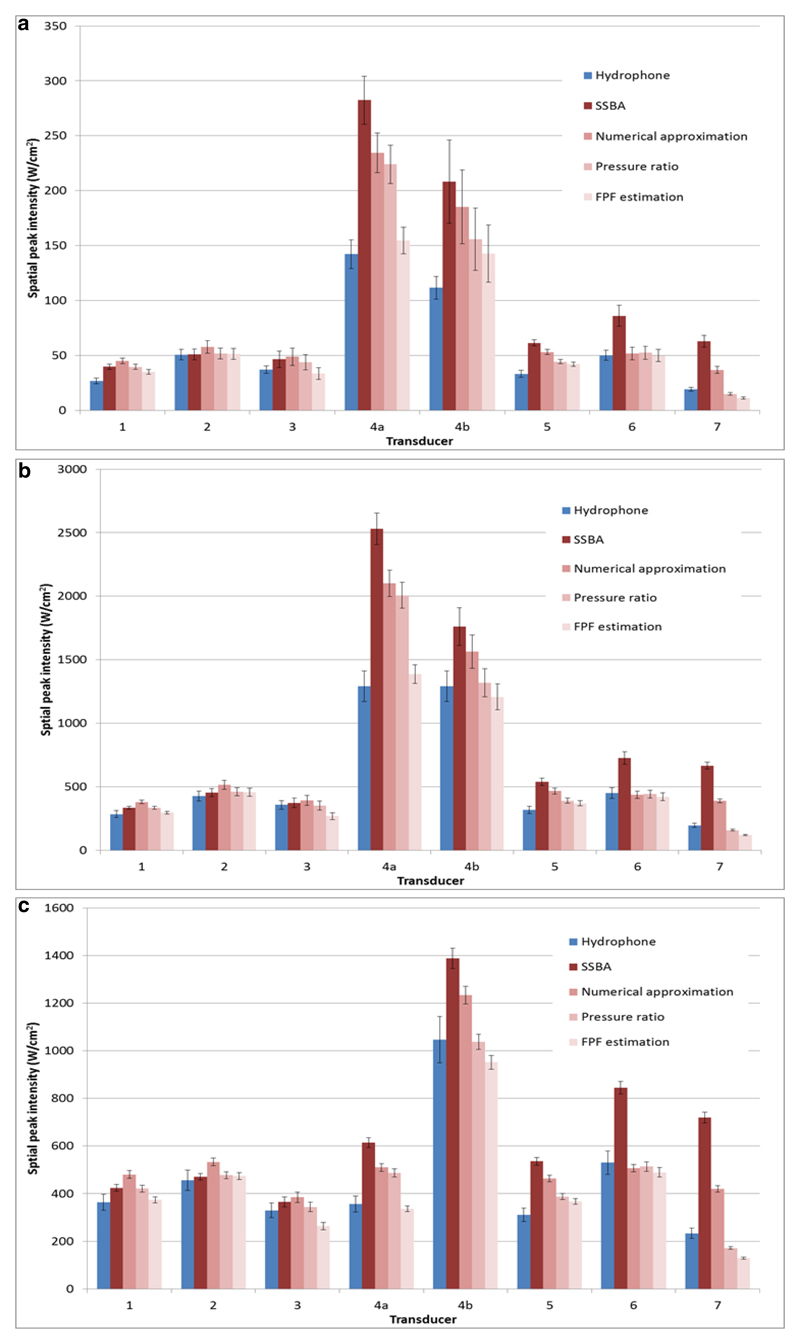
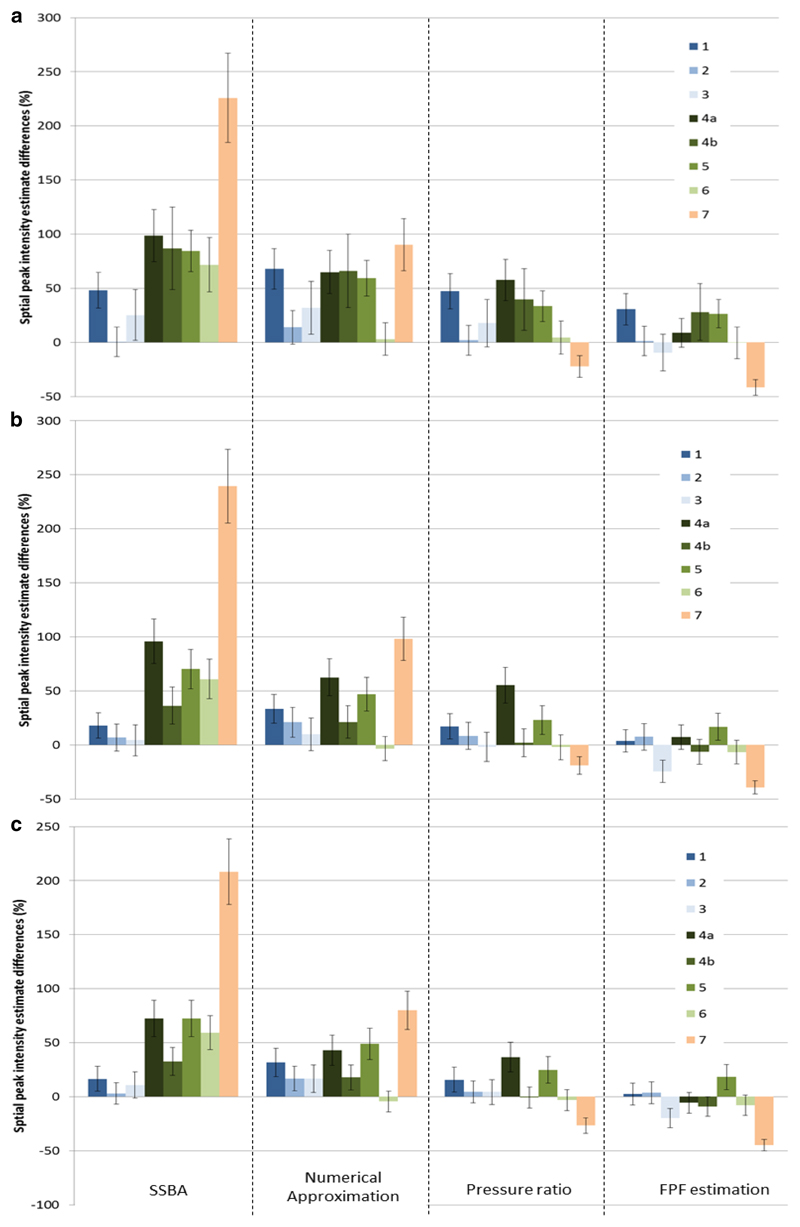
Buoyancy measurements of acoustic power, provided in Table 4, were used to estimate the focal peak intensity for all three drive settings. These estimated intensities are plotted in Figure 8 with the hydrophone measured intensities. It was not possible to drive transducer 4a at the required ‘high’ drive setting as this would have exceeded its power limit, its highest possible safe power level was used for the ‘high’ setting instead. The percentage differences (d) between buoyancy and hydrophone measured Isp are shown in Figure 9. The data are grouped according to calculation method to allow easier comparison of their relative performance. The error bars indicate the expected percentage difference uncertainty (Δd). The percentage difference analysis shows the relative accuracy of the various methods for calculating Isp indirectly from acoustic power measurements. In Figure 10, the percentage difference data are plotted as boxplots grouped by transducer (Figure 10a) and power level (Figure 10b).
Table 4.
The acoustic power measured in Watts for each transducer and drive power setting. Uncertainties indicate the standard deviation from repeat measurements (4 repeats for ‘low’, 3 repeats for ‘moderate’ and ‘high’ drive settings).
| Nominal drive setting | Acoustic Power (W) for each Transducer | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4a | 4b | 5 | 6 | 7 | |
| ‘low’ – 50mV pk-pk | 1.4±0.07 | 0.91±0.09 | 1.14±0.18 | 1.18±0.08 | 1.86±0.33 | 1.31±0.05 | 1.20±0.13 | 1.36±0.11 |
| ‘moderate’ – 150mV pk-pk | 11.86±0.21 | 8.09±0.51 | 9.15±0.88 | 10.59±0.42 | 15.73±1.23 | 11.60±0.50 | 10.12±0.60 | 14.43±0.38 |
| ‘high’ | 59.43±1.04 | 41.47±0.15 | 20.42±1.03 | 52.38±0.72 | 68.28±0.36 | 24.67±0.12 | 56.78±0.48 | 69.97±0.80 |
Figure 8.
Estimated focal peak intensities grouped according to transducer number for ‘low’ (a), ‘moderate’ (b) and ‘high’ (c) drive power setting. The hydrophone estimate is included, error bars represent the expected uncertainty (1 standard deviation) in the intensity estimates.
Figure 9.
The percentage differences in estimated focal peak intensity grouped according to estimation method, with separate graphs for ‘low’ (a), ‘moderate’ (b) and ‘high’ (c) drive power settings. The legend indicates the transducer number and error bars indicate the expected uncertainty range (standard deviation).
Figure 10.
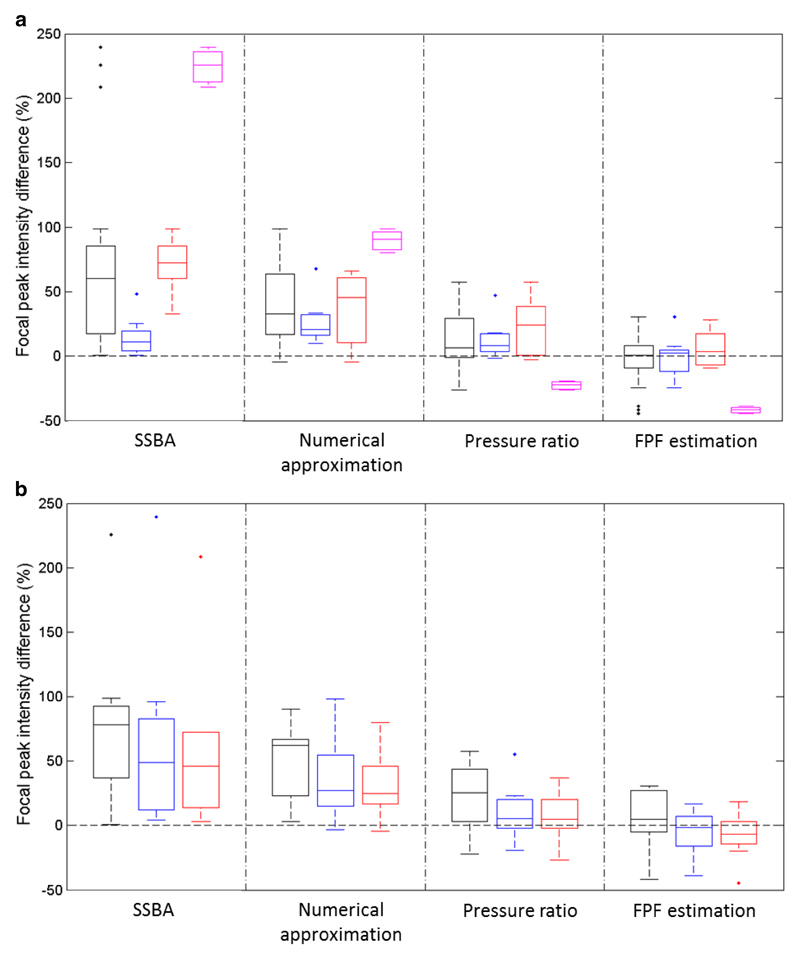
Boxplots showing the percentage differences in focal peak intensity for each estimation method compared to that calculated from hydrophone measurements. For each box the central line indicates the median, the lower and upper edges of the box indicate the 25th and 75th percentiles, the whiskers indicate the range with data points considered outliers represented by single points. In the top graph (a) the data at all power levels are averaged, with separate boxplots from left to right for all (black), solid bowl (blue - centre), annular (red - right) and non-rotationally symmetric (mauve) transducers. The bottom graph (b) shows the data averaged across all transducers and separated from left to right into ‘low’ (black), ‘moderate’ (blue) and ‘high’ (red) drive power.
Considering data across all transducers and drive settings, the methods ranked from overall ‘best’ to ‘worst’ as: FPF (average percentage difference -2.5%, and average in the absolute value of the percentage differences of 15.4%),. pressure ratio method (average percentage difference +13.3%, and average of the absolute value of the percentage differences 19.6%) numerical approximation method (average percentage difference +39.1%, average absolute value of the percentage differences of 39.8%), and SSBA method with an average percentage difference of +68.7% (all values positive).
Figure 10a shows that for the solid bowl transducers (n=3) the two top performing methods were the pressure ratio and FPF estimation methods, with average percentage differences of -0.5% and 12.8%, and average absolute value percentage differences of 11.5% and 13.2%, respectively. For these transducers the SSBA method was the next best method with an average percentage difference of +14.9%. The worst method for the solid bowl transducers was the numerical approximation method where the average percentage difference was +27. For the annular transducers (n=4) the two top methods were the FPF estimation and pressure ratio methods once again with average percentage differences of +5.8% and +22.7%, and average absolute value percentage differences of 11.8% and 23.6% respectively. For the annular transducers the numerical approach was the third best, with an average percentage difference of +35.6%, and an average of the absolute value percentage difference of 36.9. The worst method for the annular transducers was, unsurprisingly, the SSBA method where the average percentage difference was as high as +70.2
The data can also be used to assess the performance of the various methods across the different drive power settings (see Figure 10b). If the percentage differences are considered over all methods, the average differences are +39.5%, +27% and +22.5% for the ‘low’, ‘moderate’ and ‘high’ drive powers, respectively, with average absolute value percentage differences of 44.1%, 33.4% and 30.1%. Using data only from the best method, (the FPF), the average differences were +5.5%, -5.2% and -7.7% for the ‘low’, ‘moderate’ and ‘high’ drive powers, respectively, with average absolute value percentage differences of 18.3%, 14% and 13.9%. Table 5 summarises the relative amplitude of harmonic components in the measured waveforms at the focal peak for all transducers and drive settings. These data can be used to assess the degree of waveform distortion due to non-linear propagation effects. The increase in the relative amplitude of the harmonic components from “moderate” through to “high” power were not generally followed by the measured prms values which, on average, only increased by 3% (-10% to +13%). These data would therefore suggest that, overall, at the ‘high’ power drive level with the attenuator in the beam path, a small increase in the relative amount of harmonic components in the measured waveforms was detected, whilst the measured prms (and by extension the Isp) remained relatively unchanged from the ‘moderate’ level. This was in line with expectations as the “high” drive power setting was chosen so that it would generate similar Isp values to the “moderate” drive setting. The small increase in the relative harmonic content at the “high” drive power setting was probably due to a higher B/A parameter of the castor oil in the attenuator compared to the lower power measurement. It is interesting to note that the relative increase in the percentage harmonic amplitude is greatest for transducers 3 and 5. The harmonic components for transducers 3 and 5 at the low and moderate settings are very low compared to the other transducers. When the drive power was increased the harmonic component percentages remained lower than those of the other transducers, however these represented a much larger percentage increase. Both these transducers have a relatively short focal length and low drive frequency, characteristics which are less favourable for the generation of higher harmonics.
Table 5.
Summary of the harmonic components measured during Isp measurements at the focal peak using the Onda hydrophone. The components at the 2nd, 3rd and 4th harmonics are included and expressed as a percentage of the prms value. The effect of the attenuator and increase in drive power at the ‘high’ setting, compared to the ‘moderate’ setting, is expressed as a percentage change in the measured harmonic components and the prms values
| Focal peak pressure harmonic/rms | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Drive setting | Harmonic | Transducer | |||||||
| 1 | 2 | 3 | 4a | 4b | 5 | 6 | 7 | ||
| low | 2nd | 13.4% | 8.9% | 3.3% | 10.8% | 9.4% | 3.4% | 10.8% | 10.9% |
| 3rd | 2.1% | 0.7% | 0.3% | 0.8% | 0.9% | 0.3% | 1.0% | 1.1% | |
| 4th | 0.3% | 0.1% | 0.2% | 0.1% | 0.1% | 0.1% | 0.1% | 0.1% | |
| moderate | 2nd | 35.1% | 26.1% | 10.0% | 31.9% | 24.5% | 10.2% | 32.6% | 30.3% |
| 3rd | 17.3% | 8.6% | 1.2% | 9.2% | 8.5% | 1.3% | 13.4% | 12.1% | |
| 4th | 8.3% | 2.8% | 0.2% | 3.2% | 2.8% | 0.2% | 5.2% | 4.6% | |
| high | 2nd | 36.4% | 28.3% | 15.3% | 18.1%* | 28.6% | 12.6% | 34.0% | 26.9% |
| 3rd | 18.3% | 10.1% | 3.5% | 2.6%* | 10.4% | 2.2% | 14.8% | 10.4% | |
| 4th | 8.9% | 3.5% | 0.9% | 0.5%* | 3.3% | 0.4% | 6.0% | 3.6% | |
| Pressure high/moderate %change | |||||||||
| 2nd | +3.8% | +8.3% | +53.7% | -43.2%* | +16.7% | +23.8% | +4.3% | -11.3% | |
| 3rd | +5.6% | +17.8% | +190.0% | -72.1%* | +22.6% | +67.4% | +10.5% | -14.3% | |
| 4th | +6.9% | +26.8% | +506.7% | -84.9%* | +21.0% | +137.5% | +16.1% | -21.8% | |
| Prms | +13.1% | +3.6% | -3.9% | -47.5%* | -10.0% | -0.9% | +8.4% | +9.1% | |
Required increase in drive level at ‘high’ power setting not possible due to transducer power limit.
Discussion
The main aim of this paper is to assess the performance of a number of approaches to estimating the Isp of HIFU transducers from acoustic power measurements. As part of this work computer simulations were used to study the acoustic field of annular transducers, (spherically focused transducers with a hole in the centre). These computations predicted a reduction of focusing efficiency for annular transducers, quantified in terms of the FPF, which are also manifested in terms of an increase in the sidelobe to focal peak pressure ratio. A relationship was found between these parameters, and was quantified using a fourth order polynomial. Computations based on 8 experimentally tested transducers, giving simulated values for the D2, FPF and pressure ratio were also performed.
The measured D2 (beam width parameter) was often more than 10% larger than the simulated value (for transducers 1, 2 and 7) indicating a broadening of the cross sectional focal area compared to theory. While understanding the reason for any discrepancy was not strictly part of this study, it is interesting to note the direct effect of D2 on the Isp estimate for all methods except the numerical approximation method, and indeed for these transducers lower and more accurate Isp estimates were almost always obtained compared to the numerical approximation method. The only exception for this rule was the SSBA method for transducer 7. For other transducers (4a, 4b, 5 and 6) the measured D2 was slightly less (for a maximum difference of less than 5%) than the simulated values. Interestingly, in these cases the Isp estimated with the pressure ratio and FPF estimation methods were also found to be lower and more accurate than the numerical approximation method estimates despite the reduction in D2. These results indicate how, in general, theoretical predictions may not always closely match measurement; however, for Isp estimates it also suggests that factors other than changes in the D2 value are important. The experimentally measured pressure ratio and FPF values (Figure 7) show how a discrepancy ranging from -17% to +24% was observed for these experimentally measured values compared to theoretical predicitions. The measured ratio was greater than 5% larger than the predicted value for 5 transducers (1, 3, 4b, 5, and 7) and less than 5% smaller for transducer 2 only. The FPF values estimated experimentally (method iv) were found to be lower than those simulated for all transducers (range -0.1 to -63%) and hence suggest that in practice transducers do not focus acoustic power as efficiently as might be predicted by theory. Estimation of Isp may therefore be improved by experimental measurement of field parameters (sidelobe to peak ratio, FPF). It is not possible to draw any firm conclusions from this study as to the root cause of systematic over-estimation of Isp by the numerical theory based approach. Possible reasons may be inhomogeneity in power output at the surface of the transducer, manufacturing defects, peculiarities in the resonance mode of the piezoelectric material, or invalid assumptions regarding transducer geometry. Overall, numerical estimates of Isp for annular transducers were found to be more accurate (within 37% on average) than for the solid bowl assumption of the SSBA method (within 70% on average). This suggests that the simulation or numerical approach to estimating Isp is likely to be more accurate for annular transducers, because it accounts for the presence of the central hole, despite its general tendency to overestimate Isp. For solid bowl transducers however this was not the case (accuracy within 15% and 27% on average for the SSBA and numerical approximation methods respectively).
The pressure ratio and FPF estimation methods were consistently found to be the best methods for estimating Isp. Of the two methods, the FPF estimation method was found to be slightly more accurate (15% vs. 20% on average) for both solid bowl and annular types of transducers. This is unsurprising as the FPF estimation method requires more detailed measurement of the acoustic field.
No method was found to be accurate in predicting the Isp for the non-rotationally symmetric transducer (7). For this device the SSBA method gave very large over-estimates (>200%), the numerical approximation also produced a large over-estimate (>80%) while the remaining methods produced under-estimates (>20% and >40% respectively for the pressure ratio and FPF estimation methods respectively). For this transducer the pressure ratio method estimate was closer to the hydrophone measurement than the FPF estimation method, a result outside the general trend observed in the study. A possible explanation for this is that for asymmetric transducers, and by extension for asymmetric acoustic fields, the direct measurement method may prove to be very sensitive to the exact alignment of the transducer and the orthogonal cross measurement axes. The pressure ratio method as set out in this study samples only two positions in the radial profile (the first sidelobe and the focal peak) but it does so at several angular alignments (16 positions around the sidelobe ring in the trans-axial plane). The FPF estimation method however finely samples a large portion of the radial pressure profile but only over 4 branches oriented at 90° to each other. This result may therefore in part be due to the particular way the study was conducted and not so much due to inherent shortcomings of the different methods. This is likely to be important as clinical HIFU transducers can be asymmetric in their outer edge profile, as in Transducer 8, but may also have non-circular shaped central apertures. Clearly the theory presented here based on circular apertures is unsatisfactory for such devices, and therefore more complex strategies may be required to better estimate FPF. Theoretically it may be possible to develop O’Neil’s approach for square or rectangular apertures. Experimentally modifications of the methods presented here may be required, including full but lengthy 2D scans in the focal plane.
An important aspect to be considered is the impact of the acoustic power required in HIFU experiments and clinical treatments and the consequent ability to estimate Isp. As the acoustic power output from a transducer increases, the generation of higher harmonics due to non-linear propagation leads to a narrowing of the beam cross-sectional area at the focal plane and potentially to a non-linear increase in the focal peak intensity (Khokhlova et al 2006). Non-linear effects can therefore become significant above a certain threshold, and more sophisticated methods for estimating Isp become necessary. In this study we took the approach of measuring relevant field parameters at low power levels, where there was minimal distortion due to non-linear propagation in water. This is an inherently safer measurement, with less risk of damage to equipment, and allows comparison with simple linear acoustic field simulations. It was possible however to test whether field parameters measured under low power conditions can be used to predict Isp at higher drive levels. This was achieved using the ‘moderate’ drive level (200-1300 W/cm2) to determine Isp at levels that could deliver sufficient thermal dose to lesion soft tissue if maintained for exposures of several seconds, at relatively superficial depths. It is important to emphasise therefore that, while measurements were not performed at ‘full’ power (due to the risk of hydrophone damage), they do represent power or intensity levels that could deliver a not insignificant thermal dose. The use of the acoustic attenuator allowed a further increase in drive power to more clinically relevant levels (up to 70W acoustic power) whilst maintaining the focal intensities at approximately those measured at ‘moderate’ power. The purpose of this was to mimic, in a very approximate way, the effects of overlying tissue which may distort the propagation of the HIFU beam by virtue of attenuation, and changes in B/A parameter, leading to possible changes in Isp. In calculating Isp, the power loss due to the attenuator was accounted for by direct insertion-loss estimation using the intensity measured at the ‘moderate’ drive setting before and after insertion of the attenuator. At the ‘high’ power setting it is likely the overall losses due to attenuation were higher due to increased attenuation of the higher harmonic components. This effect was ignored here as it was considered to be small when compared to the sources of uncertainty in the measurement. Whilst not applicable in a clinical setting, this approach allowed comparison of Isp estimates with minimised uncertainty in the power loss due to the attenuator. Our results show that the percentage differences in Isp at ‘high’ drive power were comparable to those measured using the ‘moderate’ drive level, which in turn were lower than those obtained at the ‘low’ power setting. While the difference in uncertainty magnitudes between ‘low’ and ‘moderate’ levels can be explained in terms of the larger relative uncertainties associated with measurements at ‘low’ power, it is interesting to note that at the ‘moderate’ drive level a measurable degree of distortion due to non-linear propagation in the water could be detected (Table 5). Furthermore the similarity in Isp percentage difference between the moderate and high power data suggests that the intensity estimation methods performed as well at the ‘high’ drive power setting as they did under the ‘moderate’ drive setting (within experimental uncertainties). The data also provides some evidence that the use of the acoustic field parameters (D2, pressure ratio and FPF) determined under nominally linear (‘low’ power) conditions can also be employed to calculate Isp at the higher power settings used in this study. These findings need verification. It will be important to determine conditions under which the effects of non-linear propagation are sufficiently large to give significant changes in focal size and Isp. Such a study would almost certainly require a robust hydrophone or pressure sensor.
Conclusion
In this study we have considered methods which help clinicians and researchers to estimate the focal peak intensity of HIFU transducers from a calibration of acoustic power output. We have found from simulation and experiment that an existing expression (Hill et al 1994) based on simple spherical bowl radiating transducers is only strictly applicable to transducers with this type of geometry. The presence of a central imaging aperture reduces the power delivered to the main focal region, by a factor which we have defined as the FPF. We have found that the FPF can be estimated with a hydrophone with two different techniques: measurement of the mean first sidelobe/focal peak pressure magnitude ratio; and a detailed orthogonal cross scan in the focal plane. Both methods sample the acoustic field and can be used to estimate the FPF. We have tested these techniques on a range of solid bowl (n=3), annular (n=4), and non-symmetric (n=1) shaped transducers by comparing the focal peak intensity estimates with those determined using a calibrated hydrophone. The orthogonal cross scan method was found to be the most accurate (±15.4% agreement with the hydrophone measurement), being better than the pressure ratio method (±19.6%). A third method derived from theory which requires no hydrophone measurement was found to over-estimate focal peak intensity (40%), but was however more reliable than using the simple spherical bowl assumption from Hill (1994) for annular transducers.
Our findings suggest methods by which researchers can quantify acoustic field parameters as set out in the recommendations in ter Haar et al (2011). Where appropriate, researchers should estimate focal peak intensity with one or more of the methods described here.
Acknowledgements
The authors would like to thank the EPSRC (research grant # EP/F016816/1) for funding this research and the establishment of a state-of-the-art calibration facility at The Institute of Cancer Research; the National Physical Laboratories, UK, for advice; Dr Cyril Lafon from Université de Lyon for kindly lending us a transducer; Mr Chris Bunton from The Institute of Cancer Research’s mechanical workshop for constructing the buoyancy power calibration system; Prof Constantin Coussios from Oxford University for useful discussions, and Precision Acoustics for their support with developing and enhancing the beamplotting system and software.
References
- Alkhorayef M, Mahmoud M, Alzimami KS, Sulieman A, Fagiri MA. High-Intensity Focused Ultrasound (HIFU) in Localized Prostate Cancer Treatment. Polish Journal of Radiology. 2015;13(80):131–141. doi: 10.12659/PJR.892341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auboiroux V, Dumont E, Petrusca L, Viallon M, Salomir R. An MR-compliant phased-array HIFU transducer with augmented steering range, dedicated to abdominal thermotherapy. Phys Med Biol. 2011;56(12):3563–3582. doi: 10.1088/0031-9155/56/12/008. [DOI] [PubMed] [Google Scholar]
- Beissner K. Ultrasonic exposimetry. Boca Raton, Florida: CRC Press; 1993. Radiation force and force balances; pp. 128–140. [Google Scholar]
- Bradley WG., Jr MR-guided focused ultrasound: a potentially disruptive technology. J Am Coll Radiol. 2009;6(7):510–513. doi: 10.1016/j.jacr.2009.01.004. [DOI] [PubMed] [Google Scholar]
- Chen L, Wang K, Chen Z, Meng Z, Chen H, Gao H, Wang P, Zhu H, Lin J, Liu L. High intensity focused ultrasound ablation for patients with inoperable liver cancer. Hepatogastroenterology. 2015;62:140–143. [PubMed] [Google Scholar]
- Civale J, Clarke RL, Rivens IH, ter Haar GR. The use of a segmented transducer for rib sparing in HIFU treatments. Ult Med Biol. 2006;32(11):1753–1761. doi: 10.1016/j.ultrasmedbio.2006.06.005. [DOI] [PubMed] [Google Scholar]
- Coussios CC, Farny CH, Haar GT, Roy RA. Role of acoustic cavitation in the delivery and monitoring of cancer treatment by high-intensity focused ultrasound (HIFU) Int J Hyperthermia. 2007;23(2):105–120. doi: 10.1080/02656730701194131. [DOI] [PubMed] [Google Scholar]
- Crouzet S, Murat FJ, Pasticier G, Cassier P, Chapelon JY, Gelet A. High intensity focused ultrasound (HIFU) for prostate cancer: current clinical status, outcomes and future perspectives. Int J Hyperthermia. 2010;26(8):796–803. doi: 10.3109/02656736.2010.498803. [DOI] [PubMed] [Google Scholar]
- Farny CH, Glynn HR, Roy RA. Temporal and Spatial Detection of HIFU-Induced Inertial and Hot-Vapor Cavitation with a Diagnostic Ultrasound System. Ultrasound in Medicine and Biology. 2009;35(4):603–615. doi: 10.1016/j.ultrasmedbio.2008.09.025. [DOI] [PubMed] [Google Scholar]
- Farny CH, Glynn HR, Roy RA. The correlation between bubble-enhanced HIFU heating and cavitation power. IEEE Trans Biomed Eng. 2010;57(1):175–184. doi: 10.1109/TBME.2009.2028133. [DOI] [PubMed] [Google Scholar]
- Gyongy M, Coussios CC. Passive spatial mapping of inertial cavitation during HIFU exposure. IEEE Trans Biomed Eng. 2010;57(1):48–56. doi: 10.1109/TBME.2009.2026907. [DOI] [PubMed] [Google Scholar]
- Hand JW, Shaw A, Sadhoo N, Rajagopal S, Dickinson RJ, Gavrilov LR. A random phased array device for delivery of high intensity focused ultrasound. Phys Med Biol. 2009;54(19):5675–5693. doi: 10.1088/0031-9155/54/19/002. [DOI] [PubMed] [Google Scholar]
- Hill CR, Rivens I, Vaughan MG, ter Haar GR. Lesion development in focused ultrasound surgery: a general model. Ultrasound Med Biol. 1994;20(3):259–269. doi: 10.1016/0301-5629(94)90066-3. [DOI] [PubMed] [Google Scholar]
- Huisman M, Lam MK, Bartels LW, Nijenhuis RJ, Moonen CT, Knuttel FM, Verkooijen HM, van Vulpen M, van den Bosch MA. Feasibility of volumetric MRI-guided high intensity focused ultrasound (MR-HIFU) for painful bone metastases. Journal of Therapeutic ultrasound. 2014;10:2. doi: 10.1186/2050-5736-2-16. 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang JH, Wang YN, Warren C, Upton MP, Starr F, Zhou Y, Mitchell SB. Preclinical in vivo evaluation of an extracorporeal HIFU device for ablation of pancreatic tumors. Ultrasound Med Biol. 2009;35(6):967–975. doi: 10.1016/j.ultrasmedbio.2008.12.006. [DOI] [PubMed] [Google Scholar]
- Illing RO, Kennedy JE, Wu F, ter Haar GR, Protheroe AS, Friend PJ, Gleeson FV, Cranston DW, Phillips RR, Middleton MR. The safety and feasibility of extracorporeal high-intensity focused ultrasound (HIFU) for the treatment of liver and kidney tumours in a Western population. Br J Cancer. 2005;93(8):890–895. doi: 10.1038/sj.bjc.6602803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara Y, Calderon A, Watanabe H, Okamoto K, Suzuki Y, Kuroda K, Suzuki Y. A precise and fast temperature mapping using water proton chemical shift. Magn Reson Med. 1995;34:814–823. doi: 10.1002/mrm.1910340606. [DOI] [PubMed] [Google Scholar]
- Jensen CR, Ritchie RW, Gyöngy M, Collin JRT, Leslie T, Coussios CC. Spatiotemporal monitoring of high-intensity focused ultrasound therapy with passive acoustic mapping. Radiology. 2012;262:252–261. doi: 10.1148/radiol.11110670. [DOI] [PubMed] [Google Scholar]
- Khokhlova VA, Bailey MR, Reed JA, Cunitz BW, Kaczkowski PJ, Crum LA. Effects of nonlinear propagation, cavitation, and boiling in lesion formation by high intensity focused ultrasound in a gel phantom. Journal of Acoustic Society of America. 2006;119:1834–1848. doi: 10.1121/1.2161440. [DOI] [PubMed] [Google Scholar]
- Marinova M, Rauch M, Mücke M, Rolke R, Gonzalez-Carmona MA, Henseler J, Cuhls H, Radbruch L, Strassburg CP, Zhang L, Schild HH, et al. High-intensity focused ultrasound (HIFU) for pancreatic carcinoma: evaluation of feasibility, reduction of tumour volume and pain intensity. European Radiology. 2016;26:4047–4056. doi: 10.1007/s00330-016-4239-0. [DOI] [PubMed] [Google Scholar]
- O'Neil HT. Theory of focusing radiators. Journal of Acoustic Society of America. 1949;21(5):516–526. [Google Scholar]
- Orgera G, Monfardini L, Della VP, Zhang L, Bonomo G, Arnone P, Padrenostro M, Orsi F. High-intensity focused ultrasound (HIFU) in patients with solid malignancies: evaluation of feasibility, local tumour response and clinical results. Radiol Med. 2011;116(5):734–748. doi: 10.1007/s11547-011-0634-4. [DOI] [PubMed] [Google Scholar]
- Orsi F, Arnone P, Chen W, Zhang L. High intensity focused ultrasound ablation: a new therapeutic option for solid tumors. J Cancer Res Ther. 2010;6(4):414–420. doi: 10.4103/0973-1482.77064. [DOI] [PubMed] [Google Scholar]
- Pernot M, Aubry JF, Tanter M, Thomas JL, Fink M. High power transcranial beam steering for ultrasonic brain therapy. Phys Med Biol. 2003;48:2577–2589. doi: 10.1109/TMI.2010.2076829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pernot M, Aubry JF, Tanter M, Boch AL, Marquet F, Kujas M, Seilhean D, Fink M. In vivo transcranial brain surgery with an ultrasonic time reversal mirror. J Neurosurg. 2007;106:1061–1066. doi: 10.3171/jns.2007.106.6.1061. [DOI] [PubMed] [Google Scholar]
- Preston RC. Output Measurements for Medical Ultrasound. Springer-Verlag; 1991. [Google Scholar]
- Rabinovici J, Inbar Y, Revel A, Zalel Y, Gomori JM, Itzchak Y, Schiff E, Yagel S. Clinical improvement and shrinkage of uterine fibroids after thermal ablation by magnetic resonance-guided focused ultrasound surgery. Ultrasound Obstet Gynecol. 2007;30(5):771–777. doi: 10.1002/uog.4099. [DOI] [PubMed] [Google Scholar]
- Ritchie RW, Leslie T, Phillips R, Wu F, Illing R, Ter Haar G, Protheroe A, Cranston D. Extracorporeal high intensity focused ultrasound for renal tumours: a 3-year follow-up. BJU Int. 2010;106(7):1004–1009. doi: 10.1111/j.1464-410X.2010.09289.x. [DOI] [PubMed] [Google Scholar]
- Roujol S, Ries M, Quesson B, Moonen C, Denis dS. Real-time MR-thermometry and dosimetry for interventional guidance on abdominal organs. Magn Reson Med. 2010;63(4):1080–1087. doi: 10.1002/mrm.22309. [DOI] [PubMed] [Google Scholar]
- Shaw A. A Buoyancy Method for the Measurement of Total Ultrasound Power Generated by HIFU Transducers. Ultrasound in Medicine & Biology. 2008;34(8):1327–1342. doi: 10.1016/j.ultrasmedbio.2008.01.008. 2008. [DOI] [PubMed] [Google Scholar]
- ter Haar G, Shaw A, Pye S, Ward B, Bottomley F, Nolan R, Coady A. Guidance on Reporting Ultrasound Exposure Conditions for Bio-Effects Studies. Ultrasound in Medicine & Biology. 2011;37(2):177–183. doi: 10.1016/j.ultrasmedbio.2010.10.021. [DOI] [PubMed] [Google Scholar]
- van Velthoven R, Aoun F, Marcelis Q, Albisinni S, Zanaty M, Lemort M, Peltier A, Limani K. A prospective clinical trial of HIFU hemiablation for clinically localized prostate cancer. Prostate ~cancer and Prostatic Diseases. 2016;19(1):79–83. doi: 10.1038/pcan.2015.55. [DOI] [PubMed] [Google Scholar]
- Visioli AG, Rivens IH, ter Haar GR, Horwich A, Huddart RA, Moskovic E, Padhani A, Glees J. Preliminary results of a phase I dose escalation clinical trial using focused ultrasound in the treatment of localised tumours. European Journal of Ultrasound. 1999;9(1):11–18. doi: 10.1016/s0929-8266(99)00009-9. [DOI] [PubMed] [Google Scholar]
- Wu F, Wang Z-B, Chen W-Z, Zhu H, Bai J, Zou J-Z, Li K-Q, Jin C-B, Xie F-L, Su H-B. Extracorporeal high intensity focused ultrasound ablation in the treatment of patients with large hepatocellular carcinoma. Ann Surg Oncol. 2004;11(12):1061–1069. doi: 10.1245/ASO.2004.02.026. [DOI] [PubMed] [Google Scholar]
- Yoon SW, Cha SH, Ji YG, Kim HC, Lee MH, Cho JH. Magnetic resonance imaging-guided focused ultrasound surgery for symptomatic uterine fibroids: estimation of treatment efficacy using thermal dose calculations. European Journal of Obstet Gynecol Reprod Biol. 2013;169:304–308. doi: 10.1016/j.ejogrb.2013.02.023. [DOI] [PubMed] [Google Scholar]