Comparing ActiGraph equations for estimating energy expenditure in older adults

Abstract

Accurate estimation of energy expenditure (EE) from accelerometer outputs remains a challenge in older adults. The aim of this study was to validate different ActiGraph (AG) equations for predicting EE in older adults. Forty older adults (age = 77.4 ± 8.1 yrs) completed a set of household/gardening activities in their residence, while wearing an AG at the hip (GT3X+) and a portable calorimeter (MetaMax 3B – criterion). Predicted EEs from AG were calculated using five equations (Freedson, refined Crouter, Sasaki and Santos-Lozano (vertical-axis, vectormagnitude)). Accuracy of equations was assessed using root-mean-square error (RMSE) and mean bias. The Sasaki equation showed the lowest RMSE for all activities (0.47 METs) and across physical activity intensities (PAIs) (range 0.18–0.48 METs). The Freedson and Santos-Lozano equations tended to overestimate EE for sedentary activities (range: 0.48 to 0.97 METs), while EEs for moderate-to-vigorous activities (MVPA) were underestimated (range: −1.02 to −0.64 METs). The refined Crouter and Sasaki equations showed no systematic bias, but they respectively overestimated and underestimated EE across PAIs. In conclusion, none of the equations was completely accurate for predicting EE across the range of PAIs. However, the refined Crouter and Sasaki equations showed better overall accuracy and precision when compared with the other methods.

INTRODUCTION

Accelerometers are widely used to assess physical activity (PA), as they have the potential to measure intensity, duration and frequency of PA in free-living environments objectively, and with detailed time-resolution. However, accurate estimation of energy expenditure (EE) from accelerometer outputs remains a challenge (Freedson, Bowles, Troiano, & Haskell, 2012; Kamada, Shiroma, Harris, & Lee, 2016; Lyden, Kozey, Staudenmeyer, & Freedson, 2011). When deciding which method to use, researchers are faced with a choice of several different equations, developed with diverse statistical approaches, including regressions, decision trees, and machine-learning methods. Researchers also have to choose the appropriate data extraction techniques (e.g. raw data, epochs, etc.) for the age and health of the population being studied (Crouter, Kuffel, Haas, Frongillo, & Bassett, 2010; Lyden, Keadle, Staudenmayer, & Freedson, 2014; Strath, Pfeiffer, & Whitt-Glover, 2012). Although, there are several available options for accelerometer data analysis, because of their simplicity, most researchers use cut-points derived from predictive equations.

To date, most of the equations for predicting EE from accelerometer data for adults have been developed in young and middle-aged populations, using activities such as cycling, treadmill walking and sports such as basketball (Crouter et al., 2010; Freedson, Melanson, & Sirard, 1998). Older adults show different activity and movement patterns from younger adults, reflecting the biological, physical and social changes associated with aging (Strath et al., 2012; Taraldsen, Chastin, Riphagen, Vereijken, & Helbostad, 2012). However, few studies have developed predictive equations for older adults, using activities that reflect the range or intensity of activities typically undertaken by this group.

The ActiGraph (AG) accelerometer is commonly used for objective measurement of physical activity (Montoye, Moore, Bowles, Korycinski, & Pfeiffer, 2016) with acceleration counts analysed using different equations for predicting EE in children and adults. The Freedson equation (Freedson et al., 1998) was developed for data collected with the first generation of AG in 1-minute epochs for the vertical axis. Even though its validation was based only on treadmill exercise at three different speeds (Freedson et al., 1998), it has been widely used in large-scale studies, both for estimating EE and for categorising physical activity at different intensity levels (Arnardottir et al., 2013; Gennuso, Gangnon, Matthews, Thraen-Borowski, & Colbert, 2013; Matthews et al., 2013). Another commonly used method is the two-regression model developed and refined by Crouter et al. (2010); it uses 1-second counts in 10-second increments to differentiate walk/run from lifestyle activities before assigning nonlinear EE predictive equations to each type. Estimates of EE from this method have shown good agreement with EE measured with whole-room calorimetry (24-h semi-structured protocol of activities at different intensities) and doubly labelled water (14 days in free-living conditions) in an adult sample (Rothney, Brychta, Meade, Chen, & Buchowski, 2010). The refined Crouter equation has also been tested in adults in free-living environments, but significantly underestimated time in sedentary behaviours (SB) and overestimated time spent in light, moderate, and vigorous PA (Crouter, DellaValle, Haas, Frongillo, & Bassett, 2013). Also, Sasaki, John, and Freedson (2011) developed a EE predictive equation for moderate, vigorous and very vigorous intensities in adult populations using the triaxial feature of the AG under laboratory conditions on a treadmill. A specific model for predicting EE in older adults was developed by Santos-Lozano et al. (2013) using a test protocol that comprised 6 conditions (resting, sit-to-stand and treadmill at different speeds), measured with indirect calorimetry. From this study, equations for the AG were obtained for the vertical axis (Santos-Lozano VT) and using the vector magnitude of the three axes (Santos-Lozano VM). None of these equations have been tested in older adults in free-living environments.

To reduce this knowledge gap, the primary aim of this study was to validate the accuracy of five predictive EE equations (Freedson, Refined Crouter, Sasaki, Santos-Lozano VT and Santos-Lozano VM) by comparing accelerometer data against indirect calorimetry-measured values, in a group of healthy older adults in their natural daily living settings.

Methods

Participants

Forty community-dwelling participants aged 65 and over were recruited using flyers displayed at organizations with large numbers of older adults, as well as a recruitment notice circulated through emails and letters within a network of previous volunteers. Eligibility criteria included being able to walk (with or without assistive devices but not requiring assistance from another person) and ability to sign the consent form. Exclusion criteria were cognitive or physical disabilities which limited their capacity to perform the activities that were in the protocol. Before commencing, participants gave written informed consent; the consent form and study protocol were approved by the Behavioural & Social Sciences Ethical Review Committee of the University of Queensland, Australia.

Experimental protocol

Testing was conducted in each participant’s home. Age, gender, general health information, and physical activity level were assessed with a questionnaire. Exercise capacity was estimated with the Veterans Specific Activity Questionnaire (VSAQ) (Rankin, Briffa, Morton, & Hung, 1996). Height and weight were measured using a floor scale and a stadiometer and used to calculate body mass index (BMI = kg·m⁻²). The participants wore a portable calorimetry system, MetaMax 3B (MetaMax, Cortex Biophysik GmbH, Leipzig, Germany), and a tri-axial raw-signal accelerometer at the right hip, ActiGraph GT3X+ (AG; ActiGraph, Pensacola, FL, USA), during periods of sitting, lying down, self-paced walking and 4 self-selected household/gardening activities. Before commencing the tests, every participant selected activities based on their usual daily tasks.

Measured activities

In total, 16 different activities were measured across the sample. Sitting (n = 36) and lying (n = 37) were performed quietly in a comfortable position. Self-paced walking (n = 40) was measured outdoors on a flat and firm surface, which allowed walking without interruption. The participants were instructed to walk at a comfortable pace (i.e. speed used for transportation) that would allow talking. Walking speed was not measured, but step accumulation per minute was estimated using the AG (mean 82.4 ± 13.17 steps/min). Eight different household activities were measured across the whole sample, including sweeping (n = 18), tidying up (n = 5), washing windows (n = 6), dusting (n = 20), washing dishes (n = 26), vacuuming (n = 21), ironing (n = 5) and laundry, folding or hanging clothes (n = 5). Five gardening activities were measured in this sample: mowing the lawn (n = 7), trimming and weeding (n = 9), pruning (n = 11), watering plants and garden (n = 16), and raking the lawn (n = 4). No specific instructions were given on how to conduct the household and gardening activities. The activities were measured on the same day in a random order, except for the resting activities which were performed at the beginning. All the activities lasted at least 5 minutes, but participants were allowed to perform the activities for a longer duration when necessary. To avoid anticipation which may affect the activity pattern, the research team informed participants about the time remaining for each activity, as they tended to stop or slow down before the time was finished. The participants were asked to remain silent during the activity, except to indicate any inconvenience or emergency. After each activity, recovery time was allowed and the following activity started after resting heart rate values were attained.

Instruments

For each activity, ventilation and expired gas concentrations were measured breath-by-breath to measure EE with the previously validated and calibrated MetaMax as the reference standard (Macfarlane & Wong, 2012). The system included an analyser unit, which was secured to a neoprene chest harness, and a soft and flexible mask, held with a neoprene head harness. The additional weight of the equipment (650 gr) was considered in the participant body mass to compensate for the additional energy cost increase. The portable system was calibrated and prepared according to the manufacturer’s instructions before each measurement. MetaMax data were recorded and downloaded with Metasoft software v3.9.7 (Cortex Biophysik GmbH, Leipzig, Germany). To filter data and match them with accelerometry, the duration of each activity was recorded using the Metasoft software, with a synchronized watch as back up.

The AG was placed on the anterior axillary line of the iliac crest using an elastic belt. AGs were initialized and downloaded using ActiLife 5 Software v5.7.4 (ActiGraph, Pensacola, FL, USA). Data were recorded with a sampling rate of 30 Hz at all three axes.

Data analysis

In order to ensure date and time matching, all the instruments were initialized and synchronized on the same computer. For the calorimetry, a steady state was selected for each of the activities by eliminating the first 150s and retaining the remaining data, as a plateau (variability below 5% for oxygen consumption) was reached after 150s in all observations. This elimination procedure was based on a previous study (Hall, Howe, Rana, Martin, & Morey, 2013) and the overall time taken to observe a steady state in our sample. The AG 30 Hz data were integrated with Stata 13.0 (StataCorp. College Station, TX, USA) into 10-s or 1-min epochs using the start and end time for each activity. The Metamax data were averaged into the respective 10-s or 1-min epochs. This allowed precise matching of the MetaMax and AG data for the specific requirements of each equation (Table 1). Accelerometer data processing was completed with a customized Stata syntax. EE (MET_standard) was derived from calorimetry-measured VO₂ and VCO₂ using Weir’s equation (Weir, 1949) and then divided by3.5 ml·kg⁻¹·min⁻¹.

Table 1.

AG prediction equations and cut-points included in the analysis.

	EE prediction equation (METs)
Freedson	1.439008 + 0.000795·(VT cpm)
Refined Crouter	Sedentary equation  If the VT counts·10 sec−1 are ≤ 8: EE = 1.0 MET, Walk/run equation (VT cnts·10 sec−1 > 8, and CV* ≤ 10)  2.294275·(exp(0.00084679 · VT counts·10 sec−1)) Lifestyle equation (cnts·10 sec−1 > 8, and CV*>10)  0.749395+[0.716431·(Ln(VT counts·10 sec−1)] – [0.179874 · (Ln(VT counts·10 sec−1))2] + [0.033173 · (Ln(VT counts·10 sec−1))3]
Santos-Lozano VT	2.8867 + 0.00067·(VT cpm)-0.6807·Gender
Santos-Lozano VM	2.5878 + 0.00047·(VM cpm)-0.6453·Gender
Sasaki	0.000863·(VM cpm) + 0.668876

Abbreviations: AG: ActiGraph; EE: energy expenditure; SEE: standard error of measurement; METs: Metabolic equivalents; VT: vertical axis; cnts: counts; cpm: counts per minute, CV: coefficient of variation of the vertical axis in 10 seconds; G: gender (female: 1; male: 2); VM: vector magnitude.

^*The lowest coefficient of variation (CV) is selected from those calculated for each 10-second epoch, and all combinations of the five surrounding 10-second epochs. This CV is used to identify whether the 10-second epoch was part of sedentary activity, rhythmic locomotor activity (i.e. walking or running) or intermittent lifestyle activity

Statistical analysis

All statistical analyses were performed using Stata 13.0 (StataCorp. College Station, TX, USA) and p < 0.05 was considered statistically significant. Predicted EE (MET_predicted) was calculated with the AG equations (Freedson, Refined Crouter, Sasaki, Santos-Lozano VT and Santos-Lozano VM; Table 1) and compared with MET_standard values from indirect calorimetry during the protocol.

Root mean square error (RMSE; expresses deviation of the predicted values from their mean), mean absolute percent error (MAPE; measures accuracy in relative terms), and mean bias with 95% limits of agreement (compares individual differences between predicted and measured results) were used to assess the accuracy of each equation, for all activities and by PAIs. MET_predicted values, derived from the equations were compared with MET_standard for each activity using t-tests.

Results

40 participants completed the study; their average age was77.4 years (Standard Deviation [SD] = 8.13, range 66–99), mean BMI was 26.0 kg∙m⁻² (SD = 3.67, range 19.0–36.0) and median exercise capacity was 6.9 METs [interquartile range 4.59, 9.39]. Only 10% rated their health as poor or fair, and 53.9% reported less than 1 h/week of physical activity. No differences were observed between male and female participants. In total, 16 different activities were assessed and the average total measured time with indirect calorimetry in the test was 49.4 min (SD = 6.50). Preparation and breaks without the mask were not considered in the measured time estimation.

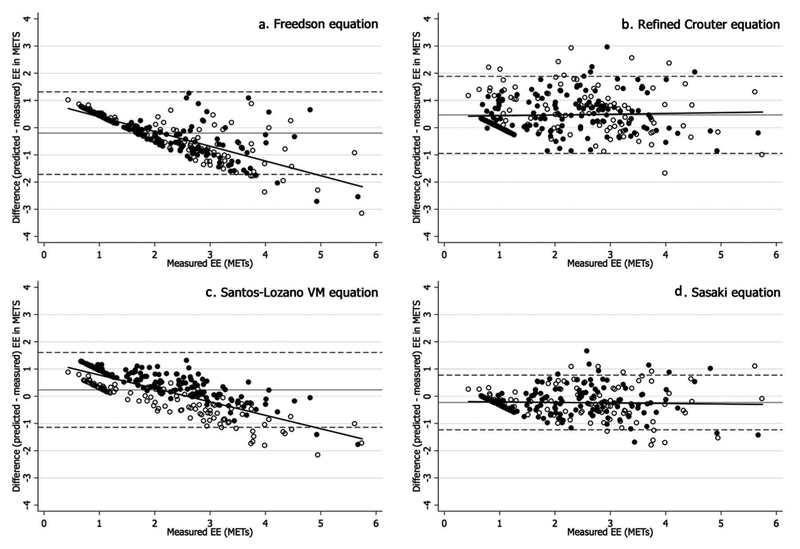
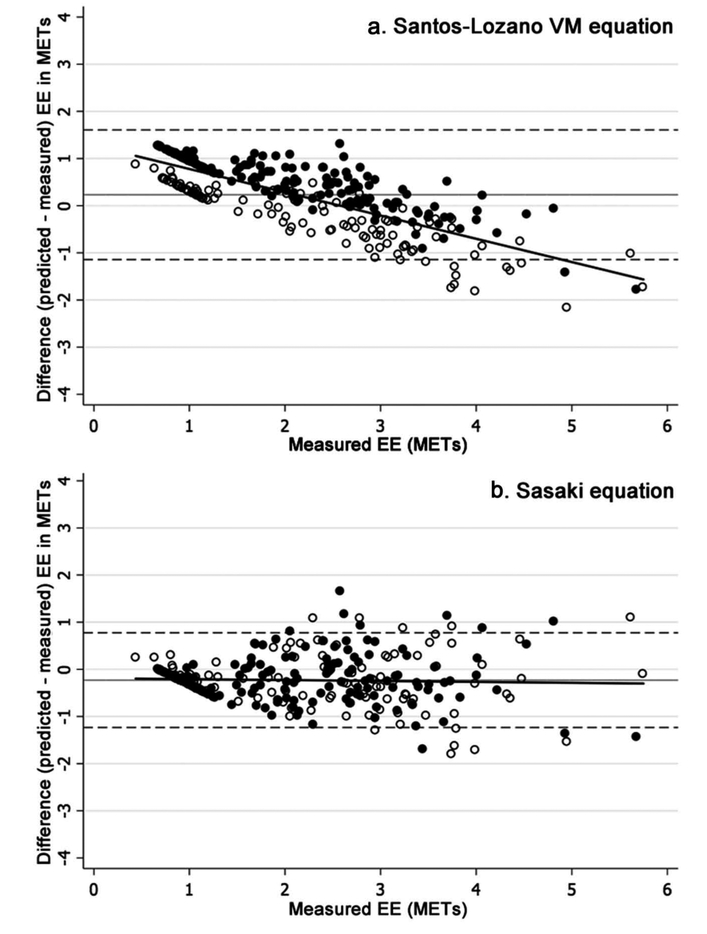
The Freedson, Santos-Lozano VT and VM equations tended to overestimate EE for lower intensity activities by about 1 MET, while EEs for activities with higher intensity were underestimated by approximately 1.5 METs (Figures 1 and 2). In contrast, both the refined Crouter and Sasaki equations showed no systematic bias when compared with indirect calorimetry. Overall mean biases between MET_standard and MET_predicted ranged from −0.23 METs (Sasaki) to 0.47 METs (refined Crouter) with wide limits of agreements (LoA, 2–3 METs) (Figures 1 and 2). Overall mean biases were different for men and women when using both the Santos-Lozano VT (0.26 (LoA: 0.11, 0.42) vs −0.54 (LoA:−0.65,−0.43) METs, p < 0.001) and VM (0.22 (LoA: 0.11, 0.34) vs −0.54 (LoA: −0.62,−0.46), p < 0.001) equations. The accuracy of the five equations for predicting energy expenditure for all activity levels is shown in Table 2. The lowest RMSE for all activities was observed with the Sasaki equation (0.47 METs), while the highest was obtained with Santos-Lozano VT (0.89 METs). For comparisons of MET_standard and MET_predicted (for overall activities) MAPE ranged from 8.6% (Freedson) to 38.6% (Santos-Lozano VT).

Figure 1.

Plots representing the difference between measured (MetaMax 3B) and predicted (ActiGraph equations using the vertical axis) energy expenditure (METs) for all activities combined The black solid line represents the trend, grey solid line represents mean bias and the dashed lines represent the 95% limits of agreement. Open circles represent women and filled circles represent men. EE: Energy expenditure; MET: Metabolic equivalent; VT: vertical axis.

Figure 2.

Plots representing the difference between measured (MetaMax 3B) and predicted (ActiGraph equations using the vector magnitude) energy expenditure (METs) for all activities combined. The black solid line represents the trend, grey solid line represents mean bias and the dashed lines represent the 95% limits of agreement. Open circles represent women and filled circles represent men. EE: Energy expenditure; MET: Metabolic equivalent; VM: vector magnitude.

Table 2.

Accuracy of equations for predicting energy expenditure for all activities (overall) and according to physical activity intensities, compared with indirect calorimetry (MetaMax 3B).

	RMSE (METs)	R2	MAPE (%)	Mean Bias (METs)	95% LoA
Freedson	0.77	0.54	8.6	−0.20	−1.75, 1.35
Overall	0.19	0.05	54.9	0.48	0.10, 0.85
Sedentary	0.38	0.24	16.5	−0.40	−1.33, 0.52
Light PA	0.58	0.20	27.2	−1.02	−2.71,0.68
MVPA
Refined Crouter	0.60	0.72	28.1	0.47	−0.98, 1.91
Overall	0.19	0.04	37.4	0.33	−0.73, 1.39
Sedentary	0.37	0.28	28.5	0.65	−0.90,2.19
Light PA	0.55	0.29	11.3	0.40	−1.31,2.10
MVPA
Santos-Lozano VT*	0.89	0.37	38.6	0.22	−1.57, 2.00
Overall	0.19	0.00	107.6	0.97	0.23, 1.72
Sedentary	0.40	0.12	4.9	0.06	−1.04, 1.16
Light PA	0.59	0.17	21.5	0.82	−2.47, 0.84
MVPA
Santos-Lozano VM*	0.68	0.64	32.8	0.23	−1.17, 1.63
Overall	0.19	0.01	82.8	0.75	0.05, 1.45
Sedentary	0.39	0.19	11.7	0.22	−0.77, 1.21
Light PA	0.53	0.32	16.5	−0.64	−1.83, 0.55
MVPA
Sasaki*	0.47	0.82	13.8	−0.23	−1.25,0.80
Overall	0.18	0.14	23.1	−0.25	−0.63, 0.14
Sedentary	0.34	0.37	7.5	−0.16	−1.30, 0.97
Light PA	0.48	0.45	8.7	−0.32	−1.79, 1.16
MVPA

LoA: limits of agreement; MAPE: mean absolute percent error; METs: metabolic equivalent; MVPA: moderate-to-vigorous physical activity; PA: physical activity; RMSE: root mean squared error; VT: vertical axis; VM: vector magnitude.

^*Santos-Lozano VT and VM equations were validated with light, moderate and vigorous intensity activities, while the Sasaki equation was developed for moderate and vigorous activities only.

When comparing predicted EE with indirect calorimetry by PAIs (Table 2), RMSEs were similar across equations for sedentary EE (range 0.18–0.19). The Sasaki equation appeared to perform best, in comparison with the other EE predictive equations, for most PAIs. Assessing sedentary PAI was challenging for all predictive equations because all showed large relative differences with the measured EE (range 23.1%−107.6%).

When comparing each activity type individually with the predicted EE from equations, mean biases ranged from −1.97 (Freedson, mowing lawn) to 0.81 METs (refined Crouter, watering plants) (Figure 3). The number of activities for which ME_Tpredicted significantly differed from MET_standard was 15 for the Freedson equation, 8 for the refined Crouter equation, 8 and 4 for the Santos-Lozano VT and VM equations and 4 for the Sasaki equation. None of the equations correctly predicted the EE for sedentary activities and mean biases ranged from −0.29 (Sasaki, sitting) to1.01 (Santos-Lozano VT, lying quietly).

Figure 3.

Mean bias and 95% limits of agreement for steady-state energy expenditure (METs) estimated from different predictive equations and indirect calorimetry (MetaMax 3B) for 16 different activities in older adults. *Significantly different from measured energy expenditure (p < 0.05). LoA: limits of agreement; EE: energy expenditure; METs: metabolic equivalent; VM: vector magnitude.

Discussion

The purpose of this study was to determine the validity of different AG equations for predicting EE in older adults in their habitual-living environments. We tested a variety of common activities, and measured individual EE with a portable indirect calorimeter.

We assessed the validity of the five equations for predicting the EE of each activity type, activities by MET intensity levels, and overall activities combined. While the performances varied widely, the refined Crouter and Sasaki equations showed no systematic bias and the Sasaki equation had the lowest RMSE and second lowest MAPE for overall activities. Our results confirmed earlier findings reported for the refined Crouter equation in adults (Crouter et al., 2013). In contrast, the Freedson, Santos-Lozano VT and Santos Lozano VM equations all tended to overestimate sedentary and light intensity activities and underestimated moderate to vigorous activities. Similar findings were reported for the Freedson equation when tested in younger adults (Lyden et al., 2011; Rothney, Schaefer, Neumann, Choi, & Chen, 2008). In our study, when using the Freedson equation, the lowest EE value when 0 counts were recorded was 1.44 METs, thus resulting in overestimation, as the EE of most resting activities is close to 1 MET.

When comparing our findings with studies conducted in adults (Crouter et al., 2013; Lyden et al., 2014), the relative differences for all activities were higher in this sample of older adults. Lyden et al. (2014) reported overall percent biases ranging from −13.0% (Freedson) to 0.7% (refined Crouter), while the equations in the current study exhibited overall differences from −13.8% (Sasaki) to38.6% (Santos-Lozano VT). Therefore, these large differences suggest that results obtained for younger to middle-aged adults may not be generalised to older adults.

Although overall absolute mean biases for the two Santos-Lozano equations were comparable with those from the Freedson and Sasaki equations, and lower than those from the refined Crouter equation, these equations exhibited high MAPE for sedentary activities (82.8–107.6%). As sedentary activities represent about 65–80% of the total activities performed by older adults on an average day (Harvey, Chastin, & Skelton, 2015), these high MAPEs would result in overestimation of the daily EE. This may be partially explained by the fact that the equations were validated in a laboratory setting that not included sendentary activities, resulting in a high intercept (2.89–2.59). Thus, the Santos-Lozano equations should be used with caution for estimating overall EE and sedentary behavior in older adults.

Evidence suggests that light PA promotes health in older adults (Foong et al., 2016), and provides a starting opportunity for changing PA behavior (Eijsvogels, George, & Thompson, 2016). When comparing the performance of the equations for estimating EE in light activities, all equations exhibited similar RMSE, but MAPEs and mean biases were particularly lower for Santos-Lozano VT(4.9%, 0.06 METs) and Sasaki (7.5%, 0.16 METs) equations. These findings are relevant, as older adults spend about 15% of their day in light PA (Husu et al., 2016). This may result, as similarly described for sedentary activities, in significant differences in total daily EE when applying some equations in this age group.

In terms of RMSE, our findings were similar across equations for estimating EE in MVPA, but the refined Crouter and Sasaki equations performed better, as they showed lower MAPEs and mean biases. The refined Crouter equation tends to overestimate EE predictions in MVPA as similarly found by Rothney et al. (2010) and Crouter et al. (2013) in heterogeneous age cohorts. The Freedson equation showed the highest MAPE (27.2%) and mean bias (−1.02 METs) of all the equations. Its application for estimating total EE for these activities is therefore limited in older adults.

The number of activities that had significantly different MET_predicted and MET_standard values varied across equations. The largest differences in relative terms were observed for sedentary activities, especially with the two Santos-Lozano equations (mean bias 0.77–1.01 METs). Importantly, the lowest EE values for the Santos-Lozano VM equation, when 0 counts per minute were recorded, were 1.30 and 1.94 METs for men and women respectively, which would lead to significant overestimation of EE at rest. Differences between MET_standard and MET_predicted for each activity may also be explained by the fact that these equations assume linear relationships between counts and EE. The relationships may not be linear when activities are performed intermittently in short bouts and at different intensities (for example, mowing lawn), as is often the case in free-living environments.

Although simple linear regression equations were widely accepted methods for model development in the past, other methods are now being employed or are in development. Crouter et al. (2006) developed the two-regression method, including more features, such as the coefficient of variation (CV), in order to differentiate walking/running from lifestyle activities. This method was refined to improve the identification of the initiation of rhythmic locomotor activities in 2010 (Crouter et al., 2010). However, both the first and refined model showed similar validity for pure sedentary or pure walking activities, with better performance for the refined Crouter equation for activities where walking was interspersed with rest periods (Crouter et al., 2010). Despite these corrections, in our study, the refined Crouter equation tended to overestimate EE in moderate intensity activities, including walking. In contrast with our findings, a study that used this method showed no difference in total EE, total minutes in bouts and the number of bouts of activity that qualify towards meeting the physical activity guidelines, when compared with direct observation in a younger sample (Lyden et al., 2014). This may suggest that CV<10 may not be appropriate for detecting locomotion in older adults in free-living environments, but this requires further research. In our study, some activities were more frequently selected by participants than others (eg indoor cleaning vs outdoor activities), which affected some comparisons. However, activities selected by few participants were were spread across ages and both genders. Therefore, differences between MET_predicted and MET_standard may be mostly explained by the diversity of skills and effort, rather than by demographic characteristics.

Strengths and limitations

To our knowledge, this is the first study to assess these methods in older adults in their habitual-living enviroments. We included a wide age range and participants with varying PA levels and exercise capacities. Moreover, a range of meaningful activities was selected by the participants. Although we used the best method available for measuring EE in free-living environments, we recognise that this method has some limitations. We were unable to conduct a valid measurement of resting metabolic rate (Compher, Frankenfield, Keim, Roth-Yousey, & Evidence Analysis Working, 2006) that may have favoured the adjustment of measured EE with this basal estimate (Kozey, Lyden, Staudenmayer, & Freedson, 2010). The calculation of METs based on the measured resting EE (rather than the standard 3.5 ml·kg⁻¹·min⁻¹) is important in older adults, as EE at rest decreases with age (Byrne, Hills, Hunter, Weinsier, & Schutz, 2005). Thus, use of standard resting EE may have led to underestimation of the estimated METs (Kozey et al., 2010; McMurray, Soares, Caspersen, & McCurdy, 2014). However, we conducted a secondary analysis with a proxy of the resting metabolic rate based on the measured EE while lying down (5 minutes) and findings were generally similar. The measurement period was limited to a period of about two hours, as these older participants would have become fatigued with a longer protocol, but this time was sufficient for measuring each activity without interruptions in all participants. Also, although the activities were self-selected (except for lying, sitting and walking), the duration was influenced by our suggestion (at least 5 minutes). Some of the selected activities may usually require less time to be completed, thus affecting the activity pattern or effort. Although we attempted to simulate free-living conditions, patterns and intensity may have been affected by our presence and the calorimeter, despite our encouragement to perform activities as they were usually done on a daily basis.

Conclusion

None of the equations was completely accurate in all domains for predicting EE and PAIs.

However, the refined Crouter and Sasaki equations showed better accuracy and precision when compared with other methods, particularly when assessing MVPA. Researchers should consider the strengths and weaknesses described here when analysing data and extrapolating results from equations, because issues such as individual variability in terms of patterns and nature of movement remain an important limitation of all these methods.