Behavior problems at ages 6 and 11 and high school academic achievement: Longitudinal latent variable modeling

Abstract

Previous studies documented long-run effects of behavior problems at the start of school on academic achievement. However, these studies did not examine whether the observed effects of early behavior problems are explained by more proximate behavior problems, given the tendency of children’s behavior problems to persist. Latent variable modeling was applied to estimate the effects of behavior problems at ages 6 and 11 on academic achievement at age 17, using data from a longitudinal study (n=823). Behavior problems at ages 6 and 11, each stage independently of the other, predicted lower math and reading test scores at age 17, controlling for intelligence quotient (IQ), birth weight, maternal characteristics, family and community environment, and taking into account behavior problems at age 17. Behavior problems at the start of school, independent of later behavior problems, exert lingering effects on achievement by impeding the acquisition of cognitive skills that are the foundation for later academic progress.

1. Introduction

Behavior problems during the early school years curtail educational attainment, adversely influencing long-term social and economic outcomes (McLeod and Kaiser, 2004; Groot and van den Brink, 2007; Breslau et al., 2008). One-way in which behavior problems influence academic attainment is by impeding the acquisition of academic skills and the successful progression in school. Duncan et al. (2007) have documented the longitudinal association of children’s attention problems at school entry with academic achievement at the end of primary school, based on data from six studies (Duncan et al., 2007). The evidence on the longitudinal association between attention and academic achievement has been subsequently extended up to the conclusion of high school (HS) (Breslau et al., 2009). In these studies, children’s attention problems were correlated with externalizing (disruptive) and internalizing (emotional) problems and all three types of problems predicted subsequent academic achievement. However, regression-adjusted estimates singled out attention as the only unique predictor, when the correlations among the three types of problems were taken into account (Duncan et al., 2007; Breslau et al., 2009). An additional analysis suggested that change in attention problems during the early school years might be followed by change in academic achievement (Breslau et al., 2010), providing a clue for the relevance of more proximate behavior problems to high school academic success.

Previous investigations did not examine whether the observed longitudinal association between early behavior problems and achievement reflect the tendency of behavior problems to persist. The long-run effects of behavior problems at the start of schooling on academic achievement at the end of high school might be explained by more proximate behavior problems. Is there evidence of an enduring effect of behavior problems at the start of school on high school achievement, even when children change or “outgrow” their early problems? This question has not been examined in previous studies.

In this study we attempt to advance the longitudinal inquiry in the following way. Using data on behavior problems atages 6, 11 and 17, we examine the contribution of behavior problems at ages 6 and 11, each adjusted for the other, to math and reading test scores at age 17, taking into account behavior problems at age 17. We use an analytic approach, latent variable modeling, which takes advantage of our rich assessment of key variables, the longitudinal design of the study, and the availability of information on important covariates.

2. Methods

2.1. Sample

Random samples of low birth weight and normal birth weight children were drawn from 1983 to 1985 newborn discharge lists of two major hospitals in southeast Michigan, one located in the City of Detroit and serving primarily the residents of the inner city (urban) and the other located in an adjacent suburb, serving residents of the surrounding middle-class suburbs. Of 1095 eligible children, 823 (75%) participated in the initial assessment in 1990–1992, when they were 6 years of age. Subsequent assessments were conducted in 1995–1997, when the children were 11 years of age (n=717), and in 2000–2002, when they were 17 years of age (n=713). Detailed information on the sample and its maintenance over the three assessments is available elsewhere (Breslau et al., 1996; Breslau and Chilcoat, 2000; Breslau et al., 2006; Breslau et al., 2009).

2.2. Measurement of key variables

At each assessment, children were rated by teachers using the Teacher’s Report Form (TRF) (Achenbach, 1991a, 1991b). The TRF asks teachers to rate children based on observations of classroom behavior during the preceding 2 months. It consists of 118 items rated from 0 to 2 (0 indicates not true; 1, somewhat or sometimes true; and 2, very or often true). The TRF consists of eight syndrome scales: withdrawn, somatic complaints, anxious/depressed, social problems, thought problems, attention problems, delinquent behavior, and aggressive behavior. The TRF also yields scores on two broadband scales measuring externalizing and internalizing spectra. The externalizing broadband scale comprises the delinquent behavior and aggressive behavior scales. The internalizing broadband scale comprises the withdrawn, somatic complaints, and anxious/depressed scales. In this analysis, we used the attention syndrome scale and the externalizing and internalizing broadband scales as indicators of a latent variable of behavior problems. The attention problems subscale consists of 20 items, and the externalizing and internalizing problems scales consist of 34 and 36 items, respectively. The TRF scale scores are standardized (T) scores based on age and sex distributions of normative samples. The TRF has excellent reliability and validity. The 15 day test–retest reliability of externalizing problems is 0.92 and internalizing problems, 0.91. Internal consistency of the subscales and broadband scales range from 9.63 to 0. 97. Construct and criterion validity are also supported in methodological studies (Achenbach, 1991a, 1991b).

Academic achievement in math and reading at age 17 was measured by the Woodcock–Johnson Psycho-Educational Battery–Revised (WJ-R) (Woodcock and Johnson, 1990). Reading was measured by Basic Reading and Reading Comprehension. Math was measured by Calculation and Applied Problems. These tests are used in this analysis as indicators of latent variables of achievement in the two core school subjects, reading and arithmetic. The WJ-R tests are age-standardized and have a mean of 100 and SD of 15 in the general population.

The Wechsler Intelligence Scale of Children–revised (WISC-R) (Wechsler, 1974) was used to measure children’s intelligence quotient (IQ) at age 6. The IQ test is agestandardized and has a mean of 100 and standard deviation of 15 in the general population. Mother’s IQ was measured by the Two-Subset Short Form of the WAIS-R (Silverstein, 1982).

Mothers rated the family environment as measured on the Family Environment Scale (FES) (Moos and Moos, 1981; Moos and Moos, 1994) at baseline assessment. In this study we use three scales: active/recreational, which measures the variety and amount of participation in social and recreational activities, cohesion, which measures the degree of commitment and support family members provide for one another, and conflict, which measures the amount of openly expressed anger and conflict among family members. Cohesion and conflict have been related to children’s behavior problems and active/recreational (as a measure of environmental complexity) can be expected to be related to children’s cognitive development. Each of these subscales comprises nine true–false items. Internal consistency reliabilities of the FES scales range from 0.61 to 0.78, and test–retest reliability ranges from 0.68 to 0.86 for a 2-month interval and 0.54 to 0.91 for a 4-month interval.

2.3. Analytic framework

We use multivariate models developed within latent variable modeling (LVM) (Muthen, 2002; Raykov and Marcoulides, 2006; Raykov and Marcoulides, 2008), using Mplus (Muthen and Muthen, 2008). Latent variables are not directly measurable; they can only be evaluated through their indicators. The LVM method offers important advantages over standard regression approaches. One, LVM allows us to examine complex models of relationships among multiple outcome and explanatory variables. Two, common sources of observed variability that underlie interrelated response variables are explicitly taken into account. Three, fallible explanatory variables, which would lead to unreliable parameter estimates if used in traditional regressions that assumes error-free predictors (Bollen, 1989), are included in the models as indicators of latent variables. Four, robust maximum likelihood estimation permits use of all available data, including those from subjects with incomplete data. This allows an efficient handling of missing data in the empirical setting of this longitudinal study, in addition to dealing with mild deviations from multinormality in response variables. Note that sample retention has been high and that the sample with complete data from all assessments has been found to represent closely the initial sample (Breslau et al., 2009). Five, latent variable models in a repeated measure context, as in this study, do not make restrictive assumptions of classical analysis-of-variance approaches, such as sphericity, covariance matrix homogeneity and error-free covariates (Bollen and Curran, 2006). Moreover, in this study, the models utilize information about temporal order of longitudinally measured variables, whereas in traditional regression approaches there is no temporal distinction among predictors (Fitzmaurice et al., 2008).

2.4. Models

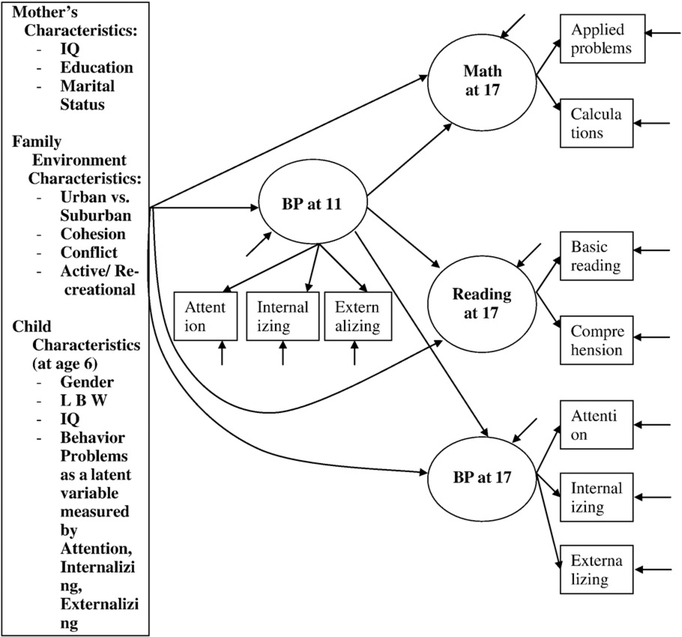
Figs. 1 and 2 display graphically the two models used in this analysis. The figures follow a path-diagram convention in LVM applications (e.g., Jöreskog and Sörbom, 1996). Observed variables are represented by squares, while latent variables are represented by circles. Long one-way lines, or curves, ending with an arrow head, symbolize assumed explanatory role played by the variables at the lines’ origin in relation to dependent variables. Two-way arrows represent correlation of the variables they connect. Short one-way arrows symbolize residual terms, such as measurement error for observed variables and disturbance terms for dependent latent variables (the combined effect of variables not included explicitly in the model). For graphic simplicity, observed covariates measured at age 6 and the latent variable behavior problems at age 6 are listed in a single vertical rectangle on the left side.

Fig. 1.

1. BP6, BP11, and BP17=behavior problems constructs at ages 6, 11 and 17, respectively. 2. Error terms of the same indicators of behavior problems constructs are correlated over time. (These are not depicted, to avoid graphical clutter).

Fig. 2.

1. BP11, BP17=behavior problems construct at ages 11 and 17, respectively. 2. Error terms of the same indicators of behavior problems constructs are correlated over time. (These are not depicted, to avoid graphical clutter). 3. Each variable listed in vertical rectangle on left assumed to affect each of the four latent variables. (Rectangle used to avoid graphical clutter by alternative multiplicity of one-way arrows and curves to denote modeled regressive relationships).

Model 1(Fig. 1) is a confirmatory factor analysis that represents the relationships of each of the five latent variables with its indicators. Model 1 can be referred to as a measurement model (Anderson and Gerbing, 1988). Model 2 (Fig. 2) uses the latent constructs of math and reading, which represent the common sources of variability in the WJ-R tests that measure their respective areas (Woodcock and Johnson, 1990). Additionally, the model uses the latent constructs of behavior problems at ages 6, 11 and 17, which represent the common sources of variability in the teacher-rated Attention, Externalizing and Internalizing scales at corresponding ages. Behavior problems constructs at ages 6 and 11 are posited as predictors for the math and reading constructs at age 17, as well as the behavior problems construct at age 17. In this model, the error terms associated with the same indicator of the behavior problems construct are assumed to be correlated over time. Such correlations are commonly used as model parameters in repeated measures analysis and reflect the residual term interrelationships of the indicator’s unique component (not explained by the common factor) that persists over repeated assessment. The model controls for the following covariates measured at age 6: (1) mother’s characteristics — IQ, education, and marital status; (2) family environment characteristics — community: urban or suburban, Cohesion, Conflict, and Active/Recreational Orientation; and (3) child characteristics — birth weight, sex, and IQ.

3. Results

3.1. Measurement model of latent variables

Model 1 (corresponding to Fig. 1) has the following fit indexes: χ²=145.333, degrees of freedom (d.f.)=54, and root mean square error of approximation (RMSEA)=0.045; 90% confidence interval 0.037, 0.054. Table 1 shows high factor loadings of the individual indicators of each latent variable. At all ages, the attention scale had the highest loading among the three indicators of the behavior problems construct. The two indicators of the math latent variable had similar size loadings, whereas reading comprehension had a higher loading than basic reading as an indicator of the reading latent variable.

Table 1.

Standardized estimates (standard errors in parentheses) for measurement model (Model 1).

Factor loadings
Behavior problem at 6
Attention	0.857	(0.025)
Internalizing	0.588	(0.022)
Externalizing	0.720	(0.022)
Behavior problem at 11
Attention	0.879	(0.023)
Internalizing	0.602	(0.025)
Externalizing	0.670	(0.027)
Behavior problem at 17
Attention	0.951	(0.023)
Internalizing	0.550	(0.041)
Externalizing	0.695	(0.038)
Math competence at 17
Problem solving	0.916	(0.013)
Calculations	0.917	(0.014)
Reading competence at 17
Comprehension	0.968	(0.011)
Basic reading	0.827	(0.015)

All coefficients are significant at p<0.001.

Table 2 presents the latent factor correlations among the latent variables. Math and reading at age 17 are highly correlated, 0.85. The negative correlations between math and reading at 17, on the one hand, and behavior problems at each age of assessment, on the other, range from −0.31 to −0.46. The correlations of the behavior problems constructs at the three ages range from 0.31 to 0.39, reflecting moderate persistence of problems over time.

Table 2.

Correlation among the latent variables (standard errors in parentheses).

Math at 17, reading at 17	0.848	(0.017)
Math at 17, behavior problem at 6	−0.486	(0.037)
Math at 17, behavior problem at 11	− 0.424	(0.035)
Math at 17, behavior problem at 17	− 0.364	(0.039)
Reading at 17, behavior problem at 6	− 0.463	(0.041)
Reading at 17, behavior problem at 11	− 0.397	(0.040)
Reading at 17, behavior problem at 17	− 0.309	(0.042)
Behavior problem at 6, behavior problem at 11	0.388	(0.043)
Behavior problem at 11, behavior problem at 17	0.316	(0.062)
Behavior problem at 6, behavior problem at 17	0.309	(0.069)

3.2. Predicting outcomes at age 17 from early behavior problems

Model 2(Fig. 2)has the following fit statistics: χ²=323.440, d.f.=134, RMSEA=0.041;90% confidence interval 0.036, 0.047.Table 3 presents the standardized regression coefficients for the explanatory relationships in Model 2. Math competence at age 17 is negatively related to behavior problems at age 11, adjusting for behavior problems at age 6 (latent regression estimate=−0.148, S.E.=0.031, Pb0.001). In addition, math is negatively related to behavior problems at age 6, adjusting for behavior problems at age 11 (latent regression estimate=−0.115, S.E.= 0.033, P=0.001). These estimates are adjusted for important predictors of academic achievement, including child’s IQ. The regression coefficients relating math at 17 to the behavior problem constructs are adjusted also for measurement error in the attention, internalizing, and externalizing measures at ages 6 and 11. The effect of the more proximate behavior problems (at age 11) is somewhat stronger than the effect of earlier behavior problems at age 6. The effect of behavior problems at ages 6 and 11 on math at age 17 is not confounded by concurrent behavior problems at age 17, because behavior problems at 17 are fully integrated in the model.

Table 3.

Predicting math and reading at age 17: Standardized regression estimates, (S.E.) and P-values.

	Beta	(S.E.)	P
Math competence at 17
Behavior problems at 6	− 0.115	(0.033)	0.001
Behavior problems at 11	− 0.148	(0.031)	<0.001
Child’s IQ	0.513	(0.033)	< 0.001
Low birth weight	− 0.029	(0.026)	0.260
Male gender	0.034	(0.026)	0.199
Active/recreational	− 0.019	(0.029)	− 0.508
Cohesion	0.034	(0.027)	0.208
Conflict	0.017	(0.028)	0.542
Urban (vs. Suburban)	− 0.104	(0.033)	0.001
Maternal IQ	0.120	(0.037)	0.001
Maternal education	0.046	(0.031)	0.129
Single mother	− 0.029	(0.028)	0.291
Reading competence at 17
Behavior problems at 6	− 0.083	(0.037)	0.027
Behavior problems at 11	− 0.109	(0.034)	0.001
Child’s IQ	0.555	(0.032)	< 0.001
Low birth weight	0.020	(0.023)	0.395
Male gender	− 0.053	(0.023)	0.021
Active/recreational	− 0.028	(0.027)	0.292
Cohesion	0.025	(0.027)	0.367
Conflict	0.006	(0.026)	0.808
Urban (vs. Suburban)	− 0.060	(0.028)	0.033
Maternal IQ	0.174	(0.033)	< 0.001
Maternal education	0.060	(0.029)	0.038
Single mother	− 0.036	(0.027)	0.185
Behavior problems at 17
Behavior problems at 6	0.198	(0.071)	0.005
Behavior problems at 11	0.191	(0.077)	0.013
Child’s IQ	− 0.025	(0.055)	0.641
Low birth weight	0.028	(0.039)	0.481
Male gender	− 0.134	(0.037)	< 0.001
Active/recreation	− 0.023	(0.046)	0.613
Cohesion	− 0.038	(0.049)	0.443
Conflict	− 0.071	(0.041)	0.080
Urban (vs. Suburban)	− 0.036	(0.052)	0.487
Maternal IQ	− 0.093	(0.052)	0.076
Maternal education	0.000	(0.060)	0.999
Single mother	0.099	(0.053)	0.061
Behavior problems at 11 (intermediate variable)
Behavior problems at 6	0.296	(0.055)	< 0.001
Child’s IQ	− 0.140	(0.049)	0.004
Low birth weight	− 0.029	(0.040)	0.457
Male gender	0.067	(0.039)	0.091
Active/recreation	0.075	(0.041)	0.066
Cohesion	− 0.097	(0.050)	0.053
Conflict	− 0.044	(0.046)	0.341
Urban (vs. Suburban)	0.112	(0.048)	0.021
Maternal IQ	0.096	(0.056)	0.084
Maternal education	− 0.080	(0.048)	0.097
Single mother	0.046	(0.049)	0.346

Math at 17 is positively related to child’s IQ (estimate=0.513, S.E.= 0.033, Pb0.001), as well as mother’s IQ (estimate=0.120, S.E.=0.037, P=0.001), and is lower among urban (vs. suburban) children (estimate=−0.104, S.E.=0.033, P=0.001), holding constant all covariates and the behavior problems constructs at ages 6 and 11. In this model, low birth weight bears no relationship to math at age 17. This is consistent with our previous findings that achievement deficits in high school associated with low birth weight were accounted for by IQ deficits measured at age 6 (Breslau et al., 2004). Comparison of the regression coefficients suggests that child IQ is by far the strongest predictor in this model. (Comparisons between standardized coefficients are used here cautiously in a descriptive rather than absolute manner (Judd et al., 2008). The reason is that standardized coefficients are affected by sampling error and possibly relevant omitted variables.)

A similar pattern of results is observed for reading at age 17. Controlling for behavior problems at age 6, behavior problems at age 11 is negatively associated with reading at age 17 (latent regression estimate=−0.109, S.E.=0.034, P=0.001). Adjusting for behavior problems at 11, behavior problems at age 6 is negatively associated with reading at age17(latent regression estimate=−0.083,S.E.=0.037, P=0.027). As in math, recent behavior problems (age 11) have a somewhat stronger effect than earlier ones on reading competence at age 17. Further, child IQ has a positive effect on reading (estimate=0.555, S.E.=0.032, Pb0.001), as do mother’s IQ (estimate=0.174, S.E.=0.033, Pb0.001) and mother’s education (estimate=0.060, S.E.=0.029, P=0.038). Urban children are at a disadvantage relative to suburban children (estimate=−0.060, S.E.=0.028, P=0.033). As is the case in math, low birth weight is unrelated to reading in this model. With respect to reading (but not math), a significant gender difference was detected (estimate=−0.053, S.E.=0.023, P=0.021), with boys being at a disadvantage relative to girls. Comparison of the standardized regression coefficientssuggeststhatchildIQisthestrongestpredictorofreading,asit is of math.

To examine the possibility that attention problems might have a unique effect on subsequent math and reading competence, apart from the behavior problems construct of which it is an indicator, we estimated a revised version of Model 2 to which we added paths from the attention scale at ages 6 and 11 to math and reading at age 17. Model fit statistics are as follows: χ² =319.539, d.f. =130, RMSEA=0.042 (90% CI, 0.036, 0.048). The analysis failed to detect evidence of unique effects of attention at ages 6 and 11, apart from what is represented by the latent construct of behavior problems on either math or reading (P-value for attention at age 6 are 0.865 and 0.906 and at age 11, 0.265 and 0.069 for math and reading, respectively). It should be noted that at all three assessments the attention scale had the highest loadings on the latent variable behavior problems, as reported above.

The results also address the continuity of behavior problems during the school years. Behavior problems at age 17 are positively related to behavior problems at age 6 (latent regression estimate=0.198, S.E.=0.071, P=0.005) and at age 11 (latent regression estimate=0.191, S.E.=0.077, P=0.013), reflecting a modest tendency for persistence from the early school years up to age 17, adjusting for other variables in the model. A sex difference in behavior problems emerged at age 17, with girls having more problems than boys (estimate=−0.134, S.E.= 0.037, Pb0.001); no significant sex difference was detected at age 11. Two significant predictors of behavior problems at age 11, as described below, have no significant direct relationship with behavior problems at age 17, child’s IQ and urban (vs. suburban) community.

Behavior problems at 11 are positively related to behavior problems at age 6 (latent regression estimate=0.296, S.E.=0.055, Pb0.001). In addition, the behavior problems construct at age 11 is negatively related to child’s IQ (estimate=−0.140, S.E.=0.049, P=0.004), controlling for behavior problems at age 6. Urban children have excess behavior problems, relative to suburban children (estimate=0.112, S.E.=0.048, P=0.021).

4. Discussion

In this longitudinal study we examined academic achievement in math and reading at age 17 in relation to behavior problems at ages 6 and 11, taking into account behavior problems at age 17. Behavior problems at ages 6 and 11, each stage independently of the other, predicted lower competence in math and reading at age 17, controlling for child IQ, maternal characteristics, family and community environment. We previously reported that behavior problems at the start of school predicted academic achievement at the end of high school, extending recent research that linked behavior problems at the start of school with achievement at the end of primary school. The previous reports did not consider the continuity of behavior problems and did not rule out the possibility that the longitudinal association (from the start of school to the time academic achievement was tested) reflected more proximate links between behavior problems and achievement. The interpretation of the longitudinal association in those studies faces an ambiguity. Do behavior problems at the start of school foreshadow later behavior problems, which in turn diminish students’ later achievement? Or do early behavior problems (even if they do not persist) exert lingering effects on achievement by impeding the acquisition of basic skills that are essential for later academic progress? This study provides evidence that the effects of behavior problems at the start of school have an independent long-run effect on high school achievement, when later behavior problems are taken into account. Further, it shows that behavior problems at the completion of primary school, at age 11, add their own influence on academic achievement, independent of behavior problems at the start of school. Behavior problems at each earlier stage exerted adverse effects on academic achievement at the conclusion of high school. Children with higher levels of behavior problems beginning at the start of school and at age 11 had lower math and reading competence at age17, compared with children whose higher behavior problems was limited to either age 6 or age 11. Academic performance at any period is determined by prior step-wise acquisition of skills (Heckman et al., 2006). Early behavior problems that impede learning basic skills would be expected to have a lingering influence on HS academic performance. The results of this study are consistent with this interpretation.

A comparison of partialled regressions show that the continuity of behavior problems decays over time. The regression estimate of behavior problem at age 11 on behavior problems at 6 is considerably larger than the estimate linking behavior problems at 17 with behavior problems at 11 (0.30 vs. 0.19). Additionally, the associations of behavior problems with IQ and key environmental variables, observed at age 11, are no longer observable at age 17. Whereas at age 11 behavior problems are negatively related to IQ and urban (vs. suburban) community, there are no such connections at age 17, when earlier behavior problems are controlled. The effects of IQ and having grown-up in the inner city on behavior problems at age 17 are indirect, through their effect at earlier ages.

In this analysis, we used latent variable modeling to estimate the longitudinal relationship of early behavior problems with academic achievement. The use of latent constructs has an important advantage particularly for the measurement of children’s behavior problems, which are based on observed indicators that have lower reliability and validity than some of the covariates (e.g. child’s IQ). By using latent variables, we were concerned with the commonality among their indicators (i.e. common sources of individual variations in the observed indicators) and thus formally forfeited the examination of the individual behavior problems scales — attention, externalizing and internalizing considered separately — pursued in the earlier studies on behavior problems and subsequent academic achievement. We found no evidence that attention problems had unique effect on math and reading, apart from the behavior problems construct. This indicates that the associations of the behavior problems constructs at ages 6 and 11 with academic achievement at age 17 capture the effects of attention problems, reported in the previous studies.

The study examines the effects of behavior problems during the early schoolyears on academic achievement at the end of high school. There is evidence supporting the importance of the pre-school period in cognitive skill formation (Cunha and Heckman, 2008). Our study does not consider the relationship between behavior problems and academic skills during the pre-school years. However, our data suggest that behavior problems during the early school years are relevant to academic skills in high school and that the early school years might be sensitive periods for the formation of these skills, even if to a lesser degree than the pre-school years.