A Stacked Sparse Autoencoder-based Detector for Automatic Identification of Neuromagnetic High Frequency Oscillations in Epilepsy

Abstract

High-frequency oscillations (HFOs) are spontaneous magnetoencephalography (MEG) patterns that have been acknowledged as a putative biomarker to identify epileptic foci. Correct detection of HFOs in the MEG signals is crucial for accurate and timely clinical evaluation. Since the visual examination of HFOs is time-consuming, error-prone and with poor inter-reviewer reliability, an automatic HFOs detector is highly desirable in clinical practice. However, existing approaches for HFOs detection may not be applicable for MEG signals with noisy background activity. Therefore, we employ the stacked sparse autoencoder (SSAE)and propose an SSAE-based MEG HFOs (SMO) detector to facilitate the clinical detection of HFOs. To the best of our knowledge, this is the first attempt to conduct HFOs detection in MEG using deep learning methods. After configuration optimization, our proposed SMO detector outperformed other classic peer models by achieving 89.9% in accuracy, 88.2% in sensitivity, and 91.6% in specificity. Furthermore, we have tested the performance consistency of our model using various validation schemes. The distribution of performance metrics demonstrate that our model can achieve steady performance.

I. INTRODUCTION

The success of epilepsy surgery depends on the accurate pre-operative localization of epileptogenic zones [1]. But, to date, there are no established marker that are able to accurately determine the location and extent of epileptogenic zones [2]. The current clinical practice to estimate the epileptogenic zones replies on a variety of diagnostic indicators. With existing methods using epileptic spikes (typically < 70 Hz), surgery is ultimately unsuccessful in controlling seizures in approximately 50% of the cases [3][4][5][6][7][8]. However, recent reports [8][9][10][11][12] show that about 80% of patients with epilepsy could be seizure free if high frequency oscillations (HFOs, typically > 70 Hz) are used to localize ictogenic zones. It has been found that [13] the interictal HFOs are useful in defining the spatial extent of the seizure onset zones. There are increasing evidences to show that HFOs is a new biomarker pinpointing to the epileptogenic zones.

The majority of previous reports on HFOs [14][9][15][16] are based on intracranial recordings, such as intracranial electroencephalography (iEEG). The detection of HFOs with intracranial recordings is limited to surgical candidates. In addition, it can be very hard to place or insert electrode into some brain areas to record HFOs safely. Furthermore,true epileptogenic areas are typically unknown before intracranial recordings or surgery [3][8][9][10][11]. Therefore, noninvasive recordings of HFOs may be helpful in most cases.

Magnetoencephalography (MEG) is a relatively new technology for noninvasive detectction of epileptic activities. Compared with conventional scalp electroencephalography (EEG), MEG has higher spatial resolution to localize epileptic activities for epilepsy surgery [17]. Previous studies [18][19][20][21] have shown that MEG can detect epileptic spikes and HFOs. Neuromagnetic HFOs are associated with epileptogenic zones [22][23]. This enables the neuromagnetic HFOs to be putative biomarkers to identify epileptic regions of the brain. Therefore, it is critical to correctly detect HFOs in MEG signals for accurate and timely clinical evaluation of epileptic patients. Current clinical practice mainly replies on the visual review of HFOs in MEG signals by human experts. However, this subjective review process is time-consuming and error prone due to the large amount of data, and inter-reviewer reliability is often inconsistent and poor [24][25].

Automatic and objective detection of HFOs in MEG with advanced machine learning method may serve as a promising computer-aided diagnosis (CAD) tool to assist human experts for the visual review of MEG signals. In fact, a number of automatic approaches [26][27][28][29] have been proposed to facilitate the HFOs detection for iEEG. Given a signal segment, the HFOs detectors for iEEG extracted handcrafted features that were manually designed based on observation or statistical analysis. For example, Burnos, et al. [27] developed handcrafted features, including high frequency peak and low frequency peak, to automatically detect HFOs in EEG signal. They optimized a threshold to recognize HFOs. Of late, another recent work [30] that focused on HFOs detection in MEG adapted the aforementioned automatic algorithm, but the threshold must be adjusted due to the high-frequency artifacts [2]. Thus, it is very challenging to directly apply existing feature extraction methods for iEEG to MEG signals due to the noisy background activity [20][21]. This circumstance hinders the identification of HFOs in MEG signals. Furthermore, these handcrafted features commonly have no theoretical evidence to guarantee an optimal performance of HFOs detection. Under such circumstances, deep learning techniques [31][32][33][34] could be helpful to recognize HFOs from complex MEG signals.

Deep learning [35] is a promising avenue towards automatic feature extraction from big data. These state-of-the-art deep learning algorithms, such as deep neural networks (NN) [32][36] and deep convolutional neural networks (CNN) [33][37], have been successfully applied to speech analysis [38], object recognition [39][40] and image classification [41]. In recent studies [42], desirable accuracy was achieved by a stacked sparse autoencoder (SSAE) on noisy audio recognition. Similarly, the SSAE has been applied on cell detection in histopathological image analysis, such as identification of prostate and breast cancer [43][44][45]. These deep learning algorithms formulate the feature extraction procedure into an optimization process of model learning, indicating that the optimized high level abstract features could be directly extracted from the raw data. In this paper, we introduce deep learning into automatic HFOs detection using MEG signals.

The objective of this study is to develop an SSAE-based MEG HFOs (SMO) detector which is able to automatically extract the abstract representations (features) from MEG data in the time domain with minimal human interference. As summarized in [2], non-invasive detection and localization of HFOs in MEG are critical for the presurgical evaluation of patients. We would like to emphasize that our current SMO detector focused on detection of HFOs in MEG signals. Our central hypothesis is that a SSAE model in our SMO detector can perform feature extraction, along with dimension reduction to detect HFOs. Our proposed method does not depend on handcrafted features, and enables us to objectively and automatically detect and localize HFOs for epilepsy surgery and many other clinical applications.

II. MATERIALS AND METHODS

A. MEG Data

MEG data were obtained from 20 clinical patients (age: 6–60 years, mean age 32; 10 female and 10 male) affected by localization related epilepsy, which is characterized by partial seizures arising from one part of the brain, and were retrospectively studied. The data were acquired under approval from an Institutional Review Board and consent was obtained from the subjects whose data were used.All patients were surgical candidates. As one part of pre-surgical evaluation, sleep deprivation and reduction of anti-epileptic drugs were used to increase the chance for capture HFOs during MEG recordings. The following additional patient inclusion criteria are used: (1) head movement during MEG recording less than 5 mm; and (2) the deflections of all MEG data within 6 pT (the MEG data were considered “clean”). These 20 patients had at least one visible lesion on structural images,underwent clinical intracranial recordings, and had epilepsy surgery.

MEG recordings were performed in a magnetically shielded room (MSR) using a 306-channel, whole-head MEG system (VectorView, Elekta Neuromag, Helsinki, Finland). The sampling rate of MEG data was set to 2,400 Hz,and approximately 60 minutes of MEG data were recorded for each patient. The noise floor in our MEG systems were calculated with MEG data acquired without subject (empty room). The noise level was about 3–5 fT/Hz. The noise floor was used to identify MEG system noise. The empty room measurements was also used to compute noise covariance matrix for localizing epileptic activities (e.g. spikes, HFOs). Before data acquisition commenced, a small coil was attached to the nasion, left and right pre-auricular points of each subject. These three coils were subsequently activated at different frequencies for measuring the subjects’ head positions relative to MEG sensors. Each subject lay comfortably in the supine position,with his or her arms resting on either side, during the entire procedure. These subjects were asked to keep still with eyes slightly closed. A head localization procedure was performed before and after each acquisition in order to locate the patient’s head relative to the coordinate system fixed to the system dewar. A three dimensional coordinate frame relative to the subject’s head was derived from these positions. The system allowed head localization to an accuracy of 1 millimeters (mm). The changes in head location before and after acquisition were required to be less than 5 mm for the study to be accepted. To identify the system and environmental noise, we routinely recorded one background MEG dataset without patients just before the experiment.

MEG data were preliminarily analyzed at a sensor level with MEG Processor [46] [47]. The conventional spike-and-wave discharges were visually identified in waveform with a band-pass filter of 1–70 Hz. HFOs were analyzed with a band-pass filter of 80–250 Hz (ripples)and a band-pass filter of 250–500Hz (fast ripples), respectively [46] [47]. These HFOs conincided with slower spikes in more than 80% of patients [23]. The HFOs was comfirmed using the HFO source analysis [12] based on intracranial recordings for these patients. We compared MEG ripples and intracranial recording ripples at source levels by comparing the MEG sources and the brain areas generating HFOs [48].

B. The SSAE-based MEG HFOs (SMO) detector

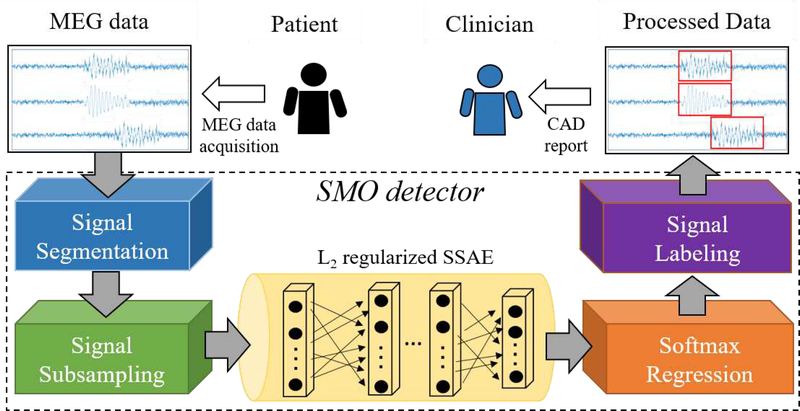
As shown in Fig 1, the proposed SMO detector is composed of three procedures: (1) signal subsampling; (2) L₂ regularized SSAE and its pre-training; (3) softmax regression and the fine tuning of SMO detector; and(4) signal labeling.

Fig. 1:

Overview of SMO detector working as a CAD tool for HFOs detection in clinical practice

1. ) Signal segmentation:

Using a moving-window technique [49], the MEG signal from multiple channels would be segmented into signal segments. Different window size and overlap could be adjusted. In the current work, we applied a 2 seconds window size without overlap to the processed MEG signal. In this way, in spite of various length of MEG recording for different subjects, the output from the signal segmentation component of SMO detector are all unified to a signal segments with 2-second length.

For the model evaluation purpose, the clinical epileptologists selected a number of HFOs and normal control (NC) signal segments based on the invasive recordings and surgical outcomes. A total of 102 signal segments (51 HFOs samples and 51 NC samples) were composed as a gold-standard dataset for model evaluation. The duration (i.e., window size) of each signal segment is 2 seconds. Namely, both HFOs and NC signal segments were represented in time domain by time series vectors with 4,800 data points.

2). Signal subsampling:

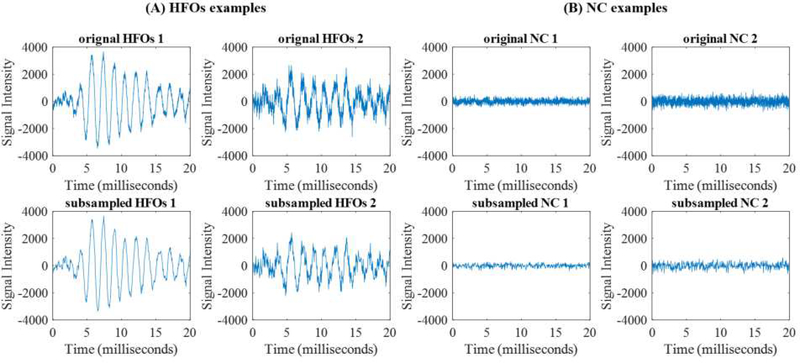
Since the sample size of our gold-standard set (a total of 102 for HFOs and NC signals) is far less than the dimension of feature (4,800), this may cause an overfitting of the machine learning model. Thus, we sought to reduce the dimension of the signal segments by a subsampling method. Fig 2 shows examples of (A) HFOs and (B) NC signals before and after subsampling. The first row is the raw data and the second row is the dimension-reduced signal. From the examples, we were able to observe that dimension-reduced segments with down sample factor 10 basically conserve the same signal patterns as the raw segments. This is essential for human experts to confirm the detected HFOs signals, since we expect that the SMO detector can work as a CAD tool to provide visualizable results.In this project, we fixed down the sample factor to be 10. It is worth noting that the down sample factor could be configured and optimized based on the sample size and the dimension of segments of the training dataset.

Fig. 2:

Examples of gold standard signals: (A) HFOs and (B) Normal signals. Original (first row) and down sample factor 10 (second row) signals for the training of our SMO detector are shown

3). L₂ regularized SSAE:

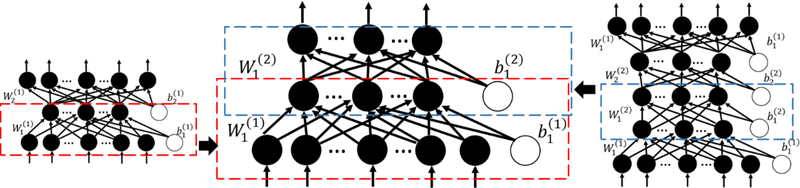
An auto-encoder (AE), the basic element of SSAE, consists of one input layer, one hidden layer and one output layer (Left part of Fig 3). Nodes between different layers of an AE are fully-connected. Multiple AEs can be stacked together to form a multi-layer neural networks. Fig 3 illustrates that two AEs (encoder parts in the boxes) are stacked into a two-layer SSAE. In terms of pre-training of the SSAE, we applied the greedy layer-wise pre-training approach [32] with the MEG signal segments. The label (HFOs or NC) information were not used, since the pre-training of SSAE is an unsupervised learning.Assume x = [x₁, x₂,..., x_n] denote an input vector of the AE,y = [y₁,y₂,...,y_n] denote the reconstructed representation vector of x,and z = [z₁, z₂,..., z_n] denote the activation vector of K hidden nodes. The AE is able to reconstruct the input features on the output layer through the intermediate hidden layer. The input x is encoded to z in layer k by encoding weights w₁ and bias b₁ by z = f(w₁x + b₁).Activation vector y in the hidden layer is then decoded the output z using the decoding weights w₂ and bias b₂. Then, the latent representation y in the hidden layer is mapped to the output z by y = f(w₂y + b₂).We implemented a L₂ regularized sparse AE, whose cost function can be modeled by:

$$E(W,b)=\frac{1}{p}{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{i=1}^n{\left(y_{ij}-x_{ij}\right)}^2}}+\lambda {\Omega }_{weights}+\beta {\Omega }_{sparsity}$$ (1)

where the first part is the mean squared error and p is the sample size of the training data. The second part of cost function is the L₂ regularization term on encoding weights,where <${\Omega }_{weights}=\frac{1}{2}{{\displaystyle {\sum }_{j=1}^p{\displaystyle {\sum }_{i=1}^n\left(w_{ji}\right)}}}^2$ and λ is the L₂ regularization penalty coefficient. The third part of the cost function is the sparsity regularization term, where β is the coefficient for the sparsity regularization term and Ω_sparsity is the Kullback-Leibler (KL) divergence [50],defined as:

$${\Omega }_{sparsity}={\displaystyle \sum _{i=1}^k\rho }\log \frac{{\rho }_j^{\prime }}{\rho }+(1-\rho )\log \frac{1-{\rho }_j^{\prime }}{1-\rho }$$ (2)

where ${\rho }_i^{\prime }=\frac{1}{p}{\displaystyle {\sum }_{j=1}^p\left[z_i\left(x_j\right)\right]}$ is the average activation of the hidden node j over the training dataset.Sparsity parameter ρ is a pre-defined small fraction constant. Using scaled conjugate gradient descent algorithm [51], weights w and bias b can be optimized for a L₂ regularized sparse AE. Then, the encoder of a sparse AE would be obtained. The output of hidden layer z of layer L-1 AE would be treated as the input x of layer L AE. At the end, as shown in Fig 3, multiple sparse AEs (encoder parts) would be stacked to form a L₂ regularized SSAE.

Fig. 3:

Stacking of a SSAE with two AEs

4. ) Softmax Regression:

We utilized a softmax regression model as a classifier in the SMO detector for distinguishing HFOs from NC signals. Softmax regression is a supervised learning multi-label classification algorithm. Assume a set with m samples is represented as(x₁,y₁),(x₂,y₂)...(x_m,y_m). In this case, the softmax regression input x_i is the output high-level features of the SSAE model. Given an input x_i, the softmax regression model is capable of estimating the probabilities p(y = j|x),j ∈ [1,...k] for a k class problem.The output of the hypothesis is a k-dimensional vector that contains k probabilities, measuring the probability of the input samples for each class label. The coefficient vector θ of the softmax regression model can be optimized by minimizing the cost function:

$$J(\theta )=-\frac{1}{m}\left[{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^{k}1}}\left\{y_i=j\right\}\log \frac{e^{{\theta }_j^T{x}_i}}{{\displaystyle {\sum }_{l=1}^k{e}^{{\theta }_l^T{x}_i}}}\right]+\frac{\lambda }{2}{\displaystyle \sum _{i=1}^k{\displaystyle \sum _{j=0}^n{\theta }_{ij}^2}}$$ (3)

In this expression, $\frac{\lambda }{2}{\displaystyle {\sum }_{i=1}^k{\displaystyle {\sum }_{j=0}^n{\theta }_{ij}^2}}$is a weight decay term, and λ is the weight decay term control parameter.

Then, we performed fine tuning of SMO detector. After training the L₂ regularized SSAE and softmax regression, we further optimized the SMO detector using a supervised learning strategy called fine tuning [32]. In this step, the pretrained SSAE and the softmax regression are stacked together to form a single model during the supervised learning process. During this process, weights from all layers of the SSAE and all parameters of the softmax regression were updated simultaneously in each iteration using scaled conjugate gradient descent algorithm [51].

5. ) Signal labeling:

Once a given signal segment was assigned to a group (either HFOs or NC), the SMO detector was designed to label the given signal segment. Using the channel and time tag, it is trivial to retrieve the source of the signal segment. Then, SMO detector would highlight those HFOs signal segments only on the MEG data. In the future application, the highlighted MEG data could be formatted as a CAD report for clinician to evaluate the subjects (Fig. 1).

C. Performance Evaluation

As mentioned in II.B. Signal segmentation, we composed a gold-standard dataset to evaluate the performance of SMO detector. The task in this work is to assign a label (HFOs or NC) for a given signal segment. We applied a repeated k-fold random subsampling validation scheme. The whole dataset would be divided into k portions. In each repeated iteration, we randomly subsampled one portion of the samples as holdout set for the test of the model, and applied the rest (k-1) portions of the samples for model training. This process would be repeated N times and the classifier can be evaluated based on the average performance.

In each repeat of the experiment, we evaluated true positive (TP), false positive (FP), true negative (TN), and false negative (FN) for the classification by comparing the predicted labels and true labels. TP is the number of HFOs samples that are classified correctly as HFOs signal, while FP is represented by the number of HFOs samples that are assigned as NC samples. Similarly, TN is the number of NC signal segments that are identified as NC signal correctly, and FN is the number of NC signal segments that are assigned as HFOs signal. The accuracy, sensitivity and specificity as the evaluation metrics were calculated by:

$$\begin{gathered} Accuracy=\frac{TP+TN}{TP+TN+FP+FN} \\ Sensitivity=\frac{TP}{TP+FN} \\ Specificity=\frac{TN}{TN+FP} \end{gathered}$$ (4)

Then, mean and standard derivation of the performance metrics would be computed over multiple repeats of the experiments.

III. EXPERIMENTAL RESULTS

A. Convergence test for the pre-training of L₂ regularized SSAE

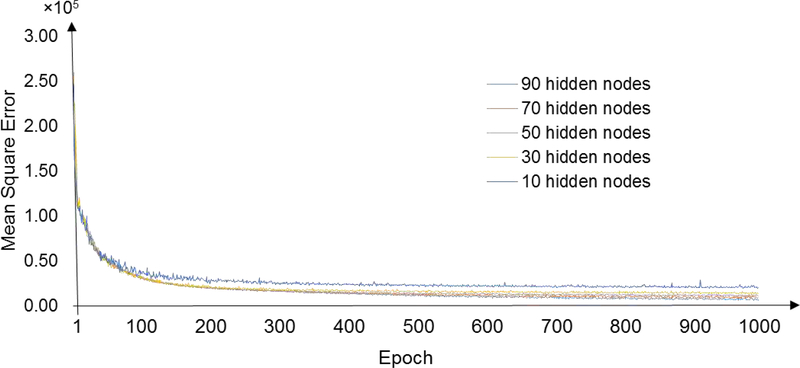
We first sought to test how many epochs the greedy layer-wise pre-training of SSAE in the SMO detector requires to guarantee the convergence of the training process. Fig 4 exemplifies the learning curves for the weights between the input layer and the first hidden layer using all gold-standard datasets. We calculated the mean square error (MSE) between input (i.e., time-series signal segments after subsampling) and reconstructed input from the AE decoder. Different empirical numbers of hidden nodes were examined in our experiments. As shown in the observations, the learning processes converged after 300 epochs across various hidden node settings. To guarantee the convergence of the training of the SSAE, we decided to apply 500 epochs as the maximal training epoch in the following HFOs detection experiments.

Fig. 4:

Learning curves for the weights between input layer and first hidden layer. Different number of hidden nodes were tested separately using all gold-standard data

B. Optimization of the architecture of SMO detector

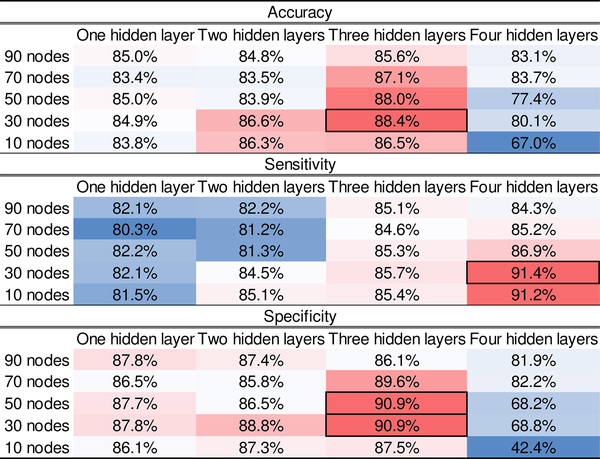
Next, we began to optimize the architecture of the SMO detector. Specifically, the number of hidden layer as well as the number of hidden nodes on each layer of the SSAE within the SMO detector had to be optimized based on a grid search. So far, there is no theoretical guide about how to select an optimal architecture of SSAE for a specific application. Thus, we selected a number of empirical values for the number of hidden nodes and layers to perform the experiments. The dimension of high level representation of data output from SSAE depended on the number of hidden nodes. Based on the sample size of the training data, we further reduced the dimension of segments. As such, we selected [90,70,50,30,10] as candidate empirical values for the number of hidden nodes. Empirical values [1,2,3,4] were tested as the number of hidden layers. The sparsity coefficients for the sparsity regularization term is set to 1 and L₂ regularized term coefficient is 0.001. For the sparsity parameter ρ, we applied a fixed value of 0.05. A 5-fold random subsampling validation strategy (i.e., gold-standard data were divided into 80% training data and 20% testing data) was applied. The performance metrics (section II-C Performance Evaluation) were calculated for all combinations of different number of hidden nodes and layers.

Fig 5 shows a heat map of the performance results. The best accuracy result (88.4%) came from the architecture of 3-hidden layer with 30 nodes on each layer. The SMO detector with the same architecture also returned a top specificity (90.9%). With respect to sensitivity, an architecture of 4-hidden layer and 30 hidden nodes provided the best result (91.4%). The architecture that offered best accuracy and specificity results achieved a decent sensitivity (85.7%). According to different criteria of the application, different architecture may be selected. Here, based on accuracy criteria, we chose the architecture (3-hidden layer/30 hidden nodes) for SSAE for the following analysis.

Fig. 5:

Performance (Accuracy, Sensitivity and Specificity) of SMO detector with various architectures. The rows are number of hidden nodes in each layer, and the columns are number of hidden layers. Best performance are marked with black boxes

C. Comparison of classification performance

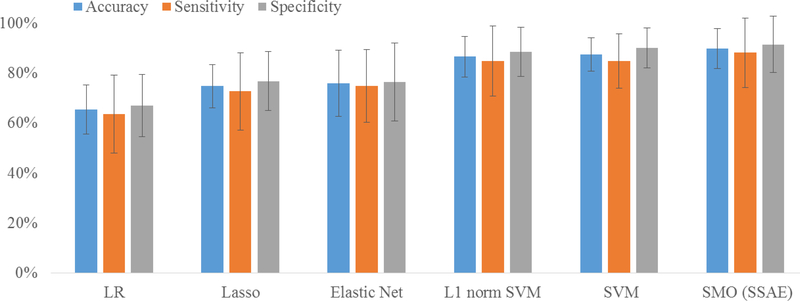
Our SMO detector was designed based on the SSAE-based classification model. Although the deep learning models have been demonstrated to outperform the classic peer models in several applications [33, 38, 42], whether the SSAE provides a superior performance compared to peer classic models for our HFOs detection application is yet to know. Using the same 5-fold random subsampling validation strategy, the SMO detector was compared with multiple advanced machine learning models, including logistic regression (LR), least absolute shrinkage and selection operator (Lasso), Elastic Net, support vector machine (SVM) as well as L₁ norm SVM. For SVM model, we deployed a 5-fold cross validation to optimize the penalty parameter with C = [2⁻¹⁰,2⁻⁹,...,2⁹,2¹⁰]. Fifty classification experiments were repeated. Fig 6 demonstrates mean and standard derivation of accuracy, sensitivity and specificity over 50 repeated experiments for three methods. In our experiments, our SMO detector achieved 89.9% in accuracy, 88.2% in sensitivity, and 91.6% in specificity. Our SMO detector slightly outperformed SVM method by 2% on accuracy, 3% on sensitivity, and 1.5% on specificity. In the test, LR model performed the worst compared to other models.

Fig. 6:

Comparison of classification performance among three methods: logistic regression (LR), support vector machine (SVM) and SMO (SSAE). Mean and standard derivation of accuracy, sensitivity and specificity over 50 repeated classification experiments are shown

D. Impact of k-fold subsampling validation on SMO detector

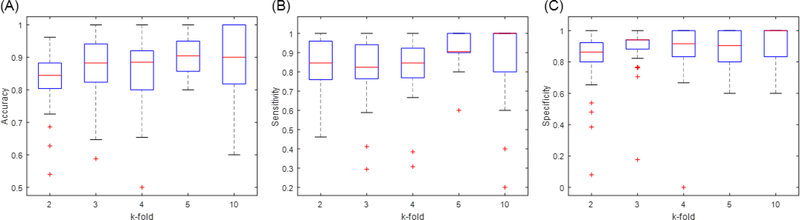
The performance consistency of our SMO detector was further tested using various k-fold random subsampling validation, since a model that is not robust may appear to perform very differently with different k. We chose the boxplot to display the distribution of the performance metrics over 50 repeated experiments. Fig 7 displays boxplots of the accuracy, sensitivity and specificity of the SMO detector over various k-fold random subsampling strategies (k=[2,3,4,5,10]). It is inspiring to see that the medium (red line) as well as the boxes mainly fall between 80% and 90%. Additionally, the boxes of all metrics were quite compact to the medium value. This indicates that the SMO detector performed consistently among various k-fold subsampling validation. However, several performance outliers were observed, especially when k was small. This is likely because the pattern or distribution of testing data were not reflected in the training data. It is common when the training data are limited. We expected that a larger gold-standard dataset may further improve the performance consistency of our SMO detector.

Fig. 7:

Boxplots of the performance metrics of the SMO detector with different repeated k-fold random subsampling validation. The box marks the first and third quartiles of data. The median value of the metrics is represented as a red band inside the box. The ends of the whiskers represent the data points within (2.7Standard derivation). The outliers are represented by ‘+’ markers

IV. DISCUSSION

To the best of our knowledge, our work is the first attempt to employ a deep learning algorithm on the automatic detection of HFOs for MEG signals. Taking advantage of superior data mining capability of deep learning on complex big data, the SMO detector demonstrated a strong ability of SSAE model on the automatic detection of HFOs in MEG signals. Our SMO detector could work as a fully automatic CAD software with minimal human interference. There is no need to select any handcrafted features for analysis or training. This is a critical characteristic of CAD for the modern clinical environments with rapid pace. Furthermore, all data analysis were performed in the time domain, which makes the identified signals compatible with human vision. Last, but not least, the deep learning model might be able to improve the performance of HFOs detection, as more HFOs segments were accumulated. Experiments have shown that deep learning models further improved the classification of complex big data when peer classic models achieved their upper limits of performance [52]. This unique benefit implicates that deep learning model might be an optimal choice for MEG data analysis.

The SSAE model employed in our SMO detector is essentially a neural network, and the convergence of the training procedure was very important. Too less training epochs of SSAE could lead to a pre-mature network easily, and desirable performance may not be achieved. As such, a convergence test is necessary to find a proper number of epochs. In our test, 500 epochs were chosen for SSAE training. This setting guaranteed the convergence of the training and avoid the unnecessary waste of time. Another important issue for neural networks is the architecture. As mentioned earlier, no universal rules are available to design the architecture of a neural network. Indeed, an optimal architecture of a neural network replies on the complexity of the data. In our case, no prior reports are available to select an optimal architecture for MEG data, and our optimization experiments could serve as the early evidence for architecture design of a SSAE for MEG data.

The results of the HFOs detection experiments were inspiring. The performance comparison experiments (Fig 5) demonstrated not only the effectiveness of our SMO detector, but also the improved ability of SSAE compared to classic peer models. We compared our SMO detector with LR and SVM under the same experiment configuration. It is noted that SVM is a popular machine learning model that often offered optimal performance in many classification applications. It is very likely that because of the high complexity of MEG signals, the SSAE outperformed SVM in our test.

While our results suggest directions to advance the performance of HFOs detection in MEG, we acknowledge that there are limitations for our SMO detector. Although the results on various k-fold validation experiments shown the performance consistency of the HFOs detector, the lower bound outliers (Fig 6) indicates that the SMO detector had undesirable classification performance in several runs of experiments. We note that our gold-standard dataset is not large enough at this stage and we expected that the consistency of the detector could be largely improved when the training data is more adequate. Moreover, we designed the down sample factor as 10 in this work for the signal down sampling component based on the sample size and dimension of segments. Without proper adjustment between sample size and dimension of segments, a SSAE mode might have an overfitting problem so as to compromise the performance. In fact, the impact of the subsampling component could be eliminated after a large gold standard dataset is accumulated.

V. CONCLUSION

In sum, we have developed a SMO detector for HFOs detection in MEG signals in this paper. A deep learning model, SSAE, was introduced for HFOs detection for the first time. After configuring key parameters such as epochs, number of hidden layers as well as number of hidden nodes, our detector achieved optimized performance compared to peer machine learning classifiers. Based on this work, there are several future directions we set to pursue. One is to extend our detector into a multi-label classifier with a function to recognize additional patterns or sub-patterns in MEG such as spike, ripple and fast-ripple. Another direction is that our HFOs detector could also be applied on EEG signal. Further comparison are required between our method and other existing approaches in EEG.