Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Oct 10;139(45):16282–16288. doi: 10.1021/jacs.7b08486

Terminal Electron–Proton Transfer Dynamics in the Quinone Reduction of Respiratory Complex I

Ana P Gamiz-Hernandez †,*, Alexander Jussupow †, Mikael P Johansson †,‡, Ville R I Kaila †,*
PMCID: PMC6300313  PMID: 29017321

Abstract

graphic file with name ja-2017-084864_0006.jpg

Complex I functions as a redox-driven proton pump in aerobic respiratory chains. By reducing quinone (Q), complex I employs the free energy released in the process to thermodynamically drive proton pumping across its membrane domain. The initial Q reduction step plays a central role in activating the proton pumping machinery. In order to probe the energetics, dynamics, and molecular mechanism for the proton-coupled electron transfer process linked to the Q reduction, we employ here multiscale quantum and classical molecular simulations. We identify that both ubiquinone (UQ) and menaquinone (MQ) can form stacking and hydrogen-bonded interactions with the conserved Q-binding-site residue His-38 and that conformational changes between these binding modes modulate the Q redox potentials and the rate of electron transfer (eT) from the terminal N2 iron–sulfur center. We further observe that, while the transient formation of semiquinone is not proton-coupled, the second eT process couples to a semiconcerted proton uptake from conserved tyrosine (Tyr-87) and histidine (His-38) residues within the active site. Our calculations indicate that both UQ and MQ have low redox potentials around −260 and −230 mV, respectively, in the Q-binding site, respectively, suggesting that release of the Q toward the membrane is coupled to an energy transduction step that could thermodynamically drive proton pumping in complex I.

1. Introduction

Respiratory complex I (NADH:ubiquinone oxidoreductase) is a redox-driven proton pump that reduces quinone (Q) by electron transfer (eT) from nicotinamide adenine dinucleotide (NADH) and couples the energy released in the process to transfer of protons (pT) across the mitochondrial or bacterial membrane,1−7 (Figure 1). The eight to nine iron–sulfur centers (ISCs) of the hydrophilic domain of complex I are responsible for catalyzing the eT reaction,8 while the proton pumping entirely takes place in the membrane domain of the enzyme.1,3−6 Remarkably, the most distant subunits responsible for the pT are separated by up to ca. 200 Å from the eT domain.9−14 This long-range coupling is believed to take place by combined conformational and electrostatic transitions, in which the terminal eT step between the N2 ISC and Q is likely to trigger the proton-pumping activity,1,3−6,8−18 but the exact molecular mechanism remains elusive.

Figure 1.

Figure 1

Open in a new tab

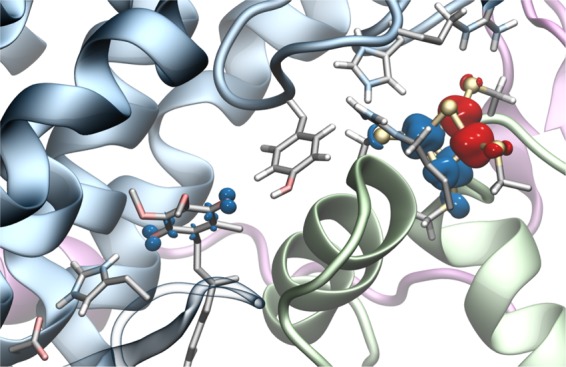
Complex I, the initial electron acceptor in aerobic respiratory chains. Electron transfer from NADH to Q via eight to nine ISCs leads to pumping of protons in the membrane domain of complex I. (inset) Q and N2 sites are located about 20 Å above the membrane plane; Q has been modeled in computationally (see the Computational Methods section).

Although the exact binding mode of Q has not been experimentally resolved in complex I, structural and biochemical studies2,9−14 show that the Q-binding site has a unique location in complex I.19 In contrast to many membrane proteins, in which the Q site is embedded within the membrane domain, the Q site in complex I is located ca. 20 Å above the membrane plane and ca. 8–11 Å from the terminal N2 ISC20 (see Figure S1 for nomenclature of ISCs in complex I), with Tyr-8721 and His-38 interacting with the Q headgroup (Figure 1).22 Although proton-coupled electron transfer (PCET) reactions of Qs in different solvents and oxidoreductases have been intensively studied over the years,23−27 a detailed understanding of the Q-reduction-linked PCET processes in complex I is still unclear. Recent electrochemical studies28 indicate that the redox potential of ubiquinone (UQ) for the Q/QH2 redox couple is unusually low, in the −300 mV range, which is considerably downshifted from the Em of Q in membranes of ca. +90 mV; electron paramagnetic resonance studies8,29 show that the Em of the terminal N2 ISC is ca. −150 mV in Escherichia coli (all Em values are relative to NHE if not otherwise stated). Moreover, experiments suggest28 that semiquinone (SQ) does not accumulate during turnover (but cf. ref (30)), further supporting that the SQ species is thermodynamically unstable and transient. Interestingly, recent experiments19 also indicate that the eT rate in complex I may be modulated by the redox state of the terminal N2 cluster, which in turn may be important for understanding the eT dynamics along the ISC chain. Importantly, elucidating the thermodynamics of the terminal eT step that is linked to the Q reduction in complex I is important for understanding how the redox energy is employed for proton pumping.

In order to address the mechanism of the Q reduction by the terminal N2 cluster and the Em of Q in complex I, we performed here first-principles quantum chemical calculations (QM), hybrid quantum mechanics/classical mechanics (QM/MM) simulations, classical molecular dynamics (MD) simulations, as well as continuum Poisson–Boltzmann (PB) electrostatics calculations on molecular models that are based on the experimentally resolved structure of complex I from Thermus thermophilus,11 for which no Q-bound structure has yet been released. Q-binding models were constructed for both UQ and menaquinone (MQ), which complex I can employ as a substrate, for example, under anaerobic conditions.31 In order to control the localization of the electron between N2 and Q, we develop here a computational approach, where we initiate the simulations from reduced or oxidized QM subsystems that are created by merging converged electronic structures from the individual donor, N2, and acceptor, Q, subsystems together. This allows us to study the energetics and dynamics of the eT process from localized diabatic electronic states of the reduced/oxidized N2 and Q. Our combined results identify important UQ- and MQ-binding configurations within the Q-binding site of complex I. We also characterize the Em of UQ/MQ in these states and show how the terminal eT from N2 is linked to coupled protonation changes of nearby residues.

2. Results and Discussion

2.1. Binding Modes of Q in the Active Site of Complex I

Our hybrid QM/MM simulations, quantum chemical density functional theory (DFT) models, as well as classical MD simulations of UQ and MQ in different oxidation states show that both species can bind in two possible conformations within the binding pocket, shown in Figure 2 for UQ and Figure S3 for MQ. In the hydrogen-bonded binding mode, UQ/MQ forms a hydrogen-bonded interaction with both His-38 and Tyr-87, while in the stacking binding mode, UQ/MQ interacts dispersively with His-38, while retaining the hydrogen bond with Tyr-87. Comparison of computed IR spectra of these conformations predict a ca. 200 cm–1 shift on the His-38 Nε-H bond, which could be employed to spectroscopically identify the two binding poses (Figure S7) by using, for example, Fourier-transform IR methodology as applied for Photosystem II.32 While UQ swaps between these two binding modes on nanosecond time scales in the oxidized state (Figure S2), MQ forms a stronger stacking interaction with His-38 in the oxidized state and favors more strongly the hydrogen-bonded interaction in the SQ state. This one-electron reduced UQ/MQ species forms an anionic semiquinone (Q•/–), without proton abstraction of the surrounding residues, consistent with previous results.17 Our QM calculations further indicate that the stacked Q conformation is favored by ca. 2 kcal mol–1 over the hydrogen-bonded binding mode and is weakly affected by the reduction of N2 (Figures 2 and S18). On the basis of the computed energetics, we expect that the hydrogen-bonded mode would have a low occupation, while structural studies might identify only the stacked conformation. In contrast to the oxidized UQ, we find that the SQ favors the hydrogen-bonded binding mode by ca. 2 kcal mol–1 (Table S1), whereas the menasemiquinone (i.e., MQ•/–) favors the hydrogen-bonded binding mode by ca. 5 kcal mol–1 due to the stronger dispersive π–π interaction between His-38 and the MQ rings in the oxidized state (Table S2). Our QM/MM calculations support these results (Figure 3), and a similar behavior is also found in our classical MD simulations (Figure S2). Structural comparison of the two binding modes for the DFT cluster models (Figure S4) shows that there is little variation between the Q and the N2 distances, but our MD simulations indicate that, in the stacked conformation, the N2–Q distance is ca. 0.5 Å shorter than in the hydrogen-bonded conformation (Figures S5 and S6), which could affect the rate of eT from N2 (see below).

Figure 2.

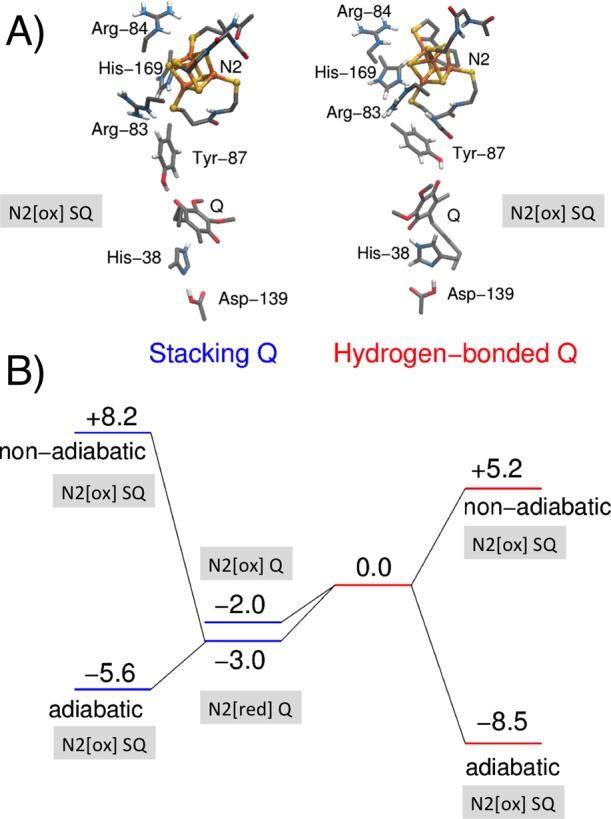
Figure 2

Open in a new tab

(A) Structure and (B) B3LYP-D3/def2-TZVPP/ε = 4 energetics (in kcal mol–1) of hydrogen-bonded (right) and stacked (left) binding modes of UQ in complex I. Q and SQ refer to oxidized quinone and semiquinone species, while N2[ox] and N2[red] refer to oxidized (2Fe[II]2Fe[III]) and reduced (3Fe[II]1Fe[III]) states of N2, respectively. Nonadiabatic and adiabatic eT energetics are calculated by relaxing the initial electron donor state (N2/Q) or by relaxing both the initial (N2[red]/Q) and final (N2[ox]/SQ) states, respectively.

Figure 3.

Figure 3

Open in a new tab

(A) pT distances between UQ and the proton donors, Y87 (r2-r1) and H38 (r4-r3), as well as between H38 and D139 (r6-r5). (B) QM/MM dynamics of eT between N2 and UQ in the stacked (in red) and hydrogen-bonded conformations (in black). The hydrogen-bonded conformation leads to formation of SQ, indicated by the higher spin population relative to the stacked conformation. The fractional spin occupation on the UQ in the stacked conformation might result from DFT charge transfer problems38 (see Figure S12). The early steps of eT indicate that, within the first 0.5 ps, the hydrogen bonds with Y87 and H38 become stronger but no pT is observed.

2.2. Energetics of eT between N2 and Q

By combining DFT (B3LYP-D3) molecular orbitals obtained from the UQ (or MQ) and N2 broken-symmetry spin-flip subsystems, we converged the electronic structure into localized diabatic electronic states of reduced/oxidized N2 and Q/SQ (MQ/MSQ). We find that the UQ reductions become thermodynamically favored by ca. −9 kcal mol–1 in the hydrogen-bonded conformation as compared to ca. −4 kcal mol–1 in the stacked conformation. This indicates that the first eT step may couple to a conformational change of the Q from the stacked to the hydrogen-bonded binding mode. The conformational change is also reflected in the rather large nonadiabatic eT energy gap of ca. 11 kcal mol–1, disfavoring formation of SQ, which is obtained without relaxing the geometry of the electron-accepting Q subsystem. In contrast, the nonadiabatic eT energy is reduced to ca. 5 kcal mol–1 in the hydrogen-bonded binding mode. This suggests that the thermodynamics of the eT between N2 and Q is nearly degenerate in the stacked conformation (Table S1). We find that the various spin-state configurations, that is, different broken-symmetry33 combinations of the unpaired electrons around the individual high-spin iron centers leading to the same total spin at the ISCs, are energetically quite different. We use the lowest energy configuration, but we note that other choices may tune the relative stability of the reduced N2 center by up to ca. 6 kcal mol–1. Interestingly, in our DFT models of the other ISCs, we do not observe such a large energy difference between different spin-state configurations, which may relate to the uniquely connected cysteine residue, Cys-45/Cys-46.2 Moreover, we observe that the relative stability of SQ is qualitatively similar using other density functionals (Table S1). For MQ, the eT from N2 to MQ is exergonic by ca. 2 kcal mol–1 and ca. 9 kcal mol–1 in the stacked and hydrogen-bonded binding modes, respectively, suggesting that Q and MQ might be redox tuned in a similar way in the Q-binding pocket (Table S2).

In order to probe the effect of the protein environment and estimate Em values, we performed classical PB continuum electrostatics calculations with Monte Carlo (MC) sampling of surrounding residues in different protonation/redox states (Figures S8 and S9). For UQ, we obtain an average Em for the Q/SQ redox couple of −260 mV with N2[ox] and −320 mV with N2[red] in the hydrogen-bonded conformation that contrast the average Em of −380 mV for the stacked Q conformation with N2[ox]. For the N2 center, we obtain an Em of −300 mV, which is considerably upshifted by ca. 200 mV from the other ISC of complex I (Figures S8 and S9). Although, somewhat downshifted from the experimental Em values of N2 (Table S1), these values are in qualitative agreement with the difference reported for Em values between N2 and other ISCs in complex I.20 The computed values are not strongly affected by applying other dielectric constants in the PB framework (Figure S10) or by the number of titrated ISCs included in the calculations (Table S4). Moreover, the values are also in qualitative agreement with electron affinities calculated based on the QM cluster models, where we find that the relative electron affinity of N2 is ca. 200 mV higher than that for a QM model of the N4 center model, giving an electron affinity of N2 in the −50 mV range, based on the employed experimental Em of N4 at ca. −250 mV (Table S1). Our calculations suggest that the negative charge of the N2 center downshifts the electron affinity of Q by ca. 400 mV, which would place the Em of Q near −300 mV, considering a reference value of +90 mV in membranes.

Similar to UQ, we obtain for MQ in its hydrogen-bonded binding mode an Em value of −230 mV (Table S5), supporting that the protein environment tunes the redox potentials of both UQ and MQ in a similar way, although MQ has a ca. 170 mV lower Em value in membranes relative to UQ.34 For the stacked MQ, we obtain a strongly downshifted Em, most likely due to the conformational switching between the two conformations upon reduction of MQ.

The Em values calculated at the PB level are thus consistent with experiments28 and the QM calculations, suggesting that the Q/SQ redox couple is less than −300 mV.28,35 Interestingly, the PB calculations suggest that reduction of N2 increases the proton affinity of a nearby His-169, consistent with site-directed mutagenesis studies by Zwicker and co-workers36 (Table S3). Our calculations thus show that the binding mode of Q, hydrogen-bonded or stacked, may modulate its redox potential, while the binding energetics itself is linked to the redox state of the N2 center. A similar stacking-induced redox-tuning effect has also been suggested for Photosystem I, where a low-potential Q stacks with a tryptophan residue.37

We next probed the energetics for the second eT between N2 and SQ, initiated by re-reduction of N2. Consistent with previous simulations,17 our DFT models suggest that the process is coupled to proton abstraction from surrounding Tyr-87 residues, whereas no complete proton abstraction from His-38 was observed, leading to the effective formation of QH–. We obtain an overall endergonicity of ca. 20 kcal mol–1 in the DFT models, which might result from the protonated His-169 that disfavors the reduction of N2. However, DFT calculations suggest that deprotonation of His-169 could stabilize this eT by ca. 5.6 kcal mol–1, which is also supported by our PB calculations. Taken together, the results suggest that reduction of N2 is linked to deprotonation of His-169 (see below and Table S3), further stabilizing the eT process.

2.3. Simulating the eT Dynamics

In order to address the eT dynamics between N2 and UQ, we performed QM/MM MD simulations, with both UQ and N2 forming the QM region and the remaining system treated classically (Figure S11). Also, for these models, the reduced donor and oxidized acceptor subsystems were generated by merging together their individual molecular orbitals to generate initial eT states with the electron on N2. The results, shown in Figure 3, indicate that the conformation of Q indeed modulates the rate of eT, consistent with the results obtained from the QM calculations and the PB calculations of Em values. In the hydrogen-bonded conformation, we observe a rapid eT between N2 and UQ (Figure 3), whereas in the stacked conformation the SQ formation is slowed down. On the basis of a Moser–Dutton treatment,39,40 by using the calculated ΔG values (−40 and +80 mV), N2–UQ edge-to-edge distance (10.5 Å), generic reorganization energy (λ = 0.7 eV), and protein-packing density (ρ = 0.76), we obtain predicted eT rates of ca 1 × 10–7 and 6 × 10–7 s–1 for the hydrogen-bonded and stacked conformations, respectively, suggesting that the eT could nevertheless be possible from both binding conformations. However, an accurate estimation of eT requires an explicit calculation of the electronic overlap, which is outside the scope of the present work.

As DFT spin energetics are known to be sensitive to the amount of exact exchange (EXX), we employed functionals with different amount of EXX in order to establish the reliability of the results. We find that the SQ is somewhat more favored when decreasing the EXX to 10% (using the TPSSh functional41), while increasing the EXX to 50% (using BHLYP) or using the range-corrected CAM-B3LYP functional42 decreases the stability of SQ (Figure S12). This indicates that the B3LYP-D3/MM calculations might somewhat overestimate the stability of SQ. However, the overall conclusions remain the same with all functionals employed, validating the robustness of the results. We do not observe any linked deprotonation of the surrounding Tyr-87 or His-38 residues, but the eT process is coupled to a spontaneous reorganization to the hydrogen-bonded conformation, further supporting the conformational reorganization of Q in the eT process. Interestingly, the eT also seems to couple to reorganization of the Arg-84 side chain near the N2 center that transiently forms a contact with the N6B center upon oxidation of the former (Figure S13).

In order to understand the role of Arg-84 and His-169 on N2 pH redox potentials,43−45 we prepared in silico H169M and R84A mutations and recomputed the Em values at different pHs (Figure S14). We estimated in our models that R84A downshifts the N2 Em value by ca. 250 mV and shows almost no pH dependence, while the H169 M mutation downshifts the Em value by 150 mV and has a pH dependence of ca. 30 mV/pH unit. His-169 has previously been suggested to function as a redox Bohr group for N2,43,44 whereas our results suggest that a combined conformational change between Arg-84 and His-169 could also be linked to N2 reduction and in part contribute to the pH dependence of the N2 center.45 The influence of other mutations43−45 could further shed light into the dynamics of the eT process and will be addressed in future work.

In order to address the dynamics of the second eT step from N2 to SQ, we re-reduced the N2 center and initiated QM/MM MD simulations. We find that, upon deprotonation of His-169 (Nε), as suggested by our PB calculations (see above), the electron moves within 0.3 ps to the SQ, which in turn, further triggers a rapid deprotonation of His-38 and Tyr-87 on the ca. 0.3–1.3 ps time scale, suggesting that the pT immediately follows the eT process (Figure 4). Interestingly, in the QM/MM trajectory, we also observe a back eT at around ca. 1.7 ps, which follows a similar but reverse PCET process, suggesting that the second eT from N2 to SQ is nearly isoenergetic; this further supports that the Em of the SQ/QH2 process is close to that of N2. We were not able to observe the second eT from N2 without deprotonation of His-169 (Figure S15), possibly due to the limited time scale of the simulations, whereas deprotonation of the Nδ proton on His-169 also resulted in a fast (>0.1 ps) eT process, coupled to a similar PCET from His-38 and Tyr-87 (Figure S16). We could not identify likely proton donors that would participate in this putative deprotonation step, but we observe that the Q-binding site is accessible to water from the bulk (Figure S17). Our QM/MM MD simulations, which treat both the eT and pT processes between the N2 and Q quantum mechanically, thus support our previous results of the Q-site dynamics, suggesting that Tyr-87 and His-38 may act as local proton donors in the QH2 formation for the second eT step (Figure 5B).17 For the first eT step, our simulations suggest that SQ formation is not linked to proton uptake (Figure 5A). Our classical MD simulations of the resulting QH2/deprotonated Tyr-87/His-38 state were further suggested to trigger conformational changes in the membrane domain Nqo8 that may in turn activate the proton pumping machinery.15

Figure 4.

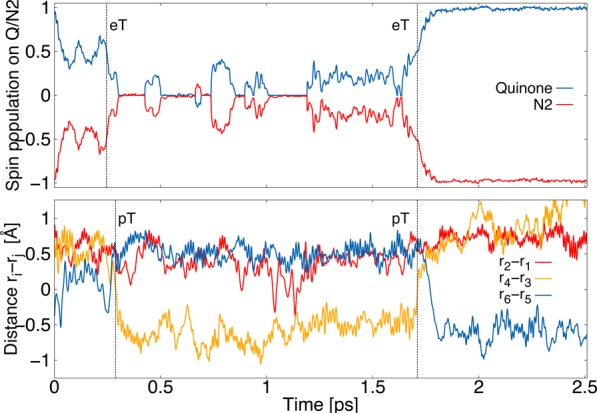
Figure 4

Open in a new tab

Dynamics of the second eT from N2 to SQ (top) upon deprotonation of His-169 and Tyr-87 (partial deprotonation at 1 ps, below). The eT process is coupled with pT from His-38 to SQ forming QH–.

Figure 5.

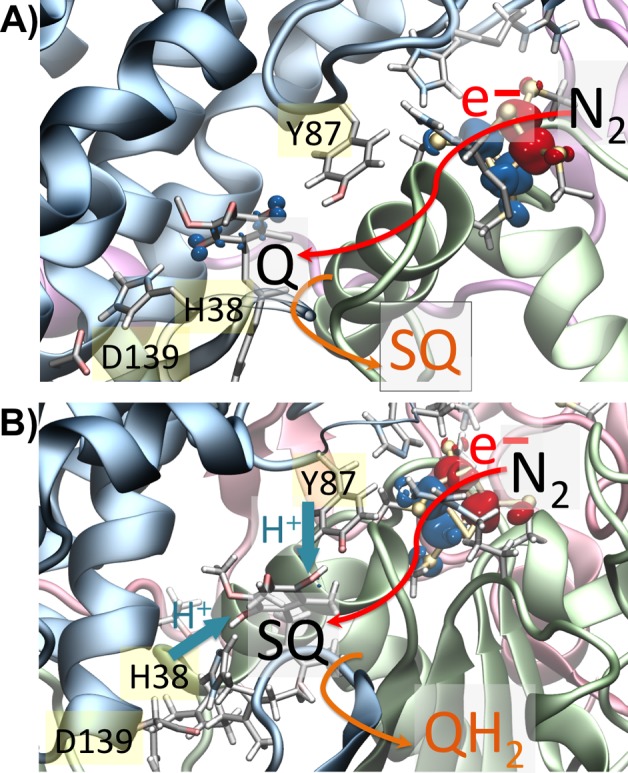
Figure 5

Open in a new tab

Sequence of eT (red arrow) and pT (blue arrow) between N2 and UQ based on QM/MM MD calculations. (A) First eT from N2 to UQ in the hydrogen-bonded conformation forming SQ. (B) Second electron moves from N2 to SQ and couples with pT from H38 and Y87, leading to formation of QH2/QH–.

3. Conclusions

Despite significant structural and biochemical work on complex I, exact structural information on the Q-binding poses in its usual binding pocket, ca. 20 Å above the membrane plane, has not been available. We have shown here by computational methods that both UQ and MQ can bind in two energetically possible binding modes to complex I: one with a hydrogen-bonded interaction with Tyr-87/His-38 of subunit Nqo4, and one where the hydrogen bond with His-38 is replaced by a stacked conformation. The latter conformation was found to be energetically favored upon N2 reduction, and the Q-binding mode was further found to tune the Em values as dispersive π–π interactions cause smaller shifts in redox potentials relative to hydrogen bonds. We obtained a redox potential of Q that is unusually low due to its interaction with N2. Our QM/MM MD simulations of the first eT steps between the reduced N2 and Q suggest that eT is linked to a conformational change of Q between stacked and hydrogen-bonded conformations that increases its electron affinity. The second eT step was further found to lead to a local PCET from Tyr-87/His-38 of subunit Nqo4 and is strongly favored by deprotonation of His-169 near the N2 center (Figure 4). Similar binding poses and Em values were also observed for MQ. Our calculations suggest that redox tuning of Q could be important for controlling the rate of the terminal eT steps in complex I, while local PCET in the Q chamber may in turn be responsible for triggering the proton pump in the membrane domain of complex I. Both eT steps between N2 and UQ were found to be nearly isoenergetic, suggesting that there might not be a large energy drop between NADH (Em = −320 mV) and UQ/MQ (Em <−300 mV). Moreover, because both Q (+90 mV) and MQ (−80 mV) have higher Em values in membranes, this further indicates that the main energy transduction event that is coupled to proton pumping could follow after Q release from its binding site near N2.

4. Computational Methods

DFT cluster and QM/MM models of complex I were built based on the X-ray structure of complex I from T. thermophilus (PDB ID: 4HEA).46 The model comprised subunits Nqo4, Nqo5, Nqo6, Nqo7, Nqo8, and Nqo9, the Q, and three ISCs N2, N6B, and N6A (Figure S11). Protonation states based on the crystal structure were assigned by PB continuum electrostatics calculations.47,48 Classical MD simulations were performed by using the whole protein and considering the UQ/MQ in oxidized (Q), SQ (i.e., Q•/–), and reduced (Q2–) states, while the ISCs were fixed in their N2[ox] state (2Fe3+ 2Fe2+) with atomic partial charges that included the inorganic iron–sulfur and four ligated cysteine residues. For the QM calculations, we also considered the N2 cluster in its N2[red] state (1Fe3+ 3Fe2+). The system was classically relaxed with NAMD2,49 for 10 ns at T = 310 K using a 1 fs integration time step with harmonic restrains on the Cα atoms and by employing the CHARMM27 force field.50 The classical MD simulations were followed by QM/MM geometry optimization and first-principles dynamics for 5 ps for each state. The QM region consisted of three models: the N2 model, the Q model, and the combined N2–Q model. The N2 model comprised the N2 center and residues Cys-45, Cys-46, Cys-111, Cys-140, Arg-86, Arg-83, and His-169. The Q model comprised the Q and residues His-38, Asp-139, Thr-135, and Tyr-87, while the combined N2–Q model comprised both subsystems (see Figure S11). The QM/MM simulations were performed at the B3LYP-D3/def2-TZVP(Fe)/def2-SVP(S, C, H, N, O) level,51−53 and the N2 center was modeled with antiferromagnetic coupling using the broken-symmetry spin-flip approach.33 QM cluster models were optimized at the dispersion corrected B3LYP-D3/def2-TZVP(Fe, S)/def2-SVP(C, H, N, O).54,55 Single point energies were computed for all atoms at B3LYP-D3 and TPSSh-D3/def2-TZVPP levels (see Table S1). The QM models comprised the Q, the N2 cluster, and residues His-38, Asp-139, Thr-135, Tyr-87, Cys-45, Cys-46, Cys-111, Cys-140, Arg-86, and Arg-83 (Figure S4); terminal carbon atoms were fixed during the optimization process. Solvation effects were treated with COSMO56 with a dielectric constant ε = 4. Calculations were performed with the CHARMM/TURBOMOLE57 interface, TURBOMOLE,58 and NWChem.59 VMD was used for visualization.60 Redox potentials were calculated based on electrostatic potentials obtained by solving numerically the linearized PB equation using APBS48,61 and MC titration sampling.47,62 The protein was described using atomic partial charges, embedded in an inhomogeneous dielectric continuum with dielectric constants of εp = 4 inside the protein and εw = 80 for the bulk water. The boundary interface between the protein and the solvent was calculated by the molecular surface routine implemented in APBS, using a solvent probe radius of 1.4 Å and modeling an implicit ionic strength of 100 mM potassium chloride. The redox potential was computed as a difference of electrostatic free energy shifts between a model compound in water and the model compound in the protein.25,62−64 To assess the influence of using a small or large model of the protein, we performed redox potential computations using the whole crystal structure and compared them with the small QM/MM models observing only a small deviation of Q/SQ and N2 Em values of ca. 40 mV (see Table S4). We also addressed the influence of the redox state of other ISCs on the Q/SQ and N2 values, suggesting that, in the current PB model, only N6B and N6A strongly influence the Q/SQ and N2 Em values (Table S4). A reference value of the UQ (MQ) Q/SQ redox couple was estimated to −188 mV (−241 mV) in water by B3LYP/def2-TZVP calculation, based on the experimental Em values of UQ and MQ in DMF and acetonitrile,25 (Table S5) by the approach of Knapp and co-workers.65−67 All our reported Em values are given relative to the NHE.

Acknowledgments

We thank Prof. Mårten Wikström for insightful discussion on complex I and Dr. Adam Kubas for technical discussions. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program/grant agreement 715311. M.P.J. is supported by the Academy of Finland (289179). The Leibniz-Rechenzentrum (LRZ), SuperMuc (project: pr48de), and CSC–The Finnish IT Center for Science provided computational resources.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.7b08486.

  • Detailed energetics, coordinates of QM and QM/MM models, and supplementary figures and tables (PDF)

  • Movie of the second eT (GIF)

The authors declare no competing financial interest.

Supplementary Material

ja7b08486_si_001.pdf (8.8MB, pdf)
ja7b08486_si_002.gif (7.6MB, gif)

References

  1. Brandt U. Annu. Rev. Biochem. 2006, 75, 69–92. 10.1146/annurev.biochem.75.103004.142539. [DOI] [PubMed] [Google Scholar]
  2. Sazanov L. A.; Hinchliffe P. Science 2006, 311, 1430–1436. 10.1126/science.1123809. [DOI] [PubMed] [Google Scholar]
  3. Verkhovskaya M.; Bloch D. A. Int. J. Biochem. Cell Biol. 2013, 45, 491–511. 10.1016/j.biocel.2012.08.024. [DOI] [PubMed] [Google Scholar]
  4. Hirst J. Annu. Rev. Biochem. 2013, 82, 551–575. 10.1146/annurev-biochem-070511-103700. [DOI] [PubMed] [Google Scholar]
  5. Sazanov L. A. Nat. Rev. Mol. Cell Biol. 2015, 16, 375–388. 10.1038/nrm3997. [DOI] [PubMed] [Google Scholar]
  6. Wikström M.; Sharma V.; Kaila V. R. I.; Hosler J. P.; Hummer G. Chem. Rev. 2015, 115, 2196–2221. 10.1021/cr500448t. [DOI] [PubMed] [Google Scholar]
  7. Hirst J.; Roessler M. M. Biochim. Biophys. Acta, Bioenerg. 2016, 1857, 872–883. 10.1016/j.bbabio.2015.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Verkhovskaya M. L.; Belevich N.; Euro L.; Wikström M.; Verkhovsky M. I. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 3763–3767. 10.1073/pnas.0711249105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Zickermann V.; Kerscher S.; Zwicker K.; Tocilescu M. A.; Radermacher M.; Brandt U. Biochim. Biophys. Acta, Bioenerg. 2009, 1787, 574–583. 10.1016/j.bbabio.2009.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hunte C.; Zickermann V.; Brandt U. Science 2010, 329, 448–451. 10.1126/science.1191046. [DOI] [PubMed] [Google Scholar]
  11. Baradaran R.; Berrisford J. M.; Minhas G. S.; Sazanov L. A. Nature 2013, 494, 443–448. 10.1038/nature11871. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Zickermann V.; Wirth C.; Nasiri H.; Siegmund K.; Schwalbe H.; Hunte C.; Brandt U. Science 2015, 347, 44–49. 10.1126/science.1259859. [DOI] [PubMed] [Google Scholar]
  13. Fiedorczuk K.; Letts J. A.; Degliesposti G.; Kaszuba K.; Skehel M.; Sazanov L. A. Nature 2016, 538, 406–410. 10.1038/nature19794. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Zhu J.; Vinothkumar K. R.; Hirst J. Nature 2016, 536, 354–358. 10.1038/nature19095. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Wikström M.; Hummer G. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 4431–4436. 10.1073/pnas.1120949109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kaila V. R. I.; Wikström M.; Hummer G. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 6988–6993. 10.1073/pnas.1319156111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Sharma V.; Belevich G.; Gamiz-Hernandez A. P.; Rog T.; Vattulainen I.; Verkhovskaya M. L.; Wikström M.; Hummer G.; Kaila V. R. I. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 11571–11576. 10.1073/pnas.1503761112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Di Luca A.; Gamiz-Hernandez A. P.; Kaila V. R. I. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E6314–E6321. 10.1073/pnas.1706278114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. de Vries S.; Dörner K.; Strampraad M. J. F.; Friedrich T. Angew. Chem., Int. Ed. 2015, 54, 2844–2848. 10.1002/anie.201410967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ohnishi T. Biochim. Biophys. Acta, Bioenerg. 1998, 1364, 186. 10.1016/S0005-2728(98)00027-9. [DOI] [PubMed] [Google Scholar]
  21. Tocilescu M. A.; Fendel U.; Zwicker K.; Dröse S.; Kerscher S.; Brandt U. Biochim. Biophys. Acta, Bioenerg. 2010, 1797, 625–632. 10.1016/j.bbabio.2010.01.029. [DOI] [PubMed] [Google Scholar]
  22. Sinha P. K.; Castro-Guerrero N.; Patki G.; Sato M.; Torres-Bacete J.; Sinha S.; Miyoshi H.; Matsuno-Yagi A.; Yagi T. Biochemistry 2015, 54, 753–764. 10.1021/bi501403t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Warren J. J.; Tronic T. A.; Mayer J. M. Chem. Rev. 2010, 110, 6961–7001. 10.1021/cr100085k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Weinberg D. R.; Gagliardi C. J.; Hull J. F.; Murphy C. F.; Kent C. A.; Westlake B. C.; Paul A.; Ess D. H.; McCafferty D. G.; Meyer T. J. Chem. Rev. 2012, 112, 4016–4093. 10.1021/cr200177j. [DOI] [PubMed] [Google Scholar]
  25. Prince R. C.; Dutton P. L.; Bruce J. M. FEBS Lett. 1983, 160, 273–276. 10.1016/0014-5793(83)80981-8. [DOI] [Google Scholar]
  26. Gunner M. R.; Madeo J.; Zhu Z. J. Bioenerg. Biomembr. 2008, 40, 509–519. 10.1007/s10863-008-9179-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Trumpower B.Function of Quinones in Energy Conserving Systems; Academic Press: New York, 1982. [Google Scholar]
  28. Verkhovskaya M.; Wikström M. Biochim. Biophys. Acta, Bioenerg. 2014, 1837, 246–250. 10.1016/j.bbabio.2013.11.001. [DOI] [PubMed] [Google Scholar]
  29. Ohnishi T. Biochim. Biophys. Acta, Bioenerg. 1998, 1364, 186–206. 10.1016/S0005-2728(98)00027-9. [DOI] [PubMed] [Google Scholar]
  30. Yano T.; Dunham W. R.; Ohnishi T. Biochemistry 2005, 44, 1744–1754. 10.1021/bi048132i. [DOI] [PubMed] [Google Scholar]
  31. Ingledew W. J.; Poole R. K. Microbiol Rev. 1984, 48, 222–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Noguchi T.; Inoue Y.; Tang X. S. Biochemistry 1999, 38, 399–403. 10.1021/bi982294v. [DOI] [PubMed] [Google Scholar]
  33. Mouesca J.-M.; Noodleman L.; Case D. A. Int. J. Quantum Chem. 1995, 56, 95–102. 10.1002/qua.560560710. [DOI] [Google Scholar]
  34. Brandt U. Annu. Rev. Biochem. 2006, 75, 69–92. 10.1146/annurev.biochem.75.103004.142539. [DOI] [PubMed] [Google Scholar]
  35. Verkhovsky M.; Bloch D. A.; Verkhovskaya M. Biochim. Biophys. Acta, Bioenerg. 2012, 1817, 1550–1556. 10.1016/j.bbabio.2012.04.013. [DOI] [PubMed] [Google Scholar]
  36. Zwicker K.; Galkin A.; Drose S.; Grgic L.; Kerscher S.; Brandt U. J. Biol. Chem. 2006, 281, 23013–7. 10.1074/jbc.M603442200. [DOI] [PubMed] [Google Scholar]
  37. Hanley J.; Deligiannakis Y.; MacMillan F.; Bottin H.; Rutherford A. W. Biochemistry 1997, 36, 11543–11549. 10.1021/bi971360a. [DOI] [PubMed] [Google Scholar]
  38. Cohen A. J.; Mori-Sánchez P.; Yang W. Science 2008, 321, 792–794. 10.1126/science.1158722. [DOI] [PubMed] [Google Scholar]
  39. Moser C. C.; Keske J. M.; Warncke K.; Farid R. S.; Dutton P. L. Nature 1992, 355, 796–802. 10.1038/355796a0. [DOI] [PubMed] [Google Scholar]
  40. Page C. C.; Moser C. C.; Chen X.; Dutton P. L. Nature 1999, 402, 47–52. 10.1038/46972. [DOI] [PubMed] [Google Scholar]
  41. Tao J.; Perdew J. P.; Staroverov V. N.; Scuseria G. E. Phys. Rev. Lett. 2003, 91, 146401. 10.1103/PhysRevLett.91.146401. [DOI] [PubMed] [Google Scholar]
  42. Yanai T.; Tew D. P.; Handy N. C. Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  43. Zwicker K.; Galkin A.; Dröse S.; Grgic L.; Kerscher S.; Brandt U. J. Biol. Chem. 2006, 281, 23013–7. 10.1074/jbc.M603442200. [DOI] [PubMed] [Google Scholar]
  44. Grgic L.; Zwicker K.; Kashani-Poor N.; Kerscher S.; Brandt U. J. Biol. Chem. 2004, 279, 21193. 10.1074/jbc.M313180200. [DOI] [PubMed] [Google Scholar]
  45. Kashani-Poor N.; Zwicker K.; Kerscher S.; Brandt U. J. Biol. Chem. 2001, 276, 24082–24087. 10.1074/jbc.M102296200. [DOI] [PubMed] [Google Scholar]
  46. Baradaran R.; Berrisford J. M.; Minhas G. S.; Sazanov L. A. Nature 2013, 494, 443–448. 10.1038/nature11871. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Kieseritzky G.; Knapp E. W. J. Comput. Chem. 2008, 29, 2575–2581. 10.1002/jcc.20999. [DOI] [PubMed] [Google Scholar]
  48. Baker N. A.; Sept D.; Joseph S.; Holst M. J.; McCammon J. A. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 10037–10041. 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kalé L.; Schulten K. J. Comput. Chem. 2005, 26, 1781–1802. 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. MacKerell A. D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Kuchnir L.; Kuczera K.; Lau F. T. K.; Mattos C.; Michnick S.; Ngo T.; Nguyen D. T.; Prodhom B.; Reiher W. E.; Roux B.; Schlenkrich M.; Smith J. C.; Stote R.; Straub J.; Watanabe M.; Wiórkiewicz-Kuczera J.; Yin D.; Karplus M. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  51. Becke A. D. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  52. Lee C. T.; Yang W. T.; Parr R. G. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  53. Schäfer A.; Horn H.; Ahlrichs R. J. Chem. Phys. 1992, 97, 2571–2577. 10.1063/1.463096. [DOI] [Google Scholar]
  54. Grimme S.; Antony J.; Ehrlich S.; Krieg H. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  55. Weigend F.; Ahlrichs R. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  56. Klamt A.; Schüürmann G. J. Chem. Soc., Perkin Trans. 2 1993, 5, 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]
  57. Riahi S.; Rowley C. N. J. Comput. Chem. 2014, 35, 2076–86. 10.1002/jcc.23716. [DOI] [PubMed] [Google Scholar]
  58. Ahlrichs R.; Bär M.; Häser M.; Horn H.; Kölmel C. Chem. Phys. Lett. 1989, 162, 165–169. 10.1016/0009-2614(89)85118-8. [DOI] [Google Scholar]
  59. Valiev M.; Bylaska E. J.; Govind N.; Kowalski K.; Straatsma T. P.; van Dam H. J. J.; Wang D.; Nieplocha J.; Apra E.; Windus T. L.; de Jong W. A. Comput. Phys. Commun. 2010, 181, 1477–1489. 10.1016/j.cpc.2010.04.018. [DOI] [Google Scholar]
  60. Humphrey W.; Dalke A.; Schulten K. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  61. Holst M.; Saied F. J. Comput. Chem. 1993, 14, 105–113. 10.1002/jcc.540140114. [DOI] [Google Scholar]
  62. Rabenstein B.; Ullmann G. M.; Knapp E. W. Eur. Biophys. J. 1998, 27, 626–637. 10.1007/s002490050174. [DOI] [Google Scholar]
  63. Ishikita H.; Knapp E. W. J. Am. Chem. Soc. 2004, 126, 8059–8064. 10.1021/ja038092q. [DOI] [PubMed] [Google Scholar]
  64. Zhu Z.; Gunner M. R. Biochemistry 2005, 44, 82–96. 10.1021/bi048348k. [DOI] [PubMed] [Google Scholar]
  65. Schmidt am Busch M.; Knapp E. W. J. Am. Chem. Soc. 2005, 127, 15730–15737. 10.1021/ja0526923. [DOI] [PubMed] [Google Scholar]
  66. Galstyan A. S.; Knapp E. W. J. Comput. Chem. 2009, 30, 203–211. 10.1002/jcc.21029. [DOI] [PubMed] [Google Scholar]
  67. Gamiz-Hernandez A. P.; Galstyan A. S.; Knapp E. W. J. Chem. Theory Comput. 2009, 5, 2898–2908. 10.1021/ct900328c. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja7b08486_si_001.pdf (8.8MB, pdf)
ja7b08486_si_002.gif (7.6MB, gif)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES