Fluctuation Analysis: Dissecting Transcriptional Kinetics with Signal Theory

Abstract

Recent live-cell microscopy techniques now allow the visualization in multiple colors of RNAs as they are transcribed on genes of interest. Following the number of nascent RNAs over time at a single locus reveals complex fluctuations originating from the underlying transcriptional kinetics. We present here a technique based on concepts from signal theory—called fluctuation analysis—to analyze and interpret multicolor transcriptional time traces and extract the temporal signatures of the underlying mechanisms. The principle is to generate, from the time traces, a set of functions called correlation functions. We explain how to compute these functions practically from a set of experimental traces and how to interpret them through different theoretical and computational means. We also present the major difficulties and pitfalls one might encounter with this technique. This approach is capable of extracting mechanistic information hidden in transcriptional fluctuations at multiple timescales and has broad applications for understanding transcriptional kinetics.

1. INTRODUCTION

Enzymatic reactions involved in the making of a mature messenger RNA (mRNA) are numerous. These include reactions to initiate transcription at the promoter, to synthesize the pre-mRNA from the DNA template, to cleave and add a poly(A) tail to the transcript once the 3^′ end of the gene is reached, and to splice the pre-mRNA into a fully mature mRNA (Craig et al., 2014). In addition to the RNA polymerase II (Pol II) and the spliceosome—the two enzymes that carry out RNA synthesis and splicing, respectively—many others act indirectly on this process, eg, by affecting the topology of DNA or depositing posttranslational marks on proteins such as histones or Pol II itself, which in turn influence the recruitment and function of other enzymes (Craig et al., 2014).

As often in enzymology, the energy-dependent nature of the reactions involved requires an out-of-equilibrium description: some of the synthesis and processing reactions are non- (or very weakly) reversible, hence maintaining a constant flux in the system turning substrates into products (Segel, 1993). In this context, certain reaction pathways can be favored simply because some reactions occur faster than others and not because the product is more energetically favorable as in an equilibrium scheme. This situation is also seen in the preinitiation steps of gene regulation and has implications for accuracy of transcriptional control (Coulon, Chow, Singer, & Larson, 2013). As a consequence, the final product of RNA synthesis and processing critically depends on the temporal coordination between the different events involved. For instance, splicing decisions are expected to be influenced by whether the pairing of splice sites occurs in a first-come-first-served basis as the transcript emerges from the elongating polymerase or happens slower than elongation, hence allowing more flexibility to pair nonadjacent splice sites (Bentley, 2014). A recurrent question in the RNA processing field is whether splicing decisions are governed by this principle of kinetic competition or if the cell has developed additional checkpoint mechanisms to ensure a predefined order between events (Bentley, 2014). Clearly, answering such questions, given the stochastic and non-equilibrium nature of these processes, requires being able to observe and dissect their dynamics at the single-molecule level.

To address this, we and others have developed tools and methods to visualize transcription and splicing in real time as it occurs in living cells (Coulon et al., 2014; Martin, Rino, Carvalho, Kirchhausen, & Carmo-Fonseca, 2013). The principle is to decorate the RNAs from a gene of interest with fluorescent proteins that are fused to an MS2 bacteriophage coat protein (MCP) that binds to MS2 RNA stem-loops present in the transcripts due to the insertion of a DNA cassette in the gene (Fig. 1A; Bertrand et al., 1998). This method allows detecting both single RNAs diffusing in the nucleoplasm as well as nascent RNAs being synthesized at the transcription site (TS) (Fig. 1B). In the latter case, one can track the TS and follow over time the fluctuations in the amount of nascent transcripts on the gene, originating from the stochastic and discrete nature of the transcription process (Fig. 1C). Combining the MS2 technique with a recent equivalent from the PP7 bacteriophage (Chao, Patskovsky, Almo, & Singer, 2007; Larson, Zenklusen, Wu, Chao, & Singer, 2011), we were able to decorate different RNAs or different regions of the same RNA with distinct fluorophores (Coulon et al., 2014; Lenstra, Coulon, Chow, & Larson, 2015).

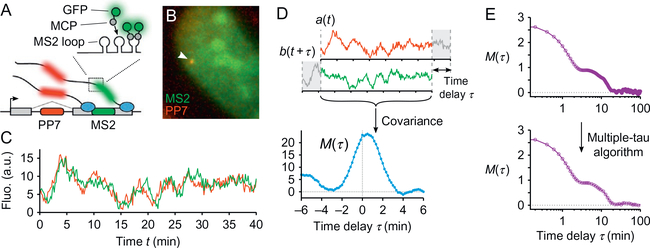
Fig. 1.

Transcriptional time traces and correlation function. (A) The MS2 and PP7 RNA-labeling technique consists in inserting, in one or two gene(s) of interest, two DNA cassettes (MS2 and PP7; here at two different locations in the same gene). They produce stem-loop structures in the nascent RNAs, which are bound by an MS2 or PP7 coat protein (MCP and PCP) fused to a fluorescent protein (eg, GFP and mCherry, respectively). (B) The transcription site (arrow) appears as a bright diffraction-limited spot in the nucleus in both fluorescence channels. (C) Recording its intensity fluctuations then yields a signal that is proportional to the number of nascent RNAs on the gene over time. (D) Using this signal as an example, the computation of a correlation function (here the covariance function) consists in shifting one signal relatively to the other and calculating the covariance between the values of the overlapping portions of the two signals as a function of the time-delay shift (Eqs. 1 and 2). (E) To analyze fluctuations at multiple timescales in a signal, computing the correlation function with the multipletau algorithm yields a somewhat uniform spacing of the time-delay points on a logarithmic scale (simulated data as in Fig. 2A). Panels (B) to (D): Data from Coulon, A., Ferguson, M. L., de Turris, V., Palangat, M., Chow, C. C., & Larson, D. R. (2014). Kinetic competition during the transcription cycle results in stochastic RNA processing. eLife, 3. http://doi.org/10.7554/eLife.03939.

Interpreting the two-color time traces resulting from the MS2/PP7 RNA-labeling technique can be nontrivial—so much so that data analysis might only focus on the rare instances in time traces where a single nascent RNA can be distinguished at the TS. An alternative approach, which we favor, consists in extracting information about the synthesis and processing kinetics of single RNAs by analyzing entire time traces using a method based on signal theory, called fluctuation analysis. This method allows an unbiased selection of all the observed transcription events, hence resulting in a high statistical power and a detailed description of the underlying kinetics (Coulon et al., 2014). In addition, it is a very general framework and can be used to interpret transcriptional fluctuations in many contexts, such as gene bursting and the kinetics of sense and antisense transcription of a single gene (Lenstra et al., 2015). In principle, it may also be applied to—or combined with—time traces from single-molecule imaging of protein recruitment at the TS (such as TFs and Pol II). By revealing the temporal relationship between specific molecular events one can now answer a wide range of questions about the mechanisms and regulation of RNA synthesis and processing.

Here, we discuss this fluctuation analysis methods, how to implement it, how to interpret its results, and the main difficulties that may arise. For reagent preparation, single-molecule 4D imaging, and time trace generation, we refer the readers to our earlier description of these methods (Ferguson & Larson, 2013).

1.1. Definitions and Terminology

Fluctuation analysis consists in computing and interpreting functions called correlation functions from a set of time traces. The term correlation function can have slightly different meanings depending on the context and the field of research. It always consist in some measure of the joint second moment between the values of a signal a(t) and the corresponding values at each time point of a signal b(t + τ) (ie, b(t) shifted by a delay τ), hence measuring the statistical correlation between fluctuations in the two signals as a function of time separation τ (Fig. 1D). Differences in the precise formulation essentially rely on how the second moment is calculated and normalized (eg, central vs raw moments, and covariance vs coefficient of variation vs Pearson correlation). In the biophysics field, the correlation between two signals is often written

$$G(\tau )=\frac{\langle \delta a(t)\delta b(t+\tau )\rangle }{\langle a(t)\rangle \langle b(t)\rangle }$$ (1)

where δa(t) = a(t) – 〈a(t)〉 and 〈·〉 denotes the temporal mean. Let us note R(τ) = 〈a(t)b(t + τ)〉 and M(τ) = 〈δa(t)δb(t + τ)〉, respectively, the raw moment and the central moment (or covariance), so that we have

$$G(\tau )=\frac{M(\tau )}{\langle a(t)\rangle \langle b(t)\rangle }=\frac{R(\tau )}{\langle a(t)\rangle \langle b(t)\rangle }-1$$ (2)

When the two signals a(t) and b(t) are the same, G(τ) and M(τ) are, respectively, called an autocorrelation and an autocovariance, and both are necessarily symmetrical by construction. When the two signals are different, G(τ) and M(τ) are, respectively, called a cross-correlation and a cross-covariance and may be asymmetrical. Note that, when one measures multicolor time traces (eg, a PP7 signal a(t) in red and an MS2 signal b(t) in green), all the pairwise correlations should be calculated (the two red and green autocorrelations and the red–green cross-correlation) since they carry complementary information about the underlying processes.

The formulation of G(τ) in Eq. (1)—akin to a squared coefficient of variation—yields a dimensionless measure that has the advantage of being insensitive to any arbitrary rescaling of either signal by an unknown multiplicative factor. This situation indeed arises frequently in microscopy data since the correspondence between fluorescence units and actual number of molecules—the fluorescence-to-RNA conversion factor—is often unknown and may change from one experiment to the next: eg, depending on the optical setup, the imaging conditions and, in the case of MS2/PP7 time traces, the expression level of coat proteins which can vary substantially between cells. Note that the Pearson correlation (ie, normalization by the product of the standard deviations rather than the means), although also dimensionless, is less informative since it is insensitive to both rescaling and offsetting the values of the signals. When the fluorescence-to-RNA conversion factor is known, the time traces can be expressed in terms of number of RNAs instead of arbitrary fluorescence units. In this case, using the covariance function M(τ) instead of G(τ) is preferable since it maximizes the information that this function reflects.

1.2. What Correlation Functions Can—and Cannot—Do

An important point to make first is that, even though a correlation function is made of many transcription events from one or several time traces (typically ~2000 transcripts in Coulon et al., 2014), the result is not an average view of the transcriptional kinetics, on the contrary. As an analogy, if X_i are Nrandom variables following a probability distribution with density P(x),then averaging together the Dirac functions δ(x – X_i) converges toward the full distribution $P(x)={\lim }_{N\to \infty }{\sum }_i\delta \left(x-X_i\right)/N$, not its average, with an accuracy that increases with N. From a theoretical point of view, this is exactly what a correlation functions reflects about the stochastic kinetics of the underlying processes (eg, X_i could be the stochastic elongation and release time of single transcripts), with the difference that the elementary functions averaged together are not Dirac functions (cf Section 3.1). In practice, full distributions are difficult to estimate accurately, but one can typically discriminate between distribution shapes (eg, Dirac, exponential, gamma), as well as the order and dependency between stochastic events (Coulon et al., 2014). These aspects are described in more details in Section 3.1.

A caveat of correlation functions to mention upfront is that it reveals the stochastic kinetics of RNAs without any distinction of whether different statistics occur in different portions of the time traces. We are currently extending the fluctuation analysis technique to circumvent this limitation and analyze transcriptional kinetics in a time-dependent manner.

Another difficulty with this approach is that correlation functions reflect all types of fluctuations in a given set of signals, including technical ones (bleaching, tracking errors, etc.) and biological ones that are not necessarily the object of the study (eg, cell cycle kinetics). Some of these aspects are specifically discussed in Sections 2.5 and 4.3.

2. COMPUTING AND AVERAGING CORRELATION FUNCTIONS

2.1. Single Correlation Functions

Calculating the numerator of Eq. (1) can be done in several ways. Let us first put aside the mean subtraction of the signals and simply discuss the calculation of R(τ) = 〈a(t)b(t + τ)〉

2.1.1. Iterative Method

The simplest method is to compute iteratively all the time-delay points. Specifically, if a₀ … a_N–1 and b₀ … b_N–1 are the values of the signals a(t) and b(t) at the N measured time points t ∈ {0, Δt, …, (N – 1)Δt}, then

$$R(i\mathrm{\Delta }t)=\frac{1}{N-i}\sum _{q=0}^{N-i-1}{a}_q{b}_{q+i}$$ (3)

An important point here is that, as signal b(t) is shifted relatively to signal a(t), one should only use the N – i pairs of time points that overlap between the two signals and discard the overhanging ends (Fig. 1D). We refer to this as overhang trimming.

2.1.2. Multiple-Tau Algorithm

If an experiment is meant to probe a broad range of timescales, one does not need the same absolute temporal resolution for fast and slow processes. For instance, if the correlation function at 20-s delay is described with 1-s resolution, it could be described at 500-s delay with 25-s resolution instead of 1-s resolution to still maintain the same relative resolution. This concept is behind the multiple-tau (or multi-tau) algorithm (Wohland, Rigler, & Vogel, 2001). It consists in down-sampling the signals (ie, reducing their temporal resolution) progressively as the correlation function is computed from small to large time delays, yielding a somewhat uniform spacing of the time-delay points of the correlation function on a logarithmic scale, ie, a somewhat constant relative resolution (Fig. 1E). In addition, reducing the resolution at long delays has the advantage of reducing the sampling noise (cf Section 4.2), which is naturally stronger for slower processes. Interestingly, this algorithm comes originally from the hardware correlators built in the 1980s and used to calculate autocorrelations in real time, while a signal is being acquired and without having to store it entirely (Schatzel, 1990).

Although we implement it differently here, this algorithm is useful in cases where a broad range of timescales need to be observed.

The principle of the multiple-tau algorithm is to choose a resampling frequency parameter m and to do the following:

1. Compute R(iΔt) as in Eq. (3) for i = 0, 1, 2, …, 2m – 1

2. When i = 2m, down-sample the signals by a factor of 2 as follows:

   • $N\leftarrow \lfloor \frac{N}{2}\rfloor$ where ⎿·⏌ denotes the integer part
   • $a_q\leftarrow \frac{a_{2q}+a_{2q+1}}{2}$ and $b_q\leftarrow \frac{b_{2q}+b_{2q+1}}{2}$ for q ∈ {0, 1, …, N – 1}
   • then Δt ⟵ 2Δt and i ⟵ m

3. Compute R(iΔt) as in Eq. (3) for i = m, …, 2m – 1 and go to step (ii). Note that, even if the length of the original signal is not a power of 2, all the time points will be used initially for the first 2m time-delay points. Only at long delays, when down-sampling occurs, one time point at the end is occasionally lost. For instance, if N = 37, it will assume the values $37\stackrel{1\text{lost}}{\to }18\to 9\stackrel{1\text{lost}}{\to }4\to 2\to 1$. This loss of a few time points is generally not a problem since significant effects only occur at the very end of the correlation function.

2.1.3. Fourier Transforms

A very fast and convenient way of computing a correlation function is to use Fourier transforms. Thanks to the Wiener–Khinchin theorem (Van Etten, 2006)

$$R(\tau )={\mathcal{F}}^{-1}[\overline{\mathcal{F}[a(t)]}\mathcal{F}[b(t)]]$$ (4)

where $\mathcal{F}[\cdot ]$ and ${\mathcal{F}}^{-1}[\cdot ]$ are the forward and inverse Fourier transforms and the bar denotes the complex conjugate. In practice, for discrete and finite signals, using the fast Fourier transform (FFT) algorithm (and its inverse form FFT^–1) translates Eq. (4) into $\frac{1}{N}{\text{FFT}}^{-1}\left(\overline{\text{FFT}\left(a_0\dots a_{N-1}\right)}\text{FFT}\left(b_0\dots b_{N-1}\right)\right)$ The FFT algorithm is very efficient and makes the computation of the correlation function orders of magnitude faster (execution time grows as N log(N), as opposed to N² for Eq. 3).

However, using Fourier transforms as such is not ideal since it wraps the nonoverlapping ends of the signals when shifting them—referred to as overhang wrapping. Indeed, FFT implicitly treat finite signals as infinite periodic signals, hence correlating not only a₀ … a_N–1–i with b_i … b_N–1 but also a_N–I … a_N–1 with b₀ … b_i–1. A way around is to extend both signals₁ by padding N zeros at their ends and to normalize the result of the FFT^–1 by |N – i| instead of N. Another advantage of this method is that, while the two halves of a cross-correlation function (at positive and negative delays) have to be computed independently if using Eq. (3), the Fourier approach provides both halves directly. More explicitly, the computation can be done as follows:

$$\begin{gathered} R(\underset{\text{positive}\text{delays}}{\underbrace{0,\mathrm{\Delta }t,\dots ,(N-1)\mathrm{\Delta }t}},\underset{\text{negative}\text{delays}}{\underbrace{-N\mathrm{\Delta }t,\dots ,-\mathrm{\Delta }t}}) \\ =\frac{{\text{FFT}}^{-1}\left(\overline{\text{FFT}(a_0,\dots ,a_{N-1},\underset{N}{\underbrace{\mathrm{0..0}}})}\text{FFT}(b_0,\dots ,b_{N-1},\underset{N}{\underbrace{\mathrm{0..0}}})\right)}{[N,N-1,N-2,\dots ,1,0,1,\dots ,N-2,N-1]} \end{gathered}$$ (5)

where products and divisions are taken term by term. Eq. (5) gives the exact same result as the iterative method of Eq. (3), but runs for instance >80 times faster on a 1000 time point signal. Down-sampling may then be performed a posterioriatdifferentdelaystomimictheresultofthemultiple-taualgorithm.

Even though computation time is generally not an issue when calculating a few tens of correlation functions on signals with hundreds of time points, the much better efficiency of this technique based on FFTs is useful when computing measurement errors on correlation functions using the bootstrap technique (Section 2.6).

2.2. Mean Subtraction of Fluorescence Traces

As developed in this section and the following one, when going from theory to practice, two important considerations arise from the application of Eq. (1) to signals of finite duration, both coming from an inaccurate estimation of the mean of the signals. As illustrated in Fig. 2 on simulated time traces, these effects become apparent when comparing the correlation function calculated on a long signal with that obtained by averaging the correlation functions calculated on a partition of the same signal. The former corresponds to an ideal case (ie, close to the theoretical situation of an infinite signal), while the latter emulates what happens in practice when we only have a set of finite—and short—time traces that are all obtained in the same experimental conditions.

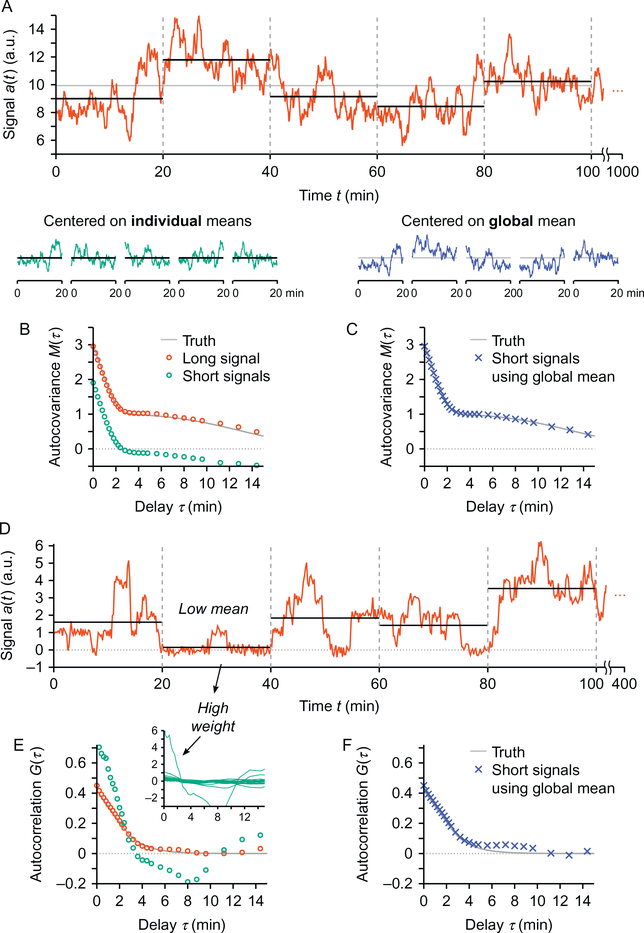
Fig. 2.

Biases due to the finiteness of time traces. (A) Shown is a portion of a signal used to illustrate the effect of inaccurate mean estimation. This 1000-min-long signal is partitioned into a set of 20-min-long signals. The true mean of the signal (ie, calculated on the long trace) is shown in gray and the inaccurate means of individual short traces are shown in black. (B) The autocovariance M(τ) of the entire signal shown in (A) is close to the expected curve (red circles vs gray curve). When averaging the autocovariances computed on each one of the 20-min-long traces, the resulting autocovariance deviates from the expected curve by a constant offset (green circles). (C) Performing the same calculation using a global estimation of the mean of the signals (ie, once over all the short signals) resolves the issue. (D) Another long signal is shown and partitioned into small sections to illustrate another artifact that may arise when averaging correlation functions G(τ). (E) The average (green circles) of the autocorrelation functions obtained on the 20-min-long sections of the signal shown in (D) deviates from the expected curve. This is due to an inaccurate weighting of the individual curves that occurs when averaging autocorrelation functions G(τ). As illustrated by the inset, the section that has a very low mean in (D) dominates the average. (F) As in (C), estimating the mean globally over all the signals solves the weighting problem. Both examples shown are simulated signals (A: Gaussian noise shaped in the Fourier domain, D: Monte Carlo simulation of transcription with Poisson initiation, distributed transcript dwell time and additive Gaussian noise). The “truth” curves in gray in (B), (C), (E), and (F) are the theoretical curves for both simulated situations.

Here, we explain why correlation functions computed on finite signals have, in many cases, an arbitrary and unknown vertical offset. It is first important to realize that, if we subtract two arbitrary constants c_a and c_b from the signals a(t) and b(t), then 〈(a(t) – c_a)(b(t + τ) – c_b)〉 equals 〈(a(t)b(t + τ)〉 up to a constant value that depends on c_a, c_b, 〈a(t)〉, and 〈b(t)〉. Hence, when computing the covariance function M(τ) = 〈δa(t)δb(t + τ)〉, an inaccurate estimation of the means of the signals would simply result in a vertical offset of the curve.

Taking finite-duration time traces of an infinite signal may imply random over- or underestimation of its mean due to sampling error, especially if some of the underlying fluctuations are at frequencies slower or in the same order as the duration of the measured time traces. In the example of Fig. 2A, the signal shows fluctuations as slow as a few tens of minutes, making the estimated mean on each 20-min-long portions (black lines) deviate from the true mean (gray line). As a result, the autocovariances of each portion are shifted toward the x-axis (loosely speaking, traces appear less variable than they should). This leads to an average autocovariance that, although having an accurate shape, is offset vertically by a constant value when compared to the autocovariance of the (virtually) infinite signal (Fig. 2B).

Fluctuations at slow temporal scales are ubiquitous in biological data (especially for in vivo transcription, eg, cell cycle, cell growth and mobility, response to cell culture passages and media changes, etc.). It is hence almost impossible to rule out this phenomenon, making experimental correlation functions always defined up to an unknown offset value. Solutions to this issue include (i) a technique to minimizes this phenomenon, presented in the next section, (ii) offsetting back the correlation funtions directly, in cases of a good separation between fast and slow timescales leading to a clearly identifiable baseline (Section 2.5), and/or (iii) performing time-lapse imaging at multiple temporal resolutions, including very slow ones, and to paste together the correlation functions from different timescales.

2.3. Averaging Methods

The second consideration resulting from the finiteness of experimental time traces is that biases may arise depending on how the average correlation functions is computed. The intuitive and classical way to calculate G(τ) from a set of traces (noted a_j(t) and b_j(t) with j ∈ [0…n – 1]) is to average together individual correlation functions

$$G(\tau )=\frac{1}{n}\sum _j{G}_j(\tau )=\frac{1}{n}\sum _j\frac{\langle \delta a_j(t)\delta b_j(t+\tau )\rangle }{\langle a_j(t)\rangle \langle b_j(t)\rangle }$$ (6)

However, as illustrated in Fig. 2D and E (in which a_j(t) = b_j(t) for simplicity), the inaccurate estimation of the mean of the signals results in an incorrect weighting of the individual correlation functions when averaging them together. Namely, traces that have, by random chance, a low mean will be artificially given a high weight because of the normalization by 〈a_j(t)〉 〈b_j(t)〉. In extreme cases, these may completely dominate the average (Fig. 2E), and even in nonextreme cases, this bias gives more importance to traces with a lower signal (eg, with fewer and/or shorter transcription events), hence influencing the result of the analysis.

A solution to both this issue and the one described in the previous section can be found if the amount of fluorescence measured per single molecule can be assumed identical between traces (ie, same experimental procedure, same imaging conditions, uniform coat protein levels between cells, uniform illumination over the field of view, etc.). In this case, rather than estimating the means of the signals individually on a trace-by-trace basis, the solution is to estimate them once globally: $\overline{a}=\frac{1}{n}\sum _j\langle a_j(t)\rangle$ and $\overline{b}=\frac{1}{n}\sum _j\langle b_j(t)\rangle$, and to use the same values on all the traces:

$$G(\tau )=\frac{1}{n\overline{a}\overline{b}}\sum _j\langle \left(a_j(t)-\overline{a}\right)\left(b_j(t+\tau )-\overline{b}\right)\rangle$$ (7)

In this case the correlation function computed from a set of short and finite time traces is much closer to what is expected for infinite signals (Fig. 2C and F). This solution, however, only works well if the fluorescence-to-RNA conversion factor is truly identical between traces (although possibly unknown). In practice, even if this factor is only expected to be roughly similar, with small trace-to-trace variations, the use of global means is also preferable (Eq. 7).

To summarize, as depicted on the decision chart of Fig. 3, the experimenter’s knowledge on the fluorescence-to-RNA conversion factor is what should guide the choice between using trace-by-trace vs global estimates of the means of the signals (Eqs. 6 and 7), and using correlation functions G(τ) vs covariance functions M(τ). In the latter case, global mean estimates should also be used:

$$M(\tau )=\frac{1}{n}\sum _j\langle \left(a_j(t)-\overline{a}\right)\left(b_j(t+\tau )-\overline{b}\right)\rangle$$ (8)

Fig. 3.

Decision chart for averaging method. To avoid introducing biases, the most appropriate method for averaging individual correlation functions depends on the experimenter’s knowledge of the fluorescence-to-RNA conversion factor, ie, the amount of fluorescence units that corresponds to a single, fully synthesized RNA.

2.4. Correct Weighting of Time-Delay Points

The above description assumes that all the traces a_j(t) and b_j(t) have the same duration. When this is not the case, correlation functions can still be averaged together, but particular care should be taken to assigning the correct weight to the different time-delay points of each correlation functions: For a given delay τ, each correlation function should be given a weight proportional to the number of pairs of time points used in its computation (this number decreases as τ becomes larger due to overhang trimming; see Section 2.1). Let us take an example where traces a₀(t) and b₀(t) have 100 time points each (at t = 0, Δt, 2Δt, …, 99Δt) and traces a₁(t) and b₁(t) have 50 time points each, and let us consider for simplicity that the multipletau algorithm (Section 2.1) is not used. In this case, G₀(τ) and G₁(τ) should have, respectively, a weight of 100 and 50 at τ = 0, a weight of 99 and 49 at τ = Δt, …, a weight of 51 and 1 at τ = 49Δt, …, a weight of 40 and 0 at τ = 60Δt, …, and a weight of 1 and 0 at τ=99Δt. This generalizes into a weight of

$$N_j-i\text{if}\text{positive}\text{and}0\text{else},\text{for}{G}_j(i\mathrm{\Delta }t)$$ (9)

where N_j denotes the number of time points of traces a_j(t) and b_j(t). This weighting applies to all three formulations of Eqs. (6)–(8) and should also be used in the computation of the global means $\overline{a}$ and $\overline{b}$. When using the multiple-tau algorithm (Section 2.1), the weight in Eq. (9) should be replaced by $\lfloor \left(N_j-i\right)/\max \left(2^{\lfloor \log 2(i/m)\rfloor },1\right)\rfloor$, where ⎿·⏌ denotes the integer part, and the values of N_j and Δt should be used before resampling.

2.5. Baseline Correction and Renormalization

Transcriptional time traces often carry many types of biological fluctuations, reflecting distinct phenomena and possibly occurring at multiple timescales (transcription initiation, RNA synthesis, gene bursting, cell cycle, etc.). Experimenters may want to focus on one or a few aspects of this kinetics and ignore or minimize the rest. To achieve this, in addition to choosing an appropriate sampling rate and time trace duration that encompass the timescales of the phenomenon of interest, one may also take advantage of potential timescale separation and scaling properties of the correlation functions.

As an example, in our earlier work (Coulon et al., 2014), we were interested in the kinetics of RNA transcription and splicing from a few seconds to a few hundreds of seconds. Slower kinetics of both biological and technical nature (such as cell cycle dynamics, gene activation/inactivation, or bleaching and imaging artifacts; see Section 4.3) were present, but with a clear timescale separation. Indeed, the correlation functions showed unambiguously a fast dynamics (up to ~4 min and with shapes fully consistent with what was expected for RNA transcription and splicing), followed by a plateau with a very slow decay (Fig. 4C). As explained in Section 2.2, the presence of such slow dynamics implies that the calculated correlation functions are defined up to an unknown vertical offset, even if the global mean estimation methods (Section 2.3) is used to minimize this artifact. In the case where a baseline is clearly visible at a certain time delay, if one only wants to focus on phenomena faster than this timescale, then the baseline may be brought to 0 by offsetting the correlation function vertically (eg, by subtracting from G(τ) its average value observed in the range |τ| ∈ [4…6 min]; Fig. 4D). This correction removes an artifactual/unwanted degree of freedom, which will turn out useful for both the computation of the standard error on the correlation functions (next section) and for fitting the data to mathematical models (Section 3.2).

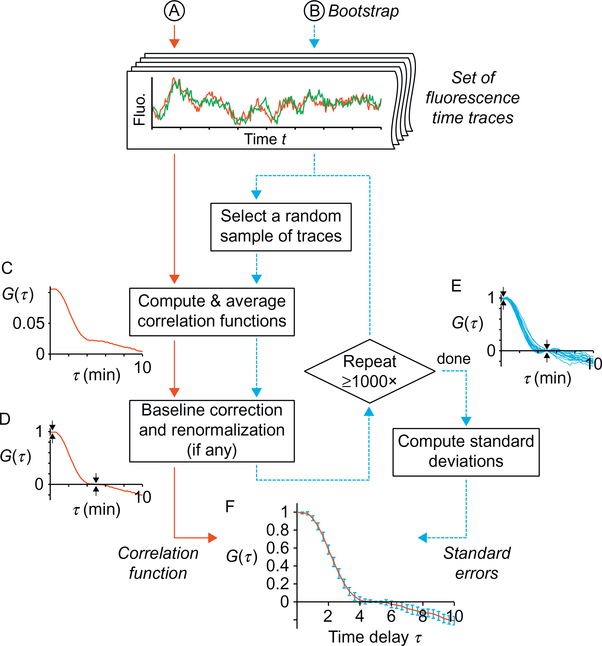
Fig. 4.

Flowchart for computing correlation functions with standard errors. (A) From a given set of time traces, one should first compute the average correlation function as appropriate (cf Fig. 3) and then perform the corrections described in Section 2.5 if needed. This yields a “corrected” correlation function. (B) To obtain the standard error by the bootstrap method, one should perform, at least 1000 times, the exact same computation as in (A), using each time a random sample of the time traces (same number of traces as the original set, and randomly drawn with replacement). This yields an estimate of the sample distribution, which standard deviation is the standard error on the correlation function calculated in (A). Intermediate results of the calculations are shown using a set of experimental time traces from Coulon et al. (2014) as an example. Shown are the average correlation function (C) before and (D) after baseline correction and renormalization, (E) multiple average correlation functions (as in D) resulting from the bootstrap loop, and (F) the average correlation function with standard errors.

When the slower dynamics decays too fast to make a clear plateau, the safest solution, although not ideal, is to include this phenomenological decay in the fit of the data (Lenstra et al., 2015). Finally, we are currently extending the fluctuation analysis technique to be able to separate source of fluctuations occurring at similar or overlapping timescales, eg, as when transcription initiation is highly nonstationary and undergoes rapid changes such as in a developing organism (Bothma et al., 2014) or during gene induction (Lenstra et al., 2015).

More anecdotal, in certain cases, another unwanted degree of freedom can be eliminated by rescaling the correlation functions: Focusing on postinitiation dynamics in our earlier study (Coulon et al., 2014), data collection/analysis was biased toward cells showing an active TS, hence making irrelevant any measure of transcription initiation rate. In addition, we realized through modeling that (i) whatever the postinitiation dynamics, varying the initiation rate simply rescales vertically all three correlation functions (autocorrelations and cross-correlation) by the same multiplicative factor, and that (ii) an important part of the correlation functions in our case was the precise shape of the cross-correlation G_cross(τ) around τ = 0. Hence, normalizing all three correlation functions by the same value G_cross(0) eliminates this extra degree of freedom (Fig. 4D). Importantly, the normalization should be performed after averaging, as to avoid introducing inappropriate weights among the different correlation functions (Fig. 4A).

2.6. Uncertainty, Error Bars, and Bootstrapping

Having a measure of uncertainty or confidence interval on a correlation function is crucial. As discussed further in Section 4.2, fallacious features or regularities may appear simply due to low sampling (ie, insufficient amount of data), hence misleading data interpretation. Calculating the uncertainty on a correlation function is however not trivial. Even though Computing 〈_a(t)b(t + τ)〉 consists in taking a temporal average, one should not use the standard deviation (or the standard error) of a(t)b(t + τ) as a measure of uncertainty. Indeed, data points from a time trace are not independent. Only time points separated by a delay longer that the slowest process involved could be considered independent. But since this slowest process is often unknown and likely longer than the measured time traces, the safest solution is to consider independent only data points from distinct traces (ie, distinct cells) as independent. Note, however, that methods have been proposed to estimate the uncertainty on the correlation function from a unique time trace (Guo et al., 2012).

In the very simple case where correlation functions are computed completely independently and then simply averaged together (ie, the method of Eq. 6) without any of the weighting described in Section 2.4 and without baseline correction or renormalization of Section 2.5, then the standard error can be computed directly as the standard deviation of the individual G_j(τ), divided by $\sqrt{n}$. But in any other case (global mean estimation, traces of different durations, baseline correction, etc.), a bootstrapping technique has to be used (Fig. 4B). If one has a pool of n time traces (possibly multicolor traces, eg, a_j(t) and b_j(t)), it consists in:

1. selecting, at random and with replacement, a sample of n time traces within this pool (hence some traces will be selected more than once and some will not be selected),

2. performing the whole computation of the correlation function from the beginning (including computation of the mean, if estimated globally) and until the end result (including weighting, baseline correction, etc.),

3. reiterating steps (i) and (ii) many times (typically ≥ 1000), and

4. computing, at each time-delay τ, the standard deviation (not the standard error) over all the correlation functions obtained in step (ii).

The standard deviation of the sampling distribution (Fig. 4E, estimated at step (iii)) is directly the standard error of the correlation function (Fig. 4F). Confidence intervals can also be computed by taking percentiles instead of standard deviations at step (iv) (eg, for a 90% confidence interval, take the 5th and the 95th percentiles).

On a technical note: In Eqs. (7) and (8), $\langle \left(a_j(t)-\overline{a}\right)\left(b_j(t+\tau )-\overline{b}\right)\rangle$ cannot be rewritten as a $\langle a_j(t)b_j(t+\tau )\rangle -\overline{a}\overline{b}$ in order to precompute 〈(a_j(t)b_j(t + τ)〉outside of the bootstrap loop; whence the advantage of a fast routine for computing correlation functions, such as the one based on FFT described in Section 2.1.

Finally, since baseline correction and normalization (if any) are included in the bootstrap loop, the correlation function will be clamped at 0 and at 1 at specific time delays, resulting in small error bars at these regions. This can be used at places where one needs to concentrate statistical power on specific features of the correlation functions, as we did in our transcription/splicing study (Coulon et al., 2014) to focus on the shape of the cross-correlation around τ = 0.

3. INTERPRETATION OF CORRELATION FUNCTIONS

A complete discussion of how to model correlation functions is clearly out of the scope of this chapter—at the very least because every experimental system and every biological question is different. Here, we give the reader an introduction to different possible options one can take to extract mechanistic information from correlation functions. We also aim at providing a basic understanding of what affects the shape of a correlation function in rather simple mathematical terms.

3.1. A Primer for Correlation Function Modeling

Transcriptional signals a(t) and b(t) can be viewed as sums of contributions ${\widehat{a}}_p(t)$ and ${\widehat{b}}_p(t)$ from $\widehat{n}$ individual RNAs occurring at times t_p

$$a(t)=\sum _p{\widehat{a}}_p\left(t-t_p\right)\text{and}b(t)=\sum _p{\widehat{b}}_p\left(t-t_p\right)$$ (10)

When transcription initiation t_p occurs at random with a constant rate k over time, it is said to follow a (homogeneous) Poisson process. In this case, the covariance function can be written simply as the mean of all the covariances of individual RNAs, multiplied by k

$$M(\tau )=k\sum _{p=0}^{\widehat{n}-1}\frac{{\widehat{M}}_p(\tau )}{\widehat{n}}$$ (11)

where ${\widehat{M}}_p(\tau )$ is the covariance function between ${\widehat{a}}_p(t)$ and ${\widehat{b}}_p(t)$. (Note that, since ${\widehat{a}}_p(t)$ and ${\widehat{b}}_p(t)$ are square integrable signals, this covariance has a slightly different formulation, ie, it uses a temporal sum ${\widehat{M}}_p(\tau )={\int }_{-\infty }^{\infty }{\widehat{a}}_p(t){\widehat{b}}_p(t+\tau )dt$ instead of a temporal average.)

This equation is central for understanding what correlation functions can reveal and is the basis for further derivations. Here, we present how Eq. (11) can be used in three different manners.

3.1.1. Understanding the Geometry of the Correlation Functions

As an illustration, let us consider the very simple example shown in Fig. 5A. Here, the fluorescence time profile of each RNA is a rectangular function of duration X_p (ie, ${\widehat{a}}_p(t)={\widehat{b}}_p(t)=1$ for t ∈ [0, X_p] and 0 elsewhere). The dwell time X_p of the RNA at the TS (which includes elongation and a potential retention at the 3^′ end of the gene) is a random variable following a probability distribution with density P(x) and a mean μ. In this case, the autocovariance of each RNA—only described for τ ≥ 0 since an autocorrelation is always symmetrical—is the triangle function ${\widehat{M}}_p(\tau )=X_p-\tau$ for τ ≤ X_p and 0 elsewhere (Fig. 5A). From Eq. (11), one can understand simple geometrical properties of the covariance function M(τ), such as that it starts at M(0) = kμ (or, if using a correlation function, G(0) = 1/kμ) with a tangent that crosses the τ-axis at τ = μ (Fig. 5B). Hence, the first few points of the correlation function already reveal two key parameters of the system: the transcription initiation rate k and the average dwell time μ of the RNA at the TS.

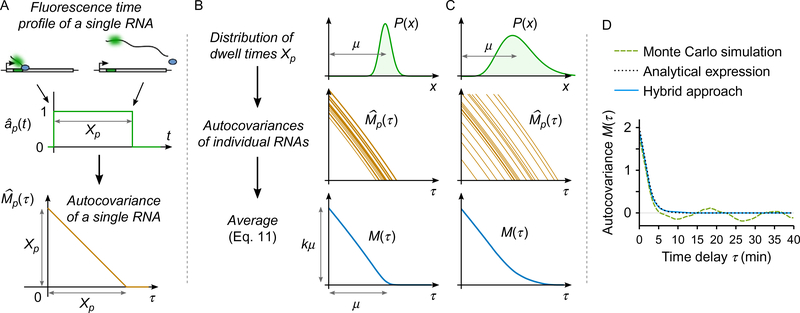
Fig. 5.

Principle of correlation function modeling. Although illustrated on a simplified single-color situation, the principle for modeling correlation functions presented here is general and holds for more complex descriptions. (A) Considering that the fluorescence time profile ${\widehat{a}}_p(t)$ recorded at the TS for a single nascent RNA is a rectangular function (rising when the MS2 cassette is transcribed and dropping when the RNA is release), then the covariance function ${\widehat{M}}_p(t)$ of this time profile is a triangle function. (B and C) When transcription initiation is considered homogeneous over time, the covariance function M(τ) can be understood as the average between individual correlation functions of single RNAs (Eq. 11). On the example of (A), if the dwell time X_p of individual RNAs is distributed, then the shape of M(τ) reveals information about initiation rate and dwell time distribution (mean, variability, etc.). (D) Several methods can be used to predict correlation functions from a given mechanistic scenario. As an alternative to a full Monte Carlo simulation approach, giving rather noisy results, and to analytical expressions, sometime difficult to derive, the hybrid approach described in Section 3.1.3 is both simple and precise. In this example, the hybrid method was performed over 100 single-RNA time profiles, and the simulation was performed over a signal that comprises 500 RNAs. The total computation time was similar in both cases. The analytical expression used is Eq. (12).

This approach does not impose a simplistic description of the fluorescence time profiles of RNAs as in the example above. For instance, using more realistic time profiles, we took a similar approach in our previous work on transcription and splicing (Coulon et al., 2014) and were able to show that a key measurement for our study (ie, the fraction of RNAs that are spliced before being released) is given by a simple geometrical feature of the correlation functions: the change of slope of the cross-correlation at τ = 0.

To develop further the example of Fig. 5, one can also show that the way M(τ) deviates from its tangent at the origin reflects the shape of the distribution P(x) of dwell times: if narrowly distributed (Fig. 5B), then M(τ) follows its tangent closely and makes a marked angle when approaching 0; if broadly distributed (Fig. 5C), this angle is smoother, making M(τ) deviate more from its tangent. This can even be generalized by realizing that, in theory, the curvature of the correlation function directly yields the full distribution $kP(\tau )=\frac{d^{2}M(\tau )}{d{\tau }^2}$. However, in practice, differentiating experimental data is problematic since it amplifies the noise, so much that only global features of the distribution can be generally extracted (eg, mean, variance, possibly skewness, etc.).

3.1.2. Analytical Expressions from Mechanistic Models

Even though a lot can be understood from the geometry of the correlation functions without making any strong assumption, it is also useful to take the opposite approach by assuming a given mechanistic model to assess if the predicted shape of the correlation functions can reproduce that of experimental data. In this context, one can derive analytical expressions of correlation functions from a given description of the underlying transcriptional kinetics. For a detailed example, the reader can refer to the supplementary derivations of Coulon et al. (2014). Briefly, we assumed different mechanistic models by describing the timing between specific events (eg, elongation through the MS2 and PP7 cassettes, removal of an intron, release of the RNA from the TS) with interdependent time distributions. We were able to express the analytical form of the correlation functions as convolutions between these distributions. As an illustration, on the simple example of Fig. 5, this approach yields

$$M(\tau )=kH(-\tau )*H(-\tau )*P(\tau )$$ (12)

defined over τ ≥ 0, where H(x) is the Heaviside function (ie, 1 if x ≥ 0 and 0 elsewhere) and where ⋆ denotes the convolution product.

This approach has several notable advantages over a simulation approach, especially for data fitting purposes: it is very fast to compute (once one has an analytical expression) and gives an exact result, hence allowing a proper parameter exploration in the fitting procedure. It also reveals which aspects of the kinetics affect the different parts of the correlation curves. However, this approach is rather mathematically cumbersome and does not offer a lot of flexibility: small modifications to the underlying mechanistic assumptions can sometime require one to rederive the equations from the beginning.

3.1.3. Hybrid Monte Carlo Approach

A much simpler alternative to the analytical method described earlier is to calculate Eq. (11) through a Monte Carlo approach. Indeed, no matter how elaborate the description of the fluorescence time profiles and the underlying mechanistic model (eg, with complicated fluorescence time profiles and intricate interdependent random variables), the correlation function M(τ) is always simply the average of individual correlation functions ${\widehat{M}}_p(\tau )$. It can hence be computed numerically from a set of individual time profiles that were randomly generated from the assumed mechanistic model. To explain this in different terms, one could perform a full Monte Carlo simulation by (i) drawing randomly all the transcription initiation times and (ii) all the fluorescence time profiles of individual RNAs, then (iii) summing them up as in Eq. (10) to obtain a simulated time trace, and finally (iv) computing its correlation function. This approach has the disadvantage of giving a rather noisy result, hence imposing to run many (or very long) simulations to reach a good converge. Instead, the hybrid method described here consist in only performing step (ii) a number of times, to compute individual correlation functions for each time profile generated, and to average them as in Eq. (11). This approach yields a much more precise estimate of the correlation function M(τ) than the full simulation approach. Fig. 5D shows a comparison between the two methods where both curves were obtained in similar amount of computation time. The precision of the result depends of course on the number of individual time profiles generated, but a few hundreds already give rather precise results (eg, the hybrid curve in Fig. 5D is generated from 100 time profiles). This hybrid approach is both easy to implement (no mathematical derivation) and very flexible (the model can be modified easily), making it an attractive alternative to the analytical approach presented earlier for fitting experimental correlation functions.

All what we just discussed in this section derives from Eq. (11), which assumes that the random transcription initiation events t_p occurs homogeneously over time. This is often not the case in reality since transcriptional activity may be time dependent, for instance if the gene of interest is induced over time, is cell cycle dependent, or switches stochastically on and off (bursting). Mathematically, taking this into account modifies Eq. (11)—we are currently working on analytical models that include these types of fluctuations. However, as explained in Section 2.5, if these fluctuations are slow compared to the timescale of single-RNA transcription, one can get rid of them and the assumption of homogeneous initiation events is then appropriate.

3.2. Data Fitting and Model Discrimination

Whether generated analytically or from the hybrid method described in the previous section, correlation functions predicted from a given mechanistic model should be compared quantitatively with experimental ones. This allows both discriminating between competing models and obtaining numerical values for the underlying physical parameters.

Since auto- and cross-correlation functions may carry information on different aspects of the transcriptional kinetics, one should predict all of them simultaneously from a given model and set of parameters, and fit them globally at once to the experimental correlation functions. Making sure to use the standard errors calculated as in Section 2.6 and to only include the relevant time-delay points (ie, up to the plateau if using baseline subtraction as in Section 2.5), one may use a regular nonlinear least square fit. It consists in minimizing

$${\chi }^2=\sum _{\tau ,G}\frac{{\left(G_{\text{exp}}(\tau )-G_{\text{theo}}(\tau )\right)}^2}{\sigma {\left[{\text{G}}_{\text{exp}}(\tau )\right]}^2}$$ (13)

where G_theo(τ) and G_exp(τ) are the theoretical and experimental correlation functions, σ[·] represents the standard error, and where the sum is taken over all relevant time-delay points and auto-/cross-correlation functions.

One important note is that a fit should always be examined visually before putting trust in the results. Especially when fitting multiple correlation functions at once (auto- and cross-correlations) with only a few parameters, one should ensure that certain features in the curves (whether real or artifactual) do not dominate the fit, hence preventing the most relevant parts from being reproduced accurately. It is hence advisable to know what part of the curves reflect what aspect(s) of the underlying processes, and to always use judgment when considering the result of a fit.

To discriminate between models, one cannot directly compare their χ² values. Indeed, if two competing models fit equally well the experimental data, the simplest one is more plausible and should be preferred. A simple way to take this into account is to find the model that minimizes the Bayesian information criterion (Konishi & Kitagawa, 2008)

$$\text{BIC}={\chi }^2+N_{\text{param}}\log N_{\text{pts}}$$ (14)

where N_param and N_pts are, respectively, the number of parameters in the model and the number of time-delay points used in the fit. Importantly, when deciding between models one should not blindly rely on the BIC. The effect of experimental perturbations should be assessed and complementary measures other than correlation functions should be used to validate or discriminate further between the retained models (see Section 4.5).

4. COMMON ISSUES AND PITFALLS

Fluctuation analysis is a powerful technique, but to apply it successfully, one needs to be aware of a number of potential difficulties and pitfalls. Section 2 focused on how to compute correlation functions properly as to avoid certain biases and artifacts. This section describes other potential issues pertaining to the design of the experimental system, the imaging conditions, and the interpretation of the resulting correlation functions.

4.1. Location of the MS2 and PP7 Cassettes

It is essential to have data analysis considerations in mind from the design stage of a project. Indeed, choices on the position and length of the MS2 and PP7 DNA cassettes to be inserted in the gene(s) of interest will crucially determine what can be concluded from the data. Poor design may make the analysis difficult and/or the interpretation ambiguous. Even though the focus of this chapter is on data analysis, a brief discussion how to design the experimental system is important here.

Design choices essentially concern the position and length of the MS2 and PP7 cassettes. These should be inserted in noncoding regions: 5^′- and 3^′-untranslated regions (UTRs) and introns. A translatable version of the PP7 cassette can also be used to place loops in open reading frames (ORFs) (Halstead et al., 2015). Every application being different, no general advice can be given and the best strategy is necessarily case specific. In this regard, it is advised to make computational predictions and/or simulations (Section 3) to understand how choices in the design will affect the ability of the approach to reflect the phenomenon of interest and/or to discriminate between competing hypotheses. From an analysis point of view, one should consider:

• signal intensity: the possibility to have a bright and easy to track TS,

• measurement sensitivity: the ability to detect subtle fluctuations coming from single RNAs, and

• temporal resolution: setting up the limit on the timescale that can be probed on the underlying processes.

The length of the cassettes, for instance, impacts the number of fluorophores per RNA molecule, hence enhancing both sensitivity and signal intensity for given imaging conditions. Another factor, the number of labeled RNAs simultaneously present at the TS may improve its brightness but will impair in return the possibility of detecting single-RNA contributions. In practice, single-RNA sensitivity is not necessary to apply fluctuation analysis, but the more one sees fluctuations due to the finite and low number of RNAs, the better the method will work. Finally, the time it takes for a single cassette to be transcribed and the time each labeled RNA dwells at the TS—both related to intensity and sensitivity—will also impact on the temporal resolution of what the data reflect.

To illustrate these points, let us give two simple examples. First, to observe the fluctuations of transcription initiation rates over time (eg, bursting, regulatory coupling between genes), placing a cassette in the 5^′ UTR will result in a strong signal (most nascent RNAs are labeled), but will mask fluctuations that are faster than the dwell time of transcripts at the TS (which comprise elongation and transcript release times). Placing the cassette in the 3^′ UTR will have the opposite effect: the signal will be weaker because only the polymerases passed the cassette in the 3^′ UTR will have a labeled RNA, but the resulting shorter dwell time will allow resolving faster fluctuations of initiation rate. However, in this latter case, any process occurring during elongation (eg, pausing, variable elongation rates) will also affect the measurement, making it more difficult to interpret. Placing the cassette in an intron toward the 5^′ end of the gene minimizes this problem while potentially keeping the advantage of a short dwell time (if the intron is spliced rapidly). In all cases, the dwell time includes unknown factors (eg, release or splicing times) that need to be taken into account for the analysis.

Another instructive example is the measure of elongation kinetics. In this case, placing the two MS2 and PP7 cassettes in both UTRs will reflect the time to elongate throughout the gene body, but without resolving the many potential pauses and variations in elongation rate along the gene. On the contrary, placing both cassettes directly around a given sequence of interest will reveal the instantaneous elongation rate and polymerase pausing kinetics over this particular sequence. Although much more revealing, this latter case is more difficult to implement. Indeed, in the former case, the long distance between the two cassettes will make the time-delay measurement rather precise, while, in the latter case, because the delay between the two signals is comparable with the time to elongate through a single cassette (ie, when the signal ramps up as the loop are being transcribed), the precision of the measurement will crucially depend the length of the cassette (ie, the steepness of the ramps). Specifically, if the cassettes are shorter, the results are more precise, hence imposing a compromise with measurement sensitivity. Also, the less the RNA dwells at the TS after passing both cassettes, the better the stochastic delay between the two cassettes can be resolved, imposing here another compromise with signal intensity.

Finally, in addition to data analysis considerations, another factor to take obviously into account is the risk of affecting endogenous processes. When choosing the location of the MS2 and PP7 cassettes, one should ensure not to disrupt functional sequences in the UTRs, introns, and ORFs (Bentley, 2014; Porrua & Libri, 2015). Length of the cassettes has also been observed to affect whether the modified RNAs behave like the endogenous ones (decay, nuclear export, aggregation, etc.). We have not yet reached a consensus for good practice since it seems context dependent. It is hence advised to perform single-molecule RNA FISH (see Section 4.5) to compare the statistics of endogenous and modified RNAs (levels, localization, number at TS, etc.) and ensure that both behave similarly.

4.2. Interpreting Single (or Too Few) Traces

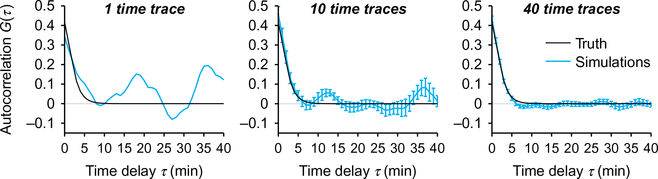
When gathering experimental data to be analyzed through fluctuation analysis, it is often tempting to interpret the data and draw conclusions based on an insufficient amount of data. Typically, one should not interpret the correlation function of a single time trace. Indeed, sampling noise—ie, the finitesize effects coming from the low number of stochastic events in a time trace (even if in the hundreds)—leads to features in the correlation function that only reflect the randomness of these events (Fig. 6). Because sampling noise produces smooth shapes in a correlation function, it does not look like what we are used to call “noise” and often produce oscillations or “bumps” in the correlation curves that only result from a lack of data. For instance, a single correlation function may show a bump at a certain time delay, not because there is a regularity at this timescale in the underlying biological process, but simply because, by random chance, there happens to be one in this particular trace (Fig. 6). Redoing the analysis on a different time trace obtained on the same experimental system may or may not show this feature. Only if this feature is present in multiple traces and is still present when averaging a number of correlation functions can it be considered a regularity (Fig. 6). To ensure that an averaged correlation function is sufficiently converged and that a given feature is statistically significant, the best way is to compute error bars (standard errors or confidence intervals; Section 2.6). Remember that nonoverlapping standard errors do not necessarily imply high significance, and that a standard error is only expected to overlap with the true, fully converged value in <80% of the cases.

Fig. 6.

Convergence when averaging correlation function. Single correlation functions are often misleading since their shape can show features that may look like regularities but are only due to the lack of data. Averaging multiple correlation functions together reduces this noise and allows one to calculate error bars. The more correlation functions are averaged together the more these spurious features disappear, leaving only the true regularities. The examples shown are simulated traces that are 100 data points eac

4.3. Technical Sources of Fluctuations

Correlation functions reflect all types of fluctuations in the observed signals. On the positive side, this has the advantage of revealing multiple biological processes at once. On the other hand, any technical source of fluctuation will also show up in a correlation function. We present here the most common types for MS2/PP7 transcriptional time traces, how to identify them and, when possible, how to correct for them:

• Bleaching: Inherent to any fluorescence microscopy experiment is the bleaching of fluorophores over time. The result is that the fluorescence intensity of the whole nucleus—and, with it, of the TS—will decay throughout an experiment. If not corrected, bleaching results essentially in an artifactual slow decay (typically exponential) in the correlation functions. It is important here to understand that, in microscopy setups where the whole nuclear volume is illuminated (eg, in widefield microscopy and to some extant in confocal microscopy when acquiring a z-stack), all the fluorophores will bleach equally fast in a nucleus regardless of being bound or not to an RNA. Hence, the relative fluorescence lost by every single RNA is statistically the same as for the whole nucleus. From this observation, it is possible to correct time traces for bleaching prior to any computation. In practice, this requires the total integrated fluorescence of the nucleus to be much higher than that of the TS—typically doable in mammalian cells (Coulon et al., 2014), but not in yeast cells (Lenstra et al., 2015). To perform this correction, sometime referred to as detrending, one needs to: (i) isolate the image of the whole nucleus (cropping the time-lapse movie around the nucleus may be sufficient as long as no other nuclei are in the resulting picture, otherwise a masking procedure of the outside of the nucleus can be used); (ii) compute the standard deviation of the pixel fluorescence intensities for each image separately, throughout the course of the time-lapse movie; (iii) ensure that the resulting time course is smooth as to avoid adding extra unwanted fluctuations; and (iv) divide the transcriptional time trace by this time course. The rational behind using the standard deviation is that the mean of a microscopy imaging often includes factors such as the autofluorescence of the media (which has its own bleaching kinetics), the digital offset of the camera/detector, etc., all of which have a negligible spatial standard deviation. Hence the mean of the pixel fluorescence intensities will be affected by these extra factors, while the standard deviation will not.

Acceptable levels of bleaching to be corrected using this technique can be empirically up to a 50–60% attenuation between the first and last frames of a time-lapse movie. More would lead to a strong difference in signal-to-noise ratio between the beginning and the end of the time traces, which may become problematic.

• Nonhomogeneous illumination of the field: Often in microscopy setups, illumination is not uniform and tends to be stronger in the center of the field of view and dimmer toward the edges. Hence, not only bleaching rate will be different for different cells, but more importantly, if a cell moves within the field and gets closer and further from the center, this will result in global fluctuations of the observed nuclear intensity and TS intensity that are not due to the transcriptional activity. As long as the spatial inhomogeneities in illumination are larger than a cell nucleus, the detrending procedure described earlier solves this problem by correcting for fluctuations in total nuclear brightness.

• Measurement noise: Many factors contribute to inexact measurements of TS fluorescence intensity. This includes Poisson noise of photon collection, current noise in the detectors, numerical inaccuracies in the fitting of the TS, etc. All of these have essentially white noise statistics, ie, the error made at a given time point is statistically independent form the error made at all the other time points. The advantage of white noise is that it will show up only in autocorrelation functions (not cross-correlations) and only at the time-delay point τ = 0. All the rest of the correlation functions are unaffected. This noise cannot be corrected without destroying additional information in the signal. Hence the simplest way to deal with it is to discard the first point (τ = 0) of any autocorrelation function, knowing that it is inaccurate.

• Tracking errors: Transcriptional time traces are generated from the time-lapse images by detecting the TSs, localizing and fitting them with Gaussians, and generating trajectories by connecting detections across different frames. Whichever software is used (eg, ours is available at http://larsonlab.net/), this process is not error free. Incorrect spot detection and/or the presence of another object in the vicinity of the tracked TS can result in inaccurate tracking. One can distinguish two situations: (i) a brief jump (eg, one frames) away from and then back to the TS, or (ii) a single jump away from the TS that does not come back (or does so after a certain number of frames, eg, ≥5 frames). In the former case, one-frame tracking errors have a similar effect as the measurement noise (if they are truly one frame long). That is, they make inaccurate the first point (at τ=0) of correlation functions (both auto- and cross-correlations in case the two channels are tracked simultaneously). Practically, a few of these errors are acceptable per trace. But if too numerous or if one needs a precise measure of the cross-correlation around τ=0, they should be corrected in the tracking procedure. In the cases where the tracking errors are long (case (ii)), the corresponding portions of the traces can be kept as such only if the TS is actually inactive (ie, showing no fluorescence signal) during this time period, and the inaccurate detections yield a signal close to background. In any other case (eg, the tracking jumps to a nuclear structure yielding a nonnull measured signal, or the tracking stays on the nuclear background while the TS is actually active), it is critical to avoid including such portions of a time trace. Two simple options are to adjust the tracking procedure as to avoid these inaccurate portions (possibly requiring manual user intervention), or to trim the traces to only keep the part where tracking is accurate (see Section 2.4 for dealing with traces of various lengths, and Section 4.4 for the biases this may cause). Note that if this type of inaccurate tracking occurs in the middle of long and otherwise good time trace, one can split the trace in two parts and treat them as two different traces.

• Volumetric imaging: Nuclei often being ≥10 μm thick in the z-axis direction, the whole nuclear volume is not always covered by the z-stack acquisition. Hence, a TS may diffuse in and out of the imaged volume through the course of the experiments, resulting in fluctuations in the measured intensity that are not due to transcriptional events. It is critical to ensure on all time traces that the TS does not reach the edge of the imaging z-range. Otherwise, these portions of the traces should be excluded (as described earlier for the long tracking errors). If not taken into account, this type of fluctuations can completely mask the transcriptional kinetics by adding a strong and short-scale decay to all the correlation functions. Along the same lines, choosing an inappropriately large Δz step between z-planes can have a similar effect. Appropriate values depend on the optical setup but are typically ~0.5 μm for a widefield microscope.

A general note on technical fluctuations is that they are not always simple to identify and may be mistaken for biological ones. A good way to confirm if a certain feature in correlation functions is of technical nature is to change the imaging conditions (eg, illumination, step and range of the z-stack, time step, coat protein level, etc.) and see if the feature is affected.

4.4. Biased Selection of Data (Cells, TS, Part of Traces)

When acquiring and analyzing data, one tends to bias the selection of fields of view and/or cells based on how the TS appears. Also, the procedure described in the previous section to exclude portions of traces where tracking is inaccurate (likely when the TS is not or weakly active) introduces a bias in the result—ie, transcription appears more frequent than it is in reality. This is acceptable if the only conclusions drawn from the data are about the postinitiation kinetics of single-RNA synthesis (Coulon et al., 2014). But in this case, it is not possible to make any statement on the frequency of transcription (eg, initiation rate, bursting kinetics, etc.) based on this data alone. To do so, one has to image and analyze cells regardless of their activity, and to generate traces where periods of transcriptional inactivity are indeed measured as such and hence included in the analysis (Lenstra et al., 2015). This is more demanding in terms of image analysis and may require extensive manual user intervention during the tracking procedure.

4.5. Validation by Complementary Measurements

Finally, an important point is that—as holds for any technique—fluctuation analysis should not be used alone. In certain cases, two distinct mechanistic scenarios about the underlying biological process may produce rather similar correlation functions. Not only perturbation experiments should be performed to ensure that the correlation functions are affected as expected, but additional techniques should also be used to corroborate the findings.

A relevant technique to use in this context is single-molecule RNA FISH (Femino, Fay, Fogarty, & Singer, 1998). It consists in hybridizing fluorescently tagged DNA oligonucleotides onto an RNA of interest in fixed cells, leading to the visualization of single RNAs in the cell and allowing the absolute quantification of nascent RNAs at each TS. This technique is also much more amenable to high-throughput acquisition and analysis, giving an unbiased view of the processes under study. Although it does not give access to dynamics, it provides a very complementary picture to fluctuation analysis of MS2/PP7 time traces. It can be performed on a gene already tagged with MS2 or PP7 (by designing oligos against the MS2/PP7 repeats) to validate/complement the conclusions obtained through the live cell approach (Lenstra et al., 2015), or it can be used to observe other genes easily (only requiring to design new oligos) to show how the conclusions of the live-cell measurements can be generalized (Coulon et al., 2014).

5. CONCLUSION

Fluctuation analysis is a powerful method for extracting mechanistic information from complex transcriptional time traces, obtained by MS2 and PP7 RNA labeling, where many RNAs are synthesized simultaneously, each one having its own stochastic transcriptional kinetics, and with potentially multiple biological processes occurring at different timescales. The added value of acquiring multicolor data on a given experimental system is often significant since one can calculate both auto- and cross-correlation functions, hence revealing much more information than an autocorrelation alone.

Implementing this technique is however not always trivial. As we have seen, calculating and interpreting correlation functions correctly requires a good knowledge and understanding of the technique and there are a number of mistakes one can make. A general advice is that, when using fluctuation analysis to interpret experimental data, one should always run numerical simulations. Whether the purpose is

• –to troubleshoot the computation of correlation functions (Section 2),
• –to estimate the effect of potential technical artifacts (Section 4.3),
• –to have an intuition on what the correlation function may reveal for a given experimental system (Section 4.1),
• –to test rapidly if a hypothetical mechanistic model is consistent with experimental observations,
• –to verify the result of mathematical predictions (Section 3.1),
• –or to assess whether the fitting procedure is able to discriminate properly between mechanistic models and to recover the underlying parameters (Section 3.2),

it is always a simple and easy tool to use, with many benefits. It provides a set of time traces to experiment with, where the underlying mechanisms at play are fully known and can be changed freely. To generate simulated signals, one can either use the Gillespie algorithm (Gillespie, 1976) or a more general Monte Carlo approach by drawing random events with the desired statistics and combining them as in Eq. (10).

Fluctuation analysis is a general technique. Its use is not restricted to transcriptional time traces. We can anticipate its future application to other related types of data, upstream and downstream of transcription. This includes, for instance, the simultaneous measurement of transcription (by MS2 or PP7 labeling) and imaging of complexes/enzymes recruitment at a given locus (transcription factors, Pol II, enhancers, etc.), as well as the time course of protein synthesis observed from a single RNA in the cytoplasm (Morisaki et al., 2016; Wu, Eliscovich, Yoon, & Singer, 2016). In many contexts, this powerful analysis technique will help to dissect complex biological mechanisms, by building upon basic concepts of signal theory.