Abstract
Introduction:
Kilohertz frequency spinal cord stimulation (kHz-SCS) deposits significantly more power in tissue compared to SCS at conventional frequencies, reflecting increased duty cycle (pulse compression). We hypothesize kHz-SCS increases local tissue temperature by joule heat, which may influence the clinical outcomes.
Methods:
To establish the role of tissue heating in KHZ-SCS, a decisive first step is to characterize the range of temperature changes expected during conventional and KHZ-SCS protocols. Fiber optic probes quantified temperature increases around an experimental SCS lead in a bath phantom. These data were used to verify a SCS lead heat-transfer model based on joule heat. Temperature increases were then predicted in a seven-compartment (soft tissue, vertebral bone, fat, intervertebral disc, meninges, spinal cord with nerve roots) geometric human spinal cord model under varied parameterization.
Results:
The experimentally constrained bio-heat model shows SCS waveform power (waveform RMS) determines tissue heating at the spinal cord and surrounding tissues. For example, we predict temperature increased at dorsal spinal cord of 0.18–1.72 °C during 3.5 mA peak 10 KHz stimulation with a 40–10–40 μs biphasic pulse pattern, 0.09–0.22 °C during 3.5 mA 1 KHz 100–100–100 μs stimulation, and less than 0.05 °C during 3.5 mA 50 Hz 200–100–200 μs stimulation. Notably, peak heating of the spinal cord and other tissues increases superlinearly with stimulation power and so are especially sensitive to incremental changes in SCS pulse amplitude or frequency (with associated pulse compression). Further supporting distinct SCS intervention strategies based on heating; the spatial profile of temperature changes is more uniform compared to electric fields, which suggests less sensitivity to lead position.
Conclusions:
Tissue heating may impact short and long-term outcomes of KHZ-SCS, and even as an adjunct mechanism, suggests distinct strategies for lead position and programming optimization.
Keywords: High rate biphasic Spinal Cord stimulation, Temperature, FEM, Bioheat modeling, Mechanism, Safety
Introduction
The emergence of kilohertz frequency (1–10 KHz) spinal cord stimulation (kHz-SCS)1–7 for the treatment of neuropathic pain has engendered studies on new mechanisms of actions (MoA)5,8–11. Divergent clinical observations for conventional rate SCS and kHZ-SCS suggest difference in MoA which could in turn inform distinct programming optimization strategies. Notably, kHZ-SCS can provide an analgesic and side-effects profile distinct from conventional frequency (~100 Hz) SCS11,12. For example, kHz-SCS does not produce the paresthesia associated with dorsal column activation in conventional SCS, and recent studies seemingly rule out direct activation of dorsal column fibers as the primary mechanism of action of kHz-SCS pain relief13,14 Wash-in time for the therapeutic benefit of conventional rate SCS is on the order of minutes, while responses to wash-in over a longer period4. Further indicating distinct MoA, kHz-SCS waveforms involve simultaneous decrease in pulse duration (well below membrane time constants) and increase in pulse frequency (beyond axon refractory periods) that challenge conventional models of stimulation15,16.
Evidence against traditional neural MoA warrants investigation of other phenomena. We note that since the decrease in interpulse-interval (e.g. from 10 ms at 0.1 KHz to 0.1 ms at 10 KHz) is more drastic than the decrease in pulse duration (e.g. from 100 μS per phase at 0.1 KHz to 40 μS per phase at 10 KHz5,9), kHZ stimulation is associated with higher duty cycle – and the RMS power of a rectangular waveform varies positively with the square root of its duty cycle. Through the principle of joule heating, the power of current flow from an implanted lead can produce temperature increases around the lead10,17–23. Thus, kHz stimulation deposits more power in the tissue than conventional spinal cord stimulation and is therefore more likely to significantly heat the tissue immediately surrounding the stimulation site. A temperature increase and resultant thermal conduction into the spinal cord can, in turn, affect neuronal function23 (e.g., via alteration of ion channel or neurotransmitters dynamics) and related biological functions (e.g., via vasodilation24, heat shock protein expression25) depending on the degree of change. Tissue heating further encourages the expression of anti-inflammatory agents, such as heat shock proteins26, over a period of time consistent with the extended wash-in times of kHz-SCS treatment.
Any form of electrical stimulation produces passive heating and the extent of induced temperature increases are specific to both the stimulation and local tissue properties, with various stimulation and environmental parameters affecting the degree to which heating occurs19,23,27. Key stimulation parameters are the stimulation waveform (based on stimulator programming) and electrode montage (based on lead placement), which together with tissue anatomy and electrical conductivity determine joule heat deposition. An implanted stimulator is a constant energy source which will produce unlimited temperature increases without passive (e.g. heat conduction by CSF) or active (e.g. spinal tissue blood perfusion) heat dissipation by the tissue. As such, heating analysis depend on tissue properties such as thermal conductivity, metabolic rate, and blood perfusion; not only of the stimulation target but surrounding tissues. Indeed, we postulate that the local environment around SCS leads is especially conducive to temperature increases, namely the low conductivity of fat and enclosed anatomy of the vertebral canal. If heating due to these factors is sufficient during kHz frequency SCS to shape beneficial responses, then joule heating by SCS may be an adjuvant mechanism underlying therapy. However, the degree of heating during kHz-SCS, including as aggravated by increased power deposition due to pulse compression and/or the enclosed spinal environment, remains unexplored.
The objective of this study was to assess, for the first time, whether an increased duty-cycle (and so power) of High-Rate spinal cord stimulation will produce significant temperature increases in the spinal cord. Prior experimental and modeling studies of conventional noninvasive and invasive forms of brain stimulation has suggested minimal heating under normal device operation (less than 1°C)18,28–31. This study predicts the degree of tissue temperature rises driven by SCS joule heat, and characterizes the role of SCS waveform (including frequency, pulse width, and amplitude) and tissue properties. We measured temperature increases around an experimental SCS lead in a bath to verify a finite-element-model of SCS joule heat. We confirmed the dependence of temperature rise only on the power of the stimulation waveform, independent of other parameters. Finally, we predicted temperature increases during conventional and kHz- SCS at the dorsal spinal cord under passive and active bio-heat conditions in a geometric human spinal cord FEM model.
Method
Bath Phantom study
Saline Bath Phantom
Thermal and electrical conductivity measurements taken to verify the general heat transfer model were performed in a cylindrical glass container (diameter: 90 mm and height: 130 mm) with three varied NaCl concentrations (154 mmol/L, 34.22 mmol/L, and 3.42 mmol/L (approximating cerebrospinal fluid, meninges, and epidural space respectively). A thermal conductivity meter (Therm Test Inc., Canada) and an electrical conductivity meter (Jenco Instruments, Inc., San Diego, CA) measured the thermal and electrical properties of the saline solutions at 37 °C (core spinal cord temperature approximation). The measured corresponding conductivity values for each molar concentrations were: electrical conductivity (σ): 1.62 S/m, 0.47 S/m, and 0.047 S/m; and thermal conductivity (κ): 0.6268 W/(m.K), 0.6317 W/(m.K), and 0.6319 W/(m.K) respectively.
In vitro Stimulation
For the saline bath experiments, an experimental polyurethane SCS lead with 4 Platinum/Iridium electrode contacts (1.35 mm electrode diameter, 3 mm electrode length, 1 mm inter-electrode spacing) was placed at the center of the cylindrical container. The cylindrical container was then immersed in a temperature-controlled water bath (280 × 160 × 150 mm3) maintained at ~37 °C (Fig 1A) and baseline temperature was stabilized for > 60 minutes. Three different waveforms, namely sinusoidal, square, and a symmetric charge-balanced biphasic pulse waveforms mimicking the characteristics and parameters of clinical SCS waveforms (described by leading pulse duration, inter-pulse interval, recovery pulse duration), were generated using a function generator (AFG320, Tektronix, Beaverton, OR, USA). The generated waveforms were passed through a custom designed high-bandwidth linear current isolator to the experimental SCS lead. (Distal) Electrode contact 1(E1) and (proximal contact) 4 (E4) of the experimental SCS lead were energized for all saline bath experiments. Tested stimulation intensities were 1– 7 mA (peak) using rates of 0.1 KHz to 10 KHz. Only for phantom verification, biphasic rectangular waveform pulse widths of each phase (40 μs) and interphases (10 μs) were kept constant such that the duty cycle increased directly with stimulation frequency.
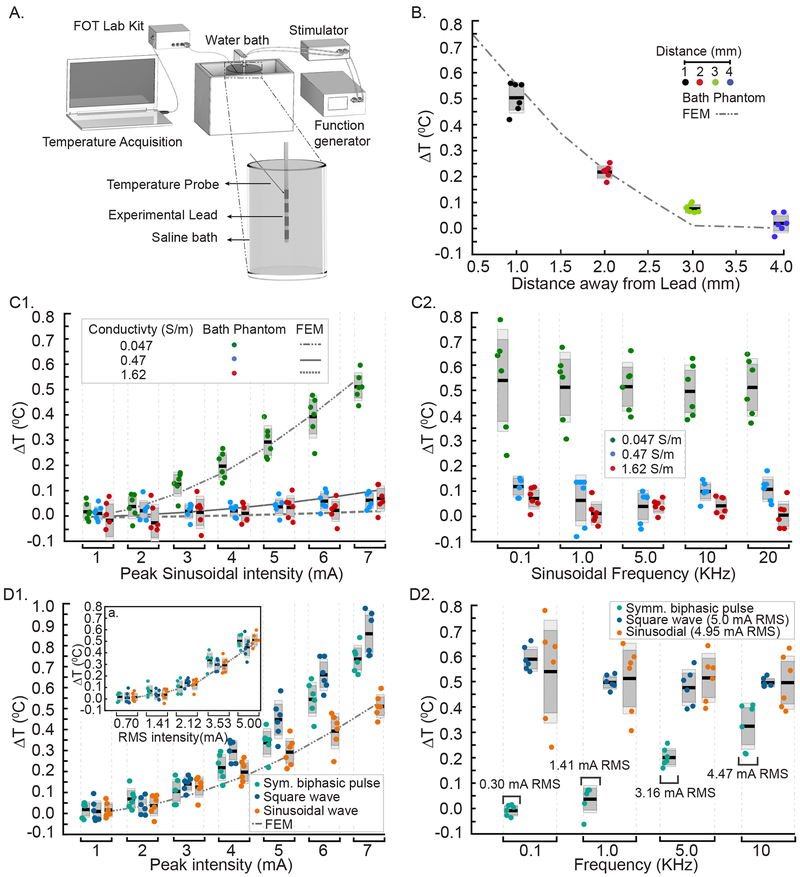
Fig 1: Measurement of temperature increases in phantom preparation across rates, waveforms (SCS, sinusoidal, square) and conductivities and verification of FEM SCS heat model.
Dark grey box: standard error of the mean; Light grey box: standard deviation; black line: mean of the data, and the dots are the individual ΔT measurements. (A) Schematic of a salt bath experimental set up with an experimental SCS lead in a salt bath heated in a water bath, function generator driving custom isolator energizing to the experimental SCS lead, and optical temperature probe mounted on a micro-manipulator. (B) ΔT measured at a radial direction away from the electrode contact (E4, positive polarity) when applying a 10 KHz Symmetric biphasic pulsed waveform at 5 mA peak in a low conductivity saline bath, and the corresponding FEM heat model. Spatial temperature field decreased with increasing radial distance as predicted with the highest temperature increases (mean ~ 0.5 °C) measured proximal to the lead (1 mm). (C1) For 10 KHz sinusoidal waveform, temperature increases as a function of peak stimulation intensity in varied saline bath conductivities: Green: 0.047 Sm−1; Blue: 0.47 S/m; Red: 1.62 S/m. Experimental (dots) and predicted (broken lines) ΔT significantly increased with stimulation intensity with higher sensitivity in lower conductivity saline baths. (C2) For 10 KHz sinusoidal waveform, ΔT measurement at varied stimulation frequencies (0.1, 1, 5, 10, 20 kHz) and conductivities. Temperature increases were independent of frequency and consistently higher for low saline conductivity (p < 0.01). (D1) ΔT across different waveforms and stimulation intensities (Main Panel: Peak; Inset: RMS matched) with frequency fixed at 10 KHz. (D2) ΔTs for the different waveforms across various frequencies at RMS stimulation intensities (Square, 5 mA; Sinusoidal, 4.95 mA; Symmetric biphasic pulsed, frequency-dependent RMS).
Temperature Measurement and Analysis
A fiber optic temperature probe (STS Probe Kit, LumaSense Technologies, Inc. CA, USA) sensed by a fiber optic thermometer (± 0.1 °C accuracy at calibration temperature, m600 FOT LAB KIT, LumaSense Technology, CA, USA) was positioned in the proximity of E4 to measure temperature increases during stimulation (Fig 1A). We measured the peak temperature change in the bath radially from E4 (1 mm, 2 mm, 3 mm, and 4 mm) during stimulation as a function of peak stimulation amplitudes (1–7 mA), over a range of stimulation frequencies (0.1 KHz, 1 KHz, 5 KHz, 10 KHz, and 20 KHz) for sinusoidal, square, and SCS pulsed waveforms. Measured temperature was digitized using TrueTemp data acquisition and graphing software (60 samples/measurement and 1 second measurement interval, LumaSense Technologies, Inc. CA, USA). Temperature was normalized with respect to the initial temperature (~37°C), which was considered baseline.
Computational Models and Solution Method
Bioheat Model of Spinal Cord
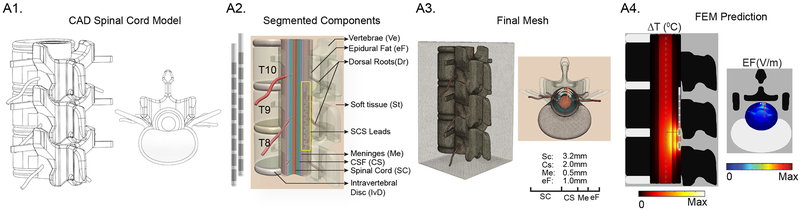
Human spinal cord was simulated as a computer-aided design (CAD) derived model comprising seven compartments namely vertebrae (lower thoracic region, T8–T11), intervertebral disc, surrounding soft-tissues (minimally perfused), epidural fat, meninges, cerebrospinal fluid, and spinal cord (white matter and grey matter combined; Fig 2). The dimensions of the individual tissues, modelled as isotropic homogenous volume conductors, were based on human cadaveric spinal cord from prior studies32. The diameter of spinal cord with dorsal roots was fixed (spinal cord, 6.4 mm; dorsal roots, 0.5 mm) and the thickness of the adjacent tissues were: CSF, 2.0 mm; meninges, 0.5 mm; and epidural fat 1.0 mm. We note that in situ, the diameter of the spinal cord varies along the vertebral column. Two SCS clinical leads were modelled and placed epidurally in a minimally staggered bilateral fashion (SCS Lead 1, 1 mm distal to the mediolateral midline at T8; SCS Lead 2, 0.5 mm away from SCS Lead 1 and proximal to the mediolateral midline at T9; Fig 2A2). We energized only the first SCS lead; the second lead was passive, positioned to mimic a clinical placement, and used to assess the impact of the presence of a passive lead on heat dispersion33. The finite element method (FEM) model was solved using Pennes’ bioheat equation governing joule heating during electrical stimulation (Laplace equation for electrostatics (Δ(σ∇V) = 0 where V is potential and σ is conductivity), metabolic heat generation rate (Qmet or MHG), and blood perfusion rate (ωb or BPer) in the tissues as mentioned below:
| (1) |
where ρ, Cp, T, σ, and κ represent tissue density, specific heat, temperature, electrical conductivity, and thermal conductivity respectively. Biological properties of blood such as density (ρb), specific heat (Cb), and temperature (Tb) were assumed constant in all vascular spinal tissues (vertebrae, meninges, spinal cord) and the corresponding values were 1057 kg /m3, 3600 J / (kg. K), and 36.7 °C respectively. Blood perfusion rate (ωb) values were tissue specific and were in the range of 0.0003–0.008 s−1 34,35. In spinal tissues, metabolic activities due to local spinal cord metabolism and enhanced metabolism in response to SCS generates thermal energy36Blood circulation also plays a significant role in transporting thermal energy across the spinal tissues through convection37. We considered the blood temperature in the spinal tissues to be 0.3 °C less than core spinal cord temperature (37 °C). We investigated how the interaction between metabolic heat generation and blood perfusion modulates kHz-SCS induced temperature increases. Prior to the application of kHz-SCS, the metabolic heat generation rate required to balance the initial spinal cord temperature was calculated using equation (2)37,38 for the aforementioned perfusion rates as:
| (2) |
where T and Tb are initial spinal cord and blood temperature. The calculated Metabolic Heat Generation (MHG) and the corresponding Blood Perfusion (BPer) values were given as; spinal cord and meninges (Qmet, 9132Wm−3; ωb, 0.008 s−1), vertebrae (Qmet, 342 Wm−3; ωb, 0.0003 s−1), and minimally perfused soft-tissues (Qmet, 457 Wm−3; ωb, 0.0004 s−1). The balanced Qmet values approximated prior experimental measurements34,35,39. CSF convection is not incorporated, but could be considered in future bio-heat models.
Fig 2: FEM SCS heat transfer model architecture and work flow.
(A1) CAD derived spinal cord model with dimensions based on human cadaver study68. (A2) Geometry of sample clinical human SCS lead and a placement of the lead in a segmented spinal cord with dorsal roots and surrounding tissues. SCS lead was positioned into the epidural space between lower thoracic (T8–T10) vertebral region. Two leads were modelled as to mimic clinical intervention, positioned in a minimally staggered bilateral fashion. Epidural space was modelled with fatty tissues. (A3) Resulting volumetric mesh of spinal tissues. (A4) The numerical solution predicted ΔT (°C) and EF (V/m) in the spinal tissues. Black line in the temperature profile plot and red line in the EF plot represent radial direction from the lead where temperature was sampled.
Mimicking clinical montages and waveforms, we energized electrode contacts E1 and E3 of the clinical SCS Lead 1 in a bipolar configuration (8 mm center-to-center electrode distance). Maximum temperature increases by conventional and kHz-SCS using rectangular waveforms for varied peak amplitudes (1, 2, 3, 3.5, 4, 5 mA), frequencies and pulse widths (50 Hz (200 μs), 100 Hz (200 μs), 1 KHz (40 μs and 100 μs), 5 KHz (40 μs), and 10 KHz (40 μs) were predicted and compared between active (bioheat) and passive heating cases at three different locations namely, at the distal edge E3 of the clinical SCS Lead 1 (~ 0.01 mm from the surface of the lead), at the proximal surface of the dorsal root to the SCS lead, and at the surface of spinal cord (~ 3.5 mm radial from the E3 electrode).
Boundary and initial condition
To model each stimulation waveform, we applied corresponding static RMS values (see phantom and model Results for justification). The accuracy of RMS intensities calculated analytically for a given intensity, frequency, and pulse width (see equation 3) were confirmed experimentally by stimulation across a resistive load (1 Kc) with voltage acquisition using a digital mixed signal oscilloscope (MSO2024, Tektronix, OR, USA, ± (100 mv + 3 % of threshold)), a DAQ (NI PCI 5922, National Instruments, TX, USA, ± 500 ppm (0.05 %) of input + 50 μV), and a digital multimeter (DMM 7510 7 ½ Digit Graphical Sampling Multimeter, Tektronix, OR, USA, ± 60 ppm 0.0014% of input). The error in calculated versus measured RMS values was less than 5 %.
| (3) |
where IPeak is the peak bipolar stimulation intensity, IRMS is the corresponding RMS value, T is the pulse duration, t is the pulse width, and D is the duty cycle.
A static inward normal current density (Jnorm, RMS) corresponding to the stimulation current intensity (IRMS, Table 1) was injected through E1, and E3 was set as the return (producing a bipolar configuration). The electrical and thermal conductivities of the electrode contacts and the inter-electrode spacing were 4 × 106 S/m and 31 W/(m.K), and σ=1 × 10−15 S/m; κ=0.0262 W/(m.K) respectively36. The outer boundaries of the spinal cord and the surrounding tissues were considered electrically insulated.
Table 1:
FEM SCS Bio-heat model predicts temperature increases (ΔT) in fat around the Lead, the surface of spinal cord (SC), and the proximal origin of dorsal Root, as a function of stimulation waveform and intensity (I), for passive (A.) and active (B.) tissue models. For each waveform (top row) the corresponding Pulse Compression Factor (PCF) is indicated (see Methods). For each waveform and intensity simulation, the corresponding RMS is indicated. In addition to increments of 1 mA peak, 3.5 mA peak is also simulation (grey rows).
| 10 KHz (40–10–40 μs) | 5 KHz (40–10–40 μs) | 1 KHz (40–100–40 μs) | 1 KHz (100–100–100 μs) | 100 Hz (200–100–200 μs) | 50 Hz (200–100–200 μs) | |||||||||||||||||||
| PCF | 6.32 | 4.47 | 2.00 | 3.16 | 1.41 | 1.00 | ||||||||||||||||||
| l (mA) | ΔT (0C) | ΔT (0C) | ΔT (0C) | ΔT (0C) | ΔT (0C) | ΔT (0C) | ||||||||||||||||||
| Peak | RMS | Lead | RMS | Lead | RMS | Lead | RMS | Lead | RMS | Lead | RMS | Lead | ||||||||||||
| 1.0 | 0.89 | 0.34 | 0.63 | 0.17 | 0.28 | 0.03 | 0.47 | 0.08 | 0.20 | 0.02 | 0.14 | 0.01 | ||||||||||||
| 2.0 | 1.78 | 1.32 | 1.26 | 0.67 | 0.56 | 0.13 | 0.89 | 0.33 | 0.40 | 0.07 | 0.28 | 0.03 | ||||||||||||
| 3.0 | 2.68 | 3.03 | 1.89 | 1.49 | 0.84 | 0.29 | 1.34 | 0.75 | 0.60 | 0.15 | 0.42 | 0.08 | ||||||||||||
| 3.5 | 3.13 | 4.11 | 2.21 | 2.05 | 0.98 | 0.40 | 1.57 | 1.01 | 0.70 | 0.21 | 0.49 | 0.10 | ||||||||||||
| 4.0 | 3.57 | 5.24 | 2.53 | 2.63 | 1.12 | 0.53 | 1.79 | 1.31 | 0.80 | 0.27 | 0.57 | 0.13 | ||||||||||||
| 5.0 | 4.47 | 8.31 | 3.16 | 4.15 | 1.41 | 0.82 | 2.24 | 2.04 | 1.00 | 0.41 | 0.71 | 0.21 | ||||||||||||
| B. Active heating (Perfusion and MHR) | ||||||||||||||||||||||||
| 10 KHz (40–10–40 μs) | 5 KHz (40–10–40 μs) | 1 KHz (40–100–40 μs) | 1 KHz (100–100–100 μs) | 100 Hz (200–100–200 μs) | 50 Hz (200–100–200 μs) | |||||||||||||||||||
| PCF | 6.32 | 4.47 | 3.16 | 2.00 | 1.41 | 1.00 | ||||||||||||||||||
| l (mA) | ΔT (0C) | ΔT (0C) | ΔT (0C) | ΔT (0C) | ΔT (0C) | ΔT (0C) | ||||||||||||||||||
| Peak | RMS | Lead | RMS | Lead | RMS | Lead | RMS | Lead | RMS | Lead | RMS | Lead | ||||||||||||
| 1.0 | 0.89 | 0.30 | 0.63 | 0.15 | 0.28 | 0.03 | 0.47 | 0.08 | 0.20 | 0.02 | 0.14 | 0.01 | ||||||||||||
| 2.0 | 1.78 | 1.19 | 1.26 | 0.59 | 0.56 | 0.12 | 0.89 | 0.31 | 0.40 | 0.06 | 0.28 | 0.03 | ||||||||||||
| 3.0 | 2.68 | 2.69 | 1.89 | 1.33 | 0.84 | 0.26 | 1.34 | 0.68 | 0.60 | 0.13 | 0.42 | 0.07 | ||||||||||||
| 3.5 | 3.13 | 3.60 | 2.21 | 1.78 | 0.98 | 0.35 | 1.57 | 0.92 | 0.70 | 0.19 | 0.49 | 0.09 | ||||||||||||
| 4.0 | 3.57 | 4.71 | 2.53 | 2.37 | 1.12 | 0.45 | 1.79 | 1.21 | 0.80 | 0.24 | 0.57 | 0.12 | ||||||||||||
| 5.0 | 4.47 | 7.25 | 3.16 | 3.69 | 1.41 | 0.73 | 2.24 | 1.89 | 1.00 | 0.39 | 0.71 | 0.19 | ||||||||||||
Pulse Compression factor (PCF)
For the thermal boundary conditions, the temperature at the outer boundaries of the spinal column was fixed at core body temperature (37 °C)35,39 with an assumption of no convective heat loss to the ambient temperature, no convective gradients across spinal surrounding tissues, and no SCS-induced heating at the model boundaries34. The initial temperature of the tissues was assumed to be 37°C, and thermo-electrical properties of biological tissues were based on average literature values40,41. Intravertebral disc (σ=0.830 S/m; κ=0.49 W/ (m.K) and csf (σ=1.65 S/m; κ=0.57 W/ (m.K) are avascular, and therefore have no BPer and MHG, whereas the other remaining tissues are vascularized and have BPer and MHG as listed: epidural fat (σ=0.25 S/m; κ=0.21 W/ (m.K), ωb= 0.0001 s−1, Qmet= 58 Wm−3) soft tissues (σ = 0.15 S/m; κ = 0.47 W/ (m.K), ωb= 0.0004 s−1, Qmet= 457 Wm−3), vertebrae (σ = 0.01 S/m; κ = 0.32 W/(m.K), ωb= 0.0003 s−1, Qmet= 342 Wm−3), meninges (σ = 0.368 S/m; κ = 0.44 W/(m.K), ωb= 0.008 ωb, Qmet = 9132 Wm−3), and spinal cord (σ = 0.126 S/m; κ = 0.51 W/(m.K), ωb= 0.008 s−1, Qmet = 9132 Wm−3). When indicated, these “standard” tissue values were manipulated by either 1) doubling or halving the electrical and/or thermal conductivities of a given compartment, or 2) by substituting properties across compartments.
Saline bath Phantom FEM
SCS saline bath phantom was modelled using equation (1) while eliminating the biological tissue parameters. The FEM Phantom model was parameterized based on the dimensions, conductivity, and initial temperature of the experimental set-up. As tested, we simulated one SCS experimental lead centrally placed in a saline bath phantom. For the electrical boundary conditions, a uniform RMS current density was applied at E4 (anode) and return at E1(cathode). The outer boundaries of the bath were considered electrically insulated. For thermal boundary conditions, the external boundary temperature and the initial temperature of the bath were fixed at 37 °C. To account for the voltage drop due to the electrode-saline interface42–44, a correction factor of 50% was applied in phantom stimulation18.
Model Construction and Computational Method
Human spinal cord and saline bath phantom models were CAD derived, assembled in SolidWorks 2016 (Dassault Systemes Americas Corp., Ma, USA), and imported using Simpleware ScanIP (Synopys Inc., CA, USA). The entire volume of the spinal tissue and the electrode assembly was 83.0 × 74 × 108 mm3. Prior to the segmentation, tissues were resampled to have an isotropic resolution of 0.2 mm3. Resampled images were segmented into seven tissues compartments along with the T8–T11 positioned SCS lead assembly using a combination of automatic and manual segmentation filters (Fig 2A2). Using a voxel-based meshing algorithms of ScanIP, an adaptive tetrahedral mesh was generated. The final model size resulting from multiple mesh densities refinement contained approximately 4,600,000 tetrahedral elements for the full anatomy of spinal cord model and approximately 320,000 tetrahedral elements for the saline bath model (Fig 2A3). The meshes were imported into COMSOL Multiphysics 5.1 (COMSOL Inc., MA, USA) to computationally solve the FEM model. The SCS model was solved for both passive heating (joule heating, without BPer and MHG) and active heating (bioheat, with BPer and MHG) conditions. The baseline temperature gradient for the active heating case was predicted by first solving the heat transfer model in the absence of electrical stimulation. In passive heating, the baseline temperature gradient was set to zero. The Saline bath model was solved only for passive heating condition. Both phantom and SCS models were solved under steady state assumption and corresponding temperature increases and field intensities were quantified. Heat flux and field intensity streamlines (seeded at selected tissue boundaries and proportional in diameter to the logarithm of corresponding magnitudes) were plotted to illustrate the overall distribution across tissues (Fig 3).
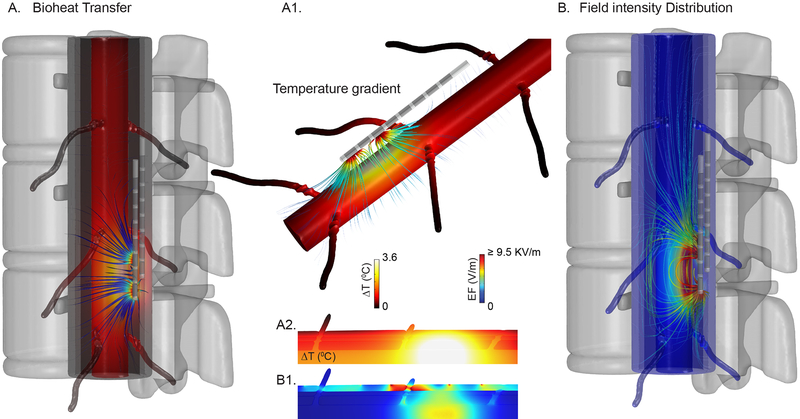
Fig 3: FEM Bioheat transfer model of Spinal Cord Stimulation predicts temperature changes and electric field intensities.
(A) Temperature increases at the spinal cord modelled with dorsal roots, and surrounding tissues for a metabolic heat and blood perfusion modulated high rate spinal cord stimulation (KHZ-SCS). Temperature gradient streamlines originated from SCS leads to the spinal cord and dorsal roots are depicted. (A1) Accumulated heat (shown as heat flux streamlines) transported throughout spinal cord and dorsal roots during kHz-SCS. (A2, B2) illustrates predicted temperature and electric field (EF) spatial distribution on a spinal cord, dorsal roots, and other adjacent tissues. (B) Field intensity distribution across spinal cord and surrounding tissues. EF strength across each tissue are depicted by electric field streamlines seeded on every tissue boundary.
Statistics and Analysis
Normality test on temperature increases were conducted using Lilliefors corrected K-S test statistical test. A two-way repeated measure analysis of variance (ANOVA) was used to access the statistical differences in ΔT across different tested conditions (stimulation intensity, waveforms, frequencies, conductivities). A critical value (p) < 0.01 was accepted as a statistical difference between the groups. Further significance between groups were verified using Post hoc Scheffe’s test (corrected multiple comparisons). The statistical relations between the experimental data the FEM data was evaluated through a simple linear regression MATLAB (R2016a, MathWorks, MA, USA).
The standard forms of power law tested super-linearity between the RMS and temperature increases, using a linear least squares fitting technique derived by Gauss and Legendre with a power function45 given as:
| (4) |
where ‘β’ is the power, and ‘A’ is the proportionality constant. The value of ‘β ‘determines the category of the relationship (β = 1, linear; β > 1, super-linear; β < 1, sublinear). Formulating the power function further on a log-log scale yields:
| (5) |
Equation (5) is a straight line with a slope ‘β’ and a y-intercept of ln (A). Linear least square fit of the logarithmic data yields the correlation (r2)45.
Pulse Compression Factor per stimulation intensity (PCF) captures the increase in RMS of a High-Rate waveform (RMSHigh-Rate) compared to a conventional 1 mA peak 50 Hz 200 μs pulse-width waveform (RMS50):
| (6) |
| (7) |
where ‘Pw’ and ‘f ‘are pulse width (sec) and frequency (Hz) for a given High-Rate waveform.
Results
Phantom Measurements and Model Verification
A specially designed chamber was used to quantify temperature increases around an experimental SCS lead in a saline bath using varied waveforms (Fig 1A). A micro-manipulator mounted optical temperature probe mapped steady-state temperature increases during stimulation with varied waveforms. As predicted by the FEM, temperature increases when applying a 10 KHz symmetric biphasic pulsed waveform at 5 mA peak intensity in a low conductivity saline phantom was maximal near energized electrodes and decreased with radial distance (Fig 1B). In separate experiments, salt bath conductivity was varied by saline concentration. The main effect of saline bath conductivity and stimulation intensities (1–7 mA peak sinusoidal) was significant (F (2, 105) = 218.95 p < 0.01 and F (6, 105) = 42.03, p < 0.01, a two-way ANOVA). The interaction between these factors on ΔT was also significant; (F (12, 105) = 19.88, p < 0.01). Temperature increases were measured to be significantly greater in the lower saline bath conductivity (0.047 S/m) than in the other two saline bath conductivities (0.47 S/m and 1.62 S/m; Post-hoc Scheffe’s test, Fig 1C1). Across different saline conductivities at different sinusoidal frequencies, the measured temperature increases were significant; F (2,75) = 256.25, p < 0.01. ΔT was higher at lower conductivity saline bath (Fig 1C2).
Temperature increased by up to ~1 °C with stimulation amplitude during stimulation using all 10 KHz waveforms (symmetric biphasic pulse, square, sinusoidal). In addition, when considering only peak intensities, higher ΔT was observed during stimulation using pulsed and square waveforms versus the sinusoidal waveform (F (2,105) =41.14, p < 0.01). However, this effect was found to be directly related to the RMS of the waveform (Figure 1D1a) and not to the specific shape of the stimulation waveform (F (2, 75) = 1.11, p > 0.01).
In a separate series, temperature increases were measured across varied frequencies for all waveforms (symmetric biphasic pulse, square, sinusoidal) in a low conductivity saline bath with 5 mA peak current intensity (corresponding RMS: sinusoidal waveform, 4.95 mA; square waveform, 5 mA; in pulsed waveform, RMS varies with frequency (Fig 1D2)). There was a main effect of stimulation waveforms on ΔT; F (2, 60) = 133.44, p < 0.01. Temperature increases (0 to ~ 0.4 °C) across frequencies for symmetric biphasic pulsed waveform were significant (p < 0.01); however, for true square and sinusoidal waveforms, ΔT did not increase significantly across frequencies (p > 0.01). Temperature rises appeared to reflect the increase in duty cycle and RMS only for the symmetric biphasic pulsed waveform. Conversely, significantly higher temperatures were measured overall at the 5 mA peak intensity for sinusoid and square waveform compared to the pulsed waveform- reflecting the 100% duty cycles and therefore higher RMS values of the sinusoid and square waveforms.
Computational FEM predictions of the phantom using the experimental lead and waveforms were correlated with experimental temperature increases measurement at varied saline conductivities ((R2= 0.24, F (1,40) = 12.20, p < 0.01, 1.62 S/m; R2= 0.26, F (1, 40) = 13.70, p < 0.01, 0.47 S/m; R2= 0.84, F (1,30) = 201.84, p < 0.01, 0.0047 S/m) (Fig 1C1). Computationally predicted and measured temperature increases were strongly correlated across different RMS stimulation intensities (R2=0.86, F (1, 27) = 167.39, p < 0.01(Fig 1D1a)). Accordingly, a strong association between ΔTs were established along radial direction away from the experimental SCS lead; R2 = 0.96, F (1, 21) = 495.59, p < 0.01 (Fig 1B).
Computational Model of Heating by SCS: Influence of waveform with standard tissue parameters
Using a FEM bio-heat computational models of human spinal cord stimulation, tissue temperature increases were predicted under varied stimulation parameters (Table 1) for passive heating and active conditions initially using “standard” tissue parameters (see Methods). Six representative SCS waveforms were simulated, with selected frequency and duty cycle (corresponding Pulse Compression Factor noted in table; see Discussion), each with varied peak intensity from 1 to 5 mA (corresponding resultant RMS noted in table). For each waveform and intensity, we tabulate the maximum ΔT around the SCS clinical lead (E3 contact), at the proximal surface of the dorsal root to the SCS lead (~ 1 mm lateral to the stimulating lead), and at the surface of spinal cord (~ 3.5 mm radial to the stimulating lead).
From this analysis, several important predictions emerge. Heating under the standard active model (which includes blood perfusion (BPer) and metabolic heat generation (MHG)) was lower than the standard passive model (where BPer and MHG were absent). Maximum temperature increases were generated around the SCS clinical lead (the epidural fat). Temperature increases were relatively higher for waveforms with a higher Pulse Compression Factor. Both active and passive heating increased with stimulation RMS, and so with intensity or Pulse Compression Factor, in a super-linear manner (e.g. doubling stimulation intensity or Pulse Compression Factor doubles RMS and results in a > 2-fold increase in temperature (Fig 4)). While relative temperature increases were more sensitive to intensity than Pulse Compression Factor, the highest temperature increase were predicted under high Pulse Compression (e.g. the 10 KHz waveform). For example, using a conventional 50 Hz waveform (PCF: 1.0), temperature at the spinal cord (SC) increased < 0.05 °C even at 5 mA peak (RMS: 0.71) while using a 10 KHz waveform (PCF: 6.32) temperature at the spinal cord (SC) increased ~1 °C at 5 mA peak (RMS: 4.47).
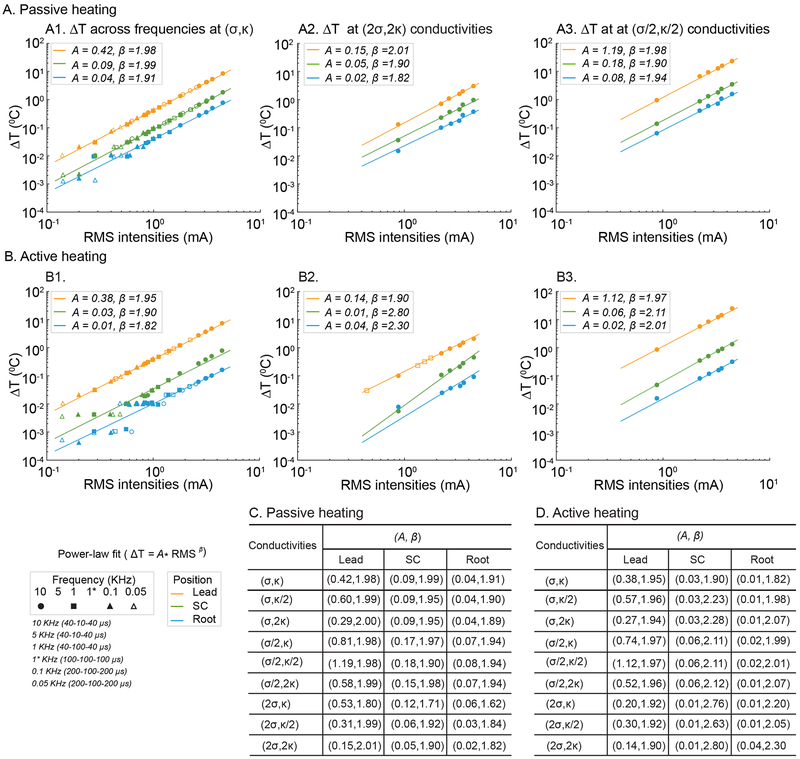
Fig 4: Power law-fit description of temperature increase with stimulation RMS in SCS model.
Temperature changes (ΔT) at three locations (Lead, orange; Spinal Cord, green; and Root, light-blue) as a function of stimulation RMS, across passive or active tissue model with varied fat electrical and thermal conductivity, were predicted by the FEM SCS model (data points). For each tissue model and compartment, we determined a best power-law fit (see Methods), which is a line with proportionality constant A and slope β (lines) on a log-RMS verse log-Temperature plot. Data plots include standard passive (A1), standard active (B1) tissue models, high thermal and electrical fat conductivity (2σ, 2κ) passive (A2) and active (B2) models, and low thermal and electrical fat conductivity (σ/2, κ/2) passive (A3) and active (B3). A and β across all 9 permutations of fat electrical (σ) and thermal (κ) conductivity are summarized for passive (C) and active (D) cases. RMS values plotted in A1 and A2 span stimulations frequencies of 0.05, 0.1, 1 (with low or high duty cycle), 5, and 10 KHz (waveforms indicated in legend and as used in Table 1). RMS values in A2, B2, A3 and B3 span 1, 5, and 10 KHz. A β > 1 indicates super-linear dependence of temperature rise on stimulation RMS; when β = 2 temperature increases with the square of RMS.
Dependence of temperature increase on RMS (and so Intensity or Pulse Compression Factor) was modeled assuming a power law relationship, which results in a linear log-log dependence (see Methods). Surprisingly, and despite the complexity of the standard tissue model, this fit sufficiently and reliability predicted temperature increases. Slope (β) approached 2 (i.e. temperature increasing with the square of RMS) - a super-linear (β >1) sensitivity of temperature to RMS. The proportionality constant (A) increased across fat (Lead), Spinal Cord, and Root compartments, all relativity higher in the passive (Fig 4A1) verse active (Fig 4B1) tissue model.
Computational Model of SCS: Parameter sensitivity analysis with fixed waveforms
Living tissue possess complex thermo-electrical properties45 and these properties are tissue specific. In the active model, we predicted the sensitivity of SCS temperature to tissue properties by halving or doubling the thermal and/or electrical conductivity (from the standard model; see Methods) of each tissue compartment. At 3.13 mA RMS (as for a 10 KHz SCS waveform with 3.5 mA peak), we considered a significant change in predicted temperature as > 0.03 °C and > 8 % from the standard model. No simulated changes in passive thermal and/or electrical conductivity at any tissue, except epidural fat (eF), produced a significant temperature change at the Lead, Spinal Cord, or Root. However, increases or decreases in epidural fat electrical conductivity significantly decreased or increased temperature across tissue compartments, respectively. The resulting predicted range of temperature increases using waveforms with 3.13 mA RMS were (Passive Model Range; Active Model Range): Lead (1.53 – 11.57 °C; 1.25 – 10.77 °C), Spinal Cord (0.42 −1.72 °C; 0.18 – 0.72 °C), and Root (0.17 – 0.75 °C; 0.04 – 0.15 °C).
We considered the sensitivity and fit of the power-law function across tissue properties, specifically varying fat electrical (σ) and thermal (k) conductivity (doubling and halving). In all tissue conditions, the linearity of log-temperature verse log-RMS confirmed a power-law fit, with consistently super-linear sensitivity (β >1). Thus, for each tissue model, temperature could be predicted reliability by simply the corresponding power law function parameters, A and β (Fig. 4). In the passive model, β approached 2 across conditions. In the active model β could exceed 2, reflecting variance at low RMS, but not sensitivity at high RMS. The proportionality constant (A) varied more significantly across model parameters and tissue compartments, particularly near the Lead (Fig. 4A1, 4B1, 4B2).
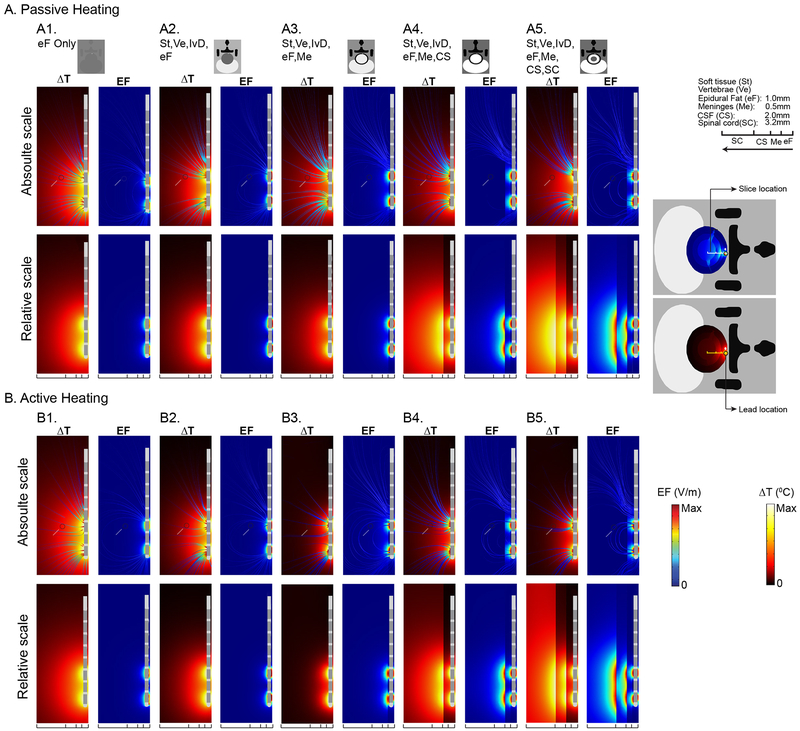
To evaluate the contribution of peripheral spinal tissues on the temperature increases, we considered series of idealized models staring with uniform epidural fat and then sequentially adding adjacent tissues, under both active and passive model conditions (Fig 5). The order of simulated tissues and predicted maximum temperature increases at locations corresponding to Lead position (“Lead”), Spinal Cord surface (“SC”), and dorsal Root surface (“Root”) are reported for both passive heating and active heating conditions (3.13 mA RMS at 10 KHz; Table 2). Maximum temperature increases and penetration (from the lead inward) is predicted in the uniform epidural fat model, with a relatively shallow electric field profile. The addition of Soft tissue (St), Vertebrae (Ve), and Intravertebral Disc (IvD) compartments and subsequent reduction of the size of the epidural fat layer(?) result in an incremental reduction in predicted temperatures increases – which is consistent with the notion that fat tissue properties are the most conducive to heating. The relative reduction in temperature between the active and passive models, as well as the reduction in electric field (which is always the same across active and passive models) emphasize these variables can change independently.
Fig 5: Tissue substitution analysis for passive and active heating conditions in SCS model.
Predicted ΔT and EF were reported in both absolute scale (data sampled at a radial distance equal to the surface of spinal cord from the surface of epidural fact, represented by a gray dot) and relative scale (data sampled at a corresponding tissue surface for all tissue combination as illustrated in the figure) from parasagittal spinal tissue slice. On an absolute scale for both passive and active heating conditions, ΔT and EF decreased as more tissues were added around the epidural fat. With an entire tissue combination (A5, B5) on this scale, the ΔT and EF were 0.84°C and 17.76 V/m in passive heating and 0.37 °C and 17.76 V/m in active heating. Similarly, on the relative scale for passive and active heating conditions, ΔT and EF decreased as more tissues were added. Maximum ΔT (7.65 °C) and EF (9.9 KV/m) were reported around the lead with only epidural fat (A1, B1, relative scale). As more tissues were added, ΔT around the lead decreased to 3.88 °C in passive heating and 3.67 °C in active heating. Maximum predicted ΔT and EF at the spinal cord was 0.37 °C and 17.76 V/m with the entire tissue combination (A5, B5, relative scale).
Table 2:
Tissue substitution order and resulting predicted temperature changes (ΔT) at the Lead, Spinal Cord, or Root tissue compartments. In this series only one waveform with 3.14 mA RMS was simulated. For each model the tissues modeled could include epidural fat (eF), vertebrae (Ve), intervertebral discs (IvD), meninges (Me), cerebral spinal fluid (CS), and spinal cord (CS).
| 3.13 mA RMS, 10 KHz | Passive Heating | Active Heating | ||||
| ΔT(0C) | ΔT(0C) | |||||
| Tissues | Lead | Lead | ||||
| eF | 7.39 | 7.32 | ||||
| eF, Ve, IvD | 5.07 | 5.02 | ||||
| eF, Ve, IvD, Me | 4.09 | 3.49 | ||||
| eF, Ve, IvD, Me, CS | 4.13 | 3.59 | ||||
| eF, Ve, IvD, Me, CS, SC | 4.11 | 3.60 | ||||
Further addition of Meninges (Me) to the model reduced predicted temperature rises notably in both relatively interior (Spinal Cord) and exterior (Lead, Root) regions - indicating that, compared to fat, the Meninges conduct heat away. The reduction in electric field at the Spinal Cord following addition of Meninges (from 165 V/m to 29.27 V/m) was comparable in scale to the temperature decreases in the active model (from 1.22 °C to 0.25 °C) while in the passive model temperature was less sensitive (from 1.37 °C to 0.92 °C) – reflecting that the Meninges are vascularized in the active model. Further addition of CSF (CS) decreased predicted temperature rises at the SC and Root for the passive model, increased predicted temperature rises at the Lead for the passive model, and increased temperature in all compartments in the active model. The avascular nature of the CSF layer is overshadowed by its high electrical/thermal conductivity. Finally, addition of Spinal Cord (SC) restores the tissue parameters of standard model.
Discussion
Thermoregulation of CNS temperature is complex and depends on a high metabolic activity46 and both passive (conduction) and active heat exchange (blood flow). Neurostimulation, such as SCS, can challenge this equilibrium in several ways by 1) altering neuronal and so metabolic activity18,47,48; with 2) changing the cellular microenvironment48,49; 3) changing vascular function as a result of both direct blood vessel stimulation24,50,51 and secondary to microenvironment changes; and 4) depositing of joule heat18,28. In the context of kHz-SCS, this study specifically addressed joule heat with the hypothesis that by increased power (pulse compression), kHz-SCS waveforms will superlinearly increase tissue temperature, potentially inducing downstream alterations in tissue function with therapeutic effects in chronic pain. Characteristic clinical responses to kHZ-SCS including as the lack of associated neural sequelae such as paresthesia and the frequency insensitivity of efficacy52 reconcile well with joule heating, while the delayed time course of effects53 may be explain by temperature homeostatic responses or heat shock protein regulation of neuroinflammation.
Bioheat SCS Model
FEM bioheat models of phantom, verified experimentally, and of human spinal cord, subjected to a broad parametric sweep (> 100 simulations in this study), are suitable for assessing our hypothesis as they enable predictions as to whether or not SCS may produce temperature rises sufficient to produce biological effects.
Heating from chronic SCS represents an exogenous non-physiological challenge. We predicted temperature increases at the dorsal spinal cord of 0.18–1.72 °C and at the lead in epidural fat of 1.25 – 11.57°C under a typical kHz-SCS setting (10 KHz, pulse at 3.5 mA peak; corresponding to 3.13 mA RMS; Figure 3, Table 1). This range depends on epidural fat electrical conductivity; the combination of high current density and low conductivity increases joule heating that is then conducted to other tissues.
The degree of heating is a super-linear function of stimulation RMS power (Fig 1D2) such that kHz-SCS can produce significantly more temperature rise than conventional frequency SCS. Assuming β ~ 2 and integrating (7) with the power-law relationship (4) yields:
| (8) |
where ‘0.02’ is the square of RMS50 at 1 mA.
Remarkably, at least across conditions considered here, temperature increases in any tissue inside the spinal canal were well fit using a power-law function (equation 8). With all lead position, electrode configuration, and passive and active tissue properties captured by a single proportionality constant (A; Figure 4). All waveform parameters collapse to Pulse Compression Factor, PCF (Equation 7). This heuristic finding has important potential consequences to SCS practice:
From a modeling standpoint, this finding could dramatically simplify future efforts to predict temperature changes as part of SCS therapy optimization and programming.
Moreover, the super-linear sensitivity to PCF warrant attentions as incremental changes in waveform can spike tissue heating.
From a mechanistic standpoint, if temperature increases underpin kHZ-SCS, then waveform power (as captured by PCF) is more important than any single waveform parameter (e.g. frequency, pulse width, shape) in generating effective therapy.
However, a heating MoA does not indicate only waveform PCF predicts outcomes as other factors (e.g. electrode placement) influence the proportionality constant (A). Nor does this imply a fixed minimum for stimulation energy (charge, battery consumption) which depends on other factors such as device efficiency and impedance.
Physiological Implications
The nervous system, including the spinal cord, is sensitive to temperature changes. Temperature increases to ~44 °C51 result in brain damage in animal models after 60 minutes36,54, with the temperature threshold for injury decreasing with increased exposure time. In animal models, significant changes in brain excitability have been noted with short-term increases of >2 °C55–57, with sensitivity to lower-temperature expected with long-term temperature increases. Brain temperature increases above 39 °C in ischemic brain injuries increases extracellular excitatory amino acids level, opening of blood-brain barrier, and elevated proteolysis of the neuronal cytoskeleton46,58. A sustained 1–2°C rise in brain temperature after injury is potentially hazardous58–60. While there are transient changes in temperature during normal function (2–3 °C46,58,60,61) a sustained temperature change may produce cumulative and profound changes in brain function. We predicted significant temperature changes in the spinal cord that met or exceeded these thresholds, specifically using kHz frequency waveforms where Pulse Compression increases heat deposition. Our findings are a surprising and important first step toward determining a new heating mechanism for kHz-SCS as well as other relatively high power (kHz frequency) neuromodulation techniques62,63.
Evidence for stimulation acutely changing neuronal firing and metabolism, perfusion18,46,47 and the extracellular environment48 is specific (limited) to sub-kHz frequencies for SCS-relevant simulation amplitudes24,49,50; and so were not modeled here (Qmet and wb were constant). Starting with kHz-stimulation joule heating, changes in brain function can derive from the acute changes in dynamics (e.g. ion channel gating, neurotransmitter clearance;64,65) or a homeostatic molecular response to chronic temperature changes (e.g. heat shock proteins). Slow temperature homeostatic changes provide a plausible explanation for the delayed onset of pain relief by kHz-SCS52,53 and suggest specific molecular pathways (MoA) for pain relief including heat shock protein producing downregulation of neuroinflammation. For example, 72-kDa heat shock protein (Hsp70) inhibits activation of the pro-neuroinflammatory transcription factor, nuclear factor-kB in satellite glial cells (NF-kB)66. Knocking out NF-kB dependent satellite glial cell activation reduces expression of neuronal colony stimulating factor 1 (Csf1)67, which can potentially reduce the inflammatory response and restore normal function of the spinal pain processing network. However, experimental measurement of expression factors associated such metabolic, genetic, and plastic changes that evolve with prolonged heating and the correlation of these changes with the function of the spinal pain processing network are required to validate this hypothesis.
Highlights.
High-Rate spinal cord stimulation (SCS) deposits significantly more power in tissue compared to conventional SCS frequencies, reflecting increased duty cycle (pulse compression).
An experimentally verified bio-heat model shows SCS waveform power determines joule tissue heating and predicts temperature increases at the spine of up to 1 °C during High-Rate stimulation.
Tissue heating by KHZ-SCS may impact short and long-term outcomes, and suggest distinct strategies for waveform optimization and lead placement.
Acknowledgements.
Source(s) of financial support: This study was partially funded by grants to MB from NIH (NIMH) and Boston Scientific Inc.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest:
The City University of New York (CUNY) has IP on neuro-stimulation system and methods with author, Niranjan Khadka and Marom Bikson as inventors. Dr. Marom Bikson has equity in Soterix Medical Inc. Tianhe Zhang, Rosana Esteller, and Brad Hershey are employees of Boston Scientific Inc.
References
- 1.Kinfe TM et al. High Frequency (10 kHz) or Burst Spinal Cord Stimulation in Failed Back Surgery Syndrome Patients With Predominant Back Pain: Preliminary Data From a Prospective Observational Study. Neuromodulation J. Int. Neuromodulation Soc. 19, 268–275 (2016). [DOI] [PubMed] [Google Scholar]
- 2.Tiede J et al. Novel spinal cord stimulation parameters in patients with predominant back pain. Neuromodulation J. Int. Neuromodulation Soc. 16, 370–375 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Van Buyten J-P, Al-Kaisy A, Smet I, Palmisani S & Smith T High-frequency spinal cord stimulation for the treatment of chronic back pain patients: results of a prospective multicenter European clinical study. Neuromodulation J. Int. Neuromodulation Soc. 16, 59–65; discussion 65–66 (2013). [DOI] [PubMed] [Google Scholar]
- 4.Al-Kaisy A et al. Sustained effectiveness of 10 kHz high-frequency spinal cord stimulation for patients with chronic, low back pain: 24-month results of a prospective multicenter study. Pain Med. Malden Mass 15, 347–354 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lempka SF, McIntyre CC, Kilgore KL & Machado AG Computational analysis of kilohertz frequency spinal cord stimulation for chronic pain management. Anesthesiology 122, 1362–1376 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Fingas M, Clark DL & Colbourne F The effects of selective brain hypothermia on intracerebral hemorrhage in rats. Exp. Neurol 208, 277–284 (2007). [DOI] [PubMed] [Google Scholar]
- 7.DiMarco AF & Kowalski KE Activation of inspiratory muscles via spinal cord stimulation. Respir. Physiol. Neurobiol 189, 438–449 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee D, Hershey B, Bradley K & Yearwood T Predicted effects of pulse width programming in spinal cord stimulation: a mathematical modeling study. Med. Biol. Eng. Comput 49, 765–774 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yearwood TL, Hershey B, Bradley K & Lee D Pulse width programming in spinal cord stimulation: a clinical study. Pain Physician 13, 321–335 (2010). [PubMed] [Google Scholar]
- 10.Miller JP et al. Parameters of Spinal Cord Stimulation and Their Role in Electrical Charge Delivery: A Review. Neuromodulation J. Int. Neuromodulation Soc 19, 373–384 (2016). [DOI] [PubMed] [Google Scholar]
- 11.Bicket MC, Dunn RY & Ahmed SU High-Frequency Spinal Cord Stimulation for Chronic Pain: Pre-Clinical Overview and Systematic Review of Controlled Trials. Pain Med. Malden Mass 17, 2326–2336 (2016). [DOI] [PubMed] [Google Scholar]
- 12.Kapural L et al. Comparison of 10-kHz High-Frequency and Traditional Low-Frequency Spinal Cord Stimulation for the Treatment of Chronic Back and Leg Pain: 24-Month Results From a Multicenter, Randomized, Controlled Pivotal Trial. Neurosurgery 79, 667–677 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Song Z, Viisanen H, Meyerson BA, Pertovaara A & Linderoth B Efficacy of kilohertz-frequency and conventional spinal cord stimulation in rat models of different pain conditions. Neuromodulation J. Int. Neuromodulation Soc. 17, 226–234; discussion 234–235 (2014). [DOI] [PubMed] [Google Scholar]
- 14.Crosby ND, Janik JJ & Grill WM Modulation of activity and conduction in single dorsal column axons by kilohertz-frequency spinal cord stimulation. J. Neurophysiol 117, 136–147 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Litvak LM, Smith ZM, Delgutte B & Eddington DK Desynchronization of electrically evoked auditory-nerve activity by high-frequency pulse trains of long duration. J. Acoust. Soc. Am 114, 2066–2078 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Linderoth B & Foreman RD Conventional and Novel Spinal Stimulation Algorithms: Hypothetical Mechanisms of Action and Comments on Outcomes. Neuromodulation J. Int. Neuromodulation Soc. 20, 525–533 (2017). [DOI] [PubMed] [Google Scholar]
- 17.Tungjitkusolmun S et al. Finite element analyses of uniform current density electrodes for radio-frequency cardiac ablation. IEEE Trans. Biomed. Eng 47, 32–40 (2000). [DOI] [PubMed] [Google Scholar]
- 18.Elwassif MM, Datta A, Rahman A & Bikson M Temperature control at DBS electrodes using a heat sink: experimentally validated FEM model of DBS lead architecture. J. Neural Eng. 9, 046009 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chang I Finite element analysis of hepatic radiofrequency ablation probes using temperature-dependent electrical conductivity. Biomed. Eng. Online 2, 12 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Labonté S Numerical model for radio-frequency ablation of the endocardium and its experimental validation. IEEE Trans. Biomed. Eng 41, 108–115 (1994). [DOI] [PubMed] [Google Scholar]
- 21.LaManna JC, McCracken KA, Patil M & Prohaska O Brain tissue temperature: activation-induced changes determined with a new multisensor probe. Adv. Exp. Med. Biol 222, 383–389 (1988). [DOI] [PubMed] [Google Scholar]
- 22.LaManna JC, McCracken KA, Patil M & Prohaska OJ Stimulus-activated changes in brain tissue temperature in the anesthetized rat. Metab. Brain Dis. 4, 225–237 (1989). [DOI] [PubMed] [Google Scholar]
- 23.Kiyatkin EA, Brown PL & Wise RA Brain temperature fluctuation: a reflection of functional neural activation. Eur. J. Neurosci 16, 164–168 (2002). [DOI] [PubMed] [Google Scholar]
- 24.Tanaka S et al. Mechanisms of sustained cutaneous vasodilation induced by spinal cord stimulation. Auton. Neurosci. Basic Clin. 114, 55–60 (2004). [DOI] [PubMed] [Google Scholar]
- 25.Eng JW-L, Reed CB, Kokolus KM & Repasky EA Housing temperature influences the pattern of heat shock protein induction in mice following mild whole body hyperthermia. Int. J. Hyperthermia 30, 540–546 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang S, Diller KR & Aggarwal SJ Kinetics study of endogenous heat shock protein 70 expression. J. Biomech. Eng 125, 794–797 (2003). [DOI] [PubMed] [Google Scholar]
- 27.Masuda H et al. Local exposure of the rat cortex to radiofrequency electromagnetic fields increases local cerebral blood flow along with temperature. J. Appl. Physiol. Bethesda Md 1985 110, 142–148 (2011). [DOI] [PubMed] [Google Scholar]
- 28.Elwassif MM, Kong Q, Vazquez M & Bikson M Bio-heat transfer model of deep brain stimulation induced temperature changes. Conf. Proc. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. IEEE Eng. Med. Biol. Soc. Annu. Conf 1, 3580–3583 (2006). [DOI] [PubMed] [Google Scholar]
- 29.Kiyatkin EA & Sharma HS Permeability of the blood-brain barrier depends on brain temperature. Neuroscience 161, 926–939 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gahwiler BH, Mamoon AM, Schlapfer WT & Tobias CA Effects of temperature on spontaneous bioelectric activity of cultured nerve cells. Brain Res. 40, 527–533 (1972). [DOI] [PubMed] [Google Scholar]
- 31.Khadka N et al. Minimal Heating at the Skin Surface During Transcranial Direct Current Stimulation. Neuromodulation J. Int. Neuromodulation Soc (2017). doi: 10.1111/ner.12554 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kameyama T, Hashizume Y & Sobue G Morphologic features of the normal human cadaveric spinal cord. Spine 21, 1285–1290 (1996). [DOI] [PubMed] [Google Scholar]
- 33.Valle-Giler EP & Sulaiman WAR Midline minimally invasive placement of spinal cord stimulators: a technical note. Ochsner J. 14, 51–56 (2014). [PMC free article] [PubMed] [Google Scholar]
- 34.Collins CM, Smith MB & Turner R Model of local temperature changes in brain upon functional activation. J. Appl. Physiol. Bethesda Md 1985 97, 2051–2055 (2004). [DOI] [PubMed] [Google Scholar]
- 35.Xu X, Tikuisis P & Giesbrecht G A mathematical model for human brain cooling during cold-water near-drowning. J. Appl. Physiol. Bethesda Md 1985 86, 265–272 (1999). [DOI] [PubMed] [Google Scholar]
- 36.Morrison SF & Nakamura K Central neural pathways for thermoregulation. Front. Biosci. Landmark Ed. 16, 74–104 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hodson DA, Barbenel JC & Eason G Modelling transient heat transfer through the skin and a contact material. Phys. Med. Biol 34, 1493–1507 (1989). [DOI] [PubMed] [Google Scholar]
- 38.Wilson SB & Spence VA A tissue heat transfer model for relating dynamic skin temperature changes to physiological parameters. Phys. Med. Biol 33, 895–912 (1988). [DOI] [PubMed] [Google Scholar]
- 39.Fiala D, Lomas KJ & Stohrer M A computer model of human thermoregulation for a wide range of environmental conditions: the passive system. J. Appl. Physiol. Bethesda Md 1985 87, 1957–1972 (1999). [DOI] [PubMed] [Google Scholar]
- 40.Gabriel S, Lau RW & Gabriel C The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol 41, 2251–2269 (1996). [DOI] [PubMed] [Google Scholar]
- 41.IT’IS Foundation. Tissue Properties Database V3.0. (2015). doi: 10.13099/VIP21000-03-0 [DOI] [Google Scholar]
- 42.Merrill DR, Bikson M & Jefferys JGR Electrical stimulation of excitable tissue: design of efficacious and safe protocols. J. Neurosci. Methods 141, 171–198 (2005). [DOI] [PubMed] [Google Scholar]
- 43.Cantrell DR, Inayat S, Taflove A, Ruoff RS & Troy JB Incorporation of the electrode–electrolyte interface into finite-element models of metal microelectrodes. J. Neural Eng. 5, 54 (2008). [DOI] [PubMed] [Google Scholar]
- 44.Richardot A & McAdams ET Harmonic analysis of low-frequency bioelectrode behavior. IEEE Trans. Med. Imaging 21, 604–612 (2002). [DOI] [PubMed] [Google Scholar]
- 45.Weisstein EW Least Squares Fitting--Power Law. Available at: http://mathworld.wolfram.com/LeastSquaresFittingPowerLaw.html. (Accessed: 1st August 2018) [Google Scholar]
- 46.LaManna JC, Rosenthal M, Novack R, Moffett DF & Jöbsis FF Temperature coefficients for the oxidative metabolic responses to electrical stimulation in cerebral cortex. J. Neurochem 34, 203–209 (1980). [DOI] [PubMed] [Google Scholar]
- 47.Mrozek S, Vardon F & Geeraerts T Brain Temperature: Physiology and Pathophysiology after Brain Injury. Anesthesiology Research and Practice (2012). doi: 10.1155/2012/989487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kim S, Tathireddy P, Normann RA & Solzbacher F In vitro and in vivo study of temperature increases in the brain due to a neural implant. in 2007 3rd International IEEE/EMBS Conference on Neural Engineering 163–166 (2007). doi: 10.1109/CNE.2007.369637 [DOI] [Google Scholar]
- 49.Bikson M et al. Suppression of epileptiform activity by high frequency sinusoidal fields in rat hippocampal slices. J. Physiol 531, 181–191 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pulgar VM Direct electric stimulation to increase cerebrovascular function. Front. Syst. Neurosci 9, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mandel Y et al. Vasoconstriction by Electrical Stimulation: New Approach to Control of Non-Compressible Hemorrhage. Sci. Rep 3, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Thomson SJ et al. Effects of Rate on Analgesia in Kilohertz Frequency Spinal Cord Stimulation: Results of the PROCO Randomized Controlled Trial. Neuromodulation J. Int. Neuromodulation Soc. 21, 67–76 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Al-Kaisy A, Palmisani S, Smith T, Harris S & Pang D The use of 10-kilohertz spinal cord stimulation in a cohort of patients with chronic neuropathic limb pain refractory to medical management. Neuromodulation J. Int. Neuromodulation Soc. 18, 18–23; discussion 23 (2015). [DOI] [PubMed] [Google Scholar]
- 54.Lawson JJ, McIlwrath SL, Woodbury CJ, Davis BM & Koerber HR TRPV1 Unlike TRPV2 Is Restricted to a Subset of Mechanically Insensitive Cutaneous Nociceptors Responding to Heat. J. Pain 9, 298–308 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Matsumi N et al. Thermal damage threshold of brain tissue--histological study of heated normal monkey brains. Neurol. Med. Chir. (Tokyo) 34, 209–215 (1994). [DOI] [PubMed] [Google Scholar]
- 56.Harris AB, Erickson L, Kendig JH, Mingrino S & Goldring S Observations on selective brain heating in dogs. J. Neurosurg 19, 514–521 (1962). [DOI] [PubMed] [Google Scholar]
- 57.Kim JA & Connors BW High temperatures alter physiological properties of pyramidal cells and inhibitory interneurons in hippocampus. Front. Cell. Neurosci 6, 27 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Tasaki I & Byrne PM Heat production associated with synaptic transmission in the bullfrog spinal cord. Brain Res. 407, 386–389 (1987). [DOI] [PubMed] [Google Scholar]
- 59.Childs C Human brain temperature: regulation, measurement and relationship with cerebral trauma: part 1. Br. J. Neurosurg 22, 486–496 (2008). [DOI] [PubMed] [Google Scholar]
- 60.Dietrich WD The importance of brain temperature in cerebral injury. J. Neurotrauma 9 Suppl 2, S475–485 (1992). [PubMed] [Google Scholar]
- 61.Wass CT, Lanier WL, Hofer RE, Scheithauer BW & Andrews AG Temperature Changes of greater or equal to 1 degree Celsius Alter Functional Neurologic Outcome and Histopathology in a Canine Model of Complete Cerebral Ischemia. Anesthesiol. J. Am. Soc. Anesthesiol 83, 325–335. (1995). [DOI] [PubMed] [Google Scholar]
- 62.Wang H et al. Brain temperature and its fundamental properties: a review for clinical neuroscientists. Front. Neurosci 8, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Patel YA, Saxena T, Bellamkonda RV & Butera RJ Kilohertz frequency nerve block enhances anti-inflammatory effects of vagus nerve stimulation. Sci. Rep 7, srep39810 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Chowdhury S, Jarecki BW & Chanda B A molecular framework for temperature-dependent gating of ion channels. Cell 158, 1148–1158 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bennetts B, Roberts ML, Bretag AH & Rychkov GY Temperature dependence of human muscle ClC-1 chloride channel. J. Physiol 535, 83–93 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zheng X, Alsop DC & Schlaug G Effects of transcranial direct current stimulation (tDCS) on human regional cerebral blood flow. NeuroImage 58, 26–33 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lim H, Lee H, Noh K & Lee SJ IKK/NF-κB-dependent satellite glia activation induces spinal cord microglia activation and neuropathic pain after nerve injury. Pain 158, 1666–1677 (2017). [DOI] [PubMed] [Google Scholar]
- 68.Kameyama T, Hashizume Y & Sobue G Morphologic features of the normal human cadaveric spinal cord. Spine 21, 1285–1290 (1996). [DOI] [PubMed] [Google Scholar]