Characterizing Inner Pressure and Stiffness of Trophoblast and Inner Cell Mass of Blastocysts

Abstract

It has long been recognized that mechanical forces underlie mammalian embryonic shape changes. Before gastrulation, the blastocyst embryo undergoes significant shape changes, namely, the blastocyst cavity emerges and expands, and the inner cell mass (ICM) forms and changes in shape. The embryo’s inner pressure has been hypothesized to be the driving mechanical input that causes the expansion of the blastocyst cavity and the shape changes of the ICM. However, how the inner pressure and the mechanics of the trophoblast and the ICM change during development is unknown because of the lack of a suitable tool for quantitative characterization. This work presents a laser-assisted magnetic tweezer technique for measuring the inner pressure and Young’s modulus of the trophoblast and ICM of the blastocyst-stage mouse embryo. The results quantitatively showed that the inner pressure and Young’s modulus of the trophoblast and ICM all increase during progression of mouse blastocysts, providing useful data for understanding how mechanical factors are physiologically integrated with other cues to direct embryo development.

Introduction

Embryonic shape and structures in morphogenesis rely on biochemical and biophysical coordination of cell behaviors during development (1). Recent advances in cell signaling have cast light on cell sorting and patterning for forming different structures in mammalian embryos, yet mechanical properties in different structures and regions of embryos remain poorly understood (2, 3).

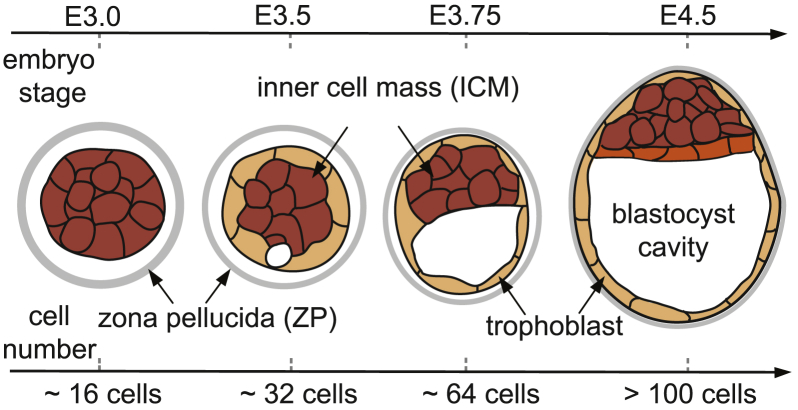
Mechanical forces are known to play a major role in regulating cell fate in the preimplantation mammalian embryo (4, 5, 6, 7). The first lineage specification occurs when some cells move to the inner aspect of the 16-cell morula to define the inner cell mass (ICM—embryo proper) that undergoes compaction and the trophoblast (extraembryonic) (4, 6, 8, 9). As cells secrete fluid, small pockets of intracellular liquid coalesce to form a blastocyst cavity that displaces the ICM eccentrically. The second lineage specification occurs in the blastula when ICM cells segregate to define the epiblast and the primitive endoderm at the margin of the cavity (Fig. 1) (10). Given the temporal correlation between cell-lineage specification and the physical shape changes of the cavity and ICM, together with the reported mechanoresponsive nature of primitive endodermal cells that separate the blastocyst cavity from the ICM (11), it is possible that the inner pressure of the blastocyst cavity mechanically drives the enlargement of the cavity and the corresponding shape changes of the ICM, thereby influencing cell rearrangements that segregate cell lineages (12, 13).

Figure 1.

Preimplantation development of the mammalian embryo. The blastocyst consists of a cavity, inner cell mass (ICM), and trophoblast, with the zona pellucida (ZP) encapsulating the embryo. As the cavity expands, the ICM undergoes significant shape changes. Primitive endoderm (orange) arises from the ICM along the margin of the cavity. E represents embryonic days since conception. To see this figure in color, go online.

To date, little is known about the inner pressure of the blastocyst cavity or mechanical properties of the trophoblast and ICM because of the lack of suitable tools for quantitative characterization. The zona pellucida (ZP) of the embryo forms a barrier for the measurement of the intraembryonic pressure and the ICM mechanics (14). For instance, the cantilevers used in atomic force microscopy (AFM) and the blunt micropipette tips used in micropipette aspiration cannot reach the inside of the embryo for measuring intraembryonic parameters without disturbing the inner pressure (15, 16).

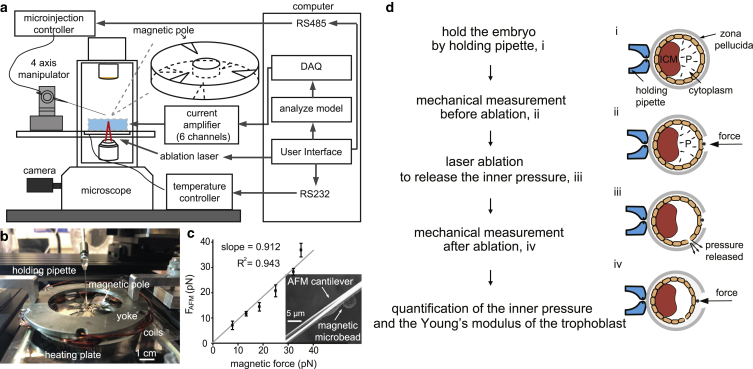
This work presents a laser-assisted magnetic tweezer technique for measuring the inner pressure and the Young’s modulus of different regions of the blastocyst. Shown in Fig. 2 a, the system consists of a multipole magnetic tweezer device, a micromanipulator (MX7600; Siskiyou, Grants Pass, OR), and a biopsy laser (LYKOS Laser, 1460 nm wavelength and 300 mW power; Hamilton Throne, Beverly, MA), which are all installed on a standard inverted microscope (Nikon Ti-S; Nikon, Tokyo, Japan). During experiments, the micromanipulator controls micropipette positioning for magnetic bead deposition, the multipole magnetic tweezer device controls the exertion of indentation forces for mechanical measurement, and the laser ablates the ZP for bead attachment and ablates trophoblast cells for releasing the embryo’s inner pressure.

Figure 2.

(a) A multipole magnetic tweezer with six magnetic poles (three in top layer and three in bottom layer, with the workspace chamber in the center), a micromanipulator, and a biopsy laser were integrated into a standard inverted microscope. (b) A picture of the multipole magnetic tweezer. (c) Magnetic force calibration using AFM, with scanning electron microscopy images showing a magnetic bead fixed onto the AFM cantilever. Error bar, SD; n = 5 measurements. (d) Measurement of embryonic inner pressure and the trophoblast’s Young’s modulus using laser and magnetic micromanipulation: i) intact embryo held by a holding pipette; ii) mechanical measurement of the trophoblast with intact embryo inner pressure; iii) release of embryo inner pressure by laser ablation of trophoblast; and iv) mechanical measurement of the trophoblast after pressure release. The results of steps (ii) and (iv) were substituted into a contact mechanics model (Eq. 2) for decoupling cavity pressure and the Young’s modulus of the trophoblast. To see this figure in color, go online.

Materials and Methods

Design and fabrication of the multipole magnetic tweezers

The multipole magnetic tweezers consist of six magnetic poles with sharp tips (three poles placed in one plane and the other three poles placed in a different plane), a magnetic yoke, and coils. To achieve a large magnetic field gradient, the magnetic poles were made of high-permeability foils (silicon iron alloys; MuShield, Londonderry, NH), and the tips were fabricated by electric discharge machining (Sodick AD325L computer numerical control wire electrical discharge machining, tolerance ± 5 μm). The magnetic yoke was fabricated through computer numerical control machining with a tolerance of ± 0.1 mm. Coils (magnetic wire, gauge 14; Digikey, Thief River Falls, MN) were wired onto the cores on the yoke. The magnetic poles were assembled onto an acrylic plate with alignment marks engraved by laser machining under a microscope to ensure the alignment of each pole pair within the same stage (either top stage or bottom stage). Detailed fabrication and assembly of the multipole magnetic tweezer device can be found in (17).

Blastocyst embryos

Mouse embryos were purchased from Embryotech Laboratories (Haverhill, MA) (four-cell mouse embryos, B4-10). The embryos at four-cell stage were first thawed, then washed in M2 medium (EMD Millipore, Burlington, MA) three times, following the thawing instructions provided by the supplier. Then, the embryos were cultured for an additional 48 h to reach the blastocyst stage in KSOM medium (EMD Millipore) covered with mineral oil to prevent evaporation. The embryo stage was quantified by cell number counting after fixation and DAPI staining.

Mechanical model

To decouple the inner pressure and the Young’s modulus of the trophoblast of an embryo, a contact mechanics model based on the Hertz model was developed. Deformation of trophoblast caused by the magnetic bead was mostly recoverable, indicating largely elastic deformation. Because the radius of the blastocyst embryos was ∼20 times the radius of the magnetic bead (50 vs. 2.5 μm), the contact was assumed to be between a sphere and a half-space. The Hertz model requires the deformation caused by an applied force to be significantly smaller than the thickness of the material under measurement (18). As quantified in our experiments, the deformation caused by the magnetic force (in the range of 0.4–1.2 μm, 0.58 ± 0.10 μm for 12 embryos quantified) was significantly smaller than the thickness of the trophoblast (in the range of 7.9–13.2 μm, 9.3 ± 1.5 μm for 12 embryos quantified). With the embryo’s inner pressure assumed to be homogenously distributed underneath the trophoblast layer, the contact mechanics model is

$$F=P\pi Rd+\frac{4}{3}\frac{E}{1-v^2}{R}^{\frac{1}{2}}{d}^{\frac{3}{2}},$$

where P is the embryo’s inner pressure, E is the Young’s modulus of the trophoblast, v is the Poisson’s ratio of the trophoblast, R is the radius of the magnetic bead, πRd is the contact area, and F and d are the force and bead indentation depths, respectively. In the mechanical model, the Poisson’s ratio of trophoblast is set to be 0.5. As in many studies on mechanical characterization of cells (19, 20, 21), the cells of blastocyst embryos were assumed to be incompressible. Thus, in the mechanical model, the Poisson’s ratio of the trophoblast was set to be 0.5. The incompressible assumption was also verified by the fact that the largest deformation caused by the magnetic bead with a force of 60 pN was very small (e.g., deformation versus cell thickness: 0.58 ± 0.10 vs. 9.3 ± 1.5 μm). Therefore, there was no significant volume change of the cells, i.e., cell volume was conserved during deformation. In experiments, measurements on the trophoblast of all embryos were made in areas without local irregular morphologies, such as local bulges.

Drug treatment

Embryos were treated with cytochalasin D (CD) (4 or 10 μg/mL in culture medium for 2 h, C8273; Sigma-Aldrich, St. Louis, MO) to specifically disrupt actin. CD powder was first dissolved in DMSO at a concentration of 4 mg/mL (or 10 mg/mL), and then 1 μL CD solution was added into 1 mL culture medium as working medium. 1 μL DMSO was added to the control group to avoid the influence from DMSO. Each working medium was added to the embryos 2 h before experiment and washed off by the culture medium three times.

Fluorescent staining

Embryonic day (E) 3.0–4.5 mouse embryos were fixed at 10 min in 4% paraformaldehyde in phosphate-buffered saline (PBS) followed by three washes in PBS. Embryos were permeabilized in 0.1% Triton X-100 in PBS for 20 min and washed three times by PBS. Embryos were then treated with phalloidin conjugate for 1 h (rhodamine phalloidin, dilution rate 1:1000). The nuclei were labeled by DAPI for 1 h (dilution rate 1:1000). Images were acquired using a Quorum Information Technologies (Calgary, Canada) spinning-disk confocal microscope, and image analysis was performed using Volocity software and Image J.

Data processing

The embryo inner pressure/ICM mechanics experiments were conducted while images/videos were collected through a Nikon TE2000-S microscope. Measurement of the embryo was completed within 30 min after it was taken out of the incubator. Trophoblast deformation was measured through tracking the bead position after force application, and the position changes were recorded over time. The centroid of the embryo was also tracked to compensating for drift of imaging during measurement. The collected force-deformation data from image processing have a displacement resolution of 0.2 μm and a force resolution of 4 pN. Data analysis for quantifying apparent Young’s modulus from force-deformation data and straightness of cell-cell contacts shown in Fig. S1 were conducted in MATLAB. The code is available at https://github.com/XianShawn/intraembryo.

Statistical analysis

The error bars presented throughout the work all represent SD. Comparisons of each group were conducted by one-way analysis of variance and Student-Newman-Keuls test for pairwise comparisons in JMP. The statistical significance in each comparison was evaluated as p < 0.05 for significance level.

Results and Discussion

The multipole magnetic tweezer device consists of six magnetic poles with sharp tips, a magnetic yoke, and coils. Distinct from traditional single-pole magnetic tweezers that can only apply pulling forces, this multipole magnetic tweezer device is capable of applying forces along three axes. To achieve a large magnetic field gradient, the magnetic poles were made of high-permeability foils (shielding alloys; MuShield) and the tips were fabricated by electrical discharge machining. The magnetic yoke strengthens the magnetic field by connecting all poles into a complete magnetic circuit. Coils were wired onto the cores on the yoke. Details of the magnetic tweezer device were previously described (17). The magnetic tweezer device was placed on a temperature-controlled heating plate (microplate heater; Cell MicroControls, Norfolk, VA). The coil current is controlled by a DAQ board with custom designed current amplifiers with feedback from current sensors.

The force exerted by the magnetic bead is quantified through the magnetic force model (17),

$${\mathit{F}}_{\mathit{mag}}=k_i{\mathit{I}}^{\mathit{T}}\mathit{NI}+k_i{I}_{max}^2\mathit{KP}\mathrm{.}$$ (1)

and

$$\mathit{K}=\left[\begin{array}{ccc}\frac{8}{l}& 0& 0\\ 0& \frac{8}{l}& 0\\ 0& 0& \frac{32}{l}\end{array}\right]$$

and

$$\mathit{P}=\left[\begin{array}{c}x\\ y\\ z\end{array}\right],$$

where I is the current matrix consisting of the current in each coil; I_max is the maximal current in each coil (2 A in this work); N is the magnetic reluctance matrix, which depends on the pole and yoke materials and coil turns (40 turns in each coil); l equals 400 μm and is the distance between the workspace center and the pole tip; P is the position of the bead; and k_i is a linear factor that was experimentally calibrated. The magnetic forces were calibrated by gluing a magnetic microbead on an AFM cantilever (see Fig. 2 c). Thermal spectroscopy (Nanoscope 8.10) was performed to accurately measure the spring constant of the AFM cantilever (spring constant 0.01 N/m, MSNL-10-C; Bruker, Billerica, MA) with the microbead fixed on its back. Applying currents to the coils exerted magnetic forces on the microbead and deformed the AFM cantilever. F_AFM was quantified through cantilever deformations and its spring constant. Fig. 2 c shows the calibration results. The root mean-square of the deviations between forces measured by the AFM cantilever and the model-calculated force reveal that resolution of the generated magnetic force is better than 3.75 pN.

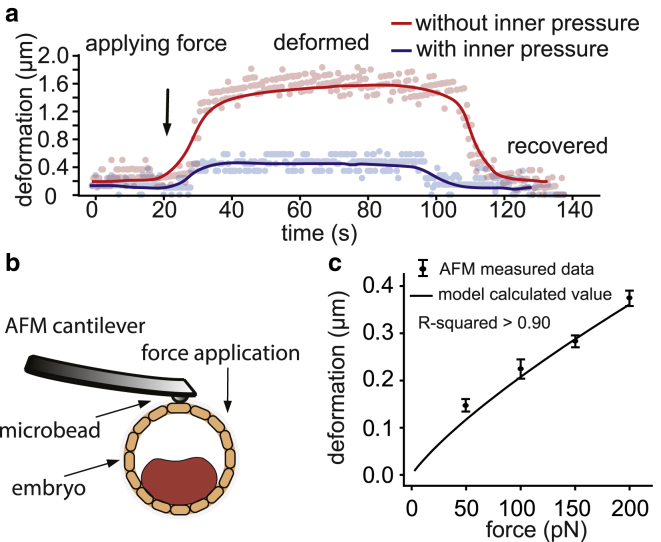
A mouse embryo was first held by a holding micropipette mounted on the micromanipulator (step i in Fig. 2 d). The laser was controlled to precisely ablate a hole in the ZP, and a magnetic bead (diameter: 5.0 μm, CFM-40-10, permeability: 0.35 H/m; Spherotech, Lake Forest, IL) was deposited directly onto the trophoblast cells (step ii in Fig. 2 d). The magnetic bead was then controlled to apply a 60 pN force to deform the trophoblast. The force-deformation data (blue curve in Fig. 3 a) reflect both the mechanical properties (Young’s modulus) of the trophoblast and the embryo’s inner pressure. The laser was then controlled to ablate a hole in the trophoblast at a different position on the embryo to release the cavity pressure (step iii in Fig. 2 d). It was observed that the blastocyst cavity of the embryo gradually collapsed during pressure release (step iv in Fig. 2 d). After the size of the embryo and cavity reached the steady state, the magnetic bead was controlled by the magnetic tweezer to apply the same force (60 pN) to the trophoblast at the same location on the embryo. The force-displacement curve collected this time (red curve in Fig. 3 a) reflects only the mechanical property of the trophoblast. The force-displacement data collected with and without the embryo’s inner pressure were then used to decouple the Young’s modulus of the trophoblast and the embryo’s inner pressure. A total of 12 mouse embryos were tested, and the embryos were fixed immediately after mechanical measurements and stained by DAPI for cell number counting.

Figure 3.

(a) Embryo deformation caused by magnetic-bead-applied force (60 pN) on trophoblast. (b) AFM characterization of blastocyst embryo after removing the ZP. (c) AFM-measured force-deformation data and the force-deformation relationship calculated using the experimentally measured embryo inner pressure and Young’s modulus of the trophoblast of the same embryo. R-squared value is larger than 0.90. n = 5 measurements for each data point; error bar: SD. To see this figure in color, go online.

To decouple the inner pressure and the Young’s modulus of the trophoblast of an embryo, a contact mechanics model based on the Hertz model was developed. Deformation of the trophoblast caused by the magnetic bead was observed to be mostly recoverable, i.e., elastic deformation (Fig. 3 a). Because the area of the trophoblast layer is significantly larger than the area of contact by the magnetic bead on trophoblast, the embryo’s inner pressure is assumed to be homogenously distributed underneath the trophoblast layer. Hence,

$$F=P\pi Rd+\frac{4}{3}\frac{E}{1-v^2}{R}^{\frac{1}{2}}{d}^{\frac{3}{2}},$$ (2)

where P is the embryo’s inner pressure (gauge pressure, which is the absolute pressure minus atmospheric pressure or medium pressure); E is the Young’s modulus of the trophoblast; v is the Poisson’s ratio of the trophoblast and set to be 0.5, assuming the trophoblast is incompressible under small deformations; R is the radius of the magnetic bead; πRd is the contact area; and F and d are the force and bead indentation depths, respectively.

To validate the measured embryo inner pressure, AFM indentation was conducted, with different forces exerted onto the trophoblast and deformations recorded. As shown in Fig. 3 b, the AFM-measured force-deformation relationship showed good agreement (R-squared > 0.90) with the force-deformation relationship calculated using our experimentally measured embryo inner pressure and trophoblast’s Young’s modulus. The maximal deviation between the AFM-measured and the model-calculated trophoblast deformations was 0.02 μm, which validates the measured embryo inner pressure. The model validation data (Fig. 3 c) also indicated that the Young’s modulus of the trophoblast is independent of the embryo inner pressure, as assumed by the model in Eq. 2.

During morula through blastocyst progression, the ICM of the embryo undergoes shape changes (Fig. 1). To measure the mechanical properties of the ICM, the magnetic microbead was introduced into the cavity of the embryo through microinjection. The injection micropipette stayed inside the embryo to maintain the embryo’s inner pressure and thus the prestress on the ICM (Fig. 4 d). The magnetic bead was navigated three-dimensionally onto the center of the ICM to apply forces of 60 pN and deform the ICM for mechanical characterization (17).

Figure 4.

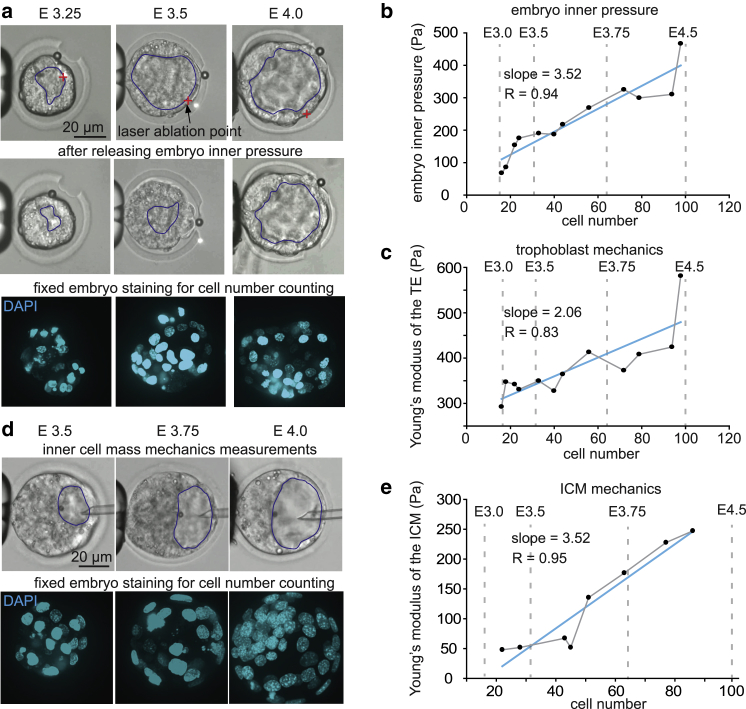
(a) Measurement on trophoblast with and without embryo inner pressure in different stages of blastocyst embryos and fixation of embryo for cell counting. The blastocyst cavity was labeled manually (blue lines) based on the clear contour of the trophectoderm. The red cross in the images indicates the laser ablation point on the trophoblast. Magnetic bead size: 4.8 ± 0.2 μm. (b) Embryo inner pressure of different embryo stages; n = 12, t-test trend analysis p < 0.0001, linear regression coefficient R = 0.94. (c) The Young’s modulus of the trophoblast of different embryo stages; n = 12, t-test trend analysis p = 0.008, linear regression coefficient R = 0.83. (d) Measurement on ICM in different stages of blastocyst embryos and fixation of embryo for cell counting. The blastocyst cavity was labeled manually (blue lines) based on the clear contour of the trophectoderm. (e) The Young’s modulus of the trophoblast of different embryo stages; n = 8, t-test trend analysis p = 0.0003, linear regression coefficient R = 0.95. To see this figure in color, go online.

The measured results from 12 embryos ranging from embryonic day E3.0 (∼16 cells) to E4.5 (>100 cells) revealed significant increase of inner pressure with embryo stages (quantified through cell number counting). The data summarized in Fig. 4 b (linear regression coefficient R = 0.94) also show a significant uphill slope, and the embryo’s inner pressure at E4.5 is ∼3.7 times that of E3.0. The increasing inner pressure can be attributed to the stronger osmotic process across the trophoblast (13). Trophoblast cells are known to be abundant with sodium and potassium pumps, which are responsible for increased ion concentrations inside the blastocyst cavity (22). The higher ion concentrations promote the osmotic process, which transports more water into the embryo, thus increasing the pressure inside the embryo (13). The increasing inner pressure enlarges the blastocyst cavity, which disrupts the radial symmetry of the embryo and establishes a symmetry along an axis called the embryonic/abembryonic axis, with the ICM at the embryonic pole and the cavity at the abembryonic pole (23). The embryonic/abembryonic axis of the embryo further aligns with the longest diameter of the ZP, thus terminating free rotation of the embryo within the ZP (24).

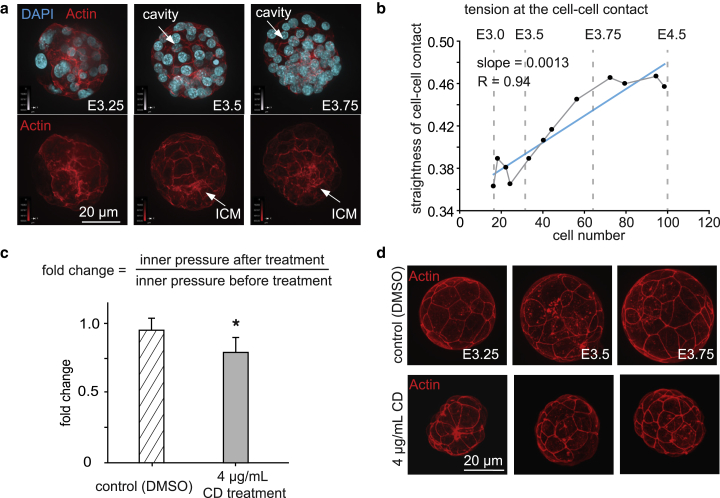
Fig. 4 c shows that Young’s modulus of the trophoblast increases during development, and linear regression shows a significant uphill slope (R = 0.83, p = 0.008). The Young’s modulus of the trophoblast at embryonic day E4.5 is ∼1.6 times that of E3.0. Fig. 4 e shows that the Young’s modulus of the ICM increased 3.6 times from E3.0 to E4.5, based on the linear regression result from eight embryos, with a significant uphill slope (R = 0.95, p = 0.0003), indicating significant stiffening of the ICM. To study the reasons for the stiffening of the trophoblast and the ICM, the cortical actin was stained in different stages of embryos. Because the straightness of cell-cell contact from cortical actin staining can indicate tension (25, 26, 27), cortical actin was stained in different stages of embryos. Straightness was defined as the ratio of the length of the reference line (a straight line connecting the start and the end of one cell-cell contact) over the summation of the distance from each sampled dot on the cell-cell contact to the reference line, as shown in Fig. S1. The results showed that, with increase in cell number, the cell density increased, and cortical actin became more clearly defined at cell-cell junctions in the trophoblast layer (Fig. 5 a); the straightness of cell-cell contact also increased (R = 0.94, p < 0.0001), indicating increased tension and tighter cell-cell junctions (Fig. 5 b). The increased inner pressure exerted on the surface of the trophoblast and ICM potentially induces mechanically sensitive pathways (11, 12) (e.g., the Rho (28) and Hippo (29) pathways), which lead to the upregulation of actin filaments and remodeling of actin organization for higher cortical tension. The updated regulated actin expression (30), together with the higher tension between the cell-cell contact (31), potentially stiffens the trophoblast and ICM.

Figure 5.

(a) Nucleus and actin staining of different embryo stages shows intercellular cortical actin is more clearly defined over time. Nucleus: DAPI (blue), actin filaments: Alexa Fluor 594 phalloidin (red). (b) Straightness of the cell-cell contacts of trophoblast of different embryo stages; n = 12, t-test trend analysis p = 0.0001, linear regression coefficient R = 0.94. The straightness value was calculated as the ratio of the length of the reference line (a straight line connecting the start and the end of one cell-cell contact) over the summation of the distance from each sampled dot on the cell-cell contact to the reference line. The value of straightness is close to 1 if the cell-cell contact line is close to a straight line. A higher value of straightness indicates a higher cortical tension in the cell-cell contact. The value straightness is close to 0 if the cell-cell contact is more curved, indicating smaller cortical tension in the cell-cell contact. The average straightness value of 20 lines in each embryo was used to represent the line straightness of the embryo. (c) Fold change of embryo inner pressure after treatment by DMSO (control group) and CD (CD) with a concentration of 4 μg/mL. n = 5 embryos, error bar: SD, p = 0.03. The fold change of embryo inner pressure is defined as the ratio of inner pressure measured after treatment over inner pressure measured before treatment. (d) Actin staining of the embryos treated by DMSO and CD. The CD-treated embryos were smaller in size compared with the control group of the same stage. The cell-cell contact was more straight in the control group, compared with the more curved shape in the CD-treated group. To see this figure in color, go online.

The stiffened trophoblast and ICM with more cell-cell junctions keep fluid from exiting through the epithelial layer, providing a tighter seal that may increase inner pressure. When the sealing was impacted through disrupting actin via CD treatment (Fig. 5, c and d; Fig. S3), the embryo inner pressure became significantly lower. As shown in Figs. 5, c and d and S3, moderate CD treatment (4 μg/mL) resulted in marginally significant change of actin intensity (Fig. S3 b), and marginally significantly decreased embryo inner pressure (Fig. 5 c). High-concentration CD treatment (10 μg/mL) resulted in larger intensity changes of actin; however, it also resulted in the collapse of the blastocyst cavity (Fig. S3 a). The result indicated the necessity of actin (and cortical tension) for maintaining the embryo’s inner pressure. However, whether actin is the primary structure that determines the embryo inner pressure and how tubulin (32), integrin subunits (33), cadherin, and other adhesion molecules (23) contribute to the embryo inner pressure require further investigations.

The growth of actin networks, driven by the tension on cell surfaces exerted by the embryo’s inner pressure (34), plays a crucial role during development (35). It has been shown that disrupting the actin organization by cytochalasin B resulted in impaired development of embryos. In addition, rescuing actin with melatonin reversed the disrupted expression patterns of genes related to actin organization (Arhgef2, Bc2, Coro2b, Flnc, and Pallld) and rescued cytochalasin-B-induced impaired embryonic development (36). Considering the mechanosensitive nature of actin and the potential role of the inner pressure as a mechanical stimulus, disrupted embryo inner pressure could potentially result in impaired embryo development.

Conclusions

In summary, we have, for the first time to our knowledge, experimentally characterized the inner pressure, Young’s modulus of the trophoblast, and ICM of preimplantation mouse embryos. The results quantitatively showed that the inner pressure and the Young’s modulus of trophoblast and ICM all increase during blastocyst stages and provide data for understanding how mechanical factors are physiologically integrated with other cues to direct embryo development.

Author Contributions

X.W., S.H., and Y.S. designed the experiments and wrote the manuscript. X.W., Z.Z., and H.T. performed experimental work. X.W., J.L., S.H., and Y.S. performed theoretical and image analyses.

Editor: Philip LeDuc.