Predicting Collective Migration of Cell Populations Defined by Varying Repolarization Dynamics

Abstract

Collective migration of heterogeneous cell populations is an essential aspect of fundamental biological processes, including morphogenesis, wound healing, and tumor invasion. Through experiments and modeling, it has been shown that cells attain front-rear polarity, generate forces, and form adhesions to migrate. However, it remains unclear how the ability of individual cells in a population to dynamically repolarize themselves into new directions could regulate the collective response. We present a vertex-based model in which each deformable cell randomly chooses a new polarization direction after every defined time interval, elongates, proportionally generates forces, and causes collective migration. Our simulations predict that cell types that repolarize at longer time intervals attain more elongated shapes, migrate faster, deform the cell sheet, and roughen the leading edge. By imaging collectively migrating epithelial cell monolayers at high temporal resolution, we found longer repolarization intervals and elongated shapes of cells at the leading edge compared to those within the monolayer. Based on these experimental measurements and simulations, we defined aggressive mutant leader cells by long repolarization interval and minimal intercellular contact. The cells with frequent and random repolarization were defined as normal cells. In simulations with uniformly dispersed leader cells in a normal cell population at a 1:10 ratio, the resulting migration and deformation of the heterogeneous cell sheet remained low. However, when the 10% mutant leaders were placed only at the leading edge, we predicted a rise in the migration of an otherwise normal cell sheet. Our model predicts that a repolarization-based definition of leader cells and their placement within a healthy population can generate myriad modes of collective cell migration, which can enhance our understanding of collective cell migration in disease and development.

Introduction

In the natural and human-made worlds, individual entities dynamically interact with each other and their heterogeneous environment, giving rise to complex collective movements that regulate fascinating processes such as migration of bird flocks, bacterial swarming, floating of icebergs, traffic movements, self-organization in animal herds, and cell migration in tissues (1, 2, 3, 4, 5). The physical principles that define these interactions among entities and their responses to external cues vary from system to system. The collective migration of living cells has emerged as a particularly complex process given that individual cells can generate forces and form adhesions by sensing a variety of physical, chemical, and biological cues presented by their extra- and intracellular environments. These cell-cell and cell-environment interactions result in several known modes of collective cell migration (6, 7). Because the ability of different cell types to migrate collectively regulates fundamental biological processes in disease, development, and regeneration (8, 9, 10), such as morphogenesis, wound healing, and tumor cell invasion across organs, it is critically important to understand the underlying biophysical principles.

As single cells move forward, they form focal adhesions with the extracellular matrix, generate forces through actin-myosin engagement, extend frontward protrusions through dynamic actin polymerization, and coordinate turnover of adhesions (11, 12). During this process, one of the key decisions the cell makes is to polarize its machinery along a given direction, which defines front and rear regions within the cell (13, 14). In the polarized form, protrusion-enabling molecules such as Rac and PI3K accumulate in the front, whereas a high activity of force-generating signals such as RhoA and myosin II is observed in the rear part of the cell (15). These intracellular gradients of mechanotransductive signals are sensitive to extracellular biochemical and mechanical cues (16, 17) and can dynamically change within seconds to minutes (18, 19, 20). This biochemical polarization of signals within the cells also gives rise to morphological elongation of the cell body, which is associated with higher mechanoactivation, migration speed, and epithelial-mesenchymal transition (EMT) in grouped cells (17, 21, 22, 23, 24, 25). In collective cell populations, elongated cell shape predicts enhanced motility (26) and “unjamming” of epithelial colonies (27). It has been shown that the social interaction of grouped cells can be orchestrated through either cellular coattraction following chemokine gradients (28) or cell-cell contact inhibition via EMT (29) during the collective migration of neural crest cells.

Over the last decade, several modeling strategies have been adopted to analyze and understand collective cell dynamics of homogeneous and heterogenous cell populations (7). Within a cellular Potts modeling framework, the polarity of leader cells has been defined in relation to external cues, and monolayer dynamics have been analyzed to better understand how cell-cell coordination may govern tumor invasion (30, 31). Through modeling and experimental measurements, the persistence time of cell polarity has been correlated with movement within the endothelial cell monolayers (32). Through active Voronoi models (27, 33, 34, 35, 36), glassy dynamics of epithelial tissues have been correlated with jamming of cellular motions, and shape factor has been associated with individual cells. A recent active vertex model combines vertex dynamics with active matter physics to simulate tissue growth, cell division, and collective motion in one framework (37). Although existing models of collective cell migration have revealed important roles of cell-cell cooperativity in collective dynamics, it remains unexplored how the ability of different cell types to dynamically polarize themselves influences the modes of collective cell migration. Furthermore, it remains unclear how the spatial placement of persistently polarized cells within a monolayer might affect the collective response. These are important gaps in our current understanding, given that cell populations involved in morphogenesis and tumor invasion are often composed of cells with heterogeneous intrinsic properties, which have been characterized in terms of generated forces, focal adhesion, oncogenic mutations, and stiffness (38, 39, 40). Along these lines, cell types that differ in their polarization dynamics could also differentially regulate grouped cell behavior. Although heterogeneous epithelial systems have been studied (30, 31, 32, 34, 41), it has not been investigated how the population would behave if specific cells are predisposed with defined repolarization dynamics. Given that cell polarity is dictated by spatiotemporally varying biochemical gradients of several signaling molecules (15), it is not easy to experimentally measure “polarization” as a cellular property. For this reason, at this stage, a computational model that specifically defines cell polarization as a time-dependent parameter can serve as an important tool for understanding the role of dynamic cell repolarization in regulating the collective cell response.

In this article, we develop a computational framework to simulate collective cell migration in which individual cells have the ability to reorient themselves in different directions and generate forces according to their shape in a spatiotemporally varying fashion. First, we assign a randomly chosen direction for each cell within a colony, and a new random direction is chosen every time after a defined repolarization time interval (RTI). Simulations are performed for RTI varying between 1 and 10 min, which were calibrated by experimental measurements. Here, the higher values of RTI caused a cell to generate protrusive force along a given direction for longer duration, causing more elongated cell shapes, faster motility, and roughening of the leading edge. Next, we assumed that more aggressive cell types pick polarization directions that minimize contact with their neighbors, which led to a further rise in cell migration and leading-edge roughness (LER). To understand how repolarization of individual cells within a monolayer occurs in reality, we performed experiments of collective migration of MCF10A mammary epithelial cells on hydrogels and found that the average repolarization interval of cells at the leading edge was higher than those in the core of the monolayer. Based on these experimental results and modeling predictions, we defined aggressive mutant cells corresponding to polarity parameters of a long RTI and minimal cell-cell contact. In contrast, normal cells possessed random repolarization with a short RTI. We simulated the migration of cell colonies with heterogeneous populations of normal and mutant cells, mimicking in vivo situations of mutants either randomly dispersed or acting as leaders of the migrating population.

Our model implements cell polarization as a defining cellular property, and these simulations and experiments provide novel, to our knowledge, insights into how the repolarization of individual cells and the placement of mutant-leader cells within a population could result in varying collective migration phenotypes. This mathematical framework can serve as a valuable tool for exploring the behavior of other biological or synthetic grouped systems in which individual entities can vary in terms of their persistence of polarization or migration in defined directions.

Materials and Methods

Computational model

Overview of the vertex model

We develop a new, to our knowledge, vertex-based collective cell model in which each cell is allowed to deform, repolarize its direction of protrusion at defined frequency, and generate forces proportional to the degree of front-rear polarization. This modified vertex dynamics model is implemented in the Cancer, Heart, and Soft Tissue Environment (CHASTE) software (42, 43). To model a monolayer, each cell is represented as a polygon. A collection of these polygonal cells is referred to as a “mesh,” which comprises a set of “elements” and “vertices,” wherein each vertex is defined as a point that moves in time and space (Fig. 1 A). Forces act upon these vertices under the assumption of an overdamped motion of vertices (44). In a two-dimensional treatment of the cell monolayer, the equation of motion for any vertex i is written as follows:

$$\frac{d{r}_i}{dt}=\frac{F_i}{\mu },$$ (1)

where r_i is the position of the ith vertex, and F_i is the total force acting on this vertex. μ = 2 × 10⁻³ N ⋅ s ⋅ m⁻¹ is the damping constant.

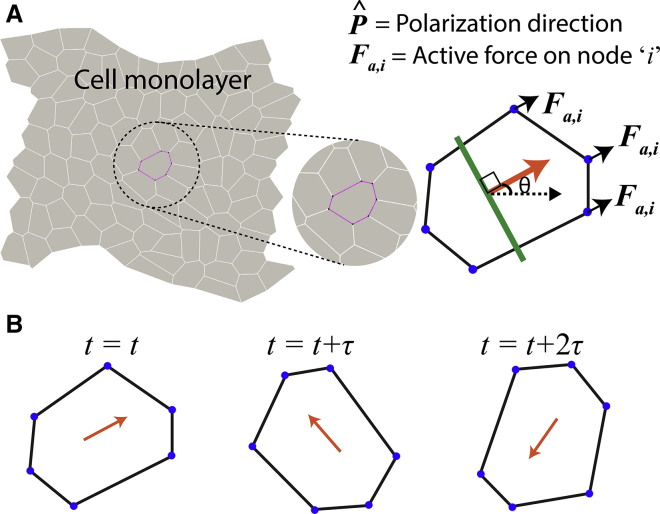
Figure 1.

(A) Vertex-based model of a cell monolayer with deformable cell bodies with active forces F_a,i acting on vertices that lie in the front of a line perpendicular (in green) to the polarization direction $\hat{P}$ (in orange) for each cell. (B) A schematic describing a new polarization direction chosen after every repolarization time interval (RTI) τ for each cell within the monolayer. To see this figure in color, go online.

Active and passive forces

The net force on any vertex has two contributions: active and passive. The passive forces arise because of cellular deformations, which are modeled by minimizing the free-energy contributions from the cell body and cell membrane. The free energy E for an element j is given by the following (45):

$$E_j=\frac{K_j}{2}{\left(A_j-A_j^0\right)}^2+\frac{{\mathit{\Gamma }}_j}{2}{\left(p_j\right)}^2+\sum _{m=0}^{n_k-1}{\mathit{\Lambda }}_{j,m}{d}_{j,m}.$$ (2)

Here, the first term represents cell elasticity, with K_j representing elastic constant and A_j and $A_j^0$ representing the actual and target cell areas, respectively. The second term represents the supracellular actin-myosin ring contractility, where Γ_j is a proportionality constant, and p_j is the perimeter. The third term represents line tension Λ_j,m at junctions between element j and its n_k neighbors, and d_j,m is the corresponding shared edge length. Edges of an element that are not shared by a neighboring element (i.e., for cells at the leading edge) can have a different line tension. The values of these parameters corresponding to “passive” properties of the cell are kept constant for all elements: $K_j=40\times {10}^{9}N/m^3,A_j^0=1\times {10}^{-12}{m}^2,{\mathit{\Gamma }}_j=0.5\times {10}^{-3}N/m$,${\mathit{\Lambda }}_{j,interior}=2.5\times {10}^{-9}N,\text{and}{\mathit{\Lambda }}_{j,boundary}=5\times {10}^{-9}N$, where interior and boundary refer to cell contacts on the interior and on the boundary of the cell cluster, respectively. Thus, the passive force acting on each vertex i is given by the following:

$$F_{passive,i}=-{\mathit{\nabla }}_{\text{i}}\sum _{j\in N_i}{E}_j,$$ (3)

where N_i denotes the set of elements that emanate from the vertex i.

Regulation of active forces through cell polarity

Higher cell elongation is a key marker of mesenchymal phenotype. It has been shown that epithelial cells that undergo EMT attain elongated morphology, form more prominent stress fibers, and generate higher forces (21, 22, 23, 46). Our recent study has shown that cells on more elongated adhesive patterns of constant area generate higher net tractions (47). Based on this knowledge, we formulate a simple phenomenological choice of higher forces for more elongated cell shapes. The forces may rise until the high elongation of the cell causes a saturation. The active forces have been modeled proportional to the elongation shape factor of the cell j, defined as the square root of the ratio of the second moments of the cell around its principal axes, written as follows:

$$F_{a,i}=\{\begin{array}{c}\begin{array}{cc}\sum _{j\in N_i}\left(\frac{K{e}_j\left|\overrightarrow{r_i^{\text{'}}}\cdot {\hat{P}}_j\right|}{{\sum }_{i\in m_j}\left|\overrightarrow{r_i^{\text{'}}}\cdot {\hat{P}}_j\right|}\right),& \overrightarrow{r_i^{\text{'}}}\cdot {\hat{P}}_j\ge 0and{e}_j\le e_{j,max}\end{array}\\ \begin{array}{cc}\sum _{j\in N_i}\left(\frac{K{e}_{j,max}\left|\overrightarrow{r_i^{\text{'}}}\cdot {\hat{P}}_j\right|}{{\sum }_{i\in m_j}\left|{\overrightarrow{r}}_i^{\text{'}}\cdot {\hat{P}}_j\right|}\right),& \overrightarrow{r_i^{\text{'}}}\cdot {\hat{P}}_j\ge 0and{e}_j>e_{j,max}\end{array}\\ \begin{array}{cc}0,& {\overrightarrow{r\text{'}}}_i\cdot {\hat{P}}_j<0\end{array}\end{array}.$$ (4)

Here, F_a,i is the active force on a vertex i, N_i is the set of cells in contact with the vertex i, K = 2.5 × 10⁻⁹ N is a scaling constant, and m_j are the vertices that are in the “front” region of the cell j with respect to its polarization direction${\hat{P}}_j$. The variable e_j is the elongation shape factor of the cell j, and e_j,max = 3 is the maximal allowed contribution toward the active force F_a,i. The front region of the cell j is defined with respect to its polarization such that any given vertex i lies in the front of the cell if $\left(\overrightarrow{r_{\mathit{i}}^{\mathit{\text{'}}}}\cdot {\hat{P}}_j\right)\ge 0$. Here, $r_i^{\text{'}}=r_i-r_{cm}$ is the position of the vertex i relative to r_cm, the position of the center of mass of the cell j. Thus, Eq. 4 captures the active force contributions from every neighboring cell j in contact with the vertex i (total N_i cells in contact with vertex i). The net force Ke_j acts on each cell, which is distributed among its front vertices proportional to $\left|\overrightarrow{r_i^{\mathit{\text{'}}}}\cdot {\hat{P}}_j\right|$.

Dynamics of cell repolarization

The direction of polarization $\hat{P}$ for each cell j is calculated from a set of 24 possible angles between 0 and 2π, equally discretized at an interval of π/12, and is chosen after a defined RTI τ_j (Fig. 1 B). In the first part (Figs. 2 and 3 and normal cells afterward), the probability of choosing a given angle of polarity is equal for all directions. In a modified version (Figs. 4 and 5 and mutant cells in Fig. 7), the probability corresponding to a given direction is weighted by the total cell-cell contact in the front of the cell. The criterion for cell polarization along the direction of minimal cell-cell contact incorporates a specific mechanism through which leading-edge cells continually polarize themselves in the outward (away from the monolayer) direction. This phenomenological choice is based on the idea that more aggressive and motile cells minimize contact with their neighbors by undergoing EMT (48). Indeed, our experimental measurements (Fig. 6; discussed ahead) show a higher RTI of the leading-edge cells compared to those within the monolayer. Wherever the cell polarity is defined by the minimal cell-cell contact criterion, a probability corresponding to every given direction is weighted by the total cell-cell contact in the front of the cell. Thus, for each of the 24 possible angles θ_n, where n ∈ [0, 24], cell-cell contact length in the front of the cell, l_n, is calculated. After this, the probability of choosing a direction θ_n depends on the value of l_n. The higher the value of l_n for a particular direction θ_n, the less likely it will be picked. We assigned a probability weight function W(l_n) = l_max − l_n, with l_max = 25 μm, corresponding to all possible angles.

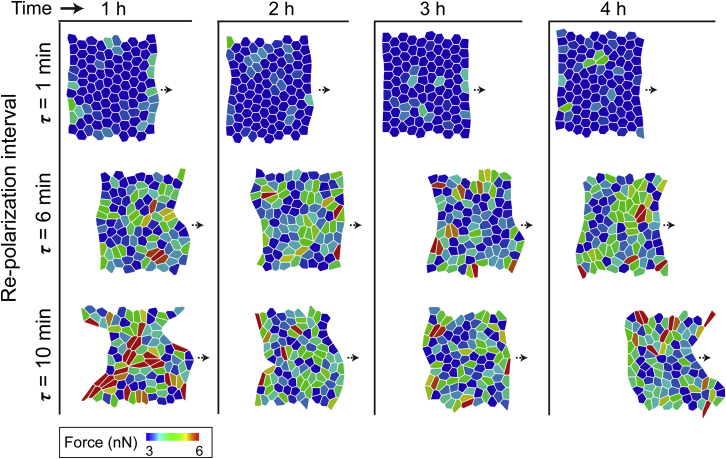
Figure 2.

Simulated configurations of cell sheets corresponding to cell repolarization intervals τ = 1, 6, and 10 min, with randomly chosen polarization directions after every RTI (τ ) at different time points over the total simulation time of 4 h. Here, each cell is color-coded by active cellular forces at a given time point. To see this figure in color, go online.

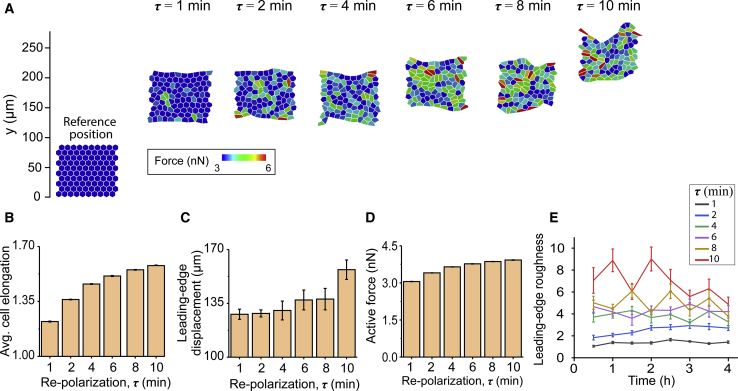
Figure 3.

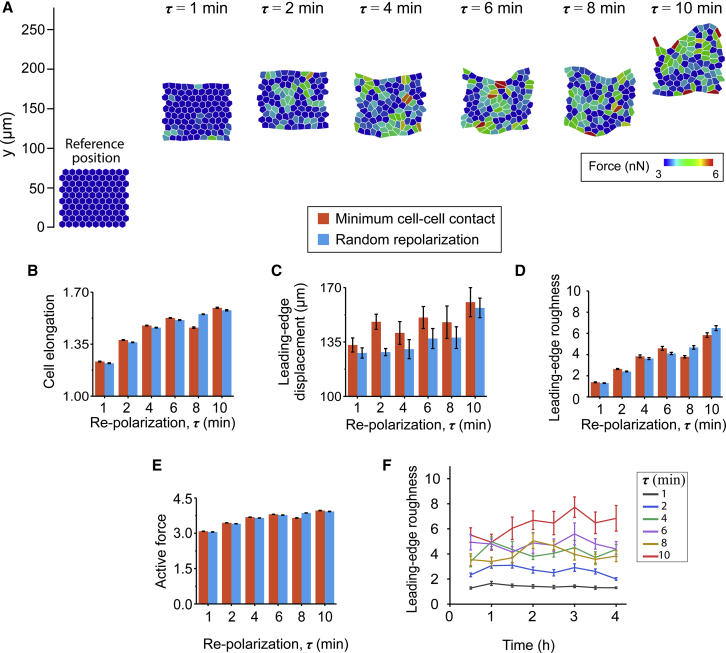
(A) The final configuration of cell sheets after 4 h of simulation time for cell repolarization intervals τ = 1, 2, 4, 6, 8, and 10 min, with randomly chosen directions after every RTI (τ ). Shown are plots of (B) average cell elongation shape factor, (C) average leading-edge displacement, and (D) active force for each repolarization condition, calculated by averaging over the entire duration of the simulation. (E) The temporal evolution of the leading-edge roughness (LER) for each case of repolarization interval. Error bars represent the standard error. To see this figure in color, go online.

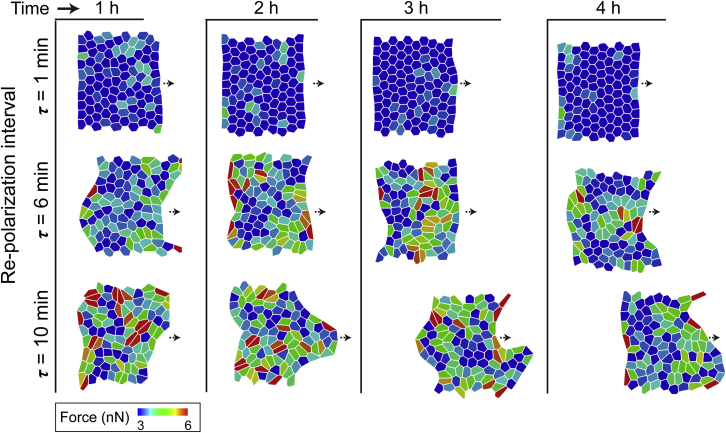
Figure 4.

For polarization directions chosen using a minimal cell-cell contact criterion, simulated configurations of cell sheets corresponding to cell repolarization intervals τ = 1, 6, and 10 min at different time points over the total simulation time of 4 h, where each cell is color-coded by active cellular forces. To see this figure in color, go online.

Figure 5.

For the case where polarization directions are chosen using a minimal cell-cell contact criterion, (A) final configuration of cell sheets after 4 h of simulation time, for cell repolarization intervals τ = 1, 2, 4, 6, 8, and 10 min. Shown are plots of (B) average cell elongation shape factor index, (C) average leading-edge displacement, (D) average leading-edge roughness (LER) for each repolarization condition, and (E) average active force, calculated by averaging over the entire duration of the simulation. (B–D) Comparisons are made between the cell polarization criteria of random directions and minimal cell-cell contact. (F) Temporal evolution of the LER for each case of repolarization interval. Error bars represent the standard error. To see this figure in color, go online.

Figure 7.

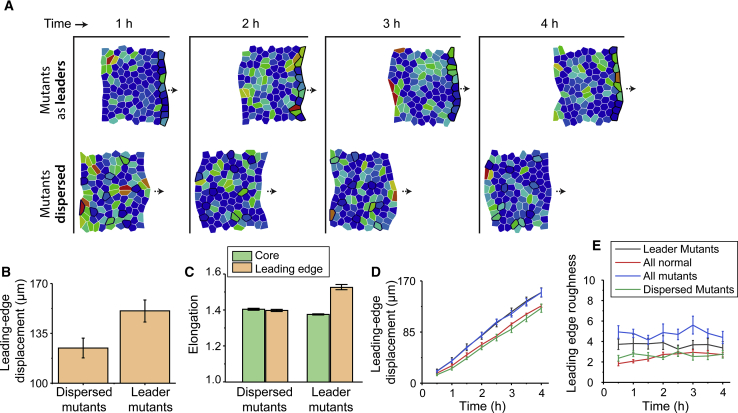
(A) Simulated configurations of cell sheets at different time points over the total simulation time of 4 h for two different heterogeneous cell populations: (bottom row) mutants dispersed within a normal cell population and (top row) mutants at the leading edge of a normal cell population. Here, mutant cells (outlined in black) are defined by minimal cell-cell contact polarization criterion and τ = 6 min. Normal cells in the core of the monolayer are defined by τ = 2 min with random repolarization. All cells are color-coded by active force magnitudes. (B) The average leading-edge displacement and (C) average cell elongation shape factor for the two cases of dispersed and leader placements of mutant cells are shown. Shown is the temporal evolution of (D) the mean leading-edge displacement and (E) the leading-edge roughness (LER) for four different cell populations: purely normal, purely mutant, mutants-as-leaders, and dispersed mutants. To see this figure in color, go online.

Figure 6.

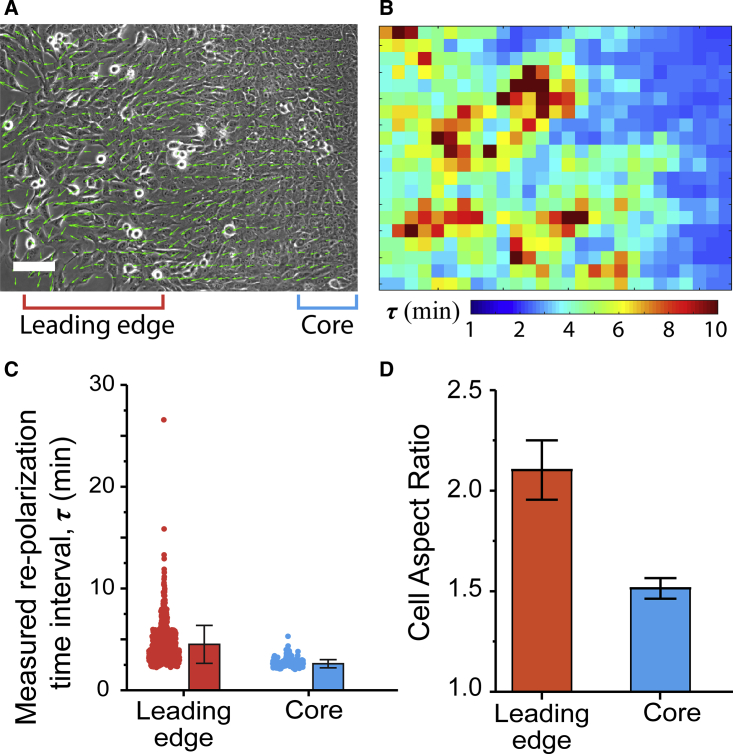
(A) A phase contrast image of a migrating cell monolayer, with arrows indicating velocity vectors. Scale bars, 100 μm. Columns 2–13 are leading-edge, and columns 25–27 are core. (B) A corresponding heat map of the measured repolarization time interval (RTI) averaged over the 4 h of the time-lapse video. (C) Beeswarm and bar plots of RTI averaged over N > 50 elements in the core and leading-edge regions of at least three monolayers. Error bar represents the SD. (D) The aspect ratio (major axis/minor axis) of cells in the core and leading-edge regions of the monolayer. N > 30. Error bar represents the standard error. To see this figure in color, go online.

We assume that all cells within the monolayer do not change their polarity in a synchronous manner. To implement asynchronous change in polarization across cells in a monolayer, we define a parameter t₀, such that a cell changes polarity every t + t₀ = nτ time interval, where t is the current simulation time, and n is an integer. Thus, higher values of t₀ would progressively reduce synchronicity. Although synchronous repolarization of all cells within the monolayer would be artificial, cells within a homogeneous colony may not be completely asynchronous. Given the 1- to 10-min range for τ, we limit this asynchronization parameter t₀ to a somewhat middle point of 4 min. This is implemented by assigning a random value of t₀ to every cell at the start of the simulation as follows:

$$t_0\in \{\begin{array}{c}\left(0,\tau \right),\tau <4\min \\ \left(\mathrm{0,4}\right),\tau \ge 4\min \end{array}.$$ (5)

Simulations of cell monolayer migration

These cellular models were integrated with the Cancer, Heart, and Soft Tissue Environment software to simulate the response of multicell networks of defined dimensions to investigate the effect of repolarization. The chosen multicell network is 10 cells wide and 10 cells long, with periodic boundary conditions imposed on the vertical edges to represent an infinite sheet in the horizontal direction. For a larger monolayer of 400 cells (see Fig. S1 for details), although the net leading-edge displacement was reduced, overall trends of increased LER, cell elongation, and net migration for a higher RTI remained consistent with the 100-cell monolayer used in this study. For the bottom horizontal edge of the monolayer, the cells are assumed to have cell-cell connections and thus do not have a free boundary. Because cell monolayers are not expected to move backward in reality, we disallow negative displacement on the bottom set of vertices. Cells are allowed to form and break bonds and are prevented from self-intersecting, which is implemented through simple operations such as cell neighbor exchange (also called a T1 transition). Cell neighbor exchange occurs when the distance between two connected vertices becomes less than a minimal threshold distance, d_min = 0.1 μm. The vertices are moved and placed at a distance d_sep apart, where d_sep = k_sepd_min, and k_sep = 3 is known as the separation ratio (49). The governing equation for vertex displacement (Eq. 1) is solved using the explicit forward Euler discretization method, with a time step of dt = 0.001 min and a total simulation time of 240 min.

Experimental measurements of cell repolarization

Fabrication of PA hydrogels and collagen coating

Polyacrylamide (PA) precursor solutions were prepared by mixing 12% acrylamide (Bio-Rad, Hercules, CA) and 0.6% bisacrylamide (Bio-Rad), resulting in the elastic modulus of 50 kPa, as previously characterized (26). To initiate polymerization, 0.5% ammonium persulfate (Sigma, St. Louis, MO) and 0.05% tetramethylethylenediamine (Sigma) were added to the precursor mixtures. 35 μL of gel precursor solution was pipetted onto a hydrophobic glass slide, which was treated with Sigmacote (Millipore Sigma, Burlington, MA), and a silanized 15-mm glass coverslip (Fisher Scientific, Waltham, MA) was placed onto the droplet. Polymerization was performed in a vacuum chamber for 45 min. After polymerization, the coverslip containing gels was rehydrated in ultrapure water and gently detached from the glass slide. The hydrogels were ultraviolet (UV) sterilized and functionalized with a UV-activated heterobifunctional cross-linker (Sulfo-SANPAH; Pierce, Rockford, IL; 0.5 mg/mL in 50 mM HEPES (pH 8.5)) under UV exposure (365 nm) for 10 min. 1 mL of 0.1 mg mL⁻¹ type I collagen (rat tail collagen; Santa Cruz Technologies, Dallas, TX) was added onto the PA surface and incubated overnight at 4°C.

Seeding and culture of epithelial cell colony

After incubation overnight at 4°C, collagen solution was aspirated, and the gels were washed three times with sterile Dulbecco’s phosphate-buffered saline (Gibco; Thermo Fisher Scientific). Before seeding MCF10A mammary epithelial cells, the surface of the gel was air dried for 30 min to facilitate the seeding of a small cell colony. MCF10A cells were seeded onto the middle of the gel by putting a tiny droplet of 5 μL cell suspension, which contains 50,000 cells. To avoid the drying out of cell suspension, several microliters of cell culture media were added in the well around the sample in such a way that the added media did not touch the seeded cell suspension. The samples were incubated at 37°C and 5% CO₂ for 1 h 10 min to let the cells attach to the matrix. Fresh cell culture media were added subsequently. Cells were cultured in DMEM/F12 (Invitrogen, Carlsbad, CA) supplemented with 5% (v/v) horse serum (Invitrogen), 20 ng/mL epidermal growth factor (Miltenyi Biotec, Sunnyvale, CA), 0.5 mg/mL hydrocortisone (Sigma-Aldrich), 100 ng/mL cholera toxin (Sigma-Aldrich), 10 μg/mL insulin (Sigma-Aldrich), and 1% (v/v) penicillin-streptomycin (Sigma-Aldrich).

Time-lapse microscopy and aspect ratio analysis

Live cell imaging was performed after 18 h of cell seeding using a Zeiss AxioObserver Z1 microscope (Carl Zeiss Microscopy, Jena, Germany) equipped with an incubation chamber capable of maintaining an environment with 37°C temperature and 5% CO₂ and a motorized, programmable stage. Phase contrast images of the leading edge of epithelial monolayer were acquired every 2 min over a 4 h period using a 10× objective. For analyzing the aspect ratio, cells were manually outlined and fit into an ellipse using ImageJ. The aspect ratio was defined as the ratio of major axis to minor axis length of the ellipse and measured for at least 30 cells per condition.

Image analysis

Experimental videos were analyzed to assess cell dynamics within the monolayer using particle image velocimetry methodology through the “PIVlab” package in Matrix Laboratory. (50). The image was discretized in to 20-μm-wide square elements, and velocity vectors for each element were recorded at every time step. Through an in-house Matrix Laboratory script, each vector was analyzed over time to ascertain the time it takes to change direction by at least a 15° angle. A vector is said to persist for time $\tau =t^{\text{'}}-t$ if $\mathit{\Delta }\theta ={\theta }_{t^{\text{'}}}-{\theta }_t\le 2\pi /24=15°$ (same as the angle discretization used in simulations). For each element in the image grid, the τ values are averaged over the duration of the video, which yields the average persistence of the velocity vector over 4 h at that location. The average τ, which is analogous to the RTI parameter used in simulations, is plotted as heat maps to show its spatial distribution within the cell monolayer.

Results

Longer cell repolarization interval causes higher cell elongation and faster migration

We performed collective migration simulations to understand the effects of varying RTI. The cells start with a random polarization direction and are allowed to pick any direction henceforth after every RTI (τ). The range of τ chosen for these simulations was based on experimental measurements discussed ahead (Fig. 6). First, we ran simulations with the RTI parameter τ = 1 min (i.e., a new random direction is picked by each cell every minute). As seen in Fig. 2 (top row) and Video S1 (second column), individual cells exhibit low forces, their shapes do not significantly change, and the leading edge of the colony remains smooth and straight over time. Next, we performed new simulations with longer RTIs of τ = 6 and 10 min, which yielded dramatically different cellular response compared to the case with τ = 1 min. In Fig. 2 (middle and bottom rows) and Video S1, we observe higher active cellular forces. Over the course of the 4-h simulation time (Fig. 2; Video S1), the longer RTIs led to progressive higher cell elongation, roughness in the leading-edge boundary, and occurrences of finger-like projections.

Video S1. Simulated Configurations of Cell Monolayers with Varying Repolarization Interval $\tau$ = 1, 2, 4, 6, 8 and 10 min over the Simulation Time of 4 h, with Randomly Chosen Polarization Directions after Every RTI,

$\tau$Cells are color-coded with active cellular force magnitudes.

To further understand the influence of RTI on collective cell responses, we ran simulations for a broader range of τ values between 1 and 10 min. We found that cellular forces and elongation steadily increased for longer RTIs (Fig. 3, A, B, and D). By plotting the state of the monolayer after 4 h of simulation time, we found a greater movement of the cell monolayer for longer RTIs (Fig. 3, A and C). The leading edge moved by ∼128 μm for the case with τ = 1 min, continued to rise to ∼140 μm for τ = 6 min, and then increased to ∼160 μm for τ = 10 min. From Fig. 3 A and Video S1, we observed that a longer RTI caused progressively less-organized leading-edge shape. Clearly, migration speed is an important aspect of the collective behavior. Moreover, the shape of the leading edge is now emerging as an important regulator of the mode of collective migration, with leading-edge instabilities generating finger-like projections and causing cell streaming from migrating monolayers (51, 52, 53). We quantified this in terms of LER, defined as 3σ, where σ is the deviation of the position vectors of the vertices at the leading edge from their mean location at a given time (54). As shown in Fig. 3 E, the longer RTI (τ) causes a rise in LER, with the values of LER ranging between ∼5 and ∼9 at different time points (i.e., a more unstable leading-edge shape over time is observed for the highest value of τ (red line)). Consequently, the difference in maximal and minimal value of LER for the case with τ = 10 min is over eightfold higher than for the case with τ = 1 min and over twofold higher than the case with τ = 6 min. Thus, our simulations show that higher RTI, that is, more persistent polarization of individual cells, causes more elongated cell shapes, higher colony movement, and more unstable leading-edge shapes.

Polarization directions with cell-cell contact reduction enhance collective cell migration and LER

One of the key hallmarks of more invasive and motile mutant cell types is reduced cell-cell cohesitivity, which has been defined in terms of EMT markers (55, 56, 57). In our model, we define aggressive cell types by assigning a higher probability for polarization directions that correspond to lower cell-cell contact, which in turn would increase cell-matrix interaction and force generation. After implementing this minimal intercellular contact criterion for the repolarization dynamics of individual cells, as described earlier in Materials and Methods, we performed simulations for collective cell migration with varying RTIs $\left(\tau \right)$, as done in the last part. Although the cell shape and forces did not show significant change over time for the case with the shortest RTI of $\tau =1\min$, there was a clear rise in active forces, cell elongation, and ruffling of the leading edge for the longest RTI of τ = 10 min (Fig. 4, bottom row; Video S2). Over the course of 4 h, the case with τ = 10 min also showed the highest leading-edge displacement compared to τ = 1 min and τ = 6 min. In comparison with the random repolarization case (Figs. 2 and 3), the minimal intercellular contact criterion in current simulations produced higher leading-edge displacements (Fig. 5 C) for all values of the RTI.

Video S2. Simulated Configurations of Cell Monolayers with Varying Repolarization Interval $\tau$ = 1, 2, 4, 6, 8 and 10 min over the Simulation Time of 4 h, with Polarization Directions Based on a Minimal Cell-Cell Contact Criterion

Cells are color-coded with active cellular force magnitudes.

We repeated simulations with this minimal intercellular contact criterion for intermediate values of RTI (τ = 2, 4, and 8 min) and compared them to the cellular responses observed in the random polarization case earlier. As shown in Fig. 5, the net leading-edge movement and cell elongation increased for longer RTIs, with higher values compared to the previous simulations with random repolarization (Figs. 2 and 3). The LER increased with longer RTI and the minimal contact criterion (Fig. 5 D). When plotted over time (Fig. 5 F), the leading-edge shape appeared to be more unstable for the higher values of RTIs with higher amplitudes of LER. Thus, the collective migration of cells that determine their polarization directions by minimizing cell-cell contact and with less frequent repolarization (higher RTI) migrates more aggressively with less structurally stable leading-edge boundaries (higher LER), even at lower RTIs (τ ≤ 6 min).

Spatial distribution of cell RTIs in collectively migrating cell sheets

To understand how cell repolarization occurs in reality and to calibrate the RTI parameter τ in migrating monolayers, we cultured MCF10A mammary epithelial cells on PA hydrogels, performed time-lapse microscopy for 4 h at high temporal resolution (at 2-min intervals), and measured how velocity vectors at given locations change their direction. The measured RTI τ was defined as the time it takes for a given velocity vector to change its direction by greater than π/12, as described earlier in Materials and Methods. Our persistence analysis showed that on an average, cells in the leading edge of the monolayer (corresponding to the monolayer migration in Video S3) had a higher repolarization interval τ (red and orange squares in Fig. 6 B) than the cells away from the monolayer (blue squares in Fig. 6 B). By plotting the distribution of τ values measured across at least three different videos (Fig. 6 C), we found that the cells in the core showed an average τ of approximately 2.4 min. In comparison, the cells in the leading edge showed a much higher average τ at ∼ 5.5 min, with some points reaching ≥8 min. We also found that the aspect ratio (a measure of elongation) of cells at the leading edge was more than twofold higher than that of cells in the core (Fig. 6 D). These measurements suggest a correlation between higher repolarization interval, that is, persistent polarity, and more elongated cell shapes.

Video S3.Time Lapse Video of MCF10A Cells PA Gels over 4 h of Real Time with 2 min Interval between Each Frame

Arrows indicate velocity vectors.

Collective migration of cell populations with varying placement of mutant cells

Based on our experiments, from the data presented in Fig. 6, we defined “mutant” cells corresponding to τ = 6 min and minimal intercellular contact criterion, which produced elongated cells in the leading edge. In contrast, the random repolarization criterion with the shortest RTI, τ = 2 min (Figs. 3 and 5), produced the most rounded cell shape, which we picked as a healthy or “normal” cell type. To validate the experimental results, we mimicked the observation of varying τ based on its position within the monolayer by assigning cells on the leading edge with τ = 6 min and minimal contact criterion and cells not on the leading edge with τ = 2 min and random polarization. Similar to previous sections, we ran the simulation for 4 h. In other situations of collective cell migration, such as wound healing and tumor invasion, cell populations are often a mixture of cell types or mutations with intrinsically dissimilar aggressiveness. To mimic such situations, we modeled a 100-cell monolayer within which 10 mutant cells were randomly dispersed among 90 normal cells, as shown in Fig. 7 A (bottom row) and Video S4 (bottom row), with mutant cells outlined in black. In this case, the leading edge of the population moved by ∼125 μm (Fig. 7 B), which was similar to the movement observed earlier for the purely normal cell population (Fig. 3 C). When plotted over time, the LER and displacement of the cell colony with dispersed mutants tracked similarly to the purely normal cell population (Fig. 7, D and E).

Video S4. Simulated Configurations of Cell Sheets over the Total Simulation Time of 4 h for Two Different Heterogeneous Cell Populations: Mutants Dispersed within a Normal Cell Population, and Mutants at the Leading-Edge of a Normal Cell Population

Here, mutant cells are outlined in black and cells are color-coded by active force magnitudes.

In collective cell migration, it is now understood that the so-called “leader” cells located at the leading edge of the migrating cell sheet generate higher forces, undergo more spreading and elongation, and exhibit mechanoactivation signaling (58, 59). Based on this idea and our experimental observations (Fig. 6 C), we hypothesized that more aggressive mutant cells might be able to better propel the sheet migration when they serve as the leaders. To understand the role of leader cells in collective migration, we modeled a monolayer in which all 10 mutant cells were placed at the leading edge (Fig. 7 A, top row; Video S4, middle row, with mutant cells outlined in black) of a 100-cell population, with 90 normal cells behind the leading edge. In the case of dispersed mutants, the elongation indexes of cells in the core and in the leading edge were similar (Fig. 7, A and C). Notably, when the mutant cells of higher RTIs served as leaders, similar to the experiments (Fig. 6), we found higher cell elongation at the leading edge (Fig. 7 C), which validates our experimental measurements of cell aspect ratio. Here, the leading edge appeared more stable compared to the earlier case with a purely mutant population. The net leading-edge displacement increased to ∼155 μm, which is over 22% higher than the case with dispersed mutants (Fig. 6 B). Over time, the leading-edge position of this 90% normal cell population, with only leading-edge cells as mutants, tracked similarly to a population in which all cells were mutants (Fig. 7 D). Although the LER for this mutants-as-leaders case was higher than the dispersed mutants case, it was surprisingly lower than a purely mutant population (Fig. 6 E). These results indicate that although mutant cells at the leading edge lead to as fast a migration as a purely mutant population, it does not cause as much structural instability for the monolayer.

Conclusions

The ability of cells to move collectively has emerged as a crucial factor in tumor invasion, wound healing, and morphogenesis. Through a range of experimental and computational studies, we are beginning to understand how the forces, adhesions, and mechanotransductive signaling of individual cells might generate varying modes of collective cell migration (7, 26, 58, 60). One of the key steps in single-cell migration is a biochemomechanical polarization of forces, adhesion, and biochemical signaling gradients into front and rear regions of the cell (15), which frequently changes as the cell moves. There is now emerging evidence that single-cell polarization might play a crucial regulatory function in tumor metastasis (61). However, it remains unknown how such dynamic polarization of individual cells within a population could alter the collective behavior. In our study, we specifically define cell polarity as a parameter that dictates the orientation of forces within a cell, causing cell elongation and movement in a given direction. We assume that different cell types repolarize themselves into a new direction at a defined time interval. This direction could either be chosen randomly or based on a criterion for minimizing cell-cell cohesiveness. Our experimental measurements and simulations provide the following key insights into how the repolarization dynamics of cells could serve as a fundamental cellular property that may regulate the modes of collective cell migration.

• 1)A longer interval between switching to a new randomly chosen polarization direction, referred to as RTI, allows higher cell elongation, generation of forces, and migration along a given direction, which results in higher overall migration of the collective population. In these cases, individual cells within a monolayer are forced to bump into each other with greater persistence, causing higher deformation of cell bodies. As a result, a longer RTI causes more structural instability of the cell sheet and roughening of the leading edge.
• 2)When a cell type is defined by its ability to choose polarization directions that minimize interaction with the neighboring cells, the efficiency of cell elongation and force generation gets enhanced, which in turn maximizes the outward polarization of leading-edge cells and enhanced overall monolayer migration. This enhancement reduces as RTI increases, suggesting a middle ground for optimal persistence.
• 3)Experimental analysis shows for the first time that cells at the leading edge maintain their polarity for a longer duration (i.e., a less frequent repolarization) compared to the cells within the core of the monolayer. The leading-edge cells are also more elongated, indicating a mesenchymal-like phenotype. Based on these findings, we speculate that the cells at the leading edge might follow a criterion of persistent outward polarity because of reduced cell-cell contact.
• 4)Based on our results, the shortest repolarization interval with randomly chosen directions corresponds to the most stable monolayer, rounded cell morphology, and slow migration, all of which could be characterized as properties of healthy or normal cells. In contrast, the longer RTI with minimal intercellular contact criterion of mutant-leader cells, according to our definition, causes more aggressive migration, chaotic deformations of the cell sheet, and instabilities at the leading edge.
• 5)In a heterogeneous cell population with mutant-leader cells uniformly dispersed within a monolayer of normal cells, the collective cell migration speed and sheet deformations do not significantly change. Here, despite the persistent elongation of the embedded leader cells, the frequent repolarization of the surrounding normal cells could continually dissipate excessive cell deformations or movements. Thus, a mere presence of leader cells within a cell population may not alter its overall migratory response.
• 6)To mimic the known function of leader cells driving the collective cell migration, we placed the more aggressive mutant leaders at the leading edge of an otherwise normal cell population. In this case, as the mutant cells led the way, the normal cells filled the space left behind through force equilibrium between the cells. As a result, the overall migration of the cell sheet dramatically increased. Surprisingly, this population of “mutant leaders” and “normal followers” migrate as fast as a purely mutant population. Moreover, we observed lesser LER and a more stable cell sheet in this case. These results indicate that the presence of aggressive cells at the leading edge of a population could dominate the collective migration phenotype even if the majority of cells in a population are slow moving (normal). In fact, the mutants-as-leaders population might yield a more efficient mode of collective cell migration as compared to a purely mutant population, given its low leading-edge ruffling and high structural stability of the cell sheet.

In summary, our computational framework of multicell deformation and migration, dictated by individual cell forces and polarity, provides new, to our knowledge, understanding of how cellular repolarization can potentially regulate various modes of collective cell migration. The insights described above can be used to define or characterize cell types of varying aggressiveness. Beyond this phenomenon of collective cell migration, the idea of dynamic repolarization of entities within a grouped population may inform the social interactions of other collective systems. From pedestrians in street traffic or global human migration to floating icebergs or the migration of birds, if individual entities within a system move or polarize along a given direction for varying durations, that could fundamentally alter the collective dynamics of the system. Our study provides a tool and fundamental insights to design better experiments and construct more sophisticated computational models to further study the regulatory function of spatiotemporally varying repolarization of entities within a moving population.

Author Contributions

A.P. and J.M. conceived the project and designed theoretical models. J.M. performed simulations and analyzed experimental data. B.S. performed experiments and analyzed data. J.M. and A.P. interpreted the data and wrote the article.

Editor: Vivek Shenoy.