Skip to main content
PMC home page
Acta Crystallographica Section A: Foundations and Advances logoLink to Acta Crystallographica Section A: Foundations and Advances
. 2019 Jan 1;75(Pt 1):82–93. doi: 10.1107/S2053273318013918

Reducing dynamical electron scattering reveals hydrogen atoms

Max T B Clabbers a, Tim Gruene b, Eric van Genderen b, Jan Pieter Abrahams a,b,c,*
PMCID: PMC6302931  PMID: 30575586

Experimental and computational reduction of dynamical electron scattering allows for visualizing of individual hydrogen atoms.

Keywords: dynamical scattering, electron diffraction, hydrogen atoms, nanocrystals, hybrid pixel detector

Abstract

Compared with X-rays, electron diffraction faces a crucial challenge: dynamical electron scattering compromises structure solution and its effects can only be modelled in specific cases. Dynamical scattering can be reduced experimentally by decreasing crystal size but not without a penalty, as it also reduces the overall diffracted intensity. In this article it is shown that nanometre-sized crystals from organic pharmaceuticals allow positional refinement of the hydrogen atoms, even whilst ignoring the effects of dynamical scattering during refinement. To boost the very weak diffraction data, a highly sensitive hybrid pixel detector was employed. A general likelihood-based computational approach was also introduced for further reducing the adverse effects of dynamic scattering, which significantly improved model accuracy, even for protein crystal data at substantially lower resolution.

1. Introduction  

Electron crystallography allows for the solving of structures of beam-sensitive macromolecules and organic compounds using sub-micron-sized three-dimensional crystals. The minute sample volumes used in electron diffraction are limiting the maximum radiation dose and the diffracted intensity (Henderson, 1995 ▸). Electrons interact with matter so strongly that the majority of 300 keV electrons will have scattered either elastically or inelastically after having passed through only 50 nm of organic matter (Clabbers & Abrahams, 2018 ▸). Because this was considered to prevent successful analysis of three-dimensional protein crystals, macromolecular electron crystallography was limited until recently to two-dimensional crystals (Unwin & Henderson, 1975 ▸; Gonen et al., 2005 ▸). Chemical electron crystallography using inorganic and organic crystals developed independently from protein crystallography (Cowley, 1953a ▸,b ▸; Vainshtein, 1964 ▸; Dorset, 1995 ▸; Kolb et al., 2007 ▸; Mugnaioli et al., 2009 ▸; Zhang et al., 2010 ▸; Zou et al., 2011 ▸). Recently, the rotation method that has been the standard for decades in X-ray protein crystallography (Arndt & Wonacott, 1977 ▸; Dauter, 1999 ▸) was adapted to electron crystallography for determining the structure of beam-sensitive macromolecules (Nederlof et al., 2013 ▸; Nannenga, Shi, Leslie et al., 2014 ▸; Nannenga, Shi, Hattne et al., 2014 ▸; Yonekura et al., 2015 ▸; Clabbers et al., 2017 ▸), organics and inorganics (Gemmi et al., 2015 ▸; van Genderen et al., 2016 ▸; Gruene et al., 2018 ▸).

Analogous to similar developments in X-ray crystallography and single-particle cryo-EM (Broennimann et al., 2006 ▸; Kühlbrandt, 2014 ▸; McMullan et al., 2016 ▸), the introduction of new camera technologies, such as the advent of hybrid pixel detectors, was of vital importance for the development of electron diffraction of beam-sensitive crystals, as they offer high sensitivity, fast read out and reduced background (van Genderen et al., 2016 ▸; Tinti et al., 2018 ▸). Electron diffraction data integration is feasible with existing X-ray crystallography packages, including profile fitting and scaling (Leslie, 1999 ▸; Kabsch, 2010 ▸; Winter et al., 2018 ▸), and requires only minor adaptations (Clabbers et al., 2018 ▸). The introduction of electron counting detectors required a Poisson error model and background estimation optimized for weak data with low-background, which were implemented for integrating very weak, few-photon, X-ray diffraction data as measured by hybrid pixel detectors (Kabsch, 2010 ▸; Parkhurst et al., 2016 ▸).

In general, crystallographic structure determination assumes single, kinematical scattering. Given the strong interaction of electrons with matter, multiple elastic or dynamical scattering is a major concern in electron crystallography, as it changes the observed structure-factor amplitudes (Cowley & Moodie, 1957 ▸; Glaeser & Downing, 1993 ▸; Dorset, 1995 ▸; Weirich et al., 2000 ▸). Dynamical scattering cannot be removed by zero-loss energy filtering, and coincides with the kinematic Bragg scattering angles. On average, dynamical scattering increases the intensity of weaker reflections, whereas the strong reflections become less intense. Typically, dynamical scattering out of intense Bragg reflections into the weaker ones predominantly affects adjacent reflections when low-resolution terms dominate (Weirich et al., 2000 ▸). Thus, it depends on the diffraction geometry and can therefore be reduced by averaging corresponding intensities obtained from multiple crystal orientations. This explains why precessing or tilting the electron beam and/or rotating the crystal in a random orientation, combined with averaging symmetry-related reflections, reduces the effects of dynamical scattering (e.g. Vincent & Midgley, 1994 ▸).

Crystal size is an important factor affecting dynamical scattering as the probability of multiple scattering events increases with sample thickness (Subramanian et al., 2015 ▸; Clabbers & Abrahams, 2018 ▸). A small crystal size combined with data acquisition using the rotation (or precession) method reduces dynamical scattering. This approach allows for full integration of the Bragg reflections resulting in a better estimate of the kinematic scattering intensity (Arndt & Wonacott, 1977 ▸; Dauter, 1999 ▸; Vincent & Midgley, 1994 ▸). It benefits from an electron-counting quantum area detector with a high dynamic range to optimize the weak diffraction signal. Dynamical refinement of electron diffraction data is an effective, independent approach for dealing with dynamical diffraction (Jansen et al., 1998 ▸; Palatinus, Petříček & Corrêa, 2015 ▸; Palatinus, Corrêa et al., 2015 ▸; Palatinus et al., 2017 ▸). It requires knowledge of the atomic crystal structure, the crystal shape or thickness, and the three-dimensional orientation of the crystal for each unmerged reflection. Because it models the electron wavefunction travelling through the entire crystal, dynamical refinement is computationally demanding and has so far only been implemented for relatively straightforward cases with small unit cells.

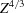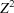A potential benefit of electron diffraction is the improved contrast of hydrogen atoms. For the lighter elements (up to about sulfur) the atomic scattering cross sections are approximately proportional to Inline graphic, instead of Inline graphic as for X-ray diffraction (Egerton, 2011 ▸). The increased contrast of light atoms relative to heavier ones implies a larger contribution from the hydrogen atoms to the overall signal (Cowley, 1953a ▸,b ▸; Vainshtein, 1964 ▸; Dorset, 1995 ▸; Clabbers & Abrahams, 2018 ▸). Localizing hydrogen atoms can be notoriously difficult in X-ray crystallography, even with high-resolution data. However, recently, hydrogen positions in organic and inorganic samples could be refined by reducing the effects of dynamical scattering by combining precession electron diffraction with dynamical refinement (Palatinus et al., 2017 ▸).

Here, we present electron diffraction data for three-dimensional nanocrystals of two pharmaceutical organic compounds, recorded at cryogenic temperature using the rotation method and a Timepix hybrid pixel detector. The small size of the crystals reduced dynamical scattering, whilst the highly sensitive hybrid pixel detector boosted the weak diffraction signal. This combination allowed for localizing of the positions of individual hydrogen atoms at a very early stage of the refinement, and allowed unconstrained refinement of the hydrogen atoms, without any modelling of dynamical scattering. Furthermore, we introduce a likelihood-based approach for correcting dynamical scattering that down-weights overestimated reflection intensities as a function of intensity and resolution, in an approach similar to Wiener filtering. These corrections significantly improved the quality of the data and the model accuracy, and even work for protein crystal data with a substantially lower resolution.

2. Methods  

2.1. Data acquisition  

Diffraction data were acquired for two pharmaceutical organic compounds (experimental data are available online at https://doi.org/10.5281/zenodo.1407682) (see Fig. S1 in the supporting information), kindly provided by Novartis, corresponding to CCDC entries IRELOH (C16O5H18) (Dai et al., 2010 ▸) and EPICZA (C18O6N2S2H16) (Deffieu et al., 1977 ▸) in the Cambridge Structural Database (CSD). Data were acquired by continuous rotation at cryogenic temperature with an ∼2.0 µm-diameter parallel beam using an FEI Polara TEM, operated at 200 kV and equipped with a 512 × 512 pixel Timepix hybrid pixel detector (van Genderen et al., 2016 ▸; Gruene et al., 2018 ▸). The effective detector distance was determined with an aluminium powder standard (Ted Pella).

2.2. Data processing  

The raw data recorded from the detector were corrected for the pixel offsets between individual chips and converted to CBF (crystallographic binary file) format (see https://strucbio.biologie.uni-konstanz.de/xdswiki/index.php/Timepix2cbf; Gruene et al., 2018 ▸). Data were integrated and scaled using XDS (Kabsch, 2010 ▸). The Laue group was constrained to mmm. Multiple crystal data sets were merged, scaled and converted to SHELX format within XDS (Kabsch, 2010 ▸). Data were truncated where there was still significant correlation at approximately I/σ(I) > 1.0 and CC 1/2 > 50% (Karplus & Diederichs, 2012 ▸; Diederichs & Karplus, 2013 ▸).

2.3. Structure determination  

2.3.1. Structure solution and model refinement  

Structures of both organic compounds were solved using SHELXT with default settings (Sheldrick, 2015b ▸). The models were refined using SHELXL (Sheldrick, 2015a ▸) and built in SHELXLE (Hübschle et al., 2011 ▸). Hydrogen atoms were placed automatically when possible using HFIX. For anisotropic refinement against incomplete data, mild restraints were applied in SHELXL to ensure similarity (RIGU) (Thorn et al., 2012 ▸) and positivity (XNPD 0.001) of the atomic displacement parameters. Electron atomic scattering factors were fitted to the nine Cromer–Mann coefficients as used by SHELXL (see also Fig. S11 in the supporting information) (Peng, 1999 ▸; Gruene et al., 2018 ▸).

2.3.2. Lattice parameter refinement  

In electron diffraction, the unit-cell dimensions and sample to detector distance are highly correlated because of the short electron wavelength. Therefore, both cannot be refined reliably at the same time from the diffraction data alone. However, the lattice can also be refined independently from the detector distance by minimizing the deviation from ideal model geometry (Gruene et al., 2018 ▸). Geometrical restraints on bond lengths (DFIX) and bond angles (DANG) for IRELOH and EPICZA were generated using the GRADE server (http://grade.globalphasing.org/cgi-bin/grade/server.cgi) (see Tables S9 and S10 in the supporting information). The unit-cell parameters were then refined against the idealized interatomic distances using SHELXL and the program CellOpt (https://github.com/JLuebben/CellOpt). The geometrical restraints were only used for lattice refinement. After the geometrical restraints were removed from the instruction file, the model was refined in SHELXL against the new unit-cell parameters.

2.3.3. Refining hydrogen positions  

To illustrate the quality of the data and the stability of the hydrogen positions, we refined their positions by subsequently removing the constraints on the hydrogen atoms (AFIX), which are normally refined using the riding model in SHELX. The hydrogen positions were then refined isotropically in SHELXL until convergence.

2.3.4. Validation  

The models were validated using R complete (Luebben & Gruene, 2015 ▸), as a more robust alterative to R free (Brünger, 1997 ▸). Since all reflections are used to calculate R complete, the model can be refined against all data; hence R work is equal to R1. The R complete was calculated with a test set size of 0.2%, running ten refinement cycles for each run, using the R_complete graphical user interface (https://github.com/JLuebben/R_complete).

To compare the quality of the model geometry, we calculated the r.m.s.d. of the electron diffraction structure bond lengths from the reference X-ray models (Deffieu et al., 1977 ▸; Dai et al., 2010 ▸). We assessed the stability of the refined hydrogen atoms by calculating the r.m.s.d. of the hydrogen-bond lengths (X—H) compared with the idealized hydrogen-bond-length tables generated by SHELXL using the NEUT command (Sheldrick, 2015a ▸). Using NEUT will list the inter-nuclei distances as neutron scattering occurs on the nuclei, and since idealized hydrogen-bond lengths determined by X-ray diffraction are generally too short, it is therefore appropriate to use the more accurate X—H distances for neutron diffraction as described previously (Gruene et al., 2014 ▸).

2.4. Dynamical scattering corrections  

2.4.1. Dynamical scattering increases intensity of weaker reflections  

We previously observed an overestimation of the weaker reflection intensities in our electron diffraction data (van Genderen et al., 2016 ▸; Clabbers et al., 2017 ▸). We confirmed that this was also the case for the two organic samples presented here by plotting the observed structure-factor amplitudes 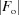Inline graphic against the structure-factor amplitudes calculated from the model 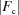Inline graphic (Figs. 3 and 4). On average, dynamical scattering increases the intensity of weaker reflections at the expense of the strong reflections, so we can expect the observed structure-factor amplitudes 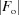Inline graphic to be overestimated for the weaker reflections (Dorset, 1995 ▸; Weirich et al., 2000 ▸; Subramanian et al., 2015 ▸; Clabbers & Abrahams, 2018 ▸). Assuming that we have a complex-valued dynamical scattering component 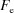Inline graphic, which is uncorrelated to the kinematical structure factor 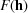Inline graphic, we can describe the expected value of 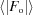Inline graphic using a hyperbolic function defined as

2.4.1.

Using least-squares fitting, we can derive the expected dynamical error term 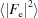Inline graphic over all observations, where the hyperbolic function describing 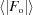Inline graphic intercepts the y axis at 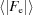Inline graphic (Figs. 3 and 4).

We determined 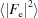Inline graphic as a function of resolution by dividing the data into ten equally sized resolution bins (in terms of number of reflections), and within each bin we determined the corresponding resolution-dependent dynamical scattering error 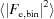Inline graphic using least-squares fitting. Using the curve-fitting tool in MATLAB we established the relation between 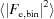Inline graphic and the resolution d (Figs. 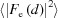3c and 4c), resulting in the continuous function Inline graphic.

In the absence of dynamical scattering (when 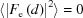Inline graphic), the measured and calculated structure factors should be linearly correlated. Thus, as a function of resolution d, we can infer the scale 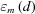Inline graphic by which an expected observed intensity 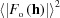Inline graphic is increased by dynamical scattering, as a function of (i) the resolution d, (ii) the strength of the dynamic effect 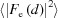Inline graphic, and (iii) the intensity 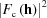Inline graphic that would be observed in the absence of errors,

2.4.1.

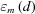Thus, Inline graphic is essentially equivalent to a reciprocal generalized Wiener filter [see equation (10) in Pratt (1972 ▸)].

2.4.2. Dynamical scattering corrections for high-resolution data  

Refinement in SHELX uses scaled observed intensities, which are assumed to be kinematic, i.e. 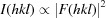Inline graphic. Instead of refining against the measured intensities, we refined against corrected intensities 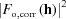Inline graphic according to

2.4.2.

These corrections were applied to each reflection, on both the intensities and their sigma values, using a single line of Awk commands that also writes the corrected HKL file with the standard formatting required for SHELX. The model was refined in SHELXL against the corrected data. The positional accuracies of the hydrogen atoms were assessed as before by refinement without any constraints on the hydrogen bonds.

2.4.3. Dynamical scattering corrections for low-resolution protein diffraction data  

In a similar fashion, the likelihood-based corrections for dynamical scattering were applied to low-resolution data. Previously, we observed the same apparent overestimation of the weaker reflections for hen egg-white lysozyme nanocrystals, solved up to a resolution of 2.1 Å (PDB ID 5o4x; experimental data are available online at https://doi.org/10.5281/zenodo.1250447; Clabbers et al., 2017 ▸). As protein data are generally refined against the amplitudes instead of intensities, we corrected structure factors according to

2.4.3.

The resolution dependency of 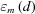Inline graphic was determined from the dynamical scattering errors 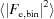Inline graphic within ten equally sized resolution bins (in terms of number of reflections). Here a discrete correction was applied for each resolution bin independently, rather than fitting a multi-parameter continuous function to describe the observed curve of 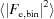Inline graphic as a function of resolution d (Fig. 5b). In all cases, the models were refined until convergence.

3. Results  

3.1. Structure determination  

3.1.1. IRELOH  

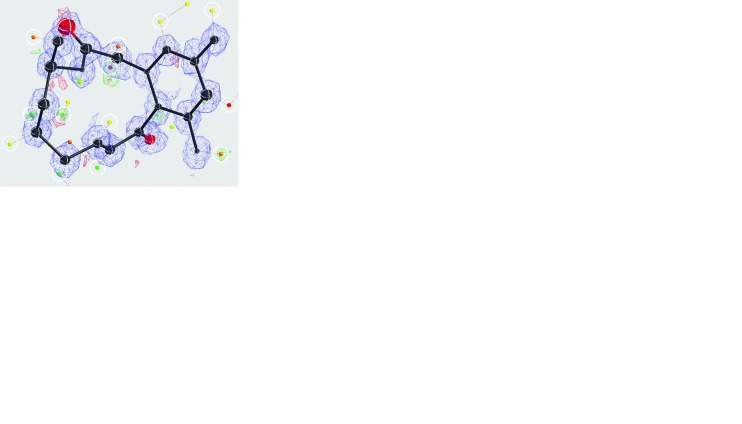
Diffraction data were acquired for three IRELOH nanocrystals over a combined tilt range of 144° using the rotation method (see Fig. S1 and Table S2 in the supporting information). Merging resulted in 85% completeness up to a resolution of 0.82 Å, which allowed phasing by direct methods (see Table 1 ▸ and Fig. S4 in the supporting information). The resulting model after phasing reveals the presence of individual hydrogen atoms as indicated by the difference map (Fig. 1 ▸ a).

Table 1. Data-merging statistics.

Reference values of unit-cell dimensions for IRELOH were obtained from Dai et al. (2010 ▸) and from Deffieu et al. (1977 ▸) for EPICZA. Values in parentheses correspond to the highest resolution shell, and data were truncated at approximately I/σ(I) > 1.0 and CC 1/2 > 50% (Karplus & Diederichs, 2012 ▸; Diederichs & Karplus, 2013 ▸), see also Fig. S4 in the supporting information.

  IRELOH EPICZA
Literature    
Chemical formula C16H18O5 C18H16N2O6S2·H2O
Space group P212121 P212121
Unit-cell dimensions    
a, b, c (Å) 8.06, 10.00, 17.73 11.11, 12.61, 13.49
α, β, γ (°) 90.00, 90.00, 90.00 90.00, 90.00, 90.00
     
Data integration    
Number of crystals† 3 4
Space group P212121 P212121
Unit-cell dimensions    
a, b, c (Å) 8.090 (2), 9.940 (2), 17.700 (4) 11.080 (2), 12.580 (2), 13.440 (3)
α, β, γ (°) 90.00, 90.00, 90.00 90.00, 90.00, 90.00
Resolution (Å) 17.60–0.82 (0.85–0.82) 12.63–0.83 (0.85–0.83)
I/σ(I) 6.47 (2.50) 5.93 (1.45)
CC 1/2 (%) 98.2 (46.2) 98.6 (67.7)
R merge (%) 16.6 (50.0) 20.6 (28.6)
R meas (%) 18.5 (61.2) 22.2 (39.8)
Completeness (%) 84.6 (78.9) 89.6 (36.4)
Reflections 6096 (352) 12039 (70)
Unique observations 1332 (135) 1761 (59)
Open in a new tab
†

See Tables S2 and S3 in the supporting information for the data-processing statistics of the individual crystal data sets.

Figure 1.

Figure 1

Open in a new tab

Structure determination of IRELOH. (a) The model after phasing using the direct methods program SHELXT. Small icosahedra represent maxima in the difference map. Peak heights are colour coded in rainbow colours (purple = high, red = low). Icosahedra that indicate the positions of individual hydrogen atoms are encircled. (b) Automated placement of the hydrogen atoms by SHELXLE confirms the quality of the model’s geometry, placing all hydrogen atoms correctly except for H5. (c) Final model after manual building and anisotropic refinement (RIGU, XNPD 0.001) in SHELXL. (d) Unconstrained positional refinement of the hydrogen atoms. (e) ORTEP plot with the numbering for the non-hydrogen atoms of the final model. Parts (a)–(d) were drawn using SHELXLE with default contour levels of 2.7σ for the 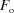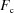Inline graphic − Inline graphic difference map and 1.2σ for the 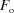Inline graphic map. The atomic displacement ellipsoids are colour coded black for carbon and red for oxygen, while the hydrogen atoms are represented in white.

Automated fixing of the hydrogen atoms can place all but one, indicating the quality of the model (Fig. 1 ▸ b). Although there was clear difference potential, position H5 was not placed automatically based on the model geometry and had to be set manually using AFIX 148 (Fig. 1 ▸ b). The final model after anisotropic refinement shows a well resolved map (Fig. 1 ▸ c) and high-quality model geometry (Fig. 1 ▸ e), although the standard crystallographic quality indications are rather poor (Table 2 ▸).

Table 2. Model building and refinement statistics without refining hydrogen atoms.
  IRELOH EPICZA
Space group P212121 P212121
Unit-cell dimensions†    
a, b, c (Å) 8.015 (2), 10.015 (2), 17.703 (4) 10.996 (2), 12.452 (2), 13.218 (3)
α, β, γ (°) 90.00, 90.00, 90.00 90.00, 90.00, 90.00
Parameters 196 259
Restraints‡ 156 267
Reflections 6096 12039
Unique 1332 1761
     
Refinement    
R1 (%)§ 16.8 (15.0) 17.2 (15.4)
R complete (%) 19.7 21.0
w R2 (%) 36.9 39.0
GooF 1.100 1.109
R.m.s.d. bond lengths (Å)†† 0.022 (18) 0.027 (19)
     
Dynamical corrections    
R1 (%)§ 13.2 (12.2) 12.7 (11.9)
R complete (%) 15.1 14.3
w R2 (%) 29.5 29.1
GooF 0.944 0.879
R.m.s.d. bond lengths (Å)†† 0.022 (17) 0.025 (13)
Open in a new tab
†

New unit-cell dimensions after lattice refinement, see also Tables S9 and S10 in the supporting information.

‡

Enhanced rigid-bond restraints (RIGU) were applied for refinement in SHELXL (Thorn et al., 2012 ▸).

§

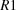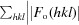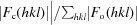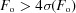Inline graphic = Inline graphic − Inline graphic where the sum is over all reflections, values in parentheses show R1 for reflections Inline graphic.

R complete was calculated over all reflections with a 0.2% test set size as a robust and unbiased validation tool (Luebben & Gruene, 2015 ▸); since all data are included, R work is equivalent to R1.

††

R.m.s.d. for all non-hydrogen atoms, calculated against reference values from high-resolution X-ray models (Dai et al., 2010 ▸; Deffieu et al., 1977 ▸); see also Tables S5 and S7 in the supporting information.

Removing the constraints on the 18 hydrogen atoms allowed refining of their positions and bond lengths despite increasing the number of free parameters from 196 to 245, with a total of 156 restraints (Table 3 ▸). The resulting structural model shows a remarkably high consistency of hydrogen atoms (Fig. 1 ▸ d).

Table 3. Model building and refinement statistics after unconstrained refinement of hydrogen atoms.
  IRELOH EPICZA
Space group P212121 P212121
Unit-cell dimensions†    
a, b, c (Å) 8.015 (2), 10.015 (2), 17.703 (4) 10.996 (2), 12.452 (2), 13.218 (3)
α, β, γ (°) 90.00, 90.00, 90.00 90.00, 90.00, 90.00
Parameters 245 305
Restraints‡ 156 267
Reflections 6096 12039
Unique 1332 1761
     
Refinement    
R1 (%)§ 15.7 (13.9) 16.6 (14.7)
R complete (%) 19.9 21.5
w R2 (%) 34.6 37.1
GooF 1.031 1.051
R.m.s.d. bond lengths (Å) 0.024 (18) 0.030 (20)
R.m.s.d. hydrogen-bond lengths (Å) 0.180 (72) 0.259 (80)
     
Dynamical corrections    
R1 (%)§ 12.5 (11.5) 12.2 (11.4)
R complete (%) 15.2 14.5
w R2 (%) 28.1 28.0
GooF 0.907 0.851
R.m.s.d. bond lengths (Å) 0.022 (13) 0.026 (13)
R.m.s.d. hydrogen-bond lengths (Å) 0.073 (52) 0.110 (56)
Open in a new tab
†

New unit-cell dimensions after lattice refinement, see also Tables S9 and S10 in the supporting information.

‡

Enhanced rigid-bond restraints (RIGU) were applied for refinement in SHELXL (Thorn et al., 2012 ▸).

§

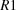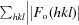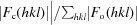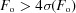Inline graphic = Inline graphic − Inline graphic where the sum is over all reflections, values in parentheses show R1 for reflections Inline graphic.

R complete was calculated over all reflections with a 0.2% test set size as a robust and unbiased validation tool (Luebben & Gruene, 2015 ▸); since all data are included, R work is equivalent to R1.

††

R.m.s.d. for all non-hydrogen atoms, calculated against reference values from high-resolution X-ray models (Dai et al., 2010 ▸; Deffieu et al., 1977 ▸).

‡‡

R.m.s.d. for the idealized hydrogen-bond lengths after unconstrained refinement of the hydrogen positions (Gruene et al., 2014 ▸; Sheldrick, 2015a ▸); see also Tables S6 and S8 in the supporting information.

3.1.2. EPICZA  

Data were acquired for four EPICZA nanocrystals using the rotation method, with a total tilt range of 213° (see Fig. S1 and Table S3 in the supporting information). Merging yielded close to complete data up to a resolution of 0.83 Å (see Table 1 ▸ and Fig. S4 in the supporting information). Although the EPICZA molecule has twofold symmetry, this was not used or imposed for structure solution or refinement. Direct methods allowed for the calculating of a map revealing difference potential peaks for localizing individual hydrogen atoms (Fig. 2 ▸ a).

Figure 2.

Figure 2

Open in a new tab

Structure determination of EPICZA. (a) The model after phasing using the direct methods program SHELXT. Small icosahedra represent maxima in the difference map. Peak heights are colour coded in rainbow colours (purple = high, red = low). Icosahedra that indicate the positions of individual hydrogen atoms are encircled. (b) Automated placement of the hydrogen atoms by SHELXLE showing the quality of the model’s geometry, placing all hydrogen atoms apart from H3, H5 and H5B. (c) Final model after building and anisotropic refinement (RIGU, XNPD 0.001) in SHELXL. (d) Unconstrained positional refinement of the hydrogen atoms where the positions of H7 and H10 are unstable and move out of bounds. (e) ORTEP plot with the numbering for the non-hydrogen atoms of the final model. Parts (a)–(d) were drawn using SHELXLE with default contour levels of 2.7σ for the 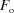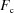Inline graphic − Inline graphic difference map and 1.2σ for the 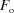Inline graphic map. The atomic displacement ellipsoids are colour coded black for carbon, red for oxygen, blue for nitro­gen and yellow for sulfur, while the hydrogen atoms are represented in white.

Most hydrogen atoms could be placed automatically, indicating good data quality (Fig. 2 ▸ b). Hydrogen atoms H3, H5, and H5B were placed with the coordinates of the corresponding difference peaks observed during refinement with AFIX 147, 23 and 147 (Fig. 2 ▸ b), respectively. After anisotropic refinement, the final model shows high quality of the map and accurate model geometry (Figs. 2 ▸ c and 2 ▸ e), but again with relatively poor quality indicators (Table 2 ▸).

In contrast to the X-ray model, we did not observe any density indicating the presence of water molecules. Perhaps this was because of evaporation after inserting the sample into the vacuum column. This would also explain the observed shrinkage of the unit cell by 90 Å3 compared with the X-ray model. Given the P212121 crystal symmetry, this shrinkage corresponds to a cube with sides of 2.83 Å per missing H2O molecule, which is very close to the volume of one H2O molecule in liquid water, which on average occupies a cube with sides of 3 Å.

All 16 hydrogen-atom positions and bond lengths were refined by removing the constraints, increasing the number of free parameters from 259 to 305, with a total of 267 restraints (Table 3 ▸). Almost all refined hydrogen-atom positions are stable, but H7 and H10 are unstable and move too far away to have a bonding interaction with the non-hydrogen atom (Fig. 2 ▸ d).

3.2. Dynamical scattering corrections  

3.2.1. IRELOH  

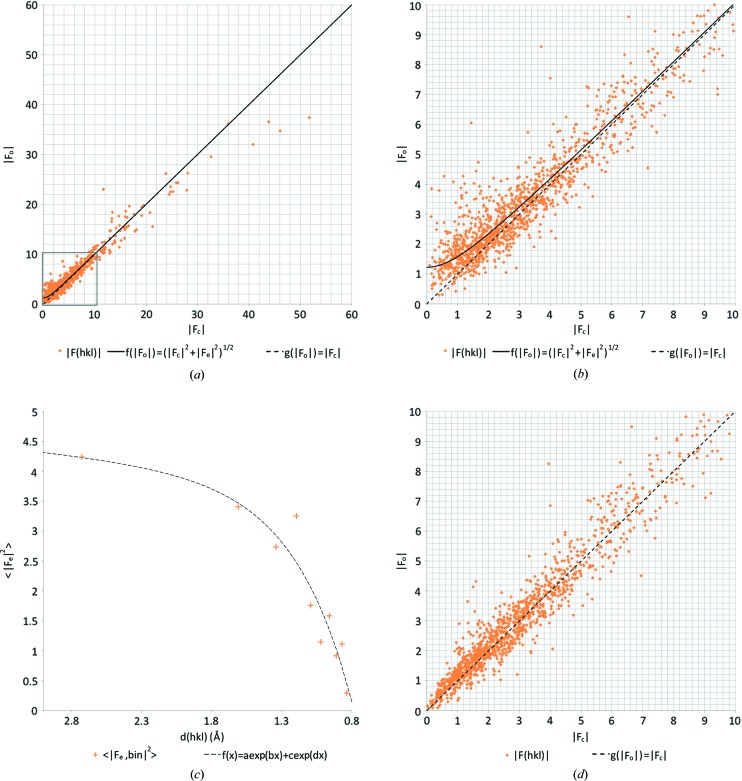
We observed considerable dynamical scattering, leading to a clear overestimation of the lower intensities (Fig. 3 ▸ a and 3b). The overestimation decreased with increasing resolution. We fitted an exponential curve to the data, thus defining 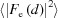Inline graphic as a continuous function of the resolution (Fig. 3 ▸ c). This allowed likelihood-based corrections of the intensities dependent on both intensity and resolution using equation (3).

Figure 3.

Figure 3

Open in a new tab

Likelihood-based corrections for dynamical scattering. (a) 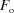Inline graphic versus 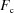Inline graphic plot for IRELOH where 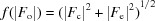Inline graphic is a hyperbolic function with an expected dynamical scattering error term of 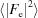Inline graphic = 1.51 as determined by least-squares fitting, and where 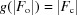Inline graphic shows a perfect linear correlation. (b) Zoomed-in version on the lower intensity reflections, as marked with a grey box in (a). (c) 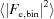Inline graphic as a function of the resolution, where we fitted an exponential curve 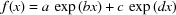Inline graphic with parameters a = 3.64, b = 0.058, c = −24.67 and d = −2.38. 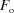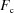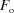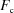(d) Inline graphic versus Inline graphic plot after applying the likelihood-based corrections shows an improved correlation between Inline graphic and Inline graphic with an error of 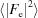Inline graphic = 0.33.

The likelihood-based corrections for dynamical scattering significantly improved the fit of the model to the data, with an R1 of 13.2% and an R complete of 15.1% (Table 2 ▸). Furthermore, the gap between R1 and R complete decreases after the likelihood-based corrections were applied, indicating reduced bias. Although the model geometry of non-hydrogen atoms was unaffected (see Table 2 ▸ and Table S5 in the supporting information), the r.m.s. deviations from the idealized hydrogen-bond lengths did improve considerably (see Table 3 ▸ and Table S6 in the supporting information). The improvement can also be inferred from the structure-factor plots that show an almost linear correlation when least-squares fitting the same hyperbolic curve (Fig. 3 ▸ d).

3.2.2. EPICZA  

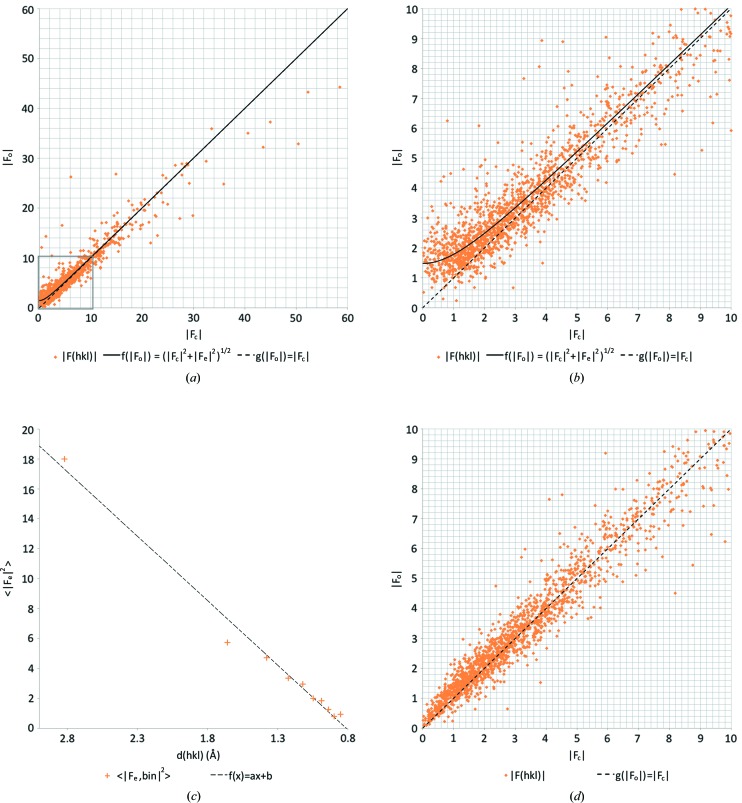
Dynamical scattering affected the observed intensities of the structure factors (Figs. 4 ▸ a and 4b). Again, the dynamical scattering error 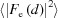Inline graphic decreased with the resolution, and a linear curve was fitted to the resulting plot (Fig. 4 ▸ c). Using equation (3) we then made likelihood-based corrections of each reflection as a function of intensity and resolution.

Figure 4.

Figure 4

Open in a new tab

Likelihood-based corrections for dynamical scattering. (a) 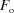Inline graphic versus 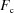Inline graphic plot for EPICZA where 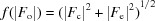Inline graphic is a hyperbolic function with an expected dynamical scattering error term of 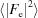Inline graphic = 2.20 as determined by least-squares fitting, and where 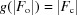Inline graphic shows a perfect linear correlation. (b) Zoomed-in version of the same plot on the lower intensity reflections, as marked with a grey box in (a). (c) 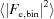Inline graphic as a function of the resolution, where we fitted an linear model 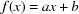Inline graphic with parameters a = 8.61 and b = −6.98. 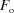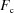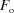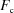(d) Inline graphic versus Inline graphic plot after applying the likelihood-based corrections shows an improved correlation between Inline graphic and Inline graphic with an error of 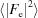Inline graphic = 0.43.

The likelihood-based corrections improved the fit between the model and the experimental data, leading to a significant improvement in R1 and R complete (Table 2 ▸). The model geometry also improved significantly. The r.m.s. deviations of bond lengths of the non-hydrogen atoms decreased (see Table 2 ▸ and Table S7 in the supporting information), as did the deviations from idealized hydrogen-bond lengths (see Table 3 ▸ and Table S8 in the supporting information). After applying the likelihood-based corrections, the 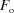Inline graphic versus 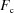Inline graphic plot improved and also showed linear correlation for the weaker reflections with a much lower value for 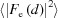Inline graphic (Fig. 4 ▸ d).

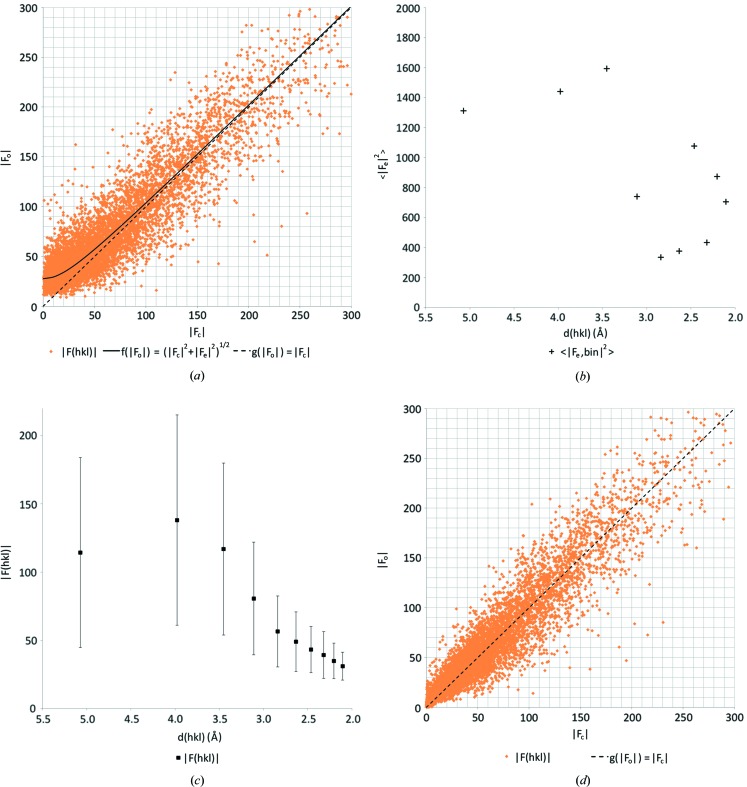
3.2.3. Lysozyme  

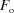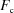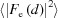The effect of dynamical scattering on the intensities had been observed previously from protein data at 2.1 Å (PDB ID 5o4x; experimental data are available online at https://doi.org/10.5281/zenodo.1250447; Clabbers et al., 2017 ▸). Again, the weaker reflections in the Inline graphic versus Inline graphic plot were overestimated (Fig. 5 ▸ a). We plotted the dynamical scattering error Inline graphic as a function of resolution, showing a non-linear relation (Fig. 5 ▸ b). We assume this non-linearity resulted from the presence of secondary structural elements and solvent contributions (Fig. 5 ▸ c). We made discrete likelihood-based corrections per resolution bin as described in Section 2.4.3.

Figure 5.

Figure 5

Open in a new tab

Likelihood-based corrections for dynamical scattering for low-resolution protein data. (a) 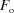Inline graphic versus 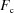Inline graphic plot for hen egg-white lysozyme where 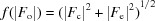Inline graphic is a hyperbolic function with an expected dynamical scattering error term of 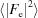Inline graphic = 768.13 as determined by least-squares fitting, and where 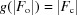Inline graphic shows a perfect linear correlation. (b) 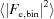Inline graphic as function of resolution. (c) Mean structure-factor amplitude 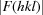Inline graphic as a function of the resolution; the same resolution bins were used as in (b) and error bars indicate the standard deviation. 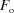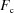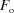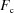(d) Inline graphic versus Inline graphic plot after applying discrete likelihood-based corrections, showing an improved correlation between Inline graphic and Inline graphic with an error of 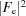Inline graphic = 53.3.

The likelihood-based correction resulted in significant improvement of the model, as indicated by the reduction of R complete from 29.1% to 26.2%. It also reduced model bias, as witnessed by the smaller gap between R1 and R complete. Furthermore, the 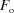Inline graphic versus 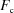Inline graphic plot improves with a lower dynamical error value (Fig. 5 ▸ d). It is unclear why the average B factor increased upon correcting for dynamical scattering. However, the model geometry after applying the corrections showed a significant improvement, since r.m.s. deviations from ideal bond lengths and bond angles dropped by about 10% (Table 4 ▸).

Table 4. Refinement statistics and dynamical scattering corrections of low-resolution protein data from seven lysozyme data sets recorded and solved previously (Clabbers et al., 2017 ▸).

Experimental data are available online at https://doi.org/10.5281/zenodo.1250447. Values in parentheses correspond to the highest resolution shell, and the data were truncated at approximately I/σ(I) > 1.0 and CC 1/2 > 50% (Diederichs & Karplus, 2013 ▸).

  Lysozyme
Data integration  
Space group P21212
Unit-cell dimensions  
a, b, c (Å) 104.56, 68.05, 32.05
α, β, γ (°) 90.0, 90.0, 90.0
Number of crystals 7
Resolution (Å) 57.03–2.11 (2.17–2.11)
R merge (%) 42.1 (57.2)
CC 1/2 (%) 90.4 (60.3)
I/σ(I) 2.7 (1.0)
Completeness (%) 62.1 (49.8)
Reflections 41191 (1462)
Unique reflections 8560 (545)
   
Refinement  
Reflections 8503
R1 (%) † 24.4
R complete (%) ‡ 29.1
〈B〉 (Å2) 33.02
R.m.s.d. bond lengths (Å) 0.074
R.m.s.d. bond angles (°) 1.0706
Ramachandran  
Favoured, allowed, outliers (%) 98.4, 1.6, 0.0
   
Dynamical corrections  
Reflections 8503
R1 (%)† 24.3
R complete (%)‡ 26.2
〈B〉 (Å2) 41.09
R.m.s.d. bond lengths (Å) 0.066
R.m.s.d. bond angles (°) 1.0072
Ramachandran  
Favoured, allowed, outliers (%) 98.0, 2.0 0.0
Open in a new tab
†

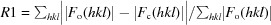
Inline graphic

‡

We present R1 and R complete instead of R work and R free. With less than 10 000 unique reflections R complete is preferred over R free since it is calculated from all reflections (Brünger, 1997 ▸; Luebben & Gruene, 2015 ▸). Since all structure factors are used in turn, this leads to a more robust calculation than R free. With this validation method, the actual refinement uses all reflections, hence R work is equivalent to R1.

4. Discussion and conclusions  

Electron diffraction allows structure solution even when only small crystals are available, and results in increased contrast of hydrogen atoms compared with X-ray diffraction. Here, we show that scattering potential at individual hydrogen-atom positions can be visualized after solving the structure by direct methods, even before interactive model improvement (Figs. 1 ▸ and 2 ▸). The refined coordinates are of comparable quality to the respective X-ray structures, indicating that organic structures can be solved with electron diffraction at sufficient quality to allow for further interpretation, for example for drug development by modelling. The positions of the individual hydrogen atoms are remarkably stable, allowing unconstrained refinement of the hydrogen-atom parameters.

Dynamical scattering was reduced experimentally by selecting for minimal crystal size, and by collecting rotation data from multiple crystals in random orientations. The signal-to-noise ratio was further boosted by measuring at cryogenic temperatures and using a highly sensitive hybrid pixel detector. Profile fitting of weak intensities allowed data to be extracted at or even below the noise level (French & Wilson, 1978 ▸; Oatley & French, 1982 ▸; Kabsch, 2010 ▸).

Acquiring more data to further increase multiplicity will always benefit data accuracy. Although it would allow a more accurate estimation of the kinematic intensity by averaging out orientation-dependent dynamical deviations, it cannot completely eliminate overestimation of weaker reflection intensities. Dynamical scattering effects could, in principle, also be further reduced by increasing the acceleration voltage, whilst data quality and structure refinement benefit from additional calibrations of the experiment (Gemmi et al., 2015 ▸; Yonekura et al., 2015 ▸), zero-loss energy filtering to remove inelastically scattered electrons (Yonekura et al., 2002 ▸) and modelling of partial charge (Yonekura & Maki-Yonekura, 2016 ▸; Yonekura et al., 2018 ▸). We consider these additional, independent measures to be important, but beyond the scope of our article, as they are enhanced, rather than replaced, by the methods we discuss here.

Existing methods of structure refinement that compensate for the effects of dynamical scattering rely on knowledge of the atomic crystal structure. Comprehensive modelling of dynamical scattering by either multi-slice or Bloch-wave simulations is computationally challenging. Current implementations assume perfect crystallinity and small unit cells with a limited number of atoms; increasing data multiplicity also increases the computational burden (Jansen et al., 1998 ▸; Palatinus, Petříček et al., 2015 ▸; Palatinus, Corrêa et al., 2015 ▸; Palatinus et al., 2017 ▸). There is currently no implementation for correcting protein data. 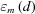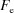Here, we introduced a likelihood-based approach, akin to the Wiener filter, that applies a straightforward scaling factor Inline graphic for down-weighting overestimated intensities as a function of intensity and resolution. It is computationally undemanding, has no underlying assumptions concerning crystal quality or thickness, and is sufficiently general to be implemented straightforwardly even for very complex cases. It is also sufficiently general to even allow corrections of single-particle cryo-EM data. We show it can substantially improve the fit between the model and experimental data, at the expense of only a few extra parameters, can reduce bias (as witnessed by a smaller difference between R1 and R complete), and has a positive effect on the model geometry (Table 2 ▸). In the absence of a predictive theory for the dependency of Inline graphic on d, the resolution dependency of 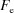Inline graphic needs to be determined heuristically. For plate-like crystals or needle-shaped crystals that are rotated about an axis normal to their longest dimension, 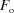Inline graphic versus 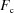Inline graphic curves should also be checked as a function of rotation angle, as at higher angles the electron beam travels through the crystal for a longer distance. This implies stronger dynamical scattering. 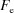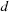In theory, the relationship between Inline graphic and Inline graphic can be derived for each crystal by means of a full dynamical simulation. In that case it would be preferable to use the simulation results. Where dynamical calculations are not possible or practical, we therefore suggest determining 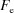Inline graphic as a function of resolution by analysing 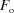Inline graphic versus 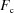Inline graphic curves for different resolution bins.

Like the other approaches, the implementation of our method requires an initial model to calculate its structure-factor amplitudes. However, it has frequently been observed that the accuracy of structure-factor amplitudes is more important for refinement than for phasing, so in practice this restriction may not limit the application of our method or other methods that require reasonably accurate 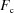Inline graphic’s. However, it may be possible to infer the required error parameters even in the absence of an initial model, using intensity statistics such as the Wilson plot. But a brute-force strategy may provide an even better alternative, since the corrections require only a few parameters. In that case, parameters within a reasonable range could be tried, generating corrected data for phasing. In marginal cases where dynamical scattering prevents initial phasing, such an approach could be helpful. The method could be further improved by implementation at the stage of data integration and/or scaling, using the fact that only reflections simultaneously in the Bragg condition for that particular frame can be affected.

Electron crystallography can produce accurate atomic models that conform to expected bonding geometries to a remarkably high degree. Yet, using current methods, X-ray diffraction models fit better to the experimental data, compared with models refined against electron diffraction data. As X-ray data are obtained from crystals that have many million times more molecules, this observation should not be too surprising. One of those components that compromises the fit between model and data is dynamical electron scattering. Here we demonstrated that experimental approaches aimed at reducing crystal size and computational reduction of the effects of dynamical scattering lead to improved refinement statistics and model geometry. As the two approaches are independent, their combined effects are multiplied, leading to structures with improved geometry that are less biased by prior assumptions and fit better to the observed diffraction data.

Supplementary Material

Crystal structure: contains datablock(s) IRELOH, EPICZA. DOI: 10.1107/S2053273318013918/td5055sup1.cif

a-75-00082-sup1.cif (557.7KB, cif)

Structure factors: contains datablock(s) IRELOH. DOI: 10.1107/S2053273318013918/td5055IRELOHsup2.hkl

Structure factors: contains datablock(s) EPICZA. DOI: 10.1107/S2053273318013918/td5055EPICZAsup3.hkl

Supporting figures and tables to the main text. DOI: 10.1107/S2053273318013918/td5055sup4.pdf

a-75-00082-sup4.pdf (2MB, pdf)

Lysozyme electron diffraction data (Timepix, CBF format) URL: https://doi.org/10.5281/zenodo.1250447

Electron diffraction data for IRELOH and EPICZA URL: https://doi.org/10.5281/zenodo.1407682

CCDC references: 1870980, 1870981

Acknowledgments

We thank Henning Stahlberg and Kenneth Goldie for discussions and support during data collection. We thank Jens Luebben for the programs CellOpt and R_complete for lattice refinement and structure validation, respectively. We thank Novartis for providing the samples.

Funding Statement

This work was funded by Swiss Nanoscience Institute grant A12.01 A3EDPI. Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung grant 200021_165669.

References

  1. Arndt, U. W. & Wonacott, A. J. (1977). The Rotation Method in Crystallography. Amsterdam: North-Holland.
  2. Broennimann, Ch., Eikenberry, E. F., Henrich, B., Horisberger, R., Huelsen, G., Pohl, E., Schmitt, B., Schulze-Briese, C., Suzuki, M., Tomizaki, T., Toyokawa, H. & Wagner, A. (2006). J. Synchrotron Rad. 13, 120–130. [DOI] [PubMed]
  3. Brünger, A. T. (1997). Methods Enzymol. 277, 366–396. [DOI] [PubMed]
  4. Clabbers, M. T. B. & Abrahams, J. P. (2018). Crystallogr. Rev. 24, 176–204.
  5. Clabbers, M. T. B., Gruene, T., Parkhurst, J. M., Abrahams, J. P. & Waterman, D. G. (2018). Acta Cryst. D74, 506–518. [DOI] [PMC free article] [PubMed]
  6. Clabbers, M. T. B., van Genderen, E., Wan, W., Wiegers, E. L., Gruene, T. & Abrahams, J. P. (2017). Acta Cryst. D73, 738–748. [DOI] [PMC free article] [PubMed]
  7. Cowley, J. M. (1953a). Acta Cryst. 6, 516–521.
  8. Cowley, J. M. (1953b). Acta Cryst. 6, 522–529.
  9. Cowley, J. M. & Moodie, A. F. (1957). Acta Cryst. 10, 609–619.
  10. Dai, J., Krohn, K., Flörke, U., Pescitelli, G., Kerti, G., Papp, T., Kövér, K. E., Bényei, A. C., Draeger, S., Schulz, B. & Kurtán, T. (2010). Eur. J. Org. Chem. 2010, 6928–6937.
  11. Dauter, Z. (1999). Acta Cryst. D55, 1703–1717. [DOI] [PubMed]
  12. Deffieu, G., Gadret, M., Leger, J. M. & Carpy, A. (1977). Acta Cryst. B33, 1474–1478.
  13. Diederichs, K. & Karplus, P. A. (2013). Acta Cryst. D69, 1215–1222. [DOI] [PMC free article] [PubMed]
  14. Dorset, D. L. (1995). Structural Electron Crystallography. New York: Plenum Press.
  15. Egerton, R. F. (2011). Electron Energy-Loss Spectroscopy in the Electron Microscope. Springer.
  16. French, S. & Wilson, K. (1978). Acta Cryst. A34, 517–525.
  17. Gemmi, M., La Placa, M. G. I., Galanis, A. S., Rauch, E. F. & Nicolopoulos, S. (2015). J. Appl. Cryst. 48, 718–727.
  18. van Genderen, E., Clabbers, M. T. B., Das, P. P., Stewart, A., Nederlof, I., Barentsen, K. C., Portillo, Q., Pannu, N. S., Nicolopoulos, S., Gruene, T. & Abrahams, J. P. (2016). Acta Cryst. A72, 236–242. [DOI] [PMC free article] [PubMed]
  19. Glaeser, R. M. & Downing, K. H. (1993). Ultramicroscopy, 52, 478–486. [DOI] [PubMed]
  20. Gonen, T., Cheng, Y., Sliz, P., Hiroaki, Y., Fujiyoshi, Y., Harrison, S. C. & Walz, T. (2005). Nature (London), 438, 633–638. [DOI] [PMC free article] [PubMed]
  21. Gruene, T., Hahn, H. W., Luebben, A. V., Meilleur, F. & Sheldrick, G. M. (2014). J. Appl. Cryst. 47, 462–466. [DOI] [PMC free article] [PubMed]
  22. Gruene, T., Li, T., van Genderen, E., Pinar, A. B. & van Bokhoven, J. A. (2018). Chem. Eur. J. 24, 2384–2388. [DOI] [PubMed]
  23. Henderson, R. (1995). Q. Rev. Biophys. 28, 171–193. [DOI] [PubMed]
  24. Hübschle, C. B., Sheldrick, G. M. & Dittrich, B. (2011). J. Appl. Cryst. 44, 1281–1284. [DOI] [PMC free article] [PubMed]
  25. Jansen, J., Tang, D., Zandbergen, H. W. & Schenk, H. (1998). Acta Cryst. A54, 91–101.
  26. Kabsch, W. (2010). Acta Cryst. D66, 125–132. [DOI] [PMC free article] [PubMed]
  27. Karplus, P. A. & Diederichs, K. (2012). Science, 336, 1030–1033. [DOI] [PMC free article] [PubMed]
  28. Kolb, U., Gorelik, T. E., Kübel, C., Otten, M. T. & Hubert, D. (2007). Ultramicroscopy, 107, 507–513. [DOI] [PubMed]
  29. Kühlbrandt, W. (2014). Science, 343, 1443–1444. [DOI] [PubMed]
  30. Leslie, A. G. W. (1999). Acta Cryst. D55, 1696–1702. [DOI] [PubMed]
  31. Luebben, J. & Gruene, T. (2015). Proc. Natl Acad. Sci. USA, 112, 8999–9003. [DOI] [PMC free article] [PubMed]
  32. McMullan, G., Faruqi, A. R. & Henderson, R. (2016). Methods Enzymol. 579, 1–17. [DOI] [PubMed]
  33. Mugnaioli, E., Gorelik, T. E. & Kolb, U. (2009). Ultramicroscopy, 109, 758–765. [DOI] [PubMed]
  34. Nannenga, B. L., Shi, D., Hattne, J., Reyes, F. E. & Gonen, T. (2014). eLife, 3, e03600. [DOI] [PMC free article] [PubMed]
  35. Nannenga, B. L., Shi, D., Leslie, A. G. W. & Gonen, T. (2014). Nat. Methods, 11, 927–930. [DOI] [PMC free article] [PubMed]
  36. Nederlof, I., van Genderen, E., Li, Y.-W. & Abrahams, J. P. (2013). Acta Cryst. D69, 1223–1230. [DOI] [PMC free article] [PubMed]
  37. Oatley, S. & French, S. (1982). Acta Cryst. A38, 537–549.
  38. Palatinus, L., Brázda, P., Boullay, P., Perez, O., Klementová, M., Petit, S., Eigner, V., Zaarour, M. & Mintova, S. (2017). Science, 355, 166–169. [DOI] [PubMed]
  39. Palatinus, L., Corrêa, C. A., Steciuk, G., Jacob, D., Roussel, P., Boullay, P., Klementová, M., Gemmi, M., Kopeček, J., Domeneghetti, M. C., Cámara, F. & Petříček, V. (2015). Acta Cryst. B71, 740–751. [DOI] [PubMed]
  40. Palatinus, L., Petříček, V. & Corrêa, C. A. (2015). Acta Cryst. A71, 235–244. [DOI] [PubMed]
  41. Parkhurst, J. M., Winter, G., Waterman, D. G., Fuentes-Montero, L., Gildea, R. J., Murshudov, G. N. & Evans, G. (2016). J. Appl. Cryst. 49, 1912–1921. [DOI] [PMC free article] [PubMed]
  42. Peng, L. M. (1999). Micron, 30, 625–648.
  43. Pratt, W. K. (1972). IEEE Trans. Comput. C-21, 636–641.
  44. Sheldrick, G. M. (2015a). Acta Cryst. C71, 3–8.
  45. Sheldrick, G. M. (2015b). Acta Cryst. A71, 3–8.
  46. Subramanian, G., Basu, S., Liu, H., Zuo, J. M. & Spence, J. C. H. (2015). Ultramicroscopy, 148, 87–93. [DOI] [PubMed]
  47. Thorn, A., Dittrich, B. & Sheldrick, G. M. (2012). Acta Cryst. A68, 448–451.
  48. Tinti, G., Fröjdh, E., van Genderen, E., Gruene, T., Schmitt, B., de Winter, D. A., Weckhuysen, B. M. & Abrahams, J. P. (2018). IUCrJ, 5, 190–199. [DOI] [PMC free article] [PubMed]
  49. Unwin, P. N. T. & Henderson, R. (1975). J. Mol. Biol. 94, 425–440. [DOI] [PubMed]
  50. Vainshtein, B. K. (1964). Structure Analysis by Electron Diffraction, edited by E. Feigl & J. A. Spink, 1st ed. Oxford: Pergamon.
  51. Vincent, R. & Midgley, P. A. (1994). Ultramicroscopy, 53, 271–282.
  52. Weirich, T. E., Zou, X. D., Ramlau, R., Simon, A., Cascarano, G. L., Giacovazzo, C. & Hovmöller, S. (2000). Acta Cryst. A56, 29–35. [DOI] [PubMed]
  53. Winter, G., Waterman, D. G., Parkhurst, J. M., Brewster, A. S., Gildea, R. J., Gerstel, M., Fuentes-Montero, L., Vollmar, M., Michels-Clark, T., Young, I. D., Sauter, N. K. & Evans, G. (2018). Acta Cryst. D74, 85–97. [DOI] [PMC free article] [PubMed]
  54. Yonekura, K., Kato, K., Ogasawara, M., Tomita, M. & Toyoshima, C. (2015). Proc. Natl Acad. Sci. USA, 112, 3368–3373. [DOI] [PMC free article] [PubMed]
  55. Yonekura, K. & Maki-Yonekura, S. (2016). J. Appl. Cryst. 49, 1517–1523.
  56. Yonekura, K., Maki-Yonekura, S. & Namba, K. (2002). Biophys. J. 82, 2784–2797. [DOI] [PMC free article] [PubMed]
  57. Yonekura, K., Matsuoka, R., Yamashita, Y., Yamane, T., Ikeguchi, M., Kidera, A. & Maki-Yonekura, S. (2018). IUCrJ, 5, 348–353. [DOI] [PMC free article] [PubMed]
  58. Zhang, D., Oleynikov, P., Hovmöller, S. & Zou, X. (2010). Z. Kristallogr. 225, 94–102.
  59. Zou, X., Hovmöller, S. & Oleynikov, P. (2011). Electron Crystallography: Electron Microscopy and Electron Diffraction. Oxford University Press.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Crystal structure: contains datablock(s) IRELOH, EPICZA. DOI: 10.1107/S2053273318013918/td5055sup1.cif

a-75-00082-sup1.cif (557.7KB, cif)

Structure factors: contains datablock(s) IRELOH. DOI: 10.1107/S2053273318013918/td5055IRELOHsup2.hkl

a-75-00082-IRELOHsup2.hkl (36.7KB, hkl)

Structure factors: contains datablock(s) EPICZA. DOI: 10.1107/S2053273318013918/td5055EPICZAsup3.hkl

a-75-00082-EPICZAsup3.hkl (48.6KB, hkl)

Supporting figures and tables to the main text. DOI: 10.1107/S2053273318013918/td5055sup4.pdf

a-75-00082-sup4.pdf (2MB, pdf)

Lysozyme electron diffraction data (Timepix, CBF format) URL: https://doi.org/10.5281/zenodo.1250447

Electron diffraction data for IRELOH and EPICZA URL: https://doi.org/10.5281/zenodo.1407682

CCDC references: 1870980, 1870981

Articles from Acta Crystallographica. Section A, Foundations and Advances are provided here courtesy of International Union of Crystallography

RESOURCES