Electric field control of magnetic domain wall motion via modulation of the Dzyaloshinskii-Moriya interaction

Magnetic domain wall speed exceeding 100 m/s is modulated by electrical gating of interfacial Dzyaloshinskii-Moriya interaction.

Abstract

We show that the electric field (EF) can control the domain wall (DW) velocity in a Pt/Co/Pd asymmetric structure. With the application of a gate voltage, a substantial change in DW velocity up to 50 m/s is observed, which is much greater than that observed in previous studies. Moreover, modulation of a DW velocity exceeding 100 m/s is demonstrated in this study. An EF-induced change in the interfacial Dzyaloshinskii-Moriya interaction (DMI) up to several percent is found to be the origin of the velocity modulation. The DMI-mediated velocity change shown here is a fundamentally different mechanism from that caused by EF-induced anisotropy modulation. Our results will pave the way for the electrical manipulation of spin structures and dynamics via DMI control, which can enhance the performance of spintronic devices.

INTRODUCTION

In a ferromagnetic metal (FM)/heavy metal (HM) layered structure, the interfacial Dzyaloshinskii-Moriya interaction (DMI) (iDMI) resulting from structural inversion asymmetry (SIA) and spin-orbit coupling stabilizes a Néel domain wall (DW) with fixed chirality (1, 2) and also a skyrmion (3, 4). The iDMI counters a substantial reduction in DW velocity v because the magnetization precession inside the DW normally caused by the Walker breakdown is suppressed (5, 6). Moreover, the invariance of the chiral DW originating from the iDMI is indispensable for its motion driven by the current-induced spin-orbit torque (7–9) and ensures the high-speed and robust operation of a race track memory (10).

An additional application of an external electric field (EF) to the FM/HM structure represents a method of tuning the SIA and thus can provide a route to efficiently control the DW dynamics via the modulation of the iDMI. A capacitor structure is used to apply an EF to the FM surface through a dielectric layer, and the resultant change in interface magnetism has been reported using various FM thin films (11–22). However, control of the DW motion caused by an “electrical iDMI gating” has never been achieved. In this study, we demonstrate that an EF application can gate the DW velocity in an iDMI-assisted flow regime. Further experiments clarify that the EF modulation of the iDMI magnitude D rather than the magnetic anisotropy explains the results.

RESULTS

Sample preparation and experimental setup

An asymmetric Pt/Co/Pd layered structure capped by a 2-nm-thick MgO layer deposited on a thermally oxidized Si substrate was used for the experiments (see also Materials and Methods). Two samples with different nominal Co thickness t_Co (0.78 and 0.98 nm) were prepared. Because of the interfacial magnetic anisotropy at the Pt/Co and Co/Pd interfaces, both samples exhibit perpendicular magnetic anisotropy (PMA). In this structure, a magnetic moment is induced in both the bottom Pt and top Pd layers because of the ferromagnetic proximity effect. The whole part of the Pd layer is expected to be magnetized because its thickness is only 0.4 nm (19). Figure 1 shows the schematic image of the device and experimental setup used in this study. The EF was applied to the sample surface through a HfO₂ dielectric layer formed by atomic layer deposition (see also Materials and Methods). Here, we defined a positive (negative) gate voltage V_G as corresponding to the direction of the increase (decrease) in the electron density near the sample surface. All experiments shown below were performed at room temperature.

Fig. 1. Experimental setup.

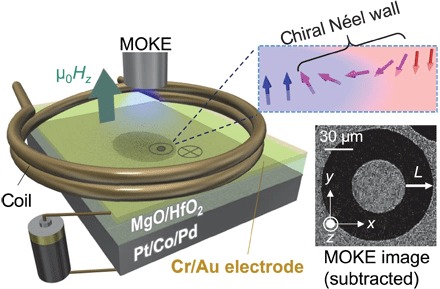
The capacitor structure consists of the Pt/Co/Pd asymmetric layers, 50-nm HfO₂ gate insulator, and Cr/Au electrode. A pulsed perpendicular magnetic field H_z was applied to drive the DW. The H_z was generated using a 500-μm-diameter coil placed on the sample. The DW motion was observed using a MOKE microscope. The typical MOKE image obtained by subtracting two MOKE images taken before and after the application of the pulsed H_z is shown. The DW velocity v was calculated from the DW displacement L by the H_z application.

The DW displacement under the application of V_G was observed using a polar magneto-optical Kerr effect (MOKE) microscope. A pulsed perpendicular magnetic field H_z with a duration τ of 150 ns was applied to nucleate a magnetic domain and drive the DW surrounding it (see also Materials and Methods). The value of v was determined by the following procedure. After making the sample a single-domain state, a domain with an opposite polarity was nucleated by applying a H_z pulse (|μ₀H_z| = 210 mT was used to nucleate a domain). Then, a H_z pulse was again applied to expand the nucleated domain. The MOKE images were taken before and after the domain expansion. A typical MOKE image after subtracting two MOKE images is shown in Fig. 1. The dark-colored part corresponds to the region swept by the DW. From the DW displacement (L) indicated on the image, v (= L/τ) can be determined.

DW velocity under application of gate voltage

First, we discuss the H_z dependence of v. Figure 2 (A and B) shows the v − μ₀H_z characteristics for both samples measured at V_G = 0, +15, and −15 V. By applying high H_z, v over 100 m/s is obtained, indicating that the DW motion is in the flow regime (23). According to the conventional one-dimensional (1D) model for DW motion, which reasonably describes a free domain expansion in unconfined systems (24), v increases linearly with H_z in the flow regime. This behavior was also confirmed experimentally in a symmetric Pt/Co/Pt system (24). In contrast, v remains almost saturated for the present asymmetric samples with t_Co = 0.78(0.98) nm above μ₀H_z ~210(~160) mT. This saturation of v in a high-field regime originated from the iDMI, which has been recently discussed in different asymmetric FM/HM systems (5, 6).

Fig. 2. Perpendicular magnetic field dependence of DW velocity.

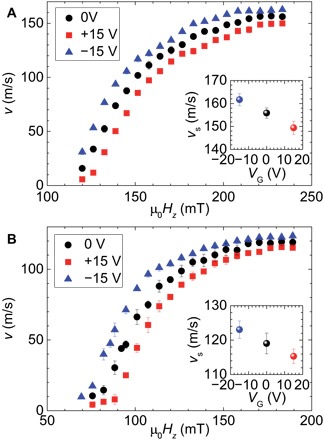
v as a function of H_z obtained under the gate voltage V_G of 0 V (circle), +15 V (square), and −15 V (triangle) for the samples with Co thickness t_Co = (A) 0.78 nm and (B) 0.98 nm is shown. The error bar is the SD of five measurements for each μ₀H_z. The insets show V_G dependence of the saturation v (v_s) in a high H_z regime. The error bar is the SD of v_s.

Our results show that the v − μ₀H_z curve is modulated by the V_G application. For example, a significant v modulation of up to 50 m/s is achieved around the DW depinning region. Such a large v change has never been reported using the EF effect (11–13). The EF-induced variation of v for the thermally activated creep regime has been in the range from 10⁻³ to 10⁻⁵ m/s (11–13). For the flow regime, only a few meters per second of v change was observed in the Ta/CoFeB/MgO system (14). The most important point here is that the saturation v (v_s) is changed by the EF application. The insets in Fig. 2 (A and B) show the v_s as a function of V_G. The ratios of v_s change between V_G = ±15 V are 8.2 and 6.7% for the t_Co = 0.78 and 0.98 nm samples, respectively.

In the saturation v region, the DW propagates with maintaining its structure as just before the Walker breakdown. It is because in the system with the DMI, the energy dissipation occurs not through the magnetization precession (Walker breakdown) but through the instantaneous nucleation and annihilation of the Bloch lines or small bubbles. Thus, using the Walker breakdown field H_W, v_s is expressed as v_s = γΔH_W/α, where γ is the gyromagnetic ratio, Δ is the DW width, and α is the damping constant. In the large DMI system, H_W ≈ παH_D/2 (6, 7), where H_D is the DMI effective field. Because H_D = Dt/(μ₀M_stΔ) (7), v_s is finally given by

$${\mathit{v}}_{\mathrm{s}}=\frac{\mathrm{\pi }}{2}\mathrm{\gamma }\frac{\mathit{D}\mathit{t}}{{\mathit{M}}_{\mathrm{s}}\mathit{t}}$$ (1)

where t is the effective thickness of a ferromagnetic layer, and Dt and M_st correspond to the areal iDMI magnitude (25) and the areal saturation magnetic moment, respectively. v_s for the Pt/Co system with large DMI can be well explained by Eq. 1, as shown in a previous report (6). Thus, this model is considered to be applicable to our Pt/Co/Pd structure. v_s is independent of K_u, i.e., a change in K_u by the EF does not affect v_s (we have also confirmed this in a 2D case; see section S2). Because the ratio of the M_st change for both samples is below 1% (see section S1), the EF modulation of Dt is the major factor underlying the v_s change. In the creep regime experiment, the change in the effective PMA is discussed as a possible origin of the creep v modulation (12). Thus, the mechanism of the EF modulation of the flow regime v presented here, i.e., v modulation via the DMI change, is largely different from the creep v modulation case. Using Eq. 1, V_G dependence of Dt is quantitatively determined, as shown in Fig. 3 (A and B). The Dt for the sample with t_Co = 0.78(0.98) nm is 0.51(0.49) pJ/m at V_G = 0 V, and the modulation ratio between ±15 V is ~8.3(~6.6)%. The modulation ratio of the iDMI in the t_Co = 0.78 nm sample is larger than that for the t_Co = 0.98 nm sample, indicating that the EF effect on the iDMI might be more effective in the thinner films. The origin of this may be, for example, the difference in the electron structure of the top Pd caused by the t_Co-dependent built in strain in the Pd (also see section S1). In this experiment, V_G of ±15 V corresponds to the EF strength applied to the Pd surface of ±0.29 V/nm in consideration of the total thickness of the dielectric layer. Thus, the efficiencies of the Dt modulation by the EF are calculated to be 7.8 × 10⁻¹¹ (t_Co = 0.78 nm) and 5.2 × 10⁻¹¹ (0.98 nm) pJ/V, respectively. These values are close to the previous study using the Au/Fe/MgO system (18).

Fig. 3. Gate voltage dependence of the areal iDMI and PMA.

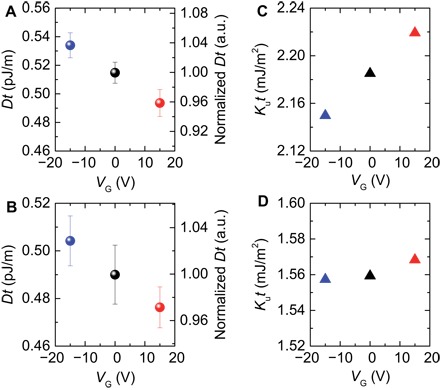
V_G dependence of the areal iDMI magnitude Dt for the sample with t_Co = (A) 0.78 nm and (B) 0.98 nm is shown. Dt is determined using the v_s and areal magnetic moment of the sample following Eq. 1. a.u., arbitrary units. The error bar indicates the error of v_s. Areal PMA energy K_ut as a function of V_G for the t_Co = (C) 0.78 nm and (D) 0.98 nm samples is shown.

Gate voltage effect on the DMI effective field

To investigate the EF effect on the iDMI more directly, the magnitude of H_D, which acts on the local magnetizations inside the DW, was determined from the H_z-driven DW motion under additional static in-plane magnetic fields (5, 6, 23). Figure 4A shows the static x-field H_x dependence of v obtained at |μ₀H_z| = 178 mT for the sample with t_Co = 0.98 nm under V_G = 0 V. Two different situations where the negatively polarized (N domain) and positively polarized (P domain) domain expands were investigated. As shown in the subtracted MOKE image in Fig. 4A, the DW displacement along the x axis is asymmetric when H_x is applied. v increases with the positive μ₀H_x when the N domain expands. The opposite μ₀H_x dependence is observed in the case of the P domain expansion. The asymmetric μ₀H_x dependence of v manifests that the magnetization inside the DW surrounding the N (P) domain directs outward (inward) normal to the DW plane, i.e., the left-handed chiral Néel DW is formed in our Pt/Co/Pd systems. The type of DW chirality in the present Pt/Co/Pd system is consistent with that for the Pt/Co systems (2, 26). Next, V_G application effect is checked. Here, the situation in which the N domain expanded by H_z is focused. In the experiments shown in Fig. 4B, DW motion was induced by a |μ₀H_z| of 100 mT under the application of H_x. In both V_G cases (+15 and −15 V), v decreased with negative H_x because of the DW chirality. For this sample, the v minimum in the v − μ₀H_x characteristics appears at approximately μ₀H_x = −88(−95) mT (≡ μ₀H_x^min) for V_G = +15(−15) V, where |H_x^min| corresponds to the H_D of this sample (6, 23). The position of H_x^min depends on V_G, i.e., H_D is modulated by the application of V_G. The ratio of the change in H_x^min between V_G = ±15 V is ~8%.

Fig. 4. In-plane field dependence of the DW velocity under gate voltage.

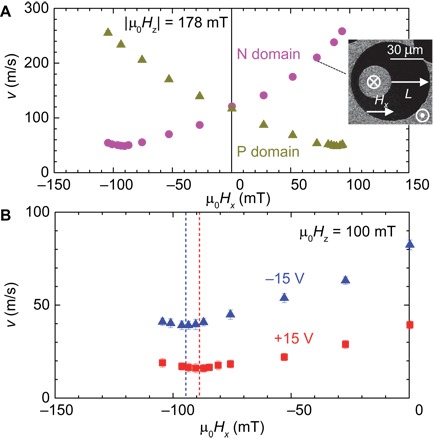
(A) v as a function of static in-plane magnetic field H_x for the sample with 0.98-nm Co thickness. The negatively polarized (N domain) and positively polarized (P domain) domain expansion cases are displayed. μ₀H_z of 178 mT was applied to drive the DW. The MOKE image is the subtracted image obtained under μ₀H_x = +72 mT for N domain case. (B) v measured under an in-plane static field H_x at V_G = +15 V (circle) and −15 V (triangle) for the sample with t_Co = 0.98 nm. |μ₀H_z| of 100 mT was applied to drive the DW. The dashed lines indicate the DMI effective fields H_D for V_G = +15 and −15 V. The error bar is the SD of 10 measurements for each μ₀H_x.

Within the framework of the 1D analytical model, H_D is also proportional to Dt as follows (7)

$${\mathit{H}}_{\mathrm{D}}=\frac{\mathit{D}\mathit{t}}{{\mathit{M}}_{\mathrm{s}}\mathit{t}\mathrm{\Delta }}$$ (2)

where Δ (= $\sqrt{\mathit{A}/{\mathit{K}}_{\mathrm{u}}}$) is the DW width parameter (K_u and A are the PMA energy density and exchange stiffness, respectively). Thus, the changes in K_u and A can represent another factor for the EF-induced H_D change. Figure 3 (C and D) shows the V_G dependences of K_ut for t_Co = 0.78 and 0.98 nm samples, respectively. K_ut increases with positive V_G in both samples, and the difference in K_ut between V_G = ±15 V for the sample with t_Co = 0.98 nm is 0.7%, as shown in Fig. 3D (see section S1). In this case, the A change must be ~17% if the EF-induced change in H_D obtained here was only caused by the modulation of Δ. However, the EF-induced change in A (or the exchange coupling) is expected to be a few percent at most (20, 21). Thus, the EF change in H_D was most likely caused by the V_G modulation of Dt. From the experimental H_D value, the Dt determined from Eq. 2 was 0.32(0.35) pJ/m for V_G = +15(−15) V by assuming a constant A = 1.6 × 10⁻¹¹ J/m (6, 7). The magnitudes of Dt determined from v_s and H_D measurements are consistent within a factor of ~1.5. The assumption of A may provide one reason for this slight difference.

DISCUSSION

The iDMI of the present sample is mainly dominated by the Pt/Co and Co/Pd interfaces. Because of the screening effect, the EF is almost shielded in the top Pd layer, i.e., the EF is hindered from reaching the deeper metallic layers (Co and Pt). Thus, the EF effect on the electronic structure (27) in the Pd layer plays a major role in the modulation of the iDMI (particularly the iDMI only at the Co/Pd interface). It is known that the iDMI in the FM/HM layered structure is attributed to the d-electron states at the Fermi level of the HM (28). Thus, in this experiment, the modulation of the outermost 4d electron state in the Pd is considered to be caused by the EF application, resulting in the change in the iDMI at the Co/Pd interface. The EF application also results in a change in the Co/Pd interfacial PMA energy. Although the iDMI is expected to positively correlate with the PMA if they originated at the same interface (9), the opposite EF response between Dt and K_u was observed in the present experiment (see Fig. 3). One possible explanation for this contradiction is as follows: the Dt (K_ut) in the present sample is the sum of the iDMIs (interfacial PMAs) at the Co/Pd and Pt/Co interfaces

$$\begin{array}{c}\mathit{D}\mathit{t}=|{\mathit{D}}^{\text{Pt}}\mathit{t}|-|{\mathit{D}}^{\text{Pd}}\mathit{t}|\\ {\mathit{K}}_{\mathrm{u}}\mathit{t}={\mathit{K}}_{\mathrm{u}}^{\text{Pt}}\mathit{t}+{\mathit{K}}_{\mathrm{u}}^{\text{Pd}}\mathit{t}\end{array}$$ (3)

where D^Pt(Pd)t [K_u^Pt(Pd)t] is the areal iDMI (areal PMA energy) at the Pt/Co (Co/Pd) interface. Note that the negative sign before the |D^Pdt| term is due to the inverted stacking of Pt/Co and Co/Pd. Equation 3 shows that the EF-induced increase in |D^Pdt| results in a decrease in the total iDMI (Dt) of the entire system because |D^Ptt|, which is the iDMI at the deeper interface, should be unchanged because of the screening effect. On the other hand, the increase in K_u^Pdt simply results in the enhancement of total PMA energy (K_ut). This may represent a scenario for understanding the opposite response of Dt and K_ut to the EF. In addition to the above interpretation, the change in iDMI and PMA may have originated at the Pd/MgO interface instead of the Co/Pd interface. In this case, the EF-induced change in the interfacial Rashba effect (29, 30) may be important for understanding the result.

In summary, we demonstrate the gating control of DW motion using Pt/Co/Pd asymmetric systems. The iDMI-stabilized v and H_D are modulated by the EF application. The change in v via the modulation of the DMI has a fundamentally different origin compared with the PMA-mediated case as reported in the Ta/CoFeB/MgO system (14). The electrical manipulation of the DMI demonstrated here is expected to provide a novel function for future spintronic devices based on chiral DWs or skyrmions.

MATERIALS AND METHODS

Film deposition and device fabrication

Layers composed of Ta(2.6 nm)/Pt(2.4)/Co(t_Co)/Pd(0.4)/MgO(2.0) were deposited on a thermally oxidized Si substrate using radio frequency sputtering. The base pressure of the sputter chamber was below 1.0 × 10⁻⁶ Pa, and Xe process gas was used for the deposition. The x-ray diffraction profile indicated that the Pt layer has a face-centered cubic (111) texture. To fabricate the capacitor structure, a 50-nm HfO₂ gate dielectric layer was deposited on the film at 150°C in an atomic layer deposition chamber. Subsequently, a Cr(2)/Au(10) gate electrode with a size of 300 × 300 μm was formed by a lift-off process. The magnitude of the leakage current under the application of V_G = ±15 V was below 500 pA. Note that the Pd layer on the Co layer acts to suppress unwanted domain nucleation; in the sample without the Pd layer, the distances between nucleated domains were too short to measure the DW velocity under the high-field regime.

Pulsed field application

H_z was generated using a small coil with a diameter of 500 μm placed on the device (see Fig. 1). To generate H_z, a pulsed current supplied from a customized high-voltage pulse generator was injected into the small coil. A rectangular-shaped pulse was confirmed by monitoring the voltage across the resistor connected with the coil in series.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/12/eaav0265/DC1

Section S1. EF effect on areal magnetic moment and anisotropy energy

Section S2. Numerical calculation of the saturation DW velocity

Fig. S1. Schematic illustration of the capacitor structure for the areal magnetization measurement.

Fig. S2. In-plane magnetization curves for the studied samples.

Fig. S3. Simulated DW velocities as a function of external magnetic field and the anisotropy and DMI dependences of the DW velocity.

Table S1. Summary of the capacitances for the capacitors.

Reference (31)