Passive Permeability of Planar Lipid Bilayers to Organic Anions

Abstract

The membrane permeability P of organic ions was reported to be governed by the structure of the permeating molecule. Thus far, it is unclear whether the ion structure alters membrane partition or translocation proper across the membrane. Here, we obtained P values for 24 anionic compounds (18 concrete values, 6 upper limits) measuring the current that they carry through folded planar lipid bilayers. The P values range over more than 10 log units. Our measured permeability values correlate well (r = 0.95; logRMSE 0.74) with the hexadecane/water partition coefficients of the respective chemicals predicted by the COSMO-RS theory. Other attempts to predict P from the partition coefficient of the neutral molecule and from the solvation energy (Born energy) that opposes transfer into the membrane once the molecule is charged were unsuccessful. The uncertainties in assigning an effective radius to nonspherical molecules were much too large. The observation underlines that the actual structure of the molecules needs to be considered to predict partition and thus P by the solubility-diffusion model.

Introduction

Passive membrane diffusion has been at the core of biophysical research for many decades. Insight into its laws is mandatory for understanding the role that channels and transporters play in membrane physiology. Transport of small neutral molecules is well described by Overton’s rule and the associated solubility-diffusion model (1, 2). The latter has been improved to account for membrane structure (3, 4, 5), but it has not lost its importance as a simple predictive tool for drug development (6). Significant efforts have been made to extend the solubility-diffusion model to charged substances. As a result, the total-membrane-energy profile was introduced, which included energetic terms 1) for stripping the molecule from its hydration shell (Born energy) and 2) that accounted for image effects and the intramembrane (dipole) potential in addition to the energetic expense for membrane partitioning of the molecule in its uncharged form (7).

Although being of potential use for the prediction of membrane permeability of charged molecules like fatty acid anions (8), uncouplers of phosphorylation (e.g., dinitrophenol (9)), antibiotics (e.g., valinomycin (10)), or drugs (e.g., verapamil (11) and aspirin (12)), the model has not been broadly used. The reason is that a simpleminded estimation of the individual energetic components based only on the molecule’s charge and size results in an unsatisfactory prediction, as we show below.

In the past, there have been a multitude of electrophysiological experiments on the conductivity of planar lipid bilayers in the presence of weak acids or permanent ions (e.g., (12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24)). Still, the collection of a diverse data set on ionic membrane permeability from literature as a basis for a sound mechanistic understanding and a predictive model remains quite difficult. One reason is that many studies were confined to molecules with a very high P, in which diffusion through the unstirred water layer (UWL)—a layer of water adjacent to the membrane in which transport is solely governed by diffusion—can be the limiting permeation process. Other factors also make it difficult to combine existing data into a consistent data set, such as varying lipid composition of the membrane and its solvents, different techniques used to form the membrane or to measure conductance, heterodimer formation and permeation in the case of weak acids, superlinearity of current voltage I/V curves, and saturation effects at high concentrations.

To allow for comparability, P is defined by the following transport equation:

$$J=P\times \mathit{\Delta }c,$$ (1)

where J is the flux density of a solute across a membrane because of a concentration difference Δc. More specifically, P here is (see Materials and Methods for details) 1) monomeric permeability, 2) membrane permeability without limiting UWL effects, 3) permeability at infinite dilution, 4) permeability in absence of a transmembrane potential, 5) permeability specific to the used lipid and its solvent, and 6) passive permeability.

Combining Eq. 1 with Fick’s first law of diffusion, passive membrane permeability can be expressed as a function of the membrane diffusion coefficient D and the partition coefficient K between the aqueous solution and the membrane of the thickness d (25):

$$P=K\times D/d.$$ (2)

Although membrane diffusion constants of different neutral organic molecules are expected to differ by less than a factor of 10 (26), the partition coefficients can vary by many orders of magnitude. Hence, the latter parameter will be the one dominating the varying P values of organic molecules. This so-called solubility-diffusion model was already established in 1899 by Overton (27), who stated that the more soluble the molecule is in lipids, the higher its permeability through the membrane will be.

Usually, the application of this solubility-diffusion model is based on the assumption that the main barrier for membrane permeation lies in the partitioning into and the diffusion through the hydrocarbon core of the lipid bilayer. The membrane is then approximated by a thin homogeneous layer of an apolar solvent such as hexadecane (Fig. S1, B and C). Indeed, for neutral compounds, the permeability seems to correlate well (26, 28) with the partition coefficient in hexadecane, which is assumed to have a dielectric constant similar to the membrane interior of solvent-depleted folded bilayers. Using this correlation established by Walter et al. (28), the permeability can be predicted if the hexadecane/water partition coefficient is known.

The solubility-diffusion model can also be applied successfully to ionic compounds (25, 29), but in that case, partitioning is not governed by the neutral H-bond and van der Waals interactions. Rather, Born energy, image energy, and effects exerted by the membrane dipole potential have to be considered (7):

$$\mathit{\Delta }{G}_{tot}\left(x\right)=\mathit{\Delta }{G}_n\left(x\right)+\mathit{\Delta }{G}_B\left(x\right)+\mathit{\Delta }{G}_i\left(x\right)+\mathit{\Delta }{G}_d\left(x\right),$$ (3)

where ΔG_tot is the total free energy of an ion in the lipid bilayer; ΔG_n is the neutral term; and Born ΔG_B, image ΔG_i, and dipole energy ΔG_d are the electrical terms of the free energy. Because of the self-solvation energy, also called Born energy—that is, the energy required to bring a charged particle from the aqueous to the organic phase—charged compounds will permeate the membrane orders of magnitude less readily than similar neutral compounds. The Born energy will be partly reduced by the image energy, which is the electrical interaction between the ion in the organic phase and the interfaces. Cation-induced membrane conductivity will be orders of magnitude smaller than membrane conductivity in the presence of anions because the membrane dipole potential increases the barrier for positively charged substances and decreases it for negatively charged molecules. Consequently, it is impossible to discriminate the cation carried direct current from the background conductivity for poorly solvable cations. Therefore, this study specializes in anionic membrane permeability.

The goal of this work was to find a mechanistically sound correlation between P of organic anions and their physicochemical properties that could eventually be used to predict P for ions for which experimental data are not available. Because no experimentally determined hexadecane/water partition coefficients for ions were available, the ionic bulk partition coefficients were either calculated from neutral partition coefficients (UFZ-LSER database (30)) corrected by the Born energy or directly via the COSMO-RS theory, using the commercial software COSMOtherm (31).

This work, therefore, involves the following working steps: 1) creation of a diverse data set from own permeability measurements on planar lipid bilayers, 2) prediction of the respective ionic water/hexadecane partition coefficients using the neutral partition coefficient and Born energy calculations or using COSMOtherm directly, 3) correlation of the permeability and the predicted partition coefficients, and 4) collection of literature data to test the predictive power of the correlation.

Materials and Methods

Chemicals

The lipids 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), and Escherichia coli polar lipid extract (PLE) were purchased from Avanti Polar Lipids (Alabaster, AL). The buffers MES hydrate (2-morpholin-4-ylethanesulfonic acid), CAPSO (3-(cyclohexylamino)-1-propanesulfonic acid), and MOPS (3-morpholinopropane-1-sulfonic acid), as well as cholesterol, methylsulfinylmethane (DMSO), 5-chloro-2-(2,4-dichlorophenoxy)phenol (triclosan), (2,3,4,5,6-pentachlorophenol (PCP), 2-hydroxybenzoic acid (salicylic acid), 2-[(3-chlorophenyl)hydrazinylidene]propanedinitrile (CCCP), anthracene-9-carboxylic acid, Sodium;tetraphenylboranuide (TPB), 3,4-dinitrophenol (3,4-Dnp), 2,4,6-tribromophenol (bromol), and 4-nitro-2-(trifluoromethyl)-1H-benzimidazole were purchased from Sigma-Aldrich (Munich, Germany). The compounds 4-nitrophenol (4-Np), 4-hydroxy-3-(3-oxo-1-phenylbutyl)chromen-2-one (warfarin), 2,4-dinitrophenol (2,4-Dnp), 2-(2-chloro-4-methylsulfonylbenzoyl)cyclohexane-1,3-dione (sulcotrione), sodium;2-[2-(2,6-dichloroanilino)phenyl]acetate (diclofenac), 2-[3-(trifluoromethyl)anilino]benzoic acid (flufenamic acid), 2-(2-Methyl-2-propanyl)-4,6-dinitrophenol (dino2terb), and 3-[1-(4-chlorophenyl)-3-oxobutyl]-4-hydroxychromen-2-one (coumachlor) were purchased from Fluka (Buchs, Switzerland). The compounds 3,5-dibromo-4-hydroxybenzonitrile (bromoxynil) and 2-butan-2-yl-4,6-dinitrophenol (dinoseb) were purchased from Dr. Ehrenstorfer (Augsburg, Germany), sodium;4-octylbenzenesulfonate was purchased from TCI (Tokyo, Japan), potassium;bis(fluorosulfonyl)azanide and sodium;9,10-dimethoxyanthracene-2-sulfonate were purchased from abcr (Karlsruhe, Germany), and 3,5-dichlorophenol (3,5-Dcp) was purchased from Riedel-de Haën AG (Seelze, Germany). 3,5-dibromo-2-(2,4-dibromophenoxy)phenol (6-OH-BDE47) was purchased from Accustandard (New Haven, CT).

Calculation of the partition coefficients

Bulk

The hexadecane/water partition coefficients were calculated using the prediction model COSMOtherm (COSMOlogic, Leverkusen, Germany). As no experimentally determined hexadecane/water partition coefficients were available in literature, we chose the COSMO-RS theory as a replacement tool. The COSMOtherm software is easy to handle for the inexperienced user and has been proven as equally or more reliable than other prediction methods (32, 33) while being significantly less computationally demanding than molecular dynamics simulations (34). The model is based on the “Conductor-like Screening Model for Realistic Solvation” (COSMO-RS) theory; see (31) for details. In brief, starting from the structure of a solute or solvent, the polarization charge density on the molecular surface in the presence of an embedding conductor is calculated via quantum chemical calculations (COSMOfiles). Next, interaction energies are quantified as local interactions of COSMO polarization charge densities. Reducing molecular interactions to pairwise interactions of surfaces and averaging thermodynamically over many ensembles then allows deriving properties such as the partition coefficient at infinite dilution.

All COSMOfiles were calculated using the software COSMOconf (v.4.1; COSMOlogic). To calculate the partition coefficients, COSMOtherm (v.C30_18.0.0; COSMOlogic) was used with the “BP_TZVPD_FINE_C30_18.ctd” parametrization at 295 K.

Membrane

For the solubility-diffusion model, two electrical interaction terms have to be considered that are not incorporated in the above bulk hexadecane/water partition coefficient (partition of the solute from a pure water phase into a pure hexadecane phase). Although the bulk calculations already include neutral interactions and the Born energy, in the membrane itself, the membrane dipole potential and the image energy have to be considered for the total membrane partition coefficient K_tot:

$$K_{tot}=K_b\times \text{exp}\left[-\left(\Delta G_d+\Delta G_i\right)/\left(RT\right)\right].$$ (4)

More generally, the partition coefficient into the membrane can be expressed as

$$K_{tot}=\exp \left[-\left(\mathit{\Delta }{G}_n+\mathit{\Delta }{G}_B+\mathit{\Delta }{G}_d+\mathit{\Delta }{G}_i\right)/\left(RT\right)\right],$$ (5)

where K_b is the bulk partition coefficient calculated with COSMOtherm, ΔG_n is the neutral energy, ΔG_B is the Born energy, ΔG_d is the dipole energy, ΔG_i is the image energy, R is the molar gas constant, and T is the temperature, here set to 295 K.

Dipole energy

ΔG_d can be calculated using the following equation:

$$\mathit{\Delta }{G}_d=N_A\times q\times \mathit{\Delta \Phi ,}$$ (6)

where N_A is the Avogadro constant, q the charge, and ΔΦ the membrane dipole potential. For further calculations, the positive membrane dipole potential of DPhPC with 228 ± 5 mV will be used (35).

Born-image energy

In accordance to Flewelling et al. (7), ΔG_B and ΔG_i in the limit of a perfect conductor can be expressed as follows:

$$\Delta G_B\left(x\right)=N_A/\left(4\pi {\epsilon }_0\right)\times q^2/\left(2{\epsilon }_{1}r\right)$$ (7)

and

$$\Delta G_i\left(x\right)=-N_A/\left(4\pi {\epsilon }_0\right)\times q^2/\left(2{\epsilon }_1\right)\times \left[1/\left(2x\right)+1.2\times \left(1/d\right){\left(x/d\right)}^2\right],$$ (8)

where N_A is the Avogadro constant, ε₀ is the electric permittivity of free space, ε₁ is the dielectric constant of the membrane interior, r is the Born radius of the ion, d is the effective electrical bilayer thickness, and x is the distance from the interface (see Fig. S1 C). For further calculations, x will be set to d/2 at the membrane center, where ΔG_i is maximal, and the dielectric constant ε₁ will be set to 2.

Membrane formation

Solvent-depleted planar lipid bilayer membranes—they are not completely “solvent free” (36)—were formed using the Montal-Mueller technique (37). Because of its high stability, the synthetic lipid DPhPC was used for all permeability measurements. To test comparability to other lipids, DOPC, DPhPC with 20 mol% cholesterol, and the negatively charged PLE were also used in experiments for measurements with two of our compounds.

A pretreated (0.5% (v/v) hexadecane in hexane) septum (25 μm thick) with a circular hole (diameter: ∼80–150 μm) separated the two compartments (1.3 mL, each) of a Teflon chamber (see Fig. S1 A). Lipid dissolved in hexane (∼5–10 μL; 20 mg/mL) was placed on top of the buffer solution in each compartment. After solvent evaporation, the buffer-air interface was lowered and raised over the aperture repetitively until a bilayer was formed. Membrane formation was judged by its membrane capacity (specific capacity range: ∼0.6–0.8 μF/cm²).

Measurement

When a stable membrane was formed, background curves for membrane-attributed conductivity were recorded before adding different concentrations of the respective chemical. The chemical was always added to the bulk phases as a concentrated solution in water or DMSO. Thereby, the volume concentration of DMSO in the aqueous phase never exceeded 1% for concentrations used in evaluation, and control measurements showed no significant effect of this DMSO concentration on the conductance. The chemical concentrations on either side of the membrane were identical (no chemical gradient).

Magnetic stirrers in each compartment allowed rapid mixing of the solutions after each addition and during the measurement. Influence of the UWL was checked by comparing the effect of different stirring velocities on the I/V characteristics.

All experiments were carried out at room temperature (21–23°C). To reduce noise, the experimental setup was placed in a Faraday cage. The aqueous buffer solutions always contained 0.1 M NaCl or KCl and 50 mM buffer (MES (pH 6); MOPS (pH 7); CAPSO (pH 9)), except for solutions at pH 12 or above, in which case no buffer was used.

The pH of the buffer solution was chosen at least 1.4 pH units above the respective pK_a of the researched chemical so c_anion ≈ c_tot could be assumed for the evaluation. The decreased fraction of neutral species also led to a reduced heterodimer concentration, ideally enabling the measurement of monomer permeation.

Data were mainly recorded with the HEKA EPC10 patch-clamp amplifier (HEKA Elektronik Dr Schulze, Lambrecht, Germany), and the built-in on-line compensation for series resistance and capacitance was used. Voltage was applied to silver-silver chloride electrodes placed in the buffer solutions in both compartments of the Teflon chamber, and the resulting current was measured. During signal acquisition, the 10 and 0.1 kHz (Bessel) filters of the EPC10 were employed.

Several ramp voltage sweeps (see Fig. S2 A) from −100 to + 100 mV at a rate of 10 mV/s were applied to measure the steady-state characteristics after each addition. Sporadic control samples measured with a 2-s-long direct current voltage, increased incrementally in 10 mV steps from −100 to + 100 mV (see Fig. S2 B), showed identical results. The only exception was TPB, which was limited by the diffusion through the UWL. To avoid this limitation, in accordance with Anderson et al. (38), its conductance was measured via voltage steps at t = 0 s after the voltage was applied (see Fig. S2 C; record rate: 0.33 kHz; filter: 8.7 kHz).

For some measurements, the eOne amplifier (ELEMENTS s.r.l., Cesena, Italy) was used, leading to the same results as the HEKA device.

Assumptions for the permeability

In this work, the permeability was understood as follows.

Monomeric permeability

In the case of permanent and strongly dissociated ions, the ion is assumed to be the sole charge carrier across the membrane (besides the membrane background conductivity (10⁻⁹–10⁻⁸ S/cm²) of the respective buffer and the salts such as Na⁺, Cl⁻, or K⁺ or H⁺ or OH⁻, which is subtracted during analysis). Measurements of the electrical membrane conductivity in their presence thus allow determining their monomeric membrane permeability. Hydrophobic weak acids (see Fig. S3) may not leave the membrane, i.e., after traversing the membrane interior in their deprotonated form [A⁻], they may diffuse back—following a local concentration gradient—in their protonated form [AH], thereby carrying an H⁺ ion from one side to the other. As the whole process is limited by the permeation of the anion itself, the anionic permeability can be measured directly. This process is also referred to as uncoupling (39).

The simultaneous permeation of the heterodimer (see Fig. S3, red frame) may add to the monomeric permeability or even replace it as the limiting permeation process (40). This will depend on the fraction of deprotonated and protonated species (i.e., on pH and pK_a), their likelihood to combine to a heterodimer (dimerization constant K_D), and the permeability of the heterodimer. Because for small concentrations, heterodimer concentration [AHA⁻] depends on the square of the total chemical concentration c_tot (see Eq. S6), conductivity measurements governed by heterodimer permeation will also show a quadratic dependence on c_tot. In contrast, conductivity measurements governed by monomer permeation will show a linear dependence on c_tot. Therefore, only linear dependencies of the conductivity on c_tot are evaluated to extract monomeric permeability.

P and UWL

We assessed the UWL effect by comparing the apparent (measured) membrane permeability P_A to the unstirred water layer permeability P_W. From

$$\frac{1}{P_A}=\frac{1}{P}+\frac{1}{P_W}$$

and P_W = D_w/δ = 5 × 10⁻⁵ cm² s⁻¹/100 μm = 5 × 10⁻³ cm s⁻¹, we find that P_W can be neglected for P < 5 × 10⁻⁴ cm s⁻¹, where D_W is the aqueous diffusion coefficient of the permeant and δ the UWL thickness. All of our investigated substances fall in that category, with only one exception: TPB. That is, unstirred layer effects can be neglected in all cases but one. In this case, P may be extracted by applying a voltage step (38) or a pulse charge (41). Instead of evaluating the current in the steady state, we measured the current just after voltage application.

Permeability at infinite dilution

At high concentrations, conductivity may stagnate or even decline, leading to a decreased P (19, 42, 43). This effect may be interpreted in terms of space-charge-limited currents (43), in which the anions entering the membrane build up a negative boundary potential as the neutralizing positive counterions remain in the aqueous phase. To explain the appearance of a conductivity maximum, Ketterer et al. (19). proposed a model of limited adsorption sites at the interface, whereas Smejtek and Paulis-Illangasekare (44) attributed the effect to a layer of absorbed molecules (oriented dipole moments) decreasing the dipole potential. To avoid the uncertainties associated with the interpretation of such saturation effects, we evaluated only linear dependencies of the conductivity on c_tot.

Permeability in absence of a transmembrane potential

The shape of the I/V curves displays superlinearity, meaning the conductance I/V increases with the applied voltage (15, 19, 43). Although some literature states the conductivity at a certain voltage (42), here, P is defined for zero applied voltage because it is more common.

Passive permeability

Synthetic lipid was used to fold solvent-depleted membranes. These purely artificial membranes contain no proteins that could promote active transport; therefore, all conductivity measurements were based on passive diffusion through the planar bilayer.

Evaluation of permeability measurements

The conductivities showed a superlinear dependence on the voltage. Therefore, in accordance with Miyauchi et al. (45), the I/V curves were fit by Eq. 9 (Igor Pro (WaveMetrics, Lake Oswego, OR), nonlinear least-squares, see Fig. S2, D and E):

$$G_V=I/V={\text{G}}_0\times \left(1+b{V}^2\right),$$ (9)

where G_V is the conductivity at the applied voltage V, I the measured current across the membrane, and b a factor indicating the curvature of the I/V curve. Specific conductivities G_s,0 were gained dividing the slope at zero voltage G₀ by the area of the septum hole. This represents the lower limit because the neglected torus surrounding the planar lipid bilayer decreases the actual membrane area.

To obtain P at zero voltage, the mean G_s,0 was related to the chemical concentration using the Goldman-Hodgkin-Katz flux equation, assuming no chemical gradient (see Fig. S2 H; weighted linear regression (Igor Pro)):

$$G_{s,0}=P\times {\left(zF\right)}^2/\left(RT\right)\times c_{ion},$$ (10)

where G_s,0 is the specific conductivity at zero voltage, P the monomeric permeability, z the valence of the ion, F the Faraday constant, R the gas constant, T the temperature set to 295 K, and c_ion the ion concentration. When conductivities showed stagnation or decreased or increased quadratically at high concentrations, only the linear part at low concentrations was used for evaluation of the permeability.

Additionally, in accordance with Miyauchi et al. (45), saturating curves were fit by a Michaelis-Menten-type equation (Eq. 11, IGOR Pro) to extract the chemical concentration K_m at which half of the saturating conductivity was reached:

$$G_{s,0}=\left(G_{s,0,max}\times c_{ion}\right)/\left(K_m+c_{ion}\right),$$ (11)

where G_s,0,max is the maximal specific conductivity at zero voltage.

Literature data

Anionic permeability data were collected from literature for validation. The list (see Results and Discussion) makes no claim to completeness, and data of experiments that did not meet our above stated specifications of permeability were excluded: if UWL effects occurred or could not be ruled out (23, 46), or if the permeability was dominated by dimer permeation (17, 23, 47, 48), the data were not taken into account. If stated, permeability values were directly adopted. If only G_s,0 was stated or could be read from a graph, Eq. 10 was used to calculate the permeability. We used the rate constants k_i and partition coefficients β reported by Benz (18) to calculate the permeability β×k_i according to Eqs. 8 and 9 in (18). Concentrations K_m at which half of the saturating conductivity was reached were extracted from literature (for both anions and cations), either directly as stated or by fitting Eq. 11 to the conductivity/concentration data extracted from figures.

Results and Discussion

Experimental anionic permeability

The measured anionic permeability data for DPhPC bilayer membranes are listed in Table 1. The monomeric permeability was determined for 18 compounds and ranged over more than 10 orders of magnitude. For six compounds, the permeability was too low to be detected, so only an upper limit of the permeability is given. For those, the conductivity never exceeded the background level in the concentration limit set by solubility in water or membrane stability or, in the case of diclofenac and triclosan, dominating heterodimer permeation prevented the determination of the monomeric permeabilities.

Table 1.

IUPAC Name, CAS Number, Abbreviation, and Experimental Logarithmic Anion Permeability through a DPhPC Bilayer Measured at Listed pH, pK_a Experimental/Predicted, and Calculated Logarithmic Anionic Bulk Partition Coefficient Hexadecane/Water K_hd/w

IUPAC name	CAS	Abbreviation	Log[(Pexp/(cm/s)]	pH	pKa	Log[Khd/wa/(Lw./Lhd)]
tetraphenylboranuide	143-66-8	TPB	−0.5b	6	NDc	−8.8
2-[(3-chlorophenyl)hydrazinylidene]propanedinitrile	555-60-2	CCCP	−3.4	7d	6.09e	−14.6
3,5-dibromo-2-(2,4-dibromophenoxy)phenol	79755-43-4	6-OH-BDE47	−5.2	12.5	7.2f	−14.8
bis(fluorosulfonyl)azanide	14984-76-0	ND	−4.7	7	−1.5f	−15.2
2-(2-Methyl-2-propanyl)-4,6-dinitrophenol	1420-07-1	dino2terb	−4.0	7	5.1f	−16.2
2-butan-2-yl-4,6-dinitrophenol	88-85-7	dinoseb	−4.4	7	4.9f	−16.6
2,3,4,5,6-pentachlorophenol	87-86-5	PCP	−4.4	7	4.8g	−16.6
3,5-dibromo-4-hydroxybenzonitrile	1689-84-5	bromoxynil	−6.2	7	5.1f	−17.5
5-chloro-2-(2,4-dichlorophenoxy)phenol	3380-34-5	triclosan	<−5.9h	12	7.7f	−17.8
3-[1-(4-chlorophenyl)-3-oxobutyl]-4-hydroxychromen-2-one	81-82-3	coumachlor	−6.8	7	5.2f	−18.2
4-nitro-2-(trifluoromethyl)-1H-benzimidazole	14689-51-1	ND	−6.1	9	7.0f	−18.4
3,4-dinitrophenol	577-71-9	3,4-Dnp	−7.5	12	5.7f	−18.9
2,4,6-tribromophenol	118-79-6	bromol	−7.3	9	6.3f	−19.0
2,4-dinitrophenol	51-28-5	2,4-Dnp	−6.5	7	4.3f	−19.2
4-hydroxy-3-(3-oxo-1-phenylbutyl)chromen-2-one	81-81-2	warfarin	−8.4	7	5.6f	−19.9
2-[3-(trifluoromethyl)anilino]benzoic acid	530-78-9	flufenamic acid	−6.8	7	3.9f	−21.1
3,5-dichlorophenol	591-35-5	3,5-Dcp	−7.9	12.5	8.1f	−21.8
4-nitrophenol	100-02-7	4-Np	−8.9	12	7.1f	−22.5
2-[2-(2,6-dichloroanilino)phenyl]acetate	15307-79-6	diclofenac	<−8.5h	7	4.0f	−23.5
4-octylbenzenesulfonate	6149-03-7	ND	<−8i	7	−1.8f	−24.9
2-(2-chloro-4-methylsulfonylbenzoyl)cyclohexane-1,3-dione	99105-77-8	sulcotrione	<−8.7i	7	4.5f	−25.2
2-hydroxybenzoic acid	69-72-7	salicylic acid	−11	7	2.8f	−26.1
9,10-dimethoxyanthracene-2-sulfonate	67580-39-6	ND	<−9i	7	−1.7f	−26.6
anthracene-9-carboxylic acid	723-62-6	ND	<−9i	7	3.2f	−27.4

^aCOSMOtherm (31), C30_18, COSMOlogic, http://www.cosmologic.de.

^bVoltage step measurement evaluated at t = 0 after voltage application because of UWL limitations; all others evaluated at steady state.

^cND, no data.

^dAt pH 7, for CCCP, c_anion ≈ 0.9c_tot. Correcting for this reduced anion fraction did not significantly change the result for P_exp.

^eFrom (16).

^fJChem for Office (Excel) was used for pK_a calculation, JChem for Office 17.14.0.1746, 2017, ChemAxon (http://www.chemaxon.com).

^gFrom (42).

^hOnly heterodimer signal detected in the experimental limit.

ⁱNo signal detected in the experimental limit.

Correlation with the partition coefficient

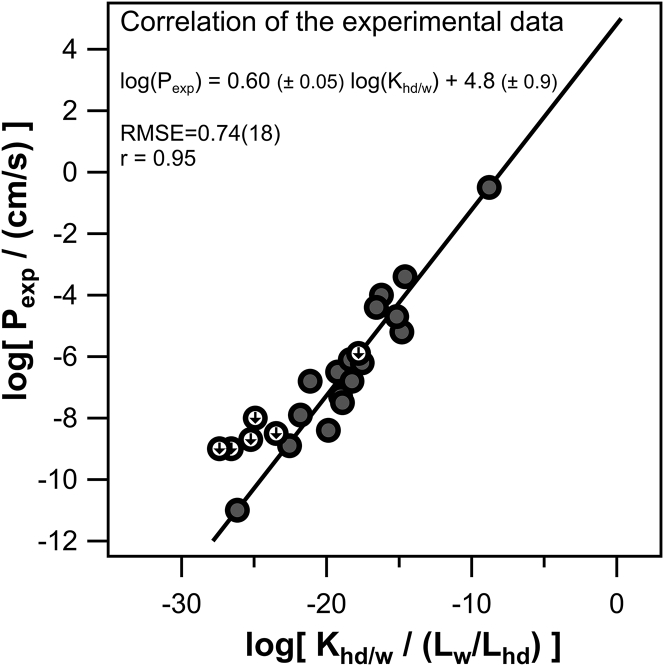
Assuming that the main barrier for anionic membrane permeability lies in the alkane-like center of the membrane, according to the solubility-diffusion model, the experimental permeability should correlate well with the partition coefficient in a hydrophobic solvent like hexadecane. And indeed, correlating (linear regression; Igor Pro) the logarithmic experimental permeability log(P_exp) values to the calculated logarithmic hexadecane/water partition coefficients (COSMOtherm) log(K_hd/w) listed in Table 1 reveals the correlation log(P_exp) = 0.60 (±0.05) log(K_hd/w) + 4.8 (±0.9) with a root-mean-squared error (RMSE) of 0.74 and an r of 0.95, shown in Fig. 1.

Figure 1.

The experimental permeability P_exp plotted against the respective hexadecane/water partition coefficients K_hd/w. P_exp was measured for 24 different anions through DPhPC bilayers, and K_hd/w (L_w and L_hd stand for litre water and litre hexadecane respectively) was calculated using the commercial prediction model COSMOtherm. The linear regression (n = 18; shaded circles) was made with IGOR Pro. Circles marked with a downward arrow indicate upper limits of P_exp and are not used for the regression. Because of its high solubility in water, P_exp for salicylate (lowest datapoint) could be determined.

This correlation should make a good semiempirical prediction model. Yet intuitively, when considering Eq. 2 and assuming that the diffusion coefficients do not vary much, one would expect the slope of the correlation to be near 1. However, with 0.60 ± 0.05, it is much smaller. This apparent discrepancy suggests that partitioning into bulk hexadecane does not completely govern P. This observation is not new. It has been made decades ago by Walter and Gutknecht (28). They found that the volume of permeating molecules plays a role: only when excluding small molecules did they find the expected 1:1 correlation of P to the partition coefficient. Nagle et al. (3) subsequently rationalized the observation by identifying the difference between the cross-sectional areas of head groups and acid chains as the area that is accessible for passage of solutes into the hydrocarbon core. Although neutral molecules are free to adopt an orientation that minimizes steric hindrance, i.e., that makes optimal use of the access area, charged molecules are not. Their orientation is governed by the intramembrane field. That is, a polar molecule must enter the positively charged membrane interior with its negatively charged residue being upfront. The orientational restrictions are less pronounced if the negative charge is buried deep within the molecule or when the molecule adopts a round shape. The different orientational bias might prevent the permeability for strongly polar compounds (highly negative K_hd/w) from going down as much as would have been predicted from a 1:1 correlation to the partition coefficient.

The slope may also be explained by taking into account that the more hydrophilic ions (see σ surfaces in Fig. S4) are unlikely to be fully dehydrated when passing the bilayer (29). Because the Born energy is the self-solvation energy, it overestimates the costs for ions that keep some water molecules. Or, in other words, if the ion locally increases the water content of the bilayer, ε changes locally and with it, the Born energy.

Calculation of P

From COSMOtherm’s K_b

We calculated P according to the solubility-diffusion model (Eq. 2). To account for the membrane dipole potential and the image energy (Eq. 4), we assumed an effective electrical bilayer thickness of 25.5 Å for DPhPC bilayers (49). Using Eqs. 6 and 8, we calculated ΔG_d to be −22.0 kJ/mol and ΔG_i at the membrane center to be equal to −17.7 kJ/mol. The resulting K_tot differed from K_b by a factor of 6.8 × 10⁷. Predicting the diffusion coefficients in the membrane interior from the molecular weight (50) and assuming a thickness of the hydrocarbon membrane core of 25.5 Å led to the P-values listed in Table S1. In Fig. S5, the logarithmic experimental permeability log(P_exp) is plotted against the logarithmic calculated permeability log(P_calc). The measured and calculated values match within one order of magnitude for the more hydrophobic compounds like TPB. However, calculated and measured P-values deviate by several orders of magnitude for the less hydrophobic, more polar compounds. Possible reasons for this discrepancy were discussed in the above paragraph.

From the membrane partition coefficient of the neutral substance

To test whether the shape of the molecule is important, we calculated P starting either from neutral permeability values or neutral hexadecane/water partition coefficients K_n using Eqs. 2, 5, 6, 7, and 8. Assuming a spherical particle, the Born radius was estimated by the van der Waals volume using JChem, and the respective Born energy terms were calculated using Eq. 7 (data listed in Table S2).

Neutral permeabilities were available in literature for CCCP (11 cm/s (16)) and salicylic acid (0.2 cm/s (1)). For those, ΔG_n was calculated using Eq. 5 while setting all electrical interaction terms to zero (−3.5 kJ/mol; 6.7 kJ/mol). Using Eqs. 2 and 5, the logarithmic anion permeability was calculated to be −10.1 for CCCP (log[P_exp/(cm/s)] = −3.4) and −14 for salicylate (log[P_exp/(cm/s)] = −11), deviating several orders of magnitude from the experimentally determined values. Fig. S6, A and B show P_exp plotted against the partition coefficients K_hd/w for the anionic species, calculated from K_n using either COSMOtherm or the UFZ-LSER database (30). In comparison to K_hd/w directly calculated using COSMOtherm (see Fig. 1; RMSE = 0.74) the correlation is more broadly distributed for both COSMOtherm (K_{hd/w,COSMOtherm}; RMSE = 1.9) and the UFZ-LSER database (K_{hd/w,UFZ-LSERD}; RMSE = 1.7) when calculating from K_n. In Fig. S6 C, K_n calculated by the UFZ-LSER database is plotted against K_n predicted by COSMOtherm. The error in K_n (RMSE from 1 to 1 line: 1.5) cannot solely explain the broad scatter in permeability in Fig. S6, A and B. This can be seen in Fig. S6 D, in which P_exp vs. P_calc based on either K_{hd/w,COSMOtherm} or K_{hd/w,UFZ-LSERD} differs only little, whereas when estimating the Born radius by the Einstein-Stokes equation instead of the van der Waals radius, the calculated anionic permeabilities increase by several orders of magnitude. In the case of, e.g., salicylate, a 30% error in radius (Einstein-Stokes: r = 3.9 Å; van der Waals: r = 3.0 Å) will result in a difference in calculated permeability of more than four orders of magnitude (Einstein-Stokes: log[P/(cm/s)] = −9.3; van der Waals: log[P/(cm/s)] = −14.0). Because of their huge impact on the Born energy, uncertainties in the radius—and the Born radius is expected to differ from the van der Waals radius (18)—render a precise prediction of the anion permeability from neutral partition coefficients impracticable.

Besides this general interpretation of the data in light of the solubility-diffusion model, it is also worthwhile to discuss some of the details of the experimental results as such.

Conductivity

I/V characteristics

Although the amplitudes of the signal ranged widely between a few hundred picoamperes and a few nanoamperes for different chemicals and concentrations, the shape of the I/V curve always displayed superlinearity, meaning the conductivity I/V increased with the applied voltage (see Fig. S2, A, D, and E). The only exception to this superlinearity was TPB, a rather large and hydrophobic permanent anion with a high membrane permeability of 0.3 cm/s. At a low concentration below 0.3 mM, its steady-state conductivity is not governed by the diffusion through the membrane core but by the diffusion through the adjacent UWL. This leads to steady-state currents saturating with increasing voltage (see Fig. S7 B) and a decay in current immediately after a voltage is applied (see Fig. S7 C). These effects due to diffusion polarization have previously been studied extensively (38, 43). The voltage ramp from −100 to +100 mV gave negative I/V characteristics (see Fig. S7 A) for TPB, a consequence of the superposition of decaying current and steady-state current (43). Therefore, a voltage step was used to measure the conductance at t = 0 (after application of the transmembrane potential) and the steady-state conductance. The former, limited by the diffusion through the membrane interior, provided the membrane permeability (0.3 cm/s), whereas the latter provided the permeability P_UWL through the UWL (7.4 × 10⁻⁴ cm/s). Using the TPB diffusion constant D_w in water (43) of 8 × 10⁻⁶ cm²/s and the simple relation P_w = D_w/δ, the overall thickness of the unstirred layers δ was estimated to be around 108 μm—a value that is consistent with direct observations of δ by scanning electrochemical microscopy (51). Increased peak and steady-state conductivities due to stirring were observed (Fig. S7 D), but the changes were not significant because the deviations between single experiments were more pronounced.

No other chemical measured in this work seemed to be limited by the UWL. Only some weak acids, like CCCP or dino2terb, showed membrane permeabilities near that of the UWL. But a high buffer concentration in the bulk solutions assured a steady supply of H⁺ at the membrane interfaces.

Permeability

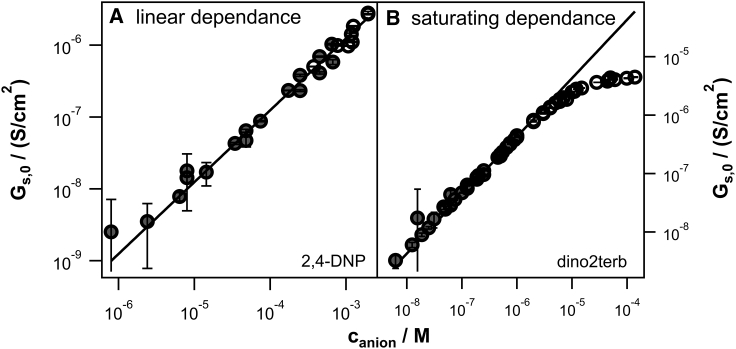
Plotting the G_s,0 values against the respective concentration ideally revealed a linear dependence (see Fig. 2 A for the example of 2,4-Dnp), indicating a constant permeability over the whole concentration range. In that case, the permeability could be extracted by fitting these curves to Eq. 10, using a linear least-squares method.

Figure 2.

(A) shows a typical case of conductivity (2,4-Dnp, p = 3.3 × 10⁻⁷ cm/s; stock solution in DMSO) depending linearly on the concentration (constant permeability). Each circle represents the mean conductivity of several voltage sweeps; the error bars mark their mean SD. Only data points at final DMSO concentrations below 1% v/v (shaded circles) were used in the linear regression (Eq. 10; IGOR Pro). (B) shows a typical case of saturating conductivity (dino2terb, p = 1.1 × 10⁻⁴ cm/s; stock solution in DMSO). At low concentration, the mean specific conductivity G_s,0 depends linearly on the concentration (constant permeability), but with increasing concentration, the conductivity saturates (decreasing permeability). Only the part showing linear dependence (shaded circles) was used in the linear regression (Eq. 10; IGOR Pro).

Saturation

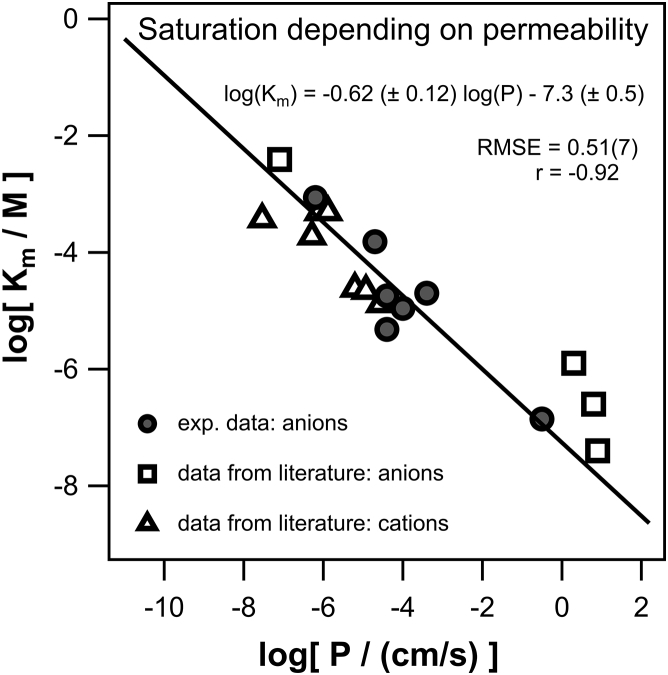
Several of the measured chemicals (see Table S3) showed a saturating or even decreasing dependence of conductivity on the respective concentration, meaning the permeability was constant for low concentrations but decreased at higher concentrations. See Fig. 2 B for the example of dino2terb. In those cases, only the linear part at low concentration was used to extract the permeability. An additional fit with a Michaelis-Menten-type kinetic (Eq. 11) allowed us to determine the chemical concentration K_m at which half of the maximal saturation conductivity is reached. This concentration may be interpreted as a measure at which saturation sets in. Plotting the logarithmic K_m against log(P_exp) revealed a good correlation (linear regression; Igor Pro) log(K_m) = −0.62(±0.1) log(P_exp) − 7.3(±0.5) with an r of −0.92 and an RMSE of 0.51. Fig. 3 shows the correlation, as well as data points of different K_m and respective permeability extracted from literature values (see Tables S3–S5). Literature data, measured with different lipid composition, and even cations, still seem to follow the correlation, indicating that the same parameters governing membrane permeation may also govern saturation behavior of both anions and cations.

Figure 3.

The concentration K_m at which half of the maximal saturation conductivity is reached plotted against the respective permeability values. K_m is extracted using Eq. 11 in IGOR Pro for seven organic anions (shaded circles) from own measurements that show saturating conductivity, and for four anions (open squares) from literature. K_m for cations (open triangles) were directly adopted from (45) (see Tables S3–S5). The linear regression was made with IGOR Pro based only on own measurements (n = 7; shaded circles). Literature data seem to follow the correlation independent of charge or used lipids.

Dimer permeation

Many weak acids showed a superposition of linear and quadratic dependence of conductivity on the concentration. Although often near the pK_a, quadratic dependence dominated the permeation, and the dependence became linear with increasing pH (except for triclosan and diclofenac). The conductivity measurements also showed mixed dependencies—linear dependencies for low concentrations and quadratic dependencies for higher concentrations (see Fig. S8 for the example of 3,4-Dnp). This effect is attributed to the formation of heterodimers that are able to traverse the membrane interior far more easily than the sole anion (see Materials and Methods). The measurement pH was raised until the conductance showed linear dependence (monomeric permeability), and in the case of mixed dependencies, only the linear part was analyzed. Final pH values at which the experiments were performed to determine the monomeric permeability are listed in Table 1.

Lipid composition

Although all permeability values in this work were measured for pure, synthetic solvent-depleted folded DPhPC (totally saturated) membranes, additional measurements with membranes of different lipid composition were done in this work to test the robustness of the system. Permeability data of two different solutes—namely coumachlor and dino2terb—measured for membranes of DOPC (unsaturated), DPhPC + 20 mol% cholesterol, or PLE (E. coli extract, negatively charged), respectively, did not deviate from the value for pure DPhPC membranes by more than a factor of 0.3 or 2.6 (see Table S6).

Comparison to literature data

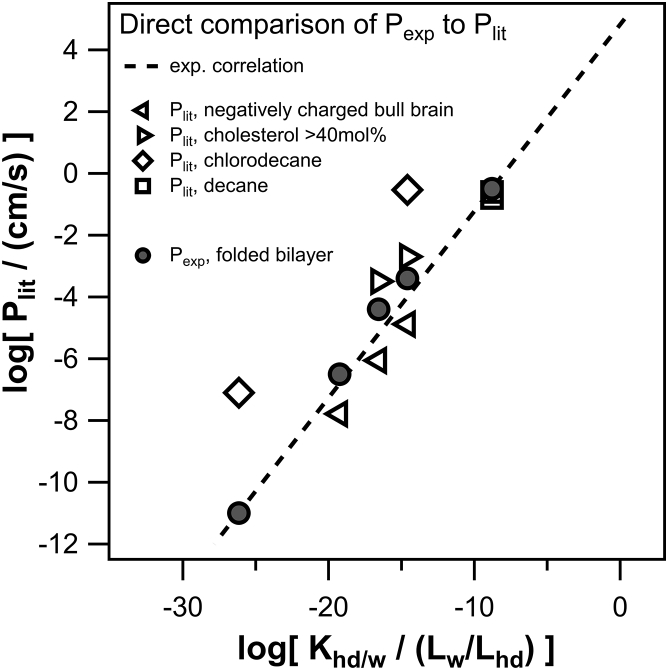
To validate our experimental data and our semiempirical correlation between the experimental anionic permeability values and the predicted anionic partition coefficients, our results are, in the following, compared to data extracted from literature. Collected logarithmic anionic permeability data from literature log(P_lit) corresponding to the criteria stated in Materials and Methods are listed in Table S7, and our own data are listed in Table 1. For five of the measured permeabilities an overlap with literature could be found: 2,4-Dnp, CCCP, PCP, salicylate and TPB.

Although TPB matched literature data within a factor of less than two, the other three compounds showed deviations of one to four orders of magnitude (see Fig. 4).

Figure 4.

Permeability values both from own experiments and literature plotted against the anionic hexadecane/water partition coefficient (COSMOtherm), for the five measured compounds for which overlapping literature data were available. From left to right are shown salicylate, 2,4-Dnp, PCP, CCCP, and TPB. The linear regression (dashed line) determined for our own permeability data (see Fig. 1) is plotted alongside literature data.

These discrepancies can be explained taking into consideration that all those measurements in literature were either done at high cholesterol contents or used chlorodecane as a solvent or negatively charged bull brain extract as lipid.

Although a small cholesterol content in our measurements only insignificantly decreased membrane conductivity, literature data show that at higher (>40 mol%) cholesterol content, anionic permeability increases significantly by around one order of magnitude. The effect may be due to a change of the membrane dipole potential (42, 52). It should, however, be noted that the cholesterol effect on membrane dipole potential may be masked by oppositely directed alterations of the local partition coefficients at the lipid headgroups and at the lipid tails (5).

Also, Dilger et al. (20) showed that the use of chlorodecane as a solvent, instead of decane or solvent-depleted bilayers, increases membrane permeability by around three orders of magnitude because of an increased dielectric constant inside the bilayer (ε_cd = 4.5). In accordance with our measurements with negatively charged PLE, P-values from literature measured with negatively charged bull brain extract are slightly lower than our P_exp.

Match to the correlation

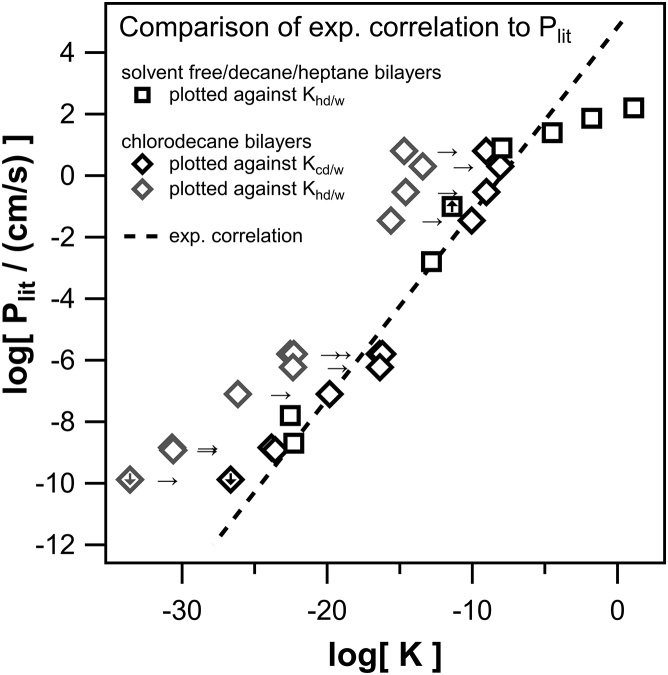
In Fig. 5, the permeability values from literature are plotted against their calculated hexadecane/water partition coefficients (COSMOtherm) listed in Table S7. For clarity, our own and the abovementioned overlapping literature data have not been plotted except for the values obtained in chlorodecane solvent. To test the determined correlation between our own experimental data and the partition coefficients (the dashed line from Fig. 1), it is plotted alongside the data from literature. All values measured with the solvent chlorodecane are shifted to higher permeabilities than predicted by the correlation, as already seen for the direct comparison. Interestingly, calculating the chlorodecane/water partition coefficient and plotting the permeability against it instead of the hexadecane/water partition coefficient eliminates the shift, and the values follow the correlation, indicating that indeed, the dielectric constant in the membrane increases.

Figure 5.

The permeability values from literature (P_lit) plotted against the respective partition coefficients K. Permeability is taken from literature for 19 different anions (see Table S7), and the anionic K-values are calculated using COSMOtherm. For validation, the linear regression determined for our own permeability data (dashed line; see Fig. 1) is plotted alongside literature data. Literature data measured for decane, heptane, or solvent depleted bilayers (open black squares) are plotted against the respective hexadecane/water partition coefficients, whereas literature data measured for chlorodecane bilayers are plotted against both the respective hexadecane/water partition coefficients (open gray diamonds) as well as the chlorodecane/water partition coefficients (open black diamonds). The respective shift to higher partition coefficients is marked by arrows. The fact that the latter data follow the correlation indicates that the solvent chlorodecane increases the dielectric constant in the membrane. The deviations from the correlation for the highest permeabilities may be due to overlooked saturation. Symbols marked with a downward/upward arrow indicate upper/lower limits of the permeability.

The values measured in decane, heptane, or solvent-depleted bilayers seem to follow the correlation except for two outliers at very high permeabilities, namely, tetrakis(3-trifluoromethylphenyl) boranuide (TTFPB) and tetrakis(4-chlorophenyl) boranuide (TCPB). Conceivably, the deviation could be explained by saturation effects. In his experiments, Benz (18) measured only at one specific concentration, namely 3 × 10⁻⁸ M. Saturation effects could therefore not be excluded. Although this low concentration was chosen specifically “to avoid the formation of boundary potentials by the adsorption of the lipophilic ions,” the correlation extracted from Fig. 4 implies that the concentrations may still have been too high because at permeabilities of 1 × 10² cm/s, the correlation predicts an onset of saturation at concentrations above 3 nM.

Conclusions

In this study, we collected passive anionic permeability data of organic molecules in planar lipid bilayers. Although our own measurements allowed establishing a predictive correlation between anionic permeability and the corresponding anionic hexadecane/water partition coefficient, permeability data collected from literature served as a validation to our model.

Equation 5 suggests that it should be possible to calculate the ion’s membrane permeability directly from the permeability of the neutral species, assuming the same neutral energy applies for both species. This assumption is plausible because of the small change in molecular size due to protonation. The most striking effect is the change in charge, which brings energies like the image, dipole, and Born energy into play. The latter energy depends on the size of the compound of interest. Uncertainties in ion radius of 30% can cause uncertainties of several orders of magnitude in the resulting expected permeability. It appears that the prediction of membrane permeability requires compound specific consideration of the Born energy like it is intrinsically done by the COSMO-RS formalism.

When using the commercial prediction model COSMOtherm to calculate the anionic partition coefficients, the only input needed to predict the permeability is the chemical structure of the anionic species. To our knowledge, at the moment, COSMOtherm is the only prediction tool for partition coefficients suited to the task because others are limited to neutral compounds.

The predictive correlation was established for solvent-depleted DPhPC membranes but may still be applied to other membranes, taking into account the contributing free-energy terms: the Born energy depends on the dielectric constant, which should be rather constant for most types of membranes, e.g., lipids dissolved in decane. If the dielectric constant differs, the correlation may still be valid using the respective solvent/water partition coefficient, as done here for chlorodecane. Depending on the type of lipid, the membrane dipole potential will vary (35). Comparing the dipole energy of DPhPC membranes (228 mV; with Eq. 6: ΔG_d = −22 kJ/mol), for example, to glycerolmonooleate (100 mV; with Eq. 6: ΔG_d = −9.6 kJ/mol), one would assume the anionic permeability to be higher by a factor of ∼150 for DPhPC than for glycerolmonooleate membranes.

A future assignment could be to create a correlation for cations, a task more difficult than for anions because of the overall lower signals in the conductivity experiments and the sparse data available in literature. However, having a tool for predicting anion permeability through lipid bilayers will help to extend the model to positively charged substances, thus being able to predict cation membrane permeability in the near future.

Author Contributions

A.E. carried out the experiments and analyzed the data. K.-U.G. conceived the project. All authors wrote the article.

Editor: Andreas Engel.

Supporting Citations

References (53, 54, 55) appear in the Supporting Material.