Effect of Substrate Stiffness on Mechanical Coupling and Force Propagation at the Infarct Boundary

Abstract

Heterogeneous intercellular coupling plays a significant role in mechanical and electrical signal transmission in the heart. Although many studies have investigated the electrical signal conduction between myocytes and nonmyocytes within the heart muscle tissue, there are not many that have looked into the mechanical counterpart. This study aims to investigate the effect of substrate stiffness and the presence of cardiac myofibroblasts (CMFs) on mechanical force propagation across cardiomyocytes (CMs) and CMFs in healthy and heart-attack-mimicking matrix stiffness conditions. The contractile forces generated by the CMs and their propagation across the CMFs were measured using a bio-nanoindenter integrated with fluorescence microscopy for fast calcium imaging. Our results showed that softer substrates facilitated stronger and further signal transmission. Interestingly, the presence of the CMFs attenuated the signal propagation in a stiffness-dependent manner. Stiffer substrates with CMFs present attenuated the signal ∼24–32% more compared to soft substrates with CMFs, indicating a synergistic detrimental effect of increased matrix stiffness and increased CMF numbers after myocardial infarction on myocardial function. Furthermore, the beating pattern of the CMF movement at the CM-CMF boundary also depended on the substrate stiffness, thereby influencing the waveform of the propagation of CM-generated contractile forces. We performed computer simulations to further understand the occurrence of different force transmission patterns and showed that cell-matrix focal adhesions assembled at the CM-CMF interfaces, which differs depending on the substrates stiffness, play important roles in determining the efficiency and mechanism of signal transmission. In conclusion, in addition to substrate stiffness, the degree and type of cell-cell and cell-matrix interactions, affected by the substrate stiffness, influence mechanical signal conduction between myocytes and nonmyocytes in the heart muscle tissue.

Introduction

Myocardial infarction (MI) is one of the leading causes of death around the world (1). MI results in the formation of scar tissue in the myocardium, which has different mechanical properties and cellular composition compared to the healthy tissue (2, 3). Specifically, the infarcted tissues have shown to be stiffer, with a measured stiffness of 100–1000 kPa (4, 5), whereas the stiffness of healthy tissue is only ∼10–20 kPa (6). In the healthy heart tissue, cardiac fibroblasts (CFs) make up ∼45–75% of the myocardial cells, depending on the species (7, 8). The adult mammalian heart has limited regenerative capacity. After an injury like MI, the lost cardiomyocytes (CMs) are replaced by a fibrotic scar tissue (9) mostly formed by the CFs near the injury area. During this process, the CFs transdifferentiate into cardiac myofibroblasts (CMFs) and constitute a significant portion of the scar tissue’s cell population (10). The formation of scar tissue triggers the remodeling of the surrounding myocardium (11, 12). Earlier studies have shown that the increase in stiffening due to fibrosis can be attributed to excessive accumulation and cross-linking of collagenous extracellular matrix (ECM) (13). Collectively, CMF-mediated formation of fibrotic tissue, increased matrix stiffness, and an increased population of CMFs impair cardiac contractility and function. Therefore, a better understanding of structural and functional interactions between CMs and CMFs and the effect of mechanical microenvironment on this interaction is necessary for the development of novel cardiac therapies.

Various studies have shown the influence of matrix stiffness, external mechanical stimuli, and the presence of CMFs on cardiac contractility (14, 15, 16). Increased ECM stiffness has also been shown to influence CM differentiation and maturation. However, most of these earlier studies have focused on the electrotonic coupling between CMs and CFs with respect to substrate stiffness (17) or investigated the variation in conduction velocity in response to an increased population of nonmyocytes (i.e., CFs or CMFs) (18, 19). In addition to electrotonic coupling, mechanical coupling also plays a major role in determining the efficiency of signal propagation between the myocardial cells (20, 21). Yet, the literature on mechanical signal propagation over CM-CMF boundaries and the effect of substrate stiffness on the mechanical propagating distance remain limited. Few recent studies have investigated the effect of external mechanical stimuli on contractile forces generated by the CMs (19, 22). Although these studies examine the effect of mechanical microenvironment on CM contractility and CM-CM coupling, to our knowledge, none of these studies have investigated the magnitude and distance of contractile force propagation in CMFs.

In this study, we developed an MI boundary model through micropatterned coculture of CMs and CMFs on substrates with varying stiffness to mimic the healthy and infarcted myocardium and investigated the mechanical signal propagation across CMFs at the CM-CMF interface. To this end, we fabricated substrates with 14, 83, and 484 kPa stiffness to mimic healthy (15 kPa) (6), 1-week (50–100 kPa) (4), and 2- to 6-week (200–1000 kPa) (5) post-MI infarcted tissues, respectively, using a biocompatible elastomeric polymer polydimethylsiloxane (PDMS). To study the effect of the presence of CMFs on mechanical signal propagation, we seeded a mixture of CM suspension containing ∼30% CFs (23) on micropatterned substrates and formed the CM-CMF boundary through self-proliferation and differentiation of the CFs into CMFs. Contractile forces of CMs and CMFs were measured at a single-cell level through dwell measurements (14, 24) using a bio-nanoindenter (25, 26). The dwell measurement method used here is similar to the technique used to measure stress relaxation behavior of cells (27). Briefly, the cell is indented to a certain degree, and the indentation probe is kept in contact with the cell for 30 s. The changes in the cell height due to beating cause changes in the cantilever deflection, which corresponds to the contractile force exerted by the cell along the transverse direction. Using the dwell measurement approach, we have shown that the microenvironmental properties of the myocardium, such as matrix stiffness and the presence of CMFs, play a critical role in regulating mechanical conduction across the MI boundary. Both the magnitude and pattern of contractile forces of CMs and CMFs were investigated to elucidate the mechanism of mechanical signal propagation in infarcted tissues. In addition to mechanical characterization, we also performed a biochemical analysis of cell-cell coupling proteins and focal adhesions. The CMFs were identified by the expressions of α-smooth-muscle-actin (α-SMA) in their stress fibers (28). Finally, we used finite element analysis (FEA) models to understand and validate our experimental results. Interestingly, we found that CMF presence attenuated the mechanical signal depending on the substrate stiffness. Furthermore, we also discovered that cell-matrix focal adhesion distribution at the CM-CMF interface controls the beating wave pattern at the CM-CMF boundary. Understanding the effects of the tissue microenvironment on resident myocardial cells is a critical step toward improving myocardial therapies. The outcomes of this study could be important in understanding the effect of CMF presence and ECM stiffness on cellular interactions and function of a healthy and infarcted heart.

Materials and Methods

Materials

4-in silicon wafers were purchased from University Wafers (Boston, MA). PDMS elastomer was purchased as a kit (base and curing agent) from Dow Corning (Midland, MI). Fibronectin (FN) from bovine plasma, Tyrode’s salt solution with sodium bicarbonate, penicillin-G sodium salt, Triton X-100, goat serum, 4,6-diamidino-2-phenylindole dihydrochloride (DAPI) powder, and Dulbecco’s phosphate buffer (PBS) were purchased from Sigma-Aldrich (St. Louis, MO). Trypsin and Hank’s balanced salt solution without calcium or magnesium were obtained from Gibco (New York, NY). Dulbecco’s modified Eagle media with 4500 mg/L glucose, 4.0 mM L-glutamine, and 110 mg/L sodium pyruvate and fetal bovine serum were obtained from Thermo Fisher Scientific (Kalamazoo, MI). Calcium Fluo-4 acetoxymethyl, cell-permeant proLong Gold antifade reagent, goat anti-rabbit immunoglobulin G (H + L) secondary antibody Alexa Fluor 647 conjugate, goat anti-mouse immunoglobulin G (H + L) secondary antibody Alexa Fluor 488 conjugate were obtained from Molecular Probes (Eugene, OR). Primary antibodies, rabbit monoclonal Cardiac Troponin-T, mouse monoclonal N-cadherin, and mouse monoclonal vinculin were obtained from Abcam (Cambridge, MA). Collagenase type-II was purchased from Worthington Biochemical Corporation (Lakewood, NJ). 30-mm borosilicate glass coverslips were purchased from Chemglass Life Sciences (Vineland, NJ), and paraformaldehyde, 16% solution EM grade, was obtained from Electron Microscopy Sciences (Hatfield, PA).

MI boundary model

Fabrication of cell culture substrates with different stiffness

PDMS substrates with different stiffness were prepared using varying ratios of base/curing agent to investigate the influence of matrix stiffness on cell function and behavior. We prepared three different substrates with stiffness around 14 kPa (soft), 83 kPa (moderate), and 484 kPa (stiff) using 1:100, 1:40, and 1:20 base/curing agent ratio combinations, respectively. Once the mixes were prepared, they were degassed and poured onto plain glass coverslips (diameter = 30 mm), spun at 750 rpm for 30 s, and then baked. The 1:40 and 1:20 PDMS samples were baked at 80°C for 5 and 2 h, respectively, whereas the 1:100 PDMS samples were baked at 95°C for 13–14 h to cure. Post curing, PDMS-coated glass substrates were glued to a 35-mm petri dish using an inert silicone glue to prevent samples from moving during the nanoindenter measurements, treated with plasma discharge for 1 min and immersed in deionized water until substrate functionalization.

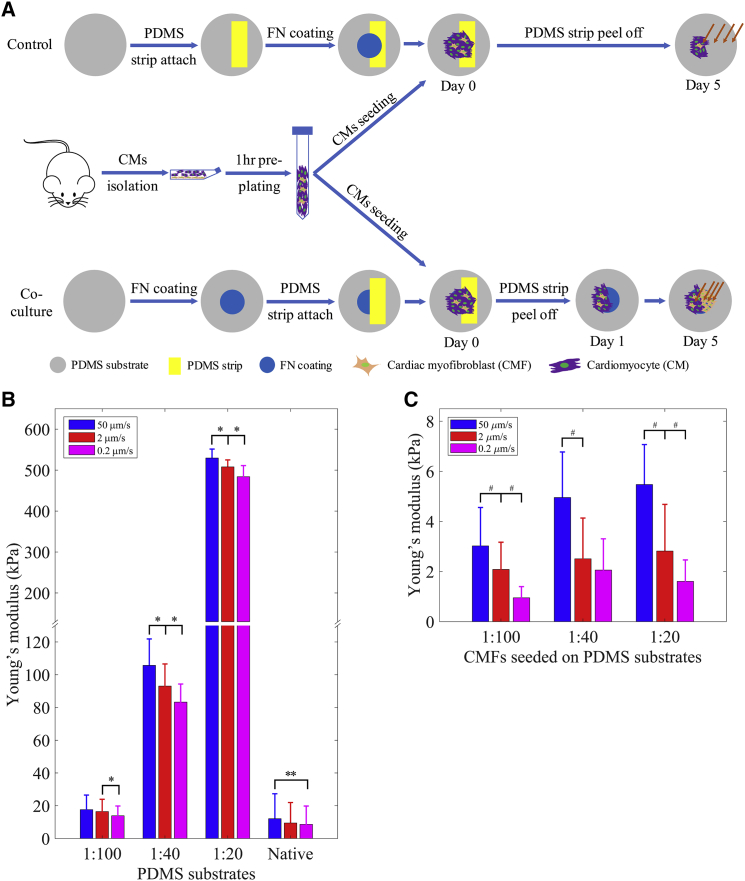
In this study, the following two groups of samples were prepared: coculture samples (i.e., CM-CMF) and control samples without any CMFs (i.e., single CM cultures). For both samples, the substrates were coated with FN before cell seeding to facilitate cell attachment onto the PDMS substrates. FN solution (50 μg/mL) was placed as a droplet at the center of the substrate, and the samples were incubated at 37°C for 1 h. After protein incubation, the solution was removed, and samples were washed and kept in PBS until cell seeding. In coculture samples, for patterning the cell attachment on the substrates, thin strips of PDMS films with 100 μm thickness were used to partially block the cell-culture substrates during cell seeding as we described before (29) (Fig. 1 A). After strip removal, CF cells proliferated, migrated, and differentiated into CMFs on the other half of the coated surface. In the case of the control samples, we placed the PDMS strip on the substrate before coating it with FN and left it in place throughout the cell culture to prevent cell migration and growth on the other half of the substrate. Placing the PDMS strip before FN coating helps the strip to adhere on the substrate stronger and prevents any detachment during media changes until we peel off the strip on day 5 of the cell culture, right before the dwell measurements.

Figure 1.

Sample preparation and stiffness characterization. (A) The preparation of the coculture samples and the control samples without CMFs. The orange arrows indicate measured locations during the dwell experiments. (B) Loading-velocity-dependent stiffness of PDMS 1:100, 1:40, and 1:20 substrates and the native heart tissues. (C) Loading-velocity-dependent stiffness of the CMFs seeded on PDMS 1:100, 1:40, and 1:20 substrates. Data are shown as the mean ± SD (^∗, ^∗∗, and # indicate statistically significant difference with p < 0.0001, p < 0.005, and p < 0.05, respectively); n = 3 with ∼390 data points for each sample condition. To see this figure in color, go online.

Cell isolation, seeding, and culture

All experiments were conducted in accordance with the Institutional Animal Care and Use Committee of the University of Notre Dame. CM isolation was carried out following a previously established protocol (23, 29, 30). Briefly, the hearts were excised from 2-day-old neonatal Sprague Dawley rat pups, diced into small parts, incubated overnight in trypsin (0.05% w/v in Hank’s balanced salt solution) followed by 0.1% collagenase type-2 treatment with mechanical trituration and enriched for CMs through 1.5 h preplating. The samples were seeded at a density of 5.7 × 10⁶ cells/mL. The existing CFs in the isolated cell suspension were allowed to self-proliferate into the regions initially covered by the PDMS strip. The low-density presence of the CFs and their rapid proliferation to fill the gap (i.e., the wound) promoted their spontaneous differentiation to CMFs essentially mimicking the wound healing process after heart injury (31, 32). The samples were cultured in standard culture media (Dulbecco’s modified Eagle media supplemented with 10% fetal bovine serum and 1% penicillin) up to 5 days under standard cell culture conditions.

Whole heart sections

Tissue pieces from whole neonatal and adult rat hearts were used for measuring the biomechanical properties of the healthy native myocardium. Dissected hearts from the 2-day-old and 9-month-old Sprague Dawley rats were sliced into 1- to 2-mm-thick pieces to obtain tissue cross sections. They were then glued onto petri dishes and rinsed with PBS two to three times before testing. Note that the samples were tested in a liquid environment (i.e., PBS) at room temperature. A total of 44 locations from two separate hearts for each sample type were tested.

Nanoindenter experimental setup

Strain-rate-dependent stiffness measurement

Stiffness of native heart tissue pieces, PDMS substrates with varying stiffness, as well as the cultured CMF cells on PDMS substrates were tested using a Piuma Chiaro nanoindenter system (Optics11, Amsterdam, the Netherlands) (26).

Colloidal probes with a tip diameter of 90 μm were used for testing the PDMS substrates with varying stiffness. The indentation probes used for the soft substrates had a spring constant of 0.43 N/m, whereas the spring constant for the probes used for the moderate and stiff substrates was 4.21 N/m. Three separate samples were tested for each PDMS substrate condition, and multiple measurements were recorded from different locations from each sample. A total of 204–390 indentation data points were recorded from all samples.

The indentation probe used for CMFs seeded on PDMS substrates had a spring constant and tip diameter of around 0.045 N/m and 41 μm, respectively. A total of 45 different CMF cells on two independent samples were tested for each substrate type. Before testing, the sensitivity calibration of the cantilever was conducted by indenting a hard surface (i.e., a glass slide). The loading velocities used were 50, 2, and 0.2 μm/s. A customized MATLAB code (The MathWorks, Natick, MA) was developed to determine contact points between the probe and samples and to identify Young’s moduli of the samples using the Hertz contact model (27, 33):

$$F=\frac{16}{9}E{R}^{1/2}{\delta }^{3/2},$$ (1)

where F is applied force, δ is indentation depth, R is the radius of the colloidal probe, and E is Young’s modulus of the samples. The samples were assumed to be incompressible (i.e., Poisson’s ratio of 0.5) because the literature studies that use this model have concluded that the measured properties change by less than 20% when varying the Poisson’s ratio from 0.3 to 0.5 (34), and as such, it is reasonable to assume incompressibility for most biological samples (35, 36). Statistics were performed using one-way analysis of variance with statistical significance reported at a 95% confidence level (p < 0.05).

Contractile force measurements

The contractile forces of individual CMs and CMFs within the cell sheets were measured with the nanoindenter through dwell experiments (23). Briefly, the nanoindenter probe was brought into contact with the samples, and the probe’s displacement was kept constant (in other words, probe was dwelled on the sample) for 30 s to dynamically measure its deflection, which is proportional to the cell’s contractile force along the transverse direction with respect to the substrates.

First, we measured the contractile forces of individual CMs adjacent to the CM-CMF boundary on the coculture samples, as well as CMs at the CM-PDMS boundary on the control samples without any CMFs. Then, the contractile forces of individual CMFs were measured sequentially, each time at a greater distance from the boundary as shown in Fig. 1 A, until there was no detectable signal. All beating force measurements were performed on the cell’s nucleus for consistency as well as to minimize the effect of cell stiffness heterogeneity. After each measurement, the cantilever was moved in the X axis, and the measurement was conducted on the nearest CMF. Therefore, all of the measurements were performed at a similar distance from the boundary with only ∼5–10% difference depending on the exact location of the nearest CMF. The probe used had a spring constant and tip diameter of 0.067 N/m and 5.4 μm, respectively. A customized MATLAB code was developed to separate each single beat and to calculate averaged contractile forces.

CMF dimension measurements

To develop the FEA models in this study, the dimensions of the CMFs (i.e., cell diameter and height) were measured through image analysis and nanoindenter measurements. First, we calculated the volume of a single CMF by measuring the diameter and height of a newly attached, spherical CMF seeded on a petri dish no more than 15 min after the cell seeding to ensure that the cells were still in spherical shape. Briefly, bright-field images of these spherical cells were captured, and diameters were measured by drawing two diagonal lines passing from the cell center using ImageJ to obtain D₀. Then, the height of these spherical cells, H₀, was measured by indenting the cell and the substrate next to it using the nanoindenter and recording the cell-substrate contact points (33). These dimensions were used to calculate the cells’ volume V₀ as follows:

$$V_0=\frac{\pi H_0^2}{3}\left(\frac{3D_0}{2}-H_0\right).$$ (2)

Finally, we measured the heights of the CMFs that were seeded and spread out on different stiffness substrates. Because of the irregular shape of the spread out CMFs, we assumed that the cell volume was preserved regardless of the shape modulation of the cells while spreading (37, 38). Based on this assumption and using the volume V₀ and measured CMF heights H of spread out CMFs on different stiffness substrates, we calculated diameter D for CMFs on different PDMS substrates using the following equation:

$$D=\frac{2V_0}{\pi H^2}+\frac{2H}{3}.$$ (3)

Together, these dimensions were used to develop the FEA models described in the following section.

FEA modeling

The porohyperelastic (PHE) model, which was developed based on the Consolidation Theory (33, 39, 40, 41), has been demonstrated as a powerful and suitable model for studying cell biomechanics (33, 42). This theory was an extension of the poroelastic theory (43) to characterize and predict large deformations and nonlinear responses in structures under loading. PHE theory assumes the cell as a continuum material consists of an incompressible fluid saturated in an impressible hyperelastic porous solid. Whereas the solid and fluid are incompressible, the whole cell is compressible because of fluid loss during deformation. The field equations for the isotropic form of this theory are summarized in Supporting Materials and Methods. This constitutive material model has hyperelastic material constants and hydraulic permeability k_ij (details of the field equations and how to identify material constants of this model are presented in previous works (27, 33)). Inverse FEA technique was employed as shown by Nguyen and Gu (33) to identify these constants. The initial conditions, including void ratio, saturation, and fluid pore pressure, were assumed to be 4, 1, and 0, respectively. The FEA commercial software ABAQUS 6.14-2 was used for simulations.

Biochemical characterization

The aim of this study is to investigate the effect of the presence of CMFs after heart injury on the propagation of mechanical signals. Therefore, it was necessary to confirm the transdifferentiation of CFs to CMF phenotype during the wound healing process. To this extent, the phenotype of the cells on the different stiffness substrates was characterized by double immunostaining as described previously (23). Briefly, all samples were cultured for 5 days with periodic media change. On day 5, they were fixed in 4% paraformaldehyde, permeabilized using 0.1% Triton X-100, and blocked with goat serum. Samples were then immunostained sequentially using a CM cytoskeleton contractile marker (cardiac Troponin-T), a CF and CMF marker (vimentin), and a CMF marker (α-SMA)).

The adherens junction and focal adhesion points were stained through N-cadherin (for cell-cell interactions) and vinculin (for cell-matrix interactions), respectively. The protein N-cadherin, as part of the adherens junction complex, aids in the intercellular mechanical coupling of the CMs with neighboring CMs and CMFs. Cell nuclei were counterstained with DAPI in all samples. All the samples were imaged under identical conditions, after the optimal exposure time and intensity were determined using the control samples. For each experimental condition, at least three samples were prepared and imaged at multiple locations (approximately n = 20 from each sample).

For characterization of the variation in expression of N-cadherin and vinculin on different substrates, the fluorescence intensity of each respective protein was quantified using ImageJ software. Five images were captured from three different samples for each condition, with fluorescence intensity measured and averaged. The total mean intensity measured for each image was normalized to total nuclei count in the respective image frame.

The CM border, cell functionality, and connectivity were characterized by fast calcium flux imaging. Briefly, CMs were loaded with fluo-4-AM ester (3 mM in 1% pluronic-F127 in Tyrode’s salt solution) and incubated at 37°C for 30 min. Propagation of calcium flux was imaged with a Zeiss Observer epifluorescence microscope and a Hamamatsu Orca-Flash4.0 digital camera C11440 (Hamamatsu, Japan) at a capture rate of 31.4 fps.

Results

Loading-velocity-dependent mechanical properties

First, we studied the viscoelastic properties of the native tissue matrix, the fabricated PDMS substrates with varying stiffness, as well as the CMFs seeded on these substrates through nanoindentation experiments. We observed variation in the measured stiffness of different PDMS substrates depending on the loading velocity of the indentation. PDMS substrate stiffness was measured at three different loading velocities (i.e., 50, 2, and 0.2 μm/s) and is shown in Fig. 1 B. The stiffness of the substrates was significantly reduced when the loading velocity was reduced from 50 to 2 μm/s and from 2 to 0.2 μm/s (p < 0.0001), except for the soft substrate, when the loading velocity was reduced from 50 to 2 μm/s (p = 0.1484). Similarly, CMFs seeded on different PDMS substrates exhibited loading-velocity-dependent stiffness (p < 0.005), except for CMFs seeded on the moderate substrate when the loading velocity was reduced from 2 to 0.2 μm/s (p = 0.1924) (Fig. 1 C). For comparison, the stiffness of native rat heart tissues was measured, which also reduced with decreasing loading velocity from 50 to 0.2 μm/s (p < 0.05).

Both PDMS substrates and CMFs seeded on PDMS substrates exhibited strain-rate-dependent stiffness. Soft substrate stiffness of around 13.9–17.66 kPa was similar to that of the native healthy heart tissue (i.e., 11.33–18.46 kPa (6)) as we measured to be 13.32 ± 8.60 kPa for healthy adult rat hearts, whereas the stiffness of moderate and stiff substrates, which were around 83.29–105.71 and 483.92–529.63 kPa, respectively, were comparable to the stiffness of infarcted heart tissues measured in earlier studies (4, 5). Similarly, the stiffness of the CMF seeded on soft, moderate, and stiff substrates was 0.95–3.02, 2.06–4.96, and 1.61–5.47 kPa, respectively. It can be seen that the cell stiffness increased with the increased substrate stiffness as expected (44). This loading-velocity-dependent stiffness is consistent with previous findings on tissues and cells (33, 45).

Effects of substrate stiffness on mechanical signal propagation

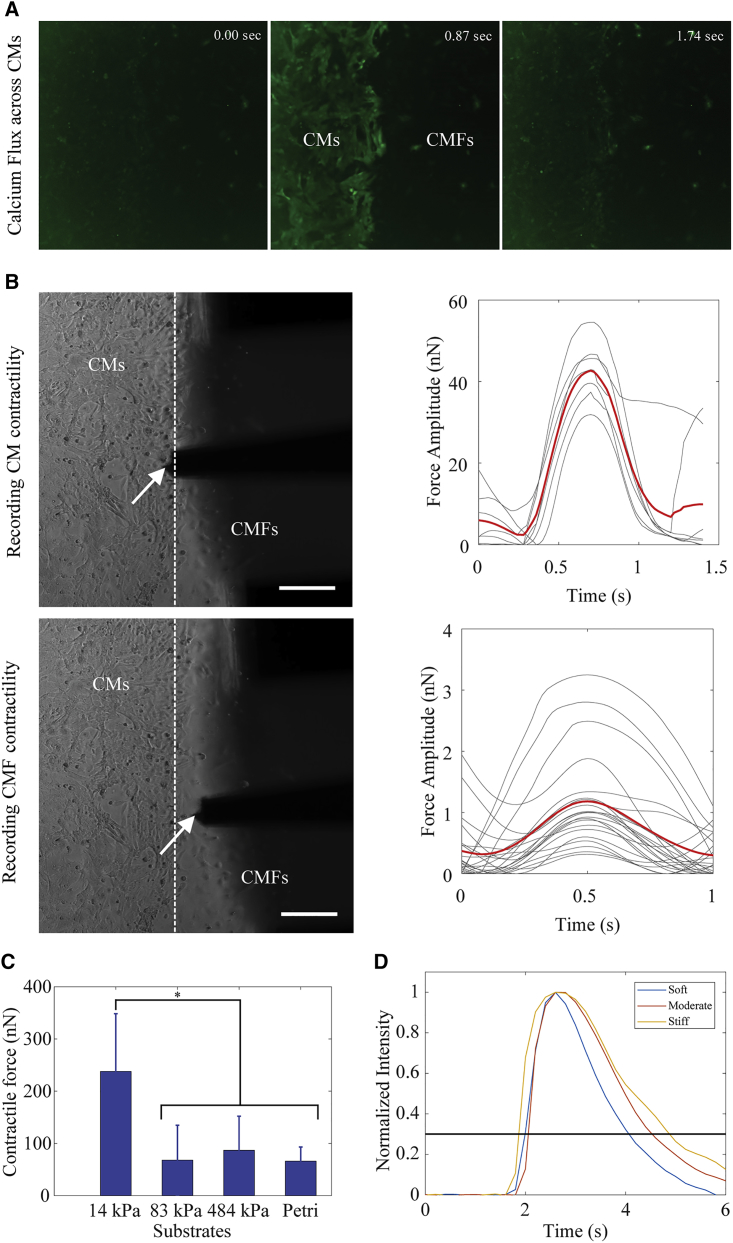
To distinguish the CMs and CMFs in the coculture samples and to correctly identify the CM-CMF boundary, samples were stained with a Ca²⁺ dye. The representative screenshots from the Ca²⁺ flux video (Video S1) on a stiff substrate sample are shown in Fig. 2. Because only CMs exhibit Ca²⁺ flux, it was used to distinguish the two cell types in real time during the live cell measurements (Fig. 2 A). We also developed a customized MATLAB code to measure calcium transient duration from these Ca²⁺ flux videos. The results were determined to be 1.00 ± 0.59, 1.17 ± 0.49, and 2.10 ± 0.37 s for CMs seeded on soft, moderate, and stiff substrates, respectively. The representative CT curves based on the Ca²⁺ imaging of CMs cultured on different stiffness substrates are shown in Fig. 2 D.

Figure 2.

Contractile force measurements of a stiff substrate coculture sample as an example showing the experimental set up as follows. (A) Screenshots of calcium flux across CMs; (B) bright-field images of the CM-CMF boundary and averaged beating force amplitude of CMs (top) and CMFs (bottom; the dashed line shows the CM-CMF boundary, and the white arrows show the nanoindenter colloidal probe) (scale bars, 100 μm); the gray and red curves represent the individual and averaged beating force of the cells, respectively; (C) contractile force magnitudes of CMs on different substrates. Data are shown as mean, and the error bar represents the SD of the measured values (^∗ indicates a statistically significant difference with p < 0.05) (n = 5); (D) fluorescence intensity representing the changes in Ca²⁺ transient in a single beat of CMs seeded on soft, moderate, and stiff substrates. To see this figure in color, go online.

The left panel of the Fig. 2 B shows representative bright-field images of the CM-CMF boundary, as well as the nanoindenter probe on the stiff substrate. The plots in the Fig. 2 B right panel show the beating force curves over time for individual CMs and CMFs at each side of the boundary, measured at the imaged position of the probe. The gray and red curves are single and averaged beats, respectively. The mean beating force magnitude was then calculated using the averaged force curve. Comparison of averaged CM contractile forces on different PDMS substrates is shown in Fig. 2 C. The CMs had a higher beating force magnitude (p < 0.05) and were beating stronger on substrates with stiffness similar to that of the native heart tissues as compared to stiffer substrates, in agreement with previous studies (15, 46). We also observed that the CMs seeded on the moderate and the stiff substrates tested in this study had similar beating force magnitude to those cultured on petri dishes.

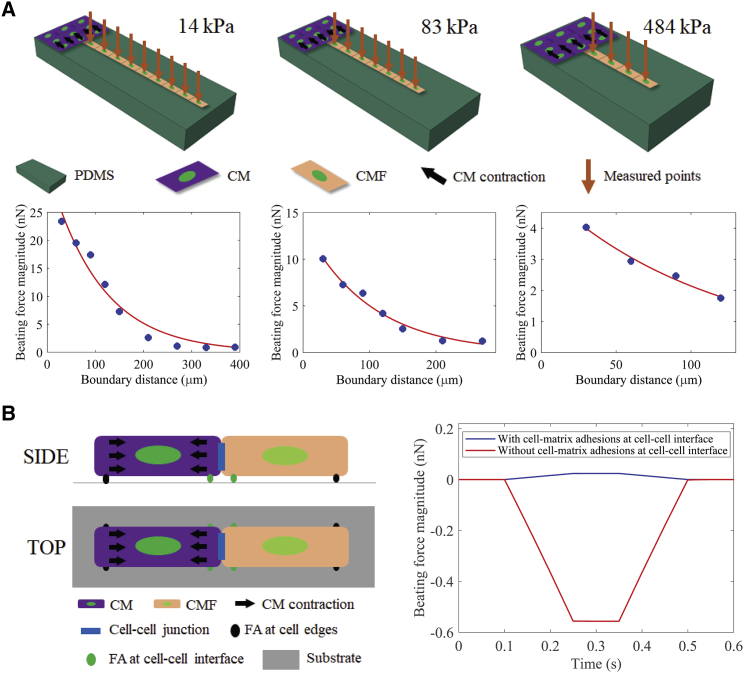
We also quantified the influence of substrate stiffness on the propagation distance of mechanical signal. “Boundary distance” refers to the distance of a certain point from the CM-CMF boundary at which the propagated mechanical signal is measured. As described earlier, the transmitted signal was measured from the CMFs on the coculture samples or from the PDMS substrate on the control samples without any CMFs. We observed that the maximal propagated distance of mechanical signal was influenced by the contractile force of the CMs, the presence of the CMFs, and the stiffness of the substrate.

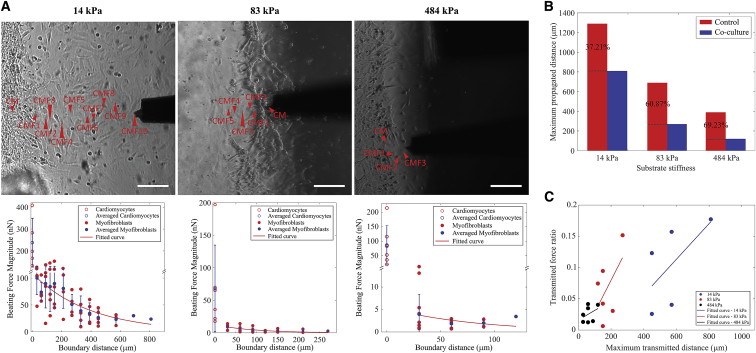
We measured the contractile force from consecutive CMFs sequentially starting from the CM-CMF boundary, as indicated by arrowheads in bright-field images in Fig. 3 A. For each condition, at least five samples were tested. The contractile force magnitude of CMFs versus the CM-CMF boundary distance for each stiffness is shown in Fig. 3 A. The red data points depict the individual beating force magnitudes at each point measured away from the CM-CMF boundary. The force measurements from the CMFs were then averaged and plotted as corresponding blue data points, which showed an exponential distribution regardless of substrate stiffness. The exponential decay of the force shows the attenuation of the mechanical signal propagating from CMs through the connected CMFs on the other side of the boundary. We also measured the deformation of the PDMS substrates using the control samples that are devoid of CMFs, to study the effect of the presence of CMFs on mechanical signal propagation. The threshold for the maximal propagation distance was determined by the resolution of the nanoindenter system. Within our current setup, the minimal beating force we can detect is ∼0.7 nN, which is the threshold force value we set in this study. The maximal propagating distance to which the contractile force of CMs can be transmitted varied with the substrate stiffness and the presence of CMFs. Soft substrates transmitted the mechanical signal the furthest (810 μm as compared to 330 and 120 μm measured for moderate and stiff substrates, respectively). These values were determined to be 1290, 690, and 390 μm on control samples, which were devoid of any CMFs (Fig. S1). Fig. 3 B shows the maximal propagating distances in samples with and without CMFs for each stiffness condition. The percentage corresponds to the ratio of attenuated distance on coculture samples caused by the presence of CMFs for each stiffness condition. Interestingly, the degree of attenuation was smaller for the softer substrates, 37.21%, as compared to 60.87 and 69.23% for moderate and stiff substrates, respectively.

Figure 3.

Mechanical signal propagation in coculture samples. (A) The top shows bright-field images of soft, moderate, and stiff substrate samples (from left to right). The red arrowheads indicate the tested locations for each sample (scale bars, 100 μm). The bottom shows the beating force magnitude (nN) versus the CM-CMF boundary distance (μm) curves of the samples. Data are shown as mean, and the error bar represents the SD of the measured values; (B) the maximal propagating distances of control and coculture samples for soft, moderate, and stiff substrates. The percentages show the ratios of these distances, corresponding to each substrate stiffness; (C) ratios of CMF and CM contractile forces at the maximal transmitted distance for different substrate stiffness. To see this figure in color, go online.

The transverse measurement method that we used in this study has limitations in terms of monitoring the substrate deformation. As discussed in earlier sections, because we measured the beating force of the cells in the Z axis, it is not possible to decouple the cell and substrate deformation. However, based on the results of Fig. 3 C, in which we observed the mechanical signals to be transmitted longer and stronger on moderate substrates than on stiff substrates, even though both had similar CM contractile force (Fig. 2 C), we conclude that the substrate stiffness is the critical factor that defines signal propagation magnitude and distance. It should be noted that despite its limitations in lateral measurements, the nanoindenter allows a robust and convenient way of single-cell-level contractile force measurement (24), while allowing for the imaging of a large field of view of cells for further analysis, which was critical in identifying the CM-CMF boundary in this study through the calcium flux imaging. In contrast, the lateral deformation measurement techniques such as traction force microscopy and micropost/micropillar arrays often require high-magnification optical objectives to measure single-cell contractility compromising concurrent imaging of several connected cells at once (16, 47).

Contractile force patterns of CMFs

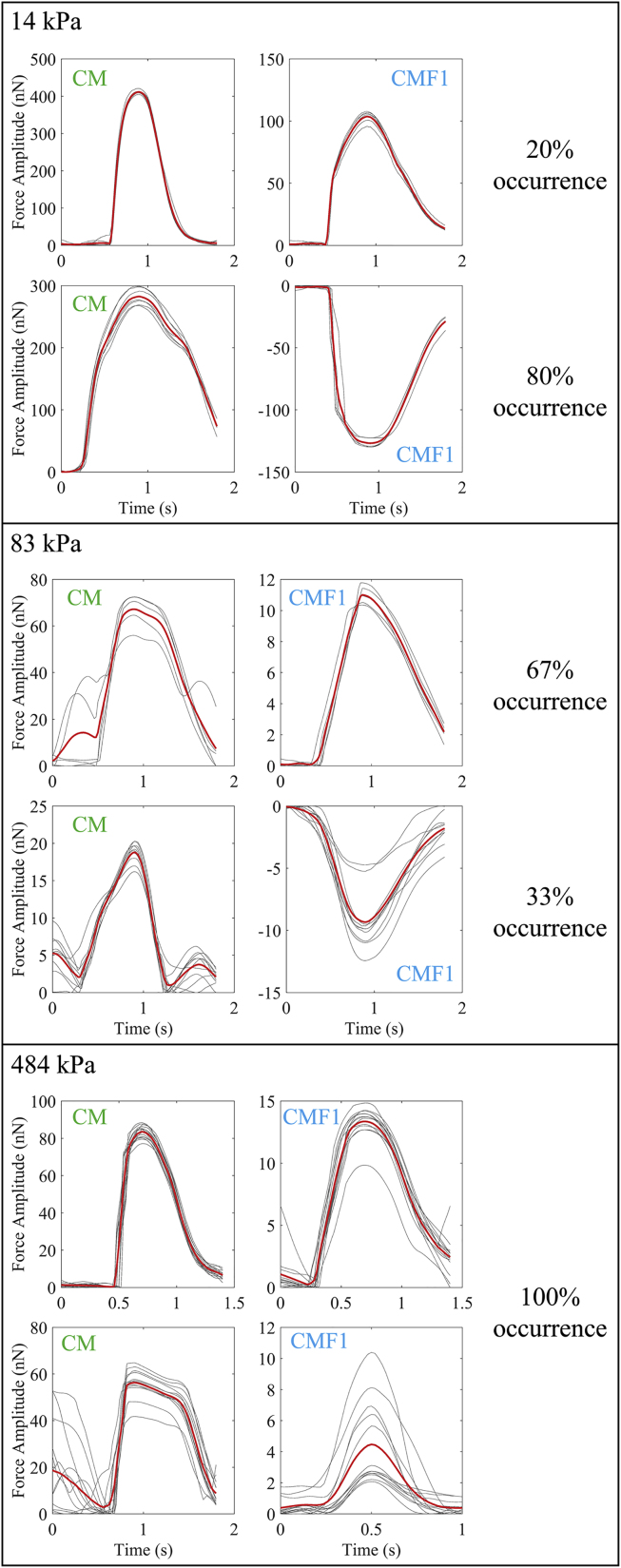
One of the interesting findings in this study is that CMFs exhibited different contractile wave patterns at the CM-CMF boundary depending on substrate stiffness as shown in Fig. 4. The first column in the figure shows the contractile force patterns of CMs, and the second column is contractile patterns from CMFs. There were two distinguishable wave patterns, one of which was denoted as “beating” because it was similar to the contractile wave pattern of CMs, whereas the other inverse wave was called “pulling” because the cells appeared to be pulled by CMs. The pulling pattern was also seen in all control samples without any CMFs regardless of substrate stiffness (Fig. S2). Notably, once a CMF within a data set (series of consecutive CMFs) had a pulling pattern, the rest of CMFs after that would also exhibit a pulling pattern. Furthermore, the occurrence probabilities of these patterns were dependent on substrate stiffness. The beating pattern occurred more frequently on stiffer substrates as indicated by the increased occurrence from 20% (i.e., one out of five measurements) on the soft substrate to 67% (i.e., four out of six measurements) on moderate and 100% (i.e., seven out of seven measurements) on the stiffest substrate (Fig. 4). This mixture of pulling and beating patterns we observed in the soft and moderate substrates is likely due to the small variability in local stiffness of the substrates. Softer materials such as PDMS have been shown to have nanoscale local variations in their stiffness (48), which is in the scale of cell surface proteins that govern cell-cell and cell-substrate interactions. As such, the amount of focal adhesions might be different at different locations within the same substrate causing the variations in the beating wave patterns we have observed.

Figure 4.

Representative images of different contractile force patterns (i.e., beating or pulling) of coculture samples for soft, moderate, and stiff substrates (from top to bottom) together with the occurrence percentages of these patterns. The gray and red curves represent the individual and averaged beating force of the cells, respectively. To see this figure in color, go online.

The difference in the beating wave patterns affected the amount of force transmission between the CMs and CMFs. Particularly, for moderate substrates, ∼52% of the force was transmitted from CMs to the first CMFs for the pulling pattern. This amount was only 4–39% for the beating pattern. Similarly, for the soft substrates, the amount of transmitted force was 36–62% and 25% for the pulling and beating patterns, respectively.

To confirm that the contractile wave pattern is dependent on substrate stiffness and not on the orientation or the contraction direction of the CMs, we developed a customized image-processing algorithm using MATLAB to detect CM contracting angle from the bright-field videos we recorded concurrently with the nanoindenter measurements (refer to the Supporting Materials and Methods). The results revealed that the contractile pattern is independent of CM beating angle, indicating that substrate stiffness likely impacts the wave pattern, which in turn influences signal propagation (Fig. S3; Tables S1–S3). We performed FEA to further study the underlying mechanism of the contractile wave pattern phenomenon we observed in this study.

Computational modeling

CMF dimensions

To develop the FEA model, we first measured the diameter and height of the CMFs. We performed our measurements 15 min after initial seeding on a petri dish to obtain attached cells without spreading. Our results showed that the diameter of the cells was 16.52 ± 1.54 μm (n = 44), and the height was 15.53 ± 2.98 μm (n = 44) (Fig. S4; Table 1). Next, we substituted these dimensions in Eq. 2 and calculated the cell’s volume, which was around 2300 μm³. After that, we measured the spread-out heights of CMFs seeded on soft, moderate, and stiff PDMS substrates and recorded the values as 5.98 ± 1.78 μm (n = 36), 5.72 ± 1.16 μm (n = 36), and 4.97 ± 1.29 μm (n = 36), respectively. It was interesting to note that the height of CMFs on the moderate substrate was similar to those on the soft substrate (p = 0.4677) but significantly larger than that of the cells on the stiff substrate (p < 0.05). These height values, together with cell volume, were used to calculate other cell parameters, including the cell’s radius (i.e., the curvature radius of the cell’s membrane) and contact radius (i.e., the radius of area that the cell attaches to the substrates) at cell-substrate interface, as shown in Table 1 below. The dimensions quantified here were later used in the FEA model (Fig. S5 A).

Table 1.

CMF Dimensions on Substrates with Different Stiffness

	Height h (μm)	Radius r (μm)	Volume V (μm3)	Contact Radius a (μm)
Petri: 15 min	15.53 ± 2.98 (n = 44)	8.26 ± 0.77 (n = 44)	2336	3.92
Soft substrate	5.98 ± 1.78 (n = 36)	22.79	2336	15.39
Moderate substrate	5.72 ± 1.16 (n = 36)	24.65	2336	15.78
Stiff substrate	4.97 ± 1.29 (n = 36)	31.81	2336	17.07

FEA modeling

In this study, we developed two different FEA models. The first model simulated our dwell measurements and was used to fit the experimental data on the contractile force versus CM-CMF boundary distance measurements. The second FEA model was used to further understand the differences we observed in the contractile wave patterns at the CM-CMF boundary on different stiffness substrates.

In the first model, we developed an FEA simulation of our indentation studies using a PHE constitutive material model to determine the loading-velocity-dependent mechanical properties of PDMS substrates as well as the CMFs seeded on these substrates (Fig. S5 B). We used quarter-symmetry models to save computational cost. Briefly, the PDMS substrate indentation simulation was created first and used to identify PHE material constants of all three substrates using the inverse FEA technique together with experimental data (33). Next, the properties of PDMS substrates were utilized in CMF indentation simulations to determine PHE material constants of CMFs seeded on the three different PDMS substrates. We observed that CMFs had negative Poisson’s ratios, which is consistent with other published data (27, 33). Notably, the hydraulic permeability (k₀) of CMFs did not change significantly with substrate stiffness. Conversely, the permeability of PDMS substrates was reduced significantly when the stiffness of the substrate increased. It is possible that higher cross-linked networks within stiffer substrates generated smaller pore sizes, which in turn reduced their permeability. In addition, PDMS substrates had a significantly increased permeability (∼1.5–410 times greater) than that of the CMFs seeded on them. During our stiffness measurements, we observed that the stiffness of the PDMS substrates was dependent on the testing velocity. This behavior is commonly observed in biphasic (i.e., solid-fluid) materials. Based on previous literature (27, 33, 49), the PHE model can precisely capture the mechanical behavior of biphasic biological materials. Thus, we used this model in our simulations. As one of the model parameters, the significant difference of hydraulic permeability k₀ demonstrated that the substrates not only had different stiffness but also had different loading-velocity-dependent deformation behavior.

We then incorporated the mechanical properties of substrates and CMFs, as well as their morphology information into a dwelling FEA model as shown in Fig. 5 A. We simulated the contractile activity of CMs as compression stress applied on the right side of CMs (black arrows in the FEA model schematics in Fig. 5 A). The contractile forces of CMFs were measured at different distances sequentially starting from the CM-CMF boundary as indicated by orange arrows in Fig. 5 A. The simulation results showed an exponential relation between the beating force magnitude and the CM-CMF boundary distance, which agreed well with our experimental data.

Figure 5.

FEA simulation models. (A) An illustration of the simulation model (top panel) and simulated beating force magnitude over the CM-CMF boundary distance (bottom panel) of CM-CMF coculture samples on soft, moderate, and stiff substrates. (B) An illustration of the simulation model (left) and beating force magnitude over time (right) of CMF when the cell-substrate adhesion is activated (blue curve) and not activated (red curve) at the cell-cell interface. FA, focal adhesion. To see this figure in color, go online.

We developed another FEA model to explain the different beating wave patterns that we observed with the CMFs (Fig. 4) at the CM-CMF boundary, as illustrated in Fig. 5 B. The wave pattern simulation model consisted of two strongly connected single CM-CMF pair seeded on deformable substrates of different stiffness values corresponding to our experimental conditions (i.e., 14, 83, and 484 kPa). In this study, the CMF cell had a dome shape to account for the effect of rounded cell topography. Specifically, we set the cell height to 4 μm at the sides and 6 μm in the middle. For simplicity, the CM was modeled as a flat cell with a uniform height of 5 μm, because the wave propagation happens through the CMFs. Moreover, we considered the relative stiffness of the CMF compared to that of the CM. The CM stiffness was assumed to be 1.5 kPa, and the stiffness of CMF was changed to 1, 1.5, and 2 kPa to investigate the effects of stiffness difference between these two cell types. The cell-cell cadherin junctions were modeled as a constraint at the CM-CMF interface surfaces. The cell-matrix adhesions were simulated as contact interactions running along the left and right bottom sides of each cell. We then applied a load on the right surface of the CM (the left cell) and measured the contractile force on the CMF (the right cell). Two separate simulations were run with and without the cell-matrix adhesions at cell-cell interface (i.e., the right-side cell-matrix adhesion of CM and the left-side cell-matrix adhesion of CMF). We observed that the beating waveforms are independent of the substrate’s and the cell’s stiffness as shown in Table S5. Particularly, we observed that CMFs had a beating contractile force pattern when focal adhesions at the cell-cell interface were activated (i.e., when focal adhesions assembled predominantly at the cell-cell interface and boundaries, as seen in the cells cultured on stiff substrate (Fig. 5 B)). On the other hand, the pulling pattern of CMFs was observed when these focal adhesions were inactivated, as observed only on substrates with soft and moderate stiffness. Notably, the force magnitude of the pulling pattern was significantly larger than that of the beating one, suggesting that the localized distribution of focal adhesions at cell-cell interface not only governs cell contractile wave patterns but also the amount of transmitted force from one cell to another. Interestingly, these waveforms are only dependent on whether the cell-substrate adhesion is activated at the cell-cell interface. Our data suggest that the increase of ECM stiffness under a pathological condition may cause the localization of focal adhesion at the cell-cell boundary (50) and influence CM function and contractility. The results observed here demonstrated the critical importance of cell-cell and cell-matrix interactions, which influence the transmission of mechanical signals.

Biochemical characterization

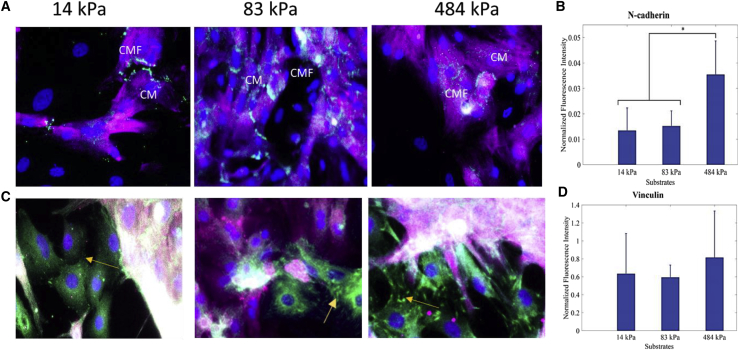
Because other similar studies on CM-CMF interactions have shown that N-cadherin expressions are comparatively higher than other cadherins such as OB-cadherin at the CM-CMF junctions, in this study, we selectively stained for N-cadherins (22). Quantification of immunostained samples revealed higher expression of N-cadherin on the stiff (∼484 kPa) substrates, whereas the expression was lower for the moderate and soft (∼83 and 14 kPa) samples. As shown in Fig. 6, the expression of N-cadherin was nearly twice as high on stiff substrates as compared to soft (14 kPa) substrates.

Figure 6.

Biochemical characterization of N-cadherin (green; A and B) and vinculin (green; C and D) at the CM-CMF boundary on soft, moderate, and stiff samples. CMs were stained with cardiac troponin-T (purple), and cell nuclei were counterstained with DAPI. The fluorescence intensity was normalized to the total number of cells on each substrate and then averaged over three samples. The yellow arrows show the distribution of vinculin at the CM-CMF interface (scale bars, 50 μm). Data are shown as mean, and the error bar represents the SD of the measured values (^∗ indicates a statistically significant difference with p < 0.05). To see this figure in color, go online.

Although substrate stiffness has been known to affect the distribution of focal adhesions, we observed no significant difference in vinculin expression for any of the tested substrate stiffnesses; however, we did notice a considerable difference in the localization of vinculin, especially at cell boundaries. The appearance of distinct focal adhesion structures is dependent on substrate stiffness (51). As observed in the higher magnification images, vinculin signal appears more diffused in the soft substrate (14 kPa), which is in line with literature observations (52).

Discussion

It is well known that CFs play a crucial role after heart injury (e.g., MI) by proliferating and differentiating into CMFs (10). Although there is growing evidence demonstrating the importance of CMFs in heart diseases, most of the studies so far have been focused on the electrotonic coupling aspect of these cells only. In this study, we investigated the effect of substrate stiffness on mechanical signal propagation between CMs and CMFs. Specifically, we characterized the mechanical properties of the CMFs connected to the CMs with a defined boundary and measured the contractile force propagation through a series of connected myocardial cells. In our studies, we used primary myocardial cells that we had enriched for CMs. One day after cell isolation (day 1), we observed that very few cells expressed α-SMA demonstrating that most of the isolated cells were CMs and CFs (Fig. S6 A). Upon seeding on the test substrates with varying stiffness, we cultured these cells for 5 days before the measurements to allow CFs to self-proliferate and form a boundary between nonproliferative CMs and proliferating CFs, essentially creating a wound-healing scenario. This condition resembles the low-density CF plating that allows for rapid CF proliferation, which eventually leads to CF to CMF differentiation as reported earlier (31, 32). We have confirmed the differentiation of the primary CFs into CMFs in all of the tested substrates by immunostaining the cells with α-SMA (Fig. S6 B). Our results showed that the stiffness of the substrate has great influence on the mechanical force propagation and characteristics of the propagated mechanical wave between the CMs and the transdifferentiated CMFs.

The mechanical microenvironment within the myocardium plays a crucial role in determining the morphology, contractility, and function of both myocytes (i.e., CM) and nonmyocytes (i.e., CF and CMF) (51, 53). For instance, studies have shown the role of matrix stiffness in modulating sarcomere alignment (54) as well as on calcium dynamics (16), both of which are majorly involved in cardiac cell contractility (55). Other studies have shown that matrix stiffness also determines cell spread area and distribution of focal adhesions (54, 56). However, recapitulating a cell’s micro niche in vitro, for which one incorporates both the physical and biochemical cues, is challenging. Many studies (57, 58) have leveraged biocompatible PDMS (23) or hydrogel-based (59) systems for investigating cell-cell or cell-matrix interactions and the effect of microenvironmental cues on these interactions. Although hydrogels can be tuned to fabricate substrates with varying stiffness to create conditions similar to native tissues in their healthy and diseased state, maximal stiffness that can be achieved is usually limited to ∼100 kPa (15, 50, 60). This is not ideal for accurately mimicking the stiffness range of infarcted heart tissue, which was reported to vary from 100 to 1000 kPa (4, 5). Because it is easier to achieve a higher and wider range of varying stiffness values with PDMS, in this study, we tuned the substrate stiffness by varying the amount of curing agent/base ratio of the PDMS and fabricated substrates with stiffness ranging from 14 kPa (stiffness of healthy heart) to 484 kPa (stiffness of 2- to 6-week infarcted heart). Furthermore, the stiffness measurements with varying loading velocity showed that the stiffness of these PDMS substrates reduced with decreasing loading velocity, much like the native heart tissues we tested (Fig. 1 B) and consistent with the earlier literature observations (61). Thus, PDMS substrates can be used to mimic the elasticity of the ECM in heart tissues. In addition, the CMFs also exhibited loading-velocity-dependent mechanical deformation behavior as shown in earlier studies for other cell types (27, 33, 62). The height of the cells was reduced, and their stiffness increased when the stiffness of the substrate increased (Table 1), indicating that CMFs spread out more and become stiffer on stiffer substrates, as expected.

Consistent with previous studies (15, 46), we noted that CMs had the strongest contractile force on the softest substrate, which was nearly 240 nN, whereas it was only 86.92 nN on the stiffest substrate. The beating force of the CMs was stronger and transmitted further on softer substrates (Figs. 2 C and 3 C), as indicated by the higher maximal CM-CMF boundary distance (Fig. 3 A). As explained earlier, stronger cell contraction force and substrate deformability can both be contributing factors, but it is difficult to decouple their individual roles through transverse measurements as performed in this study. Despite this limitation, we believe that the stiffness of the substrate plays a greater role than CM contractile force based on the results in Fig. 3 C. Fig. 3 C shows the normalized CMFs contractile force for the CMF located at the furthest measurement point (normalized to the respective CM contractile force) (i.e., the transmitted force ratio versus the maximal CM-CMF boundary distance). It was observed that mechanical signals were transmitted longer and stronger on moderate substrates than on stiff substrates, even though both had similar CM contractile force (Fig. 2 C), demonstrating that the substrate stiffness is the critical factor that defines signal propagation magnitude and distance.

Because the CMs are mechanically coupled with their neighboring cells through adherens junctions, their dynamic rhythmic beating actively stretched the CMFs (Video S2), which in turn promoted myocardial contractility. As seen from contractile measurements of the CMFs, the magnitude of the propagated contractile force of CMFs was smaller than that of CMs in all substrates and exponentially decayed with distance from the CM-CMF boundary. The amount of transmitted contractile force from CMs to CMFs depended upon the substrate stiffness, as seen from the relative contractile force measurements of the CMFs that were in direct contact with the CMs. The contractile forces of CMs were normalized to the adjacent CMF force measurements, revealing that the transmitted force was attenuated by 2.4-, 4.3-, and 21.7-fold for soft, moderate, and stiff substrates, respectively. The variation in transmitted force may be explained by larger deformations of softer substrates under the same load and thereby a higher degree of mechanical force transmission. A similar behavior was proposed in a simulation model by Chiou et al. (63) investigating mechanical signaling in the embryonic heart. They built a computational model based on the concept of “fire-diffuse-fire,” in which the mechanically excitable CMs contracted if the local strain exceeded a threshold value, which then diffused through the surrounding matrix (modeled as elastic-fluid biphasic material). As seen in this model, mechanical signal propagation is not instantaneous, unlike electrical signal conduction. Rather, the contraction of excited CMs creates local mechanical stress, which propagates to neighboring cells and matrix, eventually triggering neighboring quiescent, passive cells, such as the CMFs in the current study.

To verify that substrate stiffness influences the signal propagation, here we developed a computer simulation model using FEA to corroborate our experimental results. The PHE model has been proven to successfully capture the behavior of cells and tissues (49, 64, 65) because it can capture finite strain and nonlinear behavior as well as the fluid-solid interaction of materials. Therefore, we utilized this model to successfully simulate the behavior of myocardial cells subjected to different substrate stiffness. In our model, we assumed that PDMS, CMsc and CMFs consisted of both fluid and solid phases and, as shown in Fig. 5 A, the simulation results agreed well with experimental data except for the soft substrates. While modeling the soft substrates, as the applied stress was increased, the substrate deformation was too large, which caused the simulation to terminate. The applied CM stresses were 20, 25, and 65 kPa leading to the maximal CMF force measurements of 23.5, 10, and 4 nN for soft, moderate, and stiff substrates, respectively. CM-applied stress of the moderate substrate was 2.6-fold smaller but created a 2.5-fold larger CMF force compared to the stiff substrate, indicating that substrate stiffness is the main mechanism for mechanical signal propagation. This simulation result agreed with our experimental data shown in Figs. 2 C and 3 C.

Another important observation in our study was that the contractile force propagated longer distances on the PDMS substrates in the control samples when there were no CMFs to couple with the CMs at the boundary for all the three substrate stiffnesses we tested. It may be because in the coculture samples, CMs actively stretched both CMFs and the PDMS substrates, whereas in the control samples without any CMFs, they only deformed the PDMS substrates. Interestingly, the degree of attenuation depended on the substrate (matrix) stiffness where the reduction of the propagating distance was smaller for softer substrates (i.e., 37.21, 60.87, and 69.23% for soft, moderate, and stiff substrates, respectively). These results revealed that the level of signal attenuation increased with increasing substrate stiffness, whereas the presence of CMFs is as influential as the substrate stiffness itself, as indicated by the ratios of maximal CM-CMF boundary distance between coculture and control samples (Fig. 3 B). The reason for this observation could be that the CMF stiffness was larger on stiffer substrates, thereby attenuating the mechanical signal transmission more compared to CMFs on softer substrates. Another possible reason for a decrease in force transmission could be due to an increased presence of the focal adhesion protein vinculin at the cell-cell interface on stiff substrates compared to soft substrates. The focal adhesion proteins have been shown to localize at CM-CM interfaces during pathological stages of CMs (e.g., after an MI) when the ECM stiffness is relatively larger compared to healthy tissues (50). Similar to these findings, in our study, we observed the localized distribution of vinculin at CM-CMF boundaries. Without this localized distribution, the contractile force of one cell could be directly transmitted to its neighboring cell. With the presence of this distribution pattern on the other hand, the transmitted force would be reduced, as the cell would not only stretch its connected neighbor but also stretch the substrate underneath via focal adhesions. Finally, our immunostaining results indicate that N-cadherin expression is reduced with decreasing substrate stiffness (Fig. 6). It has been reported that N-cadherin can slow down conduction velocity when CMFs (from scar tissue) are mechanically coupled with CMs (19). Because we observed higher N-cadherin expression on stiffer substrates, smaller contractile forces on these could be due to a reduction of conduction velocity. The results reveal that the substrate stiffening and the increased presence of CMFs in the infarct tissue act synergistically to deteriorate mechanical coupling within the infarcted heart tissue.

In addition to investigating the effect of the mechanical microenvironment on the propagation of mechanical signals, we also studied the characteristics of the propagated wave. We observed, for the first time in the literature, that variations in the pattern of the mechanical wave propagated across CMFs are dependent on the stiffness of the substrate on which the cells were cultured (Fig. 4). The two types of waves that were observed were either an upward wave (i.e., beating behavior), similar to a CM beating wave observed on stiff (83–484 kPa) substrates or a downward wave (i.e., pulling action), mostly found on soft (14 kPa) substrates. Notably, we observed that both soft and moderate substrates exhibited both wave patterns with varying probabilities (Fig. 4). In contrast, only the beating pattern was observed in stiff substrate samples and was only exhibited by the first few CMFs near the CM-CMF boundary. We suggest that the localized distribution of focal adhesions at the cell-cell interface, as previously mentioned, plays a significant role in the underlying mechanism corresponding to different CMF contractile wave patterns seen on the various substrates. To verify this hypothesis, we developed an FEA model (Fig. 5 B). Both the contractile force magnitude and the pattern of CMFs were considered in this model. We observed that CMFs had a beating contractile force pattern when focal adhesions at the cell-cell interface were activated, i.e., when focal adhesions assembled predominantly at the cell-cell interface and boundaries, as seen in the cells cultured on substrates with high stiffness (Fig. 6). On the other hand, the pulling pattern of CMFs was observed when these focal adhesions were inactivated, as observed only on substrates with soft and moderate stiffness. The force magnitude of the pulling pattern was significantly larger than that of the beating one, suggesting that the localized distribution of focal adhesions at the cell-cell interface not only governs cell contractile wave patterns but also the amount of transmitted force from one cell to another. The increase of ECM matrix stiffness under pathological conditions can cause the localization of focal adhesion at the cell-cell boundary (50) and influence CM function and contractility. The results observed here demonstrated the critical importance of cell-cell and cell-matrix interactions, which influence the transmission of mechanical signals. The beating-pulling contractile pattern observed in the CM-CMF boundary on softer substrates allows the transmission of mechanical contraction and maintenance of healthy heart function. In contrast, the beating-beating pattern on the stiffer substrates might limit signal propagation at healthy-infarct tissue boundaries.

Conclusions

In this work, we studied the effect of mechanical microenvironment on mechanical signal propagation from myocytes (i.e., CMs) across nonmyocytes (i.e., CMFs). We investigated the critical role of mechanical coupling and interactions between CMs and CMFs in a healthy and infarcted tissue model. To our knowledge, our study is the first to measure and characterize contractile forces of both CMs and CMFs, the force transmission at the CM-CMF boundary, as well as its dependence on substrate stiffness. We have demonstrated that softer substrates facilitated stronger contractions and transmission of mechanical signals. Additionally, we found that the beating pattern of CMFs, which depends on substrate stiffness, plays a significant role in mechanical signal transmission, which is an interesting finding that could potentially help elucidate the effects of infarcted tissue stiffness and size on arrhythmia. We also determined the role of stiffness-dependent distribution of focal adhesions on mechanical signal transmission. The results of this project will help us gain a better understanding of the effects of scar tissues which will help explore new therapies for myocardial myopathies like infarction and arrhythmia.

Author Contributions

T.D.N. performed the substrate fabrication experiments, the nanoindenter measurements and related data analysis, the FEA simulations, and wrote the article. N.N. performed substrate fabrication experiments and the cell culture studies, biochemical characterizations and related data analysis, and wrote the article. P.Z. designed the research and wrote the article.

Editor: Philip LeDuc.