Abstract
Cells within mechanically dynamic tissues like arteries are exposed to ever-changing forces and deformations. In some pathologies, like aneurysms, complex loads may alter how cells transduce forces, driving maladaptive growth and remodeling. Here, we aimed to determine the dynamic mechanical properties of vascular smooth muscle cells (VSMCs) under biaxial load. Using cellular micro-biaxial stretching microscopy, we measured the large-strain anisotropic stress-strain hysteresis of VSMCs and found that hysteresis is strongly dependent on load orientation and actin organization. Most notably, under some cyclic loads, we found that VSMCs with elongated in-vivo-like architectures display a hysteresis loop that is reverse to what is traditionally measured in polymers, with unloading stresses greater than loading stresses. This reverse hysteresis could not be replicated using a quasilinear viscoelasticity model, but we developed a Hill-type active fiber model that can describe the experimentally observed hysteresis. These results suggest that cells in highly organized tissues, like arteries, can have strongly anisotropic responses to complex loads, which could have important implications in understanding pathological mechanotransduction.
Introduction
Many tissues undergo dynamic deformations, with strain rates ranging from ∼30% per second during cardiac contraction (1) to ∼1% per year during aneurysm growth (2). As a result, cells within the tissue are exposed to constantly changing forces. Mechanical stimulation has been shown to influence a wide range of cellular functions (3, 4, 5, 6) and alter gene expression and cell fate (7, 8, 9, 10). The process by which the cell converts extracellular mechanical stimuli into biochemical signaling, known as mechanotransduction, is implicated in a number of diseases, from traumatic brain injury (11) to cancer metastasis (12, 13). A cell’s mechanical properties, which relate its deformation to its internal forces (14), likely influence mechanotransduction. Thus, it is important to determine the dynamic material behavior of cells in mechanically responsive tissues.
Compared to most materials, cells have complex mechanical properties. Most notably, cells display temporally dynamic mechanical behaviors. For example, when a cell is rapidly stretched, its stress will initially increase but with time will decay back to a basal level (15, 16); and when cyclically stretched, cells display stress-strain hysteresis, with higher stresses during extension than during subsequent compression (17). These behaviors are well characterized in viscoelastic polymeric materials, which exhibit both fluid-like (viscous) and solid-like (elastic) properties. Thus, cells are often characterized as viscoelastic (18). However, unlike standard polymers, cells can actively adapt their stress state via actomyosin contraction and cytoskeletal remodeling, which could produce viscoelastic-like stress relaxation and hysteresis. The interplay between passive viscoelastic energy dissipation and active adaptive processes in regulation of cell stress is not fully understood.
Time-dependent properties of cells have been characterized, but existing studies either measure small strain properties or do not account for structural anisotropy of the cell (19, 20, 21, 22). Recently, using cellular micro-biaxial stretching (CμBS) microscopy, we demonstrated that vascular smooth muscle cells (VSMCs) with native-like architecture have highly anisotropic mechanical properties under large strains due to their highly aligned actomyosin cytoskeleton (23). Here, we expand on that study to examine hysteresis in cyclically stretched VSMCs. Using the CBS method, we find that hysteresis depends on the cellular architecture and that, surprisingly, under some complex loads we observed hysteresis loops that are inverse to those observed in energy-dissipating materials. We modeled VSMC anisotropic hysteresis using quasilinear viscoelasticity (QLV) theory and a Hill-type contractile fiber model and found that only the contraction model was able to capture the experimentally observed behavior. These results have important implications in in vivo mechanotransduction, when cells are exposed to complex loads, and in the development of models for better understanding cell physiology and biomechanical function within tissues.
Materials and Methods
Substrate fabrication and cell micropatterning
Micropatterned CμBS substrates were prepared as previously described (23). Briefly, VSMCs were micropatterned with aspect ratios (ARs) 4, 2, and 1 (AR4: 32 × 128 μm; AR2: 91 × 44 μm; AR1: 63 × 63 μm) on polyacrylamide gels with Young’s moduli of 13.5 kPa, which were adhered to elastomer membranes. Passages four to seven VSMCs were used for all experiments and the cells were serum starved in serum-free media for 24–48 h before experiments to induce a physiological phenotype (24).
Cell structure
Cells were fixed, stained for F-actin, and imaged using standard methods. Fiber distributions measured from two-dimensional projections of F-actin confocal stacks were fitted to a von Mises distribution function of the form
| (1) |
where is the fiber concentration factor, describing the spread of the fiber distribution around preferred orientation , and is the modified Bessel function of the first kind of order 0.
Cell stretching and traction measurement
CμBS experiments were conducted using our custom-built microscope-mounted biaxial stretcher (Fig. 1, A and B; Fig. S1 A) at 37°C in Tyrode’s buffer. Cell-seeded CμBS substrates were exposed to either uniaxial or equibiaxial stretching protocols to 25% grip strain for uniaxial or 20% grip strain for equibiaxial stretches (Fig. S1, B and C). First, a priming stretch and cell location stretch were performed. Then, active cell stretch was performed by increments of 5% loading strain (0.1%/s ramp rate) to the substrate with 2-min hold periods for image acquisition (Fig. S1, B and C). After reaching the maximal prescribed strain, cells were unloaded by performing −5% unloading strain, and images were acquired. After one cycle, cells were passivated with 100 μM HA-1077, and the load-unload cycle was repeated on the passive cells. Finally, cells were lysed with 0.1% sodium dodecyl sulfate, and the stretching protocol was repeated to acquire cell-free deformation of beads.
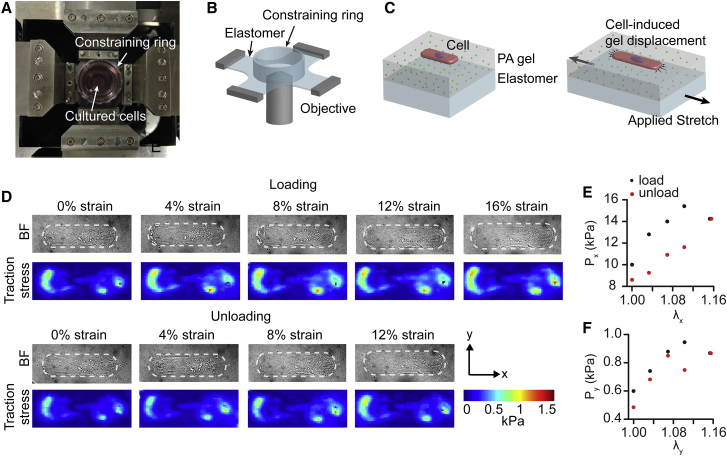
Figure 1.
CμBS and single-cell hysteresis. (A) A microscope-mounted CμBS device is shown. (B) A schematic representation of the elastomer membrane and constraining ring used to hold micropatterned cells. (C) A schematic representation of the cell and substrate construction. (D) A representative single micropatterned VSMC equibiaxially stretched. The top image set shows extensional loading. The bottom image set shows compressive unloading. The top row shows a bright-field image of the cell outlined by a dashed line. Cell-induced substrate surface tractions are shown. (E) Cellular midplane PK1 stress in the long axis of the cell (parallel to the x axis) vs stretch ratio in the x axis. (F) Cellular midplane PK1 stress in the short axis of the cell (parallel to the y axis) versus stretch ratio in the y axis. BF, bright field; PA, polyacrylamide. To see this figure in color, go online.
The total deformation F was referenced to the prestretched configuration (Fig. S2 A), and the total substrate deformation was given by substrate stretch ratios, and , which were taken as the measured cell-free substrate deformations. Cell-induced substrate displacement was given by u and determined using particle image velocimetry to compare the cell-adhered and cell-free bead position at the top surface of the gel for each applied stretch value (25) (Fig. 1 C; Fig. S2 A).
Cell-induced substrate displacement was used to calculate the midplane stresses in the cells as a function of stretch. Substrate traction stress vectors were determined from cell-induced gel displacement (u) using an unconstrained Fourier transform traction cytometry algorithm (regularization factor: 1E-9, Poisson’s ratio: 0.5), which yielded a grid of substrate traction stress vectors given by , where is the unit vector in the direction (Fig. S2 B). Substrate traction forces were given by , where is the area acts on (Fig. S2 B). Substrate forces are balanced at the cell-substrate interface by cell forces , so that . Next, forces were defined as tensile (positive) if they were oriented away from the cell midline and the total tensile forces and are given as and , where is the vector that described the location of surface with respect to the cell center (Fig. S2 B). The first Piola-Kirchhoff (PK1) stresses (force per unit undeformed cross-sectional area) at the cell’s midline were calculated as and , where and are the cell midline cross-sectional areas (Fig. S2 C), measured in a previous study to be and for VSMCs with an AR of 4, and for VSMCs with an AR of 2, and for VSMCs with an AR of 1 (23).
Modeling cell hysteresis
Two models were used to describe cell biaxial hysteresis: a QLV model and a Hill-type active fiber model.
Cell deformation and elastic constitutive description
The cell was assumed to undergo isochoric planar biaxial deformation (i.e., no shear). The deformation tensor F = diag[λx, λy, λz] was taken as the observed deformation of the cell, where λi are stretch ratios in the direction (x: parallel to the long of the cell, y: parallel to the short axis of the cell, z: perpendicular to the gel surface). Stretch ratios mimicked those of the experiments, both spatially and temporally. In a previous study, we found that cell volume does not significantly change in stretched micropatterned VSMCs (16), so for all deformations, we assumed .
The cell was treated as a distribution of discrete contractile actomyosin fibers within an isotropic matrix. The fiber contraction was modeled by altering the fiber zero-stress configuration, as shown in Fig. S3. We let the passive (stress-free) cell (B) be disassembled into the bulk matrix and individual fibers , each of which is stress free. The fibers are treated as one dimensional, so that when they contract, they shorten along the fiber axis. In this disassembled state, the shortening is stress-free and given by the active stretch ratio . When the fibers are reassembled , they are deformed from the zero-stress configuration back to their initial configuration, resulting in a stress before applied deformation. Finally, when the cell is deformed (F), a fiber deforms by the fiber stretch ratio . The fiber’s elastic deformation , or the deformation from the zero-stress configuration to the final deformation, which is used to determine the stress, is given by .
For a continuous distribution of fibers, the constitutive equation for the contribution of the fiber matrix was given by the following:
| (2) |
where is a fixed stiffness parameter, and is the fiber probability density function. The deformation of a fiber oriented with an angle from the x axis of the cell was given by the following:
| (3) |
In this model, we use discrete fibers, rather than a distribution, so for fibers was given by the following:
| (4) |
where and are the fiber stretch ratio and active stretch ratio of the fiber, respectively, and the strain energy density of a single fiber is given by the following:
| (5) |
The constitutive equation for the matrix was taken as neo-Hookean and given by the following:
| (6) |
where is shear modulus, and is the first strain invariant.
The total strain energy density for the cell is given by the following:
| (7) |
For shear-free deformation of an incompressible material, the elastic PK1 stress in the direction is given by , where is a Lagrange multiplier (14). Because the top surface of the cell is unconstrained, we let , so
| (8) |
where .
QLV model
We modeled cell hysteresis as viscoelastic relaxation using a Fung-type QLV model (26), designed for large-strain deformations and nonlinear materials. In this model, the active stretch ratio was assumed to be uniform for all fibers and constant for all times.
In the QLV model, the temporal stress was given as follows:
| (9) |
where is the reduced relaxation function. The general form for is . For simplicity, we used a first-order function given by the following:
| (10) |
where and are constants.
Hill-type active fiber model
We modeled cell hysteresis as active contraction by modeling the actomyosin fibers with the Hill equation for muscular contraction (27). In this model, we ignore viscoelastic contributions, so that the elastic stress (Eq. 8) is the total stress and temporally vary in each fiber.
A standard form of the Hill equation is given by the following:
| (11) |
where is velocity of shortening of the muscle fiber, is the constant force on the muscle, is the stall force, or force at which a tetanized muscle neither shortens nor lengthens , and and are constants. Here, we aimed to replace the shortening velocity with the rate of change of the fiber zero-stress configuration, characterized in our framework as . The stretch ratio of the fiber is decomposed into and the elastic deformation (Fig. S3), such that
| (12) |
The Hill equation is derived under constant force conditions (or constant PK1 stress), which in our model means that the fiber elastic deformation is constant, so we let . Thus, the fiber shortening velocity was given by the following:
| (13) |
The fiber force was given by the following:
| (14) |
where is the fiber PK1 stress, and is the undeformed cross-sectional area of the fiber. We assume that at the beginning of the experiment, each fiber is maintaining a homeostatic stress such that the fiber is neither contracting nor relaxing. This stress is given by and defined by the following:
| (15) |
where is the active stretch ratio at which the fibers are in stress homeostasis.
Substituting Eqs. 13, 14, and 15 into Eq. 11 and letting gives the following:
| (16) |
where and are constant parameters.
Solution method
In both models, a random family of 2000 fibers, matching the measured von Mises distribution measured of an average cell, was generated. Time was discretized into 0.01-min increments over 18 min for equibiaxial stretch and 22 min for uniaxial stretch. Initially, . Parameters were fit to the equibiaxial data via least-squares fitting of the experimentally measured stresses (both and ) and the mean model-predicted stresses during each stretch-hold period at each of the measured substrate deformations . After initially screening a large range of potential parameters to determine the most relevant range, the parameter range that was considered was , , , , , , and . After parameter optimization, uniaxial stresses for corresponding uniaxial-axial or uniaxial-transverse stretches were then computed using the fitted parameters by applying experimentally measured substrate deformations in the direction of stretch and in the off-axis direction.
Statistics
All results are expressed as means ± SD. Differences in loading and unloading stresses for at each strain for all stretching experiments were compared using paired t-tests in SigmaPlot (Systat Software, San Jose, CA). A value of p < 0.05 was considered to indicate statistical significance.
Results
VSMCs with in-vivo-like geometry display anisotropic hysteresis
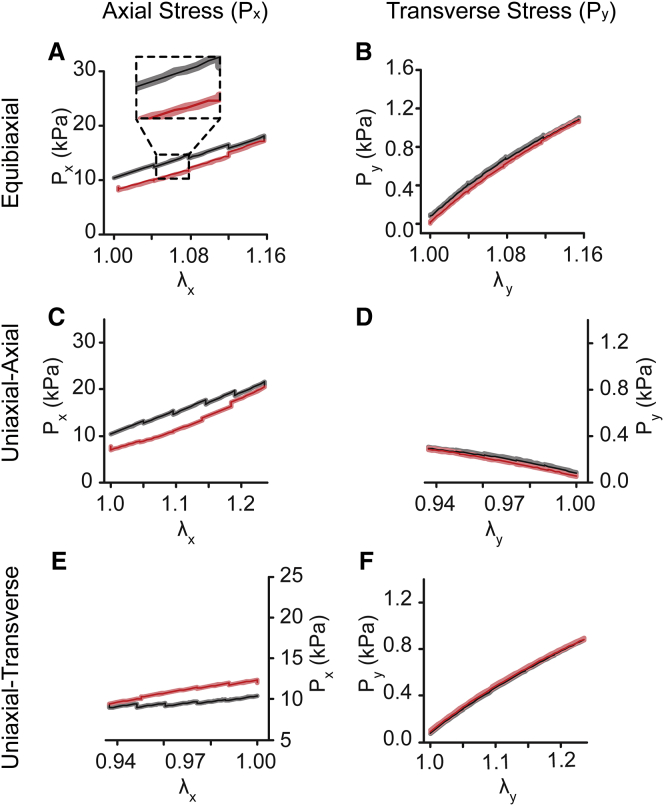
We used CμBS microscopy (23) to apply dynamic physiological deformations (up to 25% applied strain) to individual adherent VSMCs and concurrently measure the resulting stresses (Fig. 1). Briefly, VSMCs were micropatterned with an in-vivo-like elongated geometry (4:1 AR4) on a polyacrylamide gel adhered to an elastomer membrane. Using a custom-designed microscope-mounted biaxial stretcher (Fig. 1, A–C; Fig. S1 A), we applied planar strains in increments of ∼4% strain up to a maximum of 16–22%, then incrementally returned to 0% strain (Fig. S1, B and C). A representative equibiaxial stretch (stretched equally in both x and y directions) can be found in Fig. 1 D. Traction stress on the substrate surface was measured using the substrate displacement during stretching and well-established traction force microscopy methods (Fig. 1 D). The midcell stress parallel to the long axis of the cell, or axial stress (Px), and parallel to the short axis of the cell, or transverse stress (Py), were calculated from surface tractions and the cellular architecture, which was determined from confocal microscopy (23) (Fig. S2 C). Within a single cycle, stresses were dissimilar during loading and unloading, resulting in a stress-strain hysteresis loop (Fig. 1, E and F).
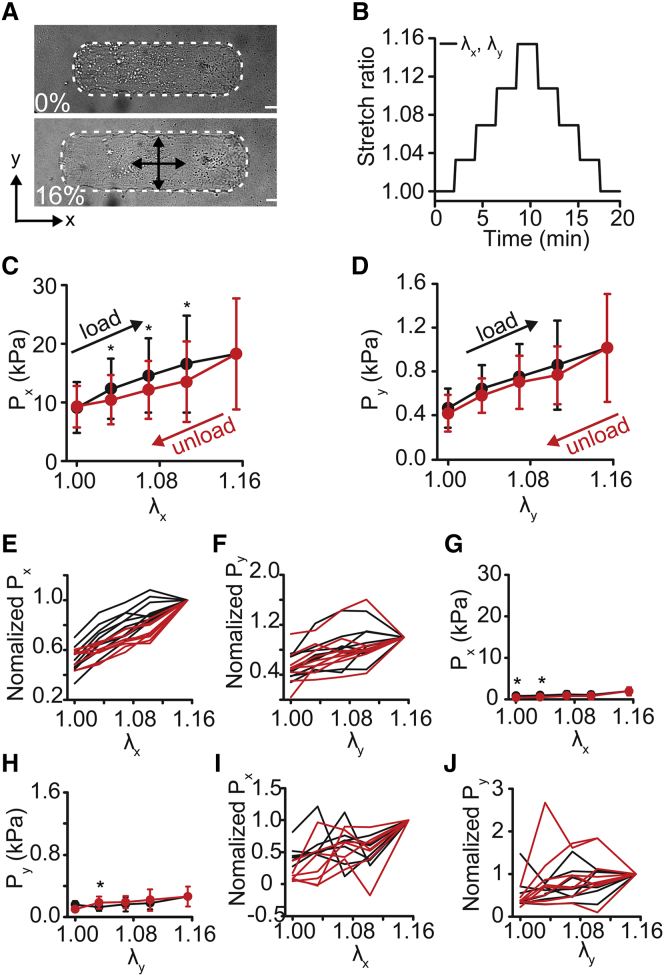
Under equibiaxial loading, both Px and Py increased when loaded and decreased when unloaded (Fig. 2, A–D). Axial stresses were an order of magnitude higher than transverse stresses (Fig. 2, C and D), consistent with previous findings (23). Within the cycle, loading stresses were higher than the subsequent unloading (Fig. 2, C and D). These data are consistent with hysteresis loops traditionally associated with viscous energy loss. Individually, normalized cell stress plots demonstrate that this trend was consistent cell to cell (Fig. 2, E and F). Next, the cells were treated with HA-1077, a Rho-kinase inhibitor, to block actomyosin contractility. After treatment, the stresses decreased by >10-fold (Fig. 2, G and H), and the cell-to-cell hysteresis decreased (Fig. 2, I and J).
Figure 2.
Equibiaxial cyclical stretch of micropatterned vascular smooth muscle cells. (A) A bright-field image of a cell before stretch and at 16% stretch (x,y-equibiaxial stretch, λx = λy). The cell is outlined in white. Scale bars, 20 μm. (B) The cell stretch ratio (λx, λy) during the equibiaxial stretch cycle. (C) Axial active cell stresses (Px) during equibiaxial stretch. (D) Transverse active cell stresses (Py) during equibiaxial stretch. (E and F) Normalized individual cell axial (E) and transverse (F) stress traces. (Each cell normalized to the stress value at maximal applied strain.) (G and H) Axial (G) and transverse (H) stress after HA-1077 treatment. (I and J) Post HA-1077 treatment normalized individual cell axial (I) and transverse (J) stress traces. (Each cell normalized to the stress value at maximal applied strain.) All graphs show mean ± SD (n = 10). ∗p < 0.05. Black represents loading. Red represents unloading. To see this figure in color, go online.
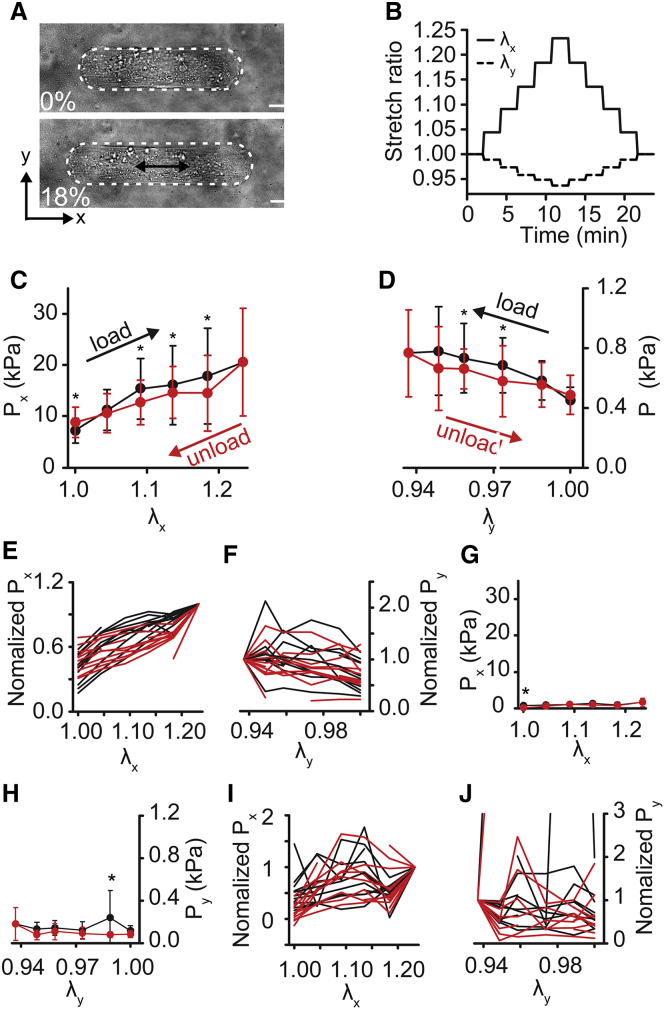
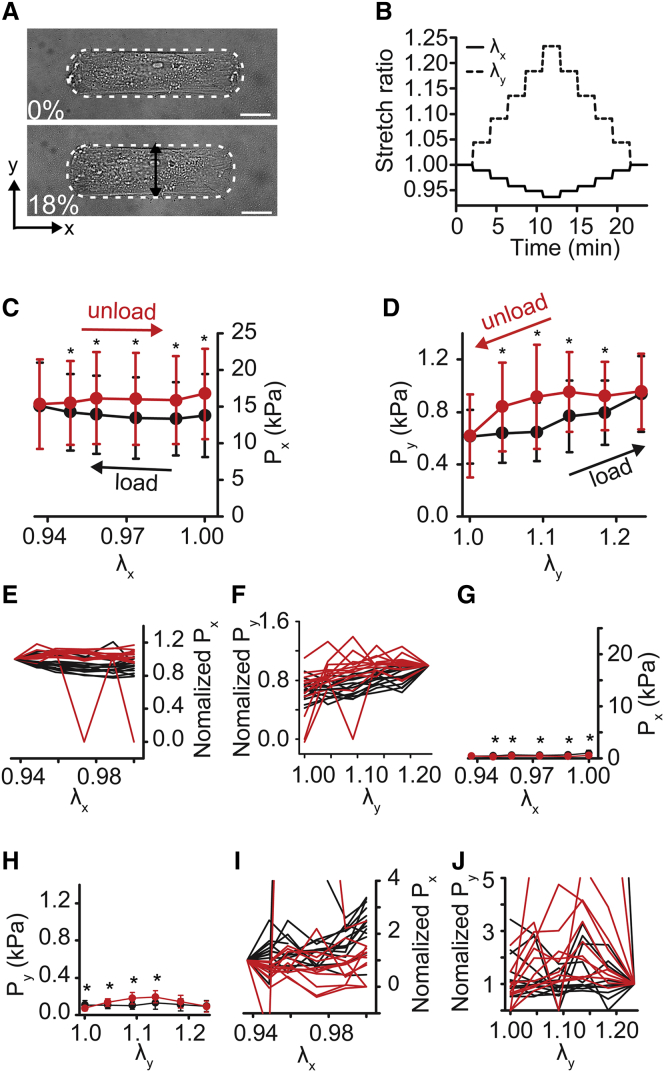
Next, we applied uniaxial deformation, where the membrane was stretched parallel to one axis and held fixed parallel to the other. Notably, because the PDMS ring is adhered to the membrane to constrain the culture media (see Fig. 1, A and B), the deformation is neither strip biaxial nor purely uniaxial. Instead, uniaxial stretching yielded some compression in the transverse direction (e.g., Fig. 3, A and B) but less compression than would be expected for uniaxial deformation of an incompressible material. When the cell was stretched parallel to its long axis (uniaxial-axial) (Fig. 3, A and B), both the stress in the direction of extension (Px) and the stress in the off-axis direction (Py) increased with strain (Fig. 3, C–F), and unloading stresses were lower than loading stresses for each increment of strain, suggesting energy loss, similar to our equibiaxial stretch experiments. Rho-kinase inhibition decreased all stresses by nearly 10-fold (Fig. 3, G and H) and decreased the degree of hysteresis (Fig. 3 and J, I). For stretching perpendicular to the cell’s long axis (uniaxial-transverse) (Fig. 4, A and B), the stress in the direction of extension (Py), increased during loading and decreased with unloading (Fig. 4, D and F). But surprisingly, unloading stresses were greater than loading stresses, creating a hysteresis loop that was opposite to the standard loop associated with energy dissipation, instead suggesting energy gain. Stresses perpendicular to the direction of stretch (Px) were nearly unchanged during loading but then increased during unloading (Fig. 4, C and E). When contraction was inhibited, passive stresses were markedly lower than contractile stresses (Fig. 4, G and H), but we observed significant differences in loading and unloading stresses for both Px and Py (Fig. 4, I and J). Notably, the hysteresis in Px was reversed in the passive state, compared to the active, with unloading stresses lower than loading stresses (Fig. 4, I and J). Taken together, these data suggest that in highly structured cells, like VSMCs in arteries, hysteresis depends on the orientation of the load with respect to cell orientation and that cytoskeletal tension is an important factor in the hysteresis magnitude.
Figure 3.
Axial cyclical stretch of micropatterned VSMCs. Cell elongation is parallel to the long axis of the cell. (A) A bright-field image of the cell before and after 18% stretch (x-direction of stretch, λx). The cell is outlined in white. Scale bars, 20 μm. (B) Cell stretch ratios (λx, λy) during uniaxial-axial stretch cycle. (C) Axial active cell stresses (Px) during uniaxial-axial stretch. (D) Transverse active cell stresses (Py) during uniaxial-axial stretch. (E and F) Normalized individual cell axial (E) and transverse (F) stress traces. (Each cell normalized to the stress value at maximal applied strain.) (G and H) Axial (G) and transverse (H) stress after HA-1077 treatment. (I and J) Post HA-1077 treatment normalized individual cell axial (I) and transverse (J) stress traces. (Each cell normalized to the stress value at maximal applied strain). All graphs show mean ± SD (n = 10). ∗p < 0.05. Black represents loading. Red represents unloading. To see this figure in color, go online.
Figure 4.
Transverse cyclical stretch of micropatterned VSMCs. Cell elongation is parallel to the short axis of the cell. (A) A bright-field image of the cell before and after 18% stretch (y-direction of stretch, λy). The cell is outlined in white. Scale bars, 20 μm. (B) Cell stretch ratios (λx, λy) during uniaxial-transverse stretch cycle. (C) Axial active cell stresses (Px) during uniaxial-transverse stretch. (D) Transverse active cell stresses (Py) during uniaxial-transverse stretch. (E and F) Normalized individual cell axial (E) and transverse (F) stress traces. (Each cell normalized to the stress value at maximal applied strain.) (G and H) Axial (G) and transverse (H) stress after HA-1077 treatment. (I and J) Post HA-1077 treatment normalized individual cell axial (I) and transverse (J) stress traces. (Each cell normalized to the stress value at maximal applied strain). All graphs show mean ± SD (n = 10). ∗p < 0.05. Black represents loading. Red represents unloading. To see this figure in color, go online.
An active fiber model describes single-cell anisotropic hysteresis
To better understand the dynamics of the observed anisotropic hysteresis, we aimed to develop a theoretical model of temporal stress in the cell during stretching. We first used a QLV model (26). QLV was used because we applied large strains to the cells, and the QLV model is designed for viscoelastic materials with nonlinear constitutive behavior undergoing large strains. The elastic strain energy density function was based on our previously published study (23), and the viscous behavior was characterized with a reduced relaxation function with an exponential decay. The parameters were fit to the equibiaxial stretching data (Fig. S4, A and B; Table S1), and the model was then applied to the uniaxial-axial and uniaxial-transverse stretch cases. For uniaxial-axial stretching, the model (Fig. S4, C and D) captured the experimental hysteresis, where unloading stresses were lower than loading stresses for each point of strain for Px and Py. But for uniaxial-transverse stretching, the model failed to predict the observed reverse hysteresis, instead predicting unloading stresses lower than loading stresses for Px and Py (Fig. S4, E and F).
The Hill equation relates muscle force generation and contraction rate (27) and has been used for decades to describe smooth muscle contraction in blood vessels (28). More recently, the Hill relationship has been used to describe discreet actomyosin fibers within cells to model cytoskeletal dynamics during cell migration (29, 30, 31). We modified our model to include active contraction via a Hill relationship between actomyosin fiber stress and contraction velocity. This model did not include passive viscoelasticity. Equibiaxial experimental data were used to optimize the parameters (Fig. 5, A and B; Table 1) and the model was then applied to uniaxial-axial and uniaxial-transverse stretch. For uniaxial-axial stretch, the model hysteresis (Fig. 5, C and D) was consistent with the experimentally observed behavior. Additionally, for uniaxial-transverse stretch, the model predicted reverse hysteresis, where unloading stresses are higher than loading stresses (Fig. 5, E and F), as seen experimentally (see Fig. 4, C and D). This result suggests that active contraction and relaxation, not passive energy dissipation, was the primary source of hysteresis in our experiments. Given this finding, our subsequent work focused on our Hill-type active fiber model.
Figure 5.
Anisotropic hysteresis is captured by a Hill-type active fiber model. (A and B) A Hill-type active fiber model for equibiaxial stretch, fitted to experimental data. (A) Model-predicted axial cell stresses (Px) during equibiaxial stretch. The inset is an enlarged image of plot showing mean stresses (dark line) and 95% confidence interval (shaded) calculated with 100 runs. (B) Model-predicted transverse cell stresses (Py) during equibiaxial stretch. (C and D) A Hill-type active fiber model for uniaxial-axial stretch, using parameters fitted to equibiaxial data. (C) Model-predicted axial cell stresses (Px) during uniaxial-axial stretch. (D) Model-predicted transverse cell stresses (Py) during uniaxial-axial stretch. (E and F) A Hill-type active fiber model for uniaxial-transverse stretch, using parameters fitted to equibiaxial data. (E) Model-predicted axial cell stresses (Px) during uniaxial-transverse stretch. (F) Model-predicted transverse cell stresses (Py) during uniaxial-transverse stretch. For all graphs, black represents loading, and red represents unloading. To see this figure in color, go online.
Table 1.
Hill-Type Active Fiber Model Parameter Values
| Parameter | Value |
|---|---|
| 1.25 kPa | |
| 4 kPa | |
| 0.675 | |
| 2 Pa | |
| 0.01 |
Actomyosin fiber orientation influences hysteresis anisotropy
To better understand why the Hill-type model replicated the experimentally measured hysteresis, we examined the model-predicted individual fiber active stretch ratios , which evolve temporally as a function of fiber stress (see Eq. 16). In equibiaxial loading, initial applied deformation caused all fibers to be uniformly stretched such that . So, increased uniformly, regardless of fiber orientation (Fig. S5 A). When individual fibers (Fig. S5 B) were examined at the same strain during loading and unloading (Fig. S5 C), the model predicted that was greater during unloading than during loading in all fibers, resulting in stresses that were higher in loading than in unloading and yielding the observed hysteresis loop. For uniaxial loading, varied with fiber orientation (Fig. S5, D and G). In uniaxial-axial loading, for fibers aligned with the long axis of the cell, increased with stretch, whereas in fibers transverse to the cell’s axis, decreased. But because the fibers in our micropatterned cells were primarily aligned with the long axis (Fig. S5 E), for individual fibers were qualitatively similar to the equibiaxial case (Fig. S5 F), resulting in lowered stresses during unloading, compared to loading. For uniaxial-transverse loading, the pattern is reverse that of the axial case (Fig. S5 G), because stretch was transverse to the cell’s long axis. But because the fibers were primarily axially aligned (Fig. S5 H), for all fibers decreased (Fig. S5 I), and the model predicted increased stress in unloading compared to loading. Thus, the compression and subsequent contraction of the fibers primarily aligned with the cell’s long axis was the source of the reverse hysteresis during uniaxial-transverse stretching in the model.
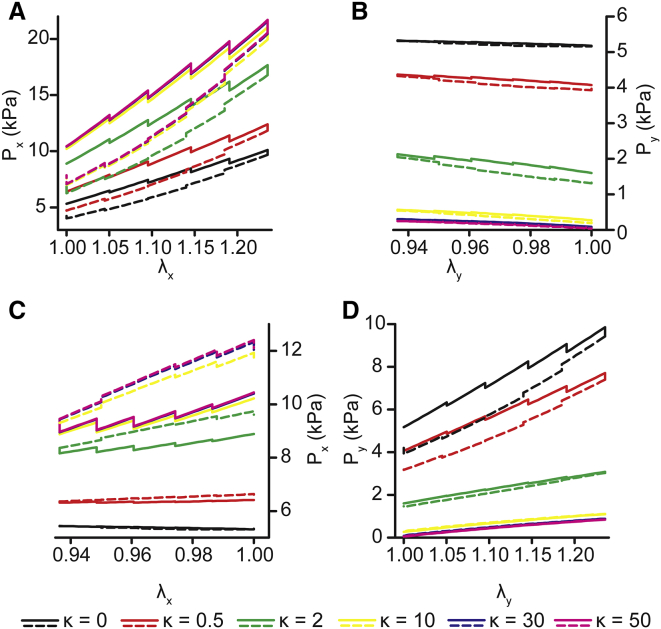
In vivo, VSMCs normally have a highly aligned actomyosin cytoskeleton. However, in vessels with complex geometries (32, 33) and in aneurysms (34), they can lose their characteristic spindle shape and, as a result, their cytoskeletal alignment. Using our Hill-type active fiber model, we tested how cytoskeletal architecture could alter the dynamic mechanics of the cells. We assumed that actomyosin fiber alignment could be described by a von Mises distribution, and we performed a parameter study for the fiber concentration factor over a range of values from isotropic ( = 0) to highly anisotropic ( = 50). For uniaxial-axial stretch, increasing fiber alignment (increasing ), the model predicted higher stresses in the direction of stretch (Px) with increased degree of hysteresis (i.e., larger loops) (Fig. 6 A), whereas stresses transverse to cell alignment (Py) decreased (Fig. 6 B) because of decreasing fiber alignment in that direction. For uniaxial-transverse stretch, increasing anisotropy led to lower stresses in the stretch direction (Py) (Fig. 6 D). Interestingly, for , the model predicts a standard hysteresis loop for dissipative viscoelastic behavior, but for 4, the model predicted reverse hysteresis similar to what we observed experimentally. A similar trend was predicted in the direction of cell alignment (Fig. 6 C). However, for values of , the reverse hysteresis behavior was observed in the axial stresses during transverse stretch (Fig. 6 C). Taken together, the model data suggest that cytoskeletal anisotropy is an important factor in the anisotropic temporal dynamics of VSMC mechanical properties.
Figure 6.
Hill-type active fiber model predicts the effect actomyosin fiber orientation has on hysteresis. (A and B) Uniaxial-axial stretch model predictions for fiber concentration factor values . (A) Axial stresses (Px) due to applied axial strain (λx). (B) Transverse stresses (Py) due to off-axis strain (λy). Solid lines represent loading stresses. Dashed lines represent unloading stresses. (C and D) Uniaxial-axial stretch model predictions for fiber concentration factor values . (C) Transverse stresses (Py) due to applied axial strain (λy). (D) Axial stresses (Px) due to off-axis strain (λx). Solid lines represent loading stresses. Dashed lines represent unloading stresses. To see this figure in color, go online.
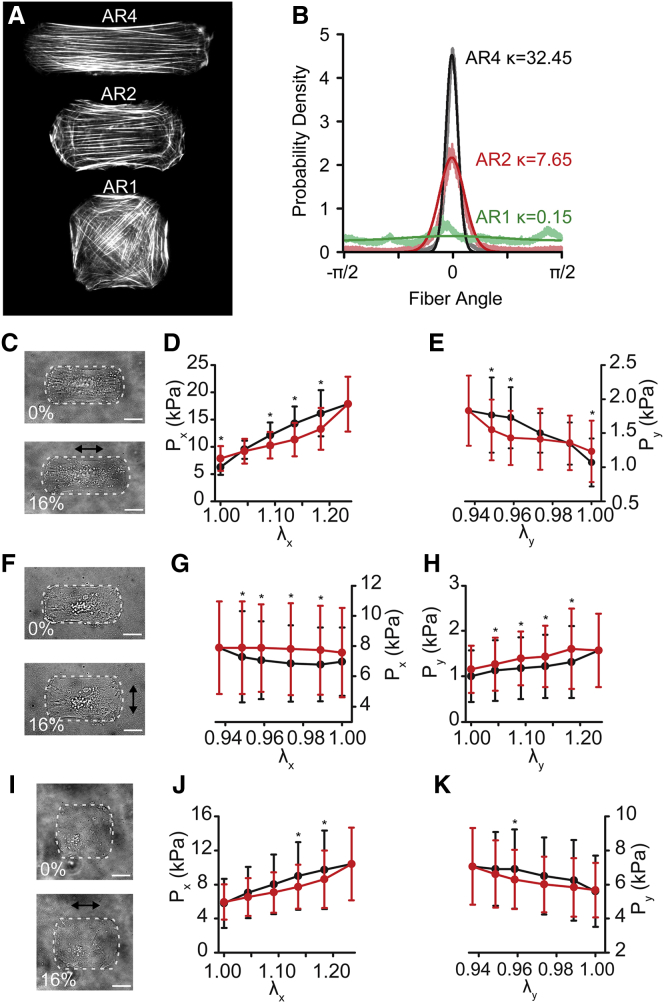
Finally, cells were micropatterned with 2:1 and 1:1 ARs (AR2, AR1) but identical spread areas (Fig. 7 A), which has been previously shown to result in more isotropic cytoskeletal alignment (23). F-actin fiber distributions were measured from confocal imaging and characterized by von Mises distributions (Fig. 7 B). When stretched using uniaxial-axial (Fig. 7 C) and uniaxial-transverse (Fig. 7 F) protocols, the stress-strain behavior and stress magnitudes closely matched those predicted by the model. AR2 cells were similar to AR4 cells with dissipative hysteresis for uniaxial-axial stretch (Fig. 7, D and E) and reverse hysteresis for uniaxial transverse stretch (Fig. 7, G and H). Uniaxial stretching performed on the nearly isotropic AR1 cell (Fig. 7 I) showed normal dissipative hysteresis, independent of stretch direction, consistent with model predictions (Fig. 7, J and K). These data demonstrate that hysteresis anisotropy is cell-architecture dependent.
Figure 7.
Cellular architecture mediates hysteresis anisotropy. (A) F-actin immunofluorescent images of cells micropatterned with ARS of 4 (AR4), 2 (AR2), and 1 (AR1). (B) Measured fiber distribution (translucent lines) and von Mises distribution fits (solid lines). (C–E) AR2 uniaxial-axial stretch. (C) A bright-field image of a representative cell outlined in white. (D and E) Axial (Px) and transverse (Py) PK1 stress. (F–H) AR2 uniaxial-transverse stretch. (F) A bright-field image of a representative cell outlined in white. (G and H) Axial (Px) and transverse (Py) PK1 stress. (I–K) AR1 uniaxial-axial stretch. (I) A bright-field image of a representative cell outlined in white. (J and K) Axial (Px) and transverse (Py) PK1 stress. All graphs show mean ± SD (n = 10). ∗p < 0.05. All scale bars, 20 μm. To see this figure in color, go online.
Discussion
It is increasingly clear that mechanical forces play an important role in the regulation of cellular function. Thus, it is important to understand how cell stresses relate to cell deformations, particularly in mechanically dynamic tissues like arteries. Here, using CμBS microscopy (23), we investigated loading and unloading dynamics of individual VSMCs exposed to large-strain biaxial stretching. Previous studies found that a cell’s time-dependent mechanical properties are dependent on both strain magnitude (17) and strain rate (35). Our study found that VSMCs with in-vivo-like architecture have markedly different hysteresis behavior under different loading regimes. Most notably, when stretched transverse to primary fiber alignment, VSMCs exhibited reverse hysteresis, with unloading stresses greater than loading stresses, suggestive of energy gain. To our knowledge, this reverse hysteresis has not been measured or characterized previously. We also found that this phenomenon was particular to anisotropic cells. The reverse hysteresis was not captured by a standard QLV model but was well described by a Hill-type active fiber model, suggesting that viscoelastic models are insufficient for modeling highly structured cells, like muscle cells, under complex loading and that contractile behavior is important for describing the constitutive behavior of cells.
The source of the observed reverse hysteresis can be inferred from the Hill-type active fiber model. In the model, we assume that all fibers are at a homeostatic stress , or stall force, before stretch. When a fiber is stretched, its stress rises above , and the fiber relaxes by altering its zero-stress configuration. Conversely, when a fiber is compressed, it contracts, raising the fiber’s tension. In highly anisotropic cells, even the fibers that provide tension in the cell’s short axis are primarily aligned with the cell’s long axis. Thus, when the cell is stretched transversely and shortens somewhat axially, these fibers contract, increasing the cell stress in both directions. In smooth muscle, contraction and relaxation are slow (28), so the fiber tension does not reestablish homeostasis in the time over which the experiment was performed, thus the fiber tension remains elevated and the unloading stress is greater than the loading stress. These results demonstrate that simple isotropic models of cell properties can miss subtle but physiologically important phenomena.
There are several limitations in our measurement of viscoelastic properties. In vivo strain rates for arteries occur on the scale of 0.25–3%/s (36, 37), whereas in the experiment, because of temporal limitations during imaging, we perform a slower stretch, taking into account stretching and imaging time, of <0.1%/s (0.5%/s during actual stretch). In addition, tissues in vivo are often exposed to continuous cyclic stretch, and in vitro studies have shown tissue properties are influenced by mechanical conditioning (38, 39, 40). Cell function can also be significantly altered by cyclic stretch (41, 42). We perform two conditioning stretches before the measured stretches and previously showed VSMCs do not exhibit a change in traction forces after four cycles of axial stretch (23) but did not investigate the ability of the cells to adapt to cyclic stretch or further conditioning stretches. In the model, we treat the cell as a bulk neo-Hookean matrix with discrete actomyosin fibers oriented with a defined distribution, but we neglect other cellular components such as the nucleus and other cytoskeletal filaments like microtubules and intermediate filaments (43, 44, 45, 46). Although these other structures undoubtedly contribute to the cell’s mechanical properties, the HA-1077 studies inhibiting actomyosin contractility eliminate nearly all tension in the cell, so we believe assuming actin fibers are the primary cytoskeletal filament is a reasonable first approximation.
Several other investigators have used Hill-type fiber contraction in models aiming to explain cytoskeletal self-organization, cell spreading, and durotaxis (29, 30, 31, 47, 48, 49). These models include both focal adhesion and cytoskeletal kinetics. Here, because our experiments take place over a relatively short time period, we have ignored both. Cytoskeletal remodeling acts in concert with contraction to modulate the stress fiber mechanics and could contribute to the temporal changes in cell stress that we observed. It is possible that these more sophisticated models can better describe the dynamics of the cell and provide more detailed insight into the mechanisms of our experimentally observed hysteresis behavior.
Finally, the large-strain mechanics of whole arteries are well characterized (50, 51), but modern biomechanical models such as constrained mixture models (52, 53) require a firm understanding of the mechanical properties of each component of tissues, including the cells. Mechanics of individual cells have been studied using a variety of tools including but not limited to micropipette aspiration, microrheology, magnetic bead twisting, atomic force microscopy, optical tweezers, and microfluidics (54, 55, 56). These measurements normally yield parameters for isotropic linear materials. Our results suggest linear isotropic properties and simple viscoelastic models are insufficient for describing cells under complex loads. Moreover, it is well known that cell function is influenced by applied loading (41, 42, 57, 58). Our results suggest that the relationship between applied deformation and mechano-adaptation is more complex in highly structured cells in tissues than isotropic descriptions of cells might suggest. These findings are particularly notable in the development of mixture models of vascular mechano-adaptation, which have potential clinical applications predicting, for example, aneurysm growth and rupture (59, 60). Cells in bifurcations or in aneurysms are necessarily exposed to complex loads (60, 61), and models that can capture the anisotropic time-dependent and architecture-dependent material behavior of the cells will be more accurate.
Author Contributions
Z.W. and P.W.A. designed the research and analysis. Z.W. and J.M.B. performed the research and analysis. Z.W. and P.W.A. wrote the article.
Acknowledgments
We acknowledge financial support from the US National Science Foundation (CMMI 1553255 (P.W.A.)), American Heart Association (13SDG14670062 (P.W.A); 16PRE27770112 (Z.W.)), and the University of Minnesota Doctoral Dissertation Fellowship (Z.W.). Parts of this work were carried out in the University Imaging Centers at the University of Minnesota and the Minnesota Nano Center, which receives partial support from the US National Science Foundation through the National Nanotechnology Infrastructure Network program.
Editor: Kinneret Keren.
Footnotes
Supporting Materials and Methods, five figures, and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)31109-3.
Supporting Material
References
- 1.Marwick T.H. Measurement of strain and strain rate by echocardiography: ready for prime time? J. Am. Coll. Cardiol. 2006;47:1313–1327. doi: 10.1016/j.jacc.2005.11.063. [DOI] [PubMed] [Google Scholar]
- 2.Villablanca J.P., Duckwiler G.R., Vinuela F.V. Natural history of asymptomatic unruptured cerebral aneurysms evaluated at CT angiography: growth and rupture incidence and correlation with epidemiologic risk factors. Radiology. 2013;269:258–265. doi: 10.1148/radiol.13121188. [DOI] [PubMed] [Google Scholar]
- 3.Trepat X., Wasserman M.R., Fredberg J.J. Physical forces during collective cell migration. Nat. Phys. 2009;5:426–430. [Google Scholar]
- 4.Shyer A.E., Tallinen T., Mahadevan L. Villification: how the gut gets its villi. Science. 2013;342:212–218. doi: 10.1126/science.1238842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Boothe S.D., Myers J.D., Jacot J.G. The effect of substrate stiffness on cardiomyocyte action potentials. Cell Biochem. Biophys. 2016;74:527–535. doi: 10.1007/s12013-016-0758-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Varner V.D., Gleghorn J.P., Nelson C.M. Mechanically patterning the embryonic airway epithelium. Proc. Natl. Acad. Sci. USA. 2015;112:9230–9235. doi: 10.1073/pnas.1504102112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Du J., Zu Y., Yang C. Extracellular matrix stiffness dictates Wnt expression through integrin pathway. Sci. Rep. 2016;6:20395. doi: 10.1038/srep20395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Alam S.G., Zhang Q., Lele T.P. The mammalian LINC complex regulates genome transcriptional responses to substrate rigidity. Sci. Rep. 2016;6:38063. doi: 10.1038/srep38063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yerrapureddy A., Tobias J., Margulies S.S. Cyclic stretch magnitude and duration affect rat alveolar epithelial gene expression. Cell. Physiol. Biochem. 2010;25:113–122. doi: 10.1159/000272056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chiu C.Z., Wang B.W., Shyu K.G. Effects of cyclic stretch on the molecular regulation of myocardin in rat aortic vascular smooth muscle cells. J. Biomed. Sci. 2013;20:50. doi: 10.1186/1423-0127-20-50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hemphill M.A., Dabiri B.E., Parker K.K. A possible role for integrin signaling in diffuse axonal injury. PLoS One. 2011;6:e22899. doi: 10.1371/journal.pone.0022899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ray A., Lee O., Provenzano P.P. Anisotropic forces from spatially constrained focal adhesions mediate contact guidance directed cell migration. Nat. Commun. 2017;8:14923. doi: 10.1038/ncomms14923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Provenzano P.P., Eliceiri K.W., Keely P.J. Collagen reorganization at the tumor-stromal interface facilitates local invasion. BMC Med. 2006;4:38. doi: 10.1186/1741-7015-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Taber L.A. World Scientific Pub Co Inc; London, UK: 2004. Nonlinear Theory of Elasticity: Applications in Biomechanics. [Google Scholar]
- 15.Weng S., Shao Y., Fu J. Mechanosensitive subcellular rheostasis drives emergent single-cell mechanical homeostasis. Nat. Mater. 2016;15:961–967. doi: 10.1038/nmat4654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Steucke K.E., Win Z., Alford P.W. Empirically determined vascular smooth muscle cell mechano-adaptation law. J. Biomech. Eng. 2017;139:071005. doi: 10.1115/1.4036454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Trepat X., Grabulosa M., Farré R. Viscoelasticity of human alveolar epithelial cells subjected to stretch. Am. J. Physiol. Lung Cell. Mol. Physiol. 2004;287:L1025–L1034. doi: 10.1152/ajplung.00077.2004. [DOI] [PubMed] [Google Scholar]
- 18.Wang N. Review of cellular mechanotransduction. J. Phys. D Appl. Phys. 2017;50:233003. doi: 10.1088/1361-6463/aa6e18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hecht F.M., Rheinlaender J., Schäffer T.E. Imaging viscoelastic properties of live cells by AFM: power-law rheology on the nanoscale. Soft Matter. 2015;11:4584–4591. doi: 10.1039/c4sm02718c. [DOI] [PubMed] [Google Scholar]
- 20.Karcher H., Lammerding J., Kaazempur-Mofrad M.R. A three-dimensional viscoelastic model for cell deformation with experimental verification. Biophys. J. 2003;85:3336–3349. doi: 10.1016/S0006-3495(03)74753-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bausch A.R., Möller W., Sackmann E. Measurement of local viscoelasticity and forces in living cells by magnetic tweezers. Biophys. J. 1999;76:573–579. doi: 10.1016/S0006-3495(99)77225-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Puig-De-Morales M., Grabulosa M., Navajas D. Measurement of cell microrheology by magnetic twisting cytometry with frequency domain demodulation. J. Appl. Physiol. (1985) 2001;91:1152–1159. doi: 10.1152/jappl.2001.91.3.1152. [DOI] [PubMed] [Google Scholar]
- 23.Win Z., Buksa J.M., Alford P.W. Cellular microbiaxial stretching to measure a single-cell strain energy density function. J. Biomech. Eng. 2017;139:071006. doi: 10.1115/1.4036440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Han M., Wen J.K., Zhang C. Serum deprivation results in redifferentiation of human umbilical vascular smooth muscle cells. Am. J. Physiol. Cell Physiol. 2006;291:C50–C58. doi: 10.1152/ajpcell.00524.2005. [DOI] [PubMed] [Google Scholar]
- 25.Tseng Q., Duchemin-Pelletier E., Théry M. Spatial organization of the extracellular matrix regulates cell-cell junction positioning. Proc. Natl. Acad. Sci. USA. 2012;109:1506–1511. doi: 10.1073/pnas.1106377109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fung Y.C. Springer-Verlag; New York: 1993. Biomechanics: mechanical properties of living tissues. [Google Scholar]
- 27.Hill A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. B Biol. Sci. 1938;126:136–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
- 28.Seow C.Y. FriesenPress; Victoria, BC, Canada: 2016. Introduction to Smooth Muscle Mechanics. [Google Scholar]
- 29.Chan C.E., Odde D.J. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 30.Bangasser B.L., Shamsan G.A., Odde D.J. Shifting the optimal stiffness for cell migration. Nat. Commun. 2017;8:15313. doi: 10.1038/ncomms15313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Deshpande V.S., McMeeking R.M., Evans A.G. A bio-chemo-mechanical model for cell contractility. Proc. Natl. Acad. Sci. USA. 2006;103:14015–14020. doi: 10.1073/pnas.0605837103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ushiwata I., Ushiki T. Cytoarchitecture of the smooth muscles and pericytes of rat cerebral blood vessels. A scanning electron microscopic study. J. Neurosurg. 1990;73:82–90. doi: 10.3171/jns.1990.73.1.0082. [DOI] [PubMed] [Google Scholar]
- 33.Krizmanich W.J., Lee R.M. Scanning electron microscopy of vascular smooth muscle cells from rat muscular arteries. Scanning Microsc. 1987;1:1749–1758. [PubMed] [Google Scholar]
- 34.Mérei F.T., Gallyas F. Role of the structural elements of the arterial wall in the formation and growth of intracranial saccular aneurysms. Neurol. Res. 1980;2:283–303. doi: 10.1080/01616412.1980.11739584. [DOI] [PubMed] [Google Scholar]
- 35.Webster K.D., Ng W.P., Fletcher D.A. Tensional homeostasis in single fibroblasts. Biophys. J. 2014;107:146–155. doi: 10.1016/j.bpj.2014.04.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wan J., He F., Wan M. Non-invasive vascular radial/circumferential strain imaging and wall shear rate estimation using video images of diagnostic ultrasound. Ultrasound Med. Biol. 2014;40:622–636. doi: 10.1016/j.ultrasmedbio.2013.10.007. [DOI] [PubMed] [Google Scholar]
- 37.Teixeira R., Monteiro R., Gonçalves L. Circumferential vascular strain rate to estimate vascular load in aortic stenosis: a speckle tracking echocardiography study. Int. J. Cardiovasc. Imaging. 2015;31:681–689. doi: 10.1007/s10554-015-0597-y. [DOI] [PubMed] [Google Scholar]
- 38.Carew E.O., Barber J.E., Vesely I. Role of preconditioning and recovery time in repeated testing of aortic valve tissues: validation through quasilinear viscoelastic theory. Ann. Biomed. Eng. 2000;28:1093–1100. doi: 10.1114/1.1310221. [DOI] [PubMed] [Google Scholar]
- 39.Schatzmann L., Brunner P., Stäubli H.U. Effect of cyclic preconditioning on the tensile properties of human quadriceps tendons and patellar ligaments. Knee. Surg. Sports Traumatol. Arthrosc. 1998;6(Suppl 1):S56–S61. doi: 10.1007/s001670050224. [DOI] [PubMed] [Google Scholar]
- 40.Miller K.S., Edelstein L., Soslowsky L.J. Effect of preconditioning and stress relaxation on local collagen fiber re-alignment: inhomogeneous properties of rat supraspinatus tendon. J. Biomech. Eng. 2012;134:031007. doi: 10.1115/1.4006340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bartolák-Suki E., Imsirovic J., Suki B. Fluctuation-driven mechanotransduction regulates mitochondrial-network structure and function. Nat. Mater. 2015;14:1049–1057. doi: 10.1038/nmat4358. [DOI] [PubMed] [Google Scholar]
- 42.Balachandran K., Alford P.W., Parker K.K. Cyclic strain induces dual-mode endothelial-mesenchymal transformation of the cardiac valve. Proc. Natl. Acad. Sci. USA. 2011;108:19943–19948. doi: 10.1073/pnas.1106954108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Guilluy C., Osborne L.D., Burridge K. Isolated nuclei adapt to force and reveal a mechanotransduction pathway in the nucleus. Nat. Cell Biol. 2014;16:376–381. doi: 10.1038/ncb2927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Guilak F., Tedrow J.R., Burgkart R. Viscoelastic properties of the cell nucleus. Biochem. Biophys. Res. Commun. 2000;269:781–786. doi: 10.1006/bbrc.2000.2360. [DOI] [PubMed] [Google Scholar]
- 45.Yamamoto S., Tsutsui H., Takeshita A. Role of microtubules in the viscoelastic properties of isolated cardiac muscle. J. Mol. Cell. Cardiol. 1998;30:1841–1853. doi: 10.1006/jmcc.1998.0747. [DOI] [PubMed] [Google Scholar]
- 46.Lin Y.-C., Koenderink G.H., Weitz D.A. Viscoelastic properties of microtubule networks. Macromolecules. 2007;40:7714–7720. [Google Scholar]
- 47.Pathak A., Deshpande V.S., Evans A.G. The simulation of stress fibre and focal adhesion development in cells on patterned substrates. J. R. Soc. Interface. 2008;5:507–524. doi: 10.1098/rsif.2007.1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.McEvoy E., Deshpande V.S., McGarry P. Free energy analysis of cell spreading. J. Mech. Behav. Biomed. Mater. 2017;74:283–295. doi: 10.1016/j.jmbbm.2017.06.006. [DOI] [PubMed] [Google Scholar]
- 49.McGarry J.P., Fu J., Deshpande V.S. Simulation of the contractile response of cells on an array of micro-posts. Philos. Trans. A Math. Phys. Eng. Sci. 2009;367:3477–3497. doi: 10.1098/rsta.2009.0097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Goto M., Kimoto Y. Hysteresis and stress-relaxation of the blood vessels studied by a universal tensile testing instrument. Jpn. J. Physiol. 1966;16:169–184. doi: 10.2170/jjphysiol.16.169. [DOI] [PubMed] [Google Scholar]
- 51.Wagenseil J.E., Mecham R.P. Vascular extracellular matrix and arterial mechanics. Physiol. Rev. 2009;89:957–989. doi: 10.1152/physrev.00041.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Humphrey J.D., Rajagopal K.R. A constrained mixture model for arterial adaptations to a sustained step change in blood flow. Biomech. Model. Mechanobiol. 2003;2:109–126. doi: 10.1007/s10237-003-0033-4. [DOI] [PubMed] [Google Scholar]
- 53.Alford P.W., Humphrey J.D., Taber L.A. Growth and remodeling in a thick-walled artery model: effects of spatial variations in wall constituents. Biomech. Model. Mechanobiol. 2008;7:245–262. doi: 10.1007/s10237-007-0101-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Bao G., Suresh S. Cell and molecular mechanics of biological materials. Nat. Mater. 2003;2:715–725. doi: 10.1038/nmat1001. [DOI] [PubMed] [Google Scholar]
- 55.Rosendahl P., Plak K., Guck J. Real-time fluorescence and deformability cytometry. Nat. Methods. 2018;15:355–358. doi: 10.1038/nmeth.4639. [DOI] [PubMed] [Google Scholar]
- 56.Harris A.R., Charras G.T. Experimental validation of atomic force microscopy-based cell elasticity measurements. Nanotechnology. 2011;22:345102. doi: 10.1088/0957-4484/22/34/345102. [DOI] [PubMed] [Google Scholar]
- 57.Alford P.W., Dabiri B.E., Parker K.K. Blast-induced phenotypic switching in cerebral vasospasm. Proc. Natl. Acad. Sci. USA. 2011;108:12705–12710. doi: 10.1073/pnas.1105860108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chen K., Vigliotti A., Holmes J.W. Role of boundary conditions in determining cell alignment in response to stretch. Proc. Natl. Acad. Sci. USA. 2018;115:986–991. doi: 10.1073/pnas.1715059115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Malkawi A.H., Hinchliffe R.J., Thompson M.M. Patient-specific biomechanical profiling in abdominal aortic aneurysm development and rupture. J. Vasc. Surg. 2010;52:480–488. doi: 10.1016/j.jvs.2010.01.029. [DOI] [PubMed] [Google Scholar]
- 60.Doyle B.J., Cloonan A.J., McGloughlin T.M. Identification of rupture locations in patient-specific abdominal aortic aneurysms using experimental and computational techniques. J. Biomech. 2010;43:1408–1416. doi: 10.1016/j.jbiomech.2009.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Delfino A., Stergiopulos N., Meister J.J. Residual strain effects on the stress field in a thick wall finite element model of the human carotid bifurcation. J. Biomech. 1997;30:777–786. doi: 10.1016/s0021-9290(97)00025-0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.