Piconewton Mechanical Forces Promote Neurite Growth

Abstract

Investigations over half a century have indicated that mechanical forces induce neurite growth, with neurites elongating at a rate of 0.1–0.3 μm h⁻¹ pN⁻¹ when mechanical force exceeds a threshold, with this being identified as 400–1000 pN for neurites of PC12 cells. In this article, we demonstrate that neurite elongation of PC12 cells proceeds at the same previously identified rate on application of mechanical tension of ∼1 pN, which is significantly lower than the force generated in vivo by axons and growth cones. This observation raises the possibility that mechanical tension may act as an endogenous signal used by neurons for promoting neurite elongation.

Introduction

With body mass growth in humans and large animals, the distance between the neuronal cell body (soma) and its cellular target increases, imposing stretch on neurites. Paul Weiss in 1941 hypothesized that the tensile force originating from this growth-induced stretch could be a signal that causes neurites to lengthen. Currently, it is widely accepted that neurites elongate when mechanical tension exceeds a threshold, the process being referred as “stretch growth” (1, 2, 3). The elongation rate was found to be very similar for both the central and peripheral nervous system (0.1–0.3 μm h⁻¹ pN⁻¹) (4, 5, 6), but various thresholds have been identified. A force threshold for elongation of ∼1 nN has been reported for neurites of PC12 cells (7) and for chick sensory neurons (6) elongated by the pulling force generated by glass microneedles and 15–100 pN in neurites of chick forebrain neurons (5) elongated by the magnetic force induced by magnetic microbeads.

Traditionally, mass addition during neurite growth was thought to occur at the leading edge, the growth cone. However, in stretch growth, mass addition occurs at any site of increased tension, e.g., at the tip when the growth cone is pulled or along the whole neurite length when the entire neurite is stretched (8, 9, 10). Indeed, neurons can regulate neurite elongation at sites other than the growth cone (11). The “stretch-growth model” was formulated on these reported observations (1). This model postulates that mechanical tension may act akin to a second messenger as a regulator of neurite initiation and elongation, being driven by tension independent of its origin, i.e., from the traction exerted by the growth cone, the mass body growth, or an external applied force. Large growth cones generate tensile forces in neurons (12), and tip growth may be regarded as a special case of stretch growth in which the growth cone is responsible for creating the tension required for neurite elongation and mass addition occurs at the tip where this tension is localized (13). Recently, it has been also recognized that force generation at the growth cone is downstream to many signaling cascades activated by neurotrophic factors, such as netrin-1 (14) and nerve growth factor (NGF) (15).

However, there are some issues concerning stretch growth as a realistic basis for a unified model of neurite growth, the most important being the established threshold. In particular, it has been reported that neurites of PC12 cells exhibit a transient elongation referred to as viscoelastic deformation when the applied tension is less than 0.4–1 nN (16, 17); in contrast, long-term extension resulting in growth is observed when the applied tension is above 0.4–1 nN. However, some studies have reported tensions of the order of 300–400 pN along PC12 neurites cultured in vitro (17), suggesting that the mechanical tension created at the growth cone is insufficient to trigger stretch growth. Similar considerations apply equally to central and peripheral nervous system neurons (18).

This study assumed that the experimental approaches used in the past to identify the threshold for stretch growth were methodologically suspect. In fact, the low detection limit (100 pN for glass microneedles and 15 pN for magnetic microbeads) together with the short observation periods (1 h or less) used in previous studies were likely inadequate for studies on the effect of pN forces. On this premise, our study aimed to investigate the effect of extremely low forces with a noncontact experimental setup based on the use of magnetic iron oxide nanoparticles (MNPs) to generate local forces under the action of external direct current magnetic fields.

Materials and Methods

Magnetic nanoparticles

MNPs used in this study are polyethyleneimine (25 kDa) Fe₃O₄ nanoparticles, which we have extensively characterized elsewhere (19). According to our previous characterization (19), we used the following data for the mathematical model: size 25 nm, saturation magnetization 58 A m² kg and density 5 × 10³ kg m³.

Cell cultures

Rat pheochromocytoma PC12 cells obtained from American Type Culture Collection (ATCC, Manassas, VA) were cultured in Dulbecco’s modified Eagle’s medium with 10% horse serum, 5% fetal bovine serum (FBS), 100 IU mL⁻¹ penicillin, 100 μg mL⁻¹ streptomycin, and 2 mM L-glutamine. Cells were cultured in petri dishes coated with poly-l-lysine (PLL, P1274; Sigma, St. Louis, MO) and maintained at 37°C in a saturated humidity atmosphere of 95% air and 5% CO₂. For cell differentiation, PC12 cells were incubated in serum-reduced media (1% FBS) supplemented with 100 ng mL⁻¹ NGF. Experiments were performed at low density, i.e., 2.5 × 10⁴ cells per cm². Cells were used at passages 6–12.

The human neuroblastoma SH-SY5Y cell line obtained from ATCC was cultured in Dulbecco’s modified Eagle’s medium with 10% FBS, 100 IU/mL penicillin, 100 μg/mL streptomycin, and 2 mM L-glutamine. For cell differentiation, SH-SY5Y cells were incubated for 5 days in a cell growth medium modified with 10 μM retinoic acid. Experiments were performed at low density, i.e., 0.5 × 10⁴ cells per cm².

Microscopy and digital image acquisitions were carried out with an Olympus 1X71/1X51 inverted microscope (Olympus, Tokyo, Japan).

Cell uptake

The amount of MNPs in cells was quantified by using the thiocyanate assay according to a protocol we published previously (19). Briefly, cell pellet was resuspended in 50 μL of a solution of 6 M HCl:65% HNO₃ v/v and incubated at 60°C for 1 h. The sample was water diluted 1:10, an equal volume of 1.5 M KSCN was added, and absorbance was recorded at 478 nm. The calibration curve was y = 0.0172x + 0.0015 (R² = 1), where y is the absorbance at 478 nm and x is the amount of MNPs (μg).

Cell viability

Cells were incubated for 72 h with MNPs. Thereafter, cells were incubated with 1 μM Hoechst for 10 min at 37°C and with 10 μg mL⁻¹ propidium iodide for an additional 5 min at 37°C. For each sample, the number of necrotic and pyknotic cells was counted on a random population of 1000 cells. For the evaluation of the cell doubling time, cells were removed by trypsinization after 48 h (t₀) or 96 h (t₁) of incubation with the particles and counted in a Burker’s chamber. Cell doubling time (T_d) was calculated by using the following formula: T_d = (t₁ − t₀) × ln(2)/ln(q₁/q₀), with q₀ and q₁ the cell number at times t₀ and t₁, respectively.

Magnetic field

Experiments were carried out in 35 mm petri dishes placed inside a Halbach-like cylinder magnetic applicator, which provided a constant magnetic field gradient of 46.5 T m⁻¹ in the radial centrifugal direction (20).

Stretching assay

PC12 cells were seeded in 35 mm dishes precoated with 1 μg mL⁻¹ PLL. Cells were differentiated with 10 μg mL⁻¹ MNP modified differentiation media (MNP⁺ groups) or differentiation media (MNP⁻ groups). 24 h after the induction of differentiation, the petri dish (M⁺ groups) was put inside the magnetic applicator. Morphological analysis was performed by using the image analysis software “Image J” (http://rsb.info.nih.gov/ij/) (21). Neurite length l was evaluated by using the plugin “Neuron J” (22), and 200 neurites were analyzed from 10× magnification images (randomly acquired). For the analysis, a cutoff of 10 μm in length was fixed, and neurites in networks were excluded. The longest path was measured for branched neurites. For neurite thickness, a population of 50 neurites was analyzed from 20× magnification images (randomly acquired). For each neurite, the thickness s was calculated as s = A/l, A being the neurite area that was precisely calculated from images after threshold normalization, binary conversion, and elimination of elements with size below the cutoff. Cell sprouting was calculated by counting the number of processes coming out from isolated cells (n = 100).

The volume of cell cytoplasm was calculated by acquiring 60× images in a population of suspended (Hoechst-stained) cells, measuring cellular and nuclear diameter (n = 25).

For stretching experiments of SH-SY5Y cell line, cells were seeded in 35 mm dishes. Cells were differentiated with 10 μg mL⁻¹ MNP-modified differentiation medium (MNP⁺ groups) or differentiation medium (MNP⁻ groups). 24 h after the induction of differentiation, the petri dish (M⁺ groups) was put inside the magnetic applicator. Analysis was performed as described for PC12 cell line.

RNaseq

For RNA sequencing (RNaseq) experiments, we analyzed three independent samples for stretched versus nonstretched condition. The stretched condition was M⁺MNP⁺, the nonstretched condition M⁻MNP⁺. Cells (passage 6) were treated as described in the previous section (stretching assay). 9 h after the application of the magnetic field, samples were chilled in liquid N2, and the RNA was extracted with RNeasy Kit (Qiagen, Hilden, Germany) according to the manufacturer’s instructions. Quality check was performed (RNA integrity number = 10). RNaseq was performed with the platform Illumina NextSeq500. The RNA library was prepared by using the polyA selection library and sequencing mode PE (paired end) 2 × 75 bp, 25–40 M. RNaseq and data analysis were performed at Glasgow Polyomics, Glasgow, UK by cutadapt 1.9.dev3 kallisto 0.43.0 software. The total numbers of reads were 34,606,835, 33,380,728, and 37,331,599 for replicates 1–3, nonstretched condition, and 35,040,903, 40,205,222, and 36,103,108 for replicates 1–3, stretched condition. No poor-quality sequences were identified in any sample. The number of protein-coding genes detected in samples was 15,350, and analysis confirmed the presence of genes (Table S1) known to be expressed in NGF-differentiated PC12 cells (23). Data are deposited in the Gene Expression Omnibus repository (GSE115474 study).

Electron microscopy

SEM/focused ion beam (FIB) cross-sectioned cells were performed using scanning electron microscopy (SEM INSPECT F50; FEI, Hillsboro, OR) and dual-beam FIB/SEM (Nova 200 NanoLab; FEI). PC12 cells were grown on coverslips coated with PLL and treated with MNPs (10 μg mL⁻¹). After 24 h of incubation, the cells were washed with phosphate-buffered saline, fixed, and dehydrated. After drying, the samples were coated with 30 nm of gold. SEM images were taken at 5 and 30 kV with a field emission gun column, and a combined Ga-based 30 kV (10 pA) ion beam was used to cross-section single cells. These investigations were completed by energy dispersive x-ray analysis (EDX) for chemical analysis.

Statistical analysis

Data were plotted with GraphPad Software, version 6.0. Values are reported as the mean ± standard error. Data distributions were analyzed by Kolmogorov-Smirnov test. Statistical significance was assessed by one-way analysis of variance. Specifically, for non-normal data distribution, we used Kruskal-Wallis analysis, followed by multicompare analysis (95% confidence), whereas for normal data distributions, we used t-test or analysis of variance followed by Bonferroni correction. Significance was set at p ≤ 0.05. Statistical analysis was performed in MATLAB R14 workspace (functions “test2,” “kstest,” “anova1,” “bonferroni,” “multicompare”) (The Mathworks, Natick, MA) or with GraphPad Software, version 6.0.

Results and Discussion

MNPs can be safely administered to neuronal cells to apply mechanical forces

We have previously confirmed the biocompatibility of MNPs in various neuronal cell lines, primary neurons, and organotypic neuronal cultures (19, 20, 24, 25, 26). In this study, MNPs were tested to exclude any batch-dependent toxicity. Dose-response assays confirm that particles can be safely administered to the cells (Fig. S1) and all experiments were performed by using the lowest concentration tested, i.e., 10 μg mL⁻¹.

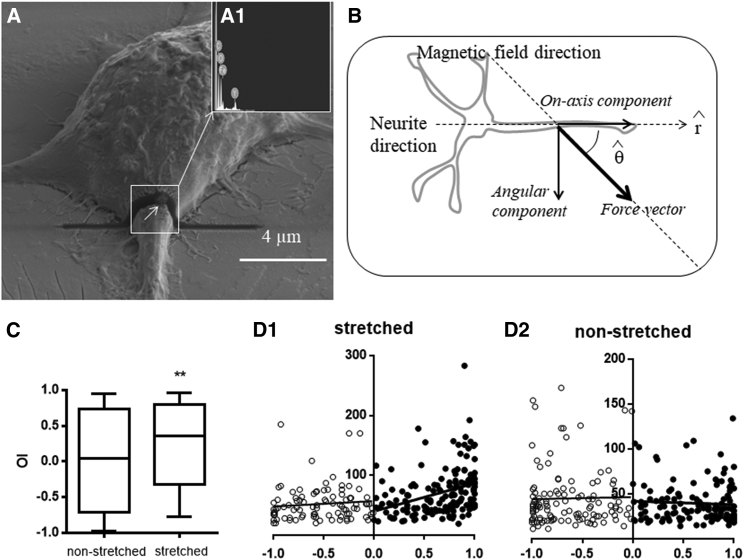
We have also extensively characterized cell-particle interactions by electron microscopy. MNPs usually stick to the cell surface as a first step (19, 20, 25). Subsequently, they are avidly internalized by the cells, and the agglomerates occupy the intracellular space. Microanalysis performed on cross-sectioned cells confirmed the particle localization within cell cytoplasm. MNPs were found to be abundant in cell neurites (Fig. 1 A), in agreement with our previous observations (20). MNPs appear as electron-dense spots (white arrows), and the iron content is confirmed by microanalysis (Fig. 1 A1). In a previous study, we demonstrated that the forces developed by MNPs entrapped in neurites, under the effect of magnetic fields, can be used to manipulate the neurites of differentiated PC12 cells (20). In fact, the MNPs entrapped in the neurites exert a force vector when exposed to an external magnetic field (Fig. 1 B): the angular component $\hat{\theta }$, being responsible for rotating the neurite, can be used for developing a tangential force against the neurite, which deviates in response to this force and preferentially aligns its direction of growth to the direction of the force vector (20) (Fig. 1 C); the on-axis component $\hat{r}$ can be used for stretching the neurite. In this study, we calculated the correlation between the neurite length and the orientation index (OI) by regression analysis. For the stretched condition, when the angle $\hat{\theta }$ is acute (i.e., positive OI), the more the neurite is aligned to the force vector, the higher the neurite lengthening is (p < 0.0001) because this is accompanied by the increase of the on-axis component of the force vector; when the angle $\hat{\theta }$ is obtuse (i.e., negative OI), neurite length is constant (the curve slope does not significantly deviate from 0, p = 0.35) (Fig. 1 C1). This suggests that the on-axis component should be positive (i.e., oriented from soma to tip) for productive neurite elongation. As expected, in the nonstretched condition, neurite length is constant with respect to both positive and negative OI (the curve slope does not significantly deviate from 0, p = 0.37 and p = 0.06, respectively). In this study, the on-axis component of force vector generated by MNPs in response to static magnetic fields was used for stretching the neurites (Fig. 1 B). For MNP labeling, we used two different procedures corresponding to the amounts 3.45 or 4.85 pg of MNPs per cell. The amount of MNP per cell was extrapolated by dose-response assays, which showed excellent data correlation (Fig. S2).

Figure 1.

Force generation in the neurite by MNP labeling. (A) SEM imaging and SEM-FIB dual-beam cross section of a differentiated MNP-labeled PC12 cell. A cross section of a neurite showing electron-dense nanoparticles (pointed out by white arrow) that contain iron (inset A1, EDX), n = 6, is shown. (B) The MNPs entrapped in the neurite exert a magnetic force under the effect of an external magnetic field: the on-axis component $\hat{r}$ along the neurite axis is responsible for stretching the neurite, and the angular component $\hat{\theta }$ is responsible for rotating the neurite. (C) A box plot of orientation index (OI = cosθ) in stretched versus nonstretched condition (t-test, p = 0.006). Stretched neurites are preferentially aligned to the force vector, in agreement to our previous observations (20) (D) Neurite length (μm) versus OI. (D1) Stretched condition: the longest neurites are preferentially aligned to the force vector for positive OI (the linear regression analysis gives a slope of 46.72 ± 10.33, whose deviation from 0 is statistically significant, p < 0.0001); the neurite length is not dependent on the force vector direction for negative OI (i.e., the deviation of the slope from 0 is not statistically significant, p = 0.35). (C2) Nonstretched condition: neurite length is constant for both positive OI (i.e., the deviation of the slope from 0 is not statistically significant, p = 0.37) and negative OI (i.e., the deviation of the slope from 0 is not statistically significant, p = 0.06). n = 200. Stretched and nonstretched conditions are M⁺MNP⁺ and M⁻MNP⁺, respectively.

Generation of a pN force along the neurite axis

The experimental setup used in this study was designed specifically to apply a constant force to each MNP in any point of the petri dish with a radial centrifugal direction (20). The only non-null component of the magnetic field gradient in the dish is thus the radial one (dB/dr = 46.5 T m⁻¹). As the particles used have a saturation magnetization M_s of 58 A m² kg⁻¹ and a coercive field H_c of 4.81 k A m⁻¹ (19), we can assume that particle magnetization saturated and the magnetic force acting on the single particle is given by

$$\text{F}=m_s\frac{dB}{dr}=\rho V{M}_s\frac{\text{dB}}{dr},$$ (1)

where ρ is the particle density and V the particle volume. The resulting force F acting on the single particle is 1.1 × 10⁻¹⁶ N. The mechanical force acting on the neurite thus depends on the number of particles inside the neurite. We made the simplest assumption that particles have a uniform distribution in cell cytoplasm, included the neurite. This assumption is strongly supported by SEM/FIB/EDX analysis, which revealed the presence of Fe in any cell sections, excluded the fractions occupied by nucleus (20). Indeed, the force F_neur acting on the single neurite can be approximated by

$$F_{\text{neur}}=\text{n}\left(\frac{V_{\text{neur}}}{V_{\text{cyt}}}\right)F,$$ (2)

where n, V_neur, and V_cyt are the number of particles in the cell, the neurite volume, and the whole cytoplasm volume, respectively.

In a local polar coordinate system, in which the on-axis coordinate $\hat{r}$ is the neurite direction and the angular coordinate is $\hat{\theta }$ (Fig. 1 B), the on-axis component of the force vector is ${\text{F}}_{\text{neur}}^{\text{r}}=F_{\text{neur}}\cos \mathit{\theta }$. In agreement with our experimental observations (Fig. 1 C), we assume that this component is able to stretch the neurite only if oriented from soma to tip (i.e., when the angle θ is acute, corresponding to positive OI). This study has been performed with a statistical approach querying a neurite population (n = 200). In this context, the mean on-axis force acting on the neurite productive for elongation $\left({\overline{F}}_{\text{on}-\text{axis}}\right)$ was considered:

$${\overline{F}}_{\text{on}-\text{axis}}=\overline{F_{\text{neur}}\cos \text{θ}}\sim \frac{2}{\text{π}}\overline{F_{\text{neur}}},\mathrm{whe}n-\frac{\pi }{2}<\theta <\frac{\pi }{2}$$ (3)

and

$${\overline{F}}_{\text{on}-\text{axis}}=0,\mathrm{when}\frac{\pi }{2}<\theta <\frac{3\pi }{2}.$$ (4)

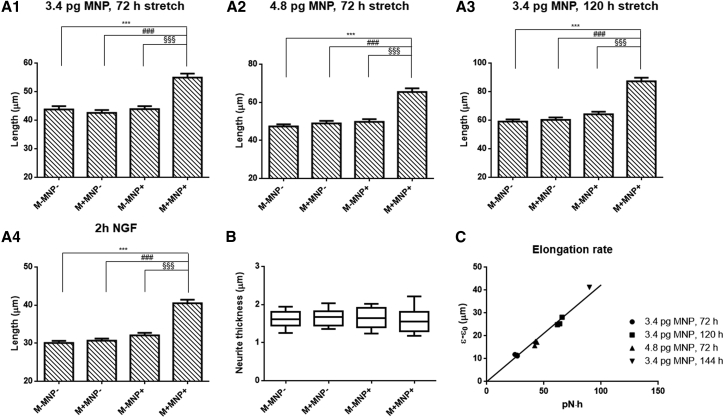
All parameters in Eqs. 1, 2, and 3 have been evaluated experimentally or extrapolated by experimental data. Specifically, the mean n has been calculated by the estimated amount of MNP per cell m (Fig. S2), the mean particle volume (8.1 × 10⁻²⁴ m³), and the mean particle weight (4.1 × 10⁻⁵ pg). V_cyt was calculated to be 542 ± 102 μm³ (n = 25). V_neu was calculated by modeling the neurite as a cylinder, being the mean length and thickness known from experimental data of Fig. 2 and Table 1.

Figure 2.

Stretching of PC12 cell neurites by pN forces tested at different stretching times and different MNP loads. (A1–4) Neurite length for stretching conditions “3.4 pg MNP, 72 h,” “3.4 pg MNP, 120 h,” “4.8 pg MNP, 72 h” and “2 h NGF,” respectively. n = 600 (from three independent assays). Kruskal Wallis test, followed by honestly significant difference (HDS) correction: p = 9.3 × 10⁻²⁰ (A1), p = 1.9 × 10⁻²⁰ (A2), p = 8.0 × 10⁻²⁵ (A3), and p = 7.5 × 10⁻³¹ (A4). “^∗” is the significance versus the control group (M⁻MNP⁻), “#” is the significance versus the group treated with the magnet (M⁺MNP⁻), and “§”is the significance versus the group treated with particles (M⁻MNP⁺). (B) A box plot (10–90 percentile) of neurite thickness (condition “4.8 pg MNP, 72 h”), n = 50. Kruskal Wallis test: p = 0.43. (C) Differential elongation versus estimated force per time. The applied force was calculated according to Eqs 3, 4, and 5. The differential elongation is expressed as the difference of elongation between the stretched and nonstretched conditions. The elongation rate (0.42 ± 0.01 μm h⁻¹ pN⁻¹) was calculated by linear regression analysis (95% of confidence level, p < 0.0001).

Table 1.

Neurite Length in μm for Each Experiment

Experiment Description	Replicate	M−MNP−	M+MNP−	M−MNP+	M+MNP+	p Value	F (pN)
3.4 pg MNP, 72 h stretch	R1	44.34 ± 2.10	44.02 ± 1.87	46.42 ± 1.69	56.45 ± 2.09∗∗∗,###, §§§	6 × 10−10	0.74
	R2	41.22 ± 1.95	39.17 ± 1.43	40.47 ± 1.60	52.13 ± 2.37∗∗∗, ###,§§§	2.6 × 10−6	0.68
	R3	45.80 ± 1.86	44.41 ± 2.00	44.75 ± 2.12	56.16 ± 2.78∗∗, ###, §§§	2.7 × 10−5	0.74
3.4 pg MNP, 120 h stretch	R1	55.82 ± 2.36	59.83 ± 3.39	63.78 ± 3.56	84.69 ± 4.37∗∗∗, §§§, ###	1.8 × 10−10	1.10
	R2	58.46 ± 2.37	62.91 ± 2.90	65.59 ± 2.73	90.47 ± 4.67∗∗∗, ###, §§	2.8 × 10−7	1.06
	R3	62.78 ± 2.82	58.04 ± 2.73	63.03 ± 2.93	86.58 ± 4.16∗∗∗, ###, §§§	1.2 × 10−8	1.03
4.8 pg MNP, 72 h stretch	R1	46.76 ± 2.12	49.38 ± 2.08	48.93 ± 2.12	64.03 ± 3.07∗∗∗,##, §§§	1.9 × 10−5	1.17
	R2	50.00 ± 1.82	47.67 ± 2.45	50.72 ± 2.39	66.66 ± 3.09∗∗, ###, §§§	5.5 × 10−8	1.19
	R3	45.21 ± 2.04	49.54 ± 2.59	49.56 ± 2.60	65.65 ± 3.53∗∗∗,##, §§	5.7 × 10−5	1.22
NGF 2 h	R1	30.38 ± 0.95	30.26 ± 0.96	30.45 ± 0.97	40.86 ± 1.60∗∗∗, ###, §§§	5.7 × 10−11	0.53
	R2	31.11 ± 1.05	32.13 ± 0.91	32.61 ± 1.18	40.29 ± 1.2∗∗∗, ##, §§§	5.8 × 10−7	0.53
	R3	28.70 ± 0.75	29.60 ± 0.94	33.02 ± 1.47	40.29 ± 1.67∗∗∗, ###, §§§	3.5 × 10−14	0.52

n = 200, Kruskal Wallis test followed by HDS correction. “^∗” is the significance versus the control group (M⁻MNP⁻), “#” is the significance versu the group treated with the magnet (M⁺MNP⁻), and “§”is the significance versus the group treated with particles (M⁻MNP⁺). F is the estimation of the mean on-axis component of force vector for positive OI.

The elongation rate e.r. was calculated by the following equation:

$$\text{e}.\text{r}.=\frac{2\mathit{\epsilon }}{{\overline{F}}_{\text{on}-\text{axis}}\cdot \text{t}},$$ (5)

ε being the differential elongation between stretched and nonstretched conditions and t the stretching time.

Based on previous assumptions, our calculation predicts that the mean on-axis component of the force vector is in the pN range (Table 1). Indeed, for the experiments, the stretching time (72–144 h) was chosen to produce neurite elongation at easily observable lengths of microns or tens of microns, in accordance with the elongation rate of 0.1–0.3 μm h⁻¹ per pN of applied force reported for PC12 cells (7).

Effects of the stretching induced by pN forces

The elongation analysis was carried on stretched cells (i.e., cells labeled with the particles and exposed to the magnetic field, hereafter labeled as M⁺MNP⁺) and on control groups, i.e., nonstretched cells treated with the same magnetic field (labeled as M⁺MNP⁻) or with the particles (labeled as M⁻MNP⁺) or untreated (labeled as M⁻MNP⁻). We tested the two doses of MNPs corresponding to the two labeling procedures (3.45 or 4.85 pg of MNPs per cell) and two stretching times (72 and 120 h). Each experiment was repeated three times, with the experiments being blinded and performed after random allocation by three different operators. Table 1 provides each experiment (n = 200) and the corresponding statistical analysis. Fig. 2 A1–3 plots overall data of three independent assays (n = 600) for each stretching condition.

In each experiment (Table 1) and under each stretching condition (Fig. 2 A1–3) tested, we found that the stretching induced by pN forces triggers a statistically highly significant increase (p < 0.01) in the length of neurites when compared to any other group, whereas the control groups (M⁻MNP⁻, M⁻MNP⁺, and M⁺MNP⁻) did not differ from each other (p > 0.05). Collectively, these observations confirm excellent experimental reproducibility. They exclude any nonspecific effect triggered by the particles or magnetic fields alone and indicate that the stretching is responsible for the length increase. Additionally, the stretching induced by pN forces was also validated in another neuron-like cell line, i.e., the human neuroblastoma SH-SY5Y cells differentiated with retinoic acid (Fig. 3), showing similar results and excluding that stretching induced by pN forces is a PC12 cell-type-specific mechanism of neurite elongation.

Figure 3.

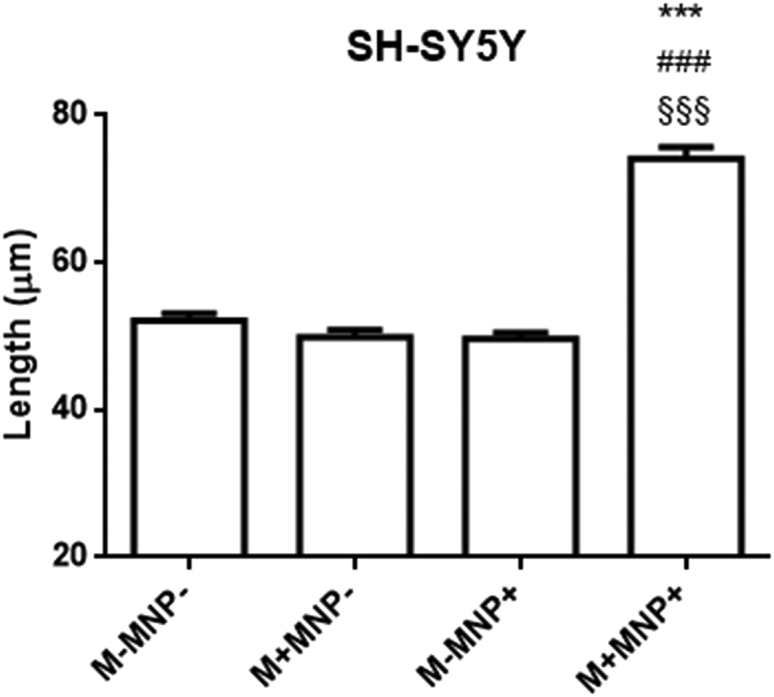
Stretching of SH-SY5Y neurites by pN forces. n = 600 (from three independent assays), Kruskal Wallis test followed by HDS correction. “^∗” is the significance versus the control group (M⁻MNP⁻), “#” is the significance versus the group treated with the magnet (M⁺MNP⁻), and “§”is the significance versus the group treated with particles (M⁻MNP⁺). p = 0.

To demonstrate that the observed length increase is not a viscoelastic deformation but genuine growth, we calculated the average thickness of neurites. The analysis was performed in the experimental condition that yielded the highest differential elongation (3.4 pg MNP, 120 h). Although the stretched neurites were 44.44 ± 3.18% longer than control groups, there was no difference in neurite thickness among all the groups (p = 0.43), indicating that the observed elongation was the result of actual growth due to mass addition (Fig. 2 B). Interestingly, the elongation rate associated with stretch growth, calculated by linear regression analysis of data obtained from 10 different experiments, was 0.42 ± 0.01 μm h⁻¹ pN⁻¹ (Fig. 2 C, p < 0.0001). It was very similar to the elongation rate calculated in previous reported studies (16, 17), in which the applied force was five orders of magnitude higher than that used in our study.

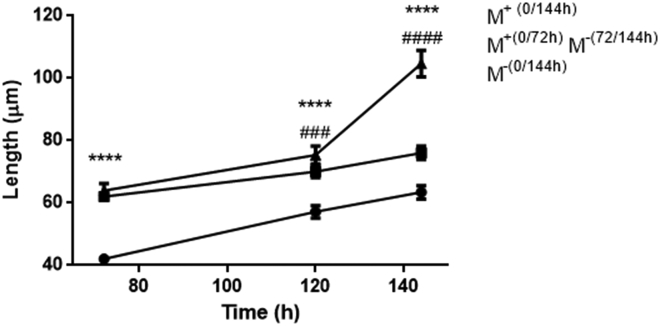
Fig. 4 compares nonstretched neurites, which elongate by tip growth, to stretched neurites, to whose elongation both stretch growth and tip growth contribute. Interestingly, when the magnet is removed after 72 h of stretch, neurites continue to elongate to the spontaneous elongation rate mediated by tip growth. Indeed, the elongation mediated by pN forces is dependent on the continuous application of force vector, and stretch growth stops when the magnetic field is removed.

Figure 4.

Neurite length (mean ± standard error) versus time. MNP-labeled differentiated PC12 cells were incubated in absence of magnetic field (M^{−(0/144 h)}), in presence of the magnetic field (M^{+(0/144 h)}) or removing the magnetic field after 72 h ((M^+(0/72h) + (M^{−(72/144 h)}). Two-way ANOVA, Bonferroni correction: n > 200, ^∗ is the significance versus the group M^{−(0/144 h)}, and # is the significance versus the group (M^{+(0/72 h)} M^{−(72/144 h)}).

We also evaluated if the stretching induced by pN forces could initiate neurite formation. Data analysis showed no difference in the number of neurites per cell among the groups. However, there is a trend of increase in the stretched samples, sometimes reaching a weak statistical significance when compared to some control groups (Table S2). We also found that the stretching induced by pN forces is not per se a signal sufficient to sustain PC12 differentiation (and neurite initiation) in absence of NGF. However, by performing a short-term exposure of the cultures to NGF (2 h incubation), stretch growth was observed in all three replicates (“NGF 2 h” and Fig. 2 A4; Table 1) and, similarly to the conditions of cells continuously exposed to NGF, the length increase was significant only for stretched neurites.

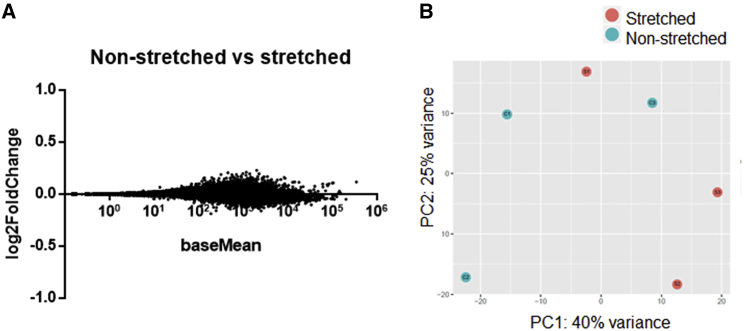
We performed RNaseq of MNP-labeled cells in stretched versus nonstretched conditions, and we did not find gene expression dysregulation (Fig. 5 A), confirming that the two samples were identical (Fig. 5 B) and excluding cytotoxicity or involvement of nuclear mechanotransduction. Indeed, local mechanisms triggered by the stretching of the MNP-labeled neurite would be responsible for neurite elongation by mass addition.

Figure 5.

(A) Logarithmic fold change of gene expression (stretched versus nonstretched condition). A value of ±1 (corresponding to a twofold increase) is typically considered a reasonable cutoff for gene dysregulation. (B) A principal component analysis plot. There is no separation between groups, which confirms that stretched and nonstretched samples are identical. The stretched condition is M⁺MNP⁺, the nonstretched condition is M⁻MNP⁺.

Conclusion

Although mechanical tension is generally recognized as a major contributor to the elongation and outgrowth of neurites, most recent theoretical models do not require the involvement of a real force threshold in stretch growth of neurites. Instead, they predict that neurite extension occurs whenever traction overcomes the cortical actomyosin contractility (27). Specifically, these models indicate that when a load Q used to stretch the neurite is below microtubule network stall force Q_μ, the neurite remains static; when Q is between Q_μ and the effective stalling stress of the entire neurite structure Q_s, the neurite extends to reach a finite length; and for values >Q_s, the neurite reaches a finite velocity (27). There is uncertainty on the exact value of Q_μ, with estimated reported values ranging widely from 9 pN (27) to 90 pN (28).

In this work, we validated stretching induced by pN forces on neurites, which spontaneously elongate by tip growth at a rate of 0.46 ± 0.02 μm h⁻¹. The stretching by pN forces of such neurites has been found to strongly enhance the elongation process by an additional rate of 0.42 ± 0.01 μm h⁻¹ pN⁻¹. Thus, based on collected data on tip-growth and stretch-growth elongation rates, the application of a 1 pN force on axis can double neurite lengthening. Obviously, these forces are markedly lower than the predicted pulling stress exerted by the microtubules, but nevertheless, stretch growth of neurites occurs, under constant loading. Indeed, the question is “How can a pN force, which is at least one order of magnitude lower than the traction force generated by the growth cone and the tension required for promoting growth of the microtubule network, double the neurite length?” Another issue highlighted by this study is the inability to confirm the force threshold reported in previous studies. A possible explanation is that stretching of neurites by pN forces occurs at a considerably longer time frame than that used in previous studies, thus shifting the response of the neurites from an initially elastic (as in previous studies, in which neurites were stretched rapidly) into a viscous state. In both instances, however, the accompanying microtubule growth is likely to be facilitated by the reduction of oppositely directed forces, leading to faster neurite growth without decreasing neurite diameters. Unknown local mechanisms activated by continuous stretching could also contribute to or sustain growth-cone-mediated cytoskeleton dynamics in regulating neurite elongation. Collectively, our finding suggests that pN forces, under the condition of constant loading, can sustain stretch growth.

Author Contributions

V.R. and A.C. conceived and designed the study. V.R., F.F., and S.D.V. performed the experiments. V.R. analyzed data. A.F. supported RNAseq data analysis. M.P.C. and G.F.G. performed MNP synthesis, characterization, and electron microscopy analysis. V.R. and A.C. wrote the manuscript.

Editor: Philip LeDuc.