Balance between Force Generation and Relaxation Leads to Pulsed Contraction of Actomyosin Networks

Abstract

Actomyosin contractility regulates various biological processes, including cell migration and cytokinesis. The cell cortex underlying the membrane of eukaryote cells exhibits dynamic contractile behaviors facilitated by actomyosin contractility. Interestingly, the cell cortex shows reversible aggregation of actin and myosin called “pulsed contraction” in diverse cellular phenomena, such as embryogenesis and tissue morphogenesis. Although contractile behaviors of actomyosin machinery have been studied extensively in several in vitro experiments and computational studies, none of them successfully reproduced the pulsed contraction observed in vivo. Recent experiments have suggested the pulsed contraction is dependent upon the spatiotemporal expression of a small GTPase protein called RhoA. This only indicates the significance of biochemical signaling pathways during the pulsed contraction. In this study, we reproduced the pulsed contraction with only the mechanical and dynamic behaviors of cytoskeletal elements. First, we observed that small pulsed clusters or clusters with fluctuating sizes may appear when there is subtle balance between force generation from motors and force relaxation induced by actin turnover. However, the size and duration of these clusters differ from those of clusters observed during the cellular phenomena. We found that clusters with physiologically relevant size and duration can appear only with both actin turnover and angle-dependent F-actin severing resulting from buckling induced by motor activities. We showed how parameters governing F-actin severing events regulate the size and duration of pulsed clusters. Our study sheds light on the underestimated significance of F-actin severing for the pulsed contraction observed in physiological processes.

Introduction

Living cells need to generate mechanical forces for their physiological functions (1). Forces are generated mainly by interactions between actin filaments (F-actin) and myosin II motor proteins in the cell cortex, which is a thin layer beneath the cell membrane (2). Myosin II proteins walk on F-actin by consuming chemical energy stored in ATP, which results in generation of tensile forces. Forces produced from actomyosin contractility facilitate a wide variety of morphogenetic phenomena at cell and tissue scales (3). For example, contractility induces cortical flows of the cortex for formation of cytokinetic furrow and drives polarization in the one-cell-stage Caenorhabditis elegans embryo (4, 5). In addition, during invagination of Drosophila mesoderm cells, anisotropic generation of forces from actomyosin cortex drives apical constriction (6). Interestingly, in these morphogenetic events, the actomyosin cortex exhibits pulsed contraction; F-actin and myosin II proteins show transient accumulation followed by scattering at various length scales rather than irreversible accumulation (5, 7). It has been suggested that the local accumulation of F-actin and myosin originates from contractile instability, which inevitably exists in the highly contractile actomyosin cortex (8, 9). The contractile instability is controlled by a spatiotemporal oscillator of RhoA that regulates myosin motor activity, which enables cells to use an intrinsically unstable contractile cortex for driving morphogenetic processes. As a result of the instability control, pulsed contraction emerges in the cortex. To understand how actomyosin contractility facilitates these morphogenetic phenomena, various methods have been applied for perturbing the constituents of actomyosin machinery in cells. However, there are limitations on the extent of perturbation, and results obtained from perturbation are often too unclear to understand how the actomyosin contractility works in cells.

Thus, alternatively, contractile behaviors driven by the actomyosin contractility have been extensively studied in recent works using computational and theoretical models as well as reconstituted actomyosin systems. It was demonstrated that the architecture and connectivity of actomyosin networks can significantly affect pattern formation (8, 10, 11). In addition, it was shown that force-dependent unbinding of actin cross-linking proteins (ACPs) from F-actin plays a critical role for a change in force generation and morphology of actomyosin networks (12, 13). Recently, buckling of F-actin was found to be crucial for large contraction of networks into small clusters (10, 14), consistent with a theoretical prediction (15). We recently suggested that buckling-induced severing of F-actin can also be very important for contraction of actomyosin networks (16). Several recent studies demonstrated that actin turnover stabilizes stress generated by actomyosin networks and helps maintain homogeneous network morphology by counteracting motor activity (17, 18, 19). Although these previous studies have provided insights into understanding of contractile behaviors of actomyosin networks in general, most of them could not recapitulate the pulsed contraction observed during morphogenetic events. They showed only existence of two different states: irreversible aggregation without disassembly of clusters after formation or negligible contraction, which represents a homogeneous network. One study showed coalescence and breakage of actomyosin clusters observed in their in vitro experiments. However, it used an artificial assumption for the phenomenological model that the unbinding rate of motors highly increases within clusters to enforce clusters to spontaneously break into two or three pieces. In addition, their observation on the coalescence and breakage of clusters is intrinsically different from the pulsed contraction that occurs via gradual growth and shrinkage of clusters. A recent computational study claimed that pulsed contraction can appear when F-actins turn over (20). However, they simulated the actin turnover by removing and adding entire F-actins at a fixed rate, which may not be physiologically relevant. In addition, the size of clusters emerging in their simulation showed fluctuation without complete disassembly of clusters. The lack of observations on the pulsed contraction in these previous computational, theoretical, and in vitro studies raises the question of whether the spatiotemporal biochemical control is indispensable for pulsed contraction of actomyosin networks.

To address this question and identify the necessary conditions for the emergence of pulsed contraction, we employed a well-established agent-based model for simulating a very thin actomyosin network consisting of F-actin, motor, and ACPs (12, 16, 17, 21). First, we explored parametric spaces consisting of the turnover rate and length of F-actin and the density of ACPs to identify the regimes in which pulsed contraction occurs. Via quantitative analysis of dynamic changes in network morphology, we found the pulsed contraction can appear without the spatiotemporal biochemical control if force generation from motors is in the balance with force relaxation induced by F-actin treadmilling. However, we observed that the average size of clusters formed during pulsed contraction is much smaller than that observed during the morphogenetic events. If cluster size increases beyond a critical level, the clusters either continuously grow or shrink slowly. We found that inclusion of buckling-induced severing of F-actin enables larger clusters to be disassembled quickly, leading to strong pulsed contraction with much larger clusters. However, if there is only severing without treadmilling, F-actins are shortened over time and thus unable to form large pulsed clusters consistently. We concluded that both local force relaxation via F-actin severing and turnover of F-actin via treadmilling are necessary for strong pulsed contraction in actomyosin networks.

Methods

Model overview

For simulations in this study, we employed our well-established agent-based model of actomyosin networks based on Brownian dynamics (12, 16, 17, 21). Basic features and parameters of the model are described in detail in the Supporting Materials and Methods and Table S1. In the model, F-actin, motor, and ACPs are simplified by cylindrical segments (Fig. S1 a). F-actin is simplified into serially connected cylindrical segments of 140 nm in length with polarity barbed and pointed ends. Motors are modeled after myosin thick filaments: they have a backbone structure with four arms attached, and each arm represents eight myosin heads. ACPs consist of two cylindrical segments. Displacements of the cylindrical segments at each time step are calculated by the Langevin equation with Euler integration scheme in the absence of inertia. Stochastic force in the Langevin equation determined based on the fluctuation-dissipation theorem leads to thermal fluctuations (22). Deterministic forces include bending and extensional forces that maintain equilibrium angles formed by segments and equilibrium lengths of segments, respectively, as well as repulsive force between neighboring pairs of segments to consider volume-exclusion effects. ACPs bind to F-actin with no preference of cross-linking angle at a constant rate and also unbind from F-actin at a force-dependent rate described by Bell’s law (23); an unbinding rate exponentially increases as ACP experiences larger tensile forces. Each arm of motors binds to F-actin at a constant rate and then walks toward the barbed end of F-actin at a force-dependent rate; a walking rate decreases as the arm feels higher tensile force. Thus, the arm stops walking if applied force on each myosin head is larger than the stall force. The motor arm unbinds from F-actin at a rate inversely proportional to applied force. The force-dependent walking and unbinding rates of motor arms are determined by a theoretical model called the parallel cluster model (24, 25). For all simulations in this study, we employed a very thin computational domain (10 × 10 × 0.1 μm) with periodic boundary conditions only in the x and y directions (Fig. S1 b). In the z direction, boundaries of the domain exert repulsive forces on elements that are displaced beyond the boundaries. At the beginning of each simulation, a thin actomyosin network is formed via self-assembly of F-actin, ACPs, and motor.

Actin dynamics

Formation of F-actin begins from a nucleation event with appearance of one cylindrical segment with polarity in a random direction perpendicular to the z direction. Polymerization and depolymerization of actins are simulated by addition and removal of one cylindrical segment, respectively, as in our previous studies (17). Via spatiotemporal control of rate constants governing the nucleation, polymerization, and depolymerization, we can simulate various types of actin turnover facilitated by actin binding proteins, such as cofilin, formin, and capping proteins. However, to avoid unnecessary complexity and uncertainty, we employed the simplest form of actin turnover, treadmilling (17). To mimic the F-actin treadmilling, we assumed that polymerization and depolymerization occur only at barbed ends and pointed ends, respectively. It was further assumed that a rate constant governing polymerization (k_+,A) has the same value as that governing depolymerization (k_−,A), which results in a dynamic equilibrium at an actin concentration of 1 μM. We define a turnover rate (k_t,A) to indicate the rate of actin treadmilling, and the value and unit of k_t,A are identical to those of k_−,A. By adjusting the ratio of the nucleation rate constant (k_n,A) to k_t,A, the average length of F-actin (<L_f>) is varied between 0.7 and 5.0 μm. This range of <L_f> is smaller than that used in typical reconstituted actomyosin networks without control of F-actin length (∼20 μm) (26, 27). However, the range is very comparable to that estimated in the cell cortex (28, 29).

In addition, for some of the simulations, we employed angle-dependent F-actin severing as in our recent work (16). F-actin severing is mimicked in a simulation by eliminating one actin segment on F-actin. To determine a segment to eliminate, the sum of bending angles at two ends of each actin segment (θ_s,A) is calculated. Then, the severing rate (k_s,A) is calculated from the sum using the following relationship:

$$k_{\text{s,A}}=k_{\text{s,A}}^0\exp \left(\frac{{\theta }_{\text{s,A}}}{{\lambda }_{\text{s,A}}}\right),$$ (1)

where $k_{\text{s,A}}^0$ is a zero-angle severing rate constant and λ_s,A is insensitivity to θ_s,A. The insensitivity means that as λ_s,A is higher, severing events tend to occur at larger bending angles. Because θ_s,A is the sum of two angles, an increase in a bending angle on either end of an actin segment can lead to disappearance of the segment because of severing. The relationship in Eq. 1 was found empirically by comparing with in vitro experiments (30) as explained and justified in the Supporting Materials and Methods in detail. Although we devised Eq. 1 without a rigorous physical basis, it reflects an experimental observation that severing takes places only at a large bending angle (i.e., a small radius curvature). As explained in the Supporting Materials and Methods, our results are insensitive to the choice of a specific model for F-actin severing.

Analysis of motions of motors

To evaluate how fast motors move at each time point, we quantify their average speed. We track the center position of each motor over time, r_i,M, where i is an index of a motor. Because the domain is very thin in the z direction, we assumed that r_i,M has only x and y components. Then, ensemble average of speed of motors is calculated every 1 s:

$$\langle v_{\text{M}}\left(t\right)\rangle =\frac{1}{N_{\text{M}}}\sum _{i=1}^{N_{\text{M}}}{v}_{i,\text{M}}\left(t\right)=\frac{1}{N_{\text{M}}}\sum _{i=1}^{N_{\text{M}}}\frac{\left|{\mathbf{r}}_{i,\text{M}}\left(t\right)-{\mathbf{r}}_{i,\text{M}}\left(t-1\right)\right|}{1\text{s}},$$ (2)

where N_M is the total number of motors. For a certain time range, we calculate time average of the ensemble average:

$${\langle v_{\text{M}}\rangle }_{t_1\to t_2}=\frac{1}{t_2-t_1}\sum _{t=t_1}^{t_2}\langle v_{\text{M}}\left(t\right)\rangle ,$$ (3)

where t₁ and t₂ are lower and upper limits of the time range of interest. If the time interval is shorter than 1 s, the calculated speed becomes noisier because influences of thermal fluctuation on motor motions are not averaged out sufficiently. If the time interval is too long, the number of data points is not enough to calculate ${\langle v_{\text{M}}\rangle }_{t_1\to t_2}$. We therefore used the time interval of 1 s for the best analysis of motor motions.

Evaluation of network morphology

We evaluate the heterogeneity of network morphology by measuring spatial distributions of F-actins in the computational domain. For measurement, the domain is divided into N_G × N_G grids in the x and y directions, where N_G indicates the number of grids in each direction. Each grid has its coordinate, (i, j). We measure the number of actin segments located in each grid, ${\rho }_{\text{A}}^{i,j}$, to create the three-dimensional histogram representing their density map. Then, SD of ${\rho }_{\text{A}}^{i,j}$ calculated over all grids is considered as an indicator for the heterogeneity of network morphology, Q_A. Because the heterogeneity calculated in this method depends on the choice of N_G, we carefully determined the optimal range of N_G = 10–20.

As an additional measure for heterogeneity, we employ an analysis method used in a previous study (31). First, we randomly choose 1% of actin segments and calculate distances between them. We calculate a radial distribution function, g(r), as a histogram with a bin size δr:

$$g\left(r\right)=P\left(r\right)/\left(2\pi r\delta r{\rho }_a\right),$$ (4)

where ρ_a represents the density of selected actin segments calculated over a whole network and P(r) is the probability of actin segments with a separate distance between r and r + δr. r is varied from 50 nm to 1 μm with an increment of δr = 50 nm. Smaller δr enables smoother radial distribution curve and transition. Higher peaks at low r indicate that a network is highly heterogeneous. By contrast, a very homogeneous network leads to g(r) ∼ 1 for all r values.

Quantification of clustering behaviors

We probed the onset and emergence of pulsed contraction in an actomyosin network. In the density map of actin segments explained above, all adjacent grids whose density and duration are above threshold values are grouped and considered to be a single cluster (Fig. S1 c). Because results of quantification can significantly vary depending on the threshold value, we carefully chose the threshold values of density and duration as explained in the Supporting Materials and Methods. Then, we calculated the center position of each cluster and the number of actin segments that belong to each cluster. This analysis was repeated for all data recorded every 1 s. We then correlated clusters at one time point to those at the next time point. Two clusters in consecutive time points were regarded as the same cluster if two primary criteria were met. First, the distance between centers of two clusters could not be larger than a chosen threshold. The threshold value was assumed to be proportional to the size of the clusters. Second, the difference in the number of actin segments in the two clusters could not be larger than half of the number of actin segments in the cluster at a later time point. When two or more clusters were merged, one of the clusters at a previous time point would share the same identity of a merged cluster at the next time point. Only the cluster with the longest history was kept. For instance, if two clusters that were merged later started emerging from different time points, the one that formed earlier would be kept and linked to the merged cluster, whereas the other that formed later would be ignored for the analysis. In addition, we ignored clusters that lasted for less than 20 s to avoid counting trivial small structures. The threshold value for the minimal duration was also chosen carefully as explained in the Supporting Materials and Methods.

Formation of clusters requires persistent movement of motors toward a specific point. We probed how persistently motors move over time. First, we calculated the ensemble average of velocities of all motors located in each grid, ${\mathbf{v}}_{\text{M}}^{i,j}\left(t\right)$, and then analyzed the autocorrelation of ${\mathbf{v}}_{\text{M}}^{i,j}$ as a measure for persistency of the velocities over time:

$$\langle \cos \varphi \left(t\right)\rangle =\frac{1}{N_{\text{G}}^2}\sum _{i=1}^{N_{\text{G}}}\sum _{j=1}^{N_{\text{G}}}\cos {\varphi }_{i,j}\left(t\right)=\frac{1}{N_{\text{G}}^2}\sum _{i=1}^{N_{\text{G}}}\sum _{j=1}^{N_{\text{G}}}\frac{{\mathbf{v}}_{\text{M}}^{i,j}\left(t\right)\cdot {\mathbf{v}}_{\text{M}}^{i,j}\left(t+\tau \right)}{\left|{\mathbf{v}}_{\text{M}}^{i,j}\left(t\right)\right|\left|{\mathbf{v}}_{\text{M}}^{i,j}\left(t+\tau \right)\right|},$$ (5)

where τ is 1 s. Values of $\langle \cos \varphi \rangle$ are averaged between 10 and 20 s, representing dynamics of the motors at early time points when a network exhibits very active aggregating behaviors in all cases. Note that the average value of $\langle \cos \varphi \rangle$ close to 1 is indicative of very persistent motions of motors, which are the signature of clustering.

Results

In this study, we performed simulations under various conditions to study the contractile behaviors of two-dimensional actomyosin networks. We varied the turnover rate (k_t,A), severing rate (k_s,A), and average length (<L_f>) of F-actin and cross-linking density (R_ACP) in the simulations, whereas we fixed actin concentration (C_A) at 60 μM and motor density (R_M) at 0.04.

Turnover of F-actin suppresses formation of clusters

In recent computational studies (18, 19, 20, 32, 33, 34), it was shown that actin turnover prevents motors from forming aggregation in two-dimensional and three-dimensional actomyosin networks as well as stabilizing stress generated from the networks by relaxing forces produced from motor activities. As in our previous study (17), we implemented the simplest form of turnover, treadmilling of F-actin, by imposing identical rate constants for polymerization at a barbed end and depolymerization at a pointed end. Despite its simplicity, the treadmilling is more realistic turnover dynamics than the abrupt disappearance and appearance of F-actins employed in recent computational studies (18, 19, 20).

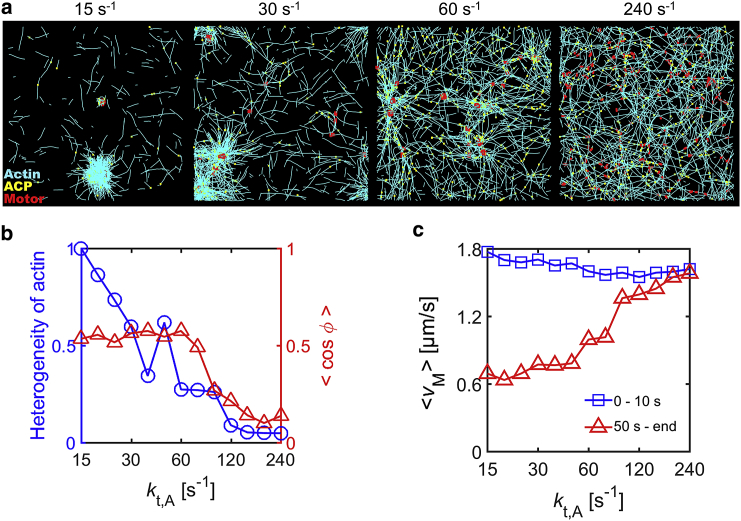
We imposed k_t,A, which represents a treadmilling rate, between 15 and 240 s⁻¹ with R_ACP = 0.02 and <L_f> = 1.6 μm. With the lowest k_t,A = 15 s⁻¹, a large portion of a network aggregates into a large cluster, resulting in very heterogeneous F-actin distribution (Fig. 1, a and b and S2 a). However, as k_t,A increases, networks tend to be more homogeneous with less distinct, smaller clusters as force relaxation is elevated. We also analyzed motor activities in a quantitative manner. With lower k_t,A, motors move persistently toward centers of the clusters and move much more slowly after formation of clusters (Fig. 1, b and c). With higher k_t,A, motors exhibit less persistent movements because motors cannot stably walk on F-actins that turn over rapidly via treadmilling (Fig. 1 b). In addition, because a network does not aggregate significantly, the average speed of motors does not change much over time (Fig. 1 c).

Figure 1.

Network contraction is regulated by F-actin turnover. We varied actin turnover rate (k_t,A) between 15 and 240 s⁻¹ at R_M = 0.04, R_ACP = 0.02, and <L_f> = 1.6 μm. (a) The morphology of networks at 65 s with four different k_t,A. (b) The heterogeneity of F-actin distribution (blue circle) and $\langle \cos \varphi \rangle$ indicating persistency of motor velocities between 10 and 20 s (red triangle) depending on k_t,A. The heterogeneity monotonically decreases as k_t,A increases. At low k_t,A, motors tend to move persistently over time, but as k_t,A increases, motors exhibit less persistent motions because F-actins undergo rapid turnover without formation of large clusters. (c) The average speed of motors at early times (0–10 s, blue square) and late times (from 50 s till end, red triangle) as a function of k_t,A. Although the average speed hardly changes at high k_t,A, it is significantly reduced over time at low k_t,A. To see this figure in color, go online.

Network connectivity critically affects contraction

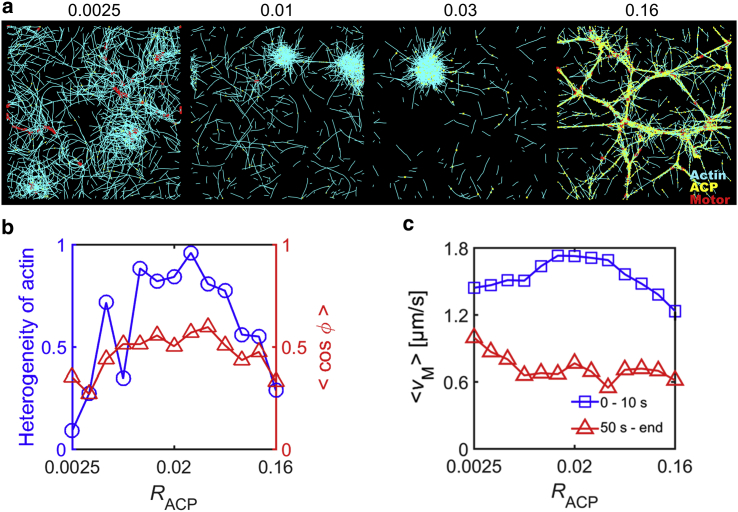
It has been shown that network connectivity plays a critical role for contractile behaviors of actomyosin networks (10). We recently demonstrated that a cross-linked actomyosin network in the absence of actin turnover shows maximal contraction at intermediate level of R_ACP because poor connectivity prevents motors from stably generating forces between pairs of F-actins, whereas too-high connectivity leads to strong resistance of the network to contraction because of high network elasticity (16). This is consistent with previous experimental results (35) and reproduced in another computational study later (20).

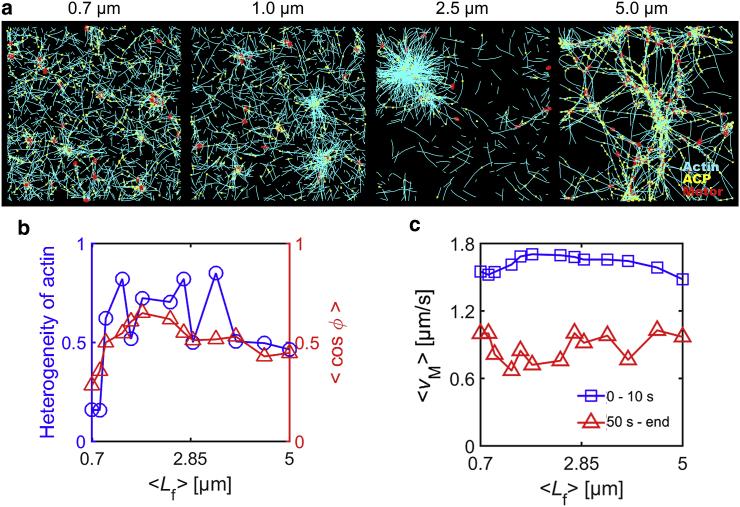
In the presence of slow actin turnover (k_t,A = 30 s⁻¹), we systematically tested influences of R_ACP and <L_f> that are likely to govern network connectivity. It was observed that a change in R_ACP and <L_f> has similar effects on network contraction. With very poor network connectivity due to low R_ACP or <L_f>, a network hardly contracts or contracts into multiple small clusters, but as connectivity increases, a single, large cluster is formed from aggregation of F-actins (Figs. 2 a and 3 a). A further increase in connectivity suppresses formation of disconnected clusters, resulting in a network consisting of interconnected bundles. Thus, at intermediate connectivity, spatial distribution of F-actins is the most heterogeneous, and motors exhibit the most persistent movements toward centers of large clusters (Figs. 2 b, 3 b, and S2, b and c). In addition, the average speed of motors at early times is the highest at intermediate connectivity because of large contraction into a single cluster (Figs. 2 c and 3 c). The average speed becomes much lower at late times in most cases in which networks show large contraction into clusters or bundle networks. However, at very low R_ACP, a decrease in the average speed of motors is less significant because the network does not form distinct clusters.

Figure 2.

Actin cross-linking proteins (ACPs) regulate contractile behaviors of networks. We changed ACP density (R_ACP) between 0.0025 and 0.16 at R_M = 0.04, <L_f> = 1.6 μm, and k_t,A = 30 s⁻¹. (a) The morphology of networks at 65 s depending on R_ACP. At small R_ACP, networks are quite homogeneous. As R_ACP increases, networks severely aggregate into disconnected clusters. At large R_ACP, very high network connectivity precludes formation of separated clusters, leading to interconnected bundles. (b) The heterogeneity of F-actin distribution (blue circle) and $\langle \cos \varphi \rangle$ representing persistency of motor velocities between 10 and 20 s (red triangle) depending on R_ACP. Consistent with (a), the heterogeneity is the highest at intermediate levels of R_ACP, and velocities of motors exhibit the most persistent motions. (c) The average speed of motors at early times (0–10 s, blue square) and late times (from 50 s till end, red triangle). Motors initially move at the highest speed at intermediate levels of R_ACP at which the largest contraction emerges. Regardless of R_ACP, the average speed is substantially decreased over time. To see this figure in color, go online.

Figure 3.

Average length of F-actins (<L_f>) highly affects network contraction in a similar fashion to R_ACP. We varied <L_f> between 0.7 and 5.0 μm at R_M = 0.04, R_ACP = 0.02, and k_t,A = 30 s⁻¹. (a) The morphology of networks at 56 s with different <L_f>. With short F-actins, only small clusters appear, whereas larger clusters are formed with longer F-actins. If F-actins are very long, enhanced network connectivity precludes formation of separated clusters, leading to interconnected bundles. (b) The heterogeneity of F-actin distribution (blue circle) and $\langle \cos \varphi \rangle$ indicative of persistency of motor velocities between 10 and 20 s (red triangle) depending on <L_f>. The heterogeneity and persistency are the largest at intermediate levels of <L_f> because of the largest contraction. (c) The average speed of motors at early times (0–10 s, blue square) and late times (from 50 s till end, red triangle) as a function of <L_f>. Initial average speed is the highest at intermediate levels of <L_f> because of the largest contraction. At all values of <L_f>, the average speed is decreased significantly over time. To see this figure in color, go online.

Weak pulsed contraction appears to be due to balance between force generation and relaxation

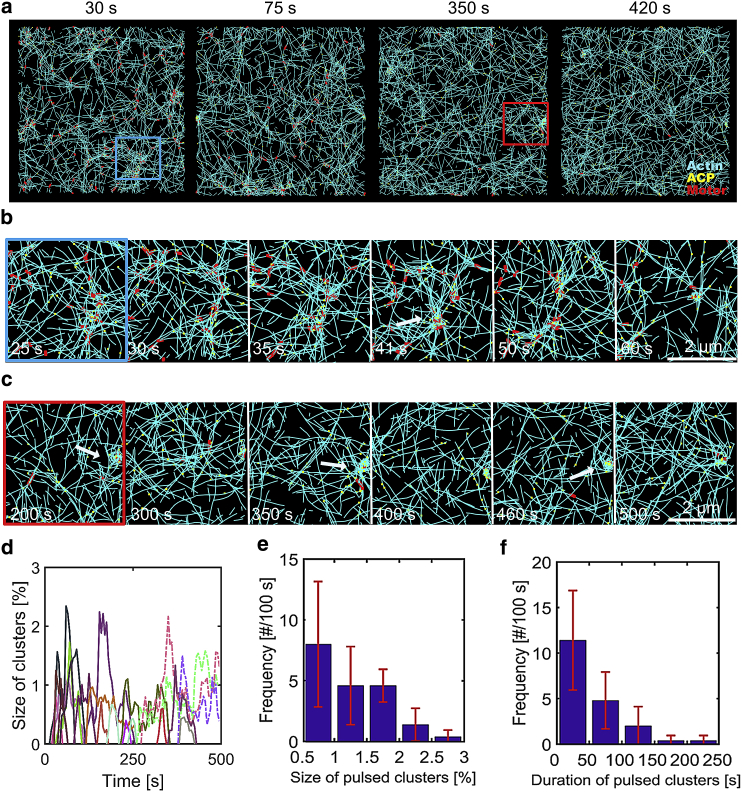
By analyzing morphological changes in networks, we probed the existence of pulsed contraction. Under specific conditions, we observed weak pulsed contraction with very small clusters. F-actins and motors aggregate toward a focal point, but nascent small clusters are disassembled shortly after formation without an increase in their size (Fig. 4, a and b), indicating pulsed contraction. This weak pulsed contraction originates from subtle balance between force generation from motor activities and force relaxation induced by actin turnover. To identify types of clusters based on size and duration, we traced individual clusters and measured the percentage of actin segments that belong to each cluster over time. These small pulsed clusters appear by themselves at higher k_t,A (Fig. S3 a; Video S1). However, at lower k_t,A, they appear with some small clusters that fluctuate in their size till the end of simulations (Fig. 4, a, c, and d; Video S2). An apparent difference between the nascent pulsed clusters and fluctuating clusters is whether or not complete disassembly occurs soon after formation. Fluctuating clusters form because force relaxation is not fast enough to relax forces generated by actomyosin components. We evaluated the size and duration of nascent clusters during the weak pulsed contraction (Fig. 4, e and f). The clusters are quite small and do not last for a long time, with lifetimes shorter than 50 s. Note that pulsed clusters observed in cells are typically ∼2–4 μm in diameter and ∼40–100 s in duration (36).

Figure 4.

Balance between force generation and relaxation causes weak pulsatile contraction with formation of very small clusters. Conditions used in a case shown here are R_M = 0.04, R_ACP = 0.01, <L_f> = 1 μm, and k_t,A = 70 s⁻¹. (a) The morphology of networks showing cluster formation taken at different time points. (b) The time evolution of a small pulsed cluster indicated by a blue box in (a). This cluster appears from ∼30 s and then becomes the largest at 41 s, as indicated by a white arrow. Then, it disassembles gradually over time. (c) The time evolution of a fluctuating cluster highlighted by a red box in (a). (d) The time evolution of the percentage of actin segments located within clusters. Random colors are assigned to curves to distinguish each cluster. Nascent pulsed clusters are shown in solid lines, whereas fluctuating clusters are shown in dot-dashed lines. (e and f) The frequency of appearance of pulsed clusters per 100 s depending on their size (e) and duration (f). Most clusters are very small and do not last for long time periods. To see this figure in color, go online.

Video S1. Contractile Movement of an Actomyosin Network Showing Emergence of Small Pulsatile Clusters with k_t,A = 80 s⁻¹

R_M = 0.04, R_ACP = 0.01, and <L_f> = 1 μm. F-actin, ACP, and motor are visualized by cyan, yellow, and red, respectively.

Video S2. Contractile Motion of an Actomyosin Network with k_t,A = 70 s⁻¹

R_M = 0.04, R_ACP = 0.01, and <L_f> = 1 μm. Fluctuating clusters are observed in addition to small pulsatile clusters. F-actin, ACP, and motor are visualized by cyan, yellow, and red, respectively.

A previous computational study that demonstrated pulsed contraction with larger clusters employed a different way to account for actin turnover (20). In their model, a whole F-actin is randomly removed in a domain, and a new F-actin appears in a different location as in other studies (18). Such turnover of entire F-actins can break down multiple connections in clusters at once, enabling large clusters to be disassembled. Although this is an efficient way to induce local, strong force relaxation for pulsed contraction, it is much less physiological than our turnover model. Indeed, pulsed contraction observed in the recent study is more similar to the behavior of fluctuating clusters in our study because sizes of their clusters showed consistent fluctuation without complete disassembly (20).

If we lower k_t,A further, most of the clusters either grow consistently for longer than 100 s until the end of simulation or show relatively fast growth followed by very slow decay, although some small nascent clusters still form at early times (Fig. S3 b; Video S3). None of these clusters are analogous to the pulsed clusters observed in cells in terms of size and duration (36). Thus, it is expected that an additional mechanism of force relaxation is necessary for enabling larger clusters to be disassembled completely within a reasonable time range. Note that in all of these simulations, the average length of F-actins remains relatively constant (∼1 μm) over time and is independent of k_t,A (Fig. S3 c).

Video S3. Irreversible Contraction of an Actomyosin Network with k_t,A = 30 s⁻¹

R_M = 0.04, R_ACP = 0.01, and <L_f> = 1 μm. Several decaying clusters and growing clusters emerge. Some small clusters still appear at early times but disappear very quickly. F-actin, ACP, and motor are visualized by cyan, yellow, and red, respectively.

In addition, we quantified cluster dynamics in a wide parametric space consisting of <L_f>, k_t,A, and R_ACP (Fig. S3, d and e). It was observed that the small nascent pulsed clusters appear only in a very narrow regime with short <L_f> (∼1 μm), intermediate actin turnover rate (∼70 s⁻¹), and low/intermediate network connectivity. It is likely that most of the previous computational studies investigating contractile behaviors of actomyosin networks neglected the appearance of the nascent pulsed clusters because they appear in such a narrow regime.

Angle-dependent severing of F-actin facilitates strong pulsed contraction

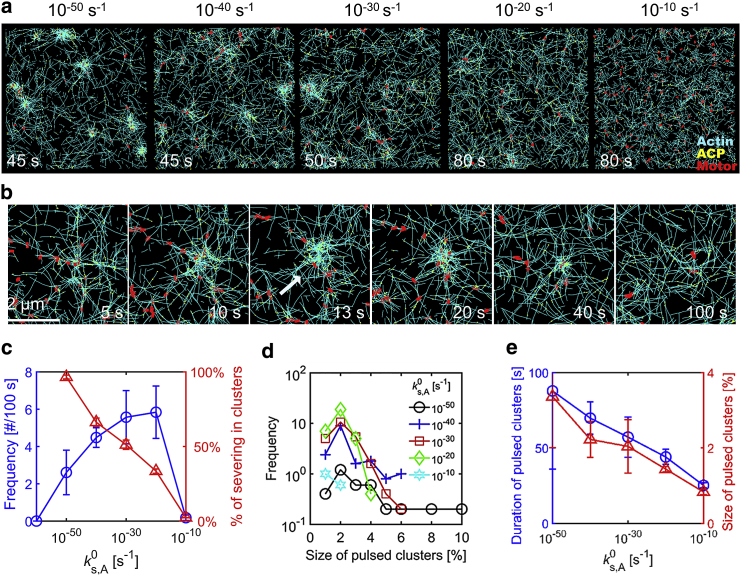
A recent in vitro experiment clearly demonstrated that F-actins undergo severe fragmentation during contraction of actomyosin networks (14). This fragmentation is likely to originate from angle-dependent severing of F-actin induced by buckling. Our recent computational study also showed that frequent severing events of F-actin can inhibit network contraction (16). Because F-actin is prone to buckling and more severing at the location where contraction takes place, the severing may relax forces locally within contracting clusters and thus help disassembly of larger clusters for more distinct pulsed contraction. We employed the model of angle-dependent F-actin severing used in our previous study to check influences of severing on the pulsed contraction (16). We incorporated F-actin severing in a case that showed formation of relatively large clusters without pulsed contraction and varied the zero-angle severing rate constant $\left(k_{\text{s,A}}^{\text{0}}\right)$ between 10⁻⁶⁰ and 10⁻¹⁰ s⁻¹. It was observed that average length of F-actins remains close to an initial value (∼1 μm) in all simulations except a case with $k_{\text{s,A}}^0$ = 10⁻¹⁰ s⁻¹ (Fig. S4 g). When $k_{\text{s,A}}^0$ is very low (=10⁻⁶⁰ s⁻¹), severing events hardly occur, so large irreversible clusters are formed (Fig. S4 a). With intermediate values of $k_{\text{s,A}}^0$ (10⁻⁵⁰–10⁻³⁰ s⁻¹), large clusters are still formed, but many of them are disassembled much faster than decaying clusters, indicative of strong pulsed contraction (Figs. 5, a and b and S4, b–d). The size and duration of these clusters are very comparable to those of pulsed clusters observed in vivo. It was found that more than half of the severing events take place within clusters at these $k_{\text{s,A}}^0$ values (Fig. 5 c), which implies that buckling arising from contraction of clusters induces F-actin severing and thus relaxation of forces generated by motors within clusters. Note that at 10⁻⁵⁰ s⁻¹ ≤ $k_{\text{s,A}}^0$ ≤ 10⁻²⁰ s⁻¹, a greater number of smaller clusters with shorter lifetime (<50 s) emerged with higher $k_{\text{s,A}}^0$ (Fig. 5, c–e). In addition, the percentage of severing events occurring within clusters decreases, meaning that severing takes place in a less selective manner. If $k_{\text{s,A}}^0$ increases more to 10⁻¹⁰ s⁻¹, only a few small pulsed clusters are formed (Fig. 5, a and c–e). If $k_{\text{s,A}}^0$ is very high, network connectivity is deteriorated, so contraction is impeded.

Figure 5.

Severing of F-actin facilitates strong pulsed contraction via selective force relaxation within clusters. We varied the zero-angle severing rate constant $\left(k_{\text{s,A}}^{\text{0}}\right)$ between 10⁻⁶⁰ and 10⁻¹⁰ s⁻¹ at R_M = 0.04, R_ACP = 0.02, <L_f> = 1 μm, k_t,A = 30 s⁻¹, and λ_s,A = 1.6°. (a) The morphology of networks with various $k_{\text{s,A}}^0$. As $k_{\text{s,A}}^0$ increases, clusters become apparently smaller. (b) The time evolution of a relatively large pulsed cluster. The cluster appears at ∼5 s and becomes the largest at 13 s, as marked by a white arrow. Then, it disassembles completely at ∼100 s. (c) The frequency of appearance of pulsed clusters per 100 s (blue circle) and percentage of severing events occurring within pulsed clusters (red triangle) depending on $k_{\text{s,A}}^0$. As $k_{\text{s,A}}^0$ increases, more pulsed clusters appear, and more severing events take place outside the pulsed clusters. However, few pulsed clusters are formed if $k_{\text{s,A}}^0$ is too high. (d) The distribution of size of pulsed clusters depending on $k_{\text{s,A}}^0$. With lower $k_{\text{s,A}}^0$, larger pulsed clusters are more likely to emerge. (e) Average duration (blue circle) and size (red triangle) of the largest pulsed clusters found from each of five simulations with different $k_{\text{s,A}}^0$. With lower $k_{\text{s,A}}^0$, more larger clusters appear and last longer before complete disassembly. To see this figure in color, go online.

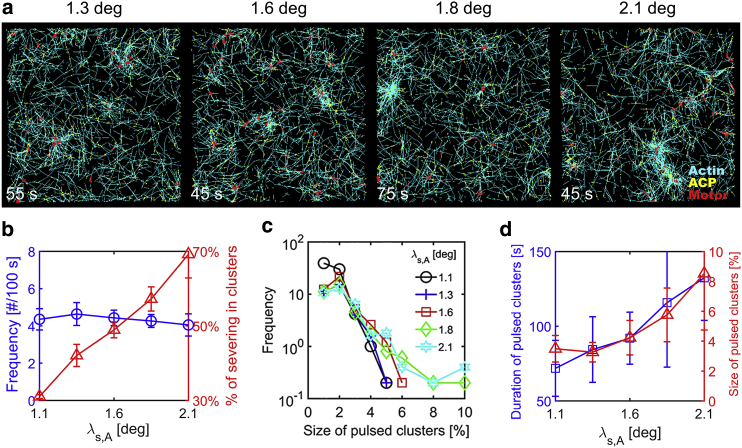
We also tested the effects of the insensitivity of F-actin severing to a bending angle (λ_s,A). As explained in the Methods, with higher λ_s,A, severing occurs at larger bending angles. At the range of λ_s,A tested in this study, the average length of F-actins does not show strong dependence on λ_s,A (Fig. S5 h). The total number of pulsed clusters is not affected much by λ_s,A (Fig. 6 b), but more large clusters appear with higher λ_s,A (Figs. 6 c and S5, a–g; Video S4). The size and duration of the largest cluster in each simulation are proportional to λ_s,A (Fig. 6 d). If severing is very sensitive to bending angles because of small λ_s,A, a large portion of F-actins within clusters are severed before substantial growth of the clusters, resulting in small pulsed clusters with short lifetime. By contrast, with large λ_s,A, the severing is delayed till F-actins are subject to greater bending angles within larger clusters, leading to formation of large pulsed clusters with relatively long lifetime. In addition, the F-actin severing is more likely to occur within clusters if λ_s,A is higher (Fig. 6 b).

Figure 6.

Dependence of the severing rate on a bending angle regulates the pulsed contraction. We modulated insensitivity of the severing rate to a bending angle (λ_s,A) at R_M = 0.04, R_ACP = 0.02, <L_f> = 1 μm, k_t,A = 30 s⁻¹, and $k_{\text{s,A}}^0$ = 10⁻³⁰ s⁻¹. Severing takes place at larger bending angles if λ_s,A is larger. (a) The morphology of networks with various λ_s,A. With higher λ_s,A, more large pulsed clusters emerge. (b) The frequency of appearance of pulsed clusters per 100 s (blue circle) and percentage of severing events occurring within pulsed clusters (red triangle) depending on λ_s,A. Although relatively the same number of clusters are formed regardless of λ_s,A, more severing events take place within clusters as λ_s,A increases. (c) The distribution of size of pulsed clusters with different λ_s,A. With larger λ_s,A, there are a greater number of large pulsed clusters, although small pulsed clusters appear at a similar frequency. (d) The average duration (blue circle) and size (red triangle) of the largest pulsed clusters found from each of five simulations depending on λ_s,A. With larger λ_s,A, there are more larger clusters, and they last longer. To see this figure in color, go online.

Video S4. Contractile Motion of an Actomyosin Network Showing Large Pulsatile Clusters with Both F-Actin Turnover and Severing

R_M = 0.04, R_ACP = 0.02, <L_f> = 1 μm, k_t,A = 30 s⁻¹, λ_s,A = 2.5°, and $k_{\text{s,A}}^0$ = 10⁻³⁰ s⁻¹. F-actin, ACP, and motor are visualized by cyan, yellow, and red, respectively.

As shown above, both an increase in λ_s,A and a decrease in $k_{\text{s,A}}^0$ lead to formation of more large pulsed clusters. However, their impacts on small pulsed clusters are quite different. Because an increase in λ_s,A hardly affects the frequency of emergence of small pulsed clusters (Fig. 6 c), large pulsed clusters coexist with small ones at high λ_s,A (Fig. 6 a). By contrast, a decrease in $k_{\text{s,A}}^0$ drastically reduces emergence of small pulsed clusters (Fig. 5 d), so large pulsed clusters appear without many small pulsed clusters (Fig. 5 a). Thus, to finely tune populations of small and large pulsed clusters, regulation of both $k_{\text{s,A}}^0$ and λ_s,A is necessary.

All of these results imply that in addition to F-actin turnover (i.e., treadmilling), severing results in local force relaxation that helps disassembly of otherwise irreversible large clusters. However, with only severing, strong pulsed contraction cannot last for long time because F-actins are gradually fragmented into shorter filaments over time (Figs. S6 and S7; Video S5). Actin turnover based on treadmilling helps remove the shorter filaments and recycle actin monomers to form another F-actin in a different location, resulting in a relatively constant average length of F-actins over time. Thus, with the presence of both actin treadmilling and severing, the strong pulsed contraction with large clusters with long lifetime can appear.

Video S5. Movements of an Actomyosin Network with F-Actin Severing without F-Actin Turnover

R_M = 0.04, R_ACP = 0.02, <L_f> = 1 μm, k_t,A = 0 s⁻¹, λ_s,A = 1.6°, and $k_{\text{s,A}}^0$ = 10⁻⁴⁰ s⁻¹. F-actin, ACP, and motor are visualized by cyan, yellow, and red, respectively.

Discussion

The actomyosin cortex facilitates various morphogenetic events by spatiotemporally regulating its cortical tension. The cortex usually shows homogeneous morphology and bears tensile forces. In our previous studies (12, 17), we showed that an actomyosin network cross-linked by transient ACPs can maintain homogeneous morphology and generate sustainable tensile forces in two ways. If there is no F-actin turnover, the number of active motors generating forces should be small enough to result in only a small load on each ACP. If F-actin undergoes relatively fast turnover, a network with a large number of active motors can be stable because the F-actin turnover prevents motors from developing large forces. Based on observations in previous experiments (10, 17, 37, 38, 39), it is likely that the actomyosin cortex in cells can be stable because of F-actin turnover. For example, when F-actin turnover was perturbed by drugs, the actomyosin cortex formed aggregates and lost most of its traction forces.

In recent experiments (7, 40, 41), it has been observed that the actomyosin cortex exhibits pulsed contraction during certain morphogenetic events. Despite efforts made by a myriad of theoretical, computational, and in vitro experimental studies, critical regulators of the pulsed contraction emerging in the actomyosin cortex remain elusive. Considering that stability of actomyosin cortex is maintained by F-actin turnover, it is likely that pulsed contraction is involved with competition and balance between force generation from motors and force relaxation induced by F-actin dynamics. In this study, we employed a computational model to illuminate the origins of pulsed contraction.

First, we demonstrated that actin turnover highly affects the contractile behaviors of a network. As F-actin turns over more slowly, a network becomes more heterogeneous, with larger irreversible clusters. This is consistent with several computational studies showing the effects of F-actin turnover on contractile behaviors of networks (18, 19, 20). To correlate motor activities with a variation in network morphology, we quantified the speed and persistency of motor movements. We found that when a network forms large clusters, motors move toward the center of the clusters in a persistent manner and then slow down after reaching the center. By contrast, when cluster formation is inhibited by fast actin turnover, motors keep moving fast and less persistently. Because treadmilling occurs toward the barbed end of F-actin, it can prevent motors from stably walking for long times, causing less persistent motions.

In addition, it has been suggested that connectivity between F-actins also plays an important role for contractile behaviors of actomyosin networks. For example, an in vitro experiment using cell extracts from Xenopus egg cells showed that a change in the amount of one type of ACPs, α-actinin, can result in distinct morphologies in the presence of actin turnover by modulating network connectivity (42). Without actin turnover, effects of network connectivity on contractile behaviors of actomyosin networks are shown to be significant (8, 10, 16). We probed effects of connectivity between F-actins on network morphology and motor movements by changing either F-actin length or ACP density at relatively low actin turnover rate. At low network connectivity, the network minimally contracts or shows formation of small clusters, leading to less persistent movements of motors. An increase in network connectivity results in formation of large clusters with very persistent motor movements. Emergence of the large clusters is related to increased ranges over which forces generated by motors are transmitted (42). A further increase in network connectivity suppresses formation of separated clusters, resulting in bundled networks with less persistent motor movements. However, the entire network will contract into a single cluster at such high connectivity in the absence of the periodic boundary condition as demonstrated in a previous study (8) because the effective size of the network becomes finite without the periodic boundary condition. It is expected that the ACP density at which the network transitions between the three states (small clusters, large clusters, and bundle network) is proportional to the actin turnover rate as shown in our previous study (17). For example, if F-actin turns over faster, the transitions will occur at higher ACP density to achieve the same degree of network connectivity.

Interestingly, we found that weak pulsed contraction with nascent clusters occurs when there is subtle balance between force generation by myosin motors and force relaxation by actin turnover. These short-lived small clusters appear by themselves or in conjunction with clusters with size fluctuating over time in a very narrow parametric regime comprised of ACP density and the turnover rate and average length of F-actin. Outside the regime, most of the clusters irreversibly grow or decay very slowly after growth. None of these clusters resemble large pulsed clusters observed in cells (5, 7, 43). Although duration of the short-lived clusters is similar to that of the in vivo pulsed clusters (∼1 min), they are much smaller in size. The fluctuating clusters show pulsed growth and shrinkage but do not disassemble completely. The decaying clusters exhibit reversibility, but they are disassembled too slowly. As mentioned earlier, using turnover of entire F-actins, a recent computational study demonstrated emergence of clusters showing pulsed behaviors (20), but they are close to fluctuating clusters rather than the in vivo pulsed clusters. All of these imply that force relaxation only via F-actin turnover is not enough to form the large distinct pulsed clusters. As size of clusters increases, more F-actins are entangled and cross-linked heavily with each other within the clusters. Then, it becomes very hard to disassemble the clusters because of very high connectivity between F-actins, resulting in very slow decay or irreversible growth. If actin turnover is very fast, disassembly of large clusters might be possible, but such large clusters are not formed because force relaxation by actin turnover dominates force generation by motors. Therefore, formation of the distinct large pulsed clusters requires an additional mechanism for locally reducing F-actin connectivity within clusters and thus relaxing forces generated by motors.

We found that angle-dependent severing of F-actin can be the additional mechanism. Buckling-induced F-actin severing has been observed during myosin-driven contraction of actin networks (14) and membrane-bound F-actins (44). Severing of F-actin can decrease network connectivity by breaking F-actin into two fragments, which may facilitate force relaxation and cluster disassembly. We demonstrated that F-actin severing enables large clusters to be disassembled quickly, resulting in a significant increase in the size and duration of the pulsed clusters. If F-actin severing tends to occur slower or at larger bending angles, a larger portion of severing events take place within the clusters, leading to the appearance of larger pulsed clusters. This indicates that F-actin severing can induce local force relaxation selectively in large clusters. However, if F-actin severing hardly occurs because of either a very low base rate or very low insensitivity to bending angles, clusters become irreversible or decay very slowly. By contrast, if severing occurs too frequently, a significant reduction in filament length prevents F-actins from forming large clusters. In addition, we found that formation of large pulsed clusters requires both F-actin severing and actin turnover via treadmilling. If treadmilling does not occur (i.e., without actin polymerization or depolymerization), fragmented filaments resulting from severing cannot be completely depolymerized or elongated. As a result, F-actin length is reduced significantly, so cluster formation does not occur.

Cells have various ways to regulate the severing rate of F-actins. The activity of gelsolin, which severs F-actin by destabilizing interactions between actins and then binds to a new barbed end, is regulated by Ca²⁺ (45). In addition, previous studies have shown that binding of cofilin to F-actin promotes severing (30, 46). Depending on cofilin concentration, severing events occur with quite distinct rates and different angle insensitivities. Association of cofilin to F-actin can be enhanced significantly by diverse actin-binding proteins, such as coronin and Aip 1 (47, 48). Therefore, variations in parameters for the F-actin severing rate in this study may be related to physiological functions of cells.

Recent experiments have demonstrated that pulsed contraction results from contractile instability regulated by spatiotemporal expression of RhoA (36, 40, 41, 43). During morphogenetic events and in the one-cell-stage C. elegans embryo, myosin and RhoA colocalize with the pulsed clusters. Although results from those experiments have suggested that the pulsed contraction is a direct consequence of RhoA cycling activity (40), a recent study suggested that RhoA might act as a pacemaker (36). During one pulse, RhoA locally enhances activities of myosin motors to form clusters and then deactivate the motors later. However, after deactivation of motor activities, it is not likely that numerous connections between F-actins within clusters are broken simultaneously for disassembly of the clusters. Based on the results in our study, it is anticipated that the turnover and severing of F-actin still play a very crucial role for cluster disassembly and pulsed contraction by locally reducing connectivity within the clusters.

Thus, our study provides insights into understanding of a role of F-actin severing for the distinct pulsed contraction observed during various physiological events. In our future studies, we will incorporate the spatiotemporal expression of RhoA and then relate the RhoA activity with motor activities to recapitulate and study more physiological pulsed contraction.

Author Contributions

Q.Y. and J.L. performed simulations and analysis. J.L., Q.Y., and T.K. designed the research. J.L., Q.Y., M.P.M., and T.K. wrote the manuscript. T.K. provided the software and computational resources.

Editor: Vivek Shenoy.

Supporting Citations

References (49, 50, 51, 52, 53, 54, 55, 56, 57) appear in the Supporting Material.