Coherent backscattering of light by an anisotropic biological network

Abstract

The scattering strength of a random medium relies on the geometry and spatial distribution of its components as well as on their refractive index. Anisotropy can, therefore, play a major role in the optimization of the scattering efficiency in both biological and synthetic materials. In this study, we show that, by exploiting the coherent backscattering phenomenon, it is possible to characterize the optical anisotropy in Cyphochilus beetle scales without the need to change their orientation or their thickness. For this reason, such a static and easily accessible experimental approach is particularly suitable for the study of biological specimens. Moreover, estimation of the anisotropy in Cyphochilus beetle scales might provide inspiration for improving the scattering strength of artificial white materials.

1. Introduction

An object is opaque white when the light incident on it undergoes multiple scattering events before exiting the medium, i.e. when the object is optically thick [1]. The optical thickness is defined as the ratio between the physical thickness of an object and the transport mean free path (ℓ_t), namely the distance that light travels before losing information about its starting propagation direction [2,3]. Commonly, ℓ_t is of the order of tens of micrometres in low-refractive-index white materials [4,5]. Therefore, opacity is only achieved for relatively large thicknesses (of the order of hundreds of micrometres) to allow a sufficient number of scattering events.

Nature, however, provides a different approach that can serve as an inspiration for the manufacturing of polymeric, thin but still opaque white materials [6–8]. In particular, the brilliant whiteness shown by the Cyphochilus beetle is known to be generated by multiple scattering of light inside the extremely thin scales (≃7 µm thick) that cover its exoskeleton (figure 1a,b) [4,9–12]. The beetle's intra-scale structure is composed of a nanostructured network of chitin filaments with a filling fraction of around 45% [13]. The chitin fibres inside the beetle scales are organized anisotropically, i.e. mainly oriented parallel to the surface of the scales (figure 1c). This structural anisotropy increases the scattering strength in the orthogonal direction to the scale surface, at the expense of the in-plane scattering, which is not as relevant for the total reflectance of the insect [12]. With such morphology and geometry, the beetle achieves high total reflectance (about 70% over the whole visible range) with a thin, lightweight and anisotropic network made of low-refractive-index material [4,12,13].

Figure 1.

Images of a white beetle at different magnifications: (a) photograph of the Cyphochilus beetle; (b) micrograph of the organization of the scales; (c) SEM image of a cross-section of a Cyphochilus scale showing the interconnected network of chitin filaments which is responsible for the white appearance of the insect. Scale bar: (a) 1 cm, (b) 200 µm and (c) 1 µm.

In recent years, a number of different techniques have been used to characterize anisotropic media; for example, spatially resolved reflectance [14,15], imaging diffuse transmission [12,16,17], spatio-temporal visualization of transmitted light [18] and coherent backscattering (CBS) [19–22]. As of yet, the accuracy in determining the in-plane and out-of-plane components of the light transport mean free path in Cyphochilus beetle scales has been limited by the strong thickness dependency of the experimental techniques used [4,12].

In this study, we showed that the CBS technique is well suited for studying the scattering properties of biological samples, allowing the anisotropy of a system to be estimated without the need to change its orientation or its thickness. Moreover, the CBS provides a precise evaluation of the in-plane transport mean free path without requiring samples with different thicknesses, in contrast with other static and easily accessible techniques. Our experimental results contribute to the understanding of scattering optimization in Cyphochilus beetle scales, providing a valuable guide for the development of novel sustainable materials by showing how to obtain a strong optical response while using a low-refractive-index biopolymer as a building block.

2. Results and discussion

To characterize light propagation in Cyphochilus scales, we performed a CBS experiment. We measured the angularly resolved light scattered by the sample around the backscattering direction, which shows a characteristic peak profile [23]. The CBS is the Fourier transform of the spatial distribution of light exiting the sample in the backscattering direction [3]. This phenomenon is often understood as an interference effect that originates from the superposition of a large number of two-wave interference patterns from reciprocal waves [23–27]. These waves have travelled the same optical path inside the medium but in opposite directions (figure 2a) and are therefore phase-related. The resulting CBS intensity distribution has a conical shape whose width provides a direct measurement of the light transport mean free path of the material [3].

Figure 2.

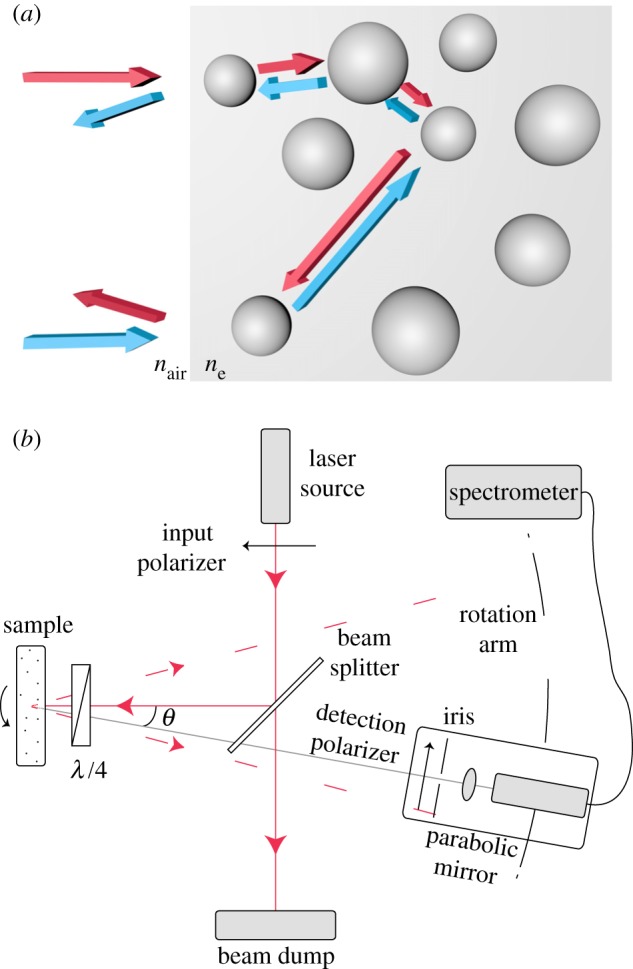
(a) Illustration of two counter-propagating photons, red and light blue arrows. For simplicity, the scattering centres are represented as spheres. (b) Schematic of the CBS set-up in an HC configuration: the red dashed lines define the cone of backscattered intensity, while the grey line represents the detection rotation. The sample was mounted on a rotation mount, whose axis was perpendicular to the propagation direction of the laser beam, to average over different disorder realizations.

The experimental set-up is shown in figure 2b. A collimated laser diode (peak wavelength of 635 nm, spot size of 2.5 mm and output power of 1.2 mW) was used as the light source. The scattered signal was focused, using a parabolic mirror, on a 100 µm core fibre connected to a spectrometer. The angular resolution of our set-up was ≃0.25 mrad. To acquire the CBS line shape, the speckle pattern, which occurs as a result of the high spatial coherence of the light source, needs to be averaged out [26]. This was done by placing the sample on a motorized rotation mount whose axis was the same as the propagation direction of the incoming laser beam. This averaging procedure precludes the possibility of investigating a potential in-plane, xy, anisotropy. However, it has recently been shown that the Cyphochilus scales are characterized by an isotropic spectral density in the xy-plane [13]. For this reason, our study focused only on the study of out-plane anisotropy.

The enhancement factor of the coherent signal, i.e. the ratio between the intensity at the exact backscattering angle and the incoherent background, strongly depends on the polarization. This is maximized when the single-scattered photons, which do not have a reciprocal counterpart and therefore contribute only to the incoherent background, are filtered out. This can be done by acquiring the CBS in the helicity-conserving (HC) channel (figure 2). The HC signal was then normalized to the one acquired in a linear non-conserving (LNC) configuration, as discussed in [28].

The measured CBS signal is reported in figure 3. The experimental data show a maximum lower than the theoretical value for semi-infinite media of 1 and a rounded top. This deviation is a consequence of the small thickness of the Cyphochilus scales and can be described by the isotropic theory for finite media [29]

$$\begin{array}{rl}& {\gamma }_c=3{\mathrm{e}}^{bv}[\cos (bu)[\left(\frac{(\nu -(\nu -\alpha )\cosh (2z_e\alpha )}{{(\nu -\alpha )}^2+u^2}\right)\\ & +\left(\frac{(\nu -(\nu -\alpha )\cosh (2z_e\alpha )}{{(\alpha -\nu )}^2+u^2}\right)]\\ & +\sin (bu)\left(\frac{u}{{(\alpha +\nu )}^2+u^2}-\frac{u}{{(\nu -\alpha )}^2+u^2}\right)\sinh (2z_e\alpha )\\ & +\frac{(\nu -\alpha )\cos h((\nu -\alpha )b-2z_e\alpha )-\nu \cos h((\nu -\alpha )b)}{{(\nu -\alpha )}^2+u^2}\\ & +\frac{(\nu +\alpha )\cos h((\nu +\alpha )b-2z_e\alpha )-\nu \cos h((\nu +\alpha )b)}{{(\alpha +\nu )}^2+u^2},\end{array}$$ 2.1

where $\mu =\cos (\theta ),\hspace{0.17em}\nu =1/2(1+1/\mu ),u=k{\ell }_t(1-\mu ),\alpha =$ $k{\ell }_t\sin (\theta ),B=b+2z_e$ The parameters k, ℓ_t and b are the wavevector, the isotropic transport mean free path and the optical thickness, respectively. For semi-infinite media, i.e. b → ∞, equation (2.1) reduces to [29]

$${\gamma }_{c,\mathrm{semi}}=\frac{3[\alpha +\nu (1-e^{-2z\alpha })]}{2\alpha \mu \nu [{(\alpha +\nu )}^2=u^2]}.$$ 2.2

The reduction of the theoretical maximum in finite media is caused by the suppression of long light paths, which are responsible for the formation of the cusp of the CBS profile for semi-infinite media [2]. To accurately determine the transport mean free path, the effect of the internal reflections at the scale interface on the light path distribution inside the chitin network was accounted for in the extrapolation length, z_e = (2/3)(1 + R)/(1 − R) [30–32]. R is the angle- and polarization-averaged reflection coefficient at the slab interface and can be obtained by an angular integration of the Fresnel coefficients [31,33]. These coefficients depend on the effective refractive index (n_e) of the chitin network, which was estimated by the Maxwell–Garnett theory [34]. The expression of z_e used in this study, and in the related literature regarding the study of the Cyphochilus beetle, is the one derived for isotropic systems. This approximation is justified by the absence of an analytical formula for the extrapolation length in anisotropic media [35].

Figure 3.

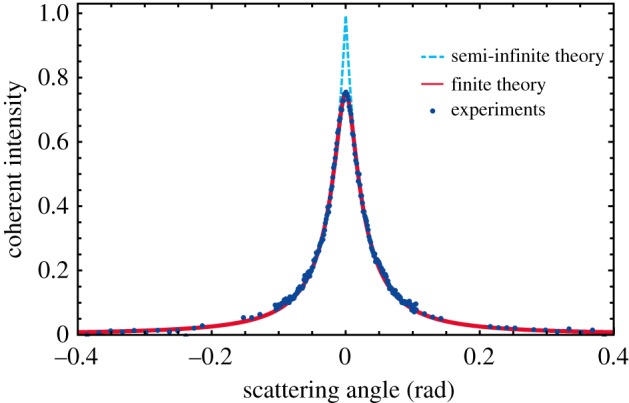
The theoretical fit of the experimental data (blue dots) using the isotropic theory for semi-infinite (light blue dashed line) and finite (red solid line) media. Both curves were normalized to the maximum value of the semi-infinite theory. The experimental points were obtained by normalizing the signal measured in the HC configuration to that acquired in the LNC set-up.

Using a filling fraction of (45 ± 6)% [13], we calculated that n_e = (1.22 ± 0.03), R = (0.32 ± 0.04) and z_e = (1.29 ± 0.11). Finally, using the extrapolation length found from the expression above, we obtained ℓ_t = (1.40 ± 0.09) µm from the fit shown in figure 3.

In the literature, the isotropic theory has been used to obtain information about media in which the anisotropy is in the plane perpendicular (xy) to the incoming beam (z-direction) [19,22]. This type of anisotropy gives rise to a CBS cone whose line shape differs when acquired along the x- and y-directions [22]. It has recently been shown that the isotropic theory cannot be used to obtain quantitatively reliable information about the anisotropic light transport along perpendicular directions [35]. However, the anisotropy can be qualitatively estimated as the ratio between the widths of the CBS line shapes acquired along the x- and y-directions, which can be individually described by the isotropic theory [22]. Similarly, in the case of birefringent media as nematic liquid crystals, the isotropic theory can be used to describe the CBS line shapes originating from different polarization configurations [20].

In the case of the Cyphochilus beetle, the anisotropy is in the xz- and yz-plane (defining z as perpendicular to the surface of the scales) [12,13] and therefore the resulting CBS profile is isotropic (for light incoming along the z-direction). Owing to the particularly small thickness of the scales (≃7 µm), the probing direction of the incoming beam cannot be changed.

As the anisotropy cannot be investigated directly, to gain insight into the light transport inside the scales we performed anisotropic Monte Carlo simulations for scalar waves. A Monte Carlo technique is well suited for describing light propagation in disordered media, where the photon paths can be mathematically mapped into random walks [2,3,36]. Monte Carlo simulations have been extensively used both to investigate theoretical aspects of anisotropic diffusion [14,35,37–40] and to accurately describe experimental results regarding light propagation in anisotropic media [15,19,21].

Here, the photons paths in the white beetle scales were modelled by a series of random steps [41]. The anisotropy of the system was introduced via a direction-dependent step size, i.e. the components of the step vector were sampled from two different negative exponential distributions with mean ℓ_xy and ℓ_z for the in-plane and out-of-plane components, respectively. The angular component of each of the random steps was sampled from a distribution of points uniformly distributed on the surface of a unit sphere [42,43]. The collection of the initial and final positions of the walkers that escaped the material from the same face they entered it, which corresponds to reflected photons, was then used to reconstruct the CBS line shape [3,29]. The effect of residual absorption on the CBS line shape is not considered, owing to the negligible absorption of chitin in the visible [44]. The only parameters required for our Monte Carlo simulations are the distribution of the random steps, the thickness of the scales and the reflection coefficient at the scale interface (R). A schematic of the simulation parameters is illustrated in figure 4a.

Figure 4.

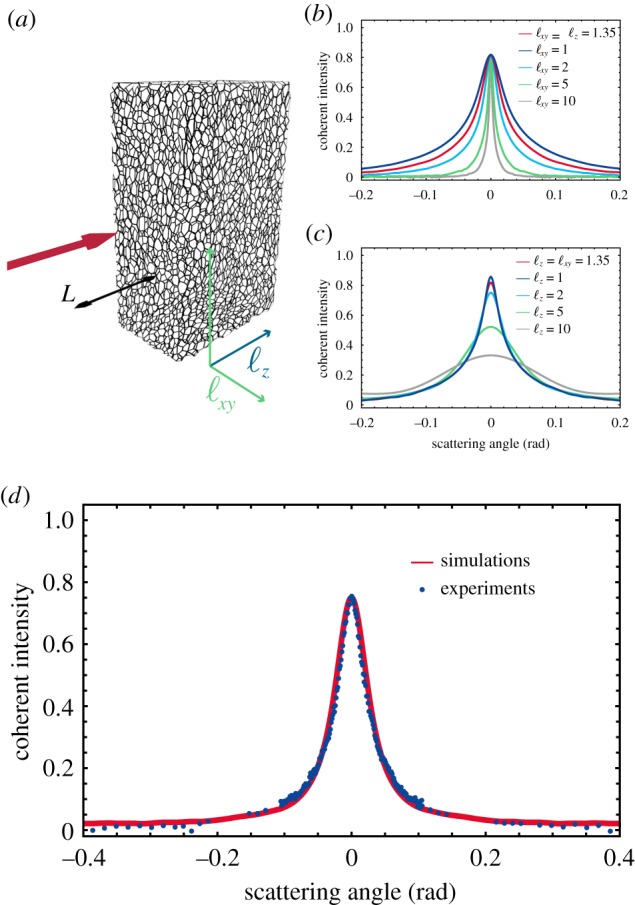
Monte Carlo simulation of the CBS line shape by an anisotropic medium: (a) illustration of the simulation parameters, (b,c) varying the in-plane and the out-of-plane components of the mean free path. For both simulations the thickness of the slab (L) was fixed at 15 µm. (d) Fit of the experimental data with the anisotropic simulation. All the simulations were performed using 1 million photons. The simulated curves were normalized to the maximum value of a simulation with OT = 1000.

Figure 4b,c shows how the CBS line shape is affected by changing both the in-plane (ℓ_xy) and out-of-plane (ℓ_z) components of the transport mean free path. In particular, ℓ_xy determines the width of the CBS profile, while the optical thickness, defined as OT = L/ℓ_z (where L is the thickness of the medium), specifies the enhancement of the coherent signal. These results can be qualitatively explained by the fact that the CBS depends only on the distance between the positions of the first scattering event (when the photon enters the medium) and the last (when the photon exits the medium). When a large number of photons is considered, these two positions have on average the same z-coordinate (which is of the order of ℓ_z), and therefore their distance can be considered to be z-independent. However, as discussed previously for the isotropic theory, when the optical thickness of the medium is small (i.e. when long light paths are not allowed by the finite thickness of the medium) the top of the CBS is rounded. The limited influence of the optical thickness on the width of the CBS line shape allows a precise value of ℓ_xy to be obtained without requiring samples with different thicknesses. By fitting the experimental data with the Monte Carlo simulations, it is possible to disentangle the contribution of ℓ_xy and ℓ_z to the CBS line shape. In particular, we obtained a value of ℓ_xy = (1.40 ± 0.09) µm and an optical thickness (OT) = (6.89 ± 0.13). The data were fitted by minimizing the χ². The errors in ℓ_xy and OT were estimated by performing simulations in which the two parameters were gradually changed. This procedure was then repeated to take into account the uncertainty in the determination of the reflection coefficient (R).

The measured optical thickness is in good agreement with the total transmission data reported in the literature [4,12]. The total transmission (T) for slab geometry media in the diffusion approximation is

$$T=\frac{2z_e}{L+2z_e},$$ 2.3

where L is the slab thickness. Equation (2.3) is the limit for negligible absorption of the expression derived in [45]. Using T = (0.29 ± 0.02), as reported in [4,12], and the extrapolation length previously calculated we obtained OT_lit = (6.3 ± 1.2), which is consistent with what we measured.

From the measured OT and assuming L = (7 ± 1) µm, where L and its error represent the mean and 1 s.d. of the distribution reported in [12], we obtained ℓ_z = (1.02 ± 0.15) µm. The error in ℓ_z, which is mainly determined by the uncertainty in the thickness of the sample, can be affected by systematic errors given by surface roughness and curvature [3,46,47]. Comparing ℓ_z with ℓ_xy, the measured optical anisotropy (OA) is

$$\mathrm{OA}=\frac{{\ell }_{xy}-{\ell }_z}{{\ell }_z}=(0.37\pm 0.24).$$ 2.4

Our experimental result is in agreement with the three-dimensional reconstruction of the chitin network reported in [13], which predicts $\mathrm{OA}\simeq 0.5$.

3. Conclusion

In conclusion, we demonstrated that the transport mean free path and OA of light in the Cyphochilus beetle scales can be determined by measuring the CBS and that the results are in agreement with the one predicted in [13]. Exploiting the CBS effect provides a measurement of the OA which describes more accurately the scattering properties of the Cyphochilus beetle than the results reported in the literature. In addition, the experimental technique reported here allows the anisotropy of a system to be estimated without the need to change its orientation or its thickness, making the CBS a technique particularly suitable for the study of biological specimens.

Data accessibility

The raw data and the Monte Carlo code regarding the publication can be found in the electronic supplementary material.

Authors' contributions

G.J., O.D.O., A.D.L., R.S. and S.V. designed the experiments. G.J., J.B., R.S. and S.V. conceived and planned the simulations. G.J. carried out the experiments and the simulations. All authors provided critical feedback and helped shape the research, analysis and manuscript.

Competing interests

We declare we have no competing interests.

Funding

This study was supported by the European Research Council (ERC-2014-STG H2020 639088), the BBSRC David Phillips Fellowship (BB/K014617/1), the Leverhulme Trust's Philip Leverhulme Prize and the Leverhulme Trust (no. PG-2016-129), the EPSRC (grant nos. EPSRC EP/M027961), the Leverhulme Trust (grant no. RPG-2014-238), the Royal Society (grant nos. RG140457 and IE160502) and the Nanolase project (PRIN 2012).