Abstract
Global analyses of biodiversity consistently reveal recurrent patterns of species distributions worldwide. However, unveiling the specific mechanisms behind those patterns remains logistically challenging, yet necessary for reliable biodiversity forecasts. Here, we combine theory and experiments to investigate the processes underlying spatial biodiversity patterns in dendritic, river-like landscapes, iconic examples of highly threatened ecosystems. We used geometric scaling properties, common to all rivers, to show that the distribution of biodiversity in these landscapes fundamentally depends on how ecological selection is modulated across space: while uniform ecological selection across the network leads to higher diversity in downstream confluences, this pattern can be inverted by disturbances when population turnover (i.e. local mortality) is higher upstream than downstream. Higher turnover in small headwater patches can slow down ecological selection, increasing local diversity in comparison to large downstream confluences. Our results show that disturbance-mediated slowing down of competitive exclusion can generate a specific transient signature in terms of biodiversity distribution when applied over a spatial gradient of disturbance, which is a common feature of many river landscapes.
Keywords: metacommunity, dendritic networks, biodiversity, patch size, perturbations
1. Introduction
Local species diversity in dendritic, river-like landscapes is generally expected to be higher in larger, more connected downstream confluences than in upstream headwaters [1–6]. Previous theoretical, comparative, and experimental studies have all emphasized the importance of dispersal along the network structure of the landscape as a key driver of this diversity pattern, regardless of the specific local drivers of community dynamics such as ecological drift [3,7] or selection [8]. The pattern of lower local diversity in upstream habitats compared to downstream confluences (hereafter ‘classical pattern’), however, is not ubiquitous in natural river systems: recent empirical studies [9,10] have documented that diversity patterns can be completely reversed, with higher diversity in upstream headwaters rather than in downstream confluences (hereafter ‘reversed pattern’). These contrasting empirical patterns, especially the reversed one, and the transition from one to the other remain insufficiently understood and are currently not accounted for by any theoretical or experimental work. Given that river ecosystems support roughly 10% of all animal species [11], it is unfortunate that we are still lacking a general understanding of the processes driving the patterns of diversity in these ecosystems. A better understanding of the dominant mechanisms that generate contrasting diversity patterns is essential if we hope to forecast effects of global change and possibly design management strategies to counter current trends of erosion of biodiversity and ecosystem services in river ecosystems worldwide [12–14].
Riverine landscapes are structured by spatial flows of organisms and resources [1,15]. They also inherently display strong environmental gradients, both in terms of resources (habitat size/land use influence) and disturbances (current flow, erosion) [1,16]. While previous theoretical work has primarily focused on dispersal-related mechanisms [3,17,18], the latter intrinsic characteristics might be key to explain contrasting diversity patterns in such spatially structured systems where habitat size scales with position in the landscape [4,15,16,19]: small headwater patches (‘patch’ sensu [20]) can be found across a wide range of landscape connectivity, but fewer and larger downstream patches are inherently more connected [16]. The Theory of Island Biogeography [21,22] provides an explanation for one of the most established and universal ecological patterns stating that smaller and more isolated patches suffer higher extinction rates and lower immigration rates eventually leading to lower diversity than in larger and more connected patches [21–25]. In such a scenario, competitive exclusion due to ecological selection occurs more rapidly in small headwater communities because, in finite populations, extinction thresholds are reached earlier in smaller populations than in larger ones. Consequently, all else being equal, at equilibrium, smaller patches should always contain lower diversity. In that context, the ‘reversed pattern’ can only occur if (i) all else is not equal and smaller headwater patches contain, for instance, higher environmental heterogeneity or (ii) the equilibrium state is reached more slowly in smaller patches. The former represents the obvious case where headwater patches might contain a higher proportion of micro-habitats providing higher niche dimensionality and/or refugia from competition and predation. Here, we focus on the latter case, where disturbances have the potential to keep smaller patches away from their equilibrium community composition. Given that upstream headwaters are less buffered from disturbances relative to larger downstream confluences, they are naturally more affected by disturbances such as desiccation or fluctuation in contaminants [26,27] and are increasingly affected by human impacts such as mountaintop mining [28]. Therefore, our study addresses an especially likely and increasingly widespread scenario.
Disturbances are often seen as an important driver of community dynamics by constraining the growth of more competitive species, which slows down competitive exclusion, and ultimately can favour transitory coexistence periods that are long enough to be empirically observed [29,30]. If disturbances impact smaller patches more strongly than larger patches, population turnover (here referring to local mortality, its underlying mechanism) will be increased, which can potentially lead to higher species richness in these smaller headwater patches than in larger downstream patches. More specifically, under the classical biodiversity pattern, competitive exclusion by ecological selection is expected to occur faster in smaller patches relative to larger patches because of lower population sizes (i.e. closer to extinction threshold) and potentially higher encounter rates among more spatially confined species (i.e. stronger interaction strengths—see [31]). In the presence of disturbances, however, ecological selection could be slowed down, more so in smaller than in larger patches, potentially reversing the spatial biodiversity pattern. Despite strong empirical evidence on the role of disturbances in driving biodiversity patterns in riverine ecosystems, via its impact on competitive dynamics [2,32–36], it remains highly challenging to investigate this hypothesis directly in the field due to multiple interacting factors and lack of replication. Therefore, to get a mechanistic understanding, we first develop a general mathematical model, and then test the main predictions in well-established ecological microcosm landscapes [37,38].
Specifically, we here investigate the processes underlying the distribution of biodiversity in river-like landscapes and focus on characteristic patch size distributions and disturbances (i.e. local mortality). In natural riverine landscapes, patch size distribution, network configuration, and disturbances are intrinsically linked and cannot be disentangled in a causal approach [4,16,39]. Thus, here we combined theory and experiments to untangle these naturally interlinked factors. We first show theoretical results from a spatially explicit Lotka–Volterra competition metacommunity model including dispersal along dendritic networks, demographic stochasticity, and patch size-dependent mortality, that is, higher local mortality in smaller patches (see full details in Material and methods). We secondly tested experimentally the model's main predictions, using dendritic protist microcosm landscapes [38] of the same network topologies (see Material and methods and figure 1). Our work shows that patch size-dependent mortality and its effect on ecological selection can be a key mechanism shaping transient biodiversity patterns in entire river-like landscapes.
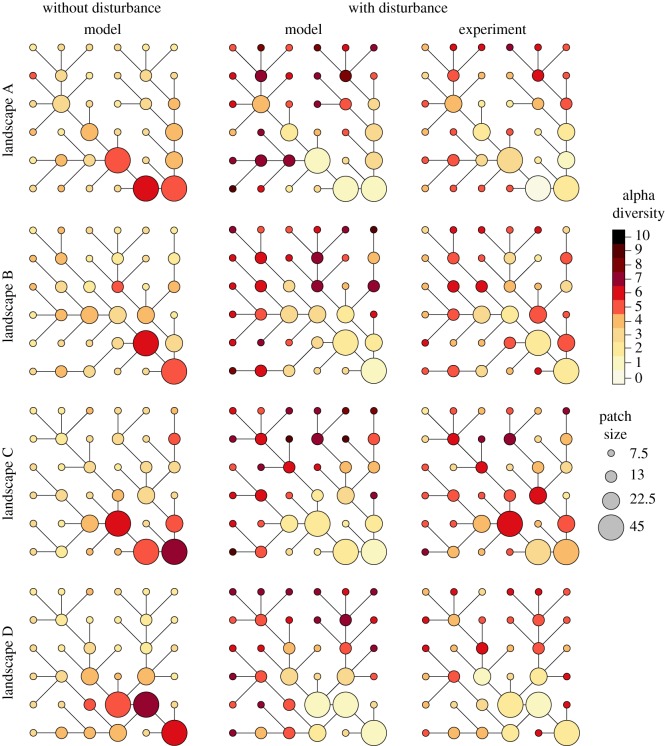
Figure 1.
Diversity distribution (local species richness) in dendritic, river-like landscapes with and without disturbance. The ‘Model’ landscapes displayed in this figure are examples of simulations made with the same replicate community. Results were qualitatively similar for each of the 10 replicate communities randomly generated (see electronic supplementary material, figure S4); model parameters specific to these simulations are dispersal δV = 0.05, mortality rates m are 0.1, 0.0868, 0.064, and 0.01, respectively, from smaller to larger patches for simulation with disturbance (patch size-dependent mortality) and 0 without. For network graphs based on experimental results, each graph represents the local diversity pattern for one of the four landscape replicates (A, B, C, and D). For illustration purposes, all network graphs are depicted at snapshots of diversity patterns at time of comparable local diversity: time 118.4 (simulations without disturbance; faster dynamics), time 167.9 (simulations with disturbance; slower dynamics), and at experimental day 29 (last sampling day). See complete dynamics over time for model simulations in electronic supplementary material, figure S4 and for experimental results in electronic supplementary material, figure S5.
2. Material and methods
(a). Model simulation
To investigate the mechanisms underlying biodiversity distributions in dendritic, river-like networks in relation to their intrinsic non-random patch connectivity/size pattern, we first used general simulations of a Lotka–Volterra competition model for 10 species, in which the temporal variation in abundance of species i located in patch x, Nix, is described by:
where ri is the intrinsic growth rate, αij the per capita effect of species j on species i (competition coefficient), Kix the carrying capacity of species i in patch x (K is higher in larger patches), dx the dispersal rate from patch x, and mx the patch size-dependent mortality rate (population turnover). Demographic stochasticity is added according to a standard method [40] with the following term . The parameter a modulates the magnitude of this drift and ρ is the random factor sampled from a Gaussian distribution. Parameters are set as in Giometto et al. [40] to produce a white noise preventing artificial persistence of very small populations (see electronic supplementary material, table S1). Species traits are parametrized in a very simple and general way, independent of our experimental organisms, to preserve the generality of our model predictions. To limit sources of variations, r, K, and d are the same for all species (see values in electronic supplementary material, table S1) and we implement species differences via competition coefficients only. Competition coefficients are drawn from a Gaussian distribution (μ = 2, σ = 0.25) with all negative coefficients multiplied by −1 to obtain a purely competitive community. The dispersal term is a sum function of the differences between immigration from patch x and each emigration from patch z to which it is connected according to the specific topology of the dendritic landscape. We scale dispersal rates with patch size to make it comparable to the experimental set-up where exchanging a constant volume between two patches was the most feasible dispersal mode. Then dispersal rate was implemented as dx = δV/Vx, with δV the fixed volume dispersed by unit of time from a patch x and Vx the volume of the patch x. In our simulations, we vary δV to alter dispersal rates. Our results are, however, robust to change in dispersal mode whether the dispersal rate is a constant rate either per edge or per patch (see electronic supplementary material, appendix A and figures S1 and S2). Moreover, while we considered only bi-directional dispersal to accommodate logistical constraints on the experimental design, we also conducted a sensitivity analysis, which attests that the results are robust to a strongly biased downstream dispersal (electronic supplementary material, appendix A and figures S2 and S3). As a minimal assumption to implement patch size dependency in turnover, we make local mortality rates follow a linear negative relationship with patch size (see sensitivity analysis below for the values). We report results with dispersal and local mortality rates set at intermediate levels (δV = 0.05, and m are 0.1, 0.0868, 0.064, and 0.01, respectively, from smaller to larger patches) in the first part of the results (figures 1–3), while we explore further the parameter space with multiple combinations of those two rates in figure 4 (see below for more details).
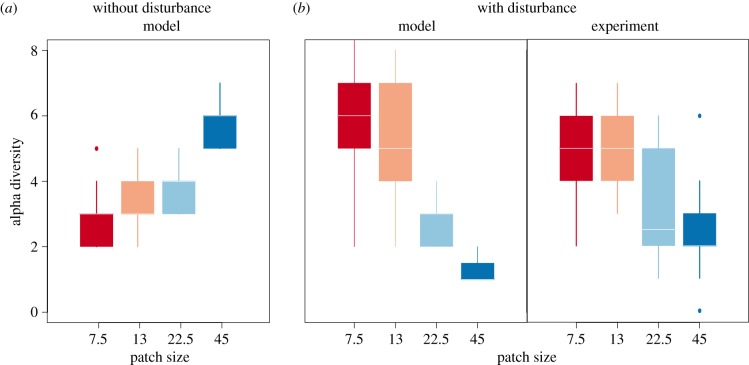
Figure 2.
Diversity distribution in dendritic, river-like landscapes (a) without and (b) with disturbance. For the panels based on simulations, each boxplot represents the distribution of diversity values across the four replicate landscapes used in the experiment, and for one of the 10 replicate communities that were used in the simulations (see electronic supplementary material, figure S4 for all 10 replicates). Parameters and data are the same as in figure 1. The two largest patch sizes of 45 (N = 11) and 22.5 ml (N = 14) show significant decline in local diversity compared to the smaller patch sizes of 13 (N = 34) and 7.5 ml (N = 85) (see electronic supplementary material, table S1 for complete linear mixed effect model results).
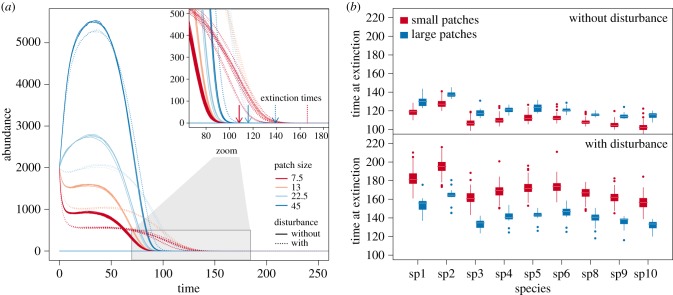
Figure 3.
Time to extinction as a function of disturbance in the simulations. (a) Example of temporal dynamics of one species in each patch of one landscape with and without disturbance (dotted and full lines, respectively). Arrows indicate time at extinction for the smallest (red) and largest (blue) patches with and without disturbance. (b) Time at extinction for each species in the smallest and the largest patches with disturbance (lower panel) or without disturbance (upper panel). Each boxplot represents the distribution of values across the patches of four replicate landscapes, and for one of the 10 different replicate communities that were used in the simulations (see electronic supplementary material, figure S4 for all replicates). Data and parameters are the same as in figure 1.
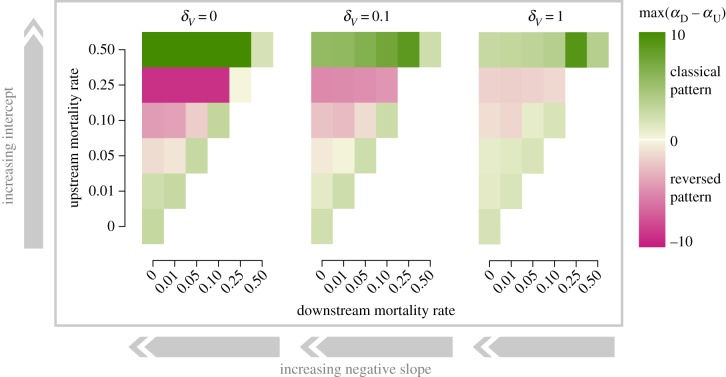
Figure 4.
Persistence of diversity patterns in dendritic, river-like landscapes. The figure illustrates the parameter space within which each diversity pattern is found as a function of the strength of disturbance (patch size—mortality rate relationship) and the magnitude of dispersal (for more dispersal rates see electronic supplementary material, figure S6). δV is the dispersal volume, with which we vary the dispersal rate (dx = δV/Vx, with Vx the volume of patch x). αD–αU corresponds to the maximum observed difference, along the temporal dynamics, in richness between the largest and smallest patches. When αD–αU is positive (green colours), the classical pattern emerges over the course of the dynamics, with higher diversity in large than in small patches, while when the difference is negative (pink colours), it is the reversed pattern, with higher diversity in small (i.e. headwater) rather than in large patches. Each case represents an average over 50 replicate simulations (five different landscapes × 10 different communities). Mortality rate increase in small upstream patches raises the intercept of the negative mortality rate–patch size relationship, while mortality rate increase in large dowstream patches reduces its slope.
For the landscapes, we use river-like networks generated from five different space-filling optimal channel networks [41] known to reproduce the scaling properties observed in real river systems [4,42]. Optimal channel networks are built under the assumption that drainage network configurations always minimize total energy dissipation, and the empirical observation that river network properties are scale-invariant (i.e. fractal, see Rinaldo et al. [42]). In order to also be able to use the same landscapes in the experiment, a coarse-graining procedure is used to reduce the five generated constructs to equivalent 6 × 6 patch networks, preserving the characteristics of the original three-dimensional basin (figure 1, for details, see appendix A in Carrara et al. [4]), but having a total patch size that was experimentally feasible. These 6 × 6 patch networks contained 36 patches of four different volumes (V): 7.5, 13, 22.5, and 45 ml (figure 1). The ratios between those different volumes are based on the known relationship between the size of a channel reach and the landscape-forming discharge at-a-station within the catchment (see [16] and appendix A in Carrara et al. 2014 [4] for more details). These volume values are also used for patch sizes Vx in the model.
Using these settings, we test the effect of patch size-dependent mortality on biodiversity patterns by contrasting simulations with and without disturbance. We have two levels of replication: we replicate our simulations over the five different dendritic landscapes to assess the independence of the results from specific network topologies, and 10 random realizations of the community matrix (replicate communities), leading to 50 simulations in total per scenario (local mortality settings at a given dispersal rate). Simulations always start with all species already present in all patches and with the same absolute abundance set to 200. The results are robust to starting conditions with the same relative abundance (scaled to patch size). Simulations of community dynamics are run with the Runge–Kutta Cash–Karp method with adaptive step-size control (GSL 1.15) to optimize the accuracy of numerical integration in continuous time. Simulations are stopped at 400 units of time, which is sufficient to observe competitive exclusion (figure 3 and electronic supplementary material, figure S4). A species for which abundance falls below 10−3 is considered extinct and its abundance set to 0. The results are robust to the decline or suppressing of this threshold but we keep it to optimize the computation time.
In addition, we also explore the persistence of the different observed diversity patterns as a function of the magnitude of dispersal and the strength of the disturbance (local mortality) versus patch size relationship (see figure 4, electronic supplementary material, figures S5 and S6). We explore six levels of dispersal with δV ∈ {0, 0.05, 0.1, 0.25, 0.5, 1} and 21 mortality rate combinations. We used all mortality rate combinations with m ∈ {0, 0.01, 0.05, 0.1, 0.25, 0.5} in the largest and smallest patches, with local mortality in the smallest patches being higher or equal to in the largest patches (electronic supplementary material, figure S5). For each parameter combination, we run 50 simulations (i.e. five replicate landscapes × 10 replicate communities) resulting in a total of 6300 simulations. We completed our exploration by running the same set of simulations but with positive slopes between mortality rate and patch size (i.e. higher mortality in downstream than in upstream patches, see electronic supplementary material, appendix B and figures S7 and S8). This allowed us to explore and contrast biodiversity patterns with our initial predictions that are based on higher perturbation upstream (negative mortality-patch size slope). In the case of a positive slope, mortality is stronger in the largest patches potentially owing to increasing human densities in downstream sites.
(b). Experimental test
To empirically test the main prediction from our simulations, that is, patch size-dependent mortality leading to a reversal of the ‘classical’ biodiversity pattern in the dendritic network, we conducted a protist metacommunity experiment. We did not experimentally test for the ‘classical’ diversity pattern without disturbances because it has already been empirically verified many times in the literature [2,3,8,26,43,44], and in the same experimental conditions [4,18]. We focused here on testing specific predictions from the simulations owing to patch size-dependent mortality and the occurrence of the predicted reversed pattern of biodiversity under this scenario. In that context, the experiment constitutes a very conservative test of our much more general simulations. The experiment consisted of seven protist species interacting and dispersing for 29 days along four different dendritic networks of 36 patches (same as four of the five landscapes used in the simulations; figure 1). Each landscape had four different patch size levels (7.5, 13, 22.5, and 45 ml) connected by dispersal along a dendritic network and preserving the scaling properties observed in real river systems (figure 1 and electronic supplementary material, figure S9 for a photo, and section ‘model simulation’ above, following Carrara et al. [4]).
Our communities were composed of six bacterivorous protist and one rotifer species (henceforth called ‘protists’): Tetrahymena sp., Paramecium caudatum, Colpidium striatum, Spirostomum sp., Chilomonas sp., Blepharisma sp., and the rotifer Cephalodella sp. The latter two species can, next to feeding on bacteria, to a lesser degree also predate on smaller protists. These protists were feeding on a common pool of bacteria (Serratia fonticola, Bacillus subtilis, and Brevibacillus brevis). Prior to the beginning of the experiment, each protist species was grown in monoculture in a solution of pre-autoclaved standard protist pellet medium (Carolina Biological Supply, Burlington NC, USA, 0.46 g protist pellets 1 l–1 tap water) and 10% bacteria inoculum, until they reached carrying capacity (for methodological details and protocols, see Altermatt et al. [38]). Protist abundance and diversity were measured by video recording combined with a trained algorithm to differentiate each species based on their morphological traits (see below).
Each microcosm in our four landscapes consisted of a 50 ml polypropylene Falcon tube (VWR, Dietikon, Switzerland). At day 0, we pipetted an equal mixture of each of the seven species into each microcosm to reach the corresponding volume (7.5, 13, 22.5, or 45 ml). Thus, protist communities were added at 15% of their carrying capacity and were allowed to grow 24 h before the first dispersal event. Dispersal and imposed local mortality (see below) occurred two times per week, while sampling of the communities for species count was done once a week (two dispersal events between each sampling with at least 48 h between the last dispersal/mortality event and sampling). Sampling events and counting were done on days 0, 7, 15, 21, 29 of the experiment, while dispersal and mortality events occurred on days 1, 4, 8, 11, 16, 19, 22, 25 of the experiment.
Dispersal was done by pipetting a fixed volume (1 ml) from one patch to each of the connected patches. Dispersal was bi-directional along each edge (1 ml from a to b and 1 ml from b to a), which ensured the maintenance of the same volume in each patch throughout the duration of the experiment. We implemented bi-directional dispersal to avoid the logistical challenge of maintaining equal patch volumes with directional dispersal. To confirm that this experimental assumption did not affect our results, we conducted a sensitivity analysis with the model including an extensive number of additional simulations that demonstrate the robustness of our results to such directional dispersal (see electronic supplementary material, appendix A and figures S2 and S3). For dispersal, we used a mirror landscape (following methods developed in Carrara et al. [18]): first, 1 ml was sampled for each edge connecting a microcosm in the real landscape and then pipetted to the recipient microcosm, but in the mirror landscape. Once this was done for all microcosms, the content of each mirror microcosm was poured to the same microcosm in the real landscape. It is noteworthy that because we started our simulations and experiment with species already assembled (all species were present at the start in all patches), we are probably underestimating the importance of dispersal dynamics in the process of early assembly [45].
Patch size-dependent mortality was experimentally reproduced by sampling, killing, and pouring back (no change in biomass) a fixed volume (1 ml) of each community regardless of patch size, which resulted in a gradient of proportionally decreasing mortality from smaller upstream to larger downstream microcosms (this 1 ml corresponds to 13%, 8%, 4%, and 2% of disturbance-induced mortality in the respective patch sizes) and can be seen as a general type of disturbance that is blind to species identity (e.g. habitat destruction, heavy pollution). More specifically, for each mortality event, 1 ml was sampled from each microcosm and microwaved until boiling to turn all living cells into detritus [46]. After a 1 h cooling period at ambient temperature (20°C), the microwaved sampled had reached ambient temperature again and was poured back into the same microcosm.
At each measurement day, 0.4 ml was sampled from each microcosm for the protist density measurements. Sampling was done semi-destructively, such that the sampled volume was not returned back to the patch to avoid cross-contamination. Therefore, sampling was acting analogously to the implemented disturbance regime. Protist abundance was measured by using a standardized video recording and analysis procedure [47,48]. In short, a constant volume (34.4 μl) of each 0.4 ml sample was measured under a dissecting microscope connected to a camera for the recording of videos (5 s per video, see electronic supplementary material, appendix B for further details on this method). Then, using a customized version of the R-package bemovi [48], we used an image processing software (ImageJ, National Institute of Health, USA) to extract the number of moving organisms per video frame along with a suite of different traits for each occurrence (e.g. speed, shape, size) that could then be used to filter out background movement noise (e.g. particles from the medium) and to identify species in a mixture (see electronic supplementary material, appendix C).
(c). Statistical analysis
To test for the effect of patch size on protist local diversity, we used a two-way linear mixed effect model testing the interactive effects of patch size and continuous time on protist species richness. To control for temporal pseudo-replication and temporal autocorrelation, we added replicate and time as nested random factors. The model was fitted by maximizing the restricted log-likelihood (‘REML’, see Pinheiro et al. [49]). The linear mixed effect model was conducted using the R-package NLME [49]. The complete results can be found in electronic supplementary material, table S2.
3. Results
(a). Shift in diversity patterns
In the simulations without disturbance (i.e. local mortality), the highest diversity levels are found in the large downstream patches (figures 1 and 2a). By contrast, the smaller, mostly upstream patches have lower diversity levels. This difference in diversity unfolded with smaller patches supporting smaller population sizes (figure 3a), which are then more prone to extinction relative to populations in larger patches (figure 3b).
In the simulations with disturbance (i.e. local mortality), the highest diversity levels are found in upstream patches (figures 1 and 2b) consistently across all the different community (different species traits) and landscape (different spatial networks) replicates. The same pattern was found in the context of our experiment with an aquatic protist community (figures 1 and 2b). As in the simulations (electronic supplementary material, figure S4), the biodiversity pattern appeared progressively over time with no apparent effects of patch size on the first sampling day (experiment day 7, 7.4 ± 0.67 species in the smallest versus 7.1 ± 0.70 species in the largest patches, mean ± s.d., electronic supplementary material, figure S10 and table S2), but by the final experimental day, i.e. 29, there was a clear and significant decline in local diversity with patch size (4.7 ± 1.3 species in the smallest patches versus 2.5 ± 1.5 species in the largest patches, mean ± s.d., figures 1 and 2b and electronic supplementary material, table S2). Those changes in species richness were mirrored by changes in community structure (electronic supplementary material, figure S11). While being homogeneous in species number across patch sizes (see above), communities at day 7 also tended to be dominated by the fast growing species Cephalodella sp. (rotifer) and Chilomonas sp. (electronic supplementary material, figure S11). By the end of the experiment at day 29, communities were much more variable in composition but with the competitor Paramecium caudatum being most often dominant (electronic supplementary material, figure S11). Communities in more disturbed patches (smaller patches) were also more even in relative abundances than in larger patches where fewer species were generally dominated by a single species (electronic supplementary material, figure S11). In terms of underlying mechanisms, the simulations show that, overall, patch size-dependent mortality slows down ecological dynamics (competitive exclusion; figure 3a), but does more so in smaller patches (figure 3a), effectively increasing the time to extinction of less competitive species in those smaller patches (figure 3b).
(b). Persistence of diversity patterns in river-like landscapes
Our model predicts both diversity scenarios to occur within specific parts of the parameter space defined by the magnitude of dispersal and the strength of disturbance (i.e. intercept [mortality upstream] and slope [rate of change in mortality with increasing patch size] of the relationship between patch size and local mortality rate, see Methods for details; figure 4). For a negative slope (higher mortality upstream), weak patch size-dependent mortality, with low intercept or slope, generates the classical diversity pattern, while intermediate to high strengths of patch size-dependent mortality, with intermediate intercept and high slope, generate the reversed diversity pattern until local mortality is so high in small patches (high intercept) that all species upstream go extinct (figure 4, mupstream = 0.5), leading to a return to the classical diversity pattern. As expected, regardless of the strength of patch size-dependent local mortality, increasing dispersal only blurs diversity patterns by homogenizing diversity in the landscape (figure 4 and electronic supplementary material, figure S6). Additional sensitivity analysis showed that the reversed biodiversity pattern is robust to strong directionality in dispersal (90 or 99% downstream, electronic supplementary material, figures S2 and S3) because competitive exclusion still occurs later in small compared with large patches. Only the combination of both high dispersal rate and strong downstream directionality can weaken the reversed biodiversity pattern (electronic supplementary material, figure S3). Finally, a positive patch size–mortality rate relationship (higher mortality downstream than upstream) strengthens the classical diversity pattern until mortality rates are so high in larger patches that species go extinct faster downstream relative to upstream, making the reversed pattern emerge (see electronic supplementary material, figure S8, mdownstream = 0.5).
4. Discussion
Testing the impact of disturbance-induced mortality on the distribution of biodiversity in river-like landscapes, we found that disturbances can alter the classical biodiversity pattern of higher diversity in larger downstream patches predicted by the Theory of Island Biogeography (TIB) [3,7,21]: the classical pattern persists only until a certain level of disturbance, at which point asymmetry in population turnover between smaller upstream and larger downstream patches will reverse the pattern completely. Such a reversed diversity pattern has been observed in case studies from multiple natural river systems [9,10] and has challenged the idea of one overarching and universal diversity pattern to be expected in river-like landscapes as proposed by some studies [3,18,50,51]. However, this reversal has hitherto neither been understood mechanistically nor been predicted by theory. Here, we identify a general mechanism responsible for the observed reversed diversity patterns based on theoretical considerations, which we then successfully tested and validated experimentally. The specific mechanism identified (patch size-dependent mortality) represents a general type of disturbance. However, any mechanism that induces differences in the speed of ecological dynamics between upstream and downstream patches should cause a reversal of diversity pattern. It could be differences in temperature, for instance, with lower temperatures at higher elevation slowing down upstream dynamics, or strong anthropogenic disturbance downstream (e.g. heavy pollution) which would speed up species extinction rather than slow down competitive exclusion, in large compared to small patches (see electronic supplementary material, figure S8, mupstream = 0.5). Moreover, our approach using five different realizations of river-like networks that follow the invariant scaling properties of real riverine networks, allows us to generalize those results and their implications to riverine networks regardless of context-specific differences.
Our work indicates that the reversed pattern generated by patch size-dependent mortality is transient over time because the perturbations slow down ecological selection in smaller patches, but do not change endpoint equilibria. Similar results, related to the transient effect of disturbance, were found by Violle et al. [30]. Our results follow the trend by which communities are dominated early on by smaller, less competitive and fast growing species (here Cephalodella sp. and Chilomonas sp.), which are then replaced by larger and more competitive species (here Paramecium caudatum). The reversed diversity pattern emerges because, across the landscape, patches are organized along a gradient in the disturbance, which effectively leads to smaller upstream and larger confluence patches being at different points in their ecological selection dynamics. As selection is weaker upstream, the downstream patches reach their low diversity equilibrium more quickly. This pattern is exacerbated by highly competitive species dominating in downstream patches due to reduced disturbance, which additionally speeds up the dynamics of an ecological selection locally. Consequently, it is the perturbation pattern, along with the invariant patch size distribution in the landscape, which creates the necessary conditions for the reversed diversity gradient to emerge. We expect this effect to be especially pronounced in communities with strong competitive asymmetries and even enhanced in systems with competition-colonization trade-offs (i.e. when a weak competitor can regionally coexist with a strong competitor because of better dispersal capacity; see [52]), as few strong competitors with low dispersal rates would lead to strong selection in the absence of turnover. Such selective processes could also affect evolutionary dynamics: dendritic networks have recently been found to inherently lead to the emergence of non-trivial abundance patterns and eco-evolutionary dynamics per se [53,54]. Thus, the network structure will impose selection gradients, likely linked to dispersal [55,56]. In addition, patch size-dependent mortality leads to another, possibly antagonistic, selection gradient, which could lead to the emergence of non-trivial evolutionary dynamics in such networks, as has already been theoretically and empirically proposed [57]. While our experimental design does not allow direct inference on evolutionary dynamics (we did not consider intraspecific variation), we suggest this to be an interesting future research direction.
Disturbance-mediated slowing down of competitive exclusion is a well-understood ecological mechanism affecting population dynamics [58–61]. Here, we show that this mechanism can generate a specific transient signature in terms of biodiversity patterns when applied over a spatial gradient of disturbance, which is a common feature of river-like landscapes. For instance, headwaters in river systems are naturally more prone to higher levels of disturbance than larger downstream patches because of their higher surface area exposed to disturbance relative to water volume [62,63]. Higher benthic surface area to water volume ratios are generally more net heterotrophic and thus show higher sensitivity to change in litter composition from terrestrial systems [64,65] and are also likely more sensitive to drought events because they are shallower. They are on average also located at a higher elevation, and thus experience stronger variations in temperature and weather conditions. Human-induced disturbances in pristine headwaters are increasingly common [58] and the general mechanisms demonstrated by our study suggest that these anthropogenic impacts can have unexpected consequences by inverting large-scale biodiversity patterns. Although more robust to change, our modelling results also suggest that very high disturbance levels in downstream locations can also lead to a reversed diversity pattern. This is likely relevant around large urban centres that are generally located at downstream confluences.
In conclusion, we show that patch size-dependent mortality (whether negative or positive), which is commonly displayed in river-like landscapes, can be a key mechanism responsible for shaping the distribution of biodiversity in riverine landscapes.
Supplementary Material
Acknowledgements
We thank S. Gut, S. Flückiger, and E. Keller for help during the laboratory work. We also thank two anonymous reviewers for comments on the manuscript. This is publication ISEM-2018-250 of the Institut des Sciences de l'Evolution - Montpellier.
Data accessibility
Data are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.pm4n81q. R code to reproduce analysis and experimental results are available at: https://github.com/harveye/Turnover_dendritic_network.
Authors' contributions
E.H., I.G., E.A.F., and F.A. designed the research; I.G. and E.A.F. designed the model; I.G. programmed and ran the model, analysed the simulation data with support from E.A.F., and produced the figures; E.H. conducted the laboratory experiment with support from I.G., E.A.F., and F.A., processed the experimental data with support from I.G., and carried out the analysis of experimental data; all authors participated in results interpretation; E.H. wrote the first draft of the manuscript; all authors significantly contributed to further manuscript revisions. E.H. and I.G. contributed equally to this work.
Competing interests
We declare we have no competing interests.
Funding
Funding is from the Swiss National Science Foundation grant no. PP00P3_150698 and PP00P3_179089, University of Zurich and Eawag.
References
- 1.Vannote RL, Minshall GW, Cummins KW, Sedell JR, Cushing CE. 1980. The river continuum concept. Can. J. Fish. Aquat. Sci. 37, 130–137. ( 10.1139/f80-017) [DOI] [Google Scholar]
- 2.Ward JV, Tockner K, Arscott DB, Claret C. 2002. Riverine landscape diversity. Freshw. Biol. 47, 517–539. ( 10.1046/j.1365-2427.2002.00893.x) [DOI] [Google Scholar]
- 3.Muneepeerakul R, Bertuzzo E, Lynch HJ, Fagan WF, Rinaldo A, Rodriguez-Iturbe I. 2008. Neutral metacommunity models predict fish diversity patterns in Mississippi–Missouri basin. Nature 453, 220–222. ( 10.1038/nature06813) [DOI] [PubMed] [Google Scholar]
- 4.Carrara F, Rinaldo A, Giometto A, Altermatt F, Roelke AEDL, Kalisz ES. 2014. Complex interaction of dendritic connectivity and hierarchical patch size on biodiversity in river-like landscapes. Am. Nat. 183, 13–25. ( 10.1086/674009) [DOI] [PubMed] [Google Scholar]
- 5.Deiner K, Fronhofer EA, Mächler E, Walser J-C, Altermatt F. 2016. Environmental DNA reveals that rivers are conveyer belts of biodiversity information. Nat. Commun. 7, 12544 ( 10.1038/ncomms12544) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Muneepeerakul R, Weitz JS, Levin SA, Rinaldo A, Rodriguez-Iturbe I. 2007. A neutral metapopulation model of biodiversity in river networks. J. Theor. Biol. 245, 351–363. ( 10.1016/j.jtbi.2006.10.005) [DOI] [PubMed] [Google Scholar]
- 7.Economo EP, Keitt TH. 2010. Network isolation and local diversity in neutral metacommunities. Oikos 119, 1355–1363. ( 10.1111/j.1600-0706.2010.18272.x) [DOI] [Google Scholar]
- 8.Seymour M, Fronhofer EA, Altermatt F. 2015. Dendritic network structure and dispersal affect temporal dynamics of diversity and species persistence. Oikos 124, 908–916. ( 10.1111/oik.02354) [DOI] [Google Scholar]
- 9.Besemer K, Singer G, Quince C, Bertuzzo E, Sloan W, Battin TJ. 2013. Headwaters are critical reservoirs of microbial diversity for fluvial networks. Proc. R. Soc. B 280, 20131760 ( 10.1098/rspb.2013.1760) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tornwall BM, Swan CM, Brown BL. 2017. Manipulation of local environment produces different diversity outcomes depending on location within a river network. Oecologia 184, 663–674. ( 10.1007/s00442-017-3891-7) [DOI] [PubMed] [Google Scholar]
- 11.Balian EV, Segers H, Lévèque C, Martens K. 2008. The freshwater animal diversity assessment: an overview of the results. Hydrobiologia 595, 627–637. ( 10.1007/s10750-007-9246-3) [DOI] [Google Scholar]
- 12.Tockner K, Stanford JA. 2002. Riverine flood plains: present state and future trends. Environ. Conserv. 29, 308–330. ( 10.1017/S037689290200022X) [DOI] [Google Scholar]
- 13.Dudgeon D, et al. 2006. Freshwater biodiversity: importance, threats, status and conservation challenges. Biol. Rev. 81, 163–182. ( 10.1017/S1464793105006950) [DOI] [PubMed] [Google Scholar]
- 14.Vörösmarty CJ, et al. 2010. Global threats to human water security and river biodiversity. Nature 467, 555–561. ( 10.1038/nature09440) [DOI] [PubMed] [Google Scholar]
- 15.Rodriguez-Iturbe I, Muneepeerakul R, Bertuzzo E, Levin SA, Rinaldo A. 2009. River networks as ecological corridors: a complex systems perspective for integrating hydrologic, geomorphologic, and ecologic dynamics. Water Resour. Res. 45, W01413 ( 10.1029/2008WR007124) [DOI] [Google Scholar]
- 16.Rodriguez-Iturbe I, Rinaldo A. 1997. Fractal river basins: chance and self-organization. New York, NY: Cambridge University Press. [Google Scholar]
- 17.Mari L, Casagrandi R, Bertuzzo E, Rinaldo A, Gatto M. 2014. Metapopulation persistence and species spread in river networks. Ecol. Lett. 17, 426–434. ( 10.1111/ele.12242) [DOI] [PubMed] [Google Scholar]
- 18.Carrara F, Altermatt F, Rodriguez-Iturbe I, Rinaldo A. 2012. Dendritic connectivity controls biodiversity patterns in experimental metacommunities. Proc. Natl Acad. Sci. USA 109, 5761–5766. ( 10.1073/pnas.1119651109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Leopold LB, Wolman MG, Miller JP. 1995. Fluvial processes in geomorphology. Trade Paperback Edition New York, NY: Dover Publications. [Google Scholar]
- 20.Leibold MA, et al. 2004. The metacommunity concept: a framework for multi-scale community ecology. Ecol. Lett. 7, 601–613. ( 10.1111/j.1461-0248.2004.00608.x) [DOI] [Google Scholar]
- 21.MacArthur RH, Wilson EO. 1963. An equilibrium theory of insular zoogeography. Evolution 17, 373 ( 10.2307/2407089) [DOI] [Google Scholar]
- 22.MacArthur RH, Wilson EO. 1967. The theory of island biogeography. Reprint edition Princeton, NJ: Princeton University Press. [Google Scholar]
- 23.Hubbell SP. 2001. The unified neutral theory of biodiversity and biogeography. Princeton, NJ: Princeton University Press. [Google Scholar]
- 24.Angela DY, Lei SA. 1998. Equilibrium theory of island biogeography: a review. Proc. RMRS, 163, 163–182. [Google Scholar]
- 25.Harvey E, MacDougall AS. 2014. Trophic island biogeography drives spatial divergence of community establishment. Ecology 95, 2870–2878. ( 10.1890/13-1683.1) [DOI] [Google Scholar]
- 26.Finn DS, Bonada N, Múrria C, Hughes JM. 2011. Small but mighty: headwaters are vital to stream network biodiversity at two levels of organization. J. North Am. Benthol. Soc. 30, 963–980. ( 10.1899/11-012.1) [DOI] [Google Scholar]
- 27.Lorenz S, Rasmussen JJ, Süß A, Kalettka T, Golla B, Horney P, Stähler M, Hommel B, Schäfer RB. 2017. Specifics and challenges of assessing exposure and effects of pesticides in small water bodies. Hydrobiologia 793, 213–224. ( 10.1007/s10750-016-2973-6) [DOI] [Google Scholar]
- 28.Palmer MA, et al. 2010. Mountaintop mining consequences. Science 327, 148–149. ( 10.1126/science.1180543) [DOI] [PubMed] [Google Scholar]
- 29.Valladares F, Bastias CC, Godoy O, Granda E, Escudero A. 2015. Species coexistence in a changing world. Front. Plant Sci. 6, 866 ( 10.3389/fpls.2015.00866) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Violle C, Pu Z, Jiang L. 2010. Experimental demonstration of the importance of competition under disturbance. Proc. Natl Acad. Sci. USA 107, 12 925–12 929. ( 10.1073/pnas.1000699107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McCann KS. 2011. Food webs. Princeton, NJ: Princeton University Press. [Google Scholar]
- 32.Hemphill N. 1991. Disturbance and variation in competition between two stream insects. Ecology 72, 864–872. ( 10.2307/1940588) [DOI] [Google Scholar]
- 33.Townsend CR, Scarsbrook MR, Dolédec S. 1997. The intermediate disturbance hypothesis, refugia, and biodiversity in streams. Limnol. Oceanogr. 42, 938–949. ( 10.4319/lo.1997.42.5.0938) [DOI] [Google Scholar]
- 34.Shea K, Roxburgh SH, Rauschert ESJ. 2004. Moving from pattern to process: coexistence mechanisms under intermediate disturbance regimes. Ecol. Lett. 7, 491–508. ( 10.1111/j.1461-0248.2004.00600.x) [DOI] [Google Scholar]
- 35.Urban MC. 2004. Disturbance heterogeneity determines freshwater metacommunity structure. Ecology 85, 2971–2978. ( 10.1890/03-0631) [DOI] [Google Scholar]
- 36.Ledger ME, Harris RML, Armitage PD, Milner AM. 2008. Disturbance frequency influences patch dynamics in stream benthic algal communities. Oecologia 155, 809–819. ( 10.1007/s00442-007-0950-5) [DOI] [PubMed] [Google Scholar]
- 37.Srivastava DS, et al. 2004. Are natural microcosms useful model systems for ecology? Trends Ecol. Evol. 19, 379–384. ( 10.1016/j.tree.2004.04.010) [DOI] [PubMed] [Google Scholar]
- 38.Altermatt, et al. 2015. Big answers from small worlds: a user's guide for protist microcosms as a model system in ecology and evolution. Methods Ecol. Evol. 6, 218–231. ( 10.1111/2041-210X.12312) [DOI] [Google Scholar]
- 39.Thorp JH, Thoms MC, Delong MD. 2006. The riverine ecosystem synthesis: biocomplexity in river networks across space and time. River Res. Appl. 22, 123–147. ( 10.1002/rra.901) [DOI] [Google Scholar]
- 40.Giometto A, Rinaldo A, Carrara F, Altermatt F. 2013. Emerging predictable features of replicated biological invasion fronts. Proc. Natl Acad. Sci. USA 111, 297–301. ( 10.1073/pnas.1321167110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rigon R, Rinaldo A, Rodriguez-Iturbe I, Bras RL, Ijjasz-Vasquez E. 1993. Optimal channel networks: a framework for the study of river basin morphology. Water Resour. Res. 29, 1635–1646. ( 10.1029/92WR02985) [DOI] [Google Scholar]
- 42.Rinaldo A, Banavar JR, Maritan A. 2006. Trees, networks, and hydrology. Water Resour. Res. 42, W06D07 ( 10.1029/2005WR004108) [DOI] [Google Scholar]
- 43.Altermatt F, Seymour M, Martinez N. 2013. River network properties shape α-diversity and community similarity patterns of aquatic insect communities across major drainage basins. J. Biogeogr. 40, 2249–2260. ( 10.1111/jbi.12178) [DOI] [Google Scholar]
- 44.Altermatt F, Alther R, Fišer C, Jokela J, Konec M, Küry D, Mächler E, Stucki P, Westram AM. 2014. Diversity and distribution of freshwater amphipod species in Switzerland (Crustacea: Amphipoda). PLoS ONE 9, e110328 ( 10.1371/journal.pone.0110328) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Walker LR, Chapin FS. 1987. Interactions among processes controlling successional change. Oikos 50, 131–135. ( 10.2307/3565409) [DOI] [Google Scholar]
- 46.Harvey E, Gounand I, Ganesanandamoorthy P, Altermatt F. 2016. Spatially cascading effect of perturbations in experimental meta-ecosystems. Proc. R. Soc. B 283, 20161496 ( 10.1098/rspb.2016.1496) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Pennekamp F, Schtickzelle N. 2013. Implementing image analysis in laboratory-based experimental systems for ecology and evolution: a hands-on guide. Methods Ecol. Evol. 4, 483–492. ( 10.1111/2041-210X.12036) [DOI] [Google Scholar]
- 48.Pennekamp F, Schtickzelle N, Petchey OL. 2015. BEMOVI, software for extracting behavior and morphology from videos, illustrated with analyses of microbes. Ecol. Evol. 5, 2584–2595. ( 10.1002/ece3.1529) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Pinheiro J, Bates D, DebRoy S, Sarkar D, R Core Team. 2016. Nlme: linear and nonlinear mixed effects model. See http://CRAN.R-project.org/package=nlme. [Google Scholar]
- 50.Widder S, Besemer K, Singer GA, Ceola S, Bertuzzo E, Quince C, Sloan WT, Rinaldo A, Battin TJ. 2014. Fluvial network organization imprints on microbial co-occurrence networks. Proc. Natl Acad. Sci. USA 111, 12 799–12 804. ( 10.1073/pnas.1411723111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Bertuzzo E, Maritan A, Gatto M, Rodriguez-Iturbe I, Rinaldo A. 2007. River networks and ecological corridors: reactive transport on fractals, migration fronts, hydrochory. Water Resour. Res. 43, W04419 ( 10.1029/2006WR005533) [DOI] [Google Scholar]
- 52.Cadotte MW. 2007. Competition–colonization trade-offs and disturbance effects at multiple scales. Ecology 88, 823–829. ( 10.1890/06-1117) [DOI] [PubMed] [Google Scholar]
- 53.Fronhofer EA, Altermatt F. 2017. Classical metapopulation dynamics and eco-evolutionary feedbacks in dendritic networks. Ecography 40, 1455–1466. ( 10.1111/ecog.02761) [DOI] [Google Scholar]
- 54.Altermatt F, Fronhofer EA. 2018. Dispersal in dendritic networks: ecological consequences on the spatial distribution of population densities. Freshw. Biol. 63, 22–32. ( 10.1111/fwb.12951) [DOI] [Google Scholar]
- 55.Tonkin JD, Altermatt F, Finn DS, Heino J, Olden JD, Pauls SU, Lytle DA. 2018. The role of dispersal in river network metacommunities: patterns, processes, and pathways. Freshw. Biol. 63, 141–163. ( 10.1111/fwb.13037) [DOI] [Google Scholar]
- 56.Anderson KE, Hayes SM. 2018. The effects of dispersal and river spatial structure on asynchrony in consumer–resource metacommunities. Freshw. Biol. 63, 100–113. ( 10.1111/fwb.12998) [DOI] [Google Scholar]
- 57.Paz-Vinas I, Loot G, Stevens VM, Blanchet S. 2015. Evolutionary processes driving spatial patterns of intraspecific genetic diversity in river ecosystems. Mol. Ecol. 24, 4586–4604. ( 10.1111/mec.13345) [DOI] [PubMed] [Google Scholar]
- 58.Sheil D. 2016. Disturbance and distributions: avoiding exclusion in a warming world. Ecol. Soc. 21, 10 ( 10.5751/ES-07920-210110) [DOI] [Google Scholar]
- 59.Chesson PL, Warner RR. 1981. Environmental variability promotes coexistence in lottery competitive systems. Am. Nat. 117, 923–943. ( 10.1086/283778) [DOI] [Google Scholar]
- 60.Chesson P. 2000. Mechanisms of maintenance of species diversity. Annu. Rev. Ecol. Syst. 31, 343–366. ( 10.1146/annurev.ecolsys.31.1.343) [DOI] [Google Scholar]
- 61.Göthlich L, Oschlies A. 2015. Disturbance characteristics determine the timescale of competitive exclusion in a phytoplankton model. Ecol. Model. 296, 126–135. ( 10.1016/j.ecolmodel.2014.10.033) [DOI] [Google Scholar]
- 62.Lowe WH, Likens GE, Power ME. 2006. Linking scales in stream ecology. BioScience 56, 591 ( 10.1641/0006-3568(2006)56%5B591:LSISE%5D2.0.CO;2) [DOI] [Google Scholar]
- 63.Battin TJ, Kaplan LA, Findlay S, Hopkinson CS, Marti E, Packman AI, Newbold JD, Sabater F. 2008. Biophysical controls on organic carbon fluxes in fluvial networks. Nat. Geosci. 1, 95–100. ( 10.1038/ngeo101) [DOI] [Google Scholar]
- 64.England LE, Rosemond AD. 2004. Small reductions in forest cover weaken terrestrial-aquatic linkages in headwater streams. Freshw. Biol. 49, 721–734. ( 10.1111/j.1365-2427.2004.01219.x) [DOI] [Google Scholar]
- 65.Rasmussen JB. 2010. Estimating terrestrial contribution to stream invertebrates and periphyton using a gradient-based mixing model for δ13C. J. Anim. Ecol. 79, 393–402. ( 10.1111/j.1365-2656.2009.01648.x) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data are available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.pm4n81q. R code to reproduce analysis and experimental results are available at: https://github.com/harveye/Turnover_dendritic_network.