Principles of niche expansion

Abstract

Niche expansion is attained by adaptations in two generalized phenotypical traits—niche position and niche width. This gives room for a wide range of conceptual ways of niche filling. The niche variation hypothesis reduces the range by predicting that expansion occurs by increasing variation in niche position, which has been debated on empirical and theoretical grounds as also other options seem possible. Here, we propose a general theory of niche expansion. We review empirical data and show with an eco-evolutionary model how resource diversity and a trade-off in resource acquisition steer niche evolution consistent with observations. We show that the range can be reduced to a discrete set of two orthogonal ways of niche filling, through (1) strict phenotypical differentiation in niche position or (2) strict individual generalization. When individual generalization is costly, niche expansion undergoes a shift from (2) to (1) at a point where the resource diversity becomes sufficiently large. Otherwise, niche expansion always follows (2), consistent with earlier results. We show that this either–or response can operate at both evolutionary and short-term time scales. This reduces the principles of niche expansion under environmental change to a notion of orthogonality, dictated by resource diversity and a resource-acquisition trade-off.

1. Introduction

For many years, the niche variation hypothesis (NVH) [1] has played a central role in providing a precept for within-species responses to ecological opportunities. It originally suggested that the variation of niche use within populations increases during niche expansion. While this effect has been observed in the field [1–3], the idea is yet debated, especially because responses with little or no increase in the variation of niche use have been observed (see review in [2,4,5]), and predicted [6,7]. This includes the outcome where population niche expansion is achieved entirely through individual generalization where all individuals in the population become only more generalized instead of further partitioning the niche space—a phenomenon which has been termed parallel release [8].

The various possible outcomes of responses to ecological opportunity can illustrate some very important features of niche dynamics, also beyond the immediate behavioural and ecological answers to changes in resources. Accessible vacant niche space may for instance induce disruptive selection and within-species differentiation [1,2,9], leading potentially in the long run to speciation [10,11]. We must therefore include both population and individual responses to new ecological opportunities if we attempt to understand the ecological and evolutionary consequences of niche expansion. Here we will use the term ecological opportunity to refer in a very general sense to a niche space that becomes accessible by evolutionary, ecological or behavioural means, and focus on within-species processes of niche expansion and contraction.

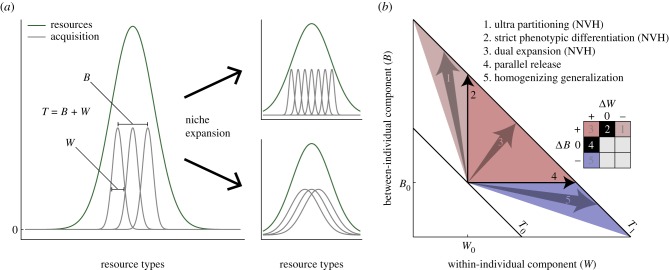
A common way to formalize, measure and think of individual and population niche use has been to view the total population niche width, T, as the sum of the between-individual component B (i.e. variation of niche positions) and the within-individual component W (i.e. average individual niche width), such that T = B + W [6]. The fraction B/T is commonly called the degree of individual specialization [12,13]. Figure 1a illustrates those basic concepts. A niche expansion (i.e. an increase in T) can be attained in five principal ways (figure 1b). The NVH predicts an increase in B [1], which can be combined with a simultaneous decrease, increase or no change of W (arrows 1–3 in figure 1b). Parallel release corresponds to an increase in W without a concomitant change in B (arrow 4, figure 1b). A fifth hypothetical way to niche expansion is when W increases while B decreases (outcome 5 in figure 1b). There is neither theoretical nor empirical support for this, but it is included here for a complete picture. There is thus room for a whole range of possible outcomes. Here we will show, however, that there is theoretical and empirical support for only two orthogonal outcomes, one of which is a special case of the NVH. Niche expansion is either acquired through parallel release (outcome 4 in figure 1b) or strict phenotypic differentiation in niche position (outcome 2). Which principal paths of niche expansion are taken by a population depends on (i) the variation of resource types in the accessible vacant niche space and (ii) what we call the cost of individual generalization, meaning a resource-acquisition trade-off between individual niche width (the number of resource types possible to use) and total consumption rate. We thus provide a theory of niche expansion that is fully consistent with available data on changes in within- and between-individual niche width, covering times scales from behavioural responses to evolutionary ones.

Figure 1.

Basic concepts of between- and within-individual components of niche width, and five conceptual ways of niche expansion. (a) Any population has some degree of phenotypic variation, represented by the between-individual component of niche width B, and each individual (or phenotype) uses some range of resources defined by respective individual's niche width w. The average individual niche width equals the within-individual components of niche width W (this figure assumes for simplicity w_i = W for any ith individual). The population's total niche width T = B + W is the sum of the two components. Niche expansion can be attained by increasing this sum principally in any way. This leads to (b) five principles cases of niche expansion: (1) increasing B and decreasing W; (2) increasing B and constant W; (3) increasing B and increasing W; (4) constant B and increasing W; (5) decreasing B and decreasing W. Cases 1–3 have in common an increasing B (i.e. all are cases of the NVH). Case 2, as we will show, is the only realization of the NVH. Case 4, falls just outside of the NVH (because NVH is an open set). Case 5 is to our knowledge not reported, neither empirically nor theoretically. Except for cases 2 and 4, the specific naming of cases does not follow from any reference and is here used just as a means of classification.

2. Material and methods

(a). Data review

In order to learn how the two niche width components B and W change with niche expansion (i.e. increasing T) in natural population, we reviewed published data that shared measures of W, B and T in comparable units and included sufficient variation in T (table 1, [2,14–18]). We settled with data on 15 major categories of taxa, where some are at species or higher level and some constitute a combination of specified taxa. The data comprise a total of 22 taxa.

Table 1.

Information on reviewed data, including, for each taxon relating to respective data, spatial and temporal context and probable processes underpinning within-taxon variation. Taxon scientific names in brackets if not directly given.

taxon	spatial	temporal	probable within-taxon processes	reference
Ameiva ameiva	distinct foraging populations	6 years	ecological and evolutionary	Costa et al. [18]
Anolis spp.	distinct foraging populations	6 years	ecological and evolutionary	Costa et al. [18]
beluga whale (Delphinapterus leucas)	distinct foraging populations	2–20 years	behavioural and ecological	Yurkowski et al. [16]
Brazilian frogs (Adenomera sp.; Eleutherodactylus sp.; Leptodactylus fuscus; Proceratophrys sp.)	one distinct foraging population per species	seasonal (wet and dry)	behavioural and ecological	Bolnick et al. [2]
chamois (Rupicapra rupicapra)	probably a single population	2 years	behavioural and ecological	Bison et al. [15]
Cnemidophorus spp.	distinct foraging population	6 years	ecological and evolutionary	Costa et al. [18]
gulls (Larus argentatus; L. canus; L. fuscus; L. marinus)	not distinct foraging populations		behavioural and ecological	Evans [17]
Micrablepharus spp.	distinct foraging population	6 years	ecological and evolutionary	Costa et al. [18]
mouflon (Ovis musimon)	probably a single population	2 years	behavioural and ecological	Bison et al. [15]
Nucella (Nucella emarginata; N. melons)	one distinct foraging population per species	1–2 years	behavioural and ecological	Bolnick et al. [2]
perch (Perca fluviatilis)	single lake	9 years	behavioural and ecological	Bolnick et al. [2]
ringed seal (Pusa hispida)	distinct foraging populations	2–19 years	behavioural and ecological	Yurkowski et al. [16]
roe deer (Capreolus capreolus)	probably a single population	2 years	behavioural and ecological	Bison et al. [15]
three-spine stickleback (Gasterosteus aculeatus)	short-term isolated populations, respectively, in experimental enclosures of 9 m2	2 weeks	behavioural	Bolnick et al. [2]; Svanbäck & Bolnick [14]
Tropidurus spp.	distinct foraging population	6 years	ecological and evolutionary	Costa et al. [18]

Measures of B, W or T in the majority of these data were results directly of Shannon index approximation or of mean proportional similarity [12], with the exception of the source data on gulls [17], which were originally represented by Hill numbers α, β and γ corresponding to, but not equivalent to, W, B and T, respectively. We here transformed these Hill numbers into Shannon indices [19], such that T = lnγ, $W=\ln \alpha -n(\mathrm{S}{\mathrm{E}}^2/2\hspace{0.17em}{\alpha }^2)$, where n is sample size, SE is standard error and B = T − W (table 2). This transformation is exact for T and approximate for W based on a second-order Taylor expansion around the mean; i.e. including the mean α and variance n SE² [17] of the distribution of individuals' niche widths.

Table 2.

Transformations from Hill numbers to total population niche width T and within-individual niche width W, in the data on gulls [17].

species	n	α	Γ	s.e.	T = ln γ	W = ln α − n SE2/(2α2)
Larus argentatus	236	4.61	5.56	0.16	1.72	1.39
Larus canus	75	4.05	5.36	0.26	1.68	1.24
Larus fuscus	49	2.66	3.74	0.19	1.32	0.85
Larus marinus	214	3.34	4.81	0.14	1.57	1.02

For each major category of taxa, the correlation between B and W was measured to test for orthogonality (appendix A).

(b). Evolutionary model

In order to understand data, we developed a model of the evolution of niche position and niche width in a consumer population. The model is based on an ecological consumer-resource model, first proposed by Ackermann & Doebeli [20], extending from MacArthur's [21] theory on competition and predation. It includes a continuous spectrum of resource types x following logistic growth. The resource carrying capacities (i.e. the resource distribution) follow a Gaussian function

$$K(x)=K_0\exp \left(-\frac{x^2}{2{\sigma }_{\mathrm{K}}^2}\right),$$ 2.1

where K₀ is the modal carrying capacity. The parameter σ_K sets the width of the resource distribution, here referred to as the resource diversity.

The resources are used by consumers depending on their ‘resource acquisition strategy’ (u, w), where u and w are traits defining a phenotype in terms of niche position and niche width, respectively. A resource-acquisition kernel a(x, u, w) determines the consumption rate of resource x by a consumer with resource acquisition strategy, or phenotype, (u, w).

A generalist phenotype, with a large niche width w, would be adapted to consume a wider range of resources compared to a specialist phenotype with a narrow one. Without a trade-off between peak performance and performance breadth, the generalist phenotype is typically always better off than a specialist. Such a type of trade-off has been a central concept for the evolution of niche width (see e.g. [22]) and, for instance, the commonly used term ‘jack of all trades, master of none’ [21], refers to a cost of generalization.

Here, similar to [20], we formulate a trade-off function in resource acquisition h(w) which functional form, or strength, is determined by the parameter c . The trade-off in resource acquisition affects the consumption rate a(x, u, w). More precisely,

$$a(x,\hspace{0.17em}u,\hspace{0.17em}w)=\frac{h(w)}{\sqrt{2\pi }w}\exp \left(-\frac{{(x-u)}^2}{2w^2}\right),$$ 2.2

and has the functional form of a normal distribution, with a mean u and a standard deviation w, multiplied by

$$h(w)=\{\begin{array}{ccc}\exp (-cw),& \mathrm{if}& c\ge 0\\ 1-\exp \left(\frac{1-cw}{c}\right),& \mathrm{if}& c<0\end{array}.$$ 2.3

This function equals the area under a(x, u, w) and thus affects the overall consumption rate of any phenotype. In that sense, it penalizes broad niches for positive c (see [20]) and rewards broad niches (penalizes narrow niches) for negative c (figure 2). As such, the parameter c accounts for the cost of individual generalization (c > 0) or the benefit of individual generalization (c < 0). We note in passing that the case c = 0, where h(w) is constant (figure 2), still imposes a trade-off in resource acquisition, because in that case, the resource utilization kernel has a fixed area. A broader niche (a higher w) thus implies a lower maximal resource utilization (at x = u). Such a trade-off becomes weaker with decreasing c but does not vanish.

Figure 2.

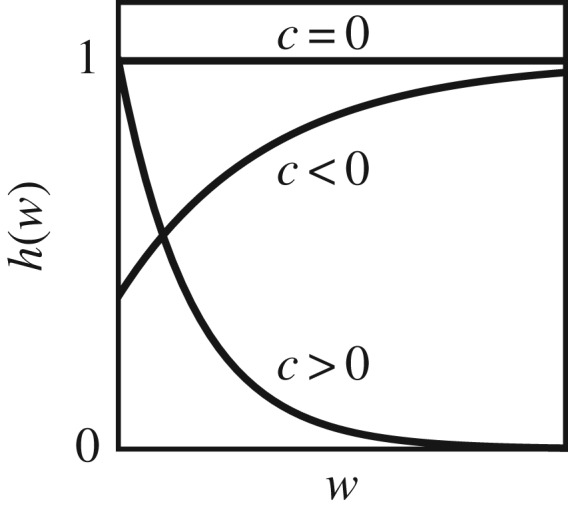
The function h(w) equals the area under the resource-acquisition kernel a(x, u, w), and thus the overall consumption rate of any phenotype with niche position u and niche width w. When the cost of individual generalization c = 0, consumption rate is independent of w. For c > 0, larger w is penalizing, which implies a cost of individual generalization. For c < 0, larger w is rewarding, which implies a benefit of individual generalization. This example uses c = −2, c = 0, c = 2.

Adding the assumption of a type I functional response gives resource dynamics following

$$\frac{\mathrm{d}R(x)}{\mathrm{d}t}=rR(x)\left(1-\frac{R(x)}{K(x)}\right)-\sum _{i}a(x,\hspace{0.17em}{u}_i,\hspace{0.17em}{w}_i)N_{i}R(x),$$ 2.4

where R(x) is the density of resource type x, r is the resource intrinsic growth rate, (u_i, w_i) is the i:th strategy present in the population and N_i is the density of that strategy (phenotype). The sum is taken across all consumer strategies. Assuming that resource growth rate is many times faster than the consumer growth rate, the resource equilibria are given by

$$R^{\ast }(x)=\left(1-\frac{{\sum }_{i}a(x,\hspace{0.17em}{u}_i,\hspace{0.17em}{w}_i)N_i}{r}\right)K(x).$$ 2.5

The growth of a consumer type i is controlled by its current consumption of resources according to

$$\frac{\mathrm{d}{N}_i}{\mathrm{d}t}=q{N}_i\left(b{\int }_{x}a(x,\hspace{0.17em}{u}_i,\hspace{0.17em}{w}_i)R^{\ast }(x)\hspace{0.17em}\mathrm{d}x-m\right),$$ 2.6

where b represents the conversion of consumed resources to energy, m is the energy required for individual maintenance and replacement and q is the number of extra offspring produced per excess unit of energy. The corresponding per capita growth rate, or fitness,

$$f(u_i,\hspace{0.17em}{w}_i)=q\left(b{\int }_{x}a(x,\hspace{0.17em}{u}_i,\hspace{0.17em}{w}_i)R^{\ast }(x)\hspace{0.17em}\mathrm{d}x-m\right),$$ 2.7

of any consumer with strategy (u_i, w_i) determines its success in the community.

By including a process of ecological trait inheritance over successive generations and occasional mutations, we account for the evolution of niche position u and niche width w in a consumer population that is using an evolutionarily inert and ecologically dynamic Gaussian resource landscape.

(c). Individual based simulations of niche evolution

To analyse the evolution of niche position and niche width under ecological opportunities, we performed individual-based simulations. These simulations were built on a discrete-time approximation of the continuous-time model presented above. Each time-step, the fitness f of all individuals was calculated from equation (2.7). Each individual then independently produced a Poisson distributed number of offspring and was discarded (died). The mean number of offspring of an individual was given by f + 1 (truncated below at 0), ensuring that a population with mean fitness $\overline{f}=0$ would on average replace itself.

All offspring inherited the trait values of their respective parent, except for mutations. Any offspring mutated with probability 0.01 to new trait values (u, w) drawn from two independent normal distributions centred at the parent values with standard deviations σ_u = σ_w = 0.02. These values are sufficient to generate adequate standing variation, and standard for this type of simulations (e.g. [23]). The mutated w was truncated below at zero.

For computational efficiency, individuals were aggregated in ‘clones’ of identical individuals. Each clone reproduced as a group rather than one individual at a time. This scheme is mathematically equivalent to the purely individual-based approach above as long as the number of offspring of a clone is also Poisson distributed and has the appropriate mean.

The simulations were run for a sufficient number of time-steps (3 × 10⁶) to allow the trait values for niche position and niche width to settle at a stationary state where the long-term averages did not change significantly with time.

(d). Niche components

In order to apply the analysis results to niche expansion in terms of B, W and T, we calculated the between-individual component of niche width, B, and the within-individual component of niche width, W, from niche position u and niche width w. B was calculated at any given time t as the variance of the individuals' niche positions u(t)₁, u(t)₂, …, u(t)_n(t), and W was calculated as the population average squared niche width, such that B(t) = Var(u) and $W(t)=\overline{w^2}$. By definition, the total niche width T(t) = B(t) + W(t). We then averaged over the last two-thirds of the temporal samples from our simulations (i.e. the stationary part) to finally obtain the equilibria B, W and consequently T.

3. Results

(a). Empirical patterns exhibit orthogonality

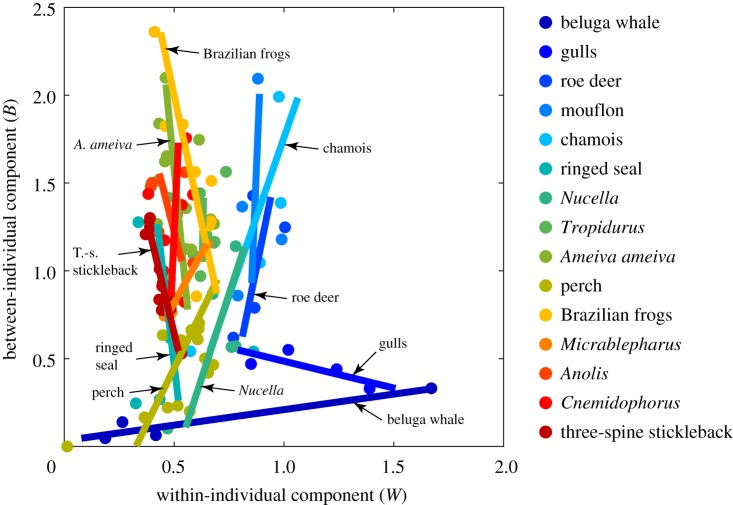
Combining independently published data (table 1) on niche expansion for a wide range of taxa under a wide range of circumstances provides a helicopter view and reveals an interesting pattern that is not discernible from looking at single-taxon or few-taxa observations (figure 3).

Figure 3.

Empirical patterns exhibit orthogonality. Combining several independently published datasets on empirical observations of niche variation for a range of taxonomic groups (see Material and methods; table 1), uncovers a dichotomous pattern. Each taxon (mainly at species level) is denoted here by a unique colour and some are also labelled. Filled circles denote data points and lines corresponding regressions. For the data on 14 out of the 15 taxa, the null hypothesis of no correlation between B and W could not be rejected. This was possible only for three-spine stickleback. As such, we cannot exclude that the respective variation in the majority of the individual-specialist taxa is orthogonal to that in the individual-generalist taxa. The colouring scheme ranges from the taxon with the smallest maximum W (three-spine stickleback; red) to that with the largest maximum W (beluga whale; blue).

Projecting the data in the plane of W and B (figure 3), indicates that expansion in one or in the other component is mutually exclusive, orthogonal, outcomes. Our data analysis suggests that this is generally the case. For 14 out of the total 15 categories of taxa observed, the null hypothesis of no correlation between B and W could not be rejected (figure 3; appendix A), and only the data on three-spine stickleback could. This suggests that niche expansion is attained strictly through individual resource-specialization (i.e. strict phenotypic differentiation in niche position), or strictly through parallel release.

(b). Niche evolution leads to orthogonality

If niche expansion occurs strictly in the between-individual component (B) or strictly in the within-individual component (W), there are two orthogonal principles of niche expansion. Our numerical results on the joint evolution of individual niche position and individual niche width indicate precisely such principles and show that this either–or response to ecological opportunity is determined by a trade-off in resource acquisition and by the diversity of resources (figure 4). The trade-off in resource acquisition dictates two general regimes as follows.

Figure 4.

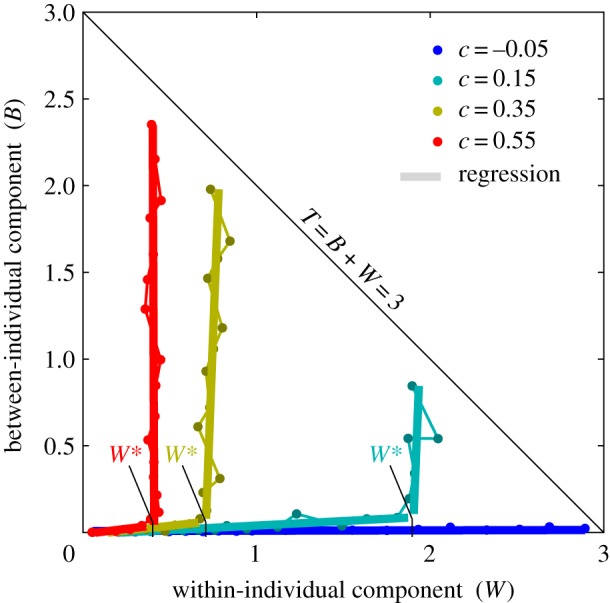
Our numerical results on niche evolution show that niche expansion follows either of two orthogonal principles determined by the cost of individual generalization c and resource diversity σ_K. For c < 0, populations inevitably achieve niche expansion by parallel release. For c > 0, populations switch between parallel release and strict phenotypic differentiation at a critical within-individual niche width W*. At low resource diversity, resulting in low total niche width T, populations achieve niche expansion by parallel release, and at high resource diversity populations achieve niche expansion by strict phenotypic differentiation. The point of switching, at the critical within-individual niche width W*, decreases with the cost of individual generalization c. Points represent simulation results for ${\sigma }_{\mathrm{K}}^2$ ranging from 0.05 to 3.0 for each uniquely coloured cost-level. Corresponding (thick) regression lines were produced by piecewise major axis regression (choosing the maximum-likelihood switch point). Here, we used q = b = 1, m = 0.1, r = 100 and K₀ = 2 (see Material and methods).

When there is a cost of individual generalization (i.e. when c > 0; equation 2.3), niche expansion is governed by an interesting phenomenon of generalist–specialist switching between the two orthogonal expansion principles (figure 4), dependent on the resource diversity (σ_K), and the cost of individual generalization. At relatively low resource diversity, niche expansion is achieved by parallel release, and when the resource diversity becomes sufficiently large, populations switch to strict phenotypic differentiation to extend to include those additional resources. Specifically, there exists a critical within-individual niche width W* such that when W = W* populations switch between parallel release and strict phenotypic differentiation. The critical within-individual niche width decreases with the cost of individual generalization, such that W* is large for small costs and small for large costs (figure 4).

Otherwise, when an individual generalization is not costly (c ≤ 0; equation 2.3), expansion is achieved strictly through parallel release, corroborating earlier theory (e.g. [20]), and we see no evidence of generalist–specialist switching (figure 4).

In either case, both resource diversity and a trade-off in resource acquisition determine niche expansion in this type of either–or manner. This signifies an important dichotomy: that there are two orthogonal outcomes of niche expansion, which is interesting in and of itself, and which considerably simplifies principles of niche expansion.

(c). Theory is consistent with observations

The orthogonal empirical patterns (figure 3) are clearly recovered by our theoretical results on niche evolution as illustrated in figure 4.

Out of the 15 observed taxonomic groups, only beluga whales and gulls appear to be under a parallel release regime, while the other remaining 13 taxa appear to be under a strict phenotypic differentiation regime. This may indicate that individual generalization, ultimately, is often costly, as also suggested by Bolnick et al. [2].

This also raises interesting questions as to the specific ecology of the respective taxa, and how that relates to their mode of niche expansion based on resources and cost of individual generalization. To answer these questions, however, one must realize that the resource-acquisition trade-offs can probably manifest in many different forms (see e.g. [20,22]), relating to internal factors like physiology and cognitive abilities, as well as external factors such as the resources and their inherent properties. While an examination to resolve this falls out of the scope of this paper, it is a promising future research problem.

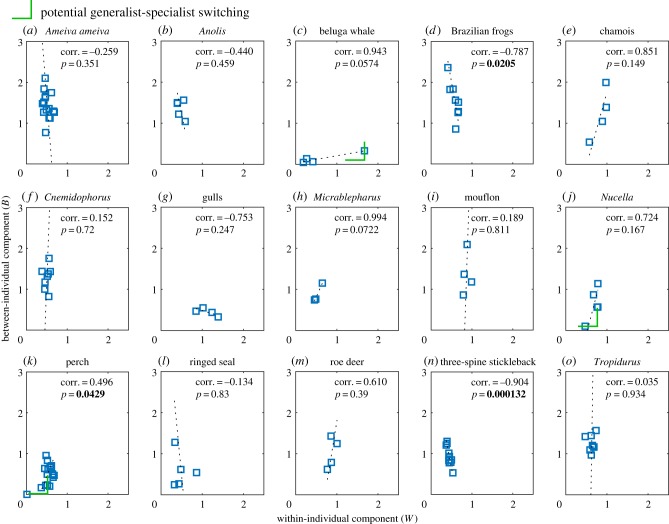
Our theory predicts a generalist–specialist switching phenomenon. Such phenomena can easily be obscured in low-resolution data. However, among the apparent individual specialists, the data on Nucella and especially that on perch display niche variation patterns that suggest that they do undergo a generalist–specialist switching (figure 3 and figure 5), where the data points of the smallest niche widths probably are within a parallel release regime. The data on the beluga whale may be an example of switching among apparent individual generalists (figure 3 and figure 5), where the data point of the largest niche width then is within a strict phenotypic differentiation regime. Thus, generalist–specialist switching seems to occur in nature. A higher data resolution (i.e. larger sample sizes within a wider range of resource diversity) would help to confirm this phenomenon.

Figure 5.

Empirical data on the 15 categories of taxa included in the analysis. Within each respective panel are noted the correlation between B and W along with corresponding p-values. Incidences of a potential generalist–specialist switching are indicated by green angular markers for beluga whale, Nucella and perch.

We can discern several different levels of organization here acting on different time scales (figure 3 and table 1). This includes behavioural processes on the shortest time scales and ecological and evolutionary processes on the larger time scales, where the latter long-term processes may also apply to data on niche variation at the above-species level. The variation on all of these levels is in line with the predicted principles based on the evolutionary processes here modelled. This suggests unified underlying fundamental principles of adaptation on evolutionary and ecological time scales.

(d). The relation to the NVH

As noted in figure 1, the NVH makes very generous predictions. Any amount of increased phenotypic variation (increased B) is permissible, regardless of the response in W. Our theory, with support from data, shows that that generosity is unwarranted and that the NVH collapses into one possible outcome: a strict increase in B without any change in W. The alternative, orthogonal response falls outside the NVH.

4. Discussion

We have outlined general principles on within-species diversification during niche expansion, and we show that there are two principal ways of filling niche space, which are orthogonal and predictable. This is the result of a synthesis between theory and empirical evidence.

We performed a meta-study on data on individual specialization and niche expansion. The data were heterogeneous and included a wide combination of very different organisms, for which respective niche responses were detected on various time scales for a variety of dietary information. This level of disorganization may easily raise doubt. Yet the data contain a strikingly strong common signal across all taxa. The theory we have presented is general and should therefore apply to a wide range of cases. We have shown with this heterogeneous data that this is exactly what the theory does.

It is not very surprising that niche dynamics occur on evolutionary time scales. However, empirical evidence shows that observable niche dynamics can occur also on short, ecological and behavioural time scales [8,14] (table 1). Expansion patterns likely to be owing to such short-term processes aligned remarkably well to the predicted relationships of evolutionary niche expansion (figure 3). One explanation of this, as already indicated, is that selection principles apply not only on large temporal scales but also on small. This is plausible as individuals, if any means for it exist, typically adapt in ways that lead to increasing payoffs, which is in agreement with optimal foraging theory and also typical in many applications of game theory. Evolutionary processes and short-term non-evolutionary processes (e.g. plastic and behavioural processes) will thus all follow similar patterns in strategy dynamics—where costs of individual generalization likely arise from a range of sources, such as Bauplan constraints, environmental heterogeneities or trophic interactions. As long as there exist means of niche adaptation, the processes and resulting patterns will follow analogous general principles regardless of scale.

We have based our analysis on the basic model by Ackermann & Doebeli [20] which extends directly from the classical work of MacArthur [21] and which formalizes the mechanism of the cost of individual generalization in a suitable and sufficient way. There are related models on the evolution of niche position and width, accounting for alternative aspects including behavioural optimal- and suboptimal-foraging processes [24], bimodal resource distributions [25] and the general assessment of branching lines of bivariate traits [26]. Such alternative models may be reviewed for additional insights or generality.

Disruptive selection and adaptive diversification are predicted to deterministically occur whenever individual generalization is costly (i.e. c > 0; e.g. [20]), because the within-individual niche width (W) is then sufficiently suppressed relative to the width (σ_K) of the resource distribution (e.g. [9]). Realistically, however, demographic and environmental stochasticity and discrete population sizes interfere with the deterministic signal [27–29], whereby adaptive diversification then occurs only for a sufficiently wide resource distribution, explaining the generalist–specialist switching phenomenon we have reported on. One conclusion is thus that the reduction of habitat diversity would in heterogeneous populations initially cause a niche contraction solely through a rapid loss of phenotypic variation, switching to a decrease in individual niche width should the degradation continue. Conversely, an increased resource diversity may at some point cause a population in a homogeneous state to shift to a state of increasing population heterogeneity (individual specialization)—a state where diversity begets diversity.

Phenotypic differentiation within species is naturally significant to speciation processes as various degrees of individual specialization would provide raw material for speciation, where one expects that higher degrees of individual specialization lead in general to a higher likelihood of speciation events. More speciose clades are therefore expected to consist to a large extent of taxa with large degrees of individual specialization. This is consistent both with that such taxa seem to be relatively common (figure 3) [13] and with that (species-rich) tropical taxa are reported to display large degrees of individual specialization [30].

5. Conclusion

Principles of niche expansion reduce to two orthogonal outcomes: strict phenotypic differentiation and parallel release. Which one depends on resource diversity and a trade-off in resource acquisition. If individual generalization is costly, a generalist–specialist switching phenomenon occurs where niche expansion is achieved by parallel release at low resource diversity and by strict phenotypic differentiation at high resource diversity. The switch occurs at a critical within-individual niche width which decreases with the cost of individual generalization. Otherwise, niche expansion is achieved exclusively by parallel release. All these theoretical results are supported by data.

Appendix A

Figure 5 summarizes the results from the analysis of the empirical data on the respective 15 taxa. p-values for the correlations between B and W were less than 0.05 only for Brazilian frogs, perch and three-spine stickleback. After Bonferroni correction, such correlations remain significant only for three-spine stickleback. This supports that niche expansion follows two strictly orthogonal principles.

Potential incidences of generalist–specialist switching are present in the data on beluga whale, Nucella and perch as indicated in figure 5.

Table 2 provides data on gulls measured in Hill numbers, and corresponding transformations into total population niche width and within-individual niche width.

Data accessibility

All data used here are previously published (see references in Material and methods).

Authors' contributions

H.S., J.R. and P.L. designed and performed research and wrote the paper. H.S. and J.R. developed models and analysed models and data.

Competing interests

We declare we have no competing interests.

Funding

This study was supported by grants from the Swedish Research Council to P.L. and J.R.