Fingering instabilities in tissue invasion: an active fluid model

Abstract

Metastatic tumours often invade healthy neighbouring tissues by forming multicellular finger-like protrusions emerging from the cancer mass. To understand the mechanical context behind this phenomenon, we here develop a minimalist fluid model of a self-propelled, growing biological tissue. The theory involves only four mechanical parameters and remains analytically trackable in various settings. As an application of the model, we study the evolution of a two-dimensional circular droplet made of our active and expanding fluid, and embedded in a passive non-growing tissue. This system could be used to model the evolution of a carcinoma in an epithelial layer. We find that our description can explain the propensity of tumour tissues to fingering instabilities, as conditioned by the magnitude of active traction and the growth kinetics. We are also able to derive predictions for the tumour size at the onset of metastasis, and for the number of subsequent invasive fingers. Our active fluid model may help describe a wider range of biological processes, including wound healing and developmental patterning.

1. Introduction

Spreading tumours often do not maintain a straight front while expanding. They instead display an interface patterned with multicellular protrusions, which are commonly referred to as fingers [1,2], invading the surrounding tissue [1–6]. Their formation generally initiates cancer metastasis [2–4,7,8], which is responsible for the vast majority of cancer-related deaths [9]. Similar structures form during wound healing, where fingers accompany re-epithelization [10,11]. In the case of glioblastoma brain tumours, these fingers usually consist of disconnected, diffusing cells [1,12]. But in carcinomas and epithelial wound healing, they tend to remain condensed, with a well-defined boundary [5,10].

What causes the formation of such fingers? Studying cancer has traditionally focused on a large number of biological (especially genetic and biochemical) cues [13]. Yet, these essentially operate by collectively affecting a smaller number of physical properties of the tissues and environments involved [1]. How these physical alterations can, in turn, lead to fingering has been investigated by several models. Various causal mechanisms, differing in their assumptions on the mechanical properties adopted for the tissues, have been proposed [14–20]. For example, reaction–diffusion models of nutrient-limited growth have been used [1,21] because the accessibility of diffusing chemicals is necessary for tumour growth. But, other models have treated the fingers’ emergence as a consequence of a mechanical instability [14,15,17,22]. Support for the latter approach was provided by experiments conducted to prevent biochemical signalling, but in which fingering occurred nevertheless [23]. Mechanical processes proposed by these models include: fracturing of an elastic surrounding medium (extracellular matrix, healthy tissue) upon pressure from a growing solid inclusion (tumour), leading to subsequent infiltration of the cracks by malignant cells [22]; branching instabilities caused by the tumour’s confinement pressure, analogous to the corona splash of a drop impacting a solid surface [24]; mechanical frustrations between an outer, proliferating ring of a growing tumour and its necrotic core [15]; buckling due to swelling of a spatially restricted gel-like tissue [17]; instability resulting from the interplay between spatially non-uniform cell division/death rates and shear in viscous tissues [14]; or a pulling mechanism by a subpopulation of leader cells at the tumour’s edges [10,25].

Many of the above mechanisms have been successfully described using continuum, analytically solvable models [14–17], thus providing deep insights into the physical context involved in tissue fingering. However, these continuum models of tumours have, in most cases, omitted one fundamental component of live tissues: cells actively apply forces (via the conversion of chemical energy into mechanical energy) to their surroundings [10,26–30]. Yet, the onset of fingering at tissue boundaries is often correlated with the dense presence of these so-called active forces and the occurrence of the resulting self-propelled motion [10,29]. In discrete models, the central role of these forces in triggering tissue fingering has been verified by simulations within several different frameworks [18,25]. But, to the best of our knowledge, only few continuum models of fingering have studied the consequences of self-propelling forces: the effect of an active rim at the boundary of the tissue has been studied by Mark et al. [31] and by Nagilla et al. [32], while the role of active forces in the tissue bulk has been discussed in wound healing models by Zimmermann et al. [33] and by Nesbitt et al. [34]. However, the analyses in the two latter works are limited to a non-dividing, rectangular tissue, either in a static state or somehow pushed on one side by a rigid barrier.

We here investigate the role of tissue bulk activity for the emergence of fingers in more general situations. We first construct a continuum mechanical model of an active and growing tissue, supported by experimental evidence, and that is analytically solvable and that involves only four physical parameters: friction, activity, growth and surface tension. We next investigate the role of activity in promoting fingering. Provided with experimentally derived estimates of the physical parameters, our model notably produces realistic predictions for the number and evolution of the fingers.

2. Model

2.1. Assumptions and equations

In our model of an active and growing tissue, the evolutions of the pressure p(r, t) and velocity v(r, t) fields at a position r and time t are governed by the following force balance and mass conservation equations,

$$\mathrm{\nabla }p=-\beta \mathbf{v}+\alpha \frac{\mathbf{v}}{|\mathbf{v}|}$$ 2.1a

and

$$\mathrm{\nabla }\cdot \mathbf{v}=k,$$ 2.1b

respectively, with $\mathrm{\nabla }$ the nabla operator, and where α and β are positive parameters, specifying the strength of the interaction between the tissue and a substrate: α describes the magnitude of the active traction, while β describes the magnitude of the effective passive friction (proportional to the tissue viscosity). In equation (2.1b), k is the net rate of growth (we are here interested in regimes in which it is also positive) of an incompressible tissue, undergoing cell division (or individual cell growth). The α-term in equation (2.1a), which accounts for the tissue activity, is discussed in detail in §2.2. The evaluation of the various parameters is examined in §2.3.

Ignoring the α-term, equation (2.1a) reduces to Darcy’s Law $\mathrm{\nabla }p=-\beta \mathbf{v}$ (originally used to describe viscous flows in porous materials and Hele–Shaw apparatus [35]), which has been widely employed to model the passive behaviour of tissues [1,36–38]. Darcy’s Law notably assumes a viscous and quasi-two-dimensional dynamics for the deformations of a tissue layer, by considering that the effects of friction against a substrate are much stronger than those of viscous shear within the plane of the layer.

Using two-dimensional models is experimentally justified by the large prevalence of in vitro tissue culture monolayers, and also because many in vivo soft tissues, including epithelium in which carcinomas develop, tend to spontaneously form quasi-two-dimensional monolayers [10,29,39]. Consequently, two-dimensional descriptions are often employed in tissue mechanics models [14,17,25].

The mechanical properties of live tissues at short timescales, up to the order of minutes, are generally dominated by an elastic constitutive behaviour. At longer timescales, however, a viscous description is better suited [30]. The crossover between the two regimes is probably related to the turnover rates of intercellular adherent junctions [40,41]. Hence, epithelial tissues become fluidized by a reduction in the number of adherent junctions, and a concomitant increase in the magnitude of active traction when becoming malignant. This well-known ‘melting’ process is often referred to as the ‘epithelial to mesenchymal transition’ [3,5,42]. Moreover, cell division and apoptosis are also known to further contribute to the fluidization of tissues [43]. As we here model the behaviour of the tissue at timescales on which it experiences substantial growth (that is, on the order of several hours at least [4]), the viscous constitutive behaviour implied by Darcy’s Law is justified. Many existing continuum models of epithelial tissues indeed make the same assumption [14,30,38,44]. Note that, by writing equations (2.1), we further assume that inertial terms are negligible on these timescales.

2.2. Tissue activity

The second term on the right-hand side of equation (2.1a) accounts for cells actively propelling themselves by exerting traction against the substrate. It will subsequently be referred to as the active term, and α specifies its strength.

We consider here that the direction of the net local active force acting on the tissue layer from the substrate is aligned with the direction of the local flow velocity. This assumption was made in previous studies modelling active tissues [18,45]. It is a consequence of cells attempting to maintain their direction of motility, as illustrated in figure 1a, and also manifested by the persistent Brownian motion of individual cells in vitro [47]. On a subcellular level, it probably results from the friction destabilizing lamellipodia [11,48] that are not aligned with the cell’s velocity [18]. It has further been shown to be consistent with experimental data [18,49,50], although this directionality is not universal [51] and other models have been proposed where the direction of the active force is treated as an independent internal variable, coupled to stress and velocity fields [44,52].

Figure 1.

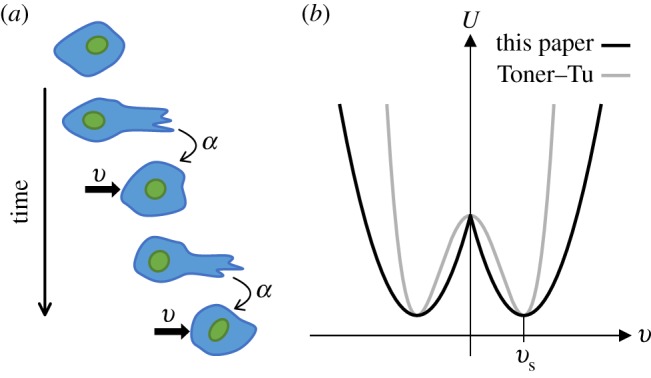
Assumptions of the active traction model. Panel (a) is a schematic illustrating how the active traction of a mesenchymal tumour cell acts in the direction of its migration velocity; filopodia and/or lamellipodia are protruding at the leading edge of the cell, which translocates in the same direction. Panel (b) compares (in one dimension) the Landau-type ‘velocity potential’ [46], U(v) such that the volumic traction force F = −∂_vU, of our description with the Toner–Tu model; both potentials select an intrinsic velocity $v_{\mathrm{s}}$ (see text), but our model introduces a discontinuity at v = 0 which has no effect on our results.

Equation (2.1a) also assumes that the active traction does not depend on the magnitude of the velocity. This assumption has been made in several numerical models of motile cells [18,53,54], and enables a distinct analysis of the role played by activity.

In the classic theory derived by Toner & Tu [55,56], often used to model active fluids [33,34,57], the net force per unit volume acting on the active fluid from the substrate, in a spatially uniform flow, follows F_T(v) = α_Tv − β_T|v|²v (ignoring here additional inertial and gradient terms; with α_T and β_T positive parameters). In comparison, our model, equation (2.1a), gives this force the expression F(v) = αv/|v| − βv. In both cases, the fluid has a ‘preferred’ spontaneous magnitude of velocity |v_s| = α/β (= (α_T/β_T) ^1/2 in the Toner–Tu model), which it would select when moving in unbounded space without being driven by an external pressure gradient or growth. For magnitudes of velocity lower than |v_s|, the fluid would be driven to move faster by the α-term, while above it, it would be slowed down by the friction (the β-term). This fluid’s constitutive behaviour may be described in terms of a Landau-type ‘velocity potential’ [46], shown in figure 1b. Although our model has a discontinuity in the direction of F(v) at v = 0 which does not exist in F_T(v), we have verified that this singularity does not significantly affect our subsequent results.

The Toner–Tu model, however, assumes that the friction force grows as |v|³ and that the active force varies linearly with |v|. Both assumptions are unrealistic when describing biological tissues. Our model, however, retains the physical interpretation of β as the friction coefficient of Darcy’s Law, and of α as the magnitude of the active force of the tissue against the substrate (per unit volume). Our approach also enables a direct comparison with classical results for viscous fingering [58], readily obtained from our model by taking the limit α → 0.

2.3. Estimation of parameters

Based on in vivo microscopy observations [4] of the time necessary for doubling a carcinoma’s size, which is on the order of a few hours, we estimate that the growth rate k is about 10⁻⁴ s⁻¹.

The passive friction β can be estimated based on in vitro force measurements of epithelial tissues against substrates [29,30,59] (admittedly, inferences about in vivo systems from these in vitro experiments are arguable). Following Pompe et al. [59], we assume that friction with the substrate is primarily the consequence of cell-substrate ligands, numbering 200–300 per cell, each of which exerts a force of about 10⁻¹² N. We thus estimate the total friction force per cellular volume to be about 10⁶ N m⁻³ for a 10⁻⁵ m cell size. From in vivo microscopy of micrometastasis growth [4], the typical velocity v of the cells falls within 10⁻¹⁰ to 10⁻⁹ m s⁻¹. Hence, dividing the volumic friction force by this velocity provides an estimate β ∼ 10¹⁵–10¹⁶ Pa s m⁻².

There is no lower limit on α, as epithelial cells may not exert any active force against the substrate. The upper limit can be estimated on the basis of force tracking microscopy applied to spreading epithelial monolayers in vitro [29,30]. It is observed that traction forces are actively exerted through the monolayers and peak at their edges, giving rise to a gradient of the stress tensor’s diagonal terms, which is up to 10⁷ Pa m⁻¹ in the study by Trepat et al. [29], and 10⁸ Pa m⁻¹ in the work of Blanch-Mercader et al. [30]. Balancing α with this typical stress gradient, one can place an upper estimate on α at approximately 10⁸ Pa m⁻¹. In agreement, the traction exerted by single fibroblasts has been reported as up to 10⁻⁷–10⁻⁵ N per cell [60], which would correspond to α ∼ 10⁸–10¹⁰ Pa m⁻¹ when dividing by the cell’s volume.

The effective surface tension of the tissue γ will also play a role in our further considerations. Its magnitude depends on the strength of intercellular adhesion and behaviour of cortical actin networks [61,62]. The surface tension was evaluated indirectly by Foty et al. [63] by measuring the energetic penalty of compression of embryonic multicellular spheroids, revealing values on the order of 3–9 mPa m. We thus presume that γ ∼ 10⁻³–10⁻² Pa m is a realistic range for our system. A summary of the estimates for the physical parameters is presented in table 1.

Table 1.

Estimates of the physical parameters.

parameter	symbol	unit	value
growth rate	k	s−1	10−4
passive friction	β	Pa s m−2	1015 to 1016
active traction	α	Pa m−1	0 to 1010
surface tension	γ	Pa m	10−3 to 10−2

2.4. Model system

The tumour is modelled as an initially circular, two-dimensional droplet of a growing active fluid described by equations (2.1), with an unperturbed, time-dependent radius r₀(t) (figure 2). The surrounding healthy tissue is modelled as a passive, non-dividing fluid, whose pressure p′(r, t) and velocity v′(r, t) fields follow the equations:

$$\mathrm{\nabla }{p}^{\prime }=-{\beta }^{\prime }{\mathbf{v}}^{\prime }$$ 2.2a

and

$$\mathrm{\nabla }\cdot {\mathbf{v}}^{\prime }=0,$$ 2.2b

where β′ is the friction parameter (analogous to β in the active fluid). In writing equation (2.2b), we effectively assume that growth in the passive fluid can be neglected on the timescale of metastasis initiation.

Figure 2.

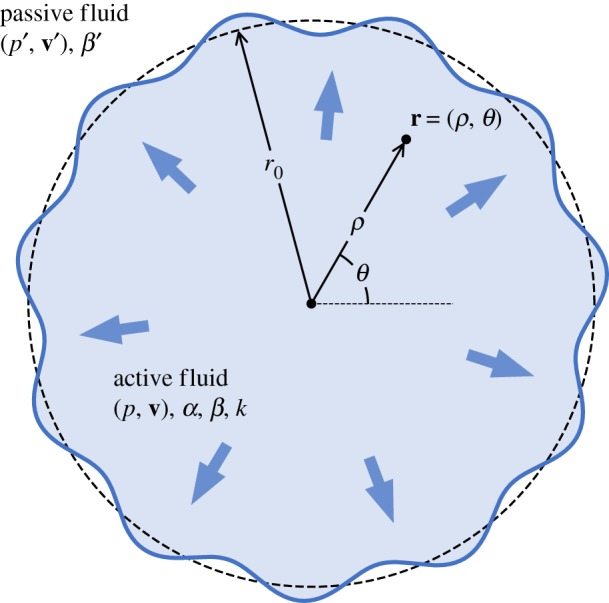
Model system of a tumour growing in an external tissue: a two-dimensional circular droplet with radius r₀ and made of an active fluid described by equations (2.1), is expanding in a passive fluid modelled by equations (2.2). The interface undergoes periodic perturbations whose linear stability is investigated in §3.

We assume that the activity α and the growth rate k are constant (independent of r and t) through the active tissue. Constant magnitude of the active force has been assumed in models of active matter before [64,65]. While not correct in all situations [30,66], it is a convenient assumption to evaluate the influence of its magnitude in fingering. Extensions to non-uniform and time-dependent behaviours of these parameters are readily possible, and we investigate a case of evolving growth rate in §3.4 (see also appendix B.2). Similarly, we assume that β and β′ are uniform within their respective regions.

We study the system in polar coordinates r = (ρ, θ) and write vector fields’ components in this system with appropriate subscripts, such as $\mathbf{v}=(v_{\rho },v_{\theta })$. The perturbed interface between the active and passive fluids, described by the line r(t, θ), must satisfy two boundary conditions. First, the continuity of the radial components of velocities is expressed as follows:

$$v_{\rho }{|}_{\rho =r}=v_{\rho }^{\prime }{|}_{\rho =r}={\mathrm{\partial }}_{t}r.$$ 2.3

Second, the pressure difference across the interface separating the two tissues must equal the Laplace pressure,

$$p{|}_{\rho =r}-p^{\prime }{|}_{\rho =r}=-\gamma \frac{r^2+2{({\mathrm{\partial }}_{\theta }r)}^2-r{\mathrm{\partial }}_{\theta \theta }^{2}r}{{[r^2+{({\mathrm{\partial }}_{\theta }r)}^2]}^{3/2}},$$ 2.4

with γ the surface tension, and the fraction being the expression of the local interfacial curvature in polar coordinates [67]. Note that our description does not account for an interfacial bending force [31,68]. We indeed assume that the corresponding energetic cost, which involves a higher order dependency in interfacial curvature when compared with surface tension [31], is negligible at the length scales considered for the linear stability analysis presented in §3.

Unless stated otherwise, we use the dimensionless variables defined as follows. Distances are re-scaled by the characteristic length $\ell ={(\frac{2\gamma }{\beta k})}^{1/3}$, which can be interpreted as a capillary length at which growth balances interfacial tension (on the order of 10 µm, based on the estimates of table 1). Times are re-scaled by k⁻¹, and we further define ϕ = β′/β the relative viscosity of the displaced tissue compared to the active growing droplet. We introduce a reference activity ${\alpha }^{\ast }=\beta \ell k\sim {10}^7\hspace{0.17em}\text{Pa}\hspace{0.17em}{\text{m}}^{-1}$ to make the active traction α dimensionless, $\alpha /{\alpha }^{\ast }\to \alpha$. Pressures and velocities are made dimensionless by $p^{\ast }=\beta {\ell }^{2}k\sim {10}^2\hspace{0.17em}\text{Pa}$ and $v^{\ast }=\ell k\sim {10}^{-9}\hspace{0.17em}\text{m}\hspace{0.17em}{\text{s}}^{-1}$, respectively. We will use the same letters for the dimensionless versions of the variables as for their dimensional counterparts.

The droplet of the active tissue grows due to a positive k, as required by equation (2.1b), and the passive fluid is displaced by it. As long as the interface between the two tissues remains circular (with the unperturbed radius r₀), hydrodynamic fields in both regions remain symmetric under rotations and are given by

$${\mathbf{v}}_0=(\frac{\rho }{2},0),p_0=\alpha (\rho -r_0)-\frac{1}{4}({\rho }^2-r_0^2)+p{|}_{\rho =r_0}$$ 2.5a

and

$${\mathbf{v}}_0^{\prime }=(\frac{r_0^2}{2\rho },0),p_0^{\prime }=-\frac{\varphi r_0^2}{2}\ln \left(\frac{\rho }{r_0}\right)-\frac{1}{2r_0}+p{|}_{\rho =r_0},$$ 2.5b

as obtained by solving equations (2.1)–(2.4) and using the dimensionless quantities defined above.

3. Results and discussion

3.1. Linear stability analysis

We investigate under which conditions the active, circular droplet of radius r₀ would start to form finger-like protrusions at its edge, while undergoing uniform growth. To do this, we perform a linear stability analysis around the circular solution given in equations (2.5), by investigating infinitesimal interfacial perturbations of the form r = r₀ + δr, with

$$\delta r\propto f_n(t)\hspace{0.17em}{\text{e}}^{\mathrm{i}n\theta },$$ 3.1

for an integer n corresponding to the mode of the periodic perturbations, and where f_n(t) is a function describing its time evolution (with lim _t→0 f_n(t) = 1 for all n). An analogous ansatz of periodicity in θ is made for the perturbations of hydrodynamic fields in both fluids, (δp, δp′, δv, δv′) ∝ f_n(t) e^inθ, around the solution given by equations (2.5). Note that our stability analysis concerns small perturbations around solutions that are themselves time-dependent. Applying the evolution equations, equations (2.1)–(2.4), to these perturbed fields provides an expression for the n-mode’s rate of growth defined by

$${\sigma }_n(r_0)=\underset{t\to 0}{lim}\frac{{\mathrm{\partial }}_t{f}_n(t)}{f_n(t)}.$$ 3.2

Positive values of σ_n(r₀) correspond to unstable, growing modes n, which may become the basis for the formation of fingers. We derive in appendix A the following expression for σ_n(r₀):

$${\sigma }_n(r_0)=\frac{1}{2}\frac{(\varphi -1)(n-1)-n(n^2-1)/r_0^3+{\mathit{\Lambda }}_{\mathit{n}}\mathit{(}\frac{\mathit{2}\alpha }{{\mathit{r}}_0}\mathit{)}}{\varphi \mathit{+}\mathit{1}\mathit{+}{\mathit{\Lambda }}_{\mathit{n}}\mathit{(}\frac{\mathit{2}\alpha }{{\mathit{r}}_0}\mathit{)}\mathit{-}\mathit{n}\frac{\mathit{2}\alpha }{{\mathit{r}}_0}},$$ 3.3

where Λ_n(x) is the function

$${\mathit{\Lambda }}_{\mathit{n}}\mathit{(}\mathit{x}\mathit{)}\mathit{=}\mathit{n}\mathit{x}\mathit{-}1\mathit{+}\mathit{n}\frac{\sum _{\mathit{k}\mathit{=}0}^{\mathit{n}}\frac{\mathit{(}\mathit{-}1{\mathit{)}}^{\hspace{0.17em}\mathit{j}}}{\mathit{n}\mathit{+}\mathit{j}}\left(\genfrac{}{}{0ex}{}{\mathit{n}\mathit{+}\mathit{j}}{\hspace{0.17em}\mathit{j}}\right)\left(\genfrac{}{}{0ex}{}{\mathit{n}}{\hspace{0.17em}\mathit{j}}\right){\mathit{x}}^{\mathit{-}\mathit{j}}}{\sum _{\hspace{0.17em}\mathit{j}\mathit{=}0}^{\mathit{n}}\mathit{j}\frac{\mathit{(}\mathit{-}1{\mathit{)}}^{\hspace{0.17em}\mathit{j}}}{\mathit{n}\mathit{+}\mathit{j}}\left(\genfrac{}{}{0ex}{}{\mathit{n}\mathit{+}\mathit{j}}{\hspace{0.17em}\mathit{j}}\right)\left(\genfrac{}{}{0ex}{}{\mathit{n}}{\hspace{0.17em}\mathit{j}}\right){\mathit{x}}^{\mathit{-}\mathit{j}}}\mathit{,}$$ 3.4

with $\left(\genfrac{}{}{0ex}{}{n}{\hspace{0.17em}j}\right)$ the binomial coefficient ‘n choose j’. Equation (3.3) holds provided α < r₀/2 (see §3.2 for a discussion). The first term in the numerator of equation (3.3) represents the effects of the viscosity mismatch, the second term embodies the effects of surface tension, while the final term shows the effects of activity.

As Λ_n(0) = 0 for all n, we obtain the following expression of σ_n(r₀) in the passive limit α → 0:

$${\sigma }_n(r_0){|}_{\alpha =0}=\frac{1}{2}[\frac{n(\varphi -1)}{\varphi +1}-1-\frac{n(n^2-1)}{r_0^3(\varphi +1)}]+\frac{1}{\varphi +1}.$$ 3.5

The first term (square brackets) of equation (3.5) is equivalent to the landmark result obtained by Paterson [58] for viscous fingering in a radial geometry (eqn. (10) in [58]), upon imposing the injection rate Q in Paterson’s formula equal to the total amount of the droplet’s growth per unit time in our setting (that is, $Q=\pi r_0^2$ in dimensionless variables). The last term 1/(ϕ + 1), however, distinguishes our result from Paterson’s, and stems from the fact that, here, the invading fluid also grows within the fingers.

Figure 3 shows σ_n(r₀) versus n for various values of ϕ and α, and for an unperturbed droplet radius r₀ = 5. Only integer values of n (circles in figure 3) have a physical interpretation. The first mode n = 1 corresponds to a translation of the droplet, and as Λ₁(x) = 0 for all x, σ₁(r₀) = 0 for all values of r₀, α and ϕ. Higher modes n ≥ 2 correspond to the formation of n fingers on the interface of the active droplet and, if unstable (that is, if σ_n(r₀) > 0), could potentially initiate the multicellular protrusions observed in tumours [4].

Figure 3.

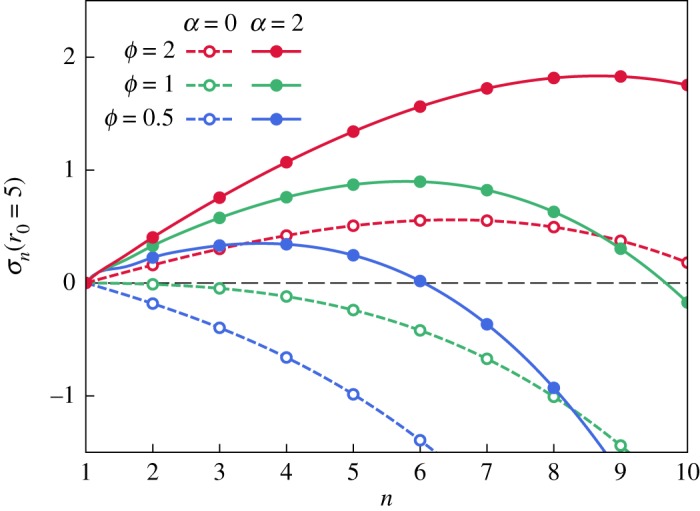
Growth rate σ_n(r₀ = 5) of periodic interfacial perturbations as a function of the number of fingers n, for a droplet of size r₀ = 5, made of a passive (α = 0; dashed lines) or an active (α = 2; solid lines) fluid, with varying ϕ.

In passive fluids, ϕ > 1 (that is, the invaded fluid is more viscous than the invading one) is a necessary condition for fingering to be initiated, as instabilities can only grow when the pressure gradient near the interface is lower in the invading fluid [69]. However, we observe that σ_n(r₀) increases with α, so that modes that are stable when α = 0 may become unstable in the presence of activity α > 0 (compare the dashed and solid blue curves, obtained with ϕ = 0.5, in figure 3). Therefore, activity can trigger fingering in systems that are stable otherwise, as well as enhance and/or change the dominant modes in droplets that are already unstable.

Activity lowers the pressure gradient of the invading fluid near the interface, hence promoting instabilities. Using the expression of p₀ and p₀′ given in equations (2.5), we find that the condition for fingering, $\mathrm{\nabla }p{|}_{\rho =r_0}<\mathrm{\nabla }{p}^{\prime }{|}_{\rho =r_0}$, is equivalent to ϕ + 2α/r₀ > 1 when the effects of surface tension are negligible.

3.2. High-activity regime

As already mentioned, |v_s| = α/β ∼ 10⁻⁹ m s⁻¹ is a characteristic velocity at which the active fluid would move in an unbounded space, under uniform pressure and without growth. If |v_s| exceeds the growth-generated velocity at the interface, the active fluid’s motion is frustrated and further instabilities occur across its entire area. We call this regime, for which dimensionless α > r₀/2, ‘high activity’. In this case, the derivation of equation (3.3) presented in the appendix, which assumes that perturbations are only arising at the interface and decaying away from it, is not valid. This regime is potentially relevant in the behaviour of real epithelial tissues, in which fingering at the boundaries is accompanied by velocity swirls forming across the entire area of the tissue [23].

Hence, equation (3.3) is only valid for the ‘low activity’ regime (α < r₀/2). Yet, even in this regime, the active droplet may feature a region of instabilities near its centre ρ < 2α, where the velocity magnitude |v₀| (given by equation (2.5a)) is less than |v_s|. In particular, this situation would have also occurred in the history of the system considered in figure 3. In practice, a separate simulation-based study would be most appropriate to obtain the velocity field throughout the whole active region and to further examine the high-activity regime. In further sections of this paper, we only examine the system’s behaviour in the low-activity regime.

3.3. Onset of fingering

For small enough radii, surface tension stabilizes the active droplet, but its strength decreases as that droplet grows. Therefore, there exists a critical radius for the onset of fingering, below which the active droplet grows circular and unperturbed. As n = 2 is always the first mode to become unstable, r_c(α, ϕ) defined by the conditions σ₂(r₀ = r_c) = 0 and ${\mathrm{\partial }}_{r_0}{\sigma }_2(r_0){|}_{r_0=r_{\mathrm{c}}}>0$ provides an estimate of that critical radius. Using equation (3.3) with Λ₂(x) = x(3x − 4)/(2x − 3), these conditions are equivalent to finding a polynomial root (first condition) within a subdomain (second condition), and have a unique positive solution.

We plot r_c(α, ϕ) versus α in figure 4, which shows that increasing activity decreases the minimum radius for fingering. When ϕ < 1 (blue curve in figure 4), there exists a minimum value of α, below which fingering cannot occur, because the higher viscosity of the invading droplet has a stabilizing effect. When ϕ = 1 (green curve in figure 4), a moderate increase of α may decrease r_c multiple times. The impact of α in fingering is, however, reduced when ϕ > 1 (the red curve in figure 4), because in that case the interface would be unstable even without activity.

Figure 4.

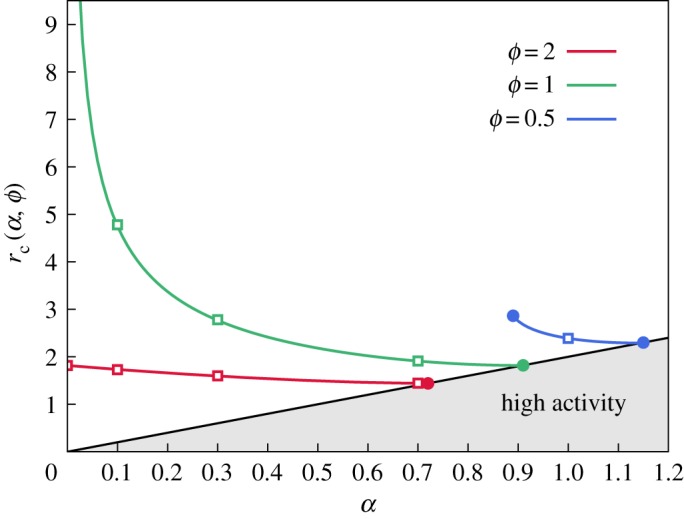
Minimum radius $r_{\mathrm{c}}(\alpha ,\varphi )$ for the initiation of fingering. The grey area on the graph signifies the high-activity regime, in which the linear stability analysis does not apply (see §3.2). The squares indicate the values of α used in figure 5 for each viscosity ratio ϕ.

The range of dimensionless r_c, presented in figure 4, would correspond to a radius of 10–100 µm; however, it can be much higher for lower values of α. This range of r_c is nevertheless in qualitative agreement with the tumour size at which the onset of fingering occurred in experimentally studied carcinomas [4].

3.4. Dominant mode

We now address the question of how many fingers are visible in practice, or, technically speaking, the question of which perturbation mode dominates during growth. Viscous fingering studies suggest the dominant mode is the one satisfying the so-called maximum-amplitude criterion [70]. The criterion is satisfied by the mode n_d experiencing the largest total aggregated growth in amplitude ζ_n over the entire history of the system [70]. Following [70], we obtain ζ_n by integrating the rate of the perturbation’s growth, as predicted by our linear stability analysis, over that history,

$${\zeta }_n(r_0)=\exp [{\int }_{R_n}^{r_0}{\sigma }_n(r)\frac{\text{d}t}{\text{d}r}\text{d}r],$$ 3.6

where R_n is the radius at which mode n is first destabilized (i.e. the minimum radius at which σ_n(R_n) becomes positive). The dominant mode n_d is then obtained for each r₀ from the conditions,

$${\mathrm{\partial }}_n{\zeta }_n(r_0){|}_{n=n_{\mathrm{d}}}=0$$ 3.7a

and

$${\mathrm{\partial }}_{nn}^2{\zeta }_n(r_0){|}_{n=n_{\mathrm{d}}}<0,$$ 3.7b

used to locate the maximum aggregated growth.

As we shall see, the selection of the dominant mode depends on the particular kinetics of the tumour growth. Some experimental studies have shown that an initially exponential growth [71] (corresponding to a constant k) subsequently slows down with time (implying a decrease in average k) as the tumour enlarges and its resource supply becomes a limiting factor [72–74]. Other kinetics have been measured for various tumours and phases of growth, including sigmoidal regimes in which the growth stalls [72–74]. The kinetics where the tumour’s radius grows linearly with time also naturally emerges when the tumour proliferates only within an outer rim [74]. Such growth can also occur as a temporary feature in a sigmoidal kinetics.

We thus proceed to discuss in detail the selection of dominant modes in two kinetic models of tumour growth: an exponentially growing tumour, where k is uniform and independent of time and $r_0(t)=r_{\mathrm{i}}\hspace{0.17em}{\text{e}}^{k(t-t_{\mathrm{i}})/2}$ (from equation (2.1b) at the interface, and with dimensional variables; r_i being the initial radius at time t_i); and a tumour with a radius growing linearly with time, r₀(t) = r_i + ν(t − t_i), with ν the constant and uniform velocity of the unperturbed interface. In the latter case, the growth rate k appearing in equation (2.1b) evolves with time.

3.4.1. Exponential growth

The integral given in equation (3.6) cannot be expressed analytically for all values of ϕ and α, and we plot in figure 5 the relationship n_d(r₀) obtained from numerical evaluation. When ϕ > 1, and for low radii close to the onset of fingering, we observe that the activity has only a moderate influence on the selection of the dominant mode. For later growth, when r₀ becomes large, the viscosity mismatch is the governing cause of fingering and the activity plays no role in the selection of the dominant mode. We numerically observe the power-law variations $n_{\mathrm{d}}\propto r_0^{3/2}$, independent of α. When ϕ = 1, higher activities promote the selection of higher modes. We obtain numerically, and for large r₀, the scaling $n_{\mathrm{d}}\propto r_0^{1/2}$, where the $\frac{1}{2}$ power law is independent of α. When ϕ < 1 and α is sufficiently high, some low-n modes will become destabilized. However, these perturbations will re-stabilize and decay as r₀ increases further, because the stabilization from viscosity mismatch dominates as the radius of the droplet grows: active terms of equation (3.3) vanish when r₀ → ∞, while terms involving ϕ remain constant in this limit.

Figure 5.

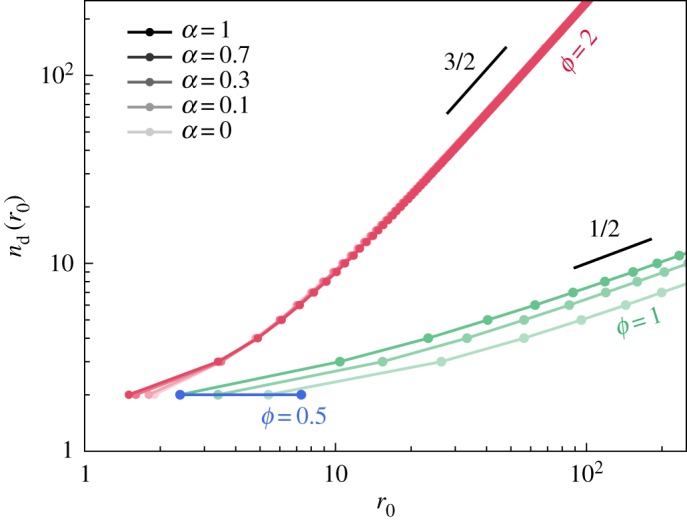
Numerical estimation of the dominant mode n_d(r₀) observed in an active droplet of radius r₀, undergoing exponential growth, for various values of α and ϕ.

We may recover analytically the observed scalings for large n_d and r₀, and for ϕ ≥ 1. We derive in appendix B.1 the following results when r₀ → ∞: $n_{\mathrm{d}}\approx {(\varphi -1)}^{1/2}\times r_0^{3/2}$ for ϕ > 1 and $n_{\mathrm{d}}\approx {[{(\alpha /2)}^2+{(\alpha /2)}^{1/2}]}^{1/2}\times r_0^{1/2}$ for ϕ = 1, which we give below in dimensional variables to highlight the influence of the various physical parameters:

$$n_{\mathrm{d}}\approx \{\begin{array}{cc}{c}^{1/2}{\left[\frac{k({\beta }^{\mathrm{\prime }}-\beta )}{2\gamma }\right]}^{1/2}\times r_0^{3/2}\hspace{0.17em}\mathrm{for}\hspace{0.17em}{\beta }^{\mathrm{\prime }}\hspace{0.17em}>\beta ,& (3.8a)\\ {\left[\frac{2\gamma }{\beta k}{\left(\frac{\alpha }{4\gamma }\right)}^2+{\left(\frac{\alpha }{4\gamma }\right)}^{1/2}\right]}^{1/2}\times r_0^{1/2}\mathrm{for}\hspace{0.17em}{\beta }^{\mathrm{\prime }}=\beta ,& (3.8b)\end{array}\hspace{0.17em}$$

when r₀ ≫ ${(\frac{2\gamma }{\beta k})}^{1/3}$, and with c ≈ 0.06 defined as the smaller of the two solutions to 3c = 3 + lnc.

3.4.2. Linear growth

We also investigate pattern selection for a tumour with a radius growing linearly with time. The derivation of σ_n(r₀) proceeds along identical lines, although in this case, the integral in equation (3.6) can be expressed analytically. Details of this calculation are given in appendix B.2, and in this case we find that n_d ≈ c(α + ϕ − 1) ^1/2 × r₀ is valid for all values of the physical parameters in the low activity regime when r₀ → ∞, and where c ≈ 0.06 is the constant defined previously. We thus write, in dimensional form,

$$n_{\mathrm{d}}\approx c{\left[\frac{\alpha +\nu ({\beta }^{\prime }-\beta )}{\gamma }\right]}^{1/2}\times r_0,$$ 3.9

when r₀ ≫ ${(\frac{\gamma }{\beta \nu })}^{1/2}$ (note that the dimensionless variables are defined differently in the linear growth, as explained in appendix B.2). The difference in the n_d versus r₀ power-law dependency between equations (3.8) and (3.9) highlights the role of the growth kinetics in the fingering pattern, and is discussed with more details in the following.

3.4.3. Comparison and discussion

We now examine the evolution of the tumour’s shape in the two growth kinetics studied above. An initially circular droplet is allowed to evolve, with the n-mode perturbation starting when the radius r₀ reaches R_n, and with an initial amplitude of 0.2 (corresponding to approx. 2 µm). The perturbation is subsequently allowed to grow according to equation (3.6), such that ζ_n(r₀) represents the weight of the n-mode at the unperturbed droplet radius r₀. We further assigned a random phase difference between each n-mode perturbation.

We present in figure 6 examples of droplet patterns obtained with this procedure, where fingering is driven by either viscosity mismatch (left) or by activity (right), in both the exponential (top) and linear (bottom) growth regimes. In the linear growth, activity-driven fingers emerge more distinctively than in the passive droplet; the opposite is observed in the exponential growth. These results, as well as the analytical scalings presented above, demonstrate that the role of activity in fingering depends on the kinetics of the tumour’s growth, and is indeed enhanced in the slower, linear growth kinetics. This assessment could potentially provide a basis for the mechanism behind the onset of metastasis, when the bulk growth of the primary tumour slows down or saturates.

Figure 6.

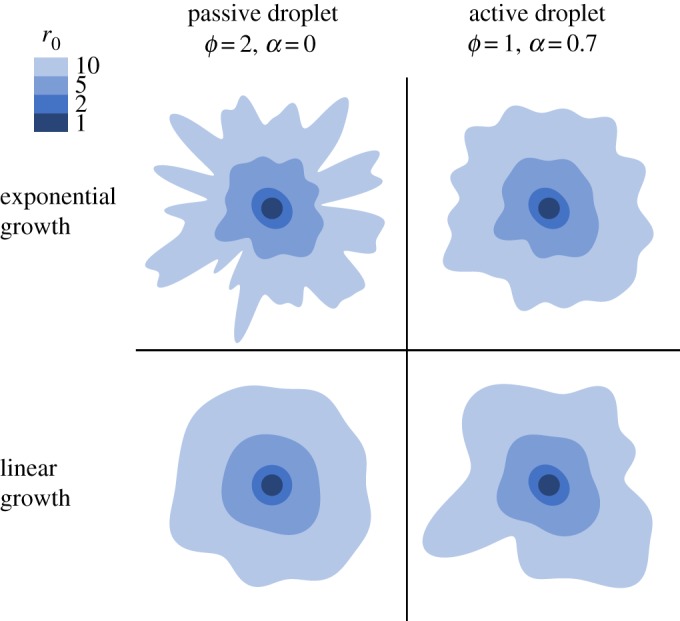
Evolution of a droplet, undergoing exponential (upper row) or linear (lower row) growth, made of a passive (left column) or active (right column) fluid. For comparison, the patterns are shown at the indicated values of the unperturbed radii r₀ (see the scale of shades), even though these are reached at different times in each growth regime. We used the initial amplitude 0.2 for all modes and, to facilitate the morphological comparison, equate the characteristic lengths introduced for each growth kinetics (see ℓ defined in §2.4 for the exponential growth, and in appendix B.2 for the linear growth): ${(\frac{2\gamma }{\beta k})}^{1/3}$ = ${(\frac{\gamma }{\beta v})}^{1/2}$ ⇔ 4βν³ = γk².

The results presented in figures 5 and 6 relate direct observables of the tumour’s geometry, and such measurements should indeed be envisaged by experimentalists. Note, however, from figure 6 that the number of fingers (approx. 10) visible at r₀ ∼ 100 µm when ϕ = 1 is in agreement with the experimental observations shown by Cheung et al. [4].

4. Conclusion

We have devised a model of a growing and self-propelled tissue that isolates the role of four mechanical parameters (summarized in table 1) on its dynamics. The theory is based on experimental evidence and is analytically trackable. We used it to describe the evolution of an embedded two-dimensional circular droplet that could model a carcinoma in an epithelial layer. In this example, we were able to highlight the basic mechanical conditioning required to form interfacial instabilities, reminiscent of the classical viscous fingering, and that could explain the tumour protrusions observed at the onset of metastasis. We notably find that the tissue’s active traction and growth kinetics are central to shape the instabilities’ pattern and evolution.

Our model, and the example of its application presented here, could further help predict the minimum tumour size for metastasis, as well as the number of subsequent invasive fingers emerging from the initial mass. To the best of our knowledge, these observable geometric quantities have yet to be measured systematically in experimental studies.

The relative analytical simplicity of our model allows the investigation of more complex settings, such as heterogeneous tumours where active forces and/or growth are not uniform, or processes where these parameters are evolving with time or are dependent on one another. It also offers constitutive equations that can be used in simulations, and we envisage such studies for systems with high traction forces, where active motions are faster than the growth velocity, and which may indeed be relevant in aggressive forms of cancer.

Appendix A. Linear stability analysis

We here follow the lines of the demonstration given by Paterson [58]. We substitute the linearized perturbations to the hydrodynamic fields in both fluids, (δp, δp′, δv, δv′), into equations (2.1)–(2.2) and obtain, to linear order

$${\mathrm{\partial }}_{\rho }\delta p=-\delta v_{\rho },$$ A 1a

$$v_{\rho }{\mathrm{\partial }}_{\theta }\delta p=\alpha \rho \delta v_{\theta }-\rho v_{\rho }\delta v_{\theta }$$ A 1b

and

$${\mathrm{\partial }}_{\rho }(\rho \delta v_{\rho })=-{\mathrm{\partial }}_{\theta }\delta v_{\theta },$$ A 1c

in the active fluid, and

$${\mathrm{\partial }}_{\rho }\delta p^{\prime }=-\varphi \delta v_{\rho }^{\prime },$$ A 2a

$${\mathrm{\partial }}_{\theta }\delta p=-\rho \varphi \delta v_{\theta }^{\prime }$$ A 2b

and

$${\mathrm{\partial }}_{\rho }(\rho \delta v_{\rho }^{\prime })=-{\mathrm{\partial }}_{\theta }\delta v_{\theta }^{\prime },$$ A 2c

in the passive fluid.

Introducing the ansatz of periodicity in θ, that is (δp, δp′, δv, δv′) ∝ e^inθ, in equations (A 1)–(A 2) allows us to calculate the partial derivatives with respect to θ. Combining the resulting equations, and using the expression of v₀ of equation (2.5a), leads to second-order differential equations for the pressure perturbations in both fluids,

$$n^2\delta p=(\rho -2\alpha ){\mathrm{\partial }}_{\rho }(\rho {\mathrm{\partial }}_{\rho }\delta p)$$ A 3a

and

$$n^2\delta p^{\prime }=\rho {\mathrm{\partial }}_{\rho }(\rho {\mathrm{\partial }}_{\rho }\delta p^{\prime }).$$ A 3b

We now assume α < r₀/2 (see §3.2). Equations (A 3) are both solved by linear combinations of two functions. One function in each of these combinations has incorrect asymptotic behaviour (diverging, instead of decaying away from the interface) and is removed. The retained functions serve to formulate the allowed forms of pressure perturbations,

$$\delta p=q(t)\left[\sum _{\hspace{0.17em}j=0}^n\frac{{(-1)}^{\hspace{0.17em}j}}{n+j}\left(\genfrac{}{}{0ex}{}{n+j}{\hspace{0.17em}j}\right)\left(\genfrac{}{}{0ex}{}{n}{\hspace{0.17em}j}\right){\left(\frac{2\alpha }{\rho }\right)}^{-j}\right]{\text{e}}^{\mathrm{i}n\theta }$$ A 4a

and

$$\delta p^{\prime }=q^{\prime }(t){\left(\frac{\rho }{r_0}\right)}^{-n}{\text{e}}^{\mathrm{i}n\theta }.$$ A 4b

The functions q(t) and q′(t) are then obtained by finding δv_ρ (using equation (A 4a) in equation (A 1a)) and δv′_ρ (using equation (A 4b) in equation (A 2a)), and substituting the resulting expressions into the kinematic boundary conditions, equation (2.3). One obtains the following:

$$\delta p=\frac{r_0}{n}[{\mathrm{\partial }}_t\delta r-\frac{\delta r}{2}][1+\frac{2\alpha }{r_0}-{\mathit{\Lambda }}_{\mathit{n}}\left(\frac{\mathit{2}\alpha }{\rho }\right)\mathit{-}\mathit{(}\mathit{n}\mathit{-}\mathit{1}\mathit{)}\frac{\mathit{2}\alpha }{\rho }]$$ A 5a

and

$$\delta p^{\prime }=\frac{\varphi r_0}{n}[{\mathrm{\partial }}_t\delta r+\frac{\delta r}{2}]{\left(\frac{\rho }{r_0}\right)}^{-n},$$ A 5b

with Λ_n the function defined by equation (3.4), and where the θ-dependency e^inθ has been incorporated into δr. Using both expressions in the pressure boundary condition, equation (2.4) linearized to first order in δr, and substituting δr ∝ f_n(t) e^inθ leads to an expression for ∂_tf_n/f_n. Upon using the definition of σ_n(r₀), equation (3.2), we finally obtain equation (3.3).

Appendix B. Scaling laws for the dominant modes

B.1. Exponential growth

We obtain the scaling of equation (3.8a) for the viscosity-controlled fingering, ϕ > 1, by only considering the passive case (α = 0). The result is valid even when α > 0, as effects of the viscosity mismatch dominate effects of activity when r₀ → ∞, as also indicated by the numerical results shown in figure 5. We then use the expression σ_n(r₀)|_α=0 given by equation (3.5) into equation (3.6), in which we substitute dt = 2dr/r for exponential growth. We calculate

$${\zeta }_n(r_0){|}_{\alpha =0}={[A_n\exp (A_n^{-1}-1)]}^{B_n},$$

with $A_n=\frac{\varphi -1}{n(n+1)}{r}_0^3$ and $B_n=\frac{(n-1)(\varphi -1)}{3(\varphi +1)}$, by using the expression of R_n obtained from solving σ_n(R_n)|_α=0 = 0. The dominant mode n_d is calculated for each r₀ from the conditions of equations (3.7). Taking the limit r₀ → ∞, and reintroducing dimensional variables, lead to equation (3.8a).

When ϕ = 1, the selection of the dominant mode depends on the activity α. We first Taylor expand Λ_n(x) to first order in x,

$${\mathit{\Lambda }}_{\mathit{n}}\mathit{(}\mathit{x}\mathit{)}\approx \frac{\mathit{2}\mathit{n}\mathit{(}\mathit{n}\mathit{-}\mathit{1}\mathit{)}}{\mathit{2}\mathit{n}\mathit{-}\mathit{1}}\mathit{x}\mathit{.}$$ B 1

This term grows linearly with n for n → ∞, while higher order coefficients in x plateau in this limit. Therefore, this expression of Λ_n is efficient even for x ∼ 1, and we use it to approximate $R_n\approx {\left[\frac{(n+1)(2n-1)}{4\alpha }\right]}^{1/2}$ and ${\sigma }_n(r_0)\approx \frac{n(n-1)}{4r_0^3}[\frac{\alpha (n^2+n-4r_0^3)}{(2n-1)r_0}-n-1]$. Upon substituting these approximations into equation (3.6), the dominant mode conditions equations (3.7) lead to equation (3.8b) for r₀ → ∞.

B.2. Linear growth

In this kinetics, the growth rate k is not a constant, as opposed to the velocity ν of the unperturbed interface which is now the adequate growth parameter. We thus use a different set of dimensionless variables, based on ν. The characteristic length is now $\ell ={(\frac{\gamma }{\beta \nu })}^{1/2}$, and times are re-scaled by ℓ/ν, activities by ${\alpha }^{\ast }=\beta \nu$, pressures by $p^{\ast }=\beta \ell \nu$ and velocities by ν. The derivation presented in appendix A proceeds similarly, and we find that the rate of perturbation’s growth σ_n(r₀) in this system of variables is written as

$${\sigma }_n(r_0)=\frac{1}{r_0}\frac{(\varphi -1)(n-1)-n(n^2-1)/r_0^2+{\mathit{\Lambda }}_{\mathit{n}}(\alpha )}{\varphi \mathit{+}\mathit{1}\mathit{+}{\mathit{\Lambda }}_{\mathit{n}}(\alpha )\mathit{-}\mathit{n}\alpha }\hspace{0.17em}.$$ B 2

The integral of equation (3.6), with the change of variables now written dt = dr, may then be calculated analytically and we obtain the following:

$${\zeta }_n(r_0)={[A_n\exp (A_n^{-1}-1)]}^{B_n}$$ B 3

with $A_n=\frac{(\varphi \hspace{0.17em}-1)(n-1)+{\mathit{\Lambda }}_{\mathit{n}}\mathit{(}\alpha \mathit{)}}{n(n^2-1)}{r}_0^2$ and $B_n=\frac{1}{2}\frac{(\varphi -1)(n-1)+{\mathit{\Lambda }}_{\mathit{n}}\mathit{(}\alpha \mathit{)}}{\varphi +1+{\mathit{\Lambda }}_{\mathit{n}}\mathit{(}\alpha \mathit{)}\mathit{-}\mathit{n}\alpha }$. Upon using the approximation of Λ_n(x) given by equation (B 1), the conditions equations (3.7) now imply equation (3.9) in the limit r₀ → ∞.

Data accessibility

This article has no additional data.

Authors' contributions

Both authors contributed equally to the research, wrote the manuscript and gave final approval for publication.

Competing interests

The authors declare no competing interests.

Funding

M.J.B. was supported by the Engineering and Physical Sciences Research Council and the Cambridge Commonwealth, European and International Trust to perform this study.