Abstract
Objectives
In the present study, we evaluated the mechanical outcome of different configurations of cannulated compression screws for the fixation of Pauwels type III femoral neck fracture and the stress distribution around the holes corresponding to fixation protocol after screws removal.
Methods
The Pauwels type III of femoral neck fracture was created in 3-matic software and the models of cannulated compression screws were constructed using UG-NX software. Five fixation systems were assembled to the fracture models. Abaqus software was used to perform the process of finite element analysis. Values of stress distribution, maximum stress, model principal strains of proximal fragment, and stress distribution around the holes of femur model were recorded.
Results
Stress of cannulated compression screws was intensely focused on the middle area of the screw near the fragment of each group. Inverted triangle model showed the highest peak stress on screws under different phases of load. Each screw dispersed some stresses, but at least one underwent the peak stress. Fracture model fixed by inverted triangle configuration showed the lowest volume of yielding strain in the proximal fragment. The area of higher stress around the holes was largest after triangle screws removal when compared with other four models.
Conclusions
Our study indicated that different cannulated compression screws fixation configurations for the unstable femoral neck fractures showed the different mechanical efficiency. Inverted triangular configuration showed the mechanical advantage and being less likely to cutout. The fixation strategy of triangle configuration was least recommended if patients tended to remove the implants.
1. Introduction
Femoral neck fracture (FNF) is a major public health problem and a common injury encountered by orthopaedic surgeons, which accounts for about 50% of hip fractures [1]. Treatment recommendations depend on the patient's age and fracture type [2]. Various treatment strategies, including compression screws, locked plates, dynamic condylar screws, and sliding hip screws, are available to treat young patients with FNFs by anatomic reduction and stable fixation to minimize the possibility of nonunion and osteonecrosis [3–5]. Despite the method of the fixation, prevalence of complications like nonunion and fixation failure has been reported between 10 and 30% [6].
Fixation by three cannulated compression screws (CCS) has been remained a standard method for fixation of FNFs for many years [7, 8], although debate continues regarding the configurations of screws fixation. Furthermore, there is no consensus on the optimal configuration of the screws. Even if fractures have healed uneventfully, internal fixation can sometimes cause functional impairment and local irritation [9, 10]. Therefore, surgeons are asked to remove implant after fracture healing by some patients with persistent complaints. But subtrochanteric fractures and other complications related to hardware removal have been well documented [11–13]. It is unclear how the holes on the proximal femur after screws removal affect the structural integrity of the bone. Seeking to analyze the stress distribution around the holes is of significant interest and medical benefit.
To our best knowledge, few biomechanical studies of finite element analysis (FEA) test are reported to evaluate the biomechanical properties of different three-CCS configurations used in the certain unstable FNFs. Therefore, we have designed this study to compare the mechanical distinction of different CCS scenarios for the fixation of unstable FNFs. We also evaluate stress distribution around the holes corresponding to fixation protocol after screws removal.
2. Materials and Methods
A geometric model of a left fourth-generation composite femur (MODEL3405#, Pacific Research Laboratories, Vashon, WA) was used in this study. Femoral neck fracture type of Pauwels III [14] was created in 3-matic software (Materialize, Belgian). The Pauwels classification is based on the angle that is formed by the fracture line and the horizontal line. Type III fractures are greater than 50 degrees. We firstly created axis of femoral shaft, through which a sagittal plane was made. The femoral neck fracture line was then created at its center by a cutting plane that was made at an angle of 20 degrees to the sagittal plane, simulating a Pauwels type III fracture (Figure 1(a)). A distal osteotomy plane was made at 10 cm above condyles (Figure 1(b)). Finally, the fracture model was created (Figure 1(c)).
Figure 1.
(a) Sagittal plane and cutting plane were made, respectively. (b) A distal osteotomy plane was made. (c) Pauwels type III model was created.
The 3-D models (Figure 2) of CCS (diameter: 6.5 mm; thread length: 16 mm) was reconstructed using the software of Unigraphics NX 8.5 (Siemens PLM Software). We completed the assemblage process of screws and bones in the 3-matic software to simulate configurations of triangle, inverted triangle, anterior triangle, posterior triangle, and vertical model (Figure 3). All the screws were perpendicular to the fracture line. Screws in each group were placed close to endosteal cortex. The inferior screw in each model was taken to avoid placing the inferior screw below the lesser trochanter level. The definition of the insertion level of CCSs could be seen in Tables 1 and 2. The threaded tunnels left by CCSs in models were also simulated using the software of 3-matic. We simulated union models after the removal of the implants (Figure 4). We meshed the models using the software of HyperMesh 11.0 (Altair Engineering, Inc., USA). The mesh was refined until the resulting displacements converged between the models. Around the screw holes, the mesh was refined.
Figure 2.

Geometric 3-D model of CCS.
Figure 3.
Assemblage of the CCSs and fracture models: (a) triangle, (b) inverted triangle, (c) anterior triangle, (d) posterior triangle, and (e) vertical model.
Table 1.
Distance from the surface of the femoral head to the tip of each screw in different models.
| Triangle | Inverted triangle | Anterior triangle | Posterior triangle | Vertical model | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | IP | IA | SP | SA | I | S | A | I | S | P | I | S | M | I | |
|
| |||||||||||||||
| Distance(mm) | 9.8 | 9.2 | 9.6 | 10.7 | 9.6 | 10.4 | 8.4 | 10.7 | 9.4 | 8.6 | 11.2 | 9.5 | 8.2 | 11.6 | 10.7 |
Abbreviation: S, superior; IP, inferoposterior; IA, inferoanterior; SP, superoposterior; SA, superoanterior; I, inferior; A, anterior; P, posterior; M, middle.
Table 2.
Distance between screws in different models.
| Triangle | Inverted triangle | Anterior triagle | Posterior triangle | Vertical model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S-IP | IP-IA | IA-S | SP-SA | SA-I | I-SP | S-A | A-I | I-S | S-P | P-I | I-S | S-M | M-I | |
|
| ||||||||||||||
| Distance(mm) | 22.7 | 12.7 | 22.6 | 17.6 | 20.7 | 21.4 | 17.3 | 18.4 | 22.5 | 17.5 | 18.5 | 22.8 | 13.6 | 14.2 |
Figure 4.
Union models after removal of the implants were simulated in 3-matic: (a) triangle, (b) inverted triangle, (c) anterior triangle, (d) posterior triangle, and (e) vertical model.
FEA process was performed in the software of Abaqus (Simulia, France). Convergence tests were performed on all models to ensure a fine enough element discretization for stress analysis. Bone was assumed to be homogeneous, isotropic with linear elastic properties [15–18]. Details of Poisson's ratio and elasticity modulus were listed in Table 3. CCS was made of Ti-6AL-4V. Finite element models were meshed using tetrahedral 10-nodes elements (C3D10). The effect of gravity was considered as negligible in the model.
Table 3.
Material properties of models in this study.
| Ti-6AL-4V | Cortical bone | Cancellous bone | |||
|---|---|---|---|---|---|
| E (GPa) | Poisson's ratio | E (GPa) | Poisson's ratio | E (GPa) | Poisson's ratio |
| 105 | 0.35 | 16.8 | 0.3 | 0.84 | 0.2 |
Contact interactions between bone and CCS, between bone fragments, were assumed to be frictional. The threaded surface of CCS was considered to be tie constraints. A friction factor of 0.3 was set as the interfaces between bone and CCS body and friction coefficient of 0.46 for bone-bone interaction [19]. The distal end of the femur surface was constrained with 0 degrees of freedom.
The finite element (FE) models were subjected to a load of 2100N corresponding to 300% body weight. The force vector applied to the femoral head laterally in the coronal plane at an angle of 13 degrees with femoral shaft axis. In the sagittal plane, the force vector applied posteriorly at an angle of 8 degrees with the femoral shaft axis [20]. In the FEA process, the force was divided into 4 steps, in order to simulate the gradually weight bearing postoperatively. Values of the von Mises stress distribution on the CCSs, maximum stress, model principal strains of proximal fragment, and stress distribution around the holes of femur model were recorded.
3. Results
Parameters of models were summarized in Table 4.
Table 4.
Parameters of the constitutive law.
| Triangle | Inverted triangle | Anterior triangle | Posterior triangle | Vertical model | ||
|---|---|---|---|---|---|---|
| Femur | Elements | 788416 | 742684 | 777827 | 752670 | 759762 |
| Nodes | 161809 | 152348 | 159510 | 154261 | 155471 | |
| Mesh size | maximum: 3mm; minimum: 0.5mm | |||||
| Screws | Elements | 56737 | 55998 | 55655 | 56435 | 57067 |
| Nodes | 101995 | 100341 | 99884 | 100885 | 101736 | |
| Mesh size | 1mm | |||||
3.1. Von Mises Stress Distribution
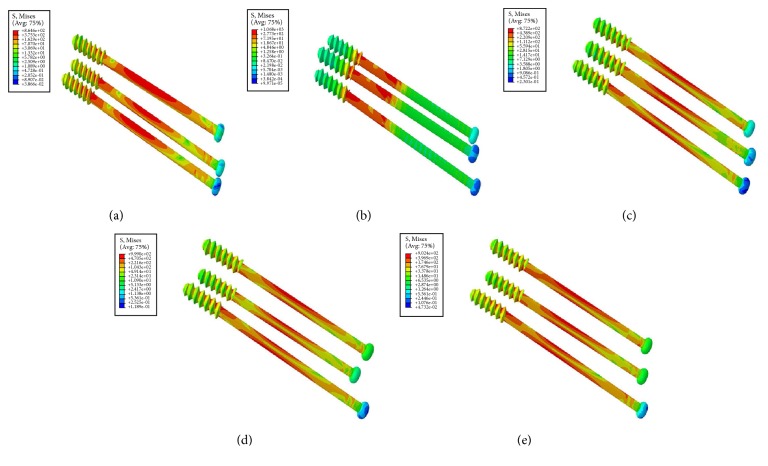
Condition of stress distribution was shown in Figure 5. Stresses were intensely focused on the middle area of the screw near the fragment of each group. Model of inverted triangle showed the highest peak stress on CCSs under different phases of loads. Lower stress values were noticed in models of triangle and anterior triangle (Figure 6). Each screw in one model dispersed some stresses, but at least one underwent the peak stress (Table 5 and Figure 7).
Figure 5.
The stress nephogram of different CCS configurations: (a) triangle, (b) inverted triangle, (c) anterior triangle, (d) posterior triangle, and (e) vertical model.
Figure 6.
Bar chart showing the peak stress variety of five CCS configurations under different phases of loads.
Table 5.
Maximum stress (Mpa) on each CCS of five models.
| Triangle | Inverted triangle | Anterior triangle | Posterior triangle | Vertical model | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | IP | IA | SP | SA | I | S | A | I | S | P | I | S | M | I | |
| 500N | 224 | 197 | 212 | 260 | 276 | 225 | 218 | 207 | 204 | 257 | 182 | 223 | 217 | 186 | 217 |
| 1000N | 444 | 400 | 426 | 524 | 543 | 451 | 437 | 416 | 419 | 511 | 372 | 454 | 432 | 368 | 441 |
| 1500N | 659 | 608 | 643 | 797 | 803 | 675 | 657 | 625 | 642 | 759 | 568 | 692 | 643 | 543 | 670 |
| 2100N | 865 | 819 | 860 | 1068 | 1068 | 899 | 872 | 837 | 872 | 990 | 768 | 934 | 846 | 709 | 902 |
Figure 7.
Bar chart showing the peak stress on each screw in five CCS configurations under different phases of loads.
3.2. Principal Strains in Proximal Fragment
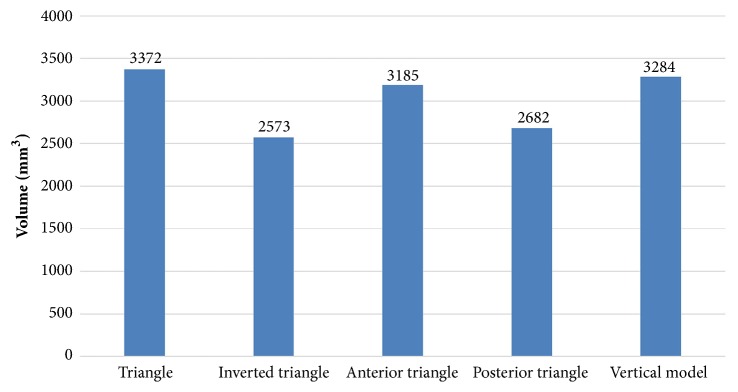
Strain nephograms demonstrated principal strains of proximal bone structure in a cross-section of proximal fragment for the different screw configurations (Figure 8). The strain nephograms is based on the hypothesis that CCS cutout from femoral head may take place as a result of high strains in the weak area of the proximal bone fragment [20]. Areas characterized by strains larger than a cutout value of 0.9% maximum principal strain were assigned orange color to emphasize the regions in which the bone structure was vulnerable to yielding [21]. Model of inverted triangle showed the lowest volume of yielding strain in proximal cancellous bone structure indicating that the CCSs configuration of inverted triangle was less likely to be cutout (Figure 9).
Figure 8.
Strain nephograms showing the principal strains plotted in percent with a yield strain value of 0.9%. Orange regions indicating the strains above 0.9% and at higher risk of cutout. (a) Triangle model. (b) Inverted triangle model. (c) Anterior triangle model. (d) Posterior triangle model. (e) Vertical model.
Figure 9.
Bar chart showing the cancellous bone volume in the proximal fragment susceptible to yielding.
3.3. Stress Distribution around Screw Holes
A comparison of the stress distribution around the holes for the five fixation protocols after screws removal was shown in Figure 10. The area of higher stress around the holes was largest after triangle screws removal when compared with other four models. In the scenario with triangle screws removal, the inferior two holes negatively affected the mechanical performance of the femur, and complication like subtrochanteric fractures may tend to occur.
Figure 10.
Stress distribution around the holes corresponding to fixation protocol after screws removal. (a) Triangle model. (b) Inverted triangle model. (c) Anterior triangle model. (d) Posterior triangle model. (e) Vertical model.
4. Discussion
In the present study, we investigated whether different three-CCS configurations had the mechanical distinction for the fixation of unstable FNF and analyzed the effect of different configurations after screws removal on the strength of femur using FEA. This study demonstrated that screws of inverted triangle configuration underwent highest stress value under the increasing loads, and the bone structure showed the minimum yielding strains when compared to other configurations. The fixation strategy of triangle configuration was least recommended if patients were willing to remove the implants.
Some studies have evaluated the outcome of different screw types for the fixation of FNFs [22, 23], but without finding the statistical difference in clinical outcomes. Selvan et al. [7] demonstrated that triangular configurations had biomechanical advantage for the fixation of Pauwels type III fractures using synthetic bone models. But mechanical tests performed by Crowell et al. [24] and Benterud et al. [25] concluded that configuration of inverted triangle and diamond patterns provides better fixation of femoral head. And Yang et al. [8] reported that the inverted triangle configuration of screws increased the union rate when compared with triangle configuration. The FEA results in this study may provide some guidance in the clinical practice. The Figures 5 and 6 illustrated that inverted triangle screws underwent higher amount of stress than other configurations. This can be explicated by the condition that CCSs of inverted triangle provide a better anchorage than others, thereby displacing the stresses transmitted by the body weight, also demonstrated in Figures 8 and 9. The maximum principal strains and corresponding yield strain were used to evaluate the risk of screw cutout. Screw stability within the head is up to the adequate anchoring force in bone structure. It is necessary to avoid the condition that the bone is beyond its yield straining. Figure 9 showed the volume of bone susceptible to yielding in proximal bone structure, which indicated that the CCSs configuration of inverted triangle was less likely to be cutout.
In FNFs, CCSs configuration of inverted triangle showed mechanical and clinical advantage compared with other configurations. This may associate with three aspects. First, the two most distal screws of triangle configuration inevitably pass through the Ward triangle within the femoral neck, which leads to the decrease of bone density because of the absence of trabeculation [26]. Second, the dense trabeculae on the central and superior portion of the femoral head could provide greater bone anchorage [24, 25]. The two screws of inverted triangle configuration inserted into the dense trabeculae area exhibit greater holding strength than the only one screw of triangle configuration. Third, drilling twice on the less area of inferior portion induces the stress concentration on the subtrochanteric area, which may increase the prevalence of subsequent subtrochanteric fractures.
Zielinski et al. [27] concluded that implant removal after internal fixation of a FNF positively influenced quality of life, especially for those who were younger and more ambulatory and more often had a Pauwels III fracture and an evident implant back-out. But subtrochanteric fractures have been reported as a serious complication following removal of screws for FNF or slipped capital femoral epiphysis [11–13]. In this study, the results of FEA research showed that different screws' configurations displayed different stress distribution on the proximal femur. As shown in Figure 10, triangular configuration showed larger stress distribution area around the screw holes, indicating that triangle construct inclined to second fracture around the subtrochanteric area.
In this study, there is no experimental validation being performed, which definitely is a limitation. Nevertheless, our objective was to show the tendency rather than the absolute value of parameters. In this way, the lack of experimental validation is rationalized. Previous experimentally validated studies [15–18] employed the same loading and boundary conditions as this study. And it was just a static simulated biomechanical study and further biomechanical researches are needed to explore the cyclic loading conditions. Even so, this is the first FEA research comparing the mechanical distinction of five CCS configurations and the stress distribution around the holes corresponding to fixation protocol after screws removal. Besides, we have simulated the threaded tunnels left by CCS in each model and refined the mesh around the areas to make the parameter level more realistic.
5. Conclusions
In conclusion, using FEA modeling, we systematically evaluated the mechanical distinction in unstable femoral neck fracture models by varying CCS configurations and the stress distribution around the holes corresponding to screw configurations after fracture union. Our study indicated that different configurations for the unstable femoral neck fractures showed the different mechanical efficiency. Inverted triangle configuration showed the mechanical advantage and being less likely to be cutout. The fixation strategy of triangle configuration was least recommended if patients tended to remove the implants.
Contributor Information
Lianting Li, Email: liliantingqd31@163.com.
Ming Hao, Email: haoming301@163.com.
Data Availability
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
There are no conflicts of interest for all authors.
Authors' Contributions
Jiantao Li, Menglin Wang, and Jianfeng Zhou contributed equally to this work.
References
- 1.Støen R. Ø., Nordsletten L., Meyer H. E., Frihagen J. F., Falch J. A., Lofthus C. M. Hip fracture incidence is decreasing in the high incidence area of Oslo, Norway. Osteoporosis International. 2012;23(10):2527–2534. doi: 10.1007/s00198-011-1888-3. [DOI] [PubMed] [Google Scholar]
- 2.Lowe J. A., Crist B. D., Bhandari M., Ferguson T. A. Optimal Treatment of Femoral Neck Fractures According to Patient's Physiologic Age: An Evidence-Based Review. Orthopedic Clinics of North America. 2010;41(2):157–166. doi: 10.1016/j.ocl.2010.01.001. [DOI] [PubMed] [Google Scholar]
- 3.Schmidt A. H., Asnis S. E., Haidukewych G. I., Koval K. J., Thorngren K.-G. Femoral neck fractures. Instructional Course Lectures. 2005;54:417–445. [PubMed] [Google Scholar]
- 4.Ly T. V., Swiontkowski M. F. Management of femoral neck fractures in young adults. Instructional Course Lectures. 2009;58:69–81. doi: 10.4103/0019-5413.38574. [DOI] [PubMed] [Google Scholar]
- 5.Swiontkowski M. F. Current concepts review: Intracapsular fractures of the hip. The Journal of Bone & Joint Surgery. 1994;76(1):129–138. doi: 10.2106/00004623-199401000-00019. [DOI] [PubMed] [Google Scholar]
- 6.Estrada L. S., Volgas D. A., Stannard J. P., Alonso J. E. Fixation failure in femoral neck fractures. Clinical Orthopaedics and Related Research. 2002;(399):110–118. doi: 10.1097/00003086-200206000-00013. [DOI] [PubMed] [Google Scholar]
- 7.Selvan V. T., Oakley M. J., Rangan A., Al-Lami M. K. Optimum configuration of cannulated hip screws for the fixation of intracapsular hip fractures: a biomechanical study. Injury. 2004;35(2):136–141. doi: 10.1016/S0020-1383(03)00059-7. [DOI] [PubMed] [Google Scholar]
- 8.Yang J.-J., Lin L.-C., Chao K.-H., et al. Risk factors for nonunion in patients with intracapsular femoral neck fractures treated with three cannulated screws placed in either a triangle or an inverted triangle configuration. The Journal of Bone & Joint Surgery—American Volume. 2013;95(1):61–69. doi: 10.2106/jbjs.k.01081. [DOI] [PubMed] [Google Scholar]
- 9.Jamil W., Allami M., Choudhury M. Z., Mann C., Bagga T., Roberts A. Do orthopaedic surgeons need a policy on the removal of metalwork? A descriptive national survey of practicing surgeons in the United Kingdom. Injury. 2008;39(3):362–367. doi: 10.1016/j.injury.2007.10.028. [DOI] [PubMed] [Google Scholar]
- 10.Hanson B., van der Werken C., Stengel D. Surgeons' beliefs and perceptions about removal of orthopaedic implants. BMC Musculoskeletal Disorders. 2008;9, article 73 doi: 10.1186/1471-2474-9-73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hafez M. A., Templeton P. A. Subtrochanteric femoral fracture following removal of screw for slipped capital femoral epiphysis. Injury. 2004;35(9):p. 953. doi: 10.1016/j.injury.2004.02.003. [DOI] [PubMed] [Google Scholar]
- 12.Ilchmann T., Parsch K. Complications at screw removal in slipped capital femoral epiphysis treated by cannulated titanium screws. Archives of Orthopaedic and Trauma Surgery. 2006;126(6):359–363. doi: 10.1007/s00402-006-0126-5. [DOI] [PubMed] [Google Scholar]
- 13.Song K. S. O., Lee S. W. O. Subtrochanteric femur fracture after removal of screws for femoral neck fracture in a child. American journal of orthopedics (Belle Mead, N.J.) 2015;44(1):40–42. [PubMed] [Google Scholar]
- 14.Rupprecht M., Grossterlinden L., Ruecker A. H., et al. A comparative biomechanical analysis of fixation devices for unstable femoral neck fractures: The Intertan versus cannulated screws or a dynamic hip screw. Journal of Trauma - Injury Infection and Critical Care. 2011;71(3):625–634. doi: 10.1097/TA.0b013e31820e86e6. [DOI] [PubMed] [Google Scholar]
- 15.Gardner M. P., Chong A. C. M., Pollock A. G., Wooley P. H. Mechanical evaluation of large-size fourth-generation composite femur and tibia models. Annals of Biomedical Engineering. 2010;38(3):613–620. doi: 10.1007/s10439-009-9887-7. [DOI] [PubMed] [Google Scholar]
- 16.Grassi L., Väänänen S. P., Amin Yavari S., et al. Experimental validation of finite element model for proximal composite femur using optical measurements. Journal of the Mechanical Behavior of Biomedical Materials. 2013;21:86–94. doi: 10.1016/j.jmbbm.2013.02.006. [DOI] [PubMed] [Google Scholar]
- 17.Heiner A. D. Structural properties of fourth-generation composite femurs and tibias. Journal of Biomechanics. 2008;41(15):3282–3284. doi: 10.1016/j.jbiomech.2008.08.013. [DOI] [PubMed] [Google Scholar]
- 18.Mei J., Liu S., Jia G., Cui X., Jiang C., Ou Y. Finite element analysis of the effect of cannulated screw placement and drilling frequency on femoral neck fracture fixation. Injury. 2014;45(12):2045–2050. doi: 10.1016/j.injury.2014.07.014. [DOI] [PubMed] [Google Scholar]
- 19.Chen W.-P., Tai C.-L., Shih C.-H., Hsieh P.-H., Leou M.-C., Lee M. S. Selection of fixation devices in proximal femur rotational osteotomy: clinical complications and finite element analysis. Clinical Biomechanics. 2004;19(3):255–262. doi: 10.1016/j.clinbiomech.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 20.Goffin J. M., Pankaj P., Simpson A. H. The importance of lag screw position for the stabilization of trochanteric fractures with a sliding hip screw: A subject-specific finite element study. Journal of Orthopaedic Research. 2013;31(4):596–600. doi: 10.1002/jor.22266. [DOI] [PubMed] [Google Scholar]
- 21.Goffin J., Pankaj P., Simpson A., Seil R., Gerich T. Does bone compaction around the helical blade of a proximal femoral nail anti-rotation (PFNA) decrease the risk of cut-out? A subject-specific computational study. Bone joint research. 2013;2(5):79–83. doi: 10.1302/2046-3758.25.2000150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Alho A., Austdal S., Benterud J. G., Blikra G., Lerud P., Raugstad T. S. Biases in a randomized comparison of three types of screw fixation in displaced femoral neck fractures. Acta Orthopaedica. 1998;69(5):463–468. doi: 10.3109/17453679808997779. [DOI] [PubMed] [Google Scholar]
- 23.Lagerby M., Asplund S., Ringqvist I. Cannulated screws for fixation of femoral neck fractures: No difference between Uppsala screws and Richards screws in a randomized prospective study of 268 cases. Acta Orthopaedica. 1998;69(4):387–391. doi: 10.3109/17453679808999052. [DOI] [PubMed] [Google Scholar]
- 24.Crowell R. R., Edwards W. T., Hayes W. C. Pullout strength of fixation devices in trabecular bone of the femoral head. Trans 31st Orthop Res Soc. 1985;10 [Google Scholar]
- 25.Benterud J. G., Husby T., Graadahl Ø., Alho A. Implant holding power of the femoral head: A cadaver study of fracture screws. Acta Orthopaedica. 1992;63(1):47–49. doi: 10.3109/17453679209154848. [DOI] [PubMed] [Google Scholar]
- 26.Singh M., Nagrath A. R., Maini P. S. Changes in trabecular pattern of the upper end of the femur as an index of osteoporosis. The Journal of Bone & Joint Surgery. 1970;52(3):457–467. doi: 10.2106/00004623-197052030-00005. [DOI] [PubMed] [Google Scholar]
- 27.Zielinski S. M., Heetveld M. J., Bhandari M., Patka P., Van Lieshout E. M. M. Implant removal after internal fixation of a femoral neck fracture: Effects on physical functioning. Journal of Orthopaedic Trauma. 2015;29(9):e285–e292. doi: 10.1097/BOT.0000000000000358. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.