Altimeter-era emergence of the patterns of forced sea-level rise in climate models and implications for the future

Significance

Regional patterns of sea-level rise have been observed from satellites since 1993 and are associated with increased coastal impacts in many regions. It is unknown whether such patterns will be transient, arising from natural climate variations, or persistent, driven by external climate forcing. Here, using climate model ensembles, we demonstrate that forced changes are likely to have contributed significantly to observed altimeter-era patterns of rise and that these patterns may persist for decades to come, with increased intensity as climate change progresses.

Abstract

The satellite altimeter record has provided an unprecedented database for understanding sea-level rise and has recently reached a major milestone at 25 years in length. A challenge now exists in understanding its broader significance and its consequences for sea-level rise in the coming decades and beyond. A key question is whether the pattern of altimeter-era change is representative of longer-term trends driven by anthropogenic forcing. In this work, two multimember climate ensembles, the Community Earth System Model (CESM) and the Earth System Model Version 2M (ESM2M), are used to estimate patterns of forced change [also known as the forced response (FR)] and their magnitudes relative to internal variability. It is found that the spatial patterns of 1993–2018 trends in the ensembles correlate significantly with the contemporaneous FRs (0.55 ± 0.10 in the CESM and 0.61 ± 0.09 in the ESM2M) and the 1950–2100 FRs (0.43 ± 0.10 in the CESM and 0.51 ± 0.11 in the ESM2M). Unforced runs for each model show such correlations to be extremely unlikely to have arisen by chance, indicating an emergence of both the altimeter-era and long-term FRs and suggesting a similar emergence in nature. Projected patterns of the FR over the coming decades resemble those simulated during the altimeter era, suggesting a continuation of the forced pattern of change in nature in the coming decades. Notably, elevated rates of rise are projected to continue in regions that are susceptible to tropical cyclones, exacerbating associated impacts in a warming climate.

Sea-level rise is among the most societally and ecologically impactful manifestations of a changing climate, yet our understanding of its historical variations and projections of its future evolution contain significant uncertainty (1–3). A major advance in its understanding has been provided by satellite altimetry since 1993 (4). At 25 y in length, this climate data record is based on the combined data records of the TOPEX/Poseidon, Jason-1, Jason-2, and Jason-3 satellites and has provided near-global coverage of open ocean sea level with remarkable accuracy and temporal sampling (samples accurate to ∼1–2 cm every ∼10 d). As a key climate metric, global mean sea level has drawn particular attention and with averaging in space and time, can be estimated for the global annual mean to ∼1 mm, with an observed rate of rise during the altimeter era of about 3.0 ± 0.4 mm/y and an acceleration of 0.084 ± 0.025 mm/y² (1σ) (5).

Altimetry has served as the basis for various other insights. For example, it has become evident that regional rates of rise can vary substantially from the global mean, with spatial variations that can be several times larger than the global average rate of rise (1–3). Our physical understanding and causal attribution of such spatial variations, however, remain limited, and the extent to which such variations are indicative of long-term trends is unclear (2, 6, 7). However, this understanding is key to regional stakeholders (2, 8), as it shapes expectations regarding whether observed trend patterns will persist in the coming decades unabated or are merely transient deviations from the global mean rate of rise, thus holding promise for a possible near-term reversal. Here, climate model simulations are used to address these and related questions, with the goal of determining whether the response in sea level to external forcing has been a major contributor to the pattern of altimeter-era trends.

Altimeter-Era Sea-Level Trends

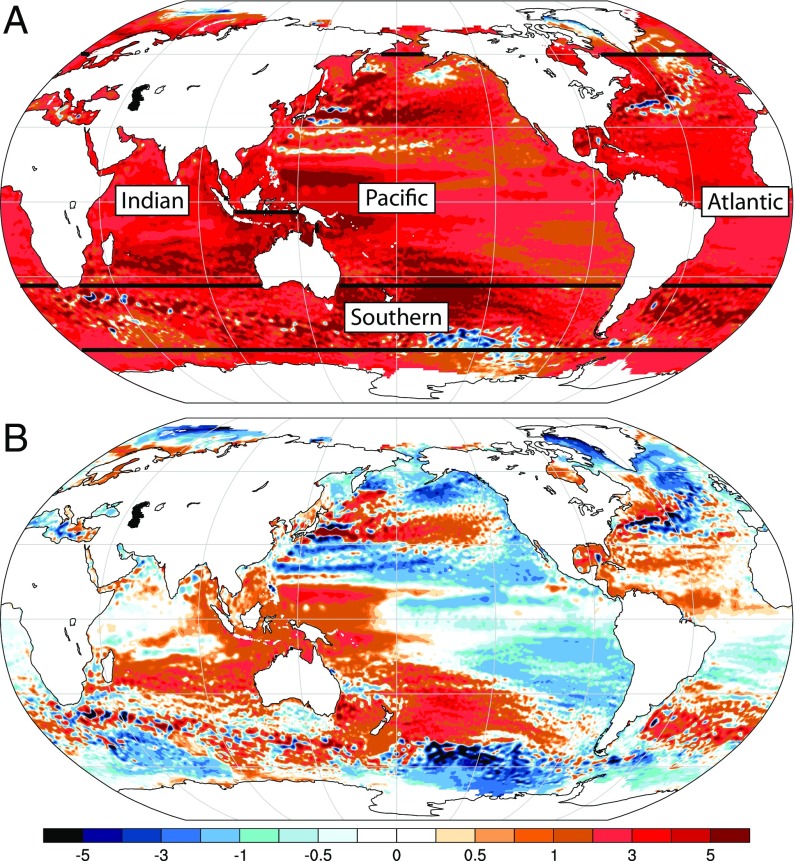
The observed regional trends estimated from just over 25 y of satellite altimeter measurements are shown in Fig. 1 with the global mean background rate of rise both included (Fig. 1A) and removed (Fig. 1B). The global mean raw trend averages ∼3.0 mm/y, and regional rates of rise are positive in all regions except for a few eddy-scale areas near the major Northern Hemisphere western boundary currents (the Kuroshio in the western north Pacific Ocean and the Gulf Stream in the North Atlantic Ocean) that perhaps reflect shifts in these currents; near Greenland, where gravitational effects can be important (9); and in the Southern Ocean (10, 11). Sea-level changes due to eddies and shifting currents are locally offset in regional averages by near-equal and opposite trends in their immediate vicinity. In this work, a focus is given to the broad-scale deviations in regional sea level that have profound significance, particularly along coastlines (2, 11, 12). In many regions and particularly in the tropics and in the eastern Indian, western Pacific, and subtropical Atlantic Ocean basins, rates of rise exceed the global average substantially and have roughly doubled the altimeter-era rate of rise (>3 mm/y) (red regions in Fig. 1B). In contrast, rates of rise in the eastern basins have been below the global mean, in some areas by over 1 mm/y (blue regions in Fig. 1B), substantially offsetting global mean changes (8, 12). The strongest large-scale deficits from the global mean rate of rise are evident in the Southern Ocean, and these can reach magnitudes exceeding 3 mm/y, entirely offsetting global mean rise, and have been associated with reduced rates of warming due to circumpolar upwelling (13).

Fig. 1.

Regional sea-level trends from altimetry (millimeters year⁻¹) from 1993 to mid-2018 (A) based on annual averages of raw AVISO estimates (https://www.aviso.altimetry.fr/en/my-aviso.html) and (B) with the global mean rate of rise removed. Also shown in A are the boundaries for the Pacific, Atlantic, Indian, and Southern Oceans used for defining ocean basins as defined in this analysis.

Observed sea-level trends are known to arise from the combined influences of internal variability due to natural variations arising within the climate system and the forced response (FR), defined as the climate response driven by forcings external to the climate system, such as from natural (i.e., volcanic) or anthropogenic aerosols, or from increases in greenhouse gas concentrations (14). Studies aimed at disentangling the FR from internal variability on regional scales have been previously attempted. In the Indo-Pacific region, diagnostic assessments have largely attributed observed trends to internal variability (15, 16). On a global scale, the relative contributions of forced and internal variability remain somewhat unclear, although many studies have concluded that altimeter-era trends are likely dominated by internal variations (6, 14, 15, 17), while others have suggested the possible emergence of the FR in the Southern Ocean (7). Studies looking at regional time of emergence based on multimodel archives show strong dependence on region (2, 6) and a benefit in removing patterns of internal variability (11), but they have yet to identify a clear emergence of major features. Considerable uncertainty surrounding these finding persists, however, as contrasts within multimodel archives include both internal variability and structural contrasts between models, with few means of separating the two (6, 7). As such, estimates of internal variability derived from multimodel ensembles may be inflated, as the representation of internal variability in the archives is often poor (18). Lastly, it is also not possible in these archives to assess the time-varying character of the FR, since they include few ensemble members for individual models, and it is often assumed that trends through the 21st century are a suitable estimate, further introducing error into the estimation of FR emergence for short periods, such as the satellite record, as discussed below.

From a purely empirical standpoint, the fact that the spatial pattern of observed trends (Fig. 1) in many ways resembles the sea surface temperature (SST) anomalies that accompany the El Niño–Southern Oscillation and Pacific Decadal Oscillation (19) supports the viewpoint that observed trends arise largely from internal variability. It is also known that strong variations in those modes occurred during the altimeter era (11, 20, 21), again suggesting a strong role. A challenge for diagnostic assessments arises, however, if the spatial pattern of internal modes resembles the pattern of long-term change, as disentangling them during altimeter era remains a challenge (21). To address this challenge, techniques for assessing the time of emergence of climate signals from internal variability have been explored for a range of variables, including temperature (22), rainfall extremes (23), and sea level (6, 7). Often, a pattern scaling approach is adopted, whereby the long-term trend, such as spanning the 20th and 21st centuries, is used to estimate the FR, as doing so provides a strong signal relative to the noise of internal variability. This approach does not, however, provide a means for estimating the time-varying character of the FR and thereby, introduces error when applied to discrete time periods. In the context of sea-level changes in the altimeter era, this assumption is particularly problematic; strong transient changes in forcing are known to occur during the era from changes in total anthropogenic aerosol emissions, their regional distributions, and natural forcings, such as those associated with the eruption of Mt. Pinatubo in 1991, the effects of which persisted for at least a decade (24). Climate models can be useful in estimating these effects; however, multimodel archives also do not allow for direct estimation of the FR on decadal timescales due to model structural contrasts (25). Here, to address these challenges, an alternative approach is taken using “large ensembles” (LEs) of climate model simulations.

Sea Level in Climate Model LEs

Climate models are powerful tools for disentangling the FR from internal variability, and as such, they play an essential role in the interpretation of short satellite records and the attribution of observed changes (24, 25). In the past decade, multimodel archives (27, 28) have been used extensively to address a range of climate issues, including sea-level rise (2, 6, 14). More recently, LEs of climate model simulations have been produced to allow for the separation of forced and internal variability, where the FR can be computed directly from the ensemble mean simulated trend across a given time period, as random internal variability averages out. LEs are created when multiple simulations using a single climate model are driven by an estimate of imposed forcings (e.g., external influences on climate, such as solar variability, volcanic and anthropogenic aerosols, and greenhouse gas emissions) initiated with different initial conditions. Unlike multimodel archives, the use of a single model eliminates any contribution of model structural uncertainty to its ensemble spread. When extremely small perturbations are made to the initial conditions of such simulations (for example, with a 10⁻¹⁴ °C change in atmospheric temperatures), chaotic effects lead them to fully diverge in their atmospheric internal states within a few months (26). Such variations in the climate system subsequently accompany the underlying change in climate state arising from external forcings. When a sufficient number of individual simulations (typically ≥ 30) are performed in this manner, their trends can be averaged together to directly compute the FR (26). Here, this is done with the goal of resolving the FR in sea level across the mid-20th century (1950–1975), the altimeter era (1993–2018), the coming decades (2020–2045), and the long-term (1950–2100). After the FRs are determined, the distribution of its pattern correlations with individual ensemble members is then derived and compared with analogous distributions derived from a control (i.e., unforced) simulation. When these distributions become statistically distinct, the FR can be concluded to have emerged. Notably, this is a distinct and somewhat more sensitive definition of emergence than time series-based methods examining the magnitude of trends relative to annual mean variance (22). However, the approach used here is arguably more suitable to the science questions pertaining to the altimeter record developed above. Lastly, after the FR has been found to emerge, an additional important question then arises as to whether a simulated FR is realistic. This question, while only tangentially related to the question of emergence, can be addressed by comparing trend patterns in altimetry with the distribution of patterns simulated in the LEs. Where the observed trend correlations lie outside of the ensemble range, biases in model variability or FRs are likely to exist.

Important caveats exist when using climate models to study sea level. Some models do not permit changes in global ocean volume, while many do not fully represent the processes that influence the total ocean mass. Dynamic ice sheets are currently not represented in most climate models, including those used here, and gravitational effects and land motion driven by ice mass loss are not represented in any current climate model (2, 29, 30). The limited resolution at which the models are run also precludes simulation of eddies in the open ocean, resulting in poor representation of western boundary currents and their extensions and an adequate treatment of coastal ocean dynamics. However, for understanding broad-scale changes in the open ocean, it is the changes in ocean heat content, near-surface winds, and salinity that are dominant, and climate models have long been able to resolve these aspects, although a role for small-scale interactions remains plausible and model validation is needed (25). Here, we use LEs based on 40 members of the Community Earth System Model (CESM) (26) spanning from 1920 to 2100 and 30 members of the Geophysical Fluid Dynamics Laboratory Earth System Model Version 2M (ESM2M) (31) run from 1950 to 2100. For the 20th century through 2005, estimated historical forcings (14) are imposed in these simulations, while from 2005 to the remainder of the 21st century, forcings are prescribed from a business-as-usual climate scenario entailing increases in greenhouse gas concentrations and reductions in anthropogenic aerosol emissions [also known as Representative Concentration Pathway 8.5 (RCP8.5)] (32), both of which are likely to influence sea level.

Simulated Patterns of Change

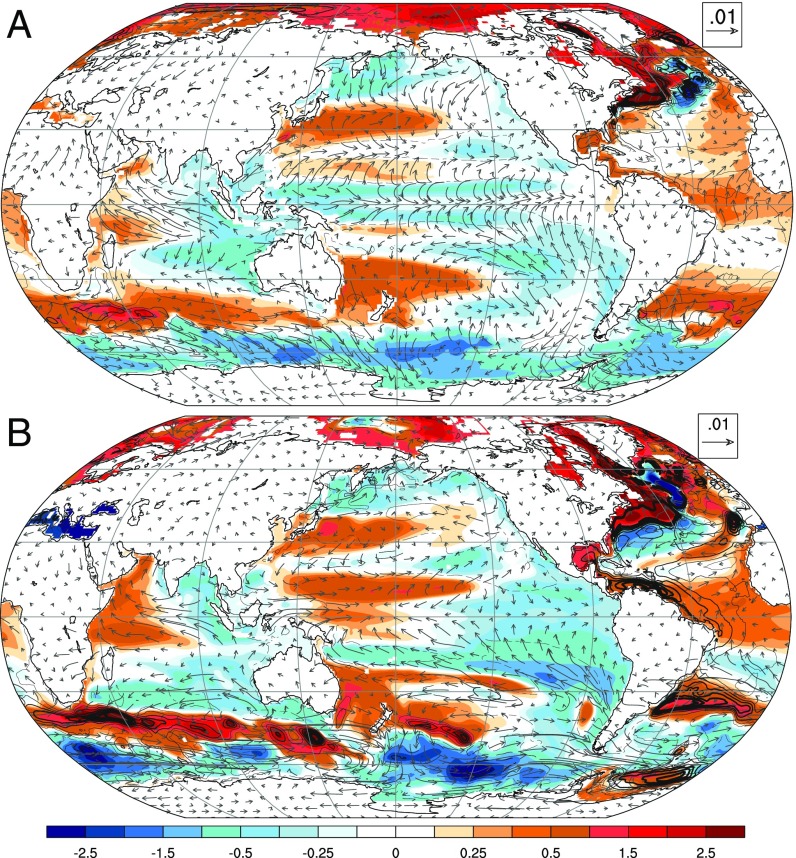
The altimeter-era (1993–2018) FR trends in sea level and near-surface winds for the CESM and the ESM2M LEs are shown in Fig. 2, where the global mean rise has been removed to highlight regional patterns. The FRs estimated from annual mean trends are shown, as seasonal contrasts in the FRs are small, with patterns for June through August and December through January correlating at 0.91 for the CESM and 0.99 for the ESM2M (SI Appendix, Fig. S1 and Table S1). In most regions, the FR sea-level trends are statistically significant based on the ensemble mean trend exceeding its ±2σ range across ensemble members (SI Appendix, Fig. S2). Various similarities in the altimeter-era FR are apparent across the two models, and these include a broad-scale relative increase in sea level in the western subtropical Pacific, tropical and northern Atlantic, and subtropical southern Atlantic and Pacific Oceans. Pronounced rates of rise are also evident in the southern midlatitude Indian Ocean near 40° S. Decreases in relative sea level are simulated in the eastern and northern Pacific, eastern and subtropical southern Indian, and polar Southern Oceans. Global ocean FR pattern correlations between the CESM and the ESM2M are strong at 0.50 for the altimeter era (Table 1), although there are likely limits to how well each model depicts nature (Discussion). Accompanying the sea-level trends are FR trends in the near-surface wind field that include an intensification of meridional convergence in the tropical central and eastern Pacific Oceans, easterly anomalies in the Indian Ocean, and westerlies in the Southern Ocean. Disagreement between the models is largest in the western tropical Pacific Ocean, where the CESM simulates a decrease in sea level, while ESM2M simulates an increase, despite both models simulating westerly surface wind FR trends. Overall, the basin-scale FR trend pattern correlations between the two models are modest at 0.37, 0.52, 0.57, and 0.54 for the Atlantic, Southern, Pacific, and Indian Ocean basins, respectively (Table 1). It is particularly notable that relative rates of rise associated with the FR are of comparable magnitude with the global mean rate of rise and that the general structure of changes simulated in the LEs in many regions resembles those in the altimeter record (Fig. 1B).

Fig. 2.

The 1993–2018 FR in sea level (millimeters per year; global mean removed), near-surface winds (vectors; meters per second per year; mean retained), and ocean heat content (contour lines; spacing of 10⁷ J/m² per year) estimated from ensemble mean trends in (A) the CESM and (B) the ESM2M. Heat content changes are shown as a function of depth and in greater detail in SI Appendix, Figs. S8, S10, and S11.

Table 1.

Pattern correlations between the FRs in the CESM and the ESM2M across various time periods

Time period	Global	Atlantic	Southern	Pacific	Indian
1950–1975	−0.21	−0.08	−0.20	−0.32	−0.26
1993–2018	0.50	0.37	0.52	0.57	0.54
2020–2045	0.63	0.59	0.67	0.81	0.51
1950–2100	0.76	0.70	0.78	0.88	0.69

The correlations demonstrate general agreement between the models’ long-term FRs while highlighting disagreement in their FRs for the mid-20th century.

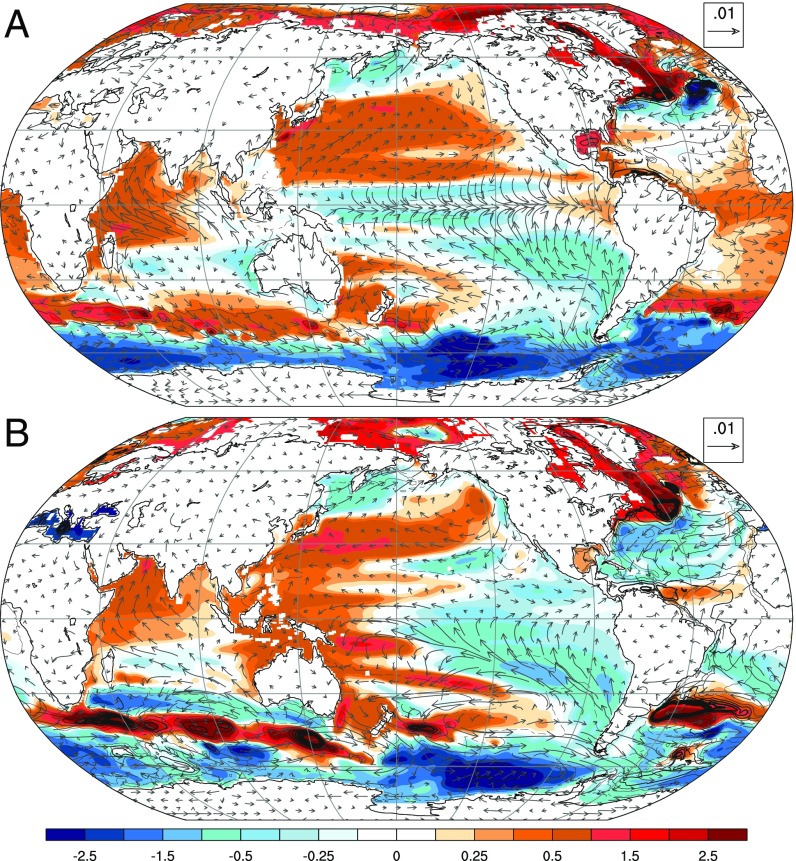
Estimates of the forced sea-level trends can also be derived for 1950–1975 (SI Appendix, Fig. S3), for the coming decades (2020–2045) (Fig. 3), and for 1950–2100 (SI Appendix, Fig. S4). It is noteworthy that the FR from 1950 to 1975, when aerosol forcing of climate increased substantially, contrasts considerably between models (r = −0.21) (Table 1) and with the altimeter era (r = −0.30 for CESM, r = 0.04 for ESM2M) and subsequent FRs, highlighting both the transient nature of the FR and associated limitations in pattern scaling approaches to estimate it. In contrast, the altimeter-era FR trend is well correlated with those simulated for 2020–2045 (r = 0.72 for CESM, r = 0.76 for ESM2M) and for 1950–2000 (Table 2 and SI Appendix, Table S2) but with an intensity that increases notably in the future (Figs. 2 and 3). The pattern correlations of the model FRs also become increasingly similar, with the global ocean pattern correlation for CESM and ESM2M FRs increasing to 0.63 for 2020–2045 and basin correlations that are about 20% stronger (except for the Indian Ocean, where they remain at about 0.51) (Table 1). A difference between the FRs persists in the western Pacific Ocean (Fig. 3), and this likely reflects the documented contrast in projections of the Walker circulation between the models (33, 34).

Fig. 3.

The 2020–2045 FR in sea level (millimeters per year; global mean removed), near-surface winds (vectors; meters per second per year; mean retained), and ocean heat content (contour lines; spacing of 10⁷ J/m² per year) estimated from ensemble mean trends in (A) the CESM and (B) the ESM2M. Heat content changes are shown as a function of depth and in greater detail in SI Appendix, Figs. S8, S10, and S11.

Table 2.

Representativeness of long-term pattern: pattern correlations between the long-term FR (1950–2100) and other time periods in the CESM for the globe and by basin

Time period	Global	Atlantic	Southern	Pacific	Indian
1950–1975	−0.10	−0.28	0.37	−0.03	0.14
1993–2018	0.78	0.78	0.86	0.78	0.79
2020–2045	0.94	0.93	0.95	0.96	0.92

The correlations demonstrate the similarity between altimeter-era and near-future (2020–2045) FR patterns of rise in the CESM while highlighting the change in those patterns from the mid-20th century.

Detection and Mechanisms of Change

It is known that climate models generally contain a number of biases, and these include, for example, an excessively westward extension of the tropical Pacific “cold tongue” of SST on the equator and a tendency for hemispheric symmetry in the Intertropical Convergence Zone (35). While the CESM and ESM2M models are among the more skillful models in reproducing observed present-day climate (36), discrepancies between their FRs are well documented (34) and are likely to result, at least in part, from shortcomings in the models’ base states (36). Given this, the main goal in this work [one that builds on the availability of altimetry data (Discussion)] is to determine whether noise from internal climate variability is likely to overwhelm the FR in the altimeter era rather than to precisely determine the structure of the FR itself. Central to this question is whether the models’ internal variability is consistent with observations, and in this sense, the CESM and the ESM2M are among the most skillful models available (34, 36, 37).

As already discussed, with LEs, the question as to whether the FR has emerged from noise can be addressed by assessing the independence of the distributions of pattern correlations derived from forced and control simulations. It is worth noting that the FR is not necessarily stationary over time but rather, evolves with both changes in forcing and the lagged climate response. A relevant question, therefore, is precisely which FR is being examined for emergence. For questions pertaining to the relative role of internal variability vs. the FR in the altimeter record, it is the contemporaneous FR (1993–2018) that may be of greatest relevance, whereas for questions pertaining to long-term impacts and planning, it is the emergence of the long-term (e.g., 1950–2100) FR that may be of interest. Here, a focus is given to analysis of the contemporaneous FR emergence, while the emergence of the 1950–2100 FR is included in SI Appendix.

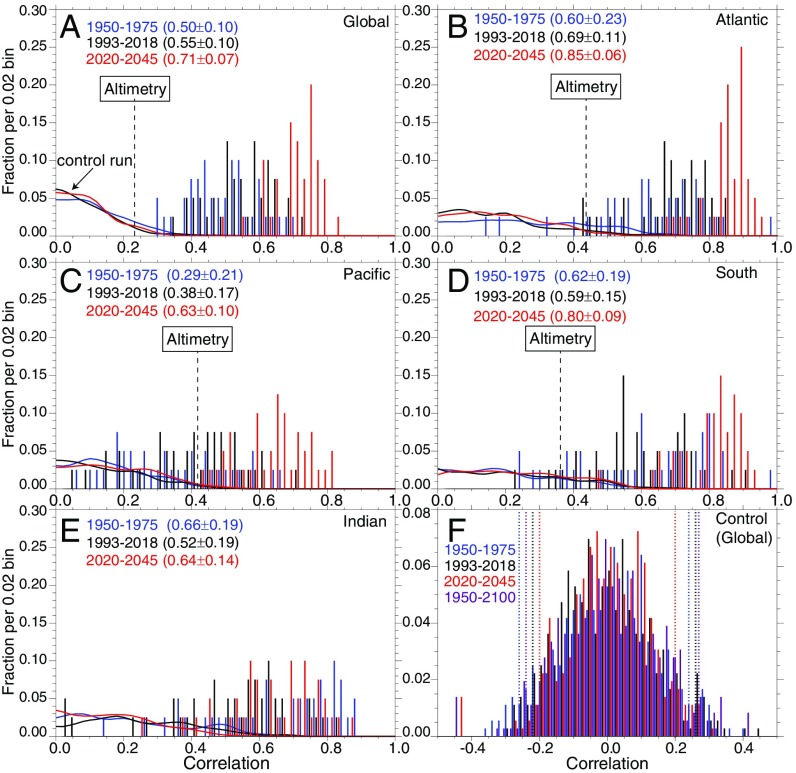
In Fig. 4, histograms are shown of the distributions of pattern correlations between the CESM FR sea-level trends and individual ensemble member trends across various intervals, including the mid-20th century (1950–1975) (blue in Fig. 4), the altimeter era (1993–2018) (black in Fig. 4), and the next 25 y (2020–2045) (red in Fig. 4). Analogous distributions from the CESM control run are also shown for each FR (colored curves in Fig. 4 A–E and in detail for the global ocean in Fig. 4F). For the global ocean (Fig. 4A), the mean pattern correlation across members from 1950 to 1975 is 0.50 ± 0.10 (1σ), and every member exceeds the 95% confidence limit (Fig. 4F), indicating a considerable contribution of the contemporary FR to simulated trends, despite exhibiting a weak relationship to the FR in other decades (for example, the mean 1950–1975 correlation with the 1950–2100 FR is negative) (Table 2 and SI Appendix, Fig. S5). In the altimeter-era contemporaneous FR pattern correlations intensify to 0.55 ± 0.10 (1σ) and strengthen further (0.71 ± 0.07) by 2020–2045. In these intervals, the long-term FR can also be seen to emerge with strong pattern correlations of individual members with the 1950–2100 FR (0.43 ± 0.10 for 1993–2018 and 0.66 ± 0.07 for 2020–2045) that are statistically distinct from those obtained from the control run (SI Appendix, Fig. S5). The facts that (i) the correlation of every member of the CESM LE exceeds the 95% confidence limit of the control simulation for the 1993–2018 FR (Fig. 4A) and that (ii) individual members strongly correlate with the long-term FR demonstrate both that the FR has emerged from the noise of internal variability during the altimeter record and that it is likely to persist. At basin scales, emergence of the altimeter-era FR is also evident, with particularly strong correlations in the Atlantic and Southern Oceans (r = 0.69 ± 0.23 and r = 0.59 ± 0.15, respectively), where significance is high, and in the Pacific and Indian Oceans (r = 0.38 ± 0.17 and r = 0.52 ± 0.19, respectively), although in these basins, with reduced significance as a number of individual members fall below the 95% significance limits. Altimetry pattern correlations with the CESM FR fall within the ensemble spread globally and in all basins, except in the Indian Ocean.

Fig. 4.

Histograms of the fractional occurrence of pattern correlations in the CESM LE of individual member trends across various eras with their contemporaneous FRs for (A) the global ocean and (B) Atlantic, (C) Pacific, (D) Southern, and (E) Indian Ocean basins (associated ocean boundaries are shown in Fig. 1A). Colored lines in A–E correspond to occurrences obtained for the FR from the three eras in the control run (for the globe shown in detail in F). Dashed lines in F correspond to 95% confidence intervals for pattern correlations in the control run. Also shown in A–D are the pattern correlations of the 1993–2018 FR with observed altimeter trends smoothed to spectral wavenumber 42 [omitted for the Indian Ocean, where the correlation is negative (−0.29)]. Plotted fractional occurrence does not sum to unity where members with negative values exist.

The identification of the recent emergence of altimeter-era and long-term FRs in the CESM is a finding that is corroborated in the ESM2M (SI Appendix, Figs. S6 and S7). This is evident, for example, in the rarity with which pattern correlations for the global ocean fall within the distribution from the control run (SI Appendix, Figs. S6A and S7A) and in the strength of correlations with the long-term (0.51 ± 0.11) and altimeter-era (0.61 ± 0.09) FRs. The transient character of the FR is also evident given the negative correlation of the long-term FR with the 1950–1975 FR and strong correlations thereafter in the altimeter era and coming decades (SI Appendix, Table S2). As for the CESM, the ESM2M’s primary contributors by ocean basin are the Atlantic and Southern Oceans. Also in agreement with the CESM is the fact that the pattern correlations are projected to strengthen considerably in the coming decades, with statistically significant increases in correlations projected for all basins. Agreement with altimetry is somewhat weaker than for CESM, however, as observed trend pattern correlations fall outside of the ESM2M distribution for the global ocean and in individual ocean basins. In the Southern and Indian Ocean basins, the correlations with the contemporary FR are negative (−0.01 and −0.27, respectively) and are outside of the ensemble distribution, suggesting error in the ESM2M FR.

A number of processes are involved in the regionally contrasting rates of sea-level rise in the FR, central among which is ocean heat content. Both the CESM and the ESM2M show anomalous ocean heat content (OHC) increases collocated with elevated rates of rise in the Atlantic (and particularly in the Gulf of Mexico) and along the East Coast of North America (SI Appendix, Figs. S8 and S9). These aspects are consistent with observed trends (38, 39). Alternatively, redistributions of OHC in the Southern Ocean coincide with regional negative OHC trend anomalies at 60° S (relative to the global mean), where sea-level anomalies are also negative, and with positive OHC trend anomalies to their north, where a sea-level rise maximum exists. The complex interaction of winds, which on their own, can drive sea-level variations and OHC, is evident across timescales in both observations and climate model simulations (40). Changes in salinity can also exert an important influence on sea-level trends in some regions and particularly, in the Atlantic, where freshening is strong, widespread, and collocated with relative increases in sea level, and the far Southern Ocean, where increased salinity coincides with relative sea-level decreases (SI Appendix, Fig. S9). In the coming decades, a similar set of processes is projected to continue to intensify sea-level trends (SI Appendix, Figs. S10 and S11).

Discussion

The altimeter record of sea level has attained remarkable success in providing an extended 25-y near-global record that is densely sampled in both space and time. However, as with all finite records and particularly those from satellites, it is unable on its own to definitively address various questions related to the attribution of long-term change. When leveraged with insights from climate models, the scope of understanding can broaden considerably. Here, climate model LEs are used to provide such additional insights. By identifying the FR explicitly in the LEs and using a method for identifying emergence based on the distribution of pattern correlations, we demonstrate that modeled internal climate variability is insufficient to obscure FR in sea-level rise in individual ensemble members in the mid-20th century, altimeter era, or coming decades. In these simulations, the FRs explain roughly 25–50% of the spatial variance in the altimeter-era trend on average across ensemble members. Furthermore, we also find that some aspects of the observed trends in regional sea-level change over the 25-y altimeter era are consistent with the FR of two different climate models driven by historical and RCP8.5 forcings, with the CESM being more consistent with altimetry. This suggests that the models might have some skill at predicting regional sea-level change due to forced ocean and atmospheric dynamics, although neither model includes the full effects of dynamic ice sheets or the effects of ocean eddies, with consequent errors in western boundary currents, which will create additional regional sea-level change (29, 41). Patterns of change in the Indian Ocean in both models, however, are particularly inconsistent with observed trends.

A key finding is that both climate models show the patterns of the FR in the altimeter era to be characteristic of the response both in coming decades and through the 21st century, implying that there will be a degree of predictable future regional sea-level change due to forced ocean and atmospheric dynamics depending on which RCP scenario we follow. While internal variability will also continue to influence regional sea level, areas of increased probability in higher sea-level rise relative to the global average arising from the FR include the East Coast of the United States, the Gulf of Mexico, and more generally, the equatorial Atlantic Ocean and western subtropical ocean basins.

These findings entail various caveats. While the emergence of the FR depends on the estimation of its overall magnitude relative to the noise of internal variability and does not depend on the detailed spatial pattern of such changes, a main concern is the fact that systematic biases exist in climate model base states relevant to both sea level and its changes. Of ultimate interest is the structure of the FRs in nature. There are indications in the altimetry record that the main aspects of both the altimeter-era and long-term CESM FRs have already been observed, particularly in the Atlantic and Southern Oceans. Given the limitations of deriving such patterns from climate models, however, techniques for removing noise directly from the altimeter record to resolve the FRs in nature are also of high interest (42). While climate models may play a central role in the testing and optimization of such techniques, ultimately the most promising method for identifying the FR in nature may be its direct estimation from altimeter data.

A number of additional findings with broad consequences have also been shown here. Most notably, the LEs underscore the transient nature of the FR (Fig. 4 and SI Appendix, Figs. S3 and S4), particularly from the mid-20th century to the altimeter era (Table 1). As a result, any attempts to resolve the FR by combining observations over several decades, such as by using both the tide gauge and altimeter sea-level records, must account for this time-varying character. In contrast, it is reasonable to expect 21st century patterns of forced change to largely be persistent, and thus, pattern-scaling approaches for prediction may be warranted. In addition, the model ensembles show that the spatial patterns of the FR and major modes of internal variability, such as the El Niño/Southern Oscillation and the Pacific Decadal Oscillation (PDO), are likely to be correlated, perhaps strongly so. As a consequence, efforts to characterize the patterns of these internal modes empirically may be subject to the conflation of internal and forced variability. For both the tide gauge record, which experiences continual changes in available data over time (43) and a general spatial sampling challenge (43, 44), and the altimeter record, during which large changes in the PDO exist (20, 21), this conflation represents a significant source of uncertainty.

Given the socioeconomic and ecological importance of sea-level rise, narrowing uncertainty in these outstanding issues is imperative. Continuation of the altimeter record and exploration with climate models and complementary sources of data remains a promising path forward for narrowing existing uncertainties.

Methods

The CESM and ESM2M climate models include coupled component models for the atmosphere, land, ocean, and sea ice. The CESM atmospheric component resolution is about 1° (288 longitude × 192 latitude), while the ESM2M atmospheric resolution is about 2° (144 longitude × 90 latitude). Ocean resolution for both models is variable in latitude and averages about 1°. The CESM ensemble initial conditions differ only in a round-off level perturbation to air temperature (25), while the ESM2M initial conditions were taken from different days in January 1950 to generate ensemble spread (31).

The datasets analyzed during this study are available on the Earth System Grid (https://www.earthsystemgrid.org, www.cesm.ucar.edu/projects/community-projects/GLENS/).