Spontaneous migration of cellular aggregates from giant keratocytes to running spheroids

Significance

The migration of cellular populations drives influential and disparate biological processes, from the establishment of embryos to the invasion of cancerous tissues. Its deregulation can lead to improper development or pathogenesis of diseases. While many of the mechanisms that promote single-cell migration have been identified, how cell assemblies coordinate these mechanisms is poorly understood. This manuscript details modes of collective migration and the role of tissue dewetting in generating a symmetry breaking, which drives the spontaneous migration of cell aggregates en masse. This discovery, its corresponding assay, and the establishment of the underlying fundamental physical principles provide a powerful platform for further in-depth studies and insights into biological migration at the mesoscopic scale.

Abstract

Despite extensive knowledge on the mechanisms that drive single-cell migration, those governing the migration of cell clusters, as occurring during embryonic development and cancer metastasis, remain poorly understood. Here, we investigate the collective migration of cell on adhesive gels with variable rigidity, using 3D cellular aggregates as a model system. After initial adhesion to the substrate, aggregates spread by expanding outward a cell monolayer, whose dynamics is optimal in a narrow range of rigidities. Fast expansion gives rise to the accumulation of mechanical tension that leads to the rupture of cell–cell contacts and the nucleation of holes within the monolayer, which becomes unstable and undergoes dewetting like a liquid film. This leads to a symmetry breaking and causes the entire aggregate to move as a single entity. Varying the substrate rigidity modulates the extent of dewetting and induces different modes of aggregate motion: “giant keratocytes,” where the lamellipodium is a cell monolayer that expands at the front and retracts at the back; “penguins,” characterized by bipedal locomotion; and “running spheroids,” for nonspreading aggregates. We characterize these diverse modes of collective migration by quantifying the flows and forces that drive them, and we unveil the fundamental physical principles that govern these behaviors, which underscore the biological predisposition of living material to migrate, independent of length scale.

While contemporary models of cancer metastasis focus on how individual cells extravasate, migrate, and invade adjacent tissue (1, 2), recent studies have shown that groups of cells are also able to dissociate from the primary site and migrate collectively (3). Furthermore, during embryonic development and regeneration, the motility of groups of cells is considered an essential mode of locomotion (4–8). The mechanisms driving multicellular migration remain poorly understood, despite their relevance to diverse biological processes. Our aim is to understand the mechanical interactions between cells and their extracellular environment, and how these interactions promote collective motion of cells.

The migration of adherent cells is induced by protrusion of F-actin–rich lamellipodia, which polymerize at the leading edge and depolymerize distal to the front (9–12) where actomyosin contractility determines the assembly, growth, and disassembly of focal contacts with the substrate (13). This process is known to depend on the mechanical and adhesive properties of the substrate and extracellular matrix (ECM). By contrast, in cell groups, the stabilization of adhesions and the generation of forces are also influenced by interactions between neighboring cells, leading to long-range collective behaviors, as it has previously been demonstrated in cell monolayers (14). However, experimental studies using monolayers display a remarkable uniformity of cell–-cell and cell–ECM interactions, as well as persistent adhesive stability. These simplifying characteristics of the monolayer model system are not necessarily present in more complex systems such as 3D geometries, as we will show below.

Although the basic principles may be similar, the motion of multicellular aggregates is much less studied than the motion of single cells. Collective migration participates in wound healing, morphogenesis, and cancer development (7, 15–18), as well as in the spreading of tissues. The migratory behavior of a multicellular aggregate will depend not only on mechanical cell–cell and cell–substrate interactions, but also on active cell behavior or collective effects.

In this work, we study the spontaneous migration of aggregates on substrates as a function of substrate rigidity. We combine traction force microscopy (TFM) of substrate deformations and particle image velocimetry (PIV) of cell motion to obtain force fields and velocity fields, respectively. Together with a theoretical model, we develop a comprehensive description of the diverse ways in which large cellular assemblies adhere and spontaneously migrate. Importantly, our work unveils that modes of single-cell motion are retrieved in the collective motion of a cellular aggregate. This is a striking result, because such motion occurs in a context where the classical regulatory pathway controlling isolated cell motility is not operating at the scale of cellular aggregates and a coherent actin cytoskeleton is absent. Our results thus indicate an unexpected robustness of the classic modes of cell motility. Our theoretical modeling provides some understanding of the foundations underlying such robustness of cell motility mechanisms across several scales.

Results

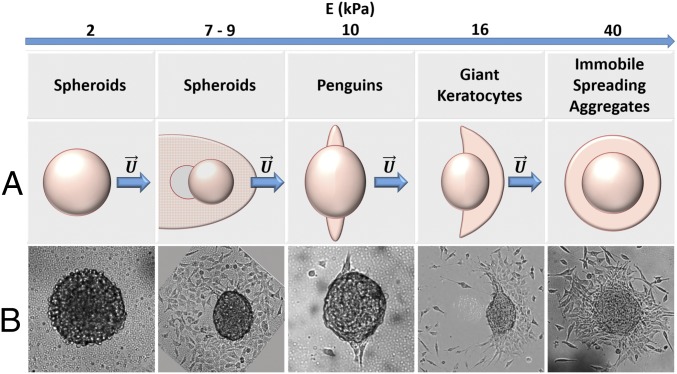
Cell aggregates, ∼100 μm in size and composed of murine sarcoma Ecad cells (19), are deposited on fibronectin-coated polyacrylamide gels (PAA) with rigidities varying from 40 to 2 kPa. The elastic modulus of the substrate E is varied, while a constant adhesive chemical environment is maintained. We observe both isotropic spreading, without motion of aggregates, and anisotropic spreading, with global motion of aggregates. The isotropic spreading of cell aggregates on substrates with different rigidities is discussed in detail in Douezan and Brochard-Wyart (20). The fraction of moving aggregates depends on the substrate stiffness and increases as E decreases. We characterize the diverse morphologies and modes of migration of aggregates upon decreasing the substrate rigidity, namely (i) polarized “giant keratocytes,” (ii) bipedal “penguins,” and (iii) “running spheroids,” the latter arising due to adhesion loss on the softest substrates (Fig. 1). For each of these modes, we describe the morphological transitions of the aggregate, their global migration kinematics, and the velocity field of cells. On soft surfaces (E < 9 kPa), where TFM can be used, we analyze the force fields generated by the cell–substrate interactions. Based on these measurements, we propose physical mechanisms to interpret the dynamics for these different regimes.

Fig. 1.

Behaviors of migrating cell aggregates deposited on substrates of increasing rigidity. (A) Schematic representation and (B) their experimental counterparts observed in bright field.

Substrate Rigidity Determines the Mode of Migration.

When cellular aggregates are deposited onto rigid substrates (glass with E = 70 GPa or PAA gel with E = 40 kPa), the spherical aggregate flattens and a circular monolayer of cells––also called precursor film below––spreads around the aggregate (Movie S1). The precursor film is isotropic and the aggregate remains immobile.

Giant keratocytes.

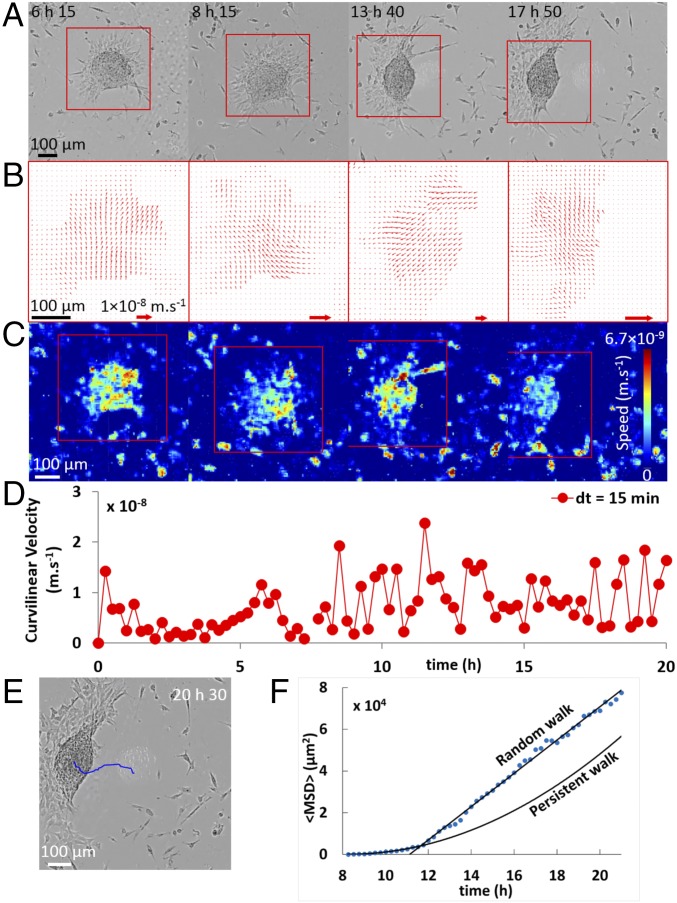
Upon decreasing the stiffness of the substrate decreases (E = 16.7 kPa), we observe the emergence of a mode of collective cell migration that resembles adherent keratocytes (Fig. 2A and Movie S2). After initial adhesion to the substrate, aggregates spread by expanding outward a circular cell monolayer, which spreads faster than in the rigid case and is apparently under tension, whereas it appears stable and firmly attached on the rigid substrate. To test this hypothesis, we have scratched with a micrometer-sized needle the cell monolayer adjacent to the aggregate on both rigid glass substrate as well as soft gel (E = 16.7 kPa, SI Appendix, Fig. S3). On the rigid substrate, cells spread to close the injury, analogous to experiments of in vitro wound healing (15, 17). On the soft substrate, the scratch induces a retraction of the film––showing that the film is under tension––and the motion of the aggregate. Importantly, scratching the film is not necessary for symmetry breaking. Indeed, when monolayers spread on soft substrate, we observe the spontaneous nucleation of holes (i.e., cell-free domains) close to the aggregate main body (Fig. 2A). These holes grow and the monolayer dewets like a liquid film (21), giving rise to a massive cell reorganization within the monolayer, eventually leading to a crescent-like shape and to collective migration (Fig. 2A). To characterize this motion, we measure the curvilinear velocity (i.e., distance traveled per unit time) of the center of mass V(t), and the directionality (defined by the ratio of the Euclidean distance to the curvilinear distance). The mean curvilinear velocity U = 10⁻² µm⋅s⁻¹ is ∼20 times lower than that of single-cell keratocytes (22) and the directionality is 0.8 (Fig. 2D). The mean-square displacement (MSD) of an aggregate trajectory (Fig. 2E) indicates a transition from persistent to random walk after about 3 h of motion (Fig. 2F). Further, the measured velocity fields in the first cell layer below the aggregate main body are all parallel to each other and point in the direction of migration (Fig. 2 B and C). The precursor film shape is anisotropic, being less expanded along the direction of motion than along the perpendicular one (Fig. 2A). At the lateral crests of these giant “lamellipodia,” we observe alternating stick (attachment) and slip (detachment) motion. Remarkably, the stick–slip cycles that are observed on the trailing edges at either side of the aggregate are in phase opposition with each other, leading to bipedal motion. The stick–slip motion of the aggregate is clearly seen from the oscillations of the curvilinear speed, with an average period of ∼1 h (Fig. 2D and Movie S2). We interpret these results with a simple one-dimensional stick–lip model (23), in which the cells at the leading front (the locomotive) pull and stretch the trailing edge at a mean velocity U (SI Appendix, Fig. S4). The period T of the stick–slip cycle is given by T = Δ/U, where Δ is the maximal deformation of the trailing edge before rupture. Inferring a deformation Δ ∼ 30 µm (from Movie S2) yields a period of T ∼ 50 min, comparable to the experimental value. As shown in ref. 22, this simple model accurately describes features of the oscillating motion of keratocytes. However, a 2D model taking into account the lateral extension of the precursor film is required to account for bipedal motion (22).

Fig. 2.

Motility of an aggregate on a PAA gel (E = 16.7 kPa). (A) Observed in bright field at different times. (B) Velocity vector fields (PIV) of aggregate migration from A. (C) Heat map of local aggregate speed corresponding to the velocity field (B). (D) Curvilinear velocity of the aggregate center of mass plotted versus time (Δt = 15 min). (E) Trajectory of an aggregate, and (F) MSD over time: blue dotted line shows the experimental MSD ($\text{MSD}\left(t\right)={\left[\mathit{r}\left(t+t_0\right)-\mathit{r}\left(t_0\right)\right]}^2$, where r(t₀) is the initial location of the cell aggregate and r(t + t₀) is the new position after time t), and black lines indicate either a persistent walk ($\text{MSD}\propto t^2)$ or a random walk ($\text{MSD}\propto t$).

Penguins.

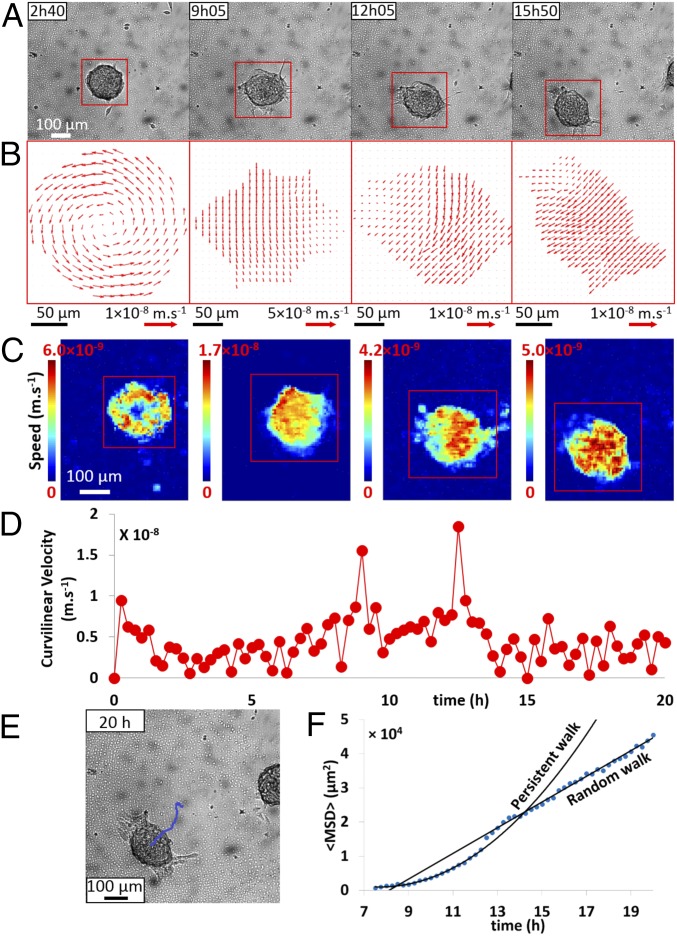
Upon further decrease of the substrate stiffness (E = 10.6 kPa), the precursor film is more unstable and unable to maintain its integrity, leading to spontaneous aggregate motion in a bipedal-like fashion, similar to the giant keratocyte mode but without a lamellipodia (Fig. 3A and Movie S3). The velocity field (Fig. 3 B and C, Left) shows that when aggregates flatten over the first few hours (24), they rotate with an angular speed Ω = 1 × 10⁻⁴ rad⋅s⁻¹ (SI Appendix, Fig. S5), which is compatible with low adhesion to the substrate. A monolayer then spreads outwards from the aggregate and holes appear as soon as it starts to form. After dewetting, two elongated cellular patches of the remaining monolayer are coupled to the aggregate motion with a succession of stick and slip steps (Fig. 3A). This leads to a fluctuating motion that resembles penguins performing bipedal motion. As shown in Fig. 3D, the curvilinear velocity exhibits two large peaks, corresponding to the initiation of the motion, and subsequently a succession of smaller peaks at steady state (t > 12 h). The MSD of an aggregate trajectory (Fig. 3E) indicates a transition from persistent to random walk after about 6 h of motion (Fig. 3F). The cell patches alternate stick and slip steps out of phase with a typical period similar to the previous case (∼1 h), suggesting that a similar mechanism might be at work (23). Between two successive steps the aggregate moves at constant speed. The velocity field under the aggregate body is uniform, corresponding to a crawling regime (Fig. 3 B and C). Compared with giant keratocytes, where the presence of the sliding film smoothens the stick–slip motion, here we observe a succession of stops and goes with a mean curvilinear speed U = 6 × 10⁻³ µm⋅s⁻¹ and directionality of 0.8 (Fig. 3D and Movie S3).

Fig. 3.

Motility of an aggregate on a PAA gel (E = 10.6 kPa). (A) Observed in bright field at different times. (B) Velocity vector fields (PIV) of aggregate migration from A. (C) Heat map of local aggregate speed corresponding to the velocity field (B). (D) Curvilinear velocity of the aggregate center of mass plotted versus time (Δt = 15 min). (E) Trajectory of an aggregate and (F) MSD over time: blue dotted line shows the experimental MSD and black lines indicate either a persistent walk ($\text{MSD}\propto t^2$) or a random walk ($\text{MSD}\propto t$).

Running spheroids.

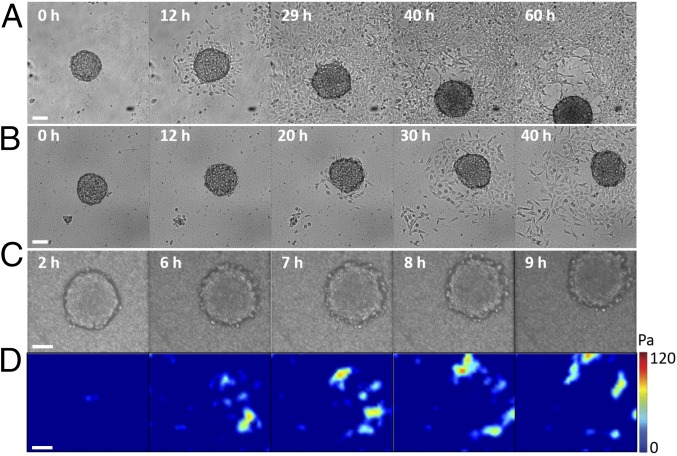
On soft substrates (9 kPa > E > 2.8 kPa), we observe another mode of collective migration, named running spheroids. The shape of the aggregate is spherical due to the loss of strong coupling with the substrate. An aggregate is imaged in bright-field microscopy as it spontaneously moves on a substrate with E = 9 kPa (Fig. 4A and Movie S4). The monolayer expanding outward from the aggregate is weakly cohesive. During the first 25 h, we observe the formation of transient holes but no clear dewetting, as opposed to what is observed for the stiffer substrates. At longer times, near the aggregate–monolayer contact line, several of these holes coalesce and grow, leading to a symmetry breaking of the film and to initiation of aggregate motion. Using PIV, we observe that the flow field at the contact area is uniform but of variable direction. Cells escaping from the running aggregates are pulled and detach, leading to small stick–slip peaks in the velocity. The motion has been characterized by measuring the curvilinear velocity of the center of mass V(t), yielding a mean curvilinear velocity U = 3 × 10⁻³ µm⋅s⁻¹ and a mean directionality of 0.8. Fig. 4B and Movie S5 show an aggregate spontaneously moving on a substrate with E = 7.4 kPa. The velocity field (SI Appendix, Fig. S6B) shows that at short time the aggregate rotates. Compared with the previous case, aggregate motion starts earlier. Initiation of motion is concomitant with the outward spreading of a weakly cohesive cell monolayer, in which transient holes form. The cells spread out from the front and the side of the aggregate, whereas no cell monolayer is observed behind the aggregate, a region that resembles a dewetted surface. We measure the cell flow field by PIV (SI Appendix, Fig. S6). As before, the flow field under the aggregate is uniform and fluctuates in direction. We also measure the curvilinear velocity of the center of mass V(t), the mean curvilinear velocity U = 3 × 10⁻³ µm⋅s⁻¹, and the mean directionality equal to 0.7 (SI Appendix, Fig. S6).

Fig. 4.

Motility of aggregates on PAA gels with different rigidities observed in bright field at different times. (A) E = 9 kPa (U = 3 × 10⁻³ µm⋅s⁻¹, directionality is 0.8), (B) E = 7.6 kPa (U = 3 × 10⁻³ µm⋅s⁻¹, directionality is 0.7), (C) E = 2.8 kPa (U = 4 × 10⁻³ µm⋅s⁻¹, directionality is 0.5). (D) Traction stresses corresponding to the aggregate for E = 2.8 kPa (C).

On soft gels, E = 2.8 kPa, the aggregate does not spread and there is no cellular monolayer spreading outward from the aggregate (Fig. 4C and Movie S6), however the aggregate still migrates. Using PIV we measure the flow of cells under the aggregate (SI Appendix, Fig. S7). We see a combination of uniform velocity field and rotation, indicating that the aggregate might not be well attached to the substrate. We also measure the curvilinear velocity of the center of mass V(t), the mean curvilinear velocity U = 4 × 10⁻³ µm⋅s⁻¹, and the directionality equal to 0.5 (SI Appendix, Fig. S7).

Traction forces of collective migration.

For the softer range of substrate stiffness we explored (9 kPa > E > 2.8 kPa), it is possible to measure traction stresses using the traction force field calculated from the displacement of embedded fluorescent beads within the PAA gel. We observe gel deformation after an aggregate has been deposited on the substrate (E = 7.4 kPa, SI Appendix, Fig. S8). The corresponding traction forces point inward, indicating that the aggregate adheres and contracts. During the first 2 h, the aggregate flattens and its contact area with the gel increases, while inward traction forces are observed at its interface with magnitudes up to 60 Pa (SI Appendix, Fig. S8). This result is consistent with previous studies on adherent liposomes (25), cell colonies (26) and droplets (26). Remarkably, for times longer than 2 h, when aggregates become motile, we observe that forces become heterogeneously distributed with hotspots of traction stresses of 120 Pa that are still concentrated near the edge of the contact area, but now higher traction forces are exerted along the direction of motion (SI Appendix, Fig. S8).

We also measure the traction force field of an aggregate on a PAA gel with E = 2.8 kPa. Our findings confirm that the applied forces are located at the periphery of the contact area and are oriented along the direction of motion (Fig. 4D). We also observe that the peak of intensity of the traction stress on these softer substrates (80 Pa) is lower than in the previous case (120 Pa), consistently with previous results (27).

Interpretation of Crawling Aggregate Motion.

Before the motion of the aggregate occurs, the first step is a dewetting of the initially circular precursor film. This dewetting can be understood from our previous work on the statics and dynamics of the isotropic spreading of cell aggregates deposited on the same substrates (24, 28–30). We also observed aggregate motion during work leading to an earlier publication (28), but this motion was not systematically studied at that time. In analogy to the wetting of liquids (31), we have defined an effective spreading parameter S = W_CS − W_CC, which is the difference between cell–cell (W_CC) and cell–substrate (W_CS) adhesion energies (24). If S is negative, the aggregate, or “living” droplets, do not spread and the wetting is partial. If S is positive, the wetting is complete with a precursor film (cell monolayer) spreading from the living droplet. Wetting transitions can be induced by tuning substrate adhesiveness (PEG-Fibronectin surface treatment) or substrate rigidity E (29). On soft substrates (E $\mathrm{\lesssim }$ 2.5 kPa), the aggregates do not spread, while on rigid substrates (E $\mathrm{\gtrsim }$ 7 kPa) complete wetting is found (30).

In the complete wetting case, we observe two regimes in the dynamics of spreading (24). At times shorter than 2 h, the aggregate flattens like a soft elastic bead on the adherent substrate. A contact area is formed, where the aggregate sticks to the substrate. At longer times, a cellular monolayer expands outward from the aggregate. The spreading dynamics of films (of radius R) obeys a diffusive law R² = D t (24). This dynamics results from a balance between viscous-like permeation forces at the aggregate–monolayer contact line and driving forces acting at the periphery of the film, equal per unit length to the spreading parameter S (28, 32). The diffusion coefficient D can be cast as D = V* R_a, where $V^{\ast }=S/\eta$ is a typical spreading velocity, η is a tissue viscosity, and $R_a$ is the aggregate radius (24, 29). D depends on the substrate rigidity E through the spreading parameter S and it presents a global maximum for rigidities close to 18 kPa (29). The fast-spreading dynamics gives rise to a tension in the monolayer, which becomes unable to maintain its integrity, and spontaneous nucleation of holes occurs. Spreading cell monolayers are also under tension due to the driving forces of leading cells (14). Dufresne and coworkers (33) have investigated the force distribution of cell colonies (from 1 to 27 cells) on adherent soft substrates. They have observed that traction stresses are generally localized at the periphery of the colony and the scaling of the total traction force with the colony radius suggests the emergence of an apparent surface tension of the order of 10⁻³ N⋅m⁻¹ (33, 34). All these studies, however, have been carried out in monolayers, where cell–cell and cell–substrate interactions are uniform. In contrast, interactions at the contact area of the aggregate with the substrate give rise to a flow of cells from 3D (aggregate) to 2D (cellular monolayer), inducing a uniform tension pattern in the monolayer with an exponential drop over a few cell lengths at the foot of the aggregate (28), where hole nucleation occurs due to large strain. The energy barrier for hole nucleation decreases on softer gels, where films appear to be increasingly unstable, because of the weakening of cell–cell contacts (35–37). The dewetting of the film starts (stochastically) on one side of the aggregate. The cell traction forces are unbalanced and the aggregates start to move with a velocity U. In the keratocyte regime, the precursor film in motion with the aggregate is less expanded in the direction of motion than in the perpendicular direction (Fig. 2A). From the analogy with the wetting dynamics of droplets (31), one can relate the length of the film along the direction of migration L to the curvilinear velocity U by the scaling relationship: L = D/U, where D is the diffusion coefficient for the spreading of the precursor film (28). Using D = V* R_a with V* ∼ 10⁻² µm⋅s⁻¹ and U ∼ 10⁻² µm⋅s⁻¹ leads to L ∼ R_a being of the order of the aggregate radius R_a, in agreement with the measured value ∼70 μm.

The migration of aggregates constitutes a mode of spontaneous motion of multicellular populations, which can be interpreted in the paradigm of wetting. Indeed, motion of droplets is ubiquitous in wetting phenomena and can generically be described as the balance between wetting and dissipative forces. For ultraviscous droplets moving at velocity U, the friction is dominated by the slippage at the interface and the balance of forces can be written as

$$\mathit{F}={\displaystyle \oint S\left(s\right)\mathit{n}ds=Ak\mathit{U}},$$ [1]

where F is the net driving force, k a friction coefficient, and A the contact area. F is the integral, over the curvilinear coordinate s, of the driving force S oriented along the normal vector to the contour n.

Here, we propose two possible mechanisms to explain the spontaneous motion of cellular aggregates: chemical modification of the substrate in analogy to reactive droplets (38), or symmetry breaking arising from cell polarization in analogy to active droplets (39).

Droplets and cellular aggregates move in a chemical gradient (SI Appendix, Fig. S8). Droplets containing a reactive solute may move also on chemically homogeneous substrates, the so-called free-running droplets (38). As a droplet moves, the surface on the front is intact and adhesive, whereas the surface on the back is chemically modified and less adhesive. This asymmetry gives rise to the sustained motion of the reactive droplet. Later, the same model was used to describe vesicles surfing on a lipid bilayer (40). The reactive-droplet model may also apply for the spontaneous motion of cellular aggregates, where a dissymmetry of wettability between the substrate in the front and the back can be induced by cell migration. It has been shown that migrating cells remove extracellular matrix proteins off the surface of gels coated using sulfo-SANPAH (27). This difference in spreading parameters generates an unbalanced capillary force, leading to the spontaneous movement of the aggregate. According to Eq. 1, the resulting force balance for a one-dimensional reactive droplet reads

$$S_a-S_r\approx kRU,$$ [2]

where S_a and S_r are the spreading parameters at the advancing (at the front) and receding (at the back) contact lines, respectively, and R is the film radius (SI Appendix, section C). After film dewetting, cells are not observed to repopulate areas over which the aggregate has moved, suggesting that the spreading parameter at the trailing edge vanishes, S_r ∼ 0 (Movie S2). The measured traction stresses are of the order of T = 100 Pa (Fig. 4) and allow one to estimate the spreading parameter at the leading edge as S_a = T l, where l is the characteristic length scale over which the traction stress is observed (SI Appendix, Eq. S5), on order of the cell length l ∼ 10 µm. We find S_a ∼ 10⁻³ N⋅m⁻¹. Taking realistic values for cell aggregates, R = 100 μm and U = 10⁻⁸ m⋅s⁻¹ leads to k ∼ 10⁹ N⋅m⁻³⋅s. This value of k is comparable to the friction coefficient k ∼ 10⁸ N⋅m⁻³⋅s (41) measured by pushing an aggregate in a nonadhesive pipette and to k ∼ 10¹⁰ N⋅m⁻³⋅s (42, 43), calculated from propulsive traction stresses in locomoting keratocytes. We postulate that it is possible to mimic a keratocyte with a droplet of oil containing a surfactant deposited on a silicon wafer or clean glass. To test our hypothesis, we have performed this experiment. In complete wetting, a reactive droplet adopts a croissant shape similar to that of a keratocyte, also seen for keratocyte fragments (44), less extended in the direction of motion than in the perpendicular direction as shown in Fig. 5 and Movie S7.

Fig. 5.

Image of a 5-µL moving reactive droplet in complete wetting. It is composed of a 0.05 M solution of 1H,1H,2H,2H,perfluorodecyltrichlorosilane in octane. The substrate is a glass slide cleaned by corona treatment. The droplet is moving from left to right with a velocity of 10.5 cm⋅s⁻¹, leaving a wake of dry substrate behind (see also Movie S7).

Active fluids or droplets can also move due to a dissymmetry in cell polarity (39). Cells can orient their planar polarity in response to forces (45). As proposed for the dynamics of spreading epithelial monolayers (46), we describe cells as interacting polar particles with the capacity to exert actively generated traction stresses on the substrate T = kv − T₀ p (SI Appendix, section D). These stresses are a linear combination of viscous (∼k v) and active (∼T₀ p) stresses. v and p correspond to the cell velocity and the cell polarity fields, respectively. T₀ sets the amplitude of the active traction stresses. In the limit where p remains finite in a narrow region near the contact line of the monolayer and vanishes elsewhere, the force balance at the level of the monolayer reduces to an equation similar to Eq. 2.

$$S_a-S_r\approx kRU,$$ [3]

where S_a = T₀ l_c p_a and S_r = T₀ l_c p_r with l_c being the width of the polarity boundary layer and R being the monolayer radius (SI Appendix, section D). S_a (S_r) and p_a (p_r) are an effective spreading parameter and the cell polarization at the advancing (receding) front, respectively. Before dewetting, monolayers spread symmetrically, meaning that p_a = p_r, and in consequence no collective migration occurs, U = 0. After dewetting, nucleation of cell-free domains breaks symmetry, leading to the spontaneous migration of the aggregate. At steady state, the migration of active droplets demands the presence of both a symmetry-breaking distribution of cell polarities (p_r $\ne$ p_a) and active traction forces (T₀ $\ne$ 0). The absence of traction stress at the trailing edge in SI Appendix, Fig. S8, suggests that the cell polarity p_r = 0 and thus S_r = 0, whereas the traction stresses at the leading edge in SI Appendix, Fig. S8 allows one to estimate T₀ = 100 Pa. For the same parameters as above, R ∼ 100 μm and U ∼ 10⁻⁸ m⋅s⁻¹ and l_c = 10 μm (46), we obtain the friction coefficient k ∼ 10⁹ N⋅m⁻³⋅ s which is compatible with that of reactive droplets.

In conclusion, the spontaneous motion of aggregates can be a combination of both mechanisms, chemical modification of the substrate, or symmetry breaking of cell polarization, which seem to be of the same order of magnitude.

Conclusions and Discussion

To summarize, cellular aggregates deposited on a rigid adhesive substrate spread with the formation of an isotropic precursor film and do not move. By contrast, cellular aggregates deposited on deformable substrates exhibit either isotropic spreading and remain immobile, or anisotropic spreading, leading to diverse motility mechanisms depending upon the stiffness of the gel. Symmetry is broken due to instabilities in the cell monolayer, which causes the aggregate to move as a single entity. When E = 16.7 kPa the aggregate moves like a giant keratocyte with the expansion of a lamellipodia in the front and a retraction in the back. For E = 10.6 kPa, the aggregate moves like a penguin with a cell patch on each side. The motion in these two cases can be described as a bipedal motion with a stationary film transported with the aggregates. On softer gels, precursor films are very unstable and less cohesive. The running aggregates become spherical. We have shown that before the symmetry breaking of the precursor film, the forces are applied radially at the edge of the film, similarly to colonies and monolayers of cells expressing E-cadherin (26, 47). On the other hand, when they become motile, the pulling forces are applied in the direction of the movement. The velocity of motion is determined by a balance between driving forces and friction forces of the crawling aggregates. The persistence of the polarity of the motion is potentially due to the difference in adhesion energy between the front and the back where cells, after their passage, have modified the substrate. This interpretation is supported by the fact that we never see any spreading of cells in the dewetted region.

To conclude, the motion of cellular aggregates on soft substrates has strong analogies with the migration of single cells, and particularly with keratocytes. As keratocytes, aggregates do not move on strong adhesive substrates (high modulus), they have a bipedal motion at intermediate rigidity with a fan-like shape, and a round shape on low (soft) adhesive substrate. The giant keratocytes described here, which carry tens of thousands of cells, move 100× slower than single-cell keratocytes. Their motion is characterized by stick and slip with a period on the order of 60 min compared with 2 min for keratocytes (22). It is striking that the collective migration of bound cells pulled by motile cells at the periphery of the leading edge generates a sophisticated motion resembling that of keratocytes, which results from the perfect interplay of actin, focal adhesions, and myosin. However, the motion of the giant keratocyte is not perfectly controlled and is more random. As the elastic modulus decreases, the precursor film loses its cohesion and the pulling forces on the aggregates are less well transmitted. Instead of bipedal motion, the running aggregates move with a stick–slip motion caused by individual cells instead of a group of cells.

Materials and Methods

Detailed experimental methods can be found in SI Appendix, Materials and Methods. We use murine sarcoma Ecad cells expressing E-cadherins at their surface. Aggregates are obtained using the agitation method. Fibronectin is either adsorbed on glass substrates or functionalized using sulfo-SANPAH on gels. We use bright-field microscopy to visualize the dynamics of the cells' and aggregates' motility. Trackings of the cells are obtained using ImageJ (National Institutes of Health). Directionality and curvilinear velocity of the cells are obtained using Chemotaxis and Migration tool. The velocity field was mapped by PIV analysis and stacks of images were analyzed by using the MatPIV software package for MATLAB (MathWorks). The MATLAB program used to calculate the tangential velocities of the velocity fields has been developed by Michael Murrell. We use spinning-disk confocal microscopy to measure force measurements. The displacements fields are calculated using PIV that runs on MATLAB. The reactive droplets were imaged using a PCO.1200hs high-speed camera (PCO imaging).