Abstract
Enhancement of Rubisco kinetics could improve photosynthetic efficiency, ultimately resulting in increased crop yield. However, imprecise knowledge of the reaction mechanism and the individual rate constants limits our ability to optimize the enzyme. Membrane inlet mass spectrometry (MIMS) may offer benefits over traditional methods for determining individual rate constants of the Rubisco reaction mechanism, as it can directly monitor concentration changes in CO2, O2, and their isotopologs during assays. However, a direct comparison of MIMS with the traditional radiolabel method of determining Rubisco kinetic parameters has not been made. Here, the temperature responses of Rubisco kinetic parameters from Arabidopsis thaliana were measured using radiolabel and MIMS methods. The two methods provided comparable parameters above 25 °C, but temperature responses deviated at low temperature as MIMS-derived catalytic rates of carboxylation, oxygenation, and CO2/O2 specificity showed thermal breakpoints. Here, we discuss the variability and uncertainty surrounding breakpoints in the Rubisco temperature response and the relevance of individual rate constants of the reaction mechanisms to potential breakpoints.
Keywords: Arabidopsis, kinetic breakpoints, membrane inlet mass spectrometery, reaction mechanisms, Rubisco, temperature
Rubisco kinetic parameters from Arabidopsis thaliana were measured using radiolabel and membrane inlet mass spectrometry to determine how the reaction mechanisms and the individual rate constants change with temperature.
Introduction
The enzyme Rubisco catalyzes the reaction of CO2 or O2 with ribulose-1,5-bisphosphate (RuBP) initiating the photosynthetic carbon reduction cycle or photorespiratory cycle, respectively (Bowes et al., 1971; Andrews et al., 1973). Kinetic studies on Rubisco typically report the Michaelis–Menten constants for carboxylation (KC) and oxygenation (KO), the catalytic rate of carboxylation (kcatCO2) and oxygenation (kcatO2), and the specificity of the enzyme for CO2 over O2 (SC/O) as these parameters are used for modeling leaf gas exchange (von Caemmerer, 2000). Each of the above Michaelis–Menten parameters is a combination of elementary rate constants that describe the reaction mechanism; however, the rate constants are less well studied as the nature of the chemical mechanism and their intermediates are uncertain (Tcherkez, 2013, 2016). Optimization of Rubisco kinetics for enhanced CO2 reduction has been proposed (Spreitzer and Salvucci, 2002), but this effort is limited by our current understanding of the reaction mechanism (Tcherkez et al., 2006; Tcherkez, 2013).
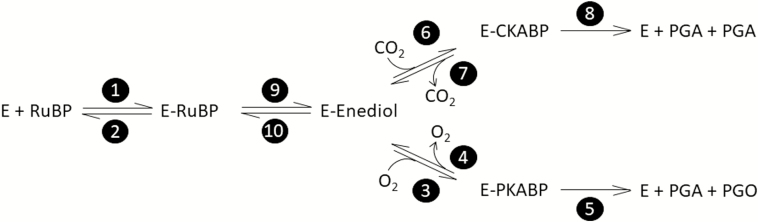
The carboxylation and oxygenation reaction mechanisms can be separated into elementary rate constant as originally proposed by Farquhar (1979), reviewed by Tcherkez (2013), and reproduced in Fig. 1. Since the initial description of the reaction mechanism (Hurwitz et al., 1956), there has been slow progress in defining rate constants due to experimental difficulties in isolating their individual effects. However, the use of membrane inlet mass spectrometry (MIMS) to study Rubisco kinetics may hold promise. The traditional radiolabel method used in most Rubisco publications relies on 14C assays to determine kcatCO2, KC, and KO, a separate 3H assay to determine SC/O, leaving kcatO2 to be calculated. Alternatively, the MIMS assay simultaneously measures changing concentrations of CO2 and O2, and can therefore determine all kinetic parameters with a single assay (Cousins et al., 2010; Boyd et al., 2015). An advantage of the MIMS method is that in addition to the abundant isotopologs of CO2 (12CO2) and O2 (16O2), the system can monitor less abundant stable isotopologs such as 13CO2 and 16O18O. Measurements of primary kinetic isotope effects have been useful in defining enzyme reaction mechanisms (O’Leary et al., 1992); therefore, the MIMS system may provide new information regarding the individual rate constants. At 25 °C the MIMS method has been used for determining both Rubisco carbon fractionation (McNevin et al., 2006, 2007; Tcherkez et al., 2013), and Michaelis–Menten constants of the carboxylation (vc) and oxygenation (vo) reactions (Cousins et al., 2010). Additionally, it was used to determine the temperature dependencies of the Rubisco kinetic parameters in the C4 species Setaria viridis, where the Arrhenius energy of activation (Ea) is used to describe the temperature dependence of chemical reaction rates (Boyd et al., 2015). However, previous work using the radiolabel method suggests lower Ea values for Vcmax in C4 species than that measured by Boyd et al. (2015) (Sage, 2002; Kubien et al., 2003; Perdomo et al., 2015; Sharwood et al., 2016). This suggests that comparisons between the MIMS Ea values and the traditional radiolabel method are needed.
Fig. 1.
Elementary reactions of Rubisco-catalyzed carboxylation and oxygenation (Farquhar,1979). Each reaction, forward and reverse, is numbered in a filled circle following the numbering from Farquhar (1979). Steps 8 and 5 are written as irreversible reactions. Step 8 includes cleavage, hydration, and reprotonation as a single step. Step 5 includes cleavage and hydration as a single step. Each step is associated with a rate constant (k) and energy of activation (ΔG‡) following the same numbering as shown in the filled circles. Abbreviations are as follows: E, free activated enzyme; RuBP, d-ribulose-1,5-bisphosphate; E-RuBP; enzyme-bound RuBP; E-Enediol, enzyme-bound 2,3-enediolate form of RuBP; CO2, carbon dioxide; E-CKABP, enzyme-bound carboxyketone intermediate; PGA, 3-phospho-d-glycerate; O2, oxygen; E-PKABP, peroxo intermediate; PGO, 2-phosphoglycolate.
Here we measured the temperature response of Rubisco kinetic parameters from Arabidopsis thaliana using two methods. First, we used the traditional method involving the use of radiolabeled substrate and analysis of labeled products following the reaction in known concentrations of CO2 and O2 (Jordan and Ogren, 1981). Secondly, we used the MIMS method following the simultaneous consumption of CO2 and O2 over time, giving a direct measure of vc, vo, CO2, and O2, leading to simultaneous determination of kcatCO2, kcatO2, KC, KO, and SC/O (Cousins et al., 2010; Boyd et al., 2015). Additionally, for the radiolabel method, we compared curve fitting CO2 responses to determine KC and kcatCO2 simultaniously in an O2-free buffer, and kcatCO2 determined at a single bicarbonate concentration in open air. The latter is a common practice for determining kcatCO2 temperature responses (Tieszen and Sigurdson, 1973; Sage et al., 1995; Crafts-Brander and Salvucci, 2000; Pittermann and Sage, 2000; Sage, 2002; Kubien et al., 2003; Perdomo et al., 2015).
Recently, the existence of thermal breakpoints in the kcatCO2 temperature response was highlighted as a source of variability in the Rubisco temperature response literature (Sharwood et al., 2016). Thermal breakpoints occur when Ea values differ between temperature ranges. Initial observations of breakpoints in Vcmax temperature responses were determined to be a methodological artifact due to the use of a single bicarbonate concentration at all temperatures and were corrected by varying the bicarbonate concentration with temperature (Björkman and Pearcy, 1970). However, breakpoints were later observed for kcatCO2, kcatO2, and KC at 15 °C using a curve fitting method (Badger and Collatz, 1977). It was suggested that these breakpoints could be due to changes in rate-limiting steps of the reaction mechanism caused by changes in enzyme conformation (Badger and Collatz, 1977). An additional breakpoint was reported in the kcatCO2 of Oryza sativa at 22 °C (Sage, 2002), and Kubien et al. (2003) observed different temperature responses when kcatCO2 was measured from 0 °C to 12 °C compared with 18 °C to 42 °C in Flaveria bidentis. Most recently, Sharwood et al. (2016) observed breakpoints in kcatCO2 at 25 °C for Panicoid grasses when using a curve fitting method. Inconsistencies are evident between studies, and it is unclear if breakpoints are universal to all temperature response studies of plant Rubisco. Here, we discuss the possible causes of breakpoints, focusing on the three previously proposed causes of breakpoints: erroneous bicarbonate concentrations, changes in the rate-limiting step of the reaction mechanism, and deactivation of Rubisco at low temperature, using the radiolabel and MIMS data sets reported here.
Materials and methods
Plant growth
Plants for the radiolabel method were grown and assayed at the University of New Brunswick, Fredericton, Canada. Arabidopsis thaliana (Col-0) seeds were stratified for 3 d at 4 °C on Promix (Plant Products, Brampton, Canada), transferred to a growth chamber (E-15, Conviron, Winnipeg, Manitoba, Canada), and grown under a photoperiod of 10 h light and14 h dark, day/night temperatures of 20/18 °C, and a photosynthetic photon flux density (PPFD) of 300 μmol m−2 s−1. Plants were watered with modified Hoagland’s solution as needed.
Plants for MIMS were grown and assayed at Washington State University, Pullman, Washington, USA. Seeds of A. thaliana, ecotype Col-0, were placed in 2 liter pots containing commercial soil (LC1 Sunshine Mix, Sun Gro Horticulture, Vancouver, Canada) and grown in an environmental growth chamber (Biochambers GC-16, Winnipeg, Manitoba, Canada) at a PPFD of 300 µmol m−2 s−1 at plant height, relative humidity was not controlled, and day/night temperature was 23/18 °C, with a 14 h photoperiod and 10 h of dark. Plants were fertilized weekly (Peters 20-20- 20, Allentown, PA, USA) and watered as needed.
Sampling for radiolabel analysis
Leaf punches were obtained at mid-day, flash-frozen in liquid nitrogen, and stored at –80 °C until extraction. Leaf tissue was ground (1.1 cm2 disks, ~20 mg) in a Tenbroeck glass tissue homogenizer containing 3 ml of ice-cold extraction buffer [100 mM HEPES pH 7.6, 2 mM Na-EDTA, 5 mM MgCl2, 5 mM DTT, 10 mg ml−1 polyvinylpolypyrolidone (PVPP), 2% (v/v) Tween-80, 2 mM NaH2PO4, 12 mM amino-n-capronic acid, and 2 mM benzamidine] and 50 μl of Protease inhibitor cocktail (Sigma, St. Louis, MO, USA). This leaf homogenate was centrifuged at 16 000 g at 4 °C for 60 s. The resulting supernatant was then desalted using an Econo Pac 1-DG column (Bio-Rad), and aliquots were incubated with 20 mM MgCl2 and 10 mM NaHCO3 at 30 °C for 20 min to carbamylate Rubisco fully. Rubisco content (number of active sites) was quantified using the [14C]carboxy-arabinitol bisphosphate (14CABP)-binding assay (Ruuska et al., 1998; Kubien et al., 2011).
Sampling for MIMS analysis
The youngest fully expanded leaves of plants 30–40 d after planting were sampled for Rubisco extraction. The mid vein was removed and ~2 g of leaf tissue was ground in 2 ml of ice-cold extraction buffer [100 mM HEPES pH 7.8, 10 mM DTT, 25 mM MgCl2, 1 mM EDTA, 10 mM NaHCO3, 1% (g ml–1) PVPP, 0.5% (v/v) Triton X-100] with a mortar and pestle on ice. Protease inhibitor cocktail (P9599, Sigma-Aldrich), 67 µl per 2 g of fresh leaf tissue, was added to the extraction buffer before grinding. The homogenized extract was centrifuged at 4 °C, for 10 min, at 17 000 g. The supernatant was collected and desalted using an Econo Pac 10DG column (Bio-Rad), filtered through a Millex GP 33 mm syringe-driven filter unit (Millipore), and then centrifuged using Amicon Ultra Ultracel 30K centrifugal filters (Millipore) at 4 °C for 1 h at 3000 g. The layer maintained above the filter unit was collected, brought to 20% glycerol (v/v), flash-frozen in liquid nitrogen, and stored at –80 °C until measured. Rubisco content was determined as described above.
Radiolabel measurement of Rubisco kinetic parameters
The maximum carboxylation rate of fully activated Rubisco (Vcmax) was measured following the methods of Kubien et al. (2011) from 0 °C to 35 °C, by the incorporation of 14C into acid-stable products. This method is later referred to as the ‘single point’ method. Assays were initiated by the addition of 50 μl of activated extract (as described above) to 250 μl of assay buffer [100 mM Bicine-NaOH (pH 8.2), 1 mM Na-EDTA, 20 mM MgCl2, 5 mM DTT, 400 μM RuBP, and 11 mM NaH14CO3 (~700 Bq nmol−1)] and stopped after 30–60 s by adding 250 μl of 1 M formic acid. Samples were dried at 90 °C, and 14C acid-stable products were counted using a scintillation counter (LS-6500, Beckman-Coulter). The catalytic rate of carboxylation (kcatCO2) was calculated using the equation
| (1) |
where active sites are measured by the 14CABP method described above. It was assumed that there is a one to one relationship between the moles of 14CABP and active sites, resulting in units for kcatCO2 of mol CO2 mol−1 active site s−1 that simplifies to s−1.
Michaelis–Menten parameters for CO2 (KC), and apparent KC at 21% O2 [KC (21% O2)] were determined by assaying the initial rate of Rubisco carboxylation (vc) in 7 ml septum-sealed, N2-sparged vials over a range of seven NaH14CO3 concentrations (Paul et al., 1991; Kubien et al., 2008). Concentrations of NaHCO3 varied depending on temperature (e.g. 0.01–3.0 mM at 10 °C, versus 0.3–13.0 mM at 35 °C). The temperature effect on pH using pKa values (Edsall and Wyman, 1958) to calculate the CO2 concentration was incorporated and the Henry coefficients (Sander, 2015) were used to account for the temperature effect on CO2 solubility (see Supplementary Table S1 at JXB online). Assays were initiated by injecting 50 μl of the activated extract into vials containing CO2-free assay buffer [100 mM Bicine-NaOH (pH 8.2 at 25 °C), 20 mM MgCl2, 1 mM Na2-EDTA, 400 μM RuBP, and 10 μg ml−1 carbonic anhydrase], stopped after 30–60 s by adding 250 μl of 1 M formic acid, and counted as described above. The response of vc to partial pressures of CO2 were fit to the Michaelis–Menten equation
| (2) |
in SigmaPlot (Systat Software, San Jose, CA, USA) solving for Vcmax and KC. This analysis, referred to as the ‘curve fitting’ method, gave a separate temperature response of kcatCO2 from the single point method described above. From the same extract, the apparent KC at 21% O2 [KC(21% O2)] was determined, and the Michaelis constant for oxygenation (KO) was calculated from the relationship
| (3) |
Rubisco specificity for CO2 over O2 (SC/O) was determined following the method described by Kane et al. (1994). Septa-sealed vials containing Rubisco, buffer [30 mM triethanolamine-acetate (pH 8.3), 20 mM Mg-acetate], and 0.2 mg ml−1 carbonic anhydrase were incubated in humidified gas (0.1% CO2 in O2, with a total flow rate of 2000 ml min−1; G400 gas mixing system, Qubit Systems, Kingston Canada) at each measurement temperature, with oscillatory shaking. Reactions were initiated by injecting 2 nmol of [3H]RuBP (3 kBq nmol−1) into the vial and terminated after 60 min by the addition of alkaline phosphatase. To prepare the sample for separation, the reaction products were applied to a 0.5 ml column of BioRad AG1-X8 anion exchange resin (200–400 mesh, formate form), washed with 10 column volumes of ddH2O, and radioactively labeled glycerate and glycolate eluted with 10% H2SO4. The [3H]glycerate and [3H]glycolate were separated via HPLC (system described in Shay and Kubien, 2013) on an Aminex HPX-87H column (BioRad, Canada) maintained at 60 °C. The mobile phase was 7.5 mM H2SO4, and the flow rate was 0.4 ml min−1. Glycerate and glycolate fractions were collected in drop-synchronization mode (Fraction Collector III, Waters), and the amount of 3H in each fraction was determined via scintillation counting. The SC/O was calculated from the ratio of [3H[glycerate to [3H]glycolate and the mole fractions of CO2 and O2 in the humidified gas, giving SC/O expressed as a ratio of partial pressures (Kane et al., 1994). Finally, the average value of each parameter was used to calculate the catalytic rate of oxygenation (kcatO2) from the relationship
| (4) |
MIMS measurement of Rubisco kinetic parameters
Rubisco assays were conducted in a 600 µl temperature-controlled cuvette linked to an isotope ratio mass spectrometer (Thermo-Fischer Delta V) and calibrated as previously described (Cousins et al., 2010; Boyd et al., 2015). Samples were measured similarly to Boyd et al. (2015); four oxygen concentrations ranging from 40 μM to 1600 μM, and five CO2 concentrations ranging from 0 μM to 200 μM at each oxygen level were made. Measurements were made in 5 °C intervals from 10 °C to 40 °C, and the same three replicates were measured at each temperature. The assay buffer contained 200 mM HEPES (pH 7.7 at each measurement temperature), 20 mM MgCl2, 0.1 mM α-hydroxypyridinemethanesulfonic acid (α-HPMS), 8 mg ml−1 carbonic anhydrase (Sigma), and 0.6 mM RuBP. A 10 µl aliquot of extract was added per measurement. Rubisco was activated by leaving the extract at room temperature for 10 min prior to returning to ice before measurement.
The measured vc, vo, and the corresponding CO2 and O2 concentrations were fit simultaneously to the following equations
| (5) |
| (6) |
solving for the parameters Vcmax, Vomax, KC, and KO. All model fits were performed in the software package Origin 8 (OriginLab) using the non-linear curve-fit function NLfit. SC/O was calculated using Equation 4. The kcatCO2 was calculated according to Equation 1 and the kcatO2 was calculated using the analogous equation
| (7) |
It should be noted that plant growth temperature, photoperiod, extraction protocol, and assay conditions were similar but not identical between the MIMS and radiolabel experiments, and, as discussed below, should be taken into account when comparing these two data sets.
Modeling temperature responses
The temperature responses of the kinetic parameters were calculated for the equation
| (8) |
where k25 is the value of the parameter at 25 °C, Ea is the Arrhenius activation energy (kJ mol−1), R is the molar gas constant (0.008314 kJ mol−1 K−1), TK is the temperature in Kelvin, and the term (298.15–TK)/298.15 is the scaling factor so that k25 may be used as the pre-exponential term. The Ea and k25 values for each Rubisco parameter were calculated by a linear regression of the natural log of the data plotted against (TK–298.15)/(TK), such that the y-intercept was equal to the natural log of k25 and the slope was equal to Ea/(298.15 R). For comparison, the non-transformed temperature responses are presented in Supplementary Fig. S1 and Supplementary Table S2. Three replicates of Ea and k25 were determined for each parameter, with the exception of radiolabel SC/O where the number of replicates was four. For all MIMS and radiolabel comparisons, other than kcatCO2, only the curve fitting methods are compared. For simplicity, we exclude the radiolabel single point when comparing ratios of kinetic parameters with MIMS. Differences in the k25 and Ea values were determined by ANOVA, followed by pair-wise comparison (Tukey HSD) with a significance cut-off of P<0.05 in Statistix 9 (Analytical Software, Tallahassee, FL, USA).
Arrhenius plots for all kinetic parameters were examined for thermal breaks using the package ‘segmented’ in R, which first tests for differences between slopes using the Davies test (Davies, 1987), and then estimates the breakpoints in linear models using maximum likelihood (Muggeo, 2003, 2008; R Core Team, 2013). When breakpoints in the Arrhenius temperature response plots were statistically valid, the Ea values above and below the break points were compared with other Ea values as described above; the k25 value was held constant when fitting for two Ea values above and below the breakpoint.
Equations for reaction mechanisms
Figure 1 depicts the currently hypothesized reaction mechanism of Rubisco as originally described by Farquhar (1979). The kinetic parameters kcatCO2, kcatO2, KC, KO, and SC/O can be described by the individual first-order rate constants (k) seen in Fig. 1 as follows:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
where the subscript indicates the transition state as numbered in Fig. 1 by the black circles. The approximations in Equations 11–13 are made by assuming that the rates of decarboxylation (k7) and deoxygenation (k4) are negligible.
These first-order rate constants can be related to temperature using transition state theory and the Eyring equation
| (14) |
where kB is the Boltzmann constant (1.3807 × 10–23 J K−1), h is the Planck constant (6.6261 × 10–34 J s), and ΔG‡ (J mol−1) is the standard free energy difference between the transition state and the substrate (or intermediate). Note that the proportionality constant κ, describing the proportion of vibrations that lead to product formation, has been assumed equal to one and left out of the equation. The ΔG‡ has components of entropy (ΔS‡) and enthalpy (ΔH‡) as defined by
| (15) |
where the double dagger symbol (‡) denotes the transition state.
Modeling rate constants (k) and ΔG‡
The proposed Rubisco reaction mechanism (Fig. 1) suggests that kcatCO2, kcatO2, KC, KO, and SC/O are described by complex terms made up of two or more elementrary reaction rates (Farquhar, 1979; Equations 9–13). The rate constant (k) is related to the energy barrier for the transition state of the reaction, often referred to as the activation energy (ΔG‡). The relationship between k, ΔG‡, and temperature is described by the Eyring equation (Equation 14), where ΔG‡ has enthalpic (ΔH‡) and entropic (ΔS‡) components (Equation 15). From Equation 15, a plot of ΔG‡ with temperature has a slope of ΔS‡ and a y-intercept of ΔH‡. For the discussion of Rubisco kinetics, all numbering of k, ΔG‡, ΔH‡, and ΔS‡ refers to reaction steps initially described by Farquhar (1979) and reproduced in Fig. 1. The Eyring equation has been previously used to calculate ΔG‡ values for kcatCO2, kcatO2, and SC/O (Chen and Spreitzer, 1992; Tcherkez et al., 2006; McNevin et al., 2007; Tcherkez, 2013). Because kcatCO2 and kcatO2 are first-order rate constants, they have been represented as
| (16) |
and
| (17) |
and because SC/O is the ratio of two first-order rate constants (Equation 13), it has been represented as
| (18) |
The ΔG‡ terms in Equations 16–18 can be calculated directly from measured values, and the ΔH‡ and ΔS‡ terms would describe a linear fit of ΔG‡ to the temperature response, assuming ΔH‡ and ΔS‡ are constant within the temperature range. However, the use of Equations 16–18 does not provide information regarding an elementary rate constant or a corresponding energy barrier. Modeling to estimate individual rate constants from the measured data is described below.
Modeling of radiolabel data
Each of the rate constants (k) in Fig. 1 has a corresponding energy of activation (ΔG‡ from Equation 14), which has a corresponding enthalpic and entropic component (ΔH‡ and ΔS‡ from Equation 15). We assumed that the values of ΔH‡ and ΔS‡ are constant within the temperature range. Therefore, we fit Michaelis–Menten parameters calculated from elementary rate constants using Equations 9–13 to the measured Michaelis–Menten parameters by varying the corresponding ΔH‡ and ΔS‡ values. All modeling used the solver function in Excel (2016, Microsoft, Redmon, WA, USA) to minimize the sum of the differences squared between modeled and measured parameters.
The rate constants k8 (cleavage of carboxylated intermediate) and k9 (enolization of RuBP) were calculated from measured kcatCO2 values following the calculations of Tcherkez et al. (2013) such that k8/k9 is 0.83 at 25 °C. The rate constant k10 (de-enolization) was modeled assuming k9/k10 is 0.43 at 25 °C following the calculations of Tcherkez et al. (2013); we further assumed that this ratio remained constant with temperature. This allowed for calculation of the rate of k6 (CO2 addition) as the only remaining unknown when fitting measured values of KC with Equation 11 assuming k7 (de-carboxylation) was negligible. After calculating k6, then k3 (O2 addition) was modeled from measured SC/O values and Equation 13, assuming rate constants k7 (decarboxylation) and k4 (deoxygenation) are negligible. Finally, the rate constant k5 (cleavage of the oxygenated intermediate) was calculated from measured KO values and Equation 14, again assuming k4 (deoxygenation) was negligible. This process allowed for estimation of the temperature response for k and ΔG‡ values for each step of the reaction mechanism listed in Equations 9–13, with the exception of the decarboxylation and deoxygenation steps that were assumed to be negligible (Tcherkez et al., 2013; Tcherkez, 2013, 2016).
Modeling of MIMS data
For the MIMS data, where measurements of kcatO2 were available and non-linearity of Arrhenious plots was observed, the rate constants and corresponding ΔG‡, ΔH‡, and ΔS‡ values were determined differently from what was described above for the radiolabel data. The ΔH‡ and ΔS‡ values corresponding to the rate constants for k8 (cleavage of carboxylated intermediate), k5 (cleavage of oxygenated intermediate), and k9 (RuBP enolization) were determined by fitting to measured kcatCO2 and kcatO2 values, assuming k8/k9 was 0.83 at 25 °C, and using Equations 9 and 10. Because kcatCO2 showed a breakpoint, it is possible that k8 and k9 have different temperature responses, with a crossover at ~25 °C. However, kcatO2 also showed a breakpoint at 25 °C and the carboxylated intermediate cleavage rate (k8) is much greater than the oxygenated cleavage rate (k5) because measured kcatCO2 values are greater than measured kcatO2. Therefore, a crossover of k5, k8, and k9 at a single temperature is not possible and a breakpoint in kcatCO2 and kcatO2 co-occuring at a single temperature cannot be modeled as a changing rate-limiting step. Therefore, we modeled the breakpoint in kcatO2 by allowing k5 to have separate ΔH‡ and ΔS‡ values above and below the breakpoint, and assuming k9 had the same values of ΔH‡ and ΔS‡ above and below the breakpoint. Because k9 (rate constant of RuBP enolization) temperature response was assumed constant for models of kcatO2, it was also assumed constant when modeling kcatCO2. Therefore, k8 was allowed to have separate values of ΔH‡ and ΔS‡ above and below the breakpoint. The k10 (rate constant of de-eneolization) was subsequently calculated assuming the ratio k9/k10 was 0.43 and constant with temperature. The value k6 (rate constant of CO2 addition) was then calculated from measured KC and the approximation of Equation 11 assuming decarboxylation is negligible. This was also done for k3 (rate constant for O2 addition) using KO and the approximation of Equation 12 assuming de-oxygenation (k4) was negligable. It was required that k6 and k3 have seperate ΔH‡ and ΔS‡ values above and below the breakpoint to model linear Arrhenious plots of KC and KO. This process provided estimates of the temperature response for k and ΔG‡ values for each step of the reaction mechanisms making up the measured Michaelis–Menten parameters (Equations 9–13), with the exception of the decarboxylation and deoxygenation steps, which were assumed to be negligable.
Results
Breakpoints
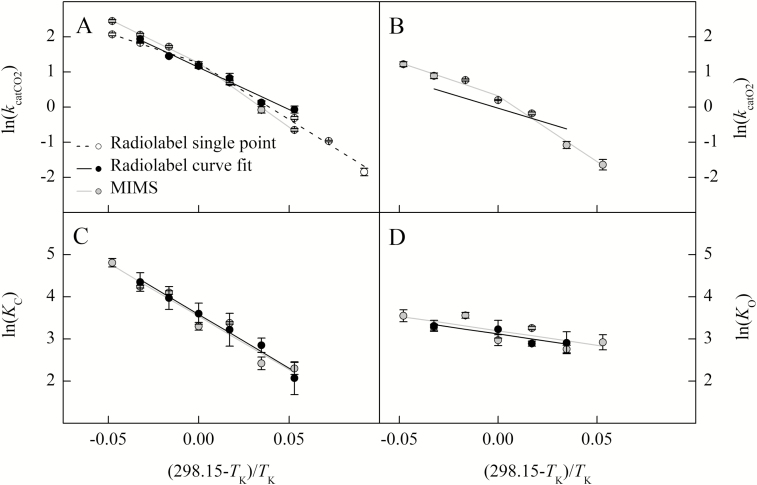
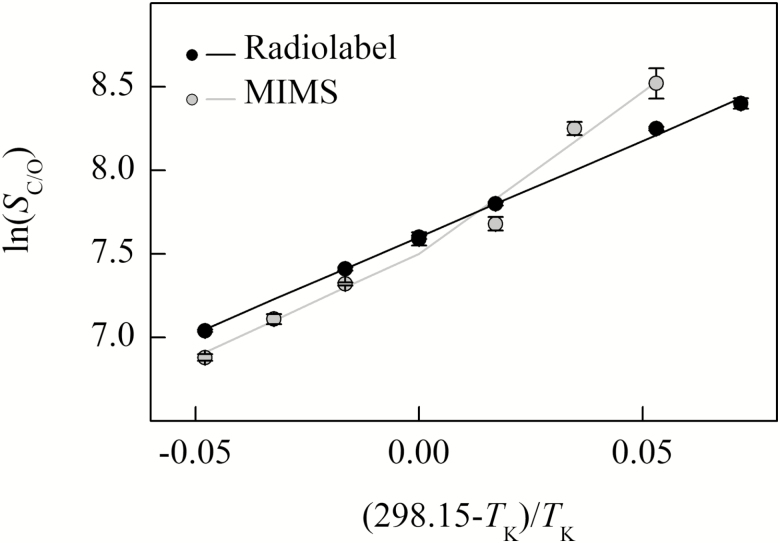
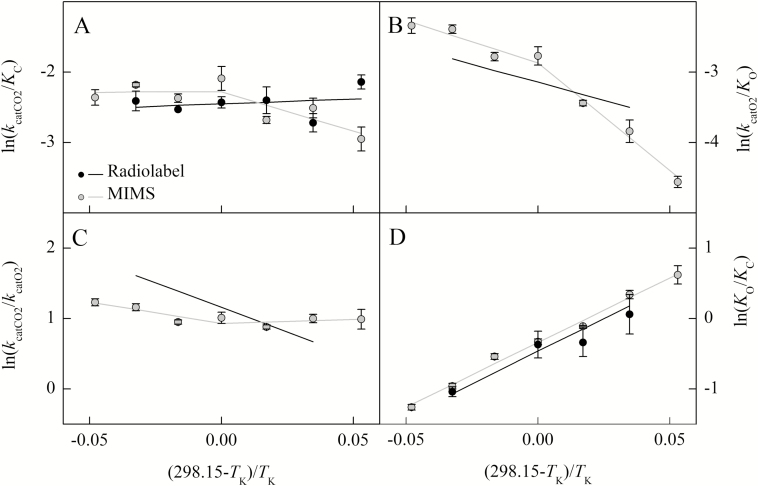
The Davies test indicated significant breakpoints for the kcatCO2, kcatO2, and SC/O temperature response for the MIMS data as well as for the radiolabel single point measurement of kcatCO2 (Table 1; Figs 2, 4). Both the Davies test and the maximum likelihood segmented analysis indicated that the breakpoints in these parameters were near 25 °C (Table 1). All other parameters showed no breakpoints in their temperature responses for either the MIMS or radiolabel data sets (Table 1; Figs 2–4).
Table 1.
Testing for thermal breaks for all kinetic parameters
| Method | Parameter | Davies test | Maximum likelihood | |||
|---|---|---|---|---|---|---|
| Estimated breakpoint (°C) | P-value | Estimated breakpoint (°C) | CI (lower) | CI (upper) | ||
| Radiolabel |
k
catCO2
single point |
26.8 | * | 25.1 | 5.3 | 36.9 |
|
k
catCO2
curve fit |
– | ns | ||||
| k catO2 | – | – | ||||
| K C | – | ns | ||||
| K O | – | ns | ||||
| S C/O | – | ns | ||||
| MIMS | k catCO2 | 25.3 | * | 25.3 | 23.1 | 31.5 |
| k catO2 | 25.3 | * | 25.5 | 24.3 | 32.6 | |
| K C | – | ns | ||||
| K O | – | ns | ||||
| S C/O | 25.4 | * | 25.2 | 15.0 | 27.6 | |
Arrhenius plots were examined using the package ‘segmented’ in R (R Core Team, 2013), which determines the significance of breakpoints in linear models and estimates breakpoint locations as described by Davies (1987). Additionally, breakpoint locations and confidence intervals (CIs, lower and upper) were independently estimated using a maximum likelihood test (Muggeo, 2003, 2008). * indicates a P-value <0.05 for the Davies test and ns is not significant.
Fig. 2.
The natural log of Rubisco parameters from Arabidopsis thaliana measured using radiolabel (single point, open circle; curve fit, black circle) and MIMS (gray circle) methods are plotted against the inverse of the temperature in Kelvin offset to a y-intercept of 25 °C. The temperature response of catalytic turnover for CO2 (kcatCO2, s−1, A) and O2 (kcatO2, s−1, B), and the Michaelis–Menten constant for CO2 (KC, Pa, C) and O2 (KO, kPa, D) are shown. The lines represent the model fit to the measured data. The radiolabel kcatO2 model in (B) was determined from the relationship with SC/O described by Equation 4.
Fig. 4.
The natural log of Rubisco specificity for CO2 over O2 (SC/O) from Arabidopsis thaliana measured using radiolabel (black circle) and MIMS (gray circle) methods are plotted against the inverse of the temperature in Kelvin offset to a y-intercept of 25 °C. The black line represents the model fit to the measured radiolabel values. The gray line was determined from the relationship of SC/O to the parameters presented in Fig. 2, described by Equation 4.
Arrhenius activation energies and modeled value at 25 °C
The modeled 25 °C values (k25) and Arrhenius activation energy (Ea) above 25 °C agree with many of the literature values for other C3-type Rubisco, including in vitro and in vivo measurements of A. thaliana (Flexas et al., 2007; Whitney et al., 2011; Walker et al., 2013; Weise et al., 2015; Galmés et al., 2016). Although, previous reports of Rubisco specificities for CO2 over O2 (SC/O) at 25 °C vary widely for C3 species, including for A. thaliana which range from below 2125 to above 2655 (Pa Pa−1; Flexas et al., 2007; Whitney et al., 2011; Walker et al., 2013; Weise et al., 2015). For the MIMS-derived parameters with breakpoints (kcatCO2, kcatO2, and SC/O), and the radiolabel single point estimate of kcatCO2, the lower temperature Ea values were larger than Ea values estimated at higher temperatures (Tables 2, 3). Above 25 °C, the Ea values were similar for all parameters between the radiolabel and MIMS curve fitting methods. The radiolabel Ea for kcatCO2 determined by curve fitting across all temperatures was intermediate to the two Ea values estimated above and below the breakpoint from the single point radiolabel data. The k25 values for kcatCO2 estimated from radiolabel and MIMS methods were not different from each other, but were larger than the k25 for kcatO2 determined by MIMS (Table 2). The Ea and k25 values for KC and KO were not significantly different between methods (Table 3). However, the MIMS SC/O measured from 10 °C to 25 °C had a lower (more negative) Ea value than the MIMS SC/OEa value measured from 25 °C to 40 °C and the radiolabel SC/OEa value (Table 3).
Table 2.
Comparison of k25 and Ea values for kcat measurements from the different methods
| Method | Temperature (°C) | Parameter | k 25 | E a |
|---|---|---|---|---|
| Radiolabel | ||||
| Single point | 0–25 | k catCO2 (s−1) | 3.50 ± 0.20 A | 79.53 ± 2.03 a |
| 25–40 | – | 42.11 ± 3.45 c | ||
| Curve fit | 10–35 | 3.10 ± 0.07 A | 59.64 ± 3.93 b | |
| MIMS | 10–25 | 3.53 ± 0.25 A | 90.36 ± 1.03 a | |
| 25–40 | – | 62.20 ± 2.68 b | ||
| 10–25 | k catO2 (s−1) | 1.38 ± 0.05 B | 92.95 ± 7.31 a | |
| 25–40 | – | 47.11 ± 2.33 b,c |
The k25 and Ea values are the mean of 3–4 replicates, calculated from linear regressions of Arrhenius plots. The temperature ranges for each regression were determined by segment analysis. Letters indicate significant differences between groups (Tukey HSD, P<0.05).
Table 3.
Comparison of KC, KO, SC/O parameters k25 and Ea resulting from the different methods
| Method | Temperature range (°C) | Parameter | k 25 (Pa) | E a (kJ mol−1) |
|---|---|---|---|---|
| Radiolabel | 10–35 | K C | 36 ± 2 | 63.09 ± 6.23 |
| MIMS | 10–40 | 34 ± 1 | 62.62 ± 3.44 | |
| Radiolabel | 15–35 | K O | 23 100 ± 3430 | 16.89 ± 2.59 |
| MIMS | 10–40 | 24 400 ± 701 | 17.01 ± 2.48 | |
| Radiolabel | 05–40 | S C/O | 2003 ± 22 | –28.66 ± 0.51 b |
| MIMS | 10–25 | 1814 ± 117 | –48.19 ± 4.17 a | |
| 25–40 | – | –30.51 ± 6.41 b |
No differences were observed in k25 between methods. No differences were observed in Ea values for KC and KO values between methods (ANOVA). Theletters next to the Ea values indicate significant differences for the SC/O values (Tukey HSD, P<0.05).
The Ea value for the carboxylation efficiency (kcatCO2/KC) below 25 °C was significantly different from zero for the MIMS method, where the carboxylation efficiency increased with temperature; however, above 25 °C, the Ea value was not significantly different from zero (Table 4). The MIMS Ea for oxygenation efficiency (kcatO2/KO) was significantly different from zero above and below 25 °C (Table 4). The Ea for the ratio of catalytic rates (kcatCO2/kcatO2) measured by MIMS was only significantly different from zero above 25 °C (Table 4). The Ea for KO/KC was significantly different from zero for both radiolabel and MIMS methods (Table 4).
Table 4.
The Ea and k25 parameters for kcatCO2/KC, kcatO2/KO, kcatCO2/kcatO2, and KO/KC ratios
| Method | Temperature range (°C) | Parameter | k 25 | E a |
|---|---|---|---|---|
| Radiolabel | 10–35 | k catCO2/KC | 0.09 ± 0.00 | –3.45 ± 3.94 |
| MIMS | 10–25 | (s−1 Pa−1) | 0.10 ± 0.01 | 27.75 ± 3.38* |
| 25–40 | – | –0.41 ± 6.10 | ||
| MIMS | 10–25 | k catO2/KO | 0.06 ± 0.00 | 75.93 ± 7.41* |
| 25–40 | (s−1 kPa−1) | – | 30.09 ± 0.70* | |
| MIMS | 10–25 | k catCO2/kcatO2 | 2.55 ± 0.16 | –2.58 ± 6.73 |
| 25–40 | – | 15.10 ± 4.92* | ||
| Radiolabel | 15–35 | K O/KC | 0.65 ± 0.11 | –46.20 ± 8.80* |
| MIMS | 10–40 | (kPa Pa−1) | 0.71 ± 0.01 | –45.60 ± 2.57* |
The Ea parameters were tested to determine if they were significantly different from zero (t-test), where the * next to the Ea values indicates a P-value <0.05.
Modeling k and ΔG‡
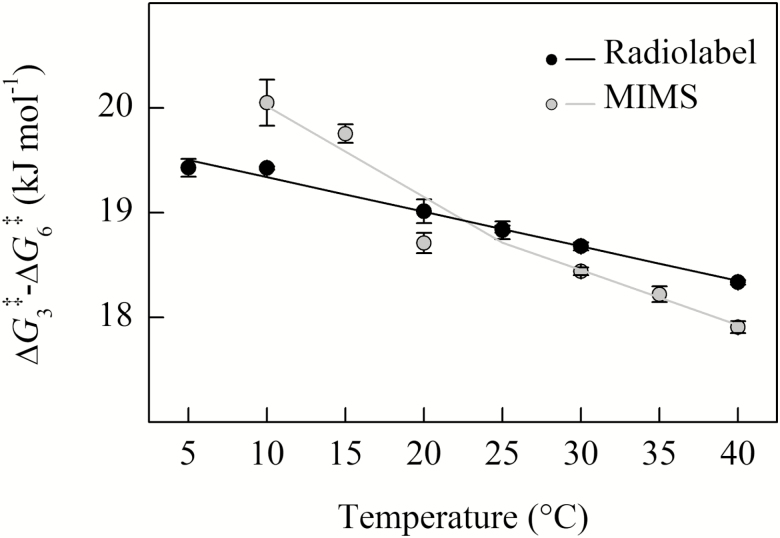
Above 25 °C, the ΔG3‡–ΔG6‡ for SC/O from radiolabel and MIMS (Fig. 5) are similar to previous calculations for C3 species reported by Tcherkez et al. (2006). However, the MIMS entropy difference between O2 and CO2 addition (ΔS3‡–ΔS6‡, slope of the line in Fig. 5; see Equation 18; see Supplemenary Table S3) from data colleted below 25 °C appear more similar to the ΔS3‡–ΔS6‡ of red algae rather than of higher plants, when compared with data presented in Tcherkez et al. (2006).
Fig. 5.
The temperature response of ΔG3‡–ΔG6‡ calculated from the data presented in Fig. 4. Both measurement methods show a decrease with temperature. Solid black circles are the mean of four replicates measured using radiolabel, filled gray circles are the means from three replicates using MIMS; the SE is shown. The solid lines indicate the linear regression fit to calculated values.
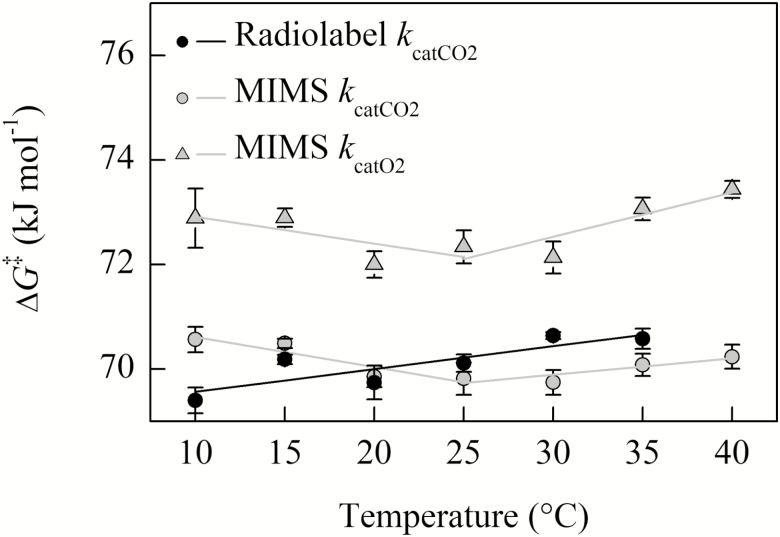
The free energy of activation associated with kcatCO2 (ΔGkcatCO2‡) plotted against temperature increased linearly for the radiolabel curve fit method, while the ΔGkcatCO2‡ calculated from MIMS measurements decreased from 10 °C to 25 °C and then increased from 25 °C to 40 °C (Fig. 6). A similar temperature response was also observed for MIMS ΔGkcatO2‡, although the absolute values of ΔGkcatO2‡ are larger than ΔGkcatCO2‡ as evident by a lower kcatO2 compared with kcatCO2 at all temperatures (i.e. larger energy barriers result in slower reactions). The slope of ΔGkcatCO2‡ values presented in Fig. 6 (equivalent to the entropy term ΔSkcatCO2‡; see Supplementary Table S4) calculated for radiolabel and MIMS above 25 °C are slightly larger than those reported for Nicotiana tabacum (McNevin et al., 2007). The MIMS ΔSkcatCO2‡ and ΔSkcatO2‡ showed a sign change above and below the breakpoint (negative slope to positive slope, Fig. 6; Supplementary Table S4).
Fig. 6.
The temperature response of ΔGkcatCO2‡ for MIMS and radiolabel methods, and ΔGkcatO2‡ for MIMS calculated from the data presented in Fig. 2. Two regressions were fit to the MIMS data on either side of the 25 °C breakpoint; a single regression is fit to the radiolabel data. Solid black circles are the mean of three replicates measured using radiolabel, filled gray circles are the means from three replicates using MIMS; the SE is shown.
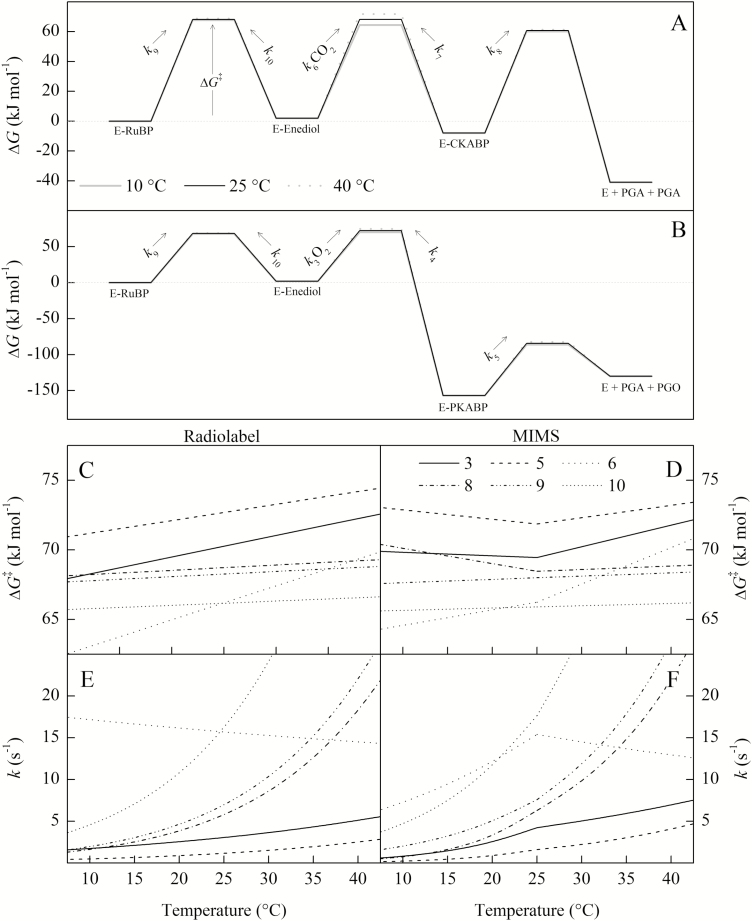
Temperature responses of the rate constants (k) and corresponding energy barriers of the transition states (ΔG‡) are shown in Fig. 7, while the modeled ΔH‡ and ΔS‡ values are presented in Suppementary Table S5. Calculations of elementary rate constants and corresponding ΔG‡ are similar to previous calculations at 25 °C from Tcherkez (2013, 2016). In order to model breakpoints in the MIMS kcatCO2, kcatO2, and SC/O parameters, breakpoints are neeeded in the rate constants for the cleavage (k8 and k5) and for gas addition (k6 and k3). This is required because it was not possible to model a simultaneous change in the rate-limiting step for both the kcatCO2 and kcatO2 parameter (Supplementary Fig. S2). This further required that breakpoints were needed in the rate constants for CO2 and O2 addition (k6 and k3, respectively) to maintain the observed linearity for the KC and KO Arrhenius plots (Fig. 2).
Fig. 7.
A kinetic energy barrier diagram showing the modeled temperature responses of the energy barrier to the transition state (ΔG‡) and the corresponding first-order rate constant k. The ΔG‡ and k are indicated by the numbered step of the reaction following Fig. 1. The assumptions made for this model are stated in the Materials and methods. For steps 3 and 6 (O2 and CO2 addition, respectively), the rate constants were multiplied by ambient concentrations O2 (21 kPa) and CO2 (41 Pa) as a pseudo-first-order approximation for comparison with the other rate constants and to calculate their respective ΔG‡. For the bottom figure, the left-hand column is modeled on the radiolabel data and the right-hand column on the MIMS data so that comparisons between continuous and breakpoint temperature responses can be made. The values for intermediates were taken from Tcherkez (2013) for (A) and Tcherkez (2016) for (B) and assumed to remain constant with temperature.
Discussion
Radiolabel single point kcatCO2 breakpoint
The radiolabel single point method reported here utilized a single bicarbonate concentration with temperature (11 mM) and resulted in a thermal breakpoint similar to Björkman and Pearcy (1970). Because Björkman and Pearcy (1970) suggested that there could be inhibition at low temperature and subsaturating concentrations at high temperature, we plotted the predicted CO2 concentration achieved by 11 mM NaHCO3 at each temperature against the measured and modeled CO2 response of the enzyme determined by both radiolabel and MIMS curve fitting methods (Supplementary Fig. S3). The CO2 concentration provided by the 11 mM NaHCO3 appears saturating at 10 °C and 15 °C, but becomes increasingly less saturating at higher temperatures, as indicated where the shaded area intersects the modeled CO2 response (Supplementary Fig. S3). This suggests that the lower Ea value of the single point method at high temperatures could be caused by subsaturating CO2 concentrations.
MIMS kcatCO2, kcatO2, and SC/O breakpoints
The non-linearity of Arrhenius plots of kcatCO2, kcatO2, and SC/O for the MIMS data were interpreted as 25 °C breakpoints. Badger and Collatz (1977) also observed breakpoints in kcatCO2, kcatO2, and SC/O; however, they observed an additional thermal breakpoint in KC, which was not observed with the MIMS data presented here. As SC/O is a ratio of kcatCO2, KC, KO, and kcatO2 (Equation 4), the differences in SC/O breakpoints between Badger and Collatz (1977) and our MIMS data could suggest different mechanisms driving the thermal response of SC/O. Furthermore, no breakpoint in SC/O has been observed in any study using the [3H]RuBP method.
The breakpoints observed in MIMS kcatCO2 and kcatO2 are unlikely to be caused by insufficient or inhibitory CO2 concentrations, as subsaturation or inhibition should be evident in the CO2 response curves (Supplementary Fig. S3). A breakpoint in both kcatCO2 and kcatO2 could be caused by deactivation of the enzyme, as was suggested by Kubien et al. (2003). However, deactivation is unlikely to change the kcatCO2/kcatO2 temperature response as was observed in Fig. 3C, because both catalytic rates are expected to be affected in the same way by deactivation. Alternatively, the observed breakpoints in MIMS could be related to methodology as the radiolabel Arrhenius plots presented here for kcatCO2 and SC/O were sufficiently linear.
Fig. 3.
The natural log of the Rubisco parameter ratios from Arabidopsis thaliana measured using radiolabel (black circle) and MIMS (gray circle) are plotted against the inverse of the temperature in Kelvin offset to a y-intercept of 25 °C. The temperature response of the catalytic efficiency of the carboxylation (kcatCO2/KC, A) and oxygenation (kcatO2/KO, B) reactions, catalytic turnover ratio for CO2 over O2 (kcatCO2/kcatO2, C), and the Michaelis–Menten constant ratio for O2 over CO2 (KO/KC, D) are shown. Lines represent the combination of models represented in Fig. 2 and are not the result of linear regressions to the ratios.
Limitations of methodological comparisons
The Rubisco kinetic parameters for A. thaliana measured with the radiolabel and MIMS curve fitting methods were similar at and above 25 °C, suggesting similar kinetic parameters under these conditions, despite slight differences in plant growth environments, as well as sample extraction and assay conditions. However, at lower temperatures, the observed breakpoints in MIMS and the corresponding linearity of the Radiolabel temperature responses could imply that plant-specific growth differences were important. For example, spinach Rubisco appears to acclimate to growth temperature, with warm-grown Rubisco showing a thermal breakpoint in the carboxylation rate at 15 °C, below which rates are lower than those of a cold-grown enzyme (Yamori et al., 2006). This is similar to the breakpoint evident in the MIMS data set presented here; however, the daytime temperature differential between plants grown for the MIMS (23 °C) and radiolabel (20 °C) plants was much smaller than the 15 °C differential used by Yamori et al. (2006). Further, the MIMS technique had a lower SC/O than radiolabel parameters at temperatures above 25 °C, and a higher value at temperatures below 25 °C, opposite to what Yamori et al. (2006) observed, suggesting that the kinetic differences between the MIIMS and radiolabel measurements were not due to temperature acclimation of Rubisco.
The possibility remains that the differences, particularly at cold temperatures, are due to methodology artifacts arising from differences in buffer composition. However, preparations of Rubisco for MIMS or radiolabel assays both include components known to affect Rubisco stability (i.e. DTT, MgCl2, and NaHCO3), albeit at different concentrations. It is also possible that either the MIMS or the radiolabel assays causes erroneous kinetic estimates at low temperatures; however, this uncertainty is difficult to explain given that breakpoints have been observed by different laboratories using varying methods and species (Badger and Collatz, 1977; Sage, 2002, Kubien et al., 2003; Sharwood et al., 2016). Therefore, additional analysis of diverse species with the MIMS system is needed to better understand if this is a technique- or species-specific phenomenon.
Nevertheless, breakpoints have persisted in the Rubisco literature for >40 years without sufficient explanation and warrant further investigations into their underlying causes. Badger and Collatz (1977) suggested that changes in the rate-limiting step of the reaction mechanism were brought about by conformational changes. If the elementary rate constants defining a specific parameter have different temperature responses then this could cause breakpoints if they cross over, causing a change in the rate-limiting step. The discussion below utilizes the currently accepted reaction mechanism of Rubisco (Fig. 1) and transition state theory to explore breakpoints as a function of changes in energy barriers to elementary reactions.
Rubisco reaction mechanisms and breakpoints
For the MIMS data, the breakpoints observed in kcatCO2 and kcatO2 could be due to changes in the rate-limiting step, as suggested by Badger and Collatz (1977). For example, kcatCO2 is a function of the rate of cleavage of the carboxylated intermediate (k8) and the rate of RuBP enolization (k9). This would mean that k8 and k9 have different a temperature response such that they cross over at around the breakpoint observed at 25 °C. However, modeling this change in rate-limiting steps due to different temperature responses cannot simultaneously explain the observed breakpoint in kcatCO2 and kcatO2, because the value of k5 defining the cleavage of the oxygenated intermediate is lower than k8. This means that k9 cannot cross over both k8 and k5 at 25 °C (Supplementary Fig. S2).
In order to model the reaction mechanism suggested by MIMS measurements, breakpoints in four elementary rate constants (k3, k5, k6, and k8) are needed to describe the breakpoints in kcatCO2, kcatO2, and SC/O (Fig. 7D, E). While it seems unlikely that such an entropy change could be driven by a conformation change in the enzyme brought about by such minimal changes in temperature, a similar change in entropy for kcatCO2 was observed between wild-type N. tabacum and a mutant (L335V) Rubisco (McNevin et al., 2007). This could suggest that the entropy changes proposed here may be possible given enzyme conformational changes with temperature.
The modeling presented here is largely based on isotope exchange studies, which suggest similar energy barriers between enolization (ΔG9‡) and cleavage (ΔG8‡). However, these measurements have been limited to 25 °C (Van Dyk and Schloss, 1986; Tcherkez et al., 2013), and extension of isotope exchange studies to temperature responses would help constrain how the elementary rate constants vary with temperature. Contrary to the above proposal that the cleavage transition state (k8) undergoes changes above and below 25 °C, is that Rubisco discrimination against 13CO2 is believed to remain constant with temperature (Christeller and Laing, 1976). If the rate of cleavage (k8) decreases, then the decarboxylation reaction (k7) may increase, or the k7/k8 ratio could increase, which would change Rubisco discrimination against 13CO2. Furthermore, the above modeling relies on the assumption that decarboxylation (k7) was negligible at all temperatures; therefore, changes in fractionation with temperature for an enzyme exhibiting breakpoints should help test the validity of these assumptions.
Conclusion
The measured temperature responses of Rubisco kinetic parameters were consistent between methods at and above 25 °C; however, there were thermal breakpoints at 25 °C in the MIMS data set for kcatCO2, kcatO2, and SC/O. Additionally, the radiolabel method using a single bicarbonate concentration showed a breakpoint for kcatCO2 probably caused by non-saturating CO2 concentrations at higher temperatures. Previous studies suggest that breakpoints are caused by either a change in the rate-limiting step of the reaction mechanism or deactivation of the enzyme at low temperatures. By modeling elementary steps of the reaction mechanism, we showed that neither cause is sufficient to explain simultaneous breakpoints in kcatCO2, kcatO2, and SC/O. Instead, breakpoints in the elementary rate constants would be needed. Because the modeling presented here is largely based on isotope exchange studies, moving forward, the temperature response of isotopic substitution experiments would advance our understanding of how elementary rate constants change in relation to one another with temperature.
Supplementary data
Supplementary data are available at JXB online.
Fig. S1. Temperature response of Rubisco parameters from Arabidopsis thaliana measured using radiolabel and MIMS methods.
Fig. S2. Two possible crossover models that result in breakpoints for kcatCO2 for MIMS data.
Fig. S3. CO2 response curves from 10 °C to 40 °C showing measured values from the radiolabel and MIMS curve fitting methods.
Table S1. pKa values used in calculations.
Table S2. Average Rubisco kinetic parameters measured at each temperature
with ±SE.
Table S3. The ΔH‡ and ΔS‡ calculated for the ΔG‡ values presented in Fig. 5 using Equation 18.
Table S4. The ΔH‡ and ΔS‡ calculated for the ΔG‡ values presented in Fig. 6 using Equations 16 and 17.
Table S5. The ΔH‡ and ΔS‡ calculated for the ΔG‡ values presented in Fig. 7 using Equations 9–15.
Acknowledgements
This work was supported by the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, Department of Energy (grant no. DE-SC0001685), the National Science Foundation (Major Research Instrumentation grant no. 0923562), the National Science and Engineering Research Council of Canada (Discovery grant no. 327103; and PGS-D scholarship to APC), and the Seattle chapter of the Achievement Rewards for College Scientists Foundation (RAB). The authors would like to thank Chuck Cody for maintaining plant growth facilities, and current members of Cousins Lab for helpful and insightful discussions. The authors have no conflicts of interest to declare.
Author contributions
ABC and DSK proposed the original concept and design for the project; RAB and APC performed the experiments and data analysis; RAB wrote the article with the contributions of all the authors; ABC supervised and complemented the writing.
References
- Andrews TJ, Lorimer GH, Tolbert NE. 1973. Ribulose diphosphate oxygenase. I. Synthesis of phosphoglycolate by fraction-1 protein of leaves. Biochemistry 12, 11–18. [DOI] [PubMed] [Google Scholar]
- Badger MR, Collatz GJ. 1977. Studies on the kinetic mechanism of ribulose-1,5-bisphosphate carboxylase and oxygenase reactions, with particular reference to the effect of temperature on kinetic parameters. Carnegie Institute of Washington, Yearbook 76, 355–361. [Google Scholar]
- Björkman O, Pearcy RW. 1970. Effect of growth temperature on the temperature dependence of photosynthesis in vivo and on CO2 fixation by carboxydismutase in vitro in C3 and C4 species. Carnegie Institution of Washington, Yearbook 70, 511–520. [Google Scholar]
- Bowes G, Ogren WL, Hageman RH. 1971. Phosphoglycolate production catalyzed by ribulose diphosphate carboxylase. Biochemical and Biophysical Research Communications 45, 716–722. [DOI] [PubMed] [Google Scholar]
- Boyd RA, Gandin A, Cousins AB. 2015. Temperature responses of C4 photosynthesis: biochemical analysis of rubisco, phosphoenolpyruvate carboxylase, and carbonic anhydrase in Setaria viridis. Plant Physiology 169, 1850–1861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z, Spreitzer RJ. 1992. How various factors influence the CO2/O2 specificity of ribulose-1,5-bisphosphate carboxylase/oxygenase. Photosynthesis Research 31, 157–164. [DOI] [PubMed] [Google Scholar]
- Christeller JT, Laing WA. 1976. Isotope discrimination by ribulose 1,5-diphosphate carboxylase: no effect of temperature or HCO3 concentration. Plant Physiology 57, 580–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cousins AB, Ghannoum O, VON Caemmerer S, Badger MR. 2010. Simultaneous determination of Rubisco carboxylase and oxygenase kinetic parameters in Triticum aestivum and Zea mays using membrane inlet mass spectrometry. Plant, Cell & Environment 33, 444–452. [DOI] [PubMed] [Google Scholar]
- Crafts-Brander SJ, Salvucci ME. 2000. Rubisco activase constrains the photosynthetic potential of leaves at high temperature and CO2. Proceedings of the National Academy of Sciences, USA 97, 13430–13435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies RB. 1987. Hypothesis testing when a nuisance parameter is present only under the alternatives. Biometrika 74, 33–43. [Google Scholar]
- Edsall JT, Wyman J. 1958. Carbon dioxide and carbonic acid. In: Edsall JT, J Wyman eds. Biophysical chemistry. New York: Academic Press, 550–590. [Google Scholar]
- Farquhar GD. 1979. Models describing the kinetics of ribulose biphosphate carboxylase-oxygenase. Archives of Biochemistry and Biophysics 193, 456–468. [DOI] [PubMed] [Google Scholar]
- Flexas J, Ortuño MF, Ribas-Carbo M, Diaz-Espejo A, Flórez-Sarasa ID, Medrano H. 2007. Mesophyll conductance to CO2 in Arabidopsis thaliana. New Phytologist 175, 501–511. [DOI] [PubMed] [Google Scholar]
- Galmés J, Hermida-Carrera C, Laanisto L, Niinemets Ü. 2016. A compendium of temperature responses of Rubisco kinetic traits: variability among and within photosynthetic groups and impacts on photosynthesis modeling. Journal of Experimental Botany 67, 5067–5091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurwitz J, Jakoby WB, Horecker BL. 1956. On the mechanism of CO2 fixation leading to phosphoglyceric acid. Biochimica et Biophysica Acta 22, 194–195. [DOI] [PubMed] [Google Scholar]
- Jordan DB, Ogren WL. 1981. A sensitive assay procedure for simultaneous determination of ribulose-1,5-bisphosphate carboxylase and oxygenase activities. Plant Physiology 67, 237–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kane HJ, Viil J, Entsch B, Paul K, Morell MK, Andrews TJ. 1994. An improved method for measuring the CO2/O2 specificity of ribulose-bisphosphate carboxylase-oxygenase. Australian Journal of Plant Physiology 21, 449–461. [Google Scholar]
- Kubien DS, Brown CM, Kane HJ. 2011. Quantifying the amount and activity of rubisco in leaves. Methods in Molecular Biology 684, 349–362. [DOI] [PubMed] [Google Scholar]
- Kubien DS, von Caemmerer S, Furbank RT, Sage RF. 2003. C4 photosynthesis at low temperature. A study using transgenic plants with reduced amounts of Rubisco. Plant Physiology 132, 1577–1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubien DS, Whitney SM, Moore PV, Jesson LK. 2008. The biochemistry of Rubisco in Flaveria. Journal of Experimental Botany 59, 1767–1777. [DOI] [PubMed] [Google Scholar]
- McNevin DB, Badger MR, Kane HJ, Farquhar GD. 2006. Measurement of (carbon) kinetic isotope effect by Rayleigh fractionation using membrane inlet mass spectrometry for CO2-consuming reactions. Functional Plant Biology 33, 1115–1128. [DOI] [PubMed] [Google Scholar]
- McNevin DB, Badger MR, Whitney SM, von Caemmerer S, Tcherkez GG, Farquhar GD. 2007. Differences in carbon isotope discrimination of three variants ofd-ribulose-1,5-bisphosphate carboxylase/oxygenase reflect differences in their catalytic mechanisms. Journal of Biological Chemistry 282, 36068–36076. [DOI] [PubMed] [Google Scholar]
- Muggeo VM. 2003. Estimating regression models with unknown break-points. Statistics in Medicine 22, 3055–3071. [DOI] [PubMed] [Google Scholar]
- Muggeo VM. 2008. Segmented: an R package to fit regression models with broken-line relationships. R News 8, 20–25. [Google Scholar]
- O’Leary MH, Madhavan S, Paneth P. 1992. Physical and chemical basis of carbon isotope fractionation in plants. Plant, Cell & Environment 15, 1099–1104. [Google Scholar]
- Paul K, Morell MK, Andrews TJ. 1991. Mutations in the small subunit of ribulosebisphosphate carboxylase affect subunit binding and catalysis. Biochemistry 30, 10019–10026. [DOI] [PubMed] [Google Scholar]
- Perdomo JA, Cavanagh AP, Kubien DS, Galmés J. 2015. Temperature dependence of in vitro Rubisco kinetics in species of Flaveria with different photosynthetic mechanisms. Photosynthesis Research 124, 67–75. [DOI] [PubMed] [Google Scholar]
- Pittermann J, Sage RF. 2000. Photosynthetic performance at low temperature of Bouteloua gracilis Lag., a high-altitude C4 grass from the Rocky Mountains, USA. Plant, Cell & Environment 23, 811–823. [Google Scholar]
- R Core Team 2013. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing, http://www.R-project.org/ [Google Scholar]
- Ruuska S, Andrews TJ, Badger MR, Hudson GS, Laisk A, Price GD, von Caemmerer S. 1998. The interplay between limiting processes in C-3 photosynthesis studied by rapid-response gas exchange using transgenic tobacco impaired in photosynthesis. Australian Journal of Plant Physiology 25, 859–870. [Google Scholar]
- Sage RF. 2002. Variation in the kcat of Rubisco in C3 and C4 plants and some implications for photosynthetic performance at high and low temperature. Journal of Experimental Botany 53, 609–620. [DOI] [PubMed] [Google Scholar]
- Sage RF, Santrucek J, Grise DJ. 1995. Temperature effects on the photosynthetic response of C3 plants to long-term CO2 enrichment. Vegetatio 121, 67–77. [Google Scholar]
- Sander R. 2015. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmospheric Chemistry and Physics 15, 4399–4981. [Google Scholar]
- Sharwood RE, Ghannoum O, Kapralov MV, Gunn LH, Whitney SM. 2016. Temperature responses of Rubisco from Paniceae grasses provide opportunities for improving C3 photosynthesis. Nature Plants 2, 16186. [DOI] [PubMed] [Google Scholar]
- Shay PE, Kubien DS. 2013. Field analysis of photoprotection in co-occurring cool climate C(3) and C(4) grasses. Physiologia Plantarum 147, 316–328. [DOI] [PubMed] [Google Scholar]
- Spreitzer RJ, Salvucci ME. 2002. Rubisco: structure, regulatory interactions, and possibilities for a better enzyme. Annual Review of Plant Biology 53, 449–475. [DOI] [PubMed] [Google Scholar]
- Tcherkez G. 2013. Modelling the reaction mechanism of ribulose-1,5-bisphosphate carboxylase/oxygenase and consequences for kinetic parameters. Plant, Cell & Environment 36, 1586–1596. [DOI] [PubMed] [Google Scholar]
- Tcherkez G. 2016. The mechanism of Rubisco-catalysed oxygenation. Plant, Cell & Environment 39, 983–997. [DOI] [PubMed] [Google Scholar]
- Tcherkez GG, Bathellier C, Stuart-Williams H, Whitney S, Gout E, Bligny R, Badger M, Farquhar GD. 2013. D2O solvent isotope effects suggest uniform energy barriers in ribulose-1,5-bisphosphate carboxylase/oxygenase catalysis. Biochemistry 52, 869–877. [DOI] [PubMed] [Google Scholar]
- Tcherkez GG, Farquhar GD, Andrews TJ. 2006. Despite slow catalysis and confused substrate specificity, all ribulose bisphosphate carboxylases may be nearly perfectly optimized. Proceedings of the National Academy of Sciences, USA 103, 7246–7251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tieszen L, Sigurdson D. 1973. Effect of temperature on carboxylase activity and stability in some Calvin cycle grasses from the arctic. Arctic, Antarctic, and Alpine Research 5, 59–66. [Google Scholar]
- Ubierna N, Gandin A, Boyd RA, Cousins AB. 2017. Temperature response of mesophyll conductance in three C4 species calculated with two methods: 18O discrimination and in vitro Vpmax. New Phytologist 214, 66–80. [DOI] [PubMed] [Google Scholar]
- Van Dyk DE, Schloss JV. 1986. Deuterium isotope effects in the carboxylase reaction of ribulose-1,5-bisphosphate carboxylase/oxygenase. Biochemistry 25, 5145–5156. [Google Scholar]
- von Caemmerer S. 2000. Biochemical models of leaf photosynthesis. Collingwood, Australia: CSIRO Publishing. [Google Scholar]
- Walker B, Ariza LS, Kaines S, Badger MR, Cousins AB. 2013. Temperature response of in vivo Rubisco kinetics and mesophyll conductance in Arabidopsis thaliana: comparisons to Nicotiana tabacum. Plant, Cell & Environment 36, 2108–2119. [DOI] [PubMed] [Google Scholar]
- Weise SE, Carr DJ, Bourke AM, Hanson DT, Swarthout D, Sharkey TD. 2015. The arc mutants of Arabidopsis with fewer large chloroplasts have a lower mesophyll conductance. Photosynthesis Research 124, 117–126. [DOI] [PubMed] [Google Scholar]
- Whitney SM, Houtz RL, Alonso H. 2011. Advancing our understanding and capacity to engineer nature’s CO2-sequestering enzyme, Rubisco. Plant Physiology 155, 27–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamori W, Suzuki K, Noguchi K, Nakai M, Terashima I. 2006. Effects of Rubisco kinetics and Rubisco activation state on the temperature dependence of the photosynthetic rate in spinach leaves from contrasting growth temperatures. Plant, Cell & Environment 29, 1659–1670. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.