Abstract
Cell-free transcription–translation provides a simplified prototyping environment to rapidly design and study synthetic networks. Despite the presence of a well characterized toolbox of genetic elements, examples of genetic networks that exhibit complex temporal behavior are scarce. Here, we present a genetic oscillator implemented in an E. coli-based cell-free system under steady-state conditions using microfluidic flow reactors. The oscillator has an activator–repressor motif that utilizes the native transcriptional machinery of E. coli: the RNAP and its associated sigma factors. We optimized a kinetic model with experimental data using an evolutionary algorithm to quantify the key regulatory model parameters. The functional modulation of the RNAP was investigated by coupling two oscillators driven by competing sigma factors, allowing the modification of network properties by means of passive transcriptional regulation.
Keywords: oscillator, cell-free systems, synthetic biology, sigma factors, competition-induced regulation
Synthetic biology employs synthetic genetic networks to re-engineer organisms for a range of applications. Synthetic genetic circuits have been designed to display higher-order temporal functions,1−4 perform logic operations in cells,5,6 and produce heterologous proteins in microorganisms.7−10 A major difficulty faced by synthetic biology concerns the implementation of synthetic genetic networks in living organisms, which presents an unnatural load for the host organism and affects the cell growth, often leading to the poor performance of engineered circuits.11
Cell-free protein synthesis (TX-TL) has the potential to serve as a biochemical breadboard that allows for the rapid prototyping of genetic networks without interference from cellular hosts.12,13 Numerous works have focused on the optimization of protein expression from bacterial cell-free systems,14−18 which has resulted in a well-characterized toolbox of genetic elements comprising a range of transcriptional and translational regulators.19−21 This toolbox extends the variety of synthetic genetic networks that can be constructed by allowing the use of essential bacterial machinery that would be difficult to achieve in vivo (E. coli), as they are important to the native functionality of the cell. Synthetic cascades, which use transcriptional machinery such as the T7 RNA polymerase (RNAP) and bacterial RNAP, have been engineered using this cell-free toolbox.19,20,22 Since such circuits exhibit linear behavior, they can be prototyped in batch TX-TL conditions, as their functioning does not depend on the balance of rates between the individual steps. To engineer networks that exhibit complex behavior—such as oscillations—batch conditions are insufficient primarily because the resources available for the synthesis of mRNAs and proteins are finite and the utilization of these resources results in byproducts that can inhibit critical TX-TL components.20 To extend the lifetime of TX-TL reactions, microfluidic platforms have been designed wherein the TX-TL components can be replenished, thereby creating an open system wherein the transcription and translation rates are sustained in a steady state.
Karzbrun et al. studied oscillatory behavior in continuous TX-TL reactions by immobilizing DNA networks within two-dimensional microfluidic compartments. Separated from the central flow channel, their system relied on the diffusion of TX-TL reagents components through capillary channels to reach the DNA compartments, enabling the dynamics of a cell-free oscillator to be tuned by changing the dimensions thereof.23 Niederholtmeyer et al. utilized pneumatically controlled microfluidic flow reactors to study numerous ring oscillators under steady-state TX-TL conditions, showing that the qualitative and quantitative performance of the oscillators in vitro reflect those in in vivo conditions.24
Despite the availability of a well characterized cell-free toolbox and long-lived TX-TL platforms, the full repertoire of available elements has not been used to engineer higher-order genetic networks. In order to expand the toolbox, it is necessary to implement the toolbox elements to design complex genetic networks, such as oscillators, in open systems where key TX-TL resources are not limiting. Oscillatory networks are important as they control key aspects of life such as circadian rhythms, cell division, metabolism and cell signaling.25 However, engineering oscillators is challenging because their design requires an optimal balance of rates of the various regulatory processes involved.26 To aid the systematic engineering of oscillators, mathematical models can be used to provide a mechanistic understanding of the system and facilitate the design of higher-order network topologies.24 In our research, we focused on engineering a synthetic genetic oscillator in an open TX-TL system, leveraging an important regulatory component of E. coli machinery: the endogenous RNAP and its associated sigma factors. Bacterial RNAP is a multisubunit enzyme that uses sigma factors to help in transcription initiation.27 Despite the regulatory role of sigma factors in vivo being well understood,28−30 their potential in engineering complex genetic networks is only starting to be realized. Recently it has been shown that bacteria use sigma factors to alter the transcriptional landscape under stressed conditions by time-sharing the core RNAP, thereby modulating its function.31 Bervoets et al. have recently engineered a sigma factor toolbox belonging to B. subtilis as an orthogonal transcriptional control mechanism that can be used in other bacterial species such as E. coli.32 Karzbrun et al. and Tayar et al. have implemented sigma-factor based oscillators in TX-TL systems to demonstrate the emergence of collective behavior such as entrainment and synchronization between coupled oscillators.23,33 Since sigma factors allow convenient reprogramming of the transcriptional machinery and exhibit versatile properties with respect to binding to RNAP and DNA, using them as regulatory molecules in oscillators will improve our ability to modulate systems-level behavior of genetic networks. Furthermore, the competition of sigma factors for the core RNAP allows for the facile coupling of multiple networks driven by different sigma factors and thereby enables the engineering of synthetic genetic networks displaying higher-order regulatory functions.
Here, we present the characterization of a two-component oscillator with an activator–repressor motif and a delayed negative feedback topology based on genetic elements from the E. coli cell-free Toolbox 2.0.20 Our initial network (Figure 1) is based on the sigma factor 28 (σ28) serving as the activator, the C1 protein serving as a repressor, and deGFP as a reporter. We have quantitatively characterized every genetic element as well as the behavior of the network, by optimizing a mathematical model with experimental data using an evolutionary algorithm. This has enabled us to map the characteristics and behavior of this oscillator. Subsequently we replaced σ28 with sigma factor 19 (σ19) to modify the oscillatory regime of the network and proceeded to investigate the influence of competition-driven passive transcriptional control between sigma factors on network behavior by coupling the two oscillators. All oscillators were characterized experimentally in a E. coli-based TX-TL system operating under steady-state conditions in microfluidic flow reactors.12
Figure 1.
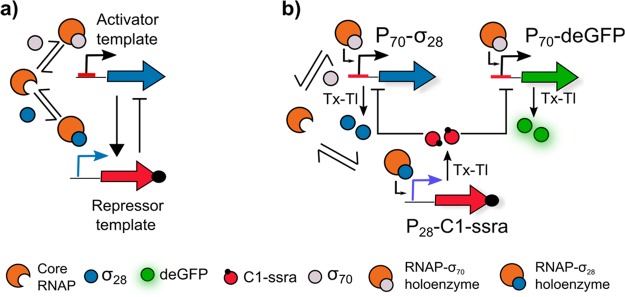
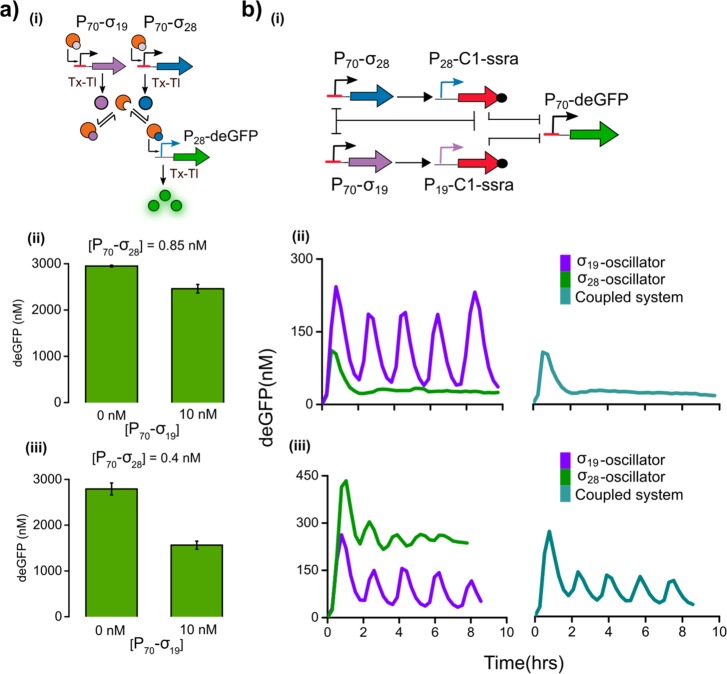
(a) The oscillator has an activator–repressor motif with the σ28 and C1 serving as activator and repressor, respectively. Critical to the functioning of the oscillator is the competitive binding between the two sigma factors to the core RNAP to form their respective holoenzymes. (b) Schematic representation of the σ28-oscillator. The network topology comprises three DNA constructs: P70-σ28, P28-C1-ssra, and P70-deGFP. The σ70 binds to the RNAP to form the RNAP-σ70 holoenzyme, which binds to the P70 promoter and initiates the expression of σ28 and deGFP. σ28 competitively binds to RNAP to form the RNAP-σ28 holoenzyme, which binds to the P28 promoter and initiates the expression of C1-ssra. C1-ssra exclusively binds to the P70 promoter and represses the production of σ28 and deGFP.
Results and Discussion
Bottom-Up Engineering of the σ28-Oscillator
The oscillator presented here is based on a delayed negative feedback topology (Figure 1a) as introduced by Stricker et al.(4) The oscillatory network constitutes an activator–repressor motif, as also found in several natural systems,34 and utilizes the σ28 as an activator and the C1 protein as the repressor (Figure 1b). In contrast to previous works, which have been performed in diffusion-limited TX-TL environments,23,33 we have implemented this design under well-mixed conditions in order to study fundamental mechanisms in the system such as the asymmetric competition between sigma factors for core RNAP. This asymmetric competition determines the amount of holoenzyme of each sigma factor—the complex formed by the association of sigma factor and RNAP—available to transcribe genes from their respective promoters.19,29 Furthermore, the sharing of critical catalytic resources, such as RNAP, in biochemical circuits plays an important role in affecting network behavior.
The oscillatory network comprises three DNA constructs: P70-σ28, P28-C1-ssra, and P70-deGFP (Figure 1b). The expression of σ28 is regulated by the P70 promoter. Transcription from this promoter is initiated when sigma factor 70 (σ70) binds to the core bacterial RNAP to form the RNAP-σ70 holoenzyme, which can subsequently bind to the P70 promoter. Once expressed, the σ28 protein binds competitively to the core RNAP to form the RNAP-σ28 holoenzyme and activates expression of genes under control of the P28 promoter. This promoter regulates the production of the λ phage protein C1, which binds exclusively at the P70 promoter, thereby inhibiting the transcription and the eventual production of σ28. Additionally, the C1 protein contains a C-terminal ssra tag for targeted protein degradation by ClpXP proteases. These proteases, along with the σ70, bacterial RNAP, and the necessary translational machinery (ribosomes, elongation factors, etc.) are present in the E. coli cell lysate.16 Finally a reporter protein, deGFP19,29—also under the control of P70 promoter—is incorporated as a fluorescent readout.
Since designing oscillators is a challenging process and involves a fine balance of rates among regulatory components, we implemented an ordinary differential equation (ODE)-based mathematical model to quantify our system and inform our experiments. We described the network using a kinetic model (SI, eq 1.1–1.11) that takes into consideration the four key processes: (i) transcription and translation of each DNA construct, (ii) competition between σ28 and σ70 for RNAP, (iii) repression by the C1 protein, and (iv) dilution (under steady-state TX-TL conditions) and degradation of mRNA and protein species. Having determined an upper and lower boundary for each model parameter based on literature, we sampled the parameter space using Latin Hypercube Sampling (LHS) to test if this motif yielded oscillatory dynamics under steady-state TX-TL conditions (Figure S1). The analysis revealed that 29% of the sampled parameter sets showed oscillations, indicating that the motif is robust in its ability to oscillate (Figure S1a).
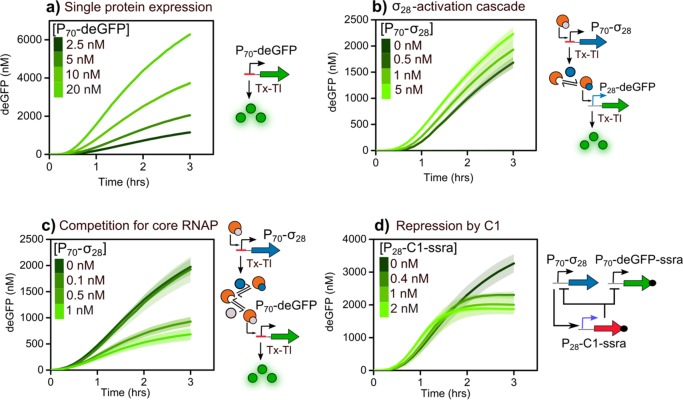
In order to identify individual parameters in our model,35 the key regulatory mechanisms of our network were implemented separately under batch TX-TL conditions (Figure 2). First, we added increasing concentrations of the P70-deGFP template to the TX-TL reaction mix (Figure 2a). We observed an increased expression of deGFP upon increasing template concentration confirming the presence of σ70 in the lysate. Next, we implemented a two-step cascade to test transcriptional activation by σ28 (Figure 2b) by adding increasing amounts of P70-σ28 template to a fixed concentration of P28-deGFP template. No deGFP fluorescence was observed in the absence of the P70-σ28 template indicating the absence of σ28 in the lysate. We observed deGFP fluorescence upon addition of 0.5 nM of P70-σ28 template indicating the production of functional σ28, which activates protein production from the P28 promoter. The onset of deGFP expression and the final yield did not improve remarkably upon increasing the P70-σ28 template concentration from 0.5 to 5 nM, highlighting the potency of σ28 as a transcriptional activator. Since the design of the network involves two sigma factors competing for the RNAP, we quantified the extent of this competition by adding increasing amounts of P70-σ28 template to a fixed concentration of P70-deGFP template (Figure 2c). The sequestration of core RNAP by σ28 and the subsequent decrease in deGFP expression serves as an indirect measurement for sigma factor competition. We observed that the addition of 0.5 nM of the P70-σ28 template is enough to produce sufficient σ28 to outcompete σ70 for the core RNAP, reducing the deGFP yield by approximately 50% when compared to the control (without any P70-σ28 template). To verify that this decrease resulted from competition between sigma factors and not from depletion of TX-TL resources, we repeated the same experiment using the P70-σ19 template instead of the P70-σ28 template (Figure S2a). The addition of 1 nM of the P70-σ19 template did not result in any significant reduction in the expression of the deGFP, indicating that the previously noted decrease is indeed caused by the competition of σ28 with σ70 for the core RNAP and is not the result of depletion of resources. The final regulatory mechanism tested is the transcriptional repression by C1 (Figure 2d). We fixed the concentration of P70-deGFP-ssra template at 5 nM and P70-σ28 template at 0.1 nM, thus ensuring that any decrease in the expression yield of deGFP is the result of inhibition via the C1 protein as opposed to competition from σ28, and added increasing concentrations of P28-C1-ssra template. We observed that the C1 protein inhibits protein production from the P70 promoter, thereby decreasing the yields of deGFP for concentrations of P28-C1-ssra template as low as 0.4 nM.
Figure 2.
Time traces of deGFP production as readout for the key regulatory mechanisms of the σ28-oscillator under batch TX-TL conditions. (a) Linear DNA template (P70-deGFP) at different concentrations. (b) Two-step σ28-activation cascade. Increasing concentrations of P70-σ28 template were added to 5 nM of P28-deGFP template. Expression of σ28 from P70-σ28 activates deGFP production. (c) Expression from P70-deGFP under competition for core RNAP between sigma factors σ70 and σ28. Increasing concentrations of P70-σ28 template were added to 5 nM of P70-deGFP. (d) Transcriptional repression by C1. The concentrations of P70-deGFP-ssra and P70-σ28 were fixed at 5 and 0.1 nM, respectively, to which increasing concentrations of P28-C1-ssra template were added. Shaded error bands are standard error of three separate measurements.
Since the lifetime of reactions in batch TX-TL conditions is limited, we used the initial expression kinetics to provide us with estimates of reaction rates and binding constants. We implemented an evolutionary algorithm (Figure S3) adapted from Smith et al.(36) to evolve model parameters to fit the batch TX-TL data (Figure S4). Using this initial parameter (Table S1) set we predicted an oscillatory regime for our network described by three experimentally controlled parameters—P70-σ28 template concentration, P28-C1-ssra template concentration, and refresh rate (vide infra)—with experimentally feasible upper and lower boundaries for each parameter, which guided our initial experiments in steady-state TX-TL conditions (Figure S5).
Steady-state TX-TL experiments were conducted in a PDMS-based, pneumatically controlled, bilayer microfluidic chip.12 Each chip comprises eight independent, 11 nL, ring reactors in which unique TX-TL reactions can be performed. The periodic inflow of fresh TX-TL reaction solutions and the simultaneous outflow of used reagents allows the system to operate such that the transcription and translation rates are in steady state and extends the lifetime of TX-TL reactions. The period between subsequent dilutions (injection of fresh reagents into reactor while removing used reagents) and the volume fraction of the reactor being replenished per dilution is represented by the refresh rate (Table S3).
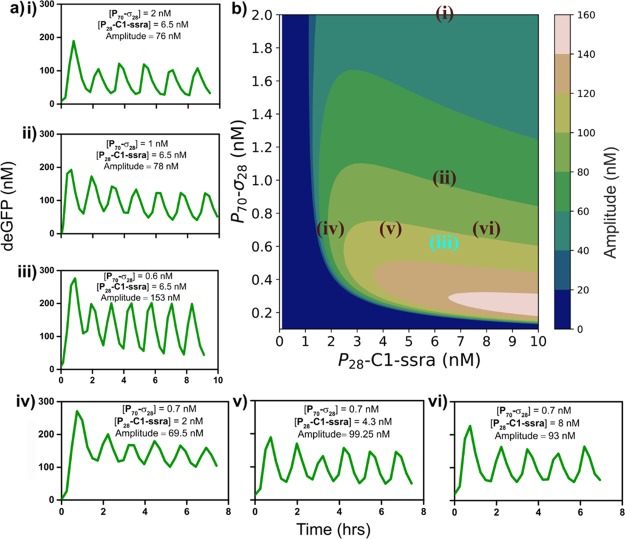
Variation of the control parameters regulates the transition of the network through three qualitatively different outputs: sustained oscillations, damped oscillations, and single-peak behavior under steady-state TX-TL conditions (Figure 3a(i–vi) and Figure S6). While the period of oscillations varied marginally (between 74 and 88 min), the amplitude of the oscillations showed significant variations, with the largest oscillation amplitude being observed at P70-σ28 and P28-C1-ssra concentrations of 0.6 and 6.5 nM, with a refresh rate of 0.026 min–1 (Figure 3a(iii)). Lowering the refresh rate for comparable concentrations of P70-σ28 and P28-C1-ssra templates resulted in the dampening of oscillations (Figure S6a). Increasing the concentration of P28-C1-ssra template, for a fixed P70-σ28 concentration and refresh rate, increased the amplitude of damped oscillations (Figure S6b,c). These results indicate that since σ28 is a transcriptionally strong sigma factor (Figure 2b) it produces C1 protein rapidly and the refresh rate needs to be sufficiently high to remove σ28 thereby generating the sufficient time delay for the negative feedback needed to observe oscillations. These results are in general agreement with our LHS analysis and previous work on similar systems.33 Increasing the concentrations of the P70-σ28 and P28-C1-ssra templates to 3 and 10 nM, respectively, results in a loss of oscillations and leads to a single transient peak (Figure S6e,f).
Figure 3.
Characterization of the σ28-oscillator. (a) (i–vi) Experimentally obtained deGFP time courses for the σ28-oscillator exhibiting sustained oscillations under steady-state TX-TL conditions for various values of [P70-σ28, P28-C1-ssra]. (b) Contour plot showing the model-predicted amplitude of oscillations mapped on to [P70-σ28, P28-C1-ssra] phase space for a given refresh rate (0.026 min–1). All points in a(i–vi) have been mapped on to the contour plot in (b). Since a(iii) was used to re-estimate model parameters and obtain the contour plot, it has been shown in blue. P70-deGFP template concentration and refresh rate were fixed at 8 nM and 0.026 min–1, respectively, in all experiments.
Characterization and Modification of Oscillator Properties
Although our initial parameter estimates from batch TX-TL data aided in finding an oscillatory regime, they did not fully capture the dynamics of the oscillator completely. To improve the accuracy of our model parameters, we re-estimated them by fitting the model to the steady-state TX-TL data using a data point within (Figure 3a(iii)) and outside (Figure S6f) the oscillating regime (Figure S7, Table S1). Using this optimized parameter set we characterized the behavior of the σ28-oscillator by simulating a control parameter space consisting of 15,625 combinations of the control parameters and estimated the subset of this control parameter space for which the model predicts stable oscillations (Figure S8a). The amplitude of oscillations, as predicted by the model, were plotted against the P70-σ28 and P28-C1-ssra template concentrations for a fixed refresh rate (0.026 min–1) (Figure 3b). In order to test the predictive ability of the model, we compared the predicted and observed oscillation amplitudes for the sustained oscillations in Figure 3a. We found that the model predicts a decrease in amplitude of oscillations with increasing P70-σ28 template concentrations, for a constant P28-C1-ssra template concentration (Figure 3b). Upon increasing the concentration of P70-σ28 template in the experiments from 1 to 2 nM (Figure 3a(ii) and (i)), for a P28-C1-ssra concentration of 6.5 nM, we observed a decrease in the amplitude of oscillations (78 and 76 nM), although the extent of decrease was much less compared to the model prediction. Furthermore, the model predicts that increasing the P28-C1-ssra template concentration, for a fixed concentration of P70-σ28 template, from 2 to 4.3 nM should lead to an increase in oscillation amplitude and upon increasing the concentration further to 8 nM should marginally decrease the oscillation amplitudes. Upon experimental verification, we observed a similar trend (Figure 3a(iv,v,vi)) wherein the amplitude increases from 69.5 nM (P28-C1-ssra = 2 nM) to 99.25 nM (P28-C1-ssra = 4.3 nM) and then decreases marginally to 93 nM (P28-C1-ssra = 8 nM).
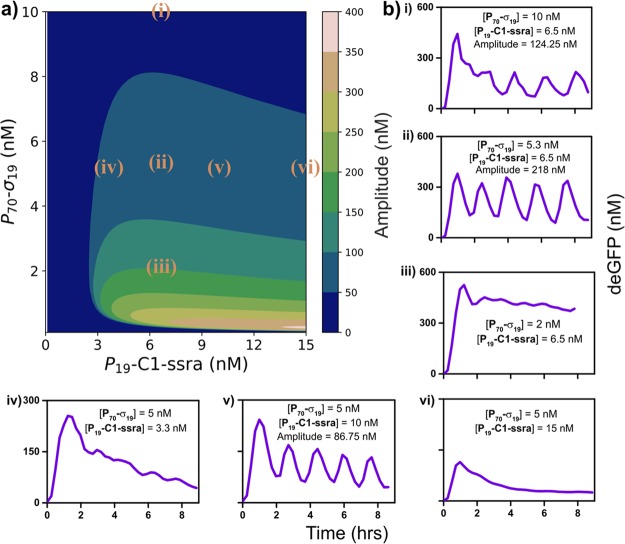
A sensitivity analysis was performed to assess the impact of changing a single system parameter on the oscillation amplitude and size of the oscillating regime (Figure S9 and S10). The analysis indicated that decreasing the competitive strength of the activator to the RNAP as a possible modification to increase the size of the oscillatory regime and the robustness of oscillations. Since the E. coli transcriptional machinery is composed of a variety of sigma factors, each with different affinities for the core RNAP, we replaced σ28 with σ19 as the activator. σ19 has been reported to be transcriptionally less potent and a weaker competitor for RNAP when compared to σ28,20 which we confirmed in batch TX-TL experiments (Figure S2). In order to compare the behavior of the two oscillators we repeated the simulations from Figures S8a and 3b by assuming a lower value for σ19 binding and accounting for increased expression dynamics that was observed in the new TX-TL mixture batch.37 Herein, it was found that the model predicts a larger oscillatory subset, in particular a broader activator template concentration range, when using σ19 as the activator in the network (Figure S11a). When characterizing the behavior of the σ19 oscillator in a phase space with a fixed refresh rate (0.026 min–1) (Figure 4a), we found that it indeed exhibited oscillations for a higher range of P70-σ19 template concentrations (from 5 to 10 nM) compared to the σ28-oscillator (from 0.6 to 2 nM) (Figure 4b(i–ii) and Figure 3). However, the model fails to accurately capture the P70-σ19 template concentration range for which the network exhibits oscillations, as it also predicts oscillations for the conditions in Figure 4b(iii). Variation of the P19-C1-ssra template concentration, while fixing the P70-σ19 template concentration at 5 nM, yielded sustained oscillations for a concentration of 10 nM, while at 3.3 and 15 nM the system does not display any oscillations despite model predictions indicating otherwise (Figure 4b(iv–vi)).
Figure 4.
Characterization of the σ19-oscillator. (a) Contour plot showing the model-predicted oscillation amplitudes mapped on to the [P70-σ19,P19-C1-ssra] phase space for a given refresh rate (0.026 min–1). (b) (i–vi) Experimentally obtained deGFP time courses for the σ19-oscillator exhibiting oscillatory and non-oscillatory behavior for various values of [P70-σ19, P19-C1-ssra]. All points have been mapped on to the contour plot (a). P70-deGFP template concentration and refresh rate were fixed at 8 nM and 0.026 min–1, respectively, in all experiments.
Effect of Passive Transcriptional Control on a Coupled Oscillator
As mentioned above, multiple sigma factors compete for the same pool of core RNAP, and thus an increase in activity of one sigma factor can exert an indirect repression on the binding of another sigma factor to the RNAP.38 This mechanism is referred to as passive transcriptional regulation.19 Although present between σ28/σ19 and σ70 in the individual oscillators, this effect is difficult to investigate as the concentration of σ70 is fixed in the lysate. To investigate the extent of such competition-induced regulation among σ28 and σ19, we allowed the sigma factors to directly compete for the core RNAP in batch TX-TL, as shown in Figure 5a(i). Comparing deGFP fluorescence in the absence or presence of 10 nM P70-σ19, we observed that with 0.85 nM of P70-σ28 template, the σ19 only marginally decreases deGFP yield (Figure 5a(ii)). In contrast, lowering the concentration of P70-σ28 template from 0.85 to 0.4 nM resulted in a decrease of approximately 40% in yield of deGFP due to passive transcriptional repression on the σ28-activation cascade by σ19 (Figure 5a(iii)).
Figure 5.
(a) (i) Schematic diagram showing the passive transcriptional regulation exerted by σ19 on the σ28 activation cascade resulting in the decrease of the deGFP yield due to competition for RNAP by σ19. (ii, iii) End-point measurement of deGFP yields for the batch TX-TL reactions shown for two different concentrations of P70-σ28: 0.85 and 0.4 nM, respectively. The concentration of P28-deGFP DNA template was fixed at 5 nM, and the concentration of P70-σ19 was varied between 0 and 10 nM. (b) (i) Schematic of the coupled oscillatory network. σ19 and σ28 regulate the expression of the C1 protein that inhibits the expression of both sigma factors and deGFP. (ii, iii) Experimentally obtained deGFP time traces of the σ28-oscillator, σ19-oscillator, and the coupled system under steady-state TX-TL conditions. The concentration of P70-deGFP, P19-C1-ssra, and P70-σ19 were kept fixed at 8, 6.5, and 10 nM, respectively. The respective concentrations of P70-σ28 and P28-C1-ssra were (ii) 0.85 and 6.5 nM and (iii) 0.4 and 1.5 nM.
In genetic networks, competition for common catalytic resources has been shown to alter network dynamics.39,40 Coupling the two oscillators within the same network, allows σ19 and σ28 to drive their respective networks while simultaneously competing for core RNAP. Both sigma factors produce C1 protein that represses the expression of σ19, σ28, and deGFP from their respective templates (Figure 5b(i)). Although multiple factors govern the behavior of such a system, a crucial factor is the competition-induced transcriptional regulation between σ28 and σ19. Under steady-state TX-TL conditions, we observed that for a concentration of 0.85 nM of P70-σ28 the σ28-oscillator displayed a single-peak behavior and at 10 nM of P70-σ19 the σ19-oscillator showed sustained oscillations. Upon coupling the networks, we found that the system exhibited single-peak behavior (Figure 5b(ii)). However, by decreasing the concentration of the P70-σ28 to 0.4 nM we found that the σ28-oscillator exhibited damped oscillations and the coupled system showed sustained oscillations (Figure 5b(iii)). This result indicates that decreasing the P70-σ28 concentration from 0.85 to 0.4 nM allows the system to enter a regime where σ19 can better compete for the core RNAP, thereby exerting greater passive transcriptional control over σ28, leading to the emergence of sustained oscillatory behavior in the coupled system. To ensure that the preservation of oscillations in the coupled system results from the coupling of oscillators and is not a consequence of extraneous factors such as pressure fluctuations within the microfluidic setup, we coupled the oscillators under conditions for which the isolated σ28-oscillator exhibited no oscillations—sustained or damped—while the σ19-oscillator exhibited sustained oscillations (Figure S12). The concentrations of the P70-σ28 and P70-σ19 templates were identical to those used in the experiments depicted in Figure 5b(iii), i.e., 0.4 and 10 nM respectively. We found that the coupled system exhibited sustained oscillations confirming that the behavior of the coupled system is caused by the passive transcriptional control exerted by σ19 over σ28.
Conclusion
In this work we have implemented cell-free genetic oscillators with an activator–repressor motif leveraging endogenous E. coli RNAP and sigma factors. Using an evolutionary algorithm, we optimized a kinetic model with batch and steady-state TX-TL data to characterize a phase space wherein the network exhibits oscillations. Since the sigma factors of both oscillators presented here share a common catalytic resource—RNAP—we were able to observe the behavior of two individual oscillators as well as the behavior of a coupled network wherein both oscillators compete for a common resource. Higher-order systems in synthetic biology are frequently engineered by combining multiple modules downstream of one another, analogous to electrical circuits.41 In our work, we rely on the RNAP to combine and thereby couple oscillators driven by different sigma factors. We found that the behavior of the coupled oscillator system depends on the extent of passive transcriptional regulation between sigma factors. Together with better understanding of the role of resource sharing42 and more robust routes to measure kinetic parameters of networks,43 our study describes a methodology to engineer complex in vitro genetic networks.
Methods
Preparation of DNA Templates
PCR for linear DNA templates was performed using Phusion High-Fidelity DNA Polymerase from ThermoFisher Scientific. PCR was carried out in a thermocycler according to the manufacturer’s protocol. DNA templates were purified using QIAGEN PCR purification kits, and concentrations were measured using a Nanodrop. P19-C1-ssra template was ordered from IDT as a gBlock fragment. All other DNA templates for this study were obtained from Arbor Biosciences.
Preparation of Cell Lysate
The energy mixture and cell lysate were prepared using protocols described previously by Sun et al.(37) and Caschera et al.(15) Briefly, BL21 Rosetta2 cells were grown to an OD600 of 1.8 in LB medium supplemented with a phosphate buffer (0.22 M sodium dihydrogen phosphate and 0.4 M disodium hydrogen phosphate, pH 7). The cells were washed with S30A buffer (14 mM magnesium glutamate, 60 mM potassium glutamate, 2 mM DTT, titrated to pH 8.2 with Tris-base). The pellet was resuspended in S30A buffer in a volume equal to 0.8 times the cell pellet weight and passed through a cell press at 16 000 lb. The extract was spun down from which the supernatant was collected, incubated at 37 °C, dialyzed in S30B buffer (14 mM magnesium glutamate, 150 mM potassium glutamate, 1 mM DTT, titrated to pH 8.2 with Tris-base) and aliquoted. The density of the cell lysate was determined to be 40 mg/mL using the Pierce BCA assay.
TX-TL Reaction Set Up
The Energy Mixture was added to the cell lysate along with 3 μM GamS, 3% w/v PEG-8000, 6 mM magnesium Glutamate and 80 mM potassium Glutamate to obtain the TX-TL reaction mixture. The final concentrations were 11 mg/mL cell lysate, 50 mM Hepes (pH 8.0), 0.9 mM cytidine triphosphate and uridine triphosphate, 1.5 mM each of adenosine triphosphate and guanosine triphosphate, 0.5 mM of each amino acid, 1 mM spermidine, 0.75 mM cyclic adenosine monophosphate, 0.33 mM nicotinamide adenine dinucleotide, 0.26 mM coenzyme A, 30 mM 3-phosphoglyceric acid, 0.067 mM folinic acid, 0.2 mg/mL tRNAs. For batch TX-TL reactions the DNA templates and necessary volume of MQ H2O were added and mixed well. Ten μL of the final reaction solution was pipetted into a Nunclon 384 well plate and the deGFP fluorescence was measured using a Tecan M200 Infinite Plate-reader. GamS was prepared using protocols described previously by Sun et al.(13)
During the steady-state TX-TL experiments, microfluidic devices were placed within an incubator set to 30 °C. The TX-TL reaction mixture, was stored within a water-cooled Peltier element, maintained at 4 °C. A short piece of tubing was used to connect the Peltier element to the microfluidic device allowing for the injection of the cooled TX-TL mix into the device. The remaining reaction components (i.e., MQ H2O and DNA solutions) were stored in Tygon tubing (0.02′′ ID, 0.06′′ OD) that was inserted directly into the microfluidic device. These solutions were maintained at 30 °C for the entirety of the experiment. Over the course of the experiments, fluorescence images were periodically captured using an inverted microscope (Nikon Eclipse) to monitor the fluorescence within the microfluidic reactors. Fluorescence was determined from the obtained images using MATLAB software. Amplitude of sustained oscillations were determined by measuring the difference between the fluorescence maxima and minima of the final two oscillations in the steady-state TX-TL experiments.
Fabrication and Design of Microfluidic device
The microfluidic devices used throughout this research were based on designs published by Niederholtmeyer et al.,12 and were manufactured according to previously described protocols. For more details refer to the Supporting Information.
Acknowledgments
We thank Frank H. T. Nelissen, Hans A. Heus and Evan Spruijt for helpful discussions and Roel Maas for his help with experiments. W.T.S.H. was supported by a TOPPUNT grant from The Netherlands Organization for Scientific Research (NWO). T.d.G was supported by the European Research Council, ERC (project no. 677313 BioCircuit) and NWO-VIDI grant from The Netherlands Organization for Scientific Research (NWO, 723.016.003), and funding from the Ministry of Education, Culture and Science (Gravity programs, 024.001.035 and 024.003.013).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acssynbio.8b00300.
Model used in the work (SI eq 1.1–1.11); Figures S1–S21; Tables S1–S3; Note on variability and DNA sequences of constructs used in this study (PDF)
Author Contributions
§ M.Y. and A.J.v.d.L. contributed equally to this work. W.T.S.H. and T.d.G. conceived and supervised the project. M.Y., A.J.v.d.L., and P.A.P. performed the experiments. M.Y., A.J.v.d.L., and B.v.S. analyzed the data. All authors contributed to writing the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Collins J. J.; Gardner T. S.; Cantor C. R. (2000) Construction of a genetic toggle switch in Escherichia coli. Nature 403, 339–342. 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- Elowitz M. B.; Leibler S. (2000) A synthetic oscillatory network of transcriptional regulators. Nature 403, 335–8. 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- Fung E.; Wong W. W.; Suen J. K.; Bulter T.; Lee S.-G.; Liao J. C. (2005) A synthetic gene – metabolic oscillator. Nature 435, 118–122. 10.1038/nature03508. [DOI] [PubMed] [Google Scholar]
- Stricker J.; Cookson S.; Bennett M. R.; Mather W. H.; Tsimring L. S.; Hasty J. (2008) A fast, robust and tunable synthetic gene oscillator. Nature 456, 516–9. 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Z.; Liu S. J.; Bleris L.; Benenson Y. (2010) Logic integration of mRNA signals by an RNAi-based molecular computer. Nucleic Acids Res. 38, 2692–2701. 10.1093/nar/gkq117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelici B.; Mailand E.; Haefliger B.; Benenson Y. (2016) Synthetic Biology Platform for Sensing and Integrating Endogenous Transcriptional Inputs in Mammalian Cells. Cell Rep. 16, 2525–2537. 10.1016/j.celrep.2016.07.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber W.; Schoenmakers R.; Keller B.; Gitzinger M.; Grau T.; Daoud-El Baba M.; Sander P.; Fussenegger M. (2008) A synthetic mammalian gene circuit reveals antituberculosis compounds. Proc. Natl. Acad. Sci. U. S. A. 105, 9994–9998. 10.1073/pnas.0800663105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao J.; Xue S.; Yu G.; Yu Y.; Yang X.; Bai Y.; Zhu S.; Yang L.; Yin J.; Wang Y.; Liao S.; Guo S.; Xie M.; Fussenegger M.; Ye H. (2017) Smartphone-controlled optogenetically engineered cells enable semiautomatic glucose homeostasis in diabetic mice. Sci. Transl. Med. 9, 1–14. 10.1126/scitranslmed.aal2298. [DOI] [PubMed] [Google Scholar]
- Ro D. K.; Paradise E. M.; Quellet M.; Fisher K. J.; Newman K. L.; Ndungu J. M.; Ho K. A.; Eachus R. A.; Ham T. S.; Kirby J.; Chang M. C. Y.; Withers S. T.; Shiba Y.; Sarpong R.; Keasling J. D. (2006) Production of the antimalarial drug precursor artemisinic acid in engineered yeast. Nature 440, 940–943. 10.1038/nature04640. [DOI] [PubMed] [Google Scholar]
- Paddon C. J.; Westfall P. J.; Pitera D. J.; Benjamin K.; Fisher K.; McPhee D.; Leavell M. D.; Tai A.; Main A.; Eng D.; Polichuk D. R.; Teoh K. H.; Reed D. W.; Treynor T.; Lenihan J.; Jiang H.; Fleck M.; Bajad S.; Dang G.; Dengrove D.; Diola D.; Dorin G.; Ellens K. W.; Fickes S.; Galazzo J.; Gaucher S. P.; Geistlinger T.; Henry R.; Hepp M.; Horning T.; Iqbal T.; Kizer L.; Lieu B.; Melis D.; Moss N.; Regentin R.; Secrest S.; Tsuruta H.; Vazquez R.; Westblade L. F.; Xu L.; Yu M.; Zhang Y.; Zhao L.; Lievense J.; Covello P. S.; Keasling J. D.; Reiling K. K.; Renninger N. S.; Newman J. D. (2013) High-level semi-synthetic production of the potent antimalarial artemisinin. Nature 496, 528–532. 10.1038/nature12051. [DOI] [PubMed] [Google Scholar]
- Borkowski O.; Ceroni F.; Stan G. B.; Ellis T. (2016) Overloaded and stressed: whole-cell considerations for bacterial synthetic biology. Curr. Opin. Microbiol. 33, 123–130. 10.1016/j.mib.2016.07.009. [DOI] [PubMed] [Google Scholar]
- Niederholtmeyer H.; Stepanova V.; Maerkl S. J. (2013) Implementation of cell-free biological networks at steady state. Proc. Natl. Acad. Sci. U. S. A. 110, 15985–90. 10.1073/pnas.1311166110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Z. Z.; Yeung E.; Hayes C. A.; Noireaux V.; Murray R. M. (2014) Linear DNA for rapid prototyping of synthetic biological circuits in an escherichia coli based TX-TL cell-free system. ACS Synth. Biol. 3, 387–397. 10.1021/sb400131a. [DOI] [PubMed] [Google Scholar]
- Shin J.; Noireaux V. (2010) Efficient cell-free expression with the endogenous E. coli RNA polymerase and sigma factor 70. J. Biol. Eng. 4, 2–10. 10.1186/1754-1611-4-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caschera F.; Noireaux V. (2014) Synthesis of 2.3 mg/mL of protein with an all Escherichia coli cell-free transcription-translation system. Biochimie 99, 162–168. 10.1016/j.biochi.2013.11.025. [DOI] [PubMed] [Google Scholar]
- Shin J.; Noireaux V. (2010) Study of messenger RNA inactivation and protein degradation in an Escherichia coli cell-free expression system. J. Biol. Eng. 4, 9. 10.1186/1754-1611-4-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iskakova M. B.; Szaflarski W.; Dreyfus M.; Remme J.; Nierhaus K. H. (2006) Troubleshooting coupled in vitro transcription-translation system derived from Escherichia coli cells: Synthesis of high-yield fully active proteins. Nucleic Acids Res. 34, e135. 10.1093/nar/gkl462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stögbauer T.; Windhager L.; Zimmer R.; Rädler J. O. (2012) Experiment and mathematical modeling of gene expression dynamics in a cell-free system. Integr. Biol. 4, 494–501. 10.1039/c2ib00102k. [DOI] [PubMed] [Google Scholar]
- Shin J.; Noireaux V. (2012) An E. coli Cell-free expression toolbox: Application to synthetic gene circuits and artificial cells. ACS Synth. Biol. 1, 29–41. 10.1021/sb200016s. [DOI] [PubMed] [Google Scholar]
- Garamella J.; Marshall R.; Rustad M.; Noireaux V. (2016) The All E. coli TX-TL Toolbox 2.0: A Platform for Cell-Free Synthetic Biology. ACS Synth. Biol. 5, 344–355. 10.1021/acssynbio.5b00296. [DOI] [PubMed] [Google Scholar]
- Marshall R.; Maxwell C. S.; Collins S. P.; Jacobsen T.; Luo M. L.; Begemann M. B.; Gray B. N.; January E.; Singer A.; He Y.; Beisel C. L.; Noireaux V. (2018) Rapid and Scalable Characterization of CRISPR Technologies Using an E. coli Cell-Free Transcription-Translation System. Mol. Cell 69, 146–157e3. 10.1016/j.molcel.2017.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adamala K. P.; Martin-Alarcon D. A.; Guthrie-Honea K. R.; Boyden E. S. (2017) Engineering genetic circuit interactions within and between synthetic minimal cells. Nat. Chem. 9, 431–439. 10.1038/nchem.2644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karzbrun E.; Tayar A. M.; Noireaux V.; Bar-Ziv R. H. (2014) Programmable on-chip DNA compartments as artificial cells. Science (Washington, DC, U. S.) 345, 829–832. 10.1126/science.1255550. [DOI] [PubMed] [Google Scholar]
- Niederholtmeyer H.; Sun Z. Z.; Hori Y.; Yeung E.; Verpoorte A.; Murray R. M.; Maerkl S. J. (2015) Rapid cell-free forward engineering of novel genetic ring oscillators. eLife 4, 1–18. 10.7554/eLife.09771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novák B.; Tyson J. J. (2008) Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 9, 981–91. 10.1038/nrm2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien E. L.; Van Itallie E.; Bennett M. R. (2012) Modeling synthetic gene oscillators. Math. Biosci. 236, 1–15. 10.1016/j.mbs.2012.01.001. [DOI] [PubMed] [Google Scholar]
- Mooney R. A.; Darst S. A.; Landick R. (2005) Sigma and RNA polymerase: An on-again, off-again relationship?. Mol. Cell 20, 335–345. 10.1016/j.molcel.2005.10.015. [DOI] [PubMed] [Google Scholar]
- Grigorova I. L.; Phleger N. J.; Mutalik V. K.; Gross C. A. (2006) Insights into transcriptional regulation and sigma competition from an equilibrium model of RNA polymerase binding to DNA. Proc. Natl. Acad. Sci. U. S. A. 103, 5332–5337. 10.1073/pnas.0600828103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maeda H.; Fujita N.; Ishihama A. (2000) Competition among seven Escherichia coli sigma subunits: relative binding affinities to the core RNA polymerase. Nucleic Acids Res. 28, 3497–503. 10.1093/nar/28.18.3497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauri M.; Klumpp S. (2014) A Model for Sigma Factor Competition in Bacterial Cells. PLoS Comput. Biol. 10, 29–34. 10.1371/journal.pcbi.1003845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park J.; Dies M.; Lin Y.; Hormoz S.; Smith-Unna S. E.; Quinodoz S.; Hernández-Jiménez M. J.; Garcia-Ojalvo J.; Locke J. C. W.; Elowitz M. B. (2018) Molecular Time Sharing through Dynamic Pulsing in Single Cells. Cell Syst. 6, 216–229e15. 10.1016/j.cels.2018.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bervoets I.; Van Brempt M.; Van Nerom K.; Van Hove B.; Maertens J.; De Mey M.; Charlier D. (2018) A sigma factor toolbox for orthogonal gene expression in Escherichia coli. Nucleic Acids Res. 46, 2133–2144. 10.1093/nar/gky010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tayar A. M.; Karzbrun E.; Noireaux V.; Bar-Ziv R. H. (2017) Synchrony and pattern formation of coupled genetic oscillators on a chip of artificial cells. Proc. Natl. Acad. Sci. U. S. A. 114, 201710620. 10.1073/pnas.1710620114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunlap J. C. (1999) Molecular bases for circadian clocks. Cell 96, 271–290. 10.1016/S0092-8674(00)80566-8. [DOI] [PubMed] [Google Scholar]
- Raue A.; Kreutz C.; Maiwald T.; Bachmann J.; Schilling M.; Klingmüller U.; Timmer J. (2009) Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 25, 1923–1929. 10.1093/bioinformatics/btp358. [DOI] [PubMed] [Google Scholar]
- Smith R. W.; van Sluijs B.; Fleck C. (2017) Designing synthetic networks in silico: A generalised evolutionary algorithm approach. BMC Syst. Biol. 11, 1–19. 10.1186/s12918-017-0499-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Z. Z.; Hayes C. A.; Shin J.; Caschera F.; Murray R. M.; Noireaux V. (2013) Protocols for implementing an Escherichia coli based TX-TL cell-free expression system for synthetic biology. J. Visualized Exp. e50762 10.3791/50762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farewell A.; Kvint K.; Nyström T. (1998) Negative regulation by RpoS: A case of sigma factor competition. Mol. Microbiol. 29, 1039–1051. 10.1046/j.1365-2958.1998.00990.x. [DOI] [PubMed] [Google Scholar]
- Rondelez Y. (2012) Competition for catalytic resources alters biological network dynamics. Phys. Rev. Lett. 108, 1–5. 10.1103/PhysRevLett.108.018102. [DOI] [PubMed] [Google Scholar]
- Kim P. M.; Tidor B. (2003) Limitations of Quantitative Gene Regulation Models : A Case Study Limitations of Quantitative Gene Regulation Models : A Case Study. Genome Res. 13, 2391–2395. 10.1101/gr.1207003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purnick P. E. M.; Weiss R. (2009) The second wave of synthetic biology: From modules to systems. Nat. Rev. Mol. Cell Biol. 10, 410–422. 10.1038/nrm2698. [DOI] [PubMed] [Google Scholar]
- Qian Y.; Huang H. H.; Jiménez J. I.; Del Vecchio D. (2017) Resource Competition Shapes the Response of Genetic Circuits. ACS Synth. Biol. 6, 1263–1272. 10.1021/acssynbio.6b00361. [DOI] [PubMed] [Google Scholar]
- Siegal-Gaskins D.; Tuza Z. A.; Kim J.; Noireaux V.; Murray R. M. (2014) Gene circuit performance characterization and resource usage in a cell-free “breadboard.. ACS Synth. Biol. 3, 416–425. 10.1021/sb400203p. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.