Resurrected Protein Interaction Networks Reveal the Innovation Potential of Ancient Whole-Genome Duplication

The ancient genome triplication at the origin of core eudicots generated many new regulatory protein complexes, innovating plant development.

Abstract

The evolution of plants is characterized by whole-genome duplications, sometimes closely associated with the origin of large groups of species. The gamma (γ) genome triplication occurred at the origin of the core eudicots, which comprise ∼75% of flowering plants. To better understand the impact of whole-genome duplication, we studied the protein interaction network of MADS domain transcription factors, which are key regulators of reproductive development. We reconstructed, synthesized, and tested the interactions of ancestral proteins immediately before and closely after the triplication and directly compared these ancestral networks to the extant networks of Arabidopsis thaliana and tomato (Solanum lycopersicum). We found that gamma expanded the MADS domain interaction network more strongly than subsequent genomic events. This event strongly rewired MADS domain interactions and allowed for the evolution of new functions and installed robustness through new redundancy. Despite extensive rewiring, the organization of the network was maintained through gamma. New interactions and protein retention compensated for its potentially destructive impact on network organization. Post gamma, the network evolved from an organization around the single hub SEP3 to a network organized around multiple hubs and well-connected proteins lost, rather than gained, interactions. The data provide a resource for comparative developmental biology in flowering plants.

INTRODUCTION

Comparative analysis of genome sequences, transcriptomes, and phylogenetic and synteny analyses of individual gene lineages placed an ancient hexaploidization event in the stem lineage of core eudicots, before the divergence of Gunnerales and after the divergence of Buxales (Bowers et al., 2003; Tang et al., 2008; Jiao et al., 2012; Vekemans et al., 2012). While this event is commonly referred to as the gamma (γ) “triplication,” a genome triplication as a mechanism is unlikely to have occurred and the resulting ancient hexaploid probably originated from the hybridization between a closely related diploid and tetraploid. Therefore, the γ triplication probably resulted from two consecutive ancient whole-genome duplications (WGDs) close in time. The exact mechanism, timing, and phylogenetic placement of the events leading to the origin of the ancient hexaploid remain unclear, but its genomic consequence is referred to as the γ triplication (Chanderbali et al., 2017). Understanding that the precise events contributing to ancient genome triplication are difficult to ascertain, our experimental design treats hexaploidization as instantaneous. At the same time, we discuss the implications of our results for a two-step process of hexaploidization.

One absolute time estimate for the γ triplication is that it occurred 120 million years ago (Mya; Figure 1) (Vekemans et al., 2012). The origin of core eudicots marks an important event in plant evolution as today this lineage comprises ∼75% of all species of flowering plants (Soltis et al., 2003; Willis and McElwain, 2013). Aside from the γ triplication and the presence of ellagic and gallic acid, the group shares few unique characteristics (Stevens and Davis, 2006). However, the Pentapetalae, which comprise most core eudicots but originated a few million years later, are morphologically more distinct and are characterized by the “canalization” or a more clear definition of flower development (Waddington, 1942; Soltis et al., 2003; Melzer and Theißen, 2016; Theißen and Melzer, 2016; Chanderbali et al., 2017). In this group, floral organs are in pentamerous whorls, and a clear separation of sepal and petal identity exists (Soltis et al., 2003; Stevens and Davis, 2006). Therefore, while core eudicots share the γ triplication, it appears that the morphological consequences of this genomic event were established only somewhat later in evolution and are more apparent from Pentapetalae onwards (Schranz et al., 2012; Vekemans et al., 2012). In the context of developmental genetics, the origin of Pentapetalae has been proposed to coincide with a transition from a fading borders model with overlapping gene expression domains of floral organ identity genes, to an ABCDE model with more strictly defined expression domains (Soltis et al., 2009; Chanderbali et al., 2016; Soltis and Soltis, 2016).

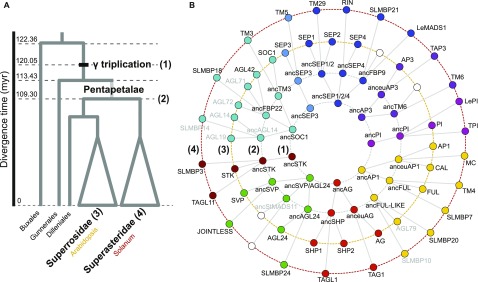
Figure 1.

Evolution of Selected MADS Box Proteins of Interest.

(A) Simplified phylogenetic tree of eudicots. The positions at which protein interaction networks were inferred are indicated: (1) PIN just before γ triplication or Pre-PIN, (2) PIN at the Asterid-Rosid split or Post-PIN, (3) PIN of Arabidopsis (Ara-PIN), and (4) PIN of tomato (Sol-PIN).

(B) Phylogenetic relationships between ancestral and extant proteins present in each reconstructed PIN. Reconstructed ancestral proteins are named after their Arabidopsis or tomato descendants preceded by “anc” for ancestral. Gray font proteins were not included in this study (see Methods). White circles indicate the absence of a specific protein due to gene loss.

The duplication patterns of MADS domain proteins—a conserved class of transcription factors that act as key regulators of reproductive development in flowering plants—indicate that many gene lineages present in extant core eudicots are derived from this whole-genome triplication with most being retained in duplicate or triplicate copies (Litt and Irish, 2003; Kramer et al., 2004, 2006; Hernández-Hernández et al., 2007; Viaene et al., 2010; Airoldi and Davies, 2012; Vekemans et al., 2012). Their molecular function as transcription factors requires them to localize in the nucleus and form specific multimeric transcriptional complexes to regulate downstream targets (Immink et al., 2010; Smaczniak et al., 2012). Considering the critical role of the specific protein binding affinities among these proteins in the induction of flowering, inflorescence meristem specification, and floral meristem and floral organ specification, the expansion of MADS box genes through the γ triplication and the protein interactions that evolved may have played an important role in establishing the derived morphology of Pentapetalae and the success of core eudicots (Veron et al., 2007; Shan et al., 2009; Liu et al., 2010; Theißen et al., 2016; Bartlett, 2017). The functional importance of protein interactions of MADS domain proteins has been characterized through genetic analysis in Arabidopsis thaliana (Liu et al., 2009a; Smaczniak et al., 2012; Yan et al., 2016) and comprehensive yeast two-hybrid protein interaction maps for MADS domain proteins are available for this model system and a few other species (de Folter et al., 2005; Leseberg et al., 2008; Angenent and Immink, 2009; Immink et al., 2009; Ruokolainen et al., 2010). While such data allow tracing of the origin and evolutionary diversification of protein interactions and some of their functions, such inferences suffer from sparse sampling and different yeast assays being used, which hampers direct comparison of data and consequently the accuracy of deep evolutionary inferences.

Biological networks are characterized by several organizational properties to which certain biological advantages can be attributed. The most often used property of nodes in a network is the degree, or the number of interactions of a protein in a protein interaction network. The degree distribution of networks is usually heterogeneous or mathematically scale free, with few nodes having many interactions and many nodes having few (Barabasi and Albert, 1999). This property indicates the presence of hubs in the network or very well-connected nodes. The origin of this property of the network is closely linked to its origin through gene duplication as more connected nodes will acquire more interactions through duplication, a mechanism referred to as preferential attachment (Eisenberg and Levanon, 2003). The presence of hubs in a network is considered to make the network more robust to random failure, as the small number of hubs decreases the likelihood of these being affected. Another important property is the degree of clustering or modularity. Modularity and hierarchy—modularity of modules—are considered to originate from a cost associated with connections between nodes (Clune et al., 2013; Mengistu et al., 2016). The evolutionary advantage of a modular organization is that it makes the network more adaptable as modules can be easily added or removed (Bassett et al., 2010; Tran and Kwon, 2013; Mengistu et al., 2016).

Specifically in plants, but of general biological importance, the role of massively concerted gene duplications at the genome level is well documented (Adams and Wendel, 2005; De Bodt et al., 2005; Conant and Wolfe, 2006; van Hoek and Hogeweg, 2009; Arabidopsis Interactome Mapping Consortium, 2011; Soltis and Soltis, 2016). Such WGD events could also have a major effect on the rewiring of protein interaction networks as predicted by the duplication-divergence model (Wagner, 2001; Arabidopsis Interactome Mapping Consortium, 2011; De Smet and Van de Peer, 2012). To understand the impact of the γ triplication on the origin of a large group of plant species, we studied the intricate ancestral protein interaction networks of MIKC^C MADS domain transcription factors. We reconstructed and resurrected ancestral proteins immediately before this genome triplication and around 10 million years later, at the diversification of rosid and asterid flowering plants. By directly comparing ancestral networks with extant networks from Arabidopsis and tomato (Solanum lycopersicum) in a single experimental setup, we are able to go beyond theoretical models and comparative analysis of present-day networks and instead investigate directly how this network diverged and which processes were responsible for its origin and divergence.

RESULTS

Resurrected Ancestral MADS Domain Proteins Reveal the Origin of Extant Networks

We reconstructed protein interaction networks (PINs) between representatives of nine MADS box gene subfamilies at three distinct points in time for a total of four PINs: (1) just before the γ triplication event coinciding with the origin of the core eudicots, (2) following the γ triplication at the Asterid-Rosid split and present-day, (3) from Arabidopsis, and (4) tomato (Figure 1; Supplemental Data Sets 1 and 2). These ancestral and extant interaction networks are respectively referred to as Pre-PIN, Post-PIN, Ara-PIN, and Sol-PIN throughout this study. The uncertainty associated with the ancestral networks includes the phylogenies used for ancestral state reconstruction, the exact timing and phylogenetic position of the events leading to the gamma triplication, the ancestral state reconstruction, and the assay used to determine protein interaction. The phylogeny used is relatively robust and the gamma events occurred in a narrow time window so we assume that they have a limited contribution to the overall uncertainty. Therefore, we explicitly address the latter two sources of uncertainty.

Reconstruction of the ancestral proteins that form the Pre-PIN and Post-PIN was performed by inferring the maximum likelihood protein sequences at the ancestral nodes of interest for each subfamily separately (see Methods; Supplemental Figure 1). MADS box genes are a good model system for ancestral sequence resurrection since there are many sequences available throughout the angiosperm phylogeny which are mostly well conserved within their subfamilies. The reconstruction accuracy of ancestral protein sequences is represented by the posterior probability of the inferred amino acids in the ancestral sequence (Supplemental Figure 2). Both the ancestral proteins before and after γ triplication were reconstructed with on average 92.8% and 94.6% of sites having a posterior probability higher than 0.95. Previous studies utilizing ancestral proteins to characterize evolutionary transitions defined ambiguously reconstructed sites as those sites for which the most likely amino acid has a posterior probability lower than 0.80 and that have an alternative amino acid state with a posterior probability higher than 0.2 (Eick et al., 2012; Voordeckers et al., 2012; McKeown et al., 2014; Anderson et al., 2016). Surveying ambiguous sites in the ancestral proteins reconstructed in this study revealed that these sites were mostly located outside of the highly conserved K-domain (Supplemental Figure 2), which plays a prominent role in interactions between MADS box proteins (Fan et al., 1997; Yang and Jack, 2004; Kaufmann et al., 2005). Out of the 26 reconstructed ancestral proteins, only 11 ambiguous sites in the K-domain had an alternative amino acid not biochemically similar to the most likely amino acid. Given the scale of our study, this represents only 0.5% of all reconstructed sites in the K-domain. Following inference, codon-optimized ancestral DNA sequences were synthesized and, analogous to their Arabidopsis and Solanum descendants, cloned into yeast two-hybrid (Y2H) expression vectors. Subsequently, all pairwise interactions for each set of MADS box protein constructs at an ancestral or extant node were determined employing a high-throughput yeast two-hybrid system using the Miller ONPG assay to measure activity of the LacZ reporter (Figure 2). In total 582 binary protein-protein interactions were tested (Supplemental Data Set 3).

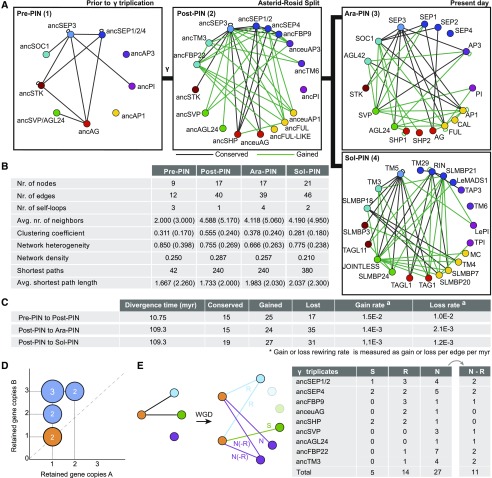
Figure 2.

Evolution of MADS Box Protein Interaction Networks Reveals Accelerated Rewiring Following γ Triplication.

(A) MADS box protein interaction networks just before the γ triplication (1), at the Asterid-Rosid split (2), for Arabidopsis (3), and for tomato (4) as assayed by Y2H. Same color nodes indicate homologous MADS box gene lineages as mentioned in Figure 1B. Conserved and gained protein interactions are indicated as black and green solid lines, respectively, and are determined by comparing Post-PIN to Pre-PIN and Ara-PIN or Sol-PIN to Post-PIN.

(B) Network topological measurements for reconstructed Y2H MADS box PINs. Values in parentheses denote the average network topological measurements of 10,000 randomly generated networks of the same network size and average degree.

(C) The rate of interaction gain and loss as determined from Pre-PIN to Post-PIN and from Post-PIN to Ara-PIN or Sol-PIN for Y2H. Gain and loss rate was defined as gained or lost edges divided by number of potential interactions (self-loops included) times the divergence time.

(D) According to the gene dosage balance hypothesis, the proteins ([A] and [B]) involved in the nine PPIs observed in Pre-PIN Y2H should be retained in similar balance after the γ triplication. The graph shows the dosage of the gene copies of these proteins. The number of interacting proteins that were retained in balance after γ are marked in orange.

(E) Schematic overview of the duplication-divergence possibilities as observed in the Y2H PINs and number of interactions that show: R, redundancy; S, subfunctionalization; or N, neofunctionalization when we compare their interactions from the Pre-PIN to the Post-PIN. N-R or neoredundant interactions are those neofunctionalized interactions that redundantly interact with the same paralogs. Genes that did not duplicate or had no interactions in Pre-PIN are excluded.

While genetic evidence has supported the functional importance of the protein interactions of MADS domain proteins as determined by Y2H, the method is prone to false positives and false negatives and dependent on the yeast strain and vector system being used (Yu et al., 2008; Chen et al., 2010; Rajagopala et al., 2012; Vidal and Fields, 2014). Therefore, we evaluated the reliability of the Y2H system used in this study in three ways. First, we analyzed the dependency of our results on the reporter used by randomly selecting 101 pairs and performing Y2H using an alternative reporter gene, MEL1 (Supplemental Figure 3A). These results show a high overlap (0.85) between the results obtained by the LacZ and the MEL1 reporter. Furthermore, in the absence of a curated interaction data set for MADS box proteins, we compared Ara-PIN and Sol-PIN to Arabidopsis and Solanum MADS box protein interaction networks described in the literature (Supplemental Figure 3B) (de Folter et al., 2005; Leseberg et al., 2008). We determined the similarity of Ara-PIN and Sol-PIN to be 0.80 and 0.74, respectively, indicating a high overlap between the Ara-PIN and Sol-PIN described here and previously constructed networks. Finally, we tested a subset of ancestral interactions from the Post-PIN using GST pull-down (Supplemental Figure 3C). We chose three post-ɣ proteins with either many, intermediate, or few interactions in the network (ancSEP3, ancFBP22, and anceuAP1) and tested these against all other proteins of the Post-PIN. We found a general overlap of 0.61 between the Y2H and the GST pull-down results and noticed that the GST pull-down system was more sensitive and picked up more interactions. However, the GST system could not identify any false positives in the Y2H data, suggesting that the Y2H method possibly underestimated the number of actual interactions in the different networks, something that has been reported previously for the Y2H system (Yu et al., 2008; Rajagopala et al., 2014). For example, like in de Folter et al. (2005), one well-known interaction that is missing in our networks is the heterodimerization of PISTILLATA (PI) and APETALA3 (AP3) (Riechmann et al., 1996). For an unknown reason, however, their interaction cannot always be detected in Y2H assays when using full-length proteins as we did in our set up (Yang et al., 2003). The effect of false negatives may influence the inferences about network evolution that follow. However, we assume that they are not likely to strongly affect our overall conclusions as there is no evidence that suggests that the different networks would be differentially impacted by false negatives and, therefore, inferences based on network comparisons would be robust. Indeed, the networks reconstructed in this study do generally correspond to known MADS domain protein interactions with SEPALLATA (SEP) proteins acting as hubs, AP3 and PI proteins being more isolated, and only a few interactions occurring between AGAMOUS (AG) and AP1 proteins (Immink et al., 2010; Liu et al., 2010).

The overall high similarity between the different yeast systems tested strengthens our confidence in the ancestral Pre-PIN and Post-PIN networks, but exposes the likely underestimation of the number of detected interactions when compared with GST pull-down systems (Supplemental Figure 3D). Because the resulting interactions do not necessarily reflect (ancestral) functional in vivo interactions, we chose to focus on large-scale changes between the networks, rather than on the evolution of individual protein interactions.

Gamma Hexaploidization Expanded MADS Domain Proteins More Strongly Than Subsequent Genomic Events

Throughout plant evolution, series of WGDs have expanded the number of nodes in major regulatory networks including the MADS box gene family (Veron et al., 2007; Jiao et al., 2011, 2012; Vekemans et al., 2012; Ruelens et al., 2013). Following the γ hexaploidization event, theoretically all genes were triplicated; however, soon afterwards, redundant genes would be silenced and lost through pseudogenization (Freeling et al., 2012; Wendel et al., 2016). Indeed, from Pre-PIN to Post-PIN not all genes were retained in three copies, generating an ancestral Post-PIN with a network size only 2-fold larger than the original Pre-PIN (Figure 2A) (Veron et al., 2007).

For proteins that function in multimeric complexes, gene retention after WGD is often explained by the dosage balance hypothesis, which states that specific types of interacting proteins, such as transcription factors, are retained in similar dosage not to disturb dosage-sensitive processes (Edger and Pires, 2009; Veitia and Potier, 2015). Since our approach provides us with ancestral interactions, it is possible that we would observe this mechanism directly. To investigate dosage balance, we plotted post-γ gene dosages of the proteins that interacted before γ by Y2H (Figure 2D). However, in line with previous findings (Guo et al., 2013), we did not observe dosage-balanced gene retention as only two out of nine protein pairs are retained in balance (SEP3-PI and SEP3-STK). However, it is likely that our data set is not large enough to observe many cases of dosage balanced gene retention since it has been shown that the MADS box gene transcription factor family is generally reciprocally retained (Tasdighian et al., 2017).

After the Asterid-Rosid split, two additional rounds of ancient WGDs occurred along the lineage toward Arabidopsis (β, 77.5 Mya; α, 23.3 Mya) and one ancient whole-genome triplication toward Solanum (T, 71 Mya) (Bowers et al., 2003; Tomato Genome Consortium, 2012). Here, the expansion of the network was limited as only 22 homologous proteins are present in Arabidopsis and 23 in Solanum compared with 19 proteins post-γ triplication (Figure 1B), suggesting that unlike the γ triplication, more recent ancient WGDs did not result in significant expansion of the MADS box PIN.

Gamma Hexaploidization Strongly Rewired MADS Domain Interactions but Did Not Affect Their Density

The γ triplication innovated the MADS domain protein network by the addition of new nodes, yet duplication is not the only force driving changes of PINs. Edges or interactions can be gained, lost, and rewired and as a consequence the functional information in the network could have evolved (Vázquez et al., 2002; Pastor-Satorras et al., 2003; De Smet and Van de Peer, 2012).

We noticed that the interaction patterns of the Post-PIN were much more similar to those of Ara-PIN and Sol-PIN compared with Pre-PIN, even though they are divided by 110 million years (myr) of evolution compared with 10 myr between Pre-PIN and Post-PIN. To investigate whether edge rewiring happened at a faster rate following genome duplication, we calculated and compared the average rate of interaction gain and loss from Pre-PIN to Post-PIN with the rates from Post-PIN to Ara-PIN and Post-PIN to Sol-PIN (Figure 2C). Our results show that from Pre- to Post-PIN, the rate in interaction gain is 1.5E-02 gained edges per total possible edges per myr, ∼1.5-fold higher than the rate of interaction loss (1.0E-02/edge/myr). In addition, from Post-PIN to Ara- and Sol-PIN, new interactions evolved at a rate of 1.4E-03 and 1.1E-03/edge/myr, respectively, while interactions were lost at 2.1E-03 and 1.2E-03/edge/myr, respectively. These results indicate that in the 10 myr following the γ triplication, the MADS box network rewired at a rate approximately 10-fold higher than over the 110 myr between Post-PIN and Ara-PIN or Sol-PIN. Moreover, from the origin of core eudicots up to the Asterid-Rosid split, the network rewired mainly through the gain of new interactions. By contrast, from the Asterid-Rosid split until present-day, not only did the overall rewiring rate decrease, interaction loss became higher than interaction gain (Figure 2C). Together, these results indicate that shortly following the γ triplication, the MADS box PIN underwent accelerated rewiring.

The γ triplication added many new interactions to the network, which may have had consequences for the selectivity with which these interactions could be maintained. To understand this specificity, it is sensible to compare network density, i.e., the ratio between the number of actually observed interactions and the number of possible interactions. Despite strong edge addition, network density did not notably change from Pre-PIN to the current PINs, Ara-PIN and Sol-PIN (Figure 2B). This relatively constant density suggests that an optimal number of specific interactions can be maintained by a set number of MADS-domain proteins, a property that possibly relates to protein structure (Zarrinpar et al., 2003).

Gamma Hexaploidization Allowed for the Evolution of New Functions and Installed Robustness through New Redundancy

Rewiring can be a consequence of neofunctionalization or subfunctionalization (He and Zhang, 2005). When applied to protein interactions, the neofunctionalization model implies that following duplication, one paralog retains all interactions, while the other is released from functional constraints and undergoes rapid diversification, resulting in the evolution of novel interactions. The subfunctionalization model posits that paralogous proteins rewire by redistributing their ancestral interactions among the different paralogs without new interactions emerging. In agreement with the rapid rewiring after the γ triplication, our data show many more instances of neofunctionalization than of subfunctionalization when comparing Pre-PIN to Post-PIN or Post-PIN to Ara-PIN and Sol-PIN. Rewiring following the γ triplication, however, cannot be explained by a strict interpretation of sub- or neofunctionalization (Figure 2E) (Voordeckers et al., 2012). Rather, the data show both rapid rewiring of all descendant paralogs by acquiring novel interactions and a combination of sub- and neofunctionalization, in which paralogs both acquire new interactions while maintaining a set of ancestral interactions.

Interestingly, we observe many cases in which new redundancy originated through the γ triplication; i.e., two newly emerged paralogs interact with the same protein, whereas their ancestor did not (Figure 2E). This observation, which we refer to as neoredundancy, can be explained by the fact that new paralogs are highly similar and as a consequence a protein evolving to interact with one of these paralogs will likely also interact with the other paralog. Together, our data suggest that the γ triplication dramatically innovated the MADS-PIN, but at the same time the network also acquired novel robustness through the redundancy that was established.

The Post Gamma Network Evolved from an Organization around the Single Hub SEP3 to a Network Organized around Multiple Hubs

We observed that the γ triplication duplicated the number of nodes and rewired the interactions between these nodes. How these edges are mathematically organized in the network is referred to as the topology of the network. The presence of hubs, the number of modules, and the organization of modules all potentially contribute to network robustness and evolvability (Clune et al., 2013; Lachowiec et al., 2016; Mengistu et al., 2016). To understand the effect of ancient hexaploidization on the topology of the network, we calculated a number of topological network parameters commonly used to describe networks (see Methods). For comparison, we also determined these parameters for random networks of equivalent size and average degree (Figure 2B).

A highly heterogeneous degree distribution is suggestive of the presence of hubs in a network as hubs have many connections while other proteins have only a few connections. By contrast, in random networks all nodes have approximately the same number of connections, with only a small deviation (Albert and Barabási, 2002). Compared with random networks, all MADS box PINs exhibit a high network heterogeneity (Figure 2B). Indeed, in Pre- and Post-PIN more than 40% of all connections involve SEP3 proteins with a degree of 7 and 16, ∼3-fold the network average degree of 2.6 and 4.7, respectively. However, both in Ara-PIN and Sol-PIN, there is no single prominent node with a high maximum degree. Rather, in the latter two networks, multiple proteins exhibit a moderately high degree between 8 and 12, only 2-fold the average degree. These new hubs are FRUITFUL (FUL), AP1, SEP3, SUPPRESSOR OF OVEREXPRESSION OF CONSTANS1 (SOC1), and SHORT VEGETATIVE PHASE (SVP) in Ara-PIN and JOINTLESS, TM5, RIPENING INHIBITOR (RIN), and SLMPB21 in Sol-PIN. SEP3 therefore lost its prominence as the sole hub protein because multiple hubs evolved in the lineages toward Ara-PIN and Sol-PIN.

Despite Extensive Rewiring through Gamma, the Organization of the Network Was Maintained

To further understand how the γ triplication affected the topology of the network, we investigated the evolution of clustering or modularity in the network. The extent of clustering is described by the average clustering coefficient of a network, which for most real-world networks is higher than comparable random networks and indicates their modular structure (Albert and Barabási, 2002). For the MADS box PINs, all Y2H networks have a higher average clustering coefficient than their corresponding random networks (Figure 2B). Moreover, the average clustering coefficient increases following the γ triplication from C_Pre-PIN = 0.311 to C_Post-PIN = 0.555, while both descendant networks, Ara-PIN and Sol-PIN, again have a lower clustering coefficient of C_Ara-PIN = 0.378 and C_Sol-PIN = 0.281. A clear negative correlation between clustering coefficient and degree can be observed for post-PIN, which is also present in pre-PIN, but such a clear correlation is lost in the extant networks of Arabidopsis and tomato (Supplemental Figure 4C). This indicates hierarchy in the ancestral networks, or a modular organization of modules. This modular and hierarchical organization is considered to originate from a cost associated with individual interactions, which is consistent with the relatively constant density of the networks and is thought to confer evolvability to the networks (Clune et al., 2013; Mengistu et al., 2016).

In addition to a high clustering coefficient, real-world networks also have a short average path length. The average shortest path length is defined as the average minimal number of edges that connect all possible pairs of nodes in a network. A short average path length ensures an efficient and fast transmission of information throughout the network (Watts and Strogatz, 1998; Barabási and Oltvai, 2004). Networks that have a higher clustering coefficient than a comparable random network, yet also have an average shortest path length similar to random networks are referred to as small world networks. The average shortest path length of each Y2H MADS box PIN was consistently smaller, albeit only slightly, than their random networks and remained relatively stable throughout evolution (Figure 2B). Together with their high clustering coefficient, this indicates that all Y2H PINs meet the requirements of small world networks. Overall, we find that the γ triplication did not establish a qualitatively different topological organization of the network.

New Interactions and Protein Retention Compensated for the Potentially Destructive Impact of Gamma on Network Organization

Because the network dynamics of the γ triplication did not disrupt network topology, we asked how network topology was maintained despite extensive rewiring. To statistically evaluate the role of elementary processes that were applied to the network, we applied the observed network dynamics between ancestral and extant networks to simulated large-scale networks (Figure 3). An initial large-scale Pre-PIN network was obtained by up-scaling the ancestral Pre-PIN of seven connected nodes to 1000 nodes by preferential attachment [Figures 3B and 3C, (i) to (ii)]. Thereafter, the up-scaled Pre-PIN was subjected to network triplication, node deletions, edge deletions, and additions as schematized in Figure 3A. To understand the role of individual elementary processes, we implemented modifications of the simulations and for comparison, we tested the effect of the measured network dynamics on a completely random network model obtained via random attachment of nodes (see Methods) (Supplemental Figure 4). For each simulation, we performed at least 10 stochastic runs.

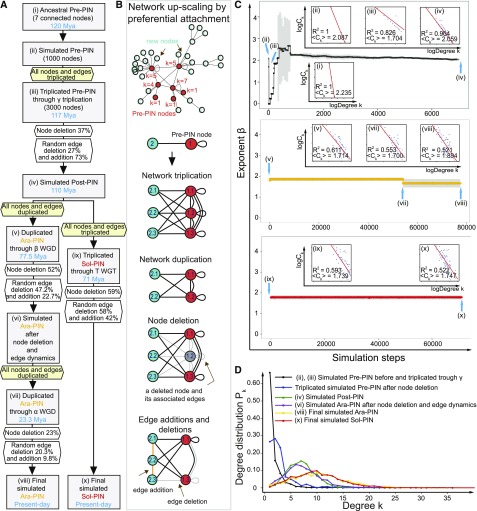
Figure 3.

Tracing Elementary Processes in Network Evolution from Pre-PIN until Extant Ara-PIN and Sol-PIN.

(A) The flowchart shows the initial up-scaled Pre-PIN model with the simulation process based on the actual ancestral and extant MADS-box PIN parameters (calculated percentages of node deletion, edge addition, and deletion). The initializing network is up-scaled to the size of 1000 nodes based on the actual Pre-PIN with 12 edges and seven connected nodes where two isolated nodes are excluded. Each simulation step reflects bins of 0.001 myr for random edge addition or deletion excluding the steps of ancient whole genome triplication or duplication and node deletions.

(B) Elementary processes of network evolution. The mechanisms of network up-scaling using preferential attachment in the initial up-scaled Pre-PIN model, network triplication, node deletion, and edge additions and deletions applied in the simulated networks. The ancestral Pre-PIN nodes are labeled in red while the new nodes are labeled in turquoise. All nodes are numbered and the number near the Pre-PIN nodes indicates their corresponding node degrees.

(C) Exponent β distribution for the initial up-scaled Pre-PIN model. The main plots show the average value of the β exponent together with the sd (plots in black, yellow, and red and error bars in gray) for a total 10 replicated simulations. Blue arrows indicate positions of several important simulated networks following the simulation steps corresponding to the simulation process from (A). There are a total of nine intrinsic log-log plots showing the relationship between degree k and C_k of each node in simulated MADS box PINs following the simulation steps (for the complete plots, see Supplemental Figure 4).

(D) Degree P_k distribution for the initial up-scaled Pre-PIN model.

Our focus was on how elementary processes contributed to hierarchy in the network, which is measured by a significant negative linear correlation between clustering coefficient C_k and degree k (plots in Figure 3C). Triplication of the nodes in the up-scaled Pre-PIN did not significantly affect network hierarchy [Figure 3C, (iii)]. However, we see that the observed 37% node deletion subsequent to node triplication would have destroyed network hierarchy without edge dynamics (Figure 3C, above β exponent distribution). Edge dynamics played an important role in restoring hierarchy in the simulated Pre-PIN [Figure 3C, (iii) to (iv)]. The approximately 3-fold edge addition frequency (73%) compared with edge deletion frequency (27%) facilitated the generation of numerous novel clusters in the simulated Post-PIN, while not many such newly created clusters were eliminated [Figure 3C, (ii) to (iv)]. This hierarchy seems subsequently to be retained from simulated Post-PIN to Ara-PIN [Figure 3C, (v) to (viii)] and simulated Sol-PIN [Figure 3C, (ix) to (x)] even though the edge deletion frequency was found to be 2- and 1.4-fold higher than the edge addition frequency, respectively (Figure 3A). A high scaling β exponent was obtained (Figure 3C, middle and bottom β exponent distribution), which is consistent with earlier studies where several biological networks such as yeast PINs have exhibited higher scaling exponents (Koonin et al., 2007).

We further evaluated the role of the node triplication in network evolution by constructing networks devoid of this major event. In this simulation, the network size from Pre-PIN to Post-PIN was retained without triplication. Here, node deletion followed by edge dynamics created clusters in the simulated networks but never hierarchy (Supplemental Figures 5C, 5E, and 5G). Indeed, the effect of the edge dynamics was too drastic on such a reduced network size. Therefore, the combination of node and edge dynamics appears to have been necessary to maintain hierarchy in the network after the γ triplication (Figure 3C, above β exponent distribution). This suggests that modularity was actively maintained through edge and node dynamics. While hierarchical modularity provides the biological advantage of modules that can be easily added or removed, it could also be that the cost associated with the interactions drove the network to retain its hierarchy (Mengistu et al., 2016). Furthermore, because the γ triplication already established many clusters in the network, subsequent WGDs observed in the lineages toward Arabidopsis (α WGD and β WGD) and tomato (T WGT) did not significantly affect hierarchy of the network anymore [Figure 3C, (v) and (vii)]. While hierarchy was not clear for Ara-PIN and Sol-PIN in the smaller experimental networks, when up-scaled through preferential attachment to a 1000 nodes, these networks also display hierarchy (Supplemental Figure 4C).

Concerning the edge dynamics, we found edge addition to be the most important step in maintaining hierarchy in the simulated networks. We applied discrete edge deletion and addition frequencies via pure random attachment to the simulated up-scaled Pre-PIN. In a first simulation, the edge deletions preceded the edge additions and in a second one, this order was reversed. We found edge addition to be a dominant step in creating hierarchical modularity in the simulated Post-PIN (Supplemental Figures 5I and 5J), and such dominance of edge addition is not dependent on the observed relatively higher edge addition frequency because the hierarchical organization could already be observed in the simulated Post-PIN when the frequency ratio (edge addition frequency to edge deletion frequency) was 40:60 (Supplemental Figures 5K and 5L). Edge additions increase the C_k of a node, which in turn increases the overall C_k of the whole network (Supplemental Figure 5A). In our simulations, random addition of edges drove the highly abundant low degree nodes to acquire more links than the lowly abundant hubs, resulting in the low degree nodes to become parts of a highly clustered neighborhood (hub-like high degree intermediates) (Ghoshal et al., 2013). Higher edge deletion frequencies which occurred from simulated Post-PIN to simulated Ara-PIN and Sol-PIN lead to hubs getting eroded of their existing links. As a result, the hubs did not gain as many interactions as compared with the low degree nodes, which rapidly acquired more edges than in the simulated Post-PIN.

As a control, we also initialized our simulations using a homogeneous random network (initial Erdős-Rényi random Pre-PIN model) (Supplemental Figure 4A). Application of the measured node and edge dynamics to such a homogeneous random network did not yield a good fitting negative linear correlation between the variables C_k and k in the simulated extant networks (Supplemental Figure 4B) and showed relatively lower β exponent values (Supplemental Figures 5D, 5F, and 5H) compared with those from the simulated up-scaled Pre-PIN model. This implies that a scale-free heterogeneous initialization network (up-scaled Pre-PIN model) with its organization was necessary for the sustenance of hierarchical modularity in our networks. We also traced the degree distribution P_k at each stage for both models. When the initialization network was random, the observed Poisson distribution at the beginning was retained in all descendant simulated networks (Supplemental Figure 5B). By contrast, in the simulated up-scaled Pre-PIN model, we found that there was a gradual transition from a pure Power Law degree P_k distribution in the simulated Pre-PIN to a bell-shaped tailed distribution in the simulated Post-PIN, Ara-PIN, and Sol-PIN (Figure 3D). The simulations illustrate that edge addition has led to an increase in the degree of low degree nodes in the extant PINs resulting in the emergence of many hub-like high degree intermediates (Figure 3D).

The Rich Did Not Become Richer: Well-Connected Proteins Lost Rather Than Gained Interactions

To understand the underlying mechanisms behind the observed evolutionary edge dynamics, we investigated the extent to which node degree can explain conservation, gain, or loss of edges (Figure 4). We define conserved interactions as those interactions that are retained between single nodes at different points in time or those interactions that are added directly by node duplication (see Methods). We first investigated whether γ-duplicated interactions follow preferential attachment, i.e., high degree nodes will grow much stronger than low degree nodes through duplication (Figure 4B). We indeed observe this effect for the conserved interactions (Figure 4A, 1 and 2). Gained interactions include only those interactions that are completely novel and do not derive from previously present interactions through duplication. This type of gained edges allows us to investigate whether highly connected nodes are more likely to acquire new edges, which could explain how hubs arise in evolution and scale-free degree distributions originate in extant networks (Barabasi and Albert, 1999; Eisenberg and Levanon, 2003). Our data set would allow direct observation of this “the rich get richer” mechanism as nodes with high initial degrees are predicted to acquire more edges. While we observe that large nodes that arose in the network acquired their size by edge gain (Figure 4A, 4) and by edge duplication (conserved interactions; Figure 4A, 2), we find that for the MADS box networks, the initial node degree does not predict the number of interactions that will be gained (Figure 4A, 3). Rather, the opposite is true, in all three evolutionary lineages the initial degree is positively correlated to the number of interactions a protein loses: large nodes tend to lose more interactions (Figure 4A, 5). The final degree is, as can be expected, not correlated to the number of lost interactions (Figure 4A, 6). Overall, we observe that throughout evolution, new intermediate degree proteins emerge by gaining novel interactions at the expense of previous high degree proteins, suggesting that the MADS box PINs rewired to gain more intermediate hubs. This clarifies how the SEPs partially lost their hub characteristics in the evolution from the ancestral to the extant networks, while other proteins gained them.

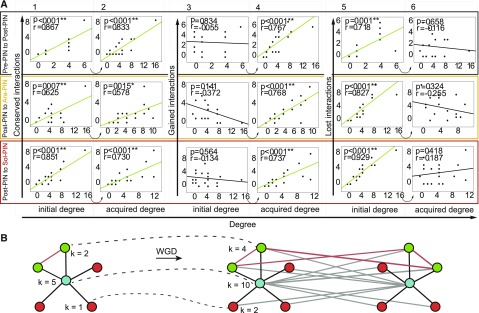
Figure 4.

Analysis of MADS Box PINs Edge Dynamics.

(A) Scatterplots indicating node degree versus conserved interactions (1 and 2), gained interactions (3 and 4), and lost interactions (5 and 6) as determined between Pre-PIN and Post-PIN (top), between Post-PIN and Ara-PIN (middle), and between Post-PIN and Sol-PIN (bottom). Correlations are represented by the Pearson correlation coefficients of the relationships and the associated p value.

(B) Example of preferential attachment as a result of WGD. k is the degree of the proteins before (left) and after (right) a WGD.

No Link between Selective Pressure, Protein Evolution, and the Number of Gained or Lost Interactions

While it is generally agreed that natural selection does not need to be inferred to explain network structure and that network topology of PINs could be explained by gene duplication (Dwight Kuo et al., 2006; Wang and Zhang, 2007), at some level natural selection needs to interact with network structure. To investigate whether the intermediate hubs that originated in the extant networks are selected for or whether different selective pressures occurred in hubs versus nonhubs, we first calculated the selective pressure (ω = d_N/d_S) for each MADS domain subfamily in general (ω_b) and more specifically for the branches following the γ triplication (ω_f). In agreement with previous studies (Shan et al., 2009), branch models showed that some subfamilies were subjected to relaxed negative selection directly after the γ triplication (Supplemental Table 1). These differences in selective pressure, however, were not linked to the protein degree or its rewiring (Supplemental Table 2). Only in the Pre-PIN network did we find that high degree nodes generally evolved more slowly (Pearson, P = 0.012), but we did not find this correlation in the Post-PIN or in the Ara- or Sol-PIN networks. Because the ω_b of a clade can be influenced by branch-specific periods of accelerated protein evolution and because we could not calculate the ω_f of all branches between the Asterid-Rosid split and Arabidopsis/Solanum, we second used sequence similarity as a proxy for the rate of protein evolution and correlated them to the node degree. Again, no significant correlations were found (Supplemental Table 2). In general, we could conclude that for the MADS domain PINs, hubs were not differently selected for than intermediate or nonhubs. Even though previously thought otherwise (Fraser, 2005), this is in line with more recent beliefs that hub proteins are not evolving more slowly (Jordan et al., 2003; Batada et al., 2006; Wang and Zhang, 2007). Finally, to more generally test whether proteins that rewired more strongly experienced natural selection, we linked the number of gained and lost interactions of each protein to their evolutionary rate (ω_b, when available ω_f, sequence similarity and identity) (Supplemental Table 2). Here, we observe that MADS subfamilies with a slower evolutionary rate (ω_b) lost more interactions (P = 0.005) in the rewiring after the γ event. However, a lack of correlation between gained or lost interactions and sequence evolution or ω_b of MADS proteins from Post-PIN to Ara-/Sol-PIN, implies that there is no generally applicable link between selective pressure, protein evolution, and the number of gained or lost interactions.

Toward a Functional History of MADS Domain Protein Interactions

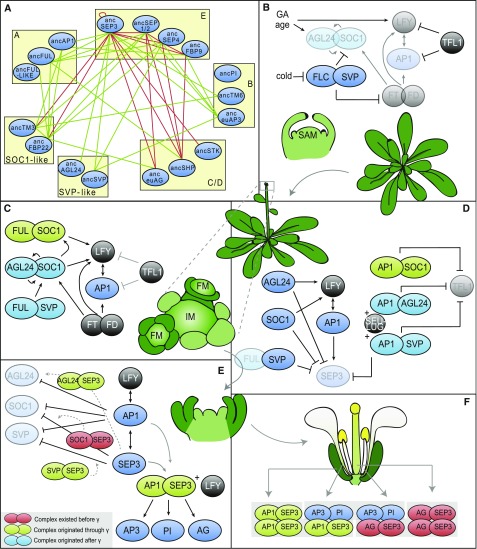
While we have to be very cautious to interpret ancestral interactions in the context of functional data available for extant species, it is interesting to explore the possible link between the evolution of the network and the evolution of developmental traits. The function of the MADS domain proteins we studied can be ordered according to the developmental transitions they control in Arabidopsis (Figure 5). The gene activation or repression steps are supported by positive or negative feedback loops that can be established through protein interactions of the upstream regulatory protein with the gene product of the gene that is regulated (de Folter et al., 2005). We asked which novel interactions originated at the origin of core eudicots and which associated functions could have evolved at this point in time (Figure 5A).

Figure 5.

Overview of all MADS Box Complexes Involved in Floral Transition in Arabidopsis.

(A) Post-PIN network. Green lines denote all interactions that originated through γ, and red lines denote interactions that existed before the γ triplication. Proteins are ordered into their subfamilies by yellow boxes.

(B) and (C) MADS domain complexes before (B) and during early floral transition (C).

(D) MADS domain complexes at the start of floral organ development (stages 1 and 2) (D), during stage 3 (E), and in the mature flower (F). Red complexes existed before the γ triplication, green complexes evolved through the γ triplication, and light-blue complexes arose later. Dark-blue ellipses are proteins not in complex or not discussed here. Black circles are non-MADS domain proteins. Transparent proteins are weaker expressed in that stage. Dotted arrows denote suggested complex formation and functions.

Before the floral transition is initiated, the FLC-SVP complex represses floral integrators SOC1 and FT at the shoot apex (Li et al., 2008; Posé et al., 2012; Mateos et al., 2015). Meanwhile, AP1 and LFY are repressed by TFL1, impeding the development of the inflorescence meristem (Figure 5B) (Liljegren et al., 1999). When FLC is downregulated by external factors like cold, a switch in interaction partner of SVP from FLC to FUL has been proposed to activate SOC1, whose protein product again interacts with FUL (Figure 5C) (Liu et al., 2009a; Balanzà et al., 2014). The floral transition is further regulated by AGL24-SOC1 dimers, which specify inflorescence meristems through a positive feedback loop (Yu et al., 2004; Liu et al., 2007, 2008, 2009b). Both AGL24-SOC1 and FUL-SOC1 dimers are thought to activate LFY expression and by consequence AP1 expression, which then both initiate inflorescence meristem identity (Liu et al., 2009a; Balanzà et al., 2014). Our data suggest that the FUL-SOC1 interaction originated through the γ triplication (Figures 5A and 5C). By contrast, AGL24-SOC1 and FUL-SVP emerged both in the lineages to Arabidopsis and tomato (Figures 5A to 5C), but possibly was not ancestral and could therefore perform a different function in these two species.

In emerging floral meristems, repression of TFL1 is eventually reached by AP1 dimerization with SOC1, AGL24, and SVP (Liu et al., 2013). To prevent precocious development of the floral organs, SEP3 is repressed by the flowering time proteins AGL24, SVP, and SOC1 in addition to the corepressor complex formed by AP1-AGL24, SEU-LUG, and AP1-SVP (Figure 5D) (Franks et al., 2002; Gregis et al., 2009; Liu et al., 2009a). The AP1-SOC1 dimer appeared to originate through γ, whereas AP1-SVP and AP1-AGL24 arose later (Figure 5D).

When SEP3 levels eventually accumulate through activation by AP1 and LFY in floral stage three, it starts to repress the flowering time proteins in return in concert with AP1 (Figure 5E) (Kaufmann et al., 2009). It would be plausible that this repression occurs through negative feedback regulation of SEP3-SOC1, SEP3-SVP, and SEP3-AGL24 complexes. While a SOC1-SEP3 interaction appears to be ancestral, our data suggest that SVP-SEP3 and AGL24-SEP3 complexes originated through γ, which thus may have supported the transition to flower development (Figure 5E). A SEP3-AP1 dimer, which also originated at the origin of core eudicots according to our data, has been proposed to activate floral organ identity genes AG, AP3, and PI together with LFY (Figure 5E) (Liu et al., 2007; Gregis et al., 2009; Kaufmann et al., 2010). The AP1-SEP3 complex also has a role in establishing the elusive A-function in Arabidopsis and in organizing sepal and petal identity and is more generally involved in the transition from floral meristem identity to floral organ identity (Figure 5F) (Litt, 2007; Causier et al., 2010; Heijmans et al., 2012). It should be noted, however, that AP1 and SEP3 were already able to interact in the pre-PIN when mediated by SEP3 in Y3H (Alhindi et al., 2017). Therefore, it could be that AP1-SEP3 already performed these functions mediated by SEP3 before the γ triplication.

Our data furthermore provide evidence for the idea that several more dimeric interactions originated at the origin of core eudicots (e.g., SEP3-euAP3 or FUL-SHP) (Figure 5A); however, for these interactions no functional data are available in Arabidopsis. While we do believe that the major functions regulated by MADS domain complexes are conserved, our data suggest that the complexes controlling and supporting these functions underwent extensive evolution in their exact assembly and composition. New complexes that originated after the γ triplication according to our data (e.g., FUL-SOC1 or SVP-SEP3) seem to be predominantly involved in redundant feedback mechanisms (Figures 5B to 5F). This might have contributed to the robustness of the timing and organization of flowering transition and floral development.

DISCUSSION

In this study, we evaluated the impact of the γ triplication at the origin of core eudicots on the protein interaction network of MADS domain transcription factors, which are key regulators of reproductive development. Rather than using extant data to infer ancestral networks, we resurrected ancestral proteins and used these and their descendant proteins from extant Arabidopsis and tomato to trace the origin and evolution of MADS domain protein interaction networks. In comparison to previous network evolution studies (Matthews et al., 2001; Wagner, 2001; Liu et al., 2010; Arabidopsis Interactome Mapping Consortium, 2011; Das et al., 2013; Reinke et al., 2013), our study contributes interactions of ancestral proteins.

We observed that the ancestral hexaploidization event, referred to as γ triplication, has strongly contributed to the growth of the MADS domain protein interaction network, while later WGDs had a smaller impact. This suggests that growth of the MADS-PIN could be constrained because the size of the network acquires an apparent maximum and network density is relatively constant through γ even after multiple additional rounds of WGD. Possibly, a mechanism operates that restricts the network size and density in which structural properties of the proteins limit the possible specificity of MADS domain proteins. In this way, the more strict control of gene expression after the γ triplication could have evolved to avoid proteins from misinteracting (Zarrinpar et al., 2003; Chanderbali et al., 2016). Alternatively, the lack of further expansions following the γ triplication could also suggest that there was no positive selection toward increased network size in later duplications.

A clear observation is that the γ triplication allowed for the rapid rewiring of the protein interaction network, consistent with the rewiring of protein interactions after WGD previously inferred from the Arabidopsis protein interaction map (Arabidopsis Interactome Mapping Consortium, 2011). This rewiring occurred predominantly by the evolution of new interactions and surprisingly some novel interactions were in turn established with paralogous proteins, a process that has not previously been detected and which we propose to call neoredundancy. This process is intuitive because recent paralogs share a similar sequence and probably therefore gain the same interaction partners even when only one interaction is adaptive. As a consequence, previous studies may have overestimated the number of ancestral interactions when inferring these from extant interactions (Liu et al., 2010; Reinke et al., 2013).

While several mechanisms that drive the evolution of protein interaction networks have been proposed, they remain plausible explanations that have not been directly validated. We found that in the case of MADS domain proteins, the loss or retention of nodes through gamma was not explained by gene dosage balance (Arabidopsis Interactome Mapping Consortium, 2011; Guo et al., 2013). This may seem surprising as MADS domain proteins could be expected to follow this proposed process given that they typically assemble into higher order complexes and are preferentially retained after WGDs (Veron et al., 2007; Smaczniak et al., 2012). While we provide a novel way of directly testing dosage balanced gene retention, the fact that we could not observe it is likely just a consequence of the still limited size of our data set. We did observe preferential attachment of conserved interactions through gene duplication; however, we did not find evidence for preferential attachment of new interactions to existing hubs. By contrast, hubs preferentially lose interactions in our data, which is in agreement with the rewiring and the origin of new hubs we observe.

The topology of the network does not seem to have been qualitatively affected by the γ triplication, as both ancestral and the extant networks are scale free and modular. While the observed node and edge dynamics of the γ triplication separately would have disrupted hierarchical modularity of the network, in combination they contributed to maintaining hierarchy, suggesting that hierarchy is maintained because this is advantageous or because a continuously present selective pressure results in hierarchy. The fact that in the simulations the hierarchical modularity is maintained in the networks through the application of essentially random network dynamics suggests that it is not maintained via selection on individual interactions. Rather, selection could act on the strength of network dynamics. This would be consistent with the relatively constant network density we observe, which suggests that a cost is associated with gaining or losing interactions (Zarrinpar et al., 2003; Clune et al., 2013; Mengistu et al., 2016).

The rapid rewiring illustrates the functional innovation potential of the γ triplication. The innovation occurred primarily by connecting flowering time proteins to floral meristem identity proteins of the SEP and AP1 lineages. We could speculate that the increased control of transition to flower development could be related to the canalization of floral development in Pentapetalae (Soltis et al., 2003; Chanderbali et al., 2016; Soltis and Soltis, 2016). The more elaborate feedforward and feedback control of the transition to a floral meristem may be one of the molecular mechanisms that established increased robustness of the number of floral organs and the origin of an AP1-SEP3 dimer might have contributed to the differentiated perianth as observed in extant core eudicots (Ronse De Craene and Brockington, 2013).

Based on our current understanding of polyploidization, the gamma triplication is unlikely to have originated from a single genomic event. Most likely, a hybrid formed between a tetraploid, resulting from a genome duplication or hybridization, and a diploid. In this study, we nevertheless treated it as a single event because the unconstrained phylogenies we obtained in an earlier study (Vekemans et al., 2012) did not point to speciation events occurring between the two events, suggesting that the two steps occurred in a relatively narrow window of evolutionary time. However, it is still possible that several millions of years have passed between the two steps. If so, how would such a lag phase affect the interpretation of our observations? It could be that the two events unequally contributed to the rewiring we observe. In that case, the increased rewiring rate is not related to the special case of hexaploidization rather than diploidization and another cause needs to be sought for the impact of this event. On the other hand, the two-step process with a lag phase may have accelerated rewiring as a lag phase could have permitted the networks to have evolved independently in the tetraploid and diploid ancestor before their hybridization brought these networks back together. In this scenario, gene dosage retention becomes less likely as paralogs may have diverged already and hexaploidization could have contributed to the origin of multiple hubs by bringing together old and new modules.

It is also important to note that our data are not always consistent with existing data for extant species or with inferences of ancestral interactions based on such data, which should caution against overinterpretation of individual interactions (Liu et al., 2010). Several reasons can explain such discrepancies. While the ancestral sequences were reconstructed with relatively few ambiguities, inaccuracies could still have contributed to false-positive or false-negative results. The yeast two-hybrid system used here also differs from the ones used in other networks. On the other hand, the available evolutionary inferences have probably been biased toward interaction as ancestors were considered to interact if one extant paralog interacts (Liu et al., 2010). Our current and previous data suggest that the reasoning to support this, namely, that interactions are more easily lost than gained, is probably not true (Ruelens et al., 2017). We also frequently observed neoredundancy, where two descendant proteins interact with a third, but the ancestor did not interact, which would interfere with the reconstruction of ancestral states. Finally, the interaction between two proteins in vivo can also be influenced by a third protein or the presence of DNA in the case of transcription factors, something we did not investigate here.

METHODS

Reconstruction of Ancestral MADS Box Proteins

Sequence Alignments

Initial nucleotide alignments of the MADS box subfamilies AP1, AP3, PI, AG, AGL2/3/4, and SOC1 were obtained from Viaene et al. (2009) and Vekemans et al. (2012). These data matrices were supplemented with sequences obtained from Genbank (http://www.ncbi.nlm.nih.gov/), oneKP (https://sites.google.com/a/ualberta.ca/onekp/home) (Matasci et al., 2014), Phytozome (Goodstein et al., 2012; Vekemans et al., 2012), or from the Gunnera maniacata and Pachysandra terminalis RNA-seq data set from (Vekemans et al., 2012). STK, SEP3, and SVP/AGL24 alignments were generated de novo from sequences obtained from the aforementioned databases. The final data matrices contained between 70 (STK) and 215 (SVP/AGL24) sequences representing all major angiosperm clades with an emphasis on taxa from orders that branched off around the γ triplication. Sequences were initially aligned with MUSCLE (Edgar, 2004) and manually curated in McClade 4.08 (Maddison and Maddison, 2005). Accession numbers of all genes used for ancestral reconstruction are listed in Supplemental Data Set 1.

Phylogenetic Reconstruction

Maximum likelihood phylogenies of MADS box subfamilies AP1, AP3, PI, AG, SEP1/2/4, and SOC1 were retrieved from Viaene et al. (2009) and Vekemans et al. (2012). STK, SEP3, and SVP/AGL24 ML phylogenies were constructed using PhyML 3.0 as implemented in Geneious 5.4 or by RAxML (Guindon and Gascuel, 2003; Stamatakis et al., 2008; Guindon et al., 2010; Kearse et al., 2012) using the GTR +I +G substitution model with SH-like or bootstrap support values generated from 100 bootstrap replicates. Even though the resulting SVP phylogeny highly insinuated that SVP, AGL24, and StMADS11 are sister clades originating at the γ triplication, we used synteny implemented in PLAZA 3.0 (Proost et al., 2015) to further confirm their origin at the triplication (Supplemental Figure 7 and Supplemental Data Sets 3 and 4). To infer ancestral proteins, a tree representing the evolutionary history of the different taxa is needed. Since the acquired ML gene trees do not always follow the consensus angiosperm phylogeny, all phylogenies were manually constrained up until the order level to match with the angiosperm phylogeny described by Moore et al. (2011). Branch lengths were estimated on these manually curated trees using RAxML 7.0.4 (Stamatakis, 2006) with the JTT+G or JTT+I+G models of protein evolution, as determined by ProtTest 2.4 (Abascal et al., 2005).

Ancestral Sequence Reconstruction

The indel history of the sequence alignments was manually reconstructed. All insertions that occurred after the γ-event were deleted from the matrix. Next, the nucleotide sequence alignments were translated to proteins. The optimized gene trees with branch lengths, the protein alignments, and best-fit model of evolution (JTT + G) were then used for maximum likelihood marginal reconstruction implemented in PAML4.4 (Yang, 2007). Ancestral sequences were estimated at the last node before the γ triplication (after the divergence of Buxales and before the divergence of Gunnerales) and at the Asterid-Rosid split. Phylogenetic trees used for ancestral reconstruction indicating ancestral nodes at which ancestral proteins were reconstructed are shown in Supplemental Figure 1. Finally, the obtained ancestral protein sequences were converted to nucleotide sequences, codon optimized for yeast and Arabidopsis, and synthesized by GenScript. All ancestral sequences are shown in Supplemental Data Set 2. AncStMADS11 and ancAGL14 could not be accurately reconstructed and were not analyzed further.

Cloning of Arabidopsis thaliana, Tomato, and Ancestral MADS Box Genes

The full-length coding sequences of Arabidopsis MADS box genes were obtained from TAIR to design primers for gene amplification. The following 17 genes were selected: AP1, CAULIFLOWER (CAL), FUL, AP3, PI, AG, SHATTERPROOF1 (SHP1), SHP2, SEEDSTICK (STK), SEP1, SEP2, SEP4, SEP3, SVP, AGAMOUS-LIKE24 (AGL24), AGL42, and SOC1. Tissue samples from Arabidopsis were frozen in liquid nitrogen and stored at −80°C. RNA was isolated from these samples using the TRIzol method following the manufacturer’s instructions. The purity and concentration of RNA samples were determined using a NanoDrop spectrophotometer. Synthesis of cDNA from RNA was performed using the GoScript reverse transcription system (Promega). Tomato (Solanum lycopersicum) MADS box genes were amplified from published yeast two-hybrid constructs. The following 21 cDNAs were subcloned into the pGADT7 (pAD) and pGBKT7 (pBD) vectors (Clontech Laboratories): MC, TM4, SLMBP7, SLMBP20, TAP3, TM6, LePI, TPI, TAG1, TAGL1, SLMBP3, TAGL11, TM29, RIN, LeMADS1, SLMBP21, TM5, JOINTLESS, SLMBP24, SLMBP18, and TM3. Ancestral genes were amplified from pUC57 constructs containing the ancestral genes obtained from GenScript and cloned into pAD and pBD vectors. Due to unknown reasons, the subcloning of TM6 into the pBD vector was not achieved. Miniprep was performed using a PureYield Plasmid Miniprep System (Promega). All Miniprep plasmid samples were sent for sequencing to confirm in frame insertion of the correct gene in the expression vectors (LGC Genomics).

High-Throughput Yeast Two-Hybrid Method

Recombinant pAD and pBD vectors containing ancestral or extant MADS box genes were cotransformed into the Y187 yeast strain. To determine possible autoactivation, recombinant pBD constructs were cotransformed with an empty pAD vector. Cotransformation of empty pAD and pBD vectors was used as a negative control to measure background signal. Yeast transformation was performed as described (Gietz and Woods, 2006). Following transformation, double transformants were selected on SD-Leu -Trp plates. To analyze protein-protein interaction, β-galactosidase activity was detected by use of ortho-nitrophenyl-β-galactoside (ONPG) as a substrate (Miller, 1972). After 4 d on selection plates, three to five independent cotransformants were pooled into cotransformant groups as we expect no significant biological variation between cotransformants given their identical genotype. These cotransformant pools were grown overnight in 2 mL SD medium at 30°C with shaking at 230 rpm. The following day, 100 μL YPD medium was transferred to each well in a 96‐well 200-μL microplate, and for each combination, 25 μL of the overnight culture was added into three different wells to perform the β-galactosidase assay in triplicate. This allowed us to accurately take into account variation during the assay. The cells were grown at 650 rpm at 30°C and harvested by centrifugation (5 min at 1000g at room temperature) when OD₆₀₀ reached 0.5 to 0.8. Cell pellets were resuspended in 150 μL Z buffer and shaken at 700 rpm at 30°C for 15 min to ensure sufficient homogenization of the cell pellets. Subsequently 100 μL of the resuspended cell culture was transferred to a 2.2-mL 96‐well plate (MegaBlock). Cells were broken by three cycles of freezing in liquid nitrogen and thawing in a 42°C water bath. Afterwards, 160 μL 4 mg/mL ONPG in Z buffer and 700 μL β‐mercaptoethanol in Z buffer (1:370, v/v) were added to each well. The MegaBlock was then incubated at 30°C for 6 h. Following incubation, 96 μL from each well was transferred to a 200-μL 96‐well plate. To stop the reaction, 40 μL of 1 M Na₂CO₃ was added to each well. Finally, absorbance at 420 nm was measured. The amount of β-galactosidase which hydrolyzes 1 μmol of ONPG to ortho‐nitrophenol and d‐galactose per minute per cell is defined as 1 unit. Therefore, β-galactosidase activity (Miller units) was calculated using the following formula: Miller units = (1000 × A₄₂₀) / (t × V × OD₆₀₀), with A₄₂₀ = absorbance at 420 nm, OD₆₀₀ = optical density at 600 nm, t = 360 min, and V = 0.1 mL.

Identification of Positive Protein-Protein Interactions

Miller units of each pairwise combination were compared with the background activity of the negative control and evaluated by Student’s t test (one-tailed). If the combination was significantly higher than the control (P value < 0.05), these combinations were considered as potentially interacting. As autoactivation can lead to false positives, we also determined for each potential interacting combination the presence of autoactivation by comparing them with their respective autoactivation samples, again using Student’s t test (one-tailed). If no autoactivation was detected, the combination was assigned as positive for interaction. For those combinations in which autoactivation was also detected, Miller units were compared with their autoactivation samples by Student’s t test (one-tailed). If the Miller units of the combinations were significantly higher than their autoactivation (P value < 0.05), these combinations were assigned as true interactions. If they were not significantly different, these combinations were considered as false positives due to autoactivation. Finally, for two proteins to be interacting, at least one direction of the two combinations has to be assigned as a true interaction (i.e., X-AD with Y-BD and/or Y-AD with X-BD).

Yeast Two-Hybrid Plate Assay Using X-Gal

Out of all tested pairs, a random sample of 101 interactions was additionally tested with the same yeast strain and vectors, but with another reporter gene, MEL1, which codes for α-galactosidase. Three to five cotransformed colonies were cultured overnight in SD-Leu-Trp medium. Then, 1 μL of saturated culture was spotted on SD-Leu-Trp supplemented with X-α-gal. Colonies were incubated at 30°C for 2 d before photographs were taken. Bait proteins combined with empty vectors were used to control autoactivation and cotransformation of empty pAD and pBD vectors acted as a negative control. An interaction was defined positive when blue coloration was visually stronger than the autoactivation control.

GST Pull-Down

GST fusion proteins of Post-PIN ancSEP3, ancFBP22, and anceuAP1 were constructed in the pGEX-T4 vector and expressed in BL21(DE3) Escherichia coli cells. All HA-tagged Post-PIN proteins were expressed through the pGADT7 vector in Y187 yeast cells. BL21(DE3) cells were lysed in E. coli lysis buffer (1× PBS, 0.4% [v/v] Triton, 2 mM MgCl₂, 1 mM EDTA, 2 mM DTT, 1 tablet protease-inhibitor mix/10 mL buffer, 0.2 mg/mL lysozyme of a 50 mg/mL stock, and 1 mM PMSF) by sonication. Yeast cells were vortexed with glass beads in yeast lysis buffer (1× PBS, 0.1% [v/v] Triton, 10% [v/v] glycerol, 2.5 mM MgCl₂, 1 mM EDTA, 2 mM DTT, 10 mM NaF, 0.4 mM Na₃VO₄, 0.1 mM β-glycerol-fosfaat, 1 tablet protease-inhibitor mix/10 mL buffer, and 1 mM PMSF). Glutathione-sepharose beads were washed twice in E. coli wash buffer (1× PBS, 0.1% [v/v] Triton, 2 mM MgCl₂, 1 mM EDTA, and 1 mM DTT). Then, 50 μL wash buffer was added to 50 μL of the beads and the samples were then added to the E. coli lysates. New Glutathione-sepharose beads were washed twice with yeast lysis buffer. Washed beads in 200 μL binding buffer (1× PBS, 0.05% [v/v] Triton, and 0.1 mM DTT) were added to the yeast lysates. Both were incubated for 1 h at 4°C and then centrifuged for 1 min at 4°C at 400g. The E. coli beads-pellet was washed four times in wash buffer before the bead-bound proteins were resuspended in 200 μL binding buffer. For the yeast extract, the supernatant was carefully taken to collect the HA-tagged proteins without touching bottom glass beads. Then, 500 μL of GST-fused proteins was combined with 500 μL of HA-tagged proteins and incubated for 1 h at 4°C in a roller drum. After centrifugation at 4°C at 400g, the pellet was washed three times with 1× PBS containing 0.1% (v/v) Triton and resuspended in 60 μL 2× SDS sample buffer (100 mM Tris-HCl, pH 8.0, 20 mM β-mercaptoethanol, 4% [w/v] SDS, 0.2% [v/v] bromophenol blue, and 20% [v/v] glycerol). GST-bound proteins were analyzed by SDS-PAGE and visualized by immunoblot analysis using Anti-HA-peroxidase, High Affinity antibody Sigma-Aldrich (Roche; catalog no. 12013819001). Lysates were used as input. Empty pGEX-T4 vector combined with HA-tagged ancestral proteins was pulled down to test the proteins’ stickiness to the beads. Interactions with TM3, euAG, FULL-like, SVP, and AGL24 were left out since lysis did not work properly on these samples.

Network Parameters

All network parameters were calculated in Cytoscape 3.2.1 (Smoot et al., 2011) or NetworkX (Hagberg et al., 2008). Degree k: the degree k of a node refers to the number of edges that connect with other nodes; degree distribution P(k): represents the probability of a randomly selected node with degree k; scale-free network: the degree distribution P(k) of a randomly selected node with degree k follows a power-law distribution which is proportional to k^-γ, where γ is the degree exponent. In an undirected scale-free protein interaction network, there are only a few highly connected proteins (hubs) that connect to a large number of individual proteins with only few interactions; network heterogeneity: reflects the tendency to contain hubs; network clustering coefficient: there is also a degree of inherent modularity or clustering representative of the interconnected subnetworks between nodes that makes the global network organized or hierarchical. The clustering coefficient C_k of each node in a protein interaction network is then defined as a ratio between the number of edges from the neighbors of that node and the maximum number of edges that could exist between the neighbors of that node. The distribution of clustering coefficient C(k) is proportional to k^‐β in a highly hierarchical network, where β is the scaling exponent.

Network Analyses Using Parameterized Simulations

All computations, network analysis, and generation of plots were performed using the R programming language (version 3.1.0) and igraph 0.7.1 (Csardi and Nepusz, 2006).

Network Up-Scaling

We initialized our simulations with the following two different network types. (1) Initial Erdős-Rényi random Pre-PIN model: An Erdős-Rényi network (1960) (Erdös and Rényi, 1960) was generated using erdos.renyi.game function of the igraph R package. We used a G(n,p) undirected graph that had n = 1000 nodes and the probability that an edge was present in the graph was P = 0.01. The resultant node connectivity in the network followed a Poisson distribution. (2) Initial up-scaled Pre-PIN model: To obtain the initial up-scaled Pre-PIN model, we implemented the Barabási-Albert model of preferential attachment (Barabasi and Albert, 1999) using R script. We started with the seven connected nodes of Pre-PIN. A new node was added each time such that the probability of node attachment was dependent on the degree k of the previous node. This network was allowed to grow to a size of 1000 nodes. The final network had a node size of 1000 and 1005 edges which followed the power law Pk ∼ k γ. We achieved this by generating a matrix of data elements created by random permutation of all the elements of a vector x. A vector of weights that can be explained as the node degree k was used to obtain the elements of vector x which was being sampled.

Simulation Process

The various events of WGDs and network dynamics were simulated on an evolutionary time scale and the empirical probabilities measured from the actual Y2H networks were applied. The networks were triplicated or duplicated to hypothetically recreate the WGD events as a result of which the whole set of nodes started interacting with their partners and their partners’ paralogs. For node deletion, random nodes were sampled and eliminated. With random node deletion several links associated with those nodes were also automatically deleted. The removal of nodes was always placed after WGD events since nonfunctional genes would be quickly silenced or lost from the genome after WGDs (Giot et al., 2003). The process of application of edge dynamics was randomized. Edges were either added or deleted, decided by random Bernoulli trials. The measured edge addition and deletion frequencies from the Pre-PIN, Post-PIN, Ara-PIN, and Sol-PIN were used as the probabilities for the Bernoulli trials and these trials were performed n times based on the calculated age estimates. A new interaction was created by appending an edge to the existing network matrix. The edges to be added were predetermined by randomly sampling any two nodes at a time from the pool of remaining nodes in the network and linking them. To eliminate an interaction, we randomly chose one existing interaction at a time and deleted it.

Statistical Analysis

Ten simulations were performed and the mean, variance, and sd were calculated. At each stage of application of network dynamics, we determined (1) degree distribution (P_k) and (2) clustering coefficients; (C_k) of the nodes in the network. To determine the scale-freeness of the network, we plotted the (P_k) of the nodes against the node degrees in the logarithmic scale. To determine the hierarchy of the network, we plotted the (C_k) of the nodes having (k) connections as a function of (k) in the logarithmic scale. Linear regression was used to model the relationships between the above variables at each step of the simulation process. The quality of the linear fit of the model was estimated using R-squared estimate of goodness of fit.

Detecting Selection Pressures

Selection pressures (ω = d_N/d_S, the ratio of nonsynonymous over synonymous substitutions) were estimated using the PAML4.4 software package (Yang, 2007) and the phylogenetic trees and (nucleotide) alignments used for ancestral reconstruction. Branch lengths were reestimated in RAxML (GTR + G) using the nucleotide alignments. To test for differences in selection pressure on the branches between two nodes compared with the selection pressures on the rest of the tree (background branches), we compared the “one-ratio” branch model (M0) to a “two-ratio” branch model (M2) in which we selected all branches between the γ triplication (or the branching of the Buxales when the gene did not duplicate) and the Rosid-Asterid split as a foreground (Yang, 1998). Nested likelihood ratio tests (LRT = 2*(lnL alternative model – lnL null model)) were performed between branch models M0 and M2. P values were obtained using the χ² distribution with a 0.05 significance at a critical value of 3.84 for 1 degree of freedom.

Determination of Interaction Changes (Rewiring) and Correlation Analyses

To examine correlations between network rewiring (as in number of changes in interactions) and selective pressure or sequence similarity, we compared the interactions of each individual protein to the interactions of its ancestor. Since there are always four possible fates that a (mis-)interaction can undergo, we used the following definitions to describe the network rewiring. Changes in interactions can be caused by gains or losses of interactions. A gained interaction is here defined as an interaction between two proteins, while their ancestors did not interact. For instance, anceuAG interacts with ancFBP22, while its pre-γ ancestor ancAG did not interact with ancSOC1 (Figure 2A). A lost interaction is defined as a lack of interaction between two proteins, while both ancestors did interact. For instance, anceuAG does not interact with ancSVP nor with ancAGL24, while their ancestors ancAG and ancSVP/AGL24 did. In this case, we counted two lost interactions, because anceuAG lost the ability to interact with both ancSVP and ancAGL24. Conservation in interactions can apply to conserved interactions or to conserved misinteractions. A conserved interaction is defined as an interaction between two proteins, when both ancestors already interacted. For instance, anceuAG interacts with ancSEP3 just like their ancestors ancAG and ancSEP3 already did. Finally, a conserved misinteraction is defined as a lack of interaction between two proteins, when both ancestors already did not interact. For instance, anceuAG does not interact with anceuAP3 or with ancTM6, while their pre-γ ancestors ancAG and ancAP3 already did not. This accounts for two conserved misinteractions.

After quantifying the changes in interactions, Pearson correlations were used to link them to the selective pressure over the whole gene-tree (background = ω_b), the d_N/d_S over the branches between the branching off Buxales and the Rosid-Asterid split (foreground = ω_f) and to the sequence similarity between the proteins and their direct ancestor. Significance was determined at the P < 0.05 level. Sequence similarity was determined at the protein level using EMBOSS Needle Pairwise sequence alignment with default parameters.

Accession Numbers

Accession numbers of all genes used for ancestral reconstruction are listed in Supplemental Data Set 1.

Supplemental Data

• Supplemental Figure 1. Simplified phylogenetic trees of the MADS box gene subfamilies used for ASR and selective pressure estimation.

• Supplemental Figure 2. Ancestral sequences and their accuracy.

• Supplemental Figure 3. Validation of the PPIs obtained in this study.

• Supplemental Figure 4. C(k) and P(k) distribution for tracing of elementary processes in network evolution from Pre-PIN, via Post-PIN until extant Ara-PIN and Sol-PIN by simulation models.

• Supplemental Figure 5. Additional simulations for understanding the consequence of initialization network size and topology, the role of γ triplication and the dominance of random edge addition.

• Supplemental Figure 6. Phylogenetic relationships of SVP, AGL24, and StMADS11.

• Supplemental Table 1. LRT and parameter estimations of different Branch models.

• Supplemental Table 2. Pearson correlations between a proteins edge rewiring (gained or lost interactions) or degree, and its rate of protein evolution (selection pressure of background branches (ωb) and foreground branches (ωf) and sequence similarity.

• Supplemental Data Set 1. List of species used in phylogenetic analyses with accession numbers and alignments.

• Supplemental Data Set 2. Reconstructed ancestral protein sequences in FASTA format.

• Supplemental Data Set 3. Calculated Miller units to determine PPIs. Derived PPIs by F- and t tests.

• Supplemental Data Set 4. Alignment of O-FUCOSYLTRANSFERASE used to generate the tree in Supplemental Figure 6.

• Supplemental Data Set 5. Alignment of MECHANOSENSITIVE ION CHANNEL PROTEIN3 used to generate the tree in Supplemental Figure 6.

Dive Curated Terms

The following phenotypic, genotypic, and functional terms are of significance to the work described in this paper:

• AGL24 Gramene: AT4G24540

• AGL24 Araport: AT4G24540

• AGL42 Gramene: AT5G62165

• AGL42 Araport: AT5G62165

• ap1 Gramene: AT1G69120

• ap1 Araport: AT1G69120

• FLC Gramene: AT5G10140

• FLC Araport: AT5G10140

• lfy Gramene: AT5G61850

• lfy Araport: AT5G61850

• SDS Gramene: AT1G14750

• SDS Araport: AT1G14750

• SEP1 Gramene: AT5G15800

• SEP1 Araport: AT5G15800

• SEP2 Gramene: AT3G02310

• SEP2 Araport: AT3G02310

• SEP3 Gramene: AT1G24260

• SEP3 Araport: AT1G24260

• SEP4 Gramene: AT2G03710

• SEP4 Araport: AT2G03710

• SHP2 Gramene: AT2G42830

• SHP2 Araport: AT2G42830

• tag1 Gramene: AT2G19450

• tag1 Araport: AT2G19450

• TFL1 Gramene: AT5G03840

• TFL1 Araport: AT5G03840

• TPI Gramene: AT3G55440

• TPI Araport: AT3G55440

• application CHEBI: CHEBI:33232

• branch AmiGo: PO:0025073

• initial AmiGo: PO:0004011

• proteins CHEBI: CHEBI:36080