Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Jun 25;58(12):2450–2459. doi: 10.1021/acs.jcim.8b00256

High-Throughput Screening Approach for the Optoelectronic Properties of Conjugated Polymers

Liam Wilbraham †, Enrico Berardo ‡, Lukas Turcani ‡, Kim E Jelfs ‡,*, Martijn A Zwijnenburg †,*
PMCID: PMC6307085  PMID: 29940733

Abstract

graphic file with name ci-2018-00256d_0007.jpg

We propose a general high-throughput virtual screening approach for the optical and electronic properties of conjugated polymers. This approach makes use of the recently developed xTB family of low-computational-cost density functional tight-binding methods from Grimme and co-workers, calibrated here to (Time-Dependent) Density Functional Theory ((TD)DFT) data computed for a representative diverse set of (co)polymers. Parameters drawn from the resulting calibration using a linear model can then be applied to the xTB derived results for new polymers, thus generating near DFT-quality data with orders of magnitude reduction in computational cost. As a result, after an initial computational investment for calibration, this approach can be used to quickly and accurately screen on the order of thousands of polymers for target applications. We also demonstrate that the (opto)electronic properties of the conjugated polymers show only a very minor variation when considering different conformers and that the results of high-throughput screening are therefore expected to be relatively insensitive with respect to the conformer search methodology applied.

Introduction

High-throughput virtual screening (HTVS) has emerged as a powerful tool across many areas of materials discovery.1 At its core, it concerns the automated data-driven discovery of promising candidate materials for a particular application. Low-computational-cost techniques are applied in an initial screening step to expose promising leads, which are then fed through more accurate, higher-cost techniques to refine computed properties.2 HTVS is applied to explore vast, complex chemical spaces in order to accelerate the discovery of promising materials, as well as to reduce experimental effort spent on negative leads. Recent examples include the successful screening of both organic and inorganic materials for applications in areas including photovoltaics,3−8 light emitting devices,9,10 information storage,11,12 gas storage,13−19 and catalysis,20,21 often resulting in materials being synthesized with record-breaking properties.10,18,19

Conjugated polymers are used as light absorbers and electron donor layers in organic photovoltaics,22−26 the light-emitting layer of organic light emitting diodes,27,28 electrodes for batteries and supercapacitors,29,30 and photocatalysts for proton reduction and overall water splitting.31−35 All of these applications exploit a combination of the optoelectronic and/or redox properties of conjugated polymers in combination with their relatively facile tunability through copolymerization and chemical modification, as well as the earth abundant nature of their constituents (if not the catalysts used to make them via Suzuki or Stille coupling). Applying HTVS approaches to polymeric materials, however, remains challenging. Because of the size of the required oligomeric models, calculations on polymers are inherently more computationally costly than for small(er) molecules. Moreover, because of the large numbers of potential monomer sequences, compositions, and the potential for disorder along the polymer chains, extremely large numbers of calculations can be required. For example, constructing simple, ordered, two-component copolymers from a pool of 500 symmetric monomer units leads to over 120 000 possible polymers. If three-component copolymers are considered for the same monomer pool, the number of possible polymer increases to more than 20 million. Finally, most conjugated polymers form amorphous or poorly crystalline solids, ruling out periodic calculations.

The fundamental optoelectronic properties of a material can be understood36 in terms of (i) the optical gap (Δo), the minimum energy to form a excited electron–hole pair bound through their mutual electrostatic interaction (an exciton) and below which the material is transparent to light, (ii) the fundamental gap, the minimum energy to form a noninteracting excited-electron and hole, (iii) the exciton binding energy, the difference between the fundamental gap and optical gap, a measure of how strong the excited electron and hole are bound in the exciton, and (iv) the ionization potential (IP) and electron affinity (EA), the energy required to remove an electron and released upon adding an electron to an oligomer, respectively. IP and EA are commonly expressed in terms of standard reduction potentials vs a standard electrode, e.g., the standard hydrogen electrode (SHE). The fundamental gap, finally, can be defined in terms of the difference between IP and EA.

Because of the lack of periodicity, properties such as the optical gap, IP, and EA of polymers are typically calculated for a single oligomeric strand; a description that can be improved upon by combining this description with embedding37−39 in a dielectric continuum model to account for environmental effects. In the latter case, one assumes that all intermolecular interaction, be it with other polymer strands or a solvent or electrolyte, can be described in terms of an (isotropic) dielectric response. Generally, the underlying calculations are performed using Density Functional Theory (DFT) or the combination of DFT with GW theory, methods that, because of their computational cost, are not ideally suited for HTVS. Hutchison and co-workers pioneered the use of semiempirical methods to perform high-throughput virtual screening for properties of conjugated polymers.3,7,40 Semiempirical methods such as AM1,41 PM6,42 and PM743 approximate Hartree–Fock or DFT by parametrizing integrals that are expensive to calculate. This parametrization, combined with the use of minimal basis-sets results, makes semiempirical calculations orders of magnitude faster than DFT but potentially less accurate.

In this paper, we introduce an approach for the fast and accurate screening of the optoelectronic properties of conjugated (co)polymers. Besides direct use for HTVS we envisage that it can also be applied to generate data to train machine-learning models. We demonstrate that, by combining the recently developed xTB44 family of density functional tight-binding methods with calibration using a linear model to properties obtained through (Time-Dependent) DFT ((TD)DFT) calculations, one can not only rapidly screen polymers but also achieve (TD)DFT-quality results. We predominantly compare with results of (TD)DFT calculations using the B3LYP density functional, since we previously showed that calculations with this density functional yield accurate potentials for conjugated polymers when compared to experimental photoelectron spectroscopy data on polymeric solids,39 while also predicting reasonable optical gap values. The difference between our approach here and previous work3,7,40,45 is 3-fold. Besides the use of xTB rather than alternative semiempirical methods, we calculate adiabatic IP and EA values directly rather than approximate them from orbital energies, include an explicit description of the dielectric environment of the polymers, and use an integrated family of methods for both electronic and optical properties of the polymers.

General workflow

Structure Library Generation

In this section, we give an overview of the general workflow of the proposed high throughput approach. As outlined in Figure 1, the process involves multiple steps. Starting from a simplified molecular-input line-entry system (SMILES)46 representation of each monomer unit, linear polymer structures were generated using the Supramolecular Toolkit (stk),47,48 a python library for the assembly, structure generation and property calculation of supramolecules, which takes base functionality from RDKit.49stk allows for flexible copolymer formation from arbitrary monomer units, control over monomer sequence within repeat units, and the automatic generation of different structural isomers where asymmetric monomer units (e.g., 2,5 linked pyridine) are concerned. We restrict polymer chain length in all cases to the approximate equivalent of 12 phenylene monomer units. For example, a copolymer of thiophene and phenylene contains 6 thiophene and 6 phenylene units (each count as 1), a copolymer of fluorene and phenylene contains 4 fluorene and 4 phenylene units (phenylene counts as 1, fluorene counts as 2), and a copolymer of fluorene and carbazole contains 3 fluorene and 3 carbazole units (each counts as 2), as shown in Figure 2b. Polymer models of this length have previously been shown to provide approximately converged properties with respect to oligomer length.39

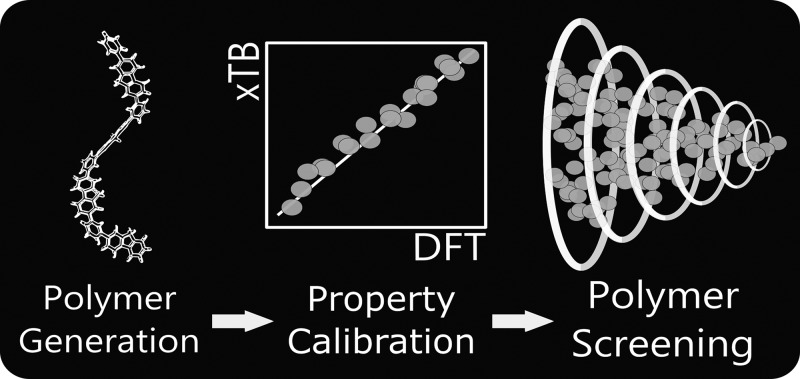
Figure 1.

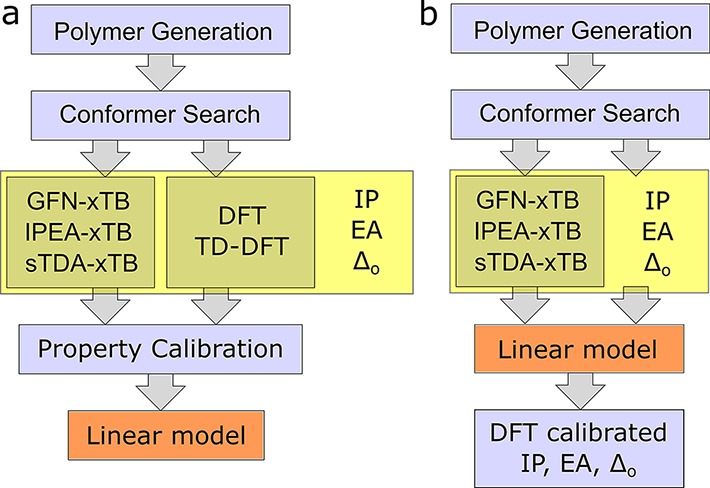
Figure 1

Open in a new tab

(a) Workflow of the calibration procedure, resulting in the linear model used to calibrate semiempirically determined properties (IP, EA, and optical gap (Δo)) to DFT-level calculations. (b) Subsequent proposed high-throughput screening approach, where the linear model produced in panel a is applied to new polymer structures for optoelectronic property screening.

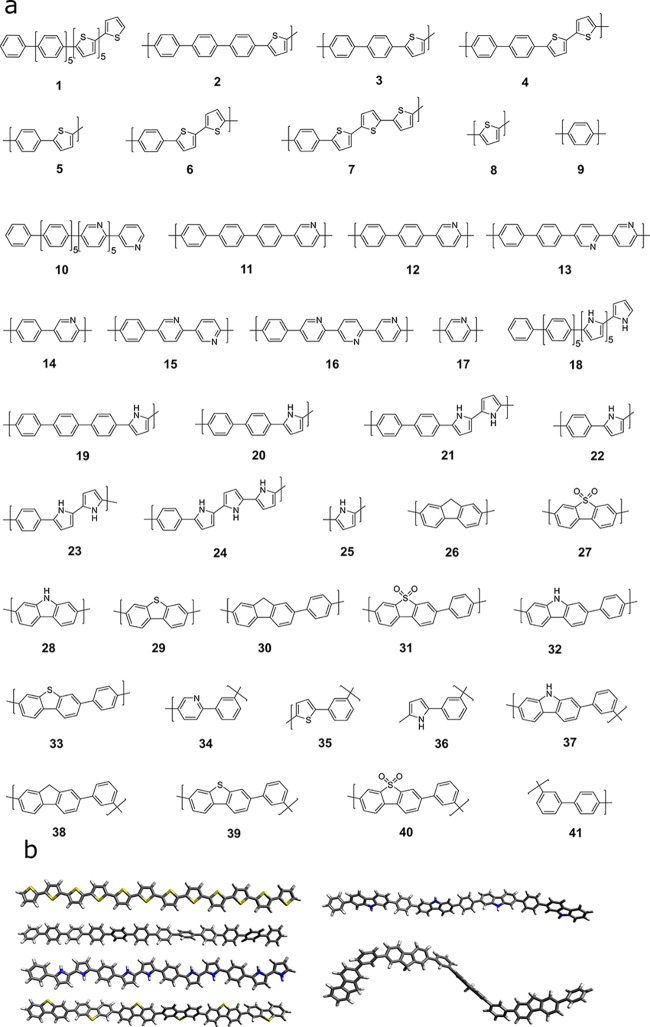
Figure 2.

Figure 2

Open in a new tab

(a) Repeat units of the polymers in the calibration set. (b) 3D geometries of the conformers of polymers with repeat units 8, 9, 23, 29, 32, and 38 as illustration of the types of conformers encountered.

Conformer Search Strategy

Linear copolymers generally contain large numbers of rotatable bonds, and therefore a conformer search on the initially generated polymer structures is warranted. Here, we make use of a stochastic rather than systematic approach, sampling the conformational space of the polymer randomly using the Experimental-Torsion Distance Geometry with additional basic knowledge (ETKDG) method,50 where we typically generate 5000 conformers per polymer. The resulting conformers are embedded in 3D space and undergo a subsequent optimization and energy ranking procedure using the Merck Molecular Force Field (MMFF)51 as implemented in RDKit. This second optimization step adds little computational cost to the overall conformer search, as the dominant contribution to computational cost stems from the initial stochastic conformer generation and embedding.

Property Calibration

At this stage, we take a set of around 40 simple copolymers that we will refer to as the calibration set. This is a set of copolymer structures composed of the monomer units shown in Figure 2a, for which the optoelectronic properties span a wide range of values. Polymer structures are generated and conformer searches are performed on each. For each system in the calibration set, both (TD)DFT and semiempirical calculations are performed on the lowest energy conformer, according to MMFF, to compute ground state geometries, ionization potentials (IP), electron affinities (EA), and optical gaps (for specific computational details, see below). This data is then used to fit linear models using Python 3.6 (numpy version 1.13.3) for IP, EA, and the optical gap; calibrating properties calculated with the semiempirical method to (TD)DFT-derived data. The motivation behind this approach is that the slopes and intercepts of this calibration step can be used to provide DFT-quality data at the cost of the associated semiempirical method. In turn, this allows a much more rapid exploration of chemical space for high-throughput screening of the intrinsic electronic properties of polymer materials, with the relatively small initial computational investment required for calibration. Naturally, this procedure relies on the semiempirical and DFT-derived data being strongly linearly correlated.

(TD)DFT Calculations

For the (TD)DFT calculations, IPs and EAs are computed using an adiabatic ΔDFT approach, based around the DFT total energies of the neutral polymer and its relaxed cationic/anionic counterparts. These calculations use the COSMO52,53 solvation model to approximate the dielectric environment of a polymer chain (e.g., at a polymer–water interface, εr 80.1, or within the polymer bulk, εr 2.0). As in our previous work,39,54,55 the (TD)DFT calculations use the B3LYP56−59 density functional and the DZP60 basis-set. The absorption spectra of the polymer models are approximated by vertical singlet excitations, calculated using (TD)B3LYP/DZP. Here, we define the optical gap, i.e., the onset of light absorption, as the energy of the lowest vertical excitation with nonzero oscillator strength. All (TD)DFT calculations described until now have been performed with Turbomole 7.01.61−63 Additional optical gap calculations were performed using the CAM-B3LYP64 and LC-ωHPBE65 range separated hybrid functionals in combination with a 6-31G(d,p) basis set, all using Gaussian 16.66

Semiempirical Calculations

Though different semiempirical methods have been applied to conjugated polymers previously,3,7,40 we make use of a recently developed density functional tight binding approach (GFN-xTB)44 for structural optimizations of the neutral polymers. For IP/EA calculations, we use an extension of the parent GFN-xTB method, IPEA-xTB,67 a differently parametrized variant of GFN-xTB for the calculation of ionization potentials and electron affinities. Essentially, IPEA-xTB performs vertical ΔSCF calculations, and has previously been shown to result in typical errors for computed vertical IP/EA values of 0.2–0.4 eV compared to DFT in vacuum.67 For optical gaps, we use the tight binding simplified Tamm–Dancoff approach (sTDA)68,69 applied to orbitals and orbital eigenvalues obtained through xTB (sTDA-xTB),70 an approach capable of ultrafast computation of entire UV–vis absorption spectra. All GFN-xTB calculations were performed using the xtb code,71 whereas the sTDA results were obtained using the sTDA72 code. All GFN-xTB calculations, but not sTDA calculations, used the generalized Born surface area solvation model, with the default parameters for benzene and water distributed with the xtb code. Finally, for comparison we also perform analogous PM6,42 PM743 (MOPAC 2016),73 and ZINDO/S74 (Gaussian 16)66 calculations on the polymers to obtain IP and EA values.

Results

In the following, we explore each stage of the high-throughput screening methodology, assessing the accuracy of the combination of the semiempirical calculation and linear calibration model, robustness of the approach when applied to various oligomer lengths and compositions, and how the conformer searching strategy ultimately affects predicted properties.

Calibration–Ionization Potential and Electron Affinity

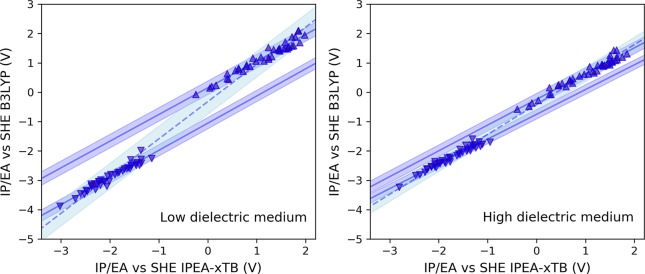
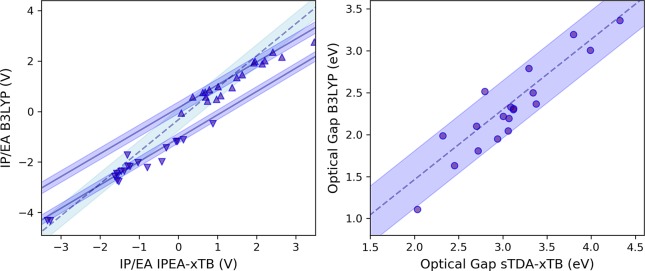
The IPs and EAs computed by IPEA-xTB and DFT/B3LYP for the calibration set are shown in Figure 3. For each dielectric environment, simple linear models are fitted to IP and EA, yielding intercept and gradient values that can be applied to calibrate semiempirical data to obtain B3LYP-quality results. All calibration parameters resulting from the regression models are given in Table 1 and Table S12. There is a strong linear correlation between the B3LYP and IPEA-xTB data, with R2 values of 0.99 for both dielectric environments. For the aqueous environment, the mean absolute differences (MAD) between IPEA-xTB and DFT data are 0.37 and 0.16 V for IP and EA, respectively. After calibration using the linear model, these are reduced to 0.08 and 0.06, respectively. The considerable reduction in MAD after calibration demonstrates that not only the trends between different copolymer properties but also the absolute values predicted by DFT are recovered well by calibrated IPEA-xTB. Furthermore, the same calibration procedure for the nonpolar (benzene) environment data results in MAD of 0.10 (IP) and 0.06 (EA) between IPEA-xTB and DFT results, indicating that the calibration quality holds across strongly differing dielectric environments with high and low dielectric constants.

Figure 3.

Figure 3

Open in a new tab

IP (up triangles) and EA (down triangles) values calculated for the copolymer calibration set using IPEA-xTB and B3LYP/DZP. In each case, properties are computed within a low dielectric screening environment resembling benzene (left) and a high dielectric environment resembling water (right). Two different fits to linear models are performed in each case. (i) Single fit performed for both IP and EA, with the predictions of the resulting model and its 95% prediction bounds shown as dashed line and light blue shaded region, respectively. (ii) Two separate fits are performed for IP and EA, with the predictions of the resulting models and its 95% confidence bounds shown as solid lines and blue shaded region, respectively. All values are presented versus the standard hydrogen electrode potential (4.44 V).

Table 1. Parameters (slope and intercept) of the Linear Models Applied to Calibrate xTB data (obtained with IPEA-xTB and sTDA-xTB for IP/EA and optical gaps, respectively) to DFT data, alongside Mean Absolute Errors of Calibrated Semiempirical Results vs DFT (B3LYP).

Property Environment Slope Intercept MAD after calibration (eV)
IP Low dielectric 0.91 0.15 0.10
EA Low dielectric 0.92 –1.05 0.06
IP and EA Low dielectric 1.27 –0.32 0.18
IP High dielectric 0.88 –0.24 0.08
EA High dielectric 0.84 –0.75 0.06
IP and EA High dielectric 1.02 –0.41 0.10
Optical Gap Low dielectric 0.83 –0.21 0.13
Optical Gap High dielectric 0.85 –0.25 0.13
Open in a new tab

The above discussion was based on linear models where IP and EA values are fitted separately. We repeated this procedure, this time fitting the IP and EA results simultaneously (Figure 3), a so-called global fit. Calibration using models based on a global fit results in slightly higher MAD values for both dielectric environments (0.18 and 0.10 V for the IP and EAs of low and high dielectric environments, respectively). The small difference in performance for each dielectric environment is reflected in the residual sum of squares, which is lower for the calibration performed in the high dielectric environment (1.23) than the low dielectric environment (2.44), indicating that, although they perform similarly, the global calibration procedure yields a better fit for the former than the latter. Here, we see that the effect of reducing the total number of parameters when moving from two separate models for IP and EA to one global fit is smallest in the high-dielectric range, indicating that a global fit may be appropriate when considering high-dielectric environments.

For each linear model, 95% prediction bands indicate that with new polymers not used for fitting, we can expect an accuracy of ±0.25 V with respect to the B3LYP calculations. Below, unless explicitly stated otherwise, all calibrated IPEA-xTB data will have been obtained using separate models for IP and EA.

We attempted analogous calibrations for PM6,42 PM7,43 and ZINDO/S74 as examples of alternative semiempirical methods. For PM6 and PM7, we calculated IP and EA both using ΔSCF and by making the orbital approximation, while only applying the latter for ZINDO/S. The orbital approximation is often made in the literature,7,75 here one approximates IP and EA by the negative of the HOMO and LUMO orbital energies of a given neutral polymer. The results of these calibration attempts can be found in the Supporting Information (Figures S15–S17). In summary, PM6/PM7 ΔSCF calculations and PM6/PM7/ZINDO/S calculations that make the orbital approximation yield poorer results than IPEA-xTB data, before, and importantly after, calibration (Table S12). However, we should note that ZINDO/S performs similarly to IPEA-xTB for IP but that IPEA-xTB offers significant improvements for EA (MAE of 0.18 V for ZINDO/S, 0.06 V for IPEA-xTB in the low dielectric case). The improved performance of IPEA-xTB over PM7, PM6, and ZINDO/S is likely to be at least partly due to the fact that IPEA-xTB was specifically developed to predict IP and EA values.

Calibration–Optical gap

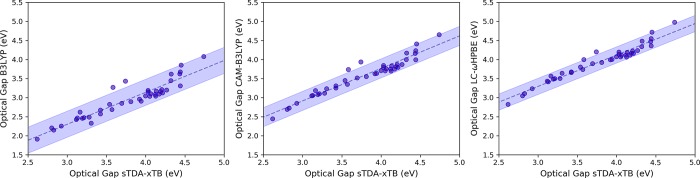
Figure 4 shows computed optical gaps (defined as the vertical excitation to the lowest excited state associated with nonzero oscillator strength) of the calibration set. In analogy to the above, we fit a linear model using data obtained with (TD)B3LYP and with sTDA-xTB. For both dielectric environments, (TD)DFT computed optical gaps are reproduced well by the combination of sTDA-xTB and a calibrated linear model. At least part of the latter shift is probably due to the fact that the (TD)B3LYP calculations employed a dielectric screening model, something that is unavailable for sTDA-xTB.

Figure 4.

Figure 4

Open in a new tab

Optical gap, defined as lowest computed vertical excitations with nonzero oscillator strength, values calculated for the copolymer calibration set at sTDA-xTB and (TD)DFT level (using B3LYP, CAM-B3LYP, and LC-ωHPBE). In each case, properties are computed using a dielectric screening model for benzene. Corresponding results for the water dielectric model can be found in the Supporting Information. Linear model fits are performed in each case, with the predictions of the fitted model and the 95% prediction bounds shown as blue dashed lines and blue solid lines, respectively.

To investigate effects of self-interaction and the potential overestimation of conjugation length by the B3LYP hybrid functional, we also employ the range-separated hybrid functional CAM-B3LYP, which has previously been shown to result in consistent agreement between experimental and DFT calculated optical gaps in conjugated polymer systems, particularly when applied to different oligomer lengths.76

CAM-B3LYP indeed improves the fit quality relative to B3LYP. However, the improvement is marginal and results in a minor change in the slope and a largely rigid shift of the DFT calculated absorption energies to higher values. This improvement upon switching to a long-range corrected functional is also exemplified when reperforming a fit against data obtained with LC-ωHPBE. The improved fits are reflected in the reduced MAD of noncalibrated sTDA-xTB optical gaps compared to density functionals with improving asymptotic behavior, which induces a more even treatment of polymers with different conjugation lengths used in the calibration set (i.e., those with meta-lined monomer units). Specifically, MAD values of optical gaps computed for the calibration set in an aqueous environment compared to B3LYP, CAM-B3LYP and LC-ωHPBE are 0.72, 0.20, and 0.18 eV, respectively. Similarly, the MADs for the nonpolar (benzene) environment are 0.83, 0.22, and 0.18 eV respectively. As we have seen above for IP and EA, these MAD values are significantly reduced through calibration (0.15, 0.10, and 0.08 eV in an aqueous environment, 0.15, 0.10, and 0.09 eV for the nonpolar (benzene) environment for B3LYP, CAM-B3LYP, and LC-wHPBE, respectively). The effect of going from B3LYP to CAM-B3LYP/LC-ωHPBE can be attributed to the improved asymptotic behavior of the exchange-correlation (electronic) potentials of these density functionals relative to B3LYP, reducing self-interaction error and subsequent over- delocalization of π orbitals along the polymer backbones.77 As the electronic potential in xTB displays the exact asymptotic behavior,70 the better quality fit is obtained when a long-range corrected density functional is expected.

Calibration and Polymer Length

Following the observations described above, we further test the robustness and versatility of calibration through a linear model by considering oligomers of varying length. To do so, we extract a subset of polymer structures from the calibration set and consider how IP, EA, and optical gap values vary with oligomer length. The results are shown in Figures S5 and S6 of the Supporting Information compared to the predictions of the linear model and 95% prediction intervals from Figures 3 and 4. Considering IP and EA, we can see that the linear relationship between IPEA-xTB and B3LYP holds for all oligomer lengths, indicating that issues with self-interaction observed in the optical gap calibration do not carry over to those of IP and EA. This is consistent with the excellent quality of fit observed in Figure 3 for IP and EA, despite the fact that the calibration set contains meta-linked polymers with a formally shorter conjugation length.

Now considering optical gaps, issues with self-interaction become apparent for B3LYP. As the oligomer length decreases from 12 to 8 and then to 4 equiv phenylene units, we see the systematic increase in optical gap relative to sTDA-xTB with decreasing oligomer length associated with the self-interaction error. Moving to CAM-B3LYP, this effect is mitigated, though not entirely eliminated, consistent with the improved (but not exact) asymptotic behavior of the exchange-correlation potential. Now considering LC-ωHPBE, the effect is further reduced compared to CAM-B3LYP, in line with the previous analysis of computed optical gaps in Figure 4.

Validation of the Approach

Here we demonstrate the robustness of the calibration procedure by introducing additional polymer systems and molecules not used during fitting. Figure 5 shows the previous IP, EA, and optical gap calibrations for the benzene dielectric screening model, alongside results for this validation set. The validation set, see Figure S3, includes polymers potentially relevant to organic photovoltaics, e.g., those based on benzothiazole or thieno[3,2-b]thiophene and polymers from the literature on photocatalytic water splitting, e.g., the carbon nitride polymer melon, consisting of a linear chain of heptazine units linked by −NH– bridges. It also includes some relevant nonpolymeric molecules, e.g., the fullerene OPV acceptor material PCBM, and even two nonconjugated polymers (fully reduced polyaniline and poly(p-xylene)). Aside from application, a crucial feature of the validation set is that it is composed of polymers that are drastically different from those used for calibration. We can see from Figure 5 that the properties of all systems in the validation set follow the same linear trends as identified for the calibration set and thus the calibration developed above is not biased to the polymers in the calibration set, but can be applied more generally to others. Differences between calibrated IPEA-xTB/sTDA-xTB and B3LYP data reflect this, with MAD values of 0.21 and 0.16 V for IP and EA and 0.17 eV for optical gaps calculated using both B3LYP and CAM-B3LYP. For the water dielectric screening model, MAD values of 0.16 and 0.14 V for IP and EA and 0.16 eV for optical gaps calculated using both B3LYP and CAM-B3LYP were obtained.

Figure 5.

Figure 5

Open in a new tab

(a) IP (triangles)/EA (circles) and (b) optical gap (circles) values computed at IPEA-xTB/sTDA-xTB and B3LYP/DZP level for the validation set (Figure S3). In each case, a dielectric screening model for benzene is used. The corresponding linear regression prediction line and 95% prediction bounds from Figures 3 and 4 are included. Analogous results obtained using a dielectric screening model for water can be found in Figure S19 of the Supporting Information.

Sensitivity of Results to Conformational and Repeat Unit Disorder

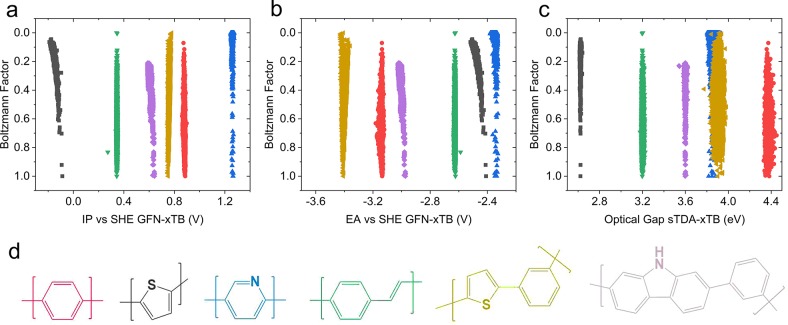
To investigate the sensitivity of calculated properties to polymer conformation, we calculate IP, EA, and optical gaps for 5000 randomly generated conformers of six selected copolymers. Each conformer is optimized at GFN-xTB level, with IP/EA and optical gaps calculated using IPEA-xTB and sTDA-xTB, respectively. Figure 6 shows the properties calculated for each conformer plotted against the calculated Boltzmann factor relative to the lowest energy conformer. None of the properties are very sensitive to the polymer conformation, with the maximum variation of a given property with respect to conformation around 0.1 (e)V, in line with previous findings.78 Further, the maximum dispersion in predicted properties lies at higher energy regions (low Boltzmann factor), with far lower variation in IP, EA, and optical gap in low-energy regions (approaching zero for IP and EA and ∼0.05 eV for optical cap). This highlights that, although an exhaustive search of all possible conformers of each polymers may be desirable, it is not necessary to predict the intrinsic electronic properties of a polymer accurately using an oligomer model. In turn, this supports our use of a stochastic approach coupled with a classical molecular mechanics optimization for conformer generation, which inherently may not necessarily be exhaustive.

Figure 6.

Figure 6

Open in a new tab

(a) IP and (b) EA values computed with IPEA-xTB and (c) optical gap values computed with sTDA-xTB for 5000 randomly generated conformers of polymers shown in panel d. The energy of each conformer is expressed as a Boltzmann factor relative to the lowest energy conformer obtained for each polymer model. In this case, each conformer structure has been optimized via GFN-xTB. Symbol colors on plots match the colors of the polymer repeat units shown in panel d. Boltzmann factors are calculated at a temperature of 298 K.

As a secondary observation, comparing the distribution of Boltzmann factors for each of the polymers, it appears that differences between the different polymers can be linked to different inter-repeat unit interactions. As an example, for polyphenylene, we calculate a broad distribution of conformers at different energies, while for polypyridine and polythiophene we obtain a narrow distribution centered at high energy, with far fewer conformers at low energy. This highlights a greater thermodynamic preference for polypyridine and polythiophene to assume particular structures, while polyphenylene and PPV remain more conformationally flexible from an energetic point of view. Finally, the lack of sensitivity of the computed properties with respect to conformation appears to hold even for two copolymers containing meta-linking 1,3-phenylene groups, where changes in conformation can lead to larger overall changes in geometry.

To test the effects of repeat unit disorder along polymer chains, i.e., the fact that for asymmetric monomers there will be different regioregular and regiorandom structures, we also produced 100 conformers of 25 randomly generated isomers of polymers comprising asymmetric repeat units, generating analogous plots to Figure 6 (see Supporting Information Figure S13). In the same vein as the above analysis, introducing random disorder along polymer chains seems to have little effect on this in all, with maximum deviations in IP, EA, and optical gap around 0.2 (e)V, which reduces to around 0.05 (e)V for lower-energy structures.

Expected Screening Rate

Within the entire process, the conformer-searching step is the clear bottleneck, predominantly because 5000 conformers per polymer are generated, but also because the full set of calculations with xTB on the lowest energy conformer are extremely rapid (typically resulting in <1 min of computation for a typical polymer model on a typical 24 core desktop machine). As an illustrative example, using such a setup we expect a screening rate of approximately 500 polymers per day. However, because of the observed relative insensitivity of IP, EA, and optical gap values to conformational degrees of freedom (Figure 6), the number of conformers sampled per polymer can be further reduced and as a result the screening rate suggested above should be viewed as a lower limit.

Perspectives

As demonstrated above, both IPEA-xTB and sTDA-xTB perform well in terms of reproducing the ordering of the IP, EA, and optical gap values predicted by (TD)B3LYP for the polymers in the calibration set. After fitting to linear models for EA, IP, and the optical gap, calibrated IPEA-xTB and sTDA-xTB also accurately reproduce the corresponding absolute values. More importantly, calibrated IPEA-xTB and sTDA-xTB also perform well when reproducing the IP/EA and optical gap values predicted by (TD)B3LYP for the polymers in the validation set, which are not included in the fitting. This ability to accurately predict properties of systems outside of the calibration set is a critical feature for high-throughput virtual screening, where one expects to screen orders of magnitude more polymers than in the calibration set. Bearing in mind that high-throughput approaches may resort to higher-level (DFT) calculations after the identification of promising leads from a low-cost approach, we show that this step could effectively be avoided altogether as a result of the inherent accuracy of the calibrated xTB data.

It is interesting to see that even if we performed our calibration exclusively for conjugated polymers, the properties of the nonconjugated polymers (fully reduced polyaniline and poly(p-xylene)) and a nonpolymeric molecule (PCBM) in our validation set are also reasonably well described. As such, the calibrated models proposed here are likely reasonably transferrable and can, for example, be used to predict open-circuit voltages and approximate energy conversions efficiencies using the Scharber model79 for bulk-heterojunction organic solar cells using a conjugated polymer as a donor and PCBM (or other molecular materials) as an acceptor.

We have performed separate calibrations for the low and high dielectric environment cases, relevant to organic photovoltaics/organic light emitting diodes and water splitting photocatalysis, respectively. However, one would expect that the same procedure would yield results of equal accuracy for the case of intermediate dielectric permittivity values relevant for polymers in contact with moderately polar solvents, relevant to the applications of conjugated polymers in batteries, as well as the characterization of their IP/EA values using cyclic voltammetry.

The accuracy of the calibrated IPEA-xTB and sTDA-xTB results is, at best, that of the DFT functional they were calibrated to. Conceptually, it would be just as easy to calibrate IPEA-xTB and sTDA-xTB to experimental data or results from higher-level quantum chemical calculations. Our rationale for calibrating to DFT rather than experimental data is that, at least for IP and EA, there is very limited experimental data to calibrate to, especially in the presence of water. Similarly, there is limited data from accurate quantum chemical calculations for adiabatic potentials of polymers in the presence of a dielectric.

Following on from the above, our usage of the word calibration is not meant to signify that (TD)DFT using a particular functional inherently yields results that are more accurate and as such we do not benchmark here the xTB family of methods or any of the other semiempirical method discussed above. Rather, the process of calibration and the fitting of a linear model means that the semiempirical methods can be used to predict the answer DFT would give for a fraction of the computational cost. A good illustration of this is the case of the optical gap, where, as discussed above, at least the trend in optical gap values predicted by sTDA-xTB might be more reliable than that predicted by (TD)B3LYP, as the former captures the correct asymptotic behavior of the electronic potential and the latter does not.

The observed relative insensitivity of the predicted IP, EA, and optical gap values to conformational degrees of freedom is an attractive property for high-throughput virtual screening for two reasons. First, it implies that the effect of not finding the true lowest energy conformer on the predicted optical and electronic properties is only very minor and that hence a minimal conformer search will suffice. Second, and perhaps more importantly, it suggests that the effect of conformational disorder on the predicted properties is likely equally minor. Based on the good correlation between properties predicted by the xTB family of methods and (TD)B3LYP, it stands to reason that the observed insensitivity to conformational degrees of freedom will translate to property predictions by (TD)DFT, even if orders of magnitude more computationally expensive to probe.

Conclusions

We demonstrate that the xTB family of density functional tight-binding methods from Grimme and co-workers form a powerful basis for a high-throughput screening method for the optoelectronic properties of conjugated polymers. We show that after fitting a linear model using a calibration set of IPEA/sTDA-xTB and (TD)B3LYP results, one can use the former to predict the latter at a fraction of the computational cost. We also demonstrate that the (opto)electronic properties of conjugated polymers are relatively insensitive to conformational degrees of freedom and that hence a minimal conformer search will probably suffice as well as, perhaps more importantly, that the effect of conformational disorder on the predicted properties is likely minor.

Acknowledgments

We thank Dr. Christoph Bannwarth, Dr. Jan Gerit Brandenburg, Prof. Andrew I. Cooper, Prof. Stefan Grimme, Prof. Piero Ugliengo and Dr. Sebastian Sprick for useful discussion. We are also grateful to Prof. Stefan Grimme for making the xtb code and IPEA-xTB parameter files available to us. The UK Engineering and Physical Sciences Research Council (EPSRC) is acknowledged for funding (EP/N004884/1, EP/M017257/1, and EP/P005543/1)). K.E.J. thanks the Royal Society for a University Research Fellowship and the ERC through grant agreement no. 758370 (ERC-StG-PE5-CoMMaD).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jcim.8b00256.

  • Underlying raw data for all figures, table of calibration parameters for all methods, fits vs polymer length, validation polymer structures, results obtained for other semiempirical methods (PM6, PM7, ZINDO/S) (PDF)

  • ESI structures (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ci8b00256_si_001.pdf (1.8MB, pdf)
ci8b00256_si_002.zip (846.1KB, zip)

References

  1. Curtarolo S.; Hart G. L. W.; Nardelli M. B.; Mingo N.; Sanvito S.; Levy O. The High-Throughput Highway to Computational Materials Design. Nat. Mater. 2013, 12, 191–201. 10.1038/nmat3568. [DOI] [PubMed] [Google Scholar]
  2. Pyzer-Knapp E. O.; Suh C.; Gómez-Bombarelli R.; Aguilera-Iparraguirre J.; Aspuru-Guzik A. What Is High-Throughput Virtual Screening? A Perspective from Organic Materials Discovery. Annu. Rev. Mater. Res. 2015, 45, 195–216. 10.1146/annurev-matsci-070214-020823. [DOI] [Google Scholar]
  3. O'Boyle N. M.; Campbell C. M.; Hutchison G. R. Computational Design and Selection of Optimal Organic Photovoltaic Materials. J. Phys. Chem. C 2011, 115, 16200–16210. 10.1021/jp202765c. [DOI] [Google Scholar]
  4. Martsinovich N.; Troisi A. High-Throughput Computational Screening of Chromophores for Dye-Sensitized Solar Cells. J. Phys. Chem. C 2011, 115, 11781–11792. 10.1021/jp2026847. [DOI] [Google Scholar]
  5. Hachmann J.; Olivares-Amaya R.; Atahan-Evrenk S.; Amador-Bedolla C.; Sánchez-Carrera R. S.; Gold-Parker A.; Vogt L.; Brockway A. M.; Aspuru-Guzik A. The Harvard Clean Energy Project: Large-Scale Computational Screening and Design of Organic Photovoltaics on the World Community Grid. J. Phys. Chem. Lett. 2011, 2, 2241–2251. 10.1021/jz200866s. [DOI] [Google Scholar]
  6. Olivares-Amaya R.; Amador-Bedolla C.; Hachmann J.; Atahan-Evrenk S.; Sánchez-Carrera R. S.; Vogt L.; Aspuru-Guzik A. Accelerated Computational Discovery of High-Performance Materials for Organic Photovoltaics by Means of Cheminformatics. Energy Environ. Sci. 2011, 4, 4849. 10.1039/c1ee02056k. [DOI] [Google Scholar]
  7. Kanal I. Y.; Owens S. G.; Bechtel J. S.; Hutchison G. R. Efficient Computational Screening of Organic Polymer Photovoltaics. J. Phys. Chem. Lett. 2013, 4, 1613–1623. 10.1021/jz400215j. [DOI] [PubMed] [Google Scholar]
  8. Lopez S. A.; Sanchez-Lengeling B.; de Goes Soares J.; Aspuru-Guzik A. Design Principles and Top Non-Fullerene Acceptor Candidates for Organic Photovoltaics. Joule 2017, 1, 857–870. 10.1016/j.joule.2017.10.006. [DOI] [Google Scholar]
  9. Halls M. D.; Giesen D. J.; Hughes T. F.; Goldberg A.; Cao Y. High-Throughput Quantum Chemistry and Virtual Screening for OLED Material Components. Proc. SPIE 2013, 8829, 882926. 10.1117/12.2025092. [DOI] [Google Scholar]
  10. Gómez-Bombarelli R.; Aguilera-Iparraguirre J.; Hirzel T. D.; Duvenaud D.; Maclaurin D.; Blood-Forsythe M. A.; Chae H. S.; Einzinger M.; Ha D. G.; Wu T.; Markopoulos G.; Jeon S.; Kang H.; Miyazaki H.; Numata M.; Kim S.; Huang W.; Hong S. I.; Baldo M.; Adams R. P.; Aspuru-Guzik A. Design of Efficient Molecular Organic Light-Emitting Diodes by a High-Throughput Virtual Screening and Experimental Approach. Nat. Mater. 2016, 15, 1120–1127. 10.1038/nmat4717. [DOI] [PubMed] [Google Scholar]
  11. Janet J. P.; Kulik H. J. Resolving Transition Metal Chemical Space: Feature Selection for Machine Learning and Structure-Property Relationships. J. Phys. Chem. A 2017, 121, 8939–8954. 10.1021/acs.jpca.7b08750. [DOI] [PubMed] [Google Scholar]
  12. Janet J. P.; Chan L.; Kulik H. J. Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network. J. Phys. Chem. Lett. 2018, 9, 1064–1071. 10.1021/acs.jpclett.8b00170. [DOI] [PubMed] [Google Scholar]
  13. van den Berg A. W. C.; Zwijnenburg M. A.; Bromley S. T.; Flikkema E.; Bell R. G.; Jansen J. C.; Schoonman J. Comparing the Influence of Framework Type on H-2 Absorption in Hypothetical and Existing Clathrasils: A Grand Canonical Monte Carlo Study. J. Mater. Chem. 2006, 16, 3285–3290. 10.1039/b604377a. [DOI] [Google Scholar]
  14. Watanabe T.; Sholl D. S. Accelerating Applications of Metal-Organic Frameworks for Gas Adsorption and Separation by Computational Screening of Materials. Langmuir 2012, 28, 14114–14128. 10.1021/la301915s. [DOI] [PubMed] [Google Scholar]
  15. Wilmer C. E.; Leaf M.; Lee C. Y.; Farha O. K.; Hauser B. G.; Hupp J. T.; Snurr R. Q. Large-Scale Screening of Hypothetical Metal-Organic Frameworks. Nat. Chem. 2012, 4, 83–89. 10.1038/nchem.1192. [DOI] [PubMed] [Google Scholar]
  16. Evans J. D.; Huang D. M.; Haranczyk M.; Thornton A. W.; Sumby C. J.; Doonan C. J. Computational Identification of Organic Porous Molecular Crystals. CrystEngComm 2016, 18, 4133–4141. 10.1039/C6CE00064A. [DOI] [Google Scholar]
  17. Chung Y. G.; Camp J.; Haranczyk M.; Sikora B. J.; Bury W.; Krungleviciute V.; Yildirim T.; Farha O. K.; Sholl D. S.; Snurr R. Q. Computation-Ready, Experimental Metal-Organic Frameworks: A Tool to Enable High-Throughput Screening of Nanoporous Crystals. Chem. Mater. 2014, 26, 6185–6192. 10.1021/cm502594j. [DOI] [Google Scholar]
  18. Pulido A.; Chen L.; Kaczorowski T.; Holden D.; Little M. A.; Chong S. Y.; Slater B. J.; McMahon D. P.; Bonillo B.; Stackhouse C. J.; Stephenson A.; Kane C. M.; Clowes R.; Hasell T.; Cooper A. I.; Day G. M. Functional Materials Discovery Using Energy-Structure-Function Maps. Nature 2017, 543, 657–664. 10.1038/nature21419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Moghadam P. Z.; Islamoglu T.; Goswami S.; Exley J.; Fantham M.; Kaminski C. F.; Snurr R. Q.; Farha O. K.; Fairen-Jimenez D. Computer-Aided Discovery of a Metal–organic Framework with Superior Oxygen Uptake. Nat. Commun. 2018, 9, 1378. 10.1038/s41467-018-03892-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Greeley J.; Jaramillo T. F.; Bonde J.; Chorkendorff I.; Nørskov J. K. Computational High-Throughput Screening of Electrocatalytic Materials for Hydrogen Evolution. Nat. Mater. 2006, 5, 909–913. 10.1038/nmat1752. [DOI] [PubMed] [Google Scholar]
  21. Nørskov J. K.; Bligaard T. The Catalyst Genome. Angew. Chem., Int. Ed. 2013, 52, 776–777. 10.1002/anie.201208487. [DOI] [PubMed] [Google Scholar]
  22. Yu G.; Gao J.; Hummelen J. C.; Wudl F.; Heeger A. J. Device Structure Consisted Polymer Photovoltaic Cells : Enhanced Efficiencies via a Network of Internal Donor-Acceptor Heterojunctions. Science 1995, 270, 1789–1791. 10.1126/science.270.5243.1789. [DOI] [Google Scholar]
  23. Facchetti A. Polymer Donor – Polymer Acceptor (All-Polymer) Solar Cells. Mater. Today 2013, 16, 123–132. 10.1016/j.mattod.2013.04.005. [DOI] [Google Scholar]
  24. Lu L.; Zheng T.; Wu Q.; Schneider A. M.; Zhao D.; Yu L. Recent Advances in Bulk Heterojunction Polymer Solar Cells. Chem. Rev. 2015, 115, 12666–12731. 10.1021/acs.chemrev.5b00098. [DOI] [PubMed] [Google Scholar]
  25. Mazzio K. A.; Luscombe C. K. The Future of Organic Photovoltaics. Chem. Soc. Rev. 2015, 44, 78–90. 10.1039/C4CS00227J. [DOI] [PubMed] [Google Scholar]
  26. Halls J. J. M.; Walsh C. A.; Greenham N. C.; Marseglia E. A.; Friend R. H.; Moratti S. C.; Holmes A. B. Efficient Photodiodes from Interpenetrating Polymer Networks. Nature 1995, 376, 498–500. 10.1038/376498a0. [DOI] [Google Scholar]
  27. Burroughes J. H.; Bradley D. D. C.; Brown A. R.; Marks R. N.; Mackay K.; Friend R. H.; Burns P. L.; Holmes A. B. Light-Emitting Diodes Based on Conjugated Polymers. Nature 1990, 347, 539–541. 10.1038/347539a0. [DOI] [Google Scholar]
  28. Akcelrud L. Electroluminescent Polymers. Prog. Polym. Sci. 2003, 28, 875–962. 10.1016/S0079-6700(02)00140-5. [DOI] [Google Scholar]
  29. Meng Q.; Cai K.; Chen Y.; Chen L. Research Progress on Conducting Polymer Based Supercapacitor Electrode Materials. Nano Energy 2017, 36, 268–285. 10.1016/j.nanoen.2017.04.040. [DOI] [Google Scholar]
  30. Xie J.; Gu P.; Zhang Q. Nanostructured Conjugated Polymers: Toward High-Performance Organic Electrodes for Rechargeable Batteries. ACS Energy Lett. 2017, 2, 1985–1996. 10.1021/acsenergylett.7b00494. [DOI] [Google Scholar]
  31. Yanagida S.; Kabumoto A.; Mizumoto K.; Pac C.; Yoshino K. Poly(pphenylene1-Catalysed Photoreduction of Water to Hydrogen. J. Chem. Soc., Chem. Commun. 1985, 8, 474–475. 10.1039/c39850000474. [DOI] [Google Scholar]
  32. Shibata T.; Kabumoto A.; Shiragami T.; Ishitani O.; Pac C.; Yanagida S. Novel Visible-Light-Driven Photocatalyst. Poly(p-Phenylene)-Catalyzed Photoreductions of Water, Carbonyl Compounds, and Olefins. J. Phys. Chem. 1990, 94, 2068–2076. 10.1021/j100368a063. [DOI] [Google Scholar]
  33. Yang C.; Ma B. C.; Zhang L.; Lin S.; Ghasimi S.; Landfester K.; Zhang K. A. I.; Wang X. Molecular Engineering of Conjugated Polybenzothiadiazoles for Enhanced Hydrogen Production by Photosynthesis. Angew. Chem., Int. Ed. 2016, 55, 9202–9206. 10.1002/anie.201603532. [DOI] [PubMed] [Google Scholar]
  34. Li L.; Cai Z.; Wu Q.; Lo W. Y.; Zhang N.; Chen L. X.; Yu L. Rational Design of Porous Conjugated Polymers and Roles of Residual Palladium for Photocatalytic Hydrogen Production. J. Am. Chem. Soc. 2016, 138, 7681–7686. 10.1021/jacs.6b03472. [DOI] [PubMed] [Google Scholar]
  35. Sprick R. S.; Bonillo B.; Clowes R.; Guiglion P.; Brownbill N. J.; Slater B. J.; Blanc F.; Zwijnenburg M. A.; Adams D. J.; Cooper A. I. Visible-Light-Driven Hydrogen Evolution Using Planarized Conjugated Polymer Photocatalysts. Angew. Chem., Int. Ed. 2016, 55, 1792–1796. 10.1002/anie.201510542. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Bredas J.-L. Mind the Gap!. Mater. Horiz. 2014, 1, 17–19. 10.1039/C3MH00098B. [DOI] [Google Scholar]
  37. van der Horst J.; Bobbert P.; de Jong P.; Michels M.; Brocks G.; Kelly P. Ab Initio Prediction of the Electronic and Optical Excitations in Polythiophene: Isolated Chains versus Bulk Polymer. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 61, 15817–15826. 10.1103/PhysRevB.61.15817. [DOI] [Google Scholar]
  38. Sun H.; Ryno S.; Zhong C.; Ravva M. K.; Sun Z.; Körzdörfer T.; Brédas J. L. Ionization Energies, Electron Affinities, and Polarization Energies of Organic Molecular Crystals: Quantitative Estimations from a Polarizable Continuum Model (PCM)-Tuned Range-Separated Density Functional Approach. J. Chem. Theory Comput. 2016, 12, 2906–2916. 10.1021/acs.jctc.6b00225. [DOI] [PubMed] [Google Scholar]
  39. Guiglion P.; Monti A.; Zwijnenburg M. A. Validating a Density Functional Theory Approach for Predicting the Redox Potentials Associated with Charge Carriers and Excitons in Polymeric Photocatalysts. J. Phys. Chem. C 2017, 121, 1498–1506. 10.1021/acs.jpcc.6b11133. [DOI] [Google Scholar]
  40. Hutchison G. R.; Ratner M. A.; Marks T. J. Accurate Prediction of Band Gaps in Neutral Heterocyclic Conjugated Polymers. J. Phys. Chem. A 2002, 106, 10596–10605. 10.1021/jp025999m. [DOI] [Google Scholar]
  41. Dewar M. J. S.; Zoebisch E. G.; Healy E. F.; Stewart J. J. P. Development and Use of Quantum Mechanical Molecular Models. 76. AM1: A New General Purpose Quantum Mechanical Molecular Model. J. Am. Chem. Soc. 1985, 107, 3902–3909. 10.1021/ja00299a024. [DOI] [Google Scholar]
  42. Stewart J. J. P. Optimization of Parameters for Semiempirical Methods V: Modification of NDDO Approximations and Application to 70 Elements. J. Mol. Model. 2007, 13, 1173–1213. 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Stewart J. J. P. Optimization of Parameters for Semiempirical Methods VI: More Modifications to the NDDO Approximations and Re-Optimization of Parameters. J. Mol. Model. 2013, 19, 1–32. 10.1007/s00894-012-1667-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Grimme S.; Bannwarth C.; Shushkov P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All Spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. 10.1021/acs.jctc.7b00118. [DOI] [PubMed] [Google Scholar]
  45. Kanal I. Y.; Hutchison G. R.. Rapid Computational Optimization of Molecular Properties Using Genetic Algorithms: Searching Across Millions of Compounds for Organic Photovoltaic Materials. arXiv:1707.02949 2017. [Google Scholar]
  46. Weininger D. SMILES, a Chemical Language and Information System: 1: Introduction to Methodology and Encoding Rules. J. Chem. Inf. Model. 1988, 28, 31–36. 10.1021/ci00057a005. [DOI] [Google Scholar]
  47. Turcani L.; Berardo E.; Jelfs K.. stk : A Python Toolkit for Macromolecular Assembly. J. Comput. Chem., 2018, 10.1002/jcc.25377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. stk : https://github.com/supramolecular-toolkit/stk/ (accessed April 2018).
  49. RDKit : open source cheminformatics software http://www.rdkit.org (accessed April 2018).
  50. Riniker S.; Landrum G. A. Better Informed Distance Geometry: Using What We Know to Improve Conformation Generation. J. Chem. Inf. Model. 2015, 55, 2562–2574. 10.1021/acs.jcim.5b00654. [DOI] [PubMed] [Google Scholar]
  51. Halgren T. a. Merck Molecular Force Field. J. Comput. Chem. 1996, 17, 490–519. . [DOI] [Google Scholar]
  52. Klamt A.; Schüürmann G. COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc., Perkin Trans. 2 1993, 2, 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]
  53. Barone V.; Cossi M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. 10.1021/jp9716997. [DOI] [Google Scholar]
  54. Guiglion P.; Butchosa C.; Zwijnenburg M. A. Polymer Photocatalysts for Water Splitting: Insights from Computational Modeling. Macromol. Chem. Phys. 2016, 217, 344–353. 10.1002/macp.201500432. [DOI] [Google Scholar]
  55. Guiglion P.; Berardo E.; Butchosa C.; Wobbe M. C. C.; Zwijnenburg M. A. Modelling Materials for Solar Fuel Synthesis by Artificial Photosynthesis; Predicting the Optical, Electronic and Redox Properties of Photocatalysts. J. Phys.: Condens. Matter 2016, 28, 074001. 10.1088/0953-8984/28/7/074001. [DOI] [PubMed] [Google Scholar]
  56. Vosko S. H.; Wilk L.; Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
  57. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  58. Becke A. D. Density-Functional thermochemistry.III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648. 10.1063/1.464913. [DOI] [Google Scholar]
  59. Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
  60. Schäfer A.; Horn H.; Ahlrichs R. Fully Optimized Contracted Gaussian Basis Sets for Atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. 10.1063/1.463096. [DOI] [Google Scholar]
  61. Ahlrichs R.; Bär M.; Häser M.; Horn H.; Kölmel C. Electronic Structure Calculations on Workstation Computers: The Program System Turbomole. Chem. Phys. Lett. 1989, 162, 165–169. 10.1016/0009-2614(89)85118-8. [DOI] [Google Scholar]
  62. Furche F.; Ahlrichs R. Erratum: “Time-Dependent Density Functional Methods for Excited State Properties” [J. Chem. Phys. 117, 7433 (2002)]. J. Chem. Phys. 2004, 121, 12772. 10.1063/1.1824903. [DOI] [Google Scholar]
  63. van Wüllen C. Shared-Memory Parallelization of the TURBOMOLE Programs AOFORCE, ESCF, and EGRAD: How to Quickly Parallelize Legacy Code. J. Comput. Chem. 2011, 32, 1195–1201. 10.1002/jcc.21692. [DOI] [PubMed] [Google Scholar]
  64. Yanai T.; Tew D. P.; Handy N. C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  65. Henderson T. M.; Izmaylov A. F.; Scalmani G.; Scuseria G. E. Can Short-Range Hybrids Describe Long-Range-Dependent Properties?. J. Chem. Phys. 2009, 131, 044108. 10.1063/1.3185673. [DOI] [PubMed] [Google Scholar]
  66. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, 2016.
  67. Ásgeirsson V.; Bauer C. A.; Grimme S. Quantum Chemical Calculation of Electron Ionization Mass Spectra for General Organic and Inorganic Molecules. Chem. Sci. 2017, 8, 4879–4895. 10.1039/C7SC00601B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Grimme S. A Simplified Tamm-Dancoff Density Functional Approach for the Electronic Excitation Spectra of Very Large Molecules. J. Chem. Phys. 2013, 138, 244104. 10.1063/1.4811331. [DOI] [PubMed] [Google Scholar]
  69. Bannwarth C.; Grimme S. A Simplified Time-Dependent Density Functional Theory Approach for Electronic Ultraviolet and Circular Dichroism Spectra of Very Large Molecules. Comput. Theor. Chem. 2014, 1040–1041, 45–53. 10.1016/j.comptc.2014.02.023. [DOI] [Google Scholar]
  70. Grimme S.; Bannwarth C. Ultra-Fast Computation of Electronic Spectra for Large Systems by Tight-Binding Based Simplified Tamm-Dancoff Approximation (sTDA-xTB). J. Chem. Phys. 2016, 145, 054103. 10.1063/1.4959605. [DOI] [PubMed] [Google Scholar]
  71. xTB : https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/xtb/xtb (accessed April 2018).
  72. sTDA : https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/stda/stda (accessed April 2018).
  73. Stewart J. J. P.Mopac2016, Stewart Computational Chemistry: Colorado Springs, CO, 2016.
  74. Ridley J.; Zerner M. An Intermediate Neglect of Differential Overlap Technique for Spectroscopy: Pyrrole and the Azines. Theor. Chim. Acta 1973, 32, 111–134. 10.1007/BF00528484. [DOI] [Google Scholar]
  75. Tsuneda T.; Song J. W.; Suzuki S.; Hirao K. On Koopmans’ Theorem in Density Functional Theory. J. Chem. Phys. 2010, 133, 174101. 10.1063/1.3491272. [DOI] [PubMed] [Google Scholar]
  76. Salzner U.; Aydin A. Improved Prediction of Properties of π-Conjugated Oligomers with Range-Separated Hybrid Density Functionals. J. Chem. Theory Comput. 2011, 7, 2568–2583. 10.1021/ct2003447. [DOI] [PubMed] [Google Scholar]
  77. Vydrov O. A.; Scuseria G. E. Assessment of a Long-Range Corrected Hybrid Functional. J. Chem. Phys. 2006, 125, 234109. 10.1063/1.2409292. [DOI] [PubMed] [Google Scholar]
  78. Jackson N. E.; Savoie B. M.; Kohlstedt K. L.; Marks T. J.; Chen L. X.; Ratner M. A. Structural and Conformational Dispersion in the Rational Design of Conjugated Polymers. Macromolecules 2014, 47, 987–992. 10.1021/ma4023923. [DOI] [Google Scholar]
  79. Scharber M. C.; Mühlbacher D.; Koppe M.; Denk P.; Waldauf C.; Heeger A. J.; Brabec C. J. Design Rules for Donors in Bulk-Heterojunction Solar Cells - Towards 10% Energy-Conversion Efficiency. Adv. Mater. 2006, 18, 789–794. 10.1002/adma.200501717. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ci8b00256_si_001.pdf (1.8MB, pdf)
ci8b00256_si_002.zip (846.1KB, zip)

Articles from Journal of Chemical Information and Modeling are provided here courtesy of American Chemical Society

RESOURCES