Abstract
Objectives
To determine whether a dual-camera markerless motion capture system can be used for lower limb kinematic evaluation in athletes in a preseason screening setting.
Design
Descriptive laboratory study.
Setting
Laboratory setting.
Participants
Thirty-four (n=34) healthy athletes.
Main outcome measures
Three dimensional lower limb kinematics during three functional tests: Single Leg Squat (SLS), Single Leg Jump, Modified Counter-movement Jump. The tests were simultaneously recorded using both a marker-based motion capture system and two Kinect v2 cameras using iPi Mocap Studio software.
Results
Excellent agreement between systems for the flexion/extension range of motion of the shin during all tests and for the thigh abduction/adduction during SLS were seen. For peak angles, results showed excellent agreement for knee flexion. Poor correlation was seen for the rotation movements.
Conclusions
This study supports the use of dual Kinect v2 configuration with the iPi software as a valid tool for assessment of sagittal and frontal plane hip and knee kinematic parameters but not axial rotation in athletes.
Keywords: 3D marker based system, markerless motion capture, Kinect, kinematics
Highlights.
Markerless (multiple Kinect v2) camera kinematic analysis a relatively inexpensive clinically useful tool.
Excellent shin range flexion-extension in all tests.
Excellent results for peak angles regarding knee flexion.
Poor results for rotations.
Introduction
Precompetition medical assessment of athletes commonly includes assessment of movement quality while athletes perform standardised testing procedures. Depending on the particular sport’s performance requirements and injury patterns, different test batteries are employed in an effort to identify at-risk individuals to target for tailored interventions. The quantification of these movement assessment tests is typically performed with simple visual analysis and rating,1 or occasionally using video recording and later 2-dimensional analysis. Such approaches have shown limited accuracy in estimating injury likelihood, and it has been suggested that this could be attributed, in part, to the reduced objectivity of these approaches in comparison to 3-dimensional kinematic analyses.
In the context of football (soccer), commonly performed functional tests include: Single Leg Squat (SLS) assessing motion in frontal plane knee motion;2–4 Single Leg Jump (SLJ)5 6 and Counter-movement Jump (CMJ) for lower limb power estimation.7 Additionally, a modification of the CMJ with the athlete landing on one leg instead of two (Modified Counter Movement Jump (MCMJ)) has been recommended as being more sport-specific.8
Marker-based motion capture is currently considered the reference method for kinematic analyses. These approaches, however, require expensive equipment, significant operator training and analysis time as well as increased subject set-up time. Accordingly, these approaches are rarely employed in settings where time and/or financial constraints exist such as preseason screening of athletes performing functional movement. Additionally, these somewhat artificial laboratory conditions can cause unknown experimental artefacts.9
Recent advances and improved access to markerless motion capture technology have made the use of low-cost motion analysis tools a possibility in the clinical setting.10 However, the validity of this technology in more complex functional movements is currently unclear. The majority of studies done so far used Kinect v1, one camera and the Software Development Kit (SDK) provided by Microsoft. Researchers have evaluated the configuration during working activities,11 functional activities,12 gait in healthy population,13 14 gait in multiple-sclerosis,15 and after cerebrovascular accident,16 and during a jump test.17 More recently, single Kinect v2 was used with Microsoft SDK to test the validity during gait10 and for balance.18 A multi-Kinect v2 configuration with Microsoft SDK was tested for its validity during gait.19 20 To our knowledge, until now, no validation of a dual-camera markerless system during dynamic, advanced movements has been done.
The goals of this study were to examine the validity of a markerless motion capture system using 2 Kinect v2 cameras with custom software during functional movements commonly performed during pre-season physical screening evaluation.
Method
Participants
Thirty-four pain-free male professional football players participated in the study(table 1). All athletes had no previous lower extremity surgery and no current injury. We followed Fleiss’ recommendation21 for reliability studies after considering previous work in the area.22 23 This study was approved by the ethical review board (Institutional Review Board E2013000003) and all participants provided written informed consent as required by the Helsinki declaration.
Table 1.
Participant information
| Participants | Mean±SD |
| Male (n=34) | |
| Age (years) | 26.63 (±4.23) |
| Weight (kg) | 73.58 (±11.44) |
| Height (cm) | 176.01 (±8.01) |
| BMI (kg/m2) | 23.62 (±2.25) |
BMI, body mass index.
Materials
Marker trajectories were measured with a 13-camera motion capture system (BTS-SMART 1000, BTS S.p.A., Italy) sampling at 250 Hz. Depth and colour image data were simultaneously recorded with 2 Kinect v2 cameras at 30 Hz (Kinect for Windows, Microsoft, Redmond, Washington, USA) and iPi Recorder (iPi Soft, Moscow, Russia). Kinect cameras were placed one in front and one to the left side of the capture area (in between the 2 Optojump sensors) at an angle of 70° between them (figure 1).
Figure 1.
Biomechanics lab setup with marker based motion capture system and dual Kinect V2 configuration. Kinect camera placement indicated by the two straight arrows, and athletes were tested within the area of the Opto-Jump sensors (curved arrow). The athletes were tested such that they were facing one Kinect camera, with the other one to their left.
Data collection
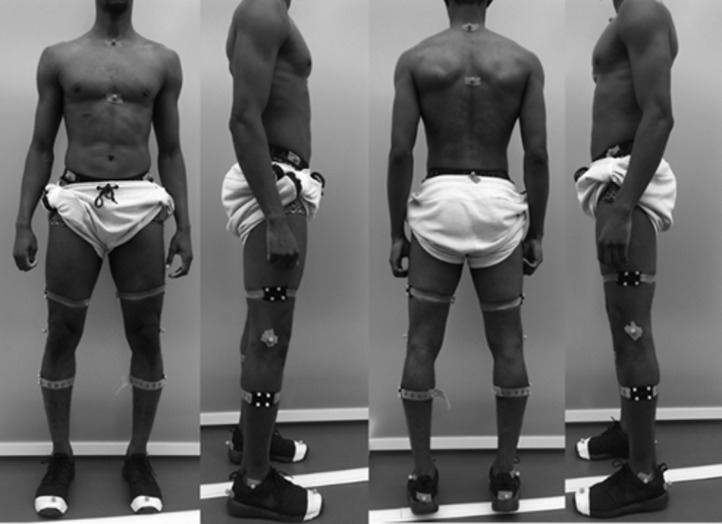
After warm up for a minimum of 5 min, 31 markers were placed using clusters for thigh and shin and on anatomical landmarks according to standard marker protocol (figure 2). Participants stood in the capture area and performed three repetitions each of a SLS, a SLJ and a MCMJ, in the same order. Each trial was captured from BTS and Kinect cameras simultaneously.
Figure 2.
Marker placement.
Data analysis
Kinematic data from the Kinect cameras were processed using biomechanics add-on software (iPi Soft, Moscow, Russia). Marker trajectories from the marker-based system were processed using the SMART Analyser application (BTS S.p.A., Italy). For this analysis, the trajectories were adjusted to iPi Software such that comparison of the extracted data could be made. Marker based data were filtered using Butterworth Low Pass Filter at 6 Hz and resampled at 30 Hz. Kinematic data from both systems were extracted in Euler angles (rotation sequence XYZ), in degrees, relative to the ground for thigh, shin and foot. For each trial, time synchronisation was performed manually by identifying the starting point of each trial as the moment of heel raise from the floor and the end point as the moment of heel contact to the floor.
The range of movement at the thigh, shin and foot and peak angles at the thigh and shin were averaged across three cycles in each exercise and used for subsequent analysis. Range of movement was calculated for each joint of interest as the difference between maximum and minimum angles for each cycle. Mean subject-based values for each test were then determined. Note that these were calculated independently for both the markerless (Kinect) and marker-based (BTS) equipment.
Statistical analysis
A two-way mixed analysis of variance (ANOVA) (absolute agreement) was performed to assess the reliability and the variability of the measurements. Between measurement agreement was assessed using intraclass correlation coefficients (ICC) (2, k; absolute agreement). Because the ICC does not allow us to fully appreciate the magnitude of within-subject variance, we also calculated the SE of measurement (SEM) and the minimal detectable change (MDC).24 SEM represents the within-subject reliability of the measure and, consequently, the reliability of the measure.24 The SEM was determined as √MSE, where MSE=mean square error from the ANOVA table. The MDC represents the threshold over which an individual change can be considered meaningful when taking into account the variability associated with both the measurement technique and the experimental sample and was calculated using the equation MDC=1.96 × √2×SEM Finally, to better understand system agreement of the peak joint angles, the 95% limits of agreement and the bias were calculated using Bland-Altman analysis.25 The bias represents the average difference in peak joint angle between the systems while the limits of agreement are the bias ±SD. Significance level was set at p<0.05. Correlation coefficients were interpreted as follows: less than 0.40 as poor, between 0.40 and 0.59 as fair, between 0.60 and 0.74 as good, between 0.75 and 1.00 as excellent.26 All analyses were performed using SPSS 23.0 (SPSS Statistics for Windows, V.23.0. Armonk, New York, USA: IBM).
Results
Mean(±SD), absolute agreement ICC, SEM and MDC values for angles and ranges of motion are provided in tables 2–4.
Table 2.
Range of angles, averaged over the three cycles during the Single Leg Squat test for BTS (considered as reference standard) and IPI software-Kinect configuration
| Test | Segment | Movement | System | Mean (SD) | 95% CI | ICC(2,k) (95% CI) | P value | SEM | MDC | |
| (deg) | Lower (deg) | Upper (deg) | (deg) | (deg) | ||||||
| SLS_L (n=34) | THIGH | Flexion/Extension | BTS | 42.5 (6.5) | 40.2 | 44.7 | 0.532 (–0.21 to 0.84) | 0.000 | 3.8 | 10.5 |
| iPi | 52.6 (7.8) | 49.8 | 55.3 | |||||||
| Rotation | BTS | 15.1 (3.2) | 14.0 | 16.2 | 0.312 (–0.31 to 0.65) | 0.069 | 3.5 | 9.6 | ||
| iPi | 13.5 (4.5) | 12.0 | 15.1 | |||||||
| Abduction/Adduction | BTS | 13.2 (4.7) | 11.6 | 14.9 | 0.775 (0.55 to 0.89) | 0.791 | 3.4 | 9.5 | ||
| iPi | 13.5 (6.4) | 11.2 | 15.7 | |||||||
| SHIN | Flexion/Extension | BTS | 26.3 (5.3) | 24.4 | 28.1 | 0.886 (0.73 to 0.95) | 0.006 | 2.4 | 6.7 | |
| iPi | 28.0 (6.2) | 25.8 | 30.2 | |||||||
| Rotation | BTS | 21.0 (4.4) | 19.5 | 22.5 | 0.126 (–0.31 to 0.47) | 0.000 | 4.7 | 12.9 | ||
| iPi | 15.5 (5.4) | 13.6 | 17.4 | |||||||
| Abduction/Adduction | BTS | 15.5 (6.7) | 13.1 | 17.8 | 0.718 (0.17 to 0.88) | 0.000 | 3.4 | 9.4 | ||
| iPi | 11.5 (5.2) | 9.7 | 13.3 | |||||||
| FOOT | Flexion/Extension | BTS | 4.7 (4.0) | 3.3 | 6.0 | 0.324 (–0.20 to 0.68) | 0.000 | 3.1 | 8.6 | |
| iPi | 12.2 (4.6) | 10.6 | 13.8 | |||||||
| Rotation | BTS | 2.4 (1.8) | 1.7 | 3.0 | 0.084 (–0.09 to 0.32) | 0.000 | 2.6 | 7.2 | ||
| iPi | 11.5 (3.8) | 10.2 | 12.8 | |||||||
| Abduction/Adduction | BTS | 11.2 (4.1) | 9.8 | 12.7 | 0.867 (0.73 to 0.93) | 0.711 | 2.1 | 6.0 | ||
| iPi | 11.4 (4.7) | 9.8 | 13.1 | |||||||
| SLS_R (n=34) | THIGH | Flexion/Extension | BTS | 43.0 (10.6) | 39.3 | 46.7 | 0.604 (–0.13 to 0.88) | 0.000 | 3.9 | 10.7 |
| iPi | 57.1 (9.6) | 53.7 | 60.4 | |||||||
| Rotation | BTS | 13.9 (4.3) | 12.4 | 15.4 | 0.515 (0.01 to 0.76) | 0.891 | 3.4 | 9.4 | ||
| iPi | 14.0 (4.0) | 12.6 | 15.4 | |||||||
| Abduction/Adduction | BTS | 16.1 (7.6) | 13.4 | 18.7 | 0.758 (0.52 to 0.88) | 0.134 | 4.1 | 11.4 | ||
| iPi | 17.6 (5.6) | 15.7 | 19.6 | |||||||
| SHIN | Flexion/Extension | BTS | 26.3 (5.7) | 24.3 | 28.3 | 0.854 (0.70 to 0.93) | 0.051 | 3.1 | 8.5 | |
| iPi | 27.8 (6.9) | 25.4 | 30.2 | |||||||
| Rotation | BTS | 20.2 (4.4) | 18.7 | 21.8 | −0.210 (–0.76 to 0.26) | 0.000 | 4.7 | 13.0 | ||
| iPi | 14.1 (4.1) | 12.6 | 15.5 | |||||||
| Abduction/Adduction | BTS | 16.5 (9.3) | 13.3 | 19.7 | 0.319 (–0.18 to 0.63) | 0.000 | 6.2 | 17.1 | ||
| iPi | 10.1 (4.1) | 8.7 | 11.5 | |||||||
| FOOT | Flexion/Extension | BTS | 5.7 (2.7) | 4.7 | 6.6 | 0.079 (–0.28 to 0.41) | 0.000 | 4.0 | 11.0 | |
| iPi | 11.1 (5.2) | 9.3 | 12.9 | |||||||
| Rotation | BTS | 2.2 (1.9) | 1.5 | 2.9 | 0.102 (–0.10 to 0.36) | 0.000 | 1.9 | 5.2 | ||
| iPi | 8.4 (2.4) | 7.6 | 9.2 | |||||||
| Abduction/Adduction | BTS | 10.2 (2.9) | 9.2 | 11.2 | 0.707 (0.42 to 0.85) | 0.070 | 2.2 | 6.0 | ||
| iPi | 11.2 (3.6) | 9.9 | 12.5 | |||||||
ICC(2,k), intraclass correlation coefficient (absolute agreement); MDC, minimal detectable change calculated as SEMx1.96x√2. P<0.05; SEM, SE of the measure calculated as the square root of the residual mean square; SLS_L, Single Leg Squat Left; SLS_R, Single Leg Squat Right.
Table 3.
Range of angles, averaged over the three cycles during the Single Leg Jump test for BTS (considered as reference standard) and IPI software-Kinect configuration
| Test | Segment | Movement | System | Mean (SD) | 95% CI | ICC(2,k) (95% CI) | P value | SEM | MDC | |
| (deg) | Lower (deg) | Upper (deg) | (deg) | (deg) | ||||||
| SLJ_L (n=31) | THIGH | Flexion/Extension | BTS | 39.0 (9.2) | 35.6 | 42.3 | 0.491 (–0.17 to 0.82) | 0.000 | 4.4 | 12.3 |
| iPi | 52.5 (7.9) | 49.6 | 55.4 | |||||||
| Rotation | BTS | 21.6 (5.9) | 19.5 | 23.8 | 0.622 (0.21 to 0.82) | 0.870 | 4.7 | 13.0 | ||
| iPi | 21.8 (6.6) | 19.4 | 24.3 | |||||||
| Abduction/Adduction | BTS | 22.2 (8.6) | 19.0 | 25.3 | 0.462 (–0.09 to 0.74) | 0.216 | 5.7 | 15.9 | ||
| iPi | 20.3 (4.5) | 18.7 | 22.0 | |||||||
| SHIN | Flexion/Extension | BTS | 28.9 (7.5) | 26.1 | 31.6 | 0.816 (0.62 to 0.91) | 0.084 | 3.6 | 9.9 | |
| iPi | 27.2 (5.4) | 25.2 | 29.2 | |||||||
| Rotation | BTS | 29.0 (4.9) | 27.2 | 30.8 | −0.260 (–0.94 to 0.28) | 0.000 | 6.0 | 16.5 | ||
| iPi | 22.2 (6.0) | 20.0 | 24.3 | |||||||
| Abduction/Adduction | BTS | 19.2 (4.4) | 17.6 | 20.8 | 0.529 (–0.20 to 0.84) | 0.000 | 2.2 | 6.1 | ||
| iPi | 13.2 (4.0) | 11.8 | 14.7 | |||||||
| FOOT | Flexion/Extension | BTS | 41.6 (10.0) | 38.0 | 45.3 | 0.487 (–0.13 to 0.82) | 0.000 | 4.2 | 11.7 | |
| iPi | 26.4 (7.9) | 23.5 | 29.3 | |||||||
| Rotation | BTS | 15.0 (4.3) | 13.4 | 16.6 | 0.461 (–0.04 to 0.73) | 0.010 | 4.3 | 11.9 | ||
| iPi | 18.0 (6.1) | 15.8 | 20.2 | |||||||
| Abduction/Adduction | BTS | 23.3 (4.5) | 21.6 | 25.0 | 0.213 (–0.18 to 0.55) | 0.000 | 3.6 | 10.1 | ||
| iPi | 15.1 (4.3) | 13.5 | 16.7 | |||||||
| SLJ_R (n=33) | THIGH | Flexion/Extension | BTS | 39.3 (9.1) | 36.0 | 42.5 | 0.658 (–0.19 to 0.88) | 0.000 | 4.5 | 12.3 |
| iPi | 47.4 (7.5) | 44.7 | 50.1 | |||||||
| Rotation | BTS | 21.2 (5.3) | 19.3 | 23.1 | 0.563 (0.15 to 0.78) | 0.063 | 3.8 | 10.5 | ||
| iPi | 19.4 (4.5) | 17.8 | 21.0 | |||||||
| Abduction/Adduction | BTS | 17.1 (5.3) | 15.2 | 19.0 | 0.725 (0.44 to 0.86) | 0.036 | 3.2 | 8.8 | ||
| iPi | 15.4 (4.6) | 13.8 | 17.0 | |||||||
| SHIN | Flexion/Extension | BTS | 27.9 (8.9) | 24.8 | 31.1 | 0.926 (0.84 to 0.96) | 0.022 | 3.0 | 8.4 | |
| iPi | 26.1 (8.3) | 23.2 | 29.1 | |||||||
| Rotation | BTS | 29.2 (5.3) | 27.3 | 31.1 | 0.297 (–0.21 to 0.63) | 0.000 | 4.1 | 11.3 | ||
| iPi | 21.6 (4.9) | 19.9 | 23.4 | |||||||
| Abduction/Adduction | BTS | 16.7 (4.6) | 15.1 | 18.3 | 0.780 (–0.16 to 0.94) | 0.000 | 1.9 | 5.2 | ||
| iPi | 12.8 (5.0) | 11.0 | 14.6 | |||||||
| FOOT | Flexion/Extension | BTS | 43.1 (9.9) | 39.6 | 46.7 | 0.443 (–0.10 to 0.80) | 0.000 | 4.4 | 12.1 | |
| iPi | 24.5 (9.7) | 21.0 | 27.9 | |||||||
| Rotation | BTS | 14.4 (4.3) | 12.9 | 15.9 | 0.421 (–0.11 to 0.71) | 0.000 | 3.3 | 9.2 | ||
| iPi | 18.0 (4.0) | 16.6 | 19.5 | |||||||
| Abduction/Adduction | BTS | 21.7 (4.9) | 19.9 | 23.4 | 0.289 (–0.20 to 0.64) | 0.000 | 3.4 | 9.5 | ||
| iPi | 13.5 (4.2) | 12.0 | 15.0 | |||||||
CC(2,k), intraclass correlation coefficient (absolute agreement); MDC, minimal detectable change calculated as SEMx1.96x√2. P<0.05; SEM, SE of the measure calculated as the square root of the residual mean square; SLJ_L, Single Leg Jump Left; SLJ_R, Single Leg Jump Right.
Table 4.
Range of angles, averaged over the three cycles during the modified counter movement test for BTS (considered as reference standard) and IPI software-Kinect configuration
| Test | Segment | Movement | System | Mean (SD) | 95% CI | ICC(2,k) (95% CI) | P value | SEM | MDC | |
| (deg) | Lower (deg) | Upper (deg) | (deg) | (deg) | ||||||
| MCMJ_L (n=33) | THIGH | Flexion/Extension | BTS | 59.8 (10.4) | 56.1 | 63.5 | 0.851 (0.07 to 0.95) | 0.000 | 3.5 | 9.8 |
| iPi | 65.7 (9.3) | 62.4 | 69.0 | |||||||
| Rotation | BTS | 26.1 (7.3) | 23.5 | 28.7 | 0.518 (0.00 to 0.77) | 0.000 | 4.7 | 13.0 | ||
| iPi | 21.4 (5.1) | 19.6 | 23.2 | |||||||
| Abduction/Adduction | BTS | 26.9 (5.8) | 24.8 | 28.9 | 0.644 (0.23 to 0.83) | 0.002 | 5.6 | 15.5 | ||
| iPi | 31.6 (10.2) | 28.0 | 35.2 | |||||||
| SHIN | Flexion/Extension | BTS | 35.1 (5.8) | 33.1 | 37.2 | 0.801 (0.60 to 0.90) | 0.578 | 3.4 | 9.5 | |
| iPi | 34.7 (6.1) | 32.5 | 36.8 | |||||||
| Rotation | BTS | 35.7 (9.5) | 32.3 | 39.1 | 0.571 (0.05 to 0.80) | 0.000 | 5.8 | 16.1 | ||
| iPi | 29.7 (6.7) | 27.3 | 32.1 | |||||||
| Abduction/Adduction | BTS | 19.6 (5.2) | 17.8 | 21.4 | 0.493 (−0.05 to 0.75) | 0.000 | 3.2 | 8.8 | ||
| iPi | 16.1 (2.9) | 15.1 | 17.1 | |||||||
| FOOT | Flexion/Extension | BTS | 47.8 (10.8) | 44.0 | 51.7 | 0.384 (−0.13 to 0.75) | 0.000 | 5.2 | 14.3 | |
| iPi | 28.7 (8.1) | 25.9 | 31.6 | |||||||
| Rotation | BTS | 22.4 (10.4) | 18.7 | 26.1 | 0.799 (0.59 to 0.90) | 0.053 | 4.8 | 13.2 | ||
| iPi | 24.8 (6.0) | 22.6 | 26.9 | |||||||
| Abduction/Adduction | BTS | 23.9 (5.6) | 21.9 | 25.9 | 0.550 (−0.23 to 0.83) | 0.000 | 2.8 | 7.7 | ||
| iPi | 18.3 (3.5) | 17.0 | 19.5 | |||||||
| MCMJ_R (n=34) | THIGH | Flexion/Extension | BTS | 56.8 (11.2) | 53.0 | 60.7 | 0.765 (−0.19 to 0.93) | 0.000 | 3.9 | 10.9 |
| iPi | 66.3 (10.0) | 62.8 | 69.8 | |||||||
| Rotation | BTS | 23.3 (4.7) | 21.7 | 25.0 | −0.280 (-1.55 to 0.36) | 0.253 | 5.8 | 15.9 | ||
| iPi | 21.7 (6.1) | 19.6 | 23.8 | |||||||
| Abduction/Adduction | BTS | 28.5 (5.8) | 26.4 | 30.5 | 0.657 (0.33 to 0.83) | 0.059 | 5.0 | 13.8 | ||
| iPi | 26.1 (8.2) | 23.2 | 29.0 | |||||||
| SHIN | Flexion/Extension | BTS | 33.7 (5.2) | 31.9 | 35.5 | 0.856 (0.71 to 0.93) | 0.887 | 3.0 | 8.2 | |
| iPi | 33.8 (6.4) | 31.5 | 36.0 | |||||||
| Rotation | BTS | 35.4 (6.3) | 33.2 | 37.6 | 0.049 (−0.50 to 0.45) | 0.001 | 6.0 | 16.5 | ||
| iPi | 30.0 (5.8) | 28.0 | 32.1 | |||||||
| Abduction/Adduction | BTS | 21.9 (7.0) | 19.5 | 24.3 | −0.030 (−0.50 to 0.36) | 0.000 | 5.4 | 14.9 | ||
| iPi | 15.8 (2.9) | 14.8 | 16.8 | |||||||
| FOOT | Flexion/Extension | BTS | 46.0 (8.6) | 43.0 | 49.0 | 0.202 (−0.13 to 0.55) | 0.000 | 5.9 | 16.3 | |
| iPi | 26.5 (7.1) | 24.0 | 29.0 | |||||||
| Rotation | BTS | 20.9 (4.0) | 19.5 | 22.2 | 0.277 (−0.22 to 0.60) | 0.000 | 4.5 | 12.5 | ||
| iPi | 25.5 (6.1) | 23.4 | 27.6 | |||||||
| Abduction/Adduction | BTS | 25.4 (4.9) | 23.7 | 27.1 | 0.238 (−0.17 to 0.58) | 0.000 | 4.5 | 12.5 | ||
| iPi | 17.1 (3.3) | 15.9 | 18.2 | |||||||
ICC(2,k), intraclass correlation coefficient (absolute agreement); MCMJ_L, Modified Counter-Movement Jump Left; MCMJ_R, Modified Counter-Movement Jump Right; MDC, minimal detectable change calculated as SEMx1.96x√2. P<0.05; SEM, standard error of the measure calculated as the square root of the residual mean square.
Our results showed excellent between system agreement for shin movement in flexion/extension in all three tests, for both legs. Additionally, during the SLS test excellent agreement was found for thigh and foot adduction/abduction motion.
Results for peak angles are shown in tables 5–7. Between systems agreement was excellent for knee flexion in all tests for both legs.
Table 5.
Peak angles averaged over the three cycles during the Single Leg Squat test for BTS (considered as reference standard) and IPI software-Kinect configuration
| Test | Movement | System | Mean (SD) | 95% CI | ICC(2,k) (95% CI) | P value | SEM | MDC | |
| (deg) | Lower (deg) | Upper (deg) | (deg) | (deg) | |||||
| SLS_L (n=34) | Hip flexion | BTS | −30.3 (17.5) | −36.4 | −24.2 | 0.896 (–0.09 to 0.97) | 0.000 | 4.1 | 11.3 |
| iPi | −40.6 (18.0) | −46.9 | −34.3 | ||||||
| Hip adduction | BTS | −18.6 (5.5) | −20.6 | −16.7 | 0.749 (0.49 to 0.88) | 0.029 | 3.3 | 9.2 | |
| iPi | −20.5 (5.4) | −22.4 | −18.6 | ||||||
| Knee flexion | BTS | 30.0 (8.6) | 27.0 | 33.0 | 0.932 (0.71 to 0.98) | 0.000 | 2.5 | 6.8 | |
| iPi | 32.8 (8.5) | 29.8 | 35.7 | ||||||
| Knee adduction | BTS | −17.5 (6.1) | −19.6 | −15.3 | 0.830 (0.57 to 0.92) | 0.001 | 2.6 | 7.3 | |
| iPi | −15.3 (4.5) | −16.8 | −13.7 | ||||||
| SLS_R (n=34) | Hip flexion | BTS | −49.1 (14.8) | −54.3 | −44.0 | 0.767 (–0.12 to 0.94) | 0.000 | 3.9 | 10.9 |
| iPi | −63.9 (14.7) | −69.0 | −58.7 | ||||||
| Hip adduction | BTS | 22.8 (4.7) | 21.1 | 24.4 | 0.684 (–0.13 to 0.89) | 0.000 | 2.6 | 7.2 | |
| iPi | 27.1 (5.1) | 25.3 | 28.9 | ||||||
| Knee flexion | BTS | 25.9 (9.8) | 22.5 | 29.4 | 0.947 (0.83 to 0.98) | 0.001 | 2.8 | 7.8 | |
| iPi | 28.5 (10.7) | 24.8 | 32.3 | ||||||
| Knee adduction | BTS | 18.3 (5.8) | 16.3 | 20.3 | 0.665 (0.08 to 0.86) | 0.000 | 3.0 | 8.2 | |
| iPi | 14.7 (3.8) | 13.4 | 16.1 | ||||||
ICC(2,k), intraclass correlation coefficient (absolute agreement); MDC, minimal detectable change calculated as SEMx1.96x√2. P<0.05; SEM, SE of the measure calculated as the square root of the residual mean square; SLS_L, Single Leg Squat Left; SLS_R, Single Leg Squat Right.
Table 6.
Peak angles averaged over the three cycles during the Single Leg Jump test for BTS (considered the gold standard) and IPI software-Kinect configuration
| Test | Movement | System | Mean (SD) | 95% CI | ICC(2,k) (95% CI) | P value | SEM | MDC | |
| (deg) | Lower (deg) | Upper (deg) | (deg) | (deg) | |||||
| SLJ_L (n=31) | Hip flexion | BTS | −27.1 (16.4) | −33.2 | −21.1 | 0.890 (−0.05 to 0.97) | 0.000 | 4.3 | 12.0 |
| iPi | −36.6 (16.6) | −42.7 | −30.5 | ||||||
| Hip adduction | BTS | −19.0 (5.5) | −21.0 | −17.0 | 0.826 (0.64 to 0.92) | 0.744 | 2.9 | 7.9 | |
| iPi | −18.7 (4.9) | −20.5 | −16.9 | ||||||
| Knee flexion | BTS | 31.4 (10.6) | 27.5 | 35.3 | 0.951 (0.90 to 0.98) | 0.694 | 3.0 | 8.3 | |
| iPi | 31.7 (8.7) | 28.5 | 34.9 | ||||||
| Knee adduction | BTS | −16.5 (4.9) | −18.3 | −14.7 | 0.883 (0.32 to 0.96) | 0.000 | 1.7 | 4.7 | |
| iPi | −14.0 (5.0) | −15.9 | −12.2 | ||||||
| SLJ_R (n=33) | Hip flexion | BTS | −46.8 (11.8) | −51.0 | −42.6 | 0.649 (−0.19 to 0.89) | 0.000 | 5.0 | 14.0 |
| iPi | −60.7 (11.6) | −64.8 | −56.6 | ||||||
| Hip adduction | BTS | 23.1 (5.5) | 21.2 | 25.0 | 0.901 (−0.04 to 0.97) | 0.002 | 3.7 | 10.2 | |
| iPi | 26.1 (5.9) | 24.0 | 28.2 | ||||||
| Knee flexion | BTS | 27.5 (11.2) | 23.6 | 31.5 | 0.956 (0.91 to 0.98) | 0.513 | 3.1 | 8.6 | |
| iPi | 28.1 (9.9) | 24.5 | 31.6 | ||||||
| Knee adduction | BTS | 18.8 (4.9) | 17.0 | 20.5 | 0.726 (–0.21 to 0.92) | 0.000 | 2.0 | 5.5 | |
| iPi | 14.3 (4.5) | 12.6 | 15.9 | ||||||
ICC(2,k), intraclass correlation coefficient (absolute agreement); MDC, minimal detectable change calculated as SEMx1.96x√2. P<0.05; SEM, SE of the measure calculated as the square root of the residual mean square; SLJ_L, Single Leg Jump Left; SLJ_R, Single Leg Jump Right.
Table 7.
Peak angles averaged over the three cycles during the modified counter movement test for BTS (considered the gold standard) and IPI software-Kinect configuration
| Test | Movement | System | Mean (SD) | 95% CI | ICC(2,k) (95% CI) | P value | SEM | MDC | |
| (deg) | Lower (deg) | Upper (deg) | (deg) | (deg) | |||||
| MCMJ_L (n=33) | Hip flexion | BTS | −49.4 (18.7) | −56.0 | −42.8 | 0.947 (0.33 to 0.99) | 0.000 | 3.7 | 10.2 |
| iPi | −56.3 (18.4) | −62.8 | −49.7 | ||||||
| Hip adduction | BTS | −18.8 (6.0) | −20.9 | −16.7 | 0.792 (0.17 to 0.92) | 0.000 | 2.5 | 7.0 | |
| iPi | −15.3 (4.8) | −17.1 | −13.6 | ||||||
| Knee flexion | BTS | 35.8 (10.1) | 32.2 | 39.4 | 0.954 (0.80 to 0.98) | 0.000 | 2.4 | 6.6 | |
| iPi | 38.4 (9.7) | 35.0 | 41.9 | ||||||
| Knee adduction | BTS | −16.3 (6.0) | −18.5 | −14.2 | 0.873 (0.59 to 0.95) | 0.000 | 2.4 | 6.5 | |
| iPi | −13.9 (5.6) | −15.9 | −12.0 | ||||||
| MCMJ_R (n=34) | Hip flexion | BTS | −65.7 (14.5) | −70.8 | −60.7 | 0.846 (–0.14 to 0.96) | 0.000 | 3.5 | 9.7 |
| iPi | −76.4 (13.9) | −81.3 | −71.6 | ||||||
| Hip adduction | BTS | 24.0 (5.9) | 21.9 | 26.0 | 0.713 (0.12 to 0.88) | 0.000 | 3.1 | 8.5 | |
| iPi | 20.1 (5.0) | 18.4 | 21.9 | ||||||
| Knee flexion | BTS | 31.0 (8.3) | 28.1 | 33.9 | 0.945 (0.81 to 0.98) | 0.000 | 2.5 | 6.8 | |
| iPi | 33.4 (9.6) | 30.1 | 36.8 | ||||||
| Knee adduction | BTS | 16.8 (5.2) | 15.0 | 18.6 | 0.742 (–0.01 to 0.91) | 0.000 | 2.5 | 6.9 | |
| iPi | 13.1 (4.8) | 11.4 | 14.7 | ||||||
ICC(2,k), intraclass correlation coefficient (absolute agreement); MCMJ_L, Modified Counter-Movement Jump Left; MCMJ_R, Modified Counter-Movement Jump Right; MDC, minimal detectable change calculated as SEMx1.96x√2. P<0.05; SEM, SE of the measure calculated as the square root of the residual mean square.
Biases and limits of agreement (table 8) (online supplementary material 1: Bland-Altman plots) were documented. The mean differences are relatively low especially for hip adduction and knee flexion and adduction. For most of the measures examined, no systematic error is detected. For hip flexion, however, there appears to be a systematic error of approximately 10°.
Table 8.
95% LOA and the bias of the motion capture systems
| Test | Movement | Lower LOA (deg) | Upper LOA (deg) | Bias (deg) |
| SLS_L | Hip flexion | −0.9 | 21.6 | 10.3 |
| Hip adduction | −7.4 | 11.1 | 1.8 | |
| Knee flexion | −9.6 | 4.1 | −2.8 | |
| Knee adduction | −9.5 | 5.0 | −2.2 | |
| SLS_R | Hip flexion | 3.8 | 25.7 | 14.7 |
| Hip adduction | −11.6 | 2.9 | −4.4 | |
| Knee flexion | −10.4 | 5.2 | −2.6 | |
| Knee adduction | −4.7 | 11.8 | 3.6 | |
| SLJ_L | Hip flexion | −2.5 | 21.4 | 9.5 |
| Hip adduction | −8.2 | 7.7 | −0.2 | |
| Knee flexion | −8.6 | 8.0 | −0.3 | |
| Knee adduction | −7.1 | 2.2 | −2.5 | |
| SLJ_R | Hip flexion | −0.1 | 27.8 | 13.9 |
| Hip adduction | −13.2 | 7.2 | −3.0 | |
| Knee flexion | −9.1 | 8.1 | −0.5 | |
| Knee adduction | −0.9 | 10.0 | 4.5 | |
| MCMJ_L | Hip flexion | −3.3 | 17.1 | 6.9 |
| Hip adduction | −10.4 | 3.6 | −3.4 | |
| Knee flexion | −9.2 | 4.0 | −2.6 | |
| Knee adduction | −8.9 | 4.1 | −2.4 | |
| MCMJ_R | Hip flexion | 1.0 | 20.4 | 10.7 |
| Hip adduction | −4.7 | 12.4 | 3.8 | |
| Knee flexion | −9.2 | 4.4 | −2.4 | |
| Knee adduction | −3.1 | 10.6 | 3.8 |
LOA, limits of agreement; MCMJ_L, Modified Counter-Movement Jump Left; MCMJ_R, Modified Counter-Movement Jump Right; SLS_L, Single Leg Squat Left; SLS_R, Single Leg Squat Right.
bmjsem-2018-000441supp001.docx (398.7KB, docx)
Discussion
Here, we have established, for the first time, validity values for SLS, CMJ and MCMJ in a cohort of professional athletes using a 2 camera markerless motion capture system (Kinect v2).
Our results indicate that a dual Kinect v2 configuration is a valid tool for assessment of sagittal plane knee range and peak angles, during squat and jumping tests. Additionally, during the SLS test excellent agreement between systems was found for thigh and foot adduction/abduction motion.
Although agreement improved when using two cameras configuration instead of one,27 the between system agreement varied widely, especially for movements of clinical interest like hip flexion, hip adduction and knee adduction. There was also variability in agreement for different joints and different parameters. For example, shin ab/adduction showed better reliability and validity when considering the peak values in comparison to the results from individual tests. Clinical interpretation is therefore recommended for each approach (eg, individual trials vs averaged values, vs peak values). It may be argued that, in the context of risk of an acute anterior cruciate ligament injury, the peak shin adduction is a more important metric than the average across a number of trials whereas in ‘overuse’ type injuries average values may be a more sensible estimator Also, poor agreement was found regarding all rotational movements. Regarding peak angles, we noticed slightly, but inconsistently, better results found for left side compared with right. Positioning one camera on the left side of the athletes may have influenced these results. Importantly, the estimation of the MDC allows better interpretation of the individual kinematic parameters of interest for future studies and allows for adequate planning (power analyses) of intervention trials. For example, it is suggested that knee abduction at initial contact and peak during a drop jump task is predictive of subsequent ACL injury—the between group differences being 8.4° and 7.6°, respectively, for those who were subsequently injured and those who were not.28 We suggest that this infers the amount of variability between trials for a given subject is likely so large as to exceed these suggested cut-points. In comparison, studies examining changes in hip and knee peak flexion during a landing task, after a fatigue protocol, report 5.1⁰ hip flexion and 6.7⁰ knee flexion29 and 7⁰ increase in peak knee flexion before and after a general fatigue protocol.30 In comparison to the displayed MDC values here, we suggest that both the markerless and marker-based approaches can readily detect such changes. Further to this, it was noted that the hip flexion angle appeared to have a systematic error of approximately 10° when comparing the markerless and marker-based systems. Post processing (ie, subtracting 10° from all measures) could simply remove this artefact and result in more accurate measures. It is uncertain from where this shift arises; however, the closed nature of the processing conducted through the markerless software capture and subsequent processing likely render this a difficult problem to resolve.
Recent studies using Kinect v2 multiple cameras19 20 found excellent between systems agreement when measuring spatiotemporal gait parameters. It should be noted, however, that these studies examined gait, not higher speed movements examined here.
The advantages of the Kinect approach were the much shorter set-up time and much lower (financial) cost of the equipment. Processing time was approximately 7 min for each test and the results derived are for the whole body. We suggest that consideration of the accuracy presented here along with these advantages will allow clinicians to better assess if this approach would be viable for their specific situation.
Some limitations should be considered in the interpretation of the results of this study. Differences in the definition of reference systems and processing between the two systems may have an important role in the extracted results. Additionally, position chosen for markerless cameras may have had a negative effect on the results obtained. Variations in footwear type and sole height may have caused variations in ankle joint centre detection, reducing measurement accuracy. Additionally, markers on the footwear may have affected results for the foot—potentially this is a source of the movement differences detected by Kinect and the BTS system. Importantly, Microsoft recently discontinued production of the Kinect v2 camera. Although the devices remain available for purchase online and in physical retail stores at the time of writing, this will change in the future.
Future studies are recommended to test the clinical utility of Kinect v2–iPi software configuration using more than two cameras. Cameras set up at 45° from the frontal plane may positively influence the extracted data. Future investigations should use standardised footwear or barefoot conditions to improve ankle visualisation and improve measurement of ankle joint kinematics. In conclusion, this study supports the use of dual Kinect v2 configuration with the iPi software as a valid tool for assessment of sagittal knee kinematic parameters in athletes.
Footnotes
Contributors: All authors contributed equally during the study design, data collection/analysis and manuscript writing/revision.
Funding: The publication of this article was funded by the Qatar National Library.
Competing interests: None declared.
Patient consent for publication: Obtained.
Ethics approval: ADLQ E2013000003.
Provenance and peer review: Not commissioned; externally peer reviewed.
Data sharing statement: The data can be accessed via the corresponding author.
References
- 1. Kiesel K, Plisky PJ, Voight ML. Can serious injury in professional football be predicted by a preseason functional movement screen? N Am J Sports Phys Ther 2007;2:147–58. [PMC free article] [PubMed] [Google Scholar]
- 2. Nakagawa TH, Moriya ET, Maciel CD, et al. . Trunk, pelvis, hip, and knee kinematics, hip strength, and gluteal muscle activation during a single-leg squat in males and females with and without patellofemoral pain syndrome. J Orthop Sports Phys Ther 2012;42:491–501. 10.2519/jospt.2012.3987 [DOI] [PubMed] [Google Scholar]
- 3. Olsen OE, Myklebust G, Engebretsen L, et al. . Injury mechanisms for anterior cruciate ligament injuries in team handball: a systematic video analysis. Am J Sports Med 2004;32:1002–12. 10.1177/0363546503261724 [DOI] [PubMed] [Google Scholar]
- 4. Zebis MK, Andersen LL, Bencke J, et al. . Identification of athletes at future risk of anterior cruciate ligament ruptures by neuromuscular screening. Am J Sports Med 2009;37:1967–73. 10.1177/0363546509335000 [DOI] [PubMed] [Google Scholar]
- 5. Gustavsson A, Neeter C, Thomeé P, et al. . A test battery for evaluating hop performance in patients with an ACL injury and patients who have undergone ACL reconstruction. Knee Surg Sports Traumatol Arthrosc 2006;14:778–88. 10.1007/s00167-006-0045-6 [DOI] [PubMed] [Google Scholar]
- 6. Young WB, MacDonald C, Flowers MA. Validity of double- and single-leg vertical jumps as tests of leg extensor muscle function. J Strength Cond Res 2001;15:6–11. [PubMed] [Google Scholar]
- 7. Markovic G, Dizdar D, Jukic I, et al. . Reliability and factorial validity of squat and countermovement jump tests. J Strength Cond Res 2004;18:551 [DOI] [PubMed] [Google Scholar]
- 8. Jacobs CA, Uhl TL, Mattacola CG, et al. . Hip abductor function and lower extremity landing kinematics: sex differences. J Athl Train 2007;42:76–83. [PMC free article] [PubMed] [Google Scholar]
- 9. Mündermann L, Corazza S, Andriacchi TP. The evolution of methods for the capture of human movement leading to markerless motion capture for biomechanical applications. J Neuroeng Rehabil 2006;3:6 10.1186/1743-0003-3-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Eltoukhy M, Oh J, Kuenze C, et al. . Improved kinect-based spatiotemporal and kinematic treadmill gait assessment. Gait Posture 2017;51:77–83. 10.1016/j.gaitpost.2016.10.001 [DOI] [PubMed] [Google Scholar]
- 11. Patrizi A, Pennestrì E, Valentini PP. Comparison between low-cost marker-less and high-end marker-based motion capture systems for the computer-aided assessment of working ergonomics. Ergonomics 2016;59:155–62. 10.1080/00140139.2015.1057238 [DOI] [PubMed] [Google Scholar]
- 12. Bonnechère B, Jansen B, Salvia P, et al. . Validity and reliability of the Kinect within functional assessment activities: comparison with standard stereophotogrammetry. Gait Posture 2014;39:593–8. 10.1016/j.gaitpost.2013.09.018 [DOI] [PubMed] [Google Scholar]
- 13. Auvinet E, Multon F, Aubin CE, et al. . Detection of gait cycles in treadmill walking using a Kinect. Gait Posture 2015;41:722–5. 10.1016/j.gaitpost.2014.08.006 [DOI] [PubMed] [Google Scholar]
- 14. Xu X, McGorry RW, Chou LS, et al. . Accuracy of the Microsoft Kinect for measuring gait parameters during treadmill walking. Gait Posture 2015;42:145–51. 10.1016/j.gaitpost.2015.05.002 [DOI] [PubMed] [Google Scholar]
- 15. Behrens J, Pfüller C, Mansow-Model S, et al. . Using perceptive computing in multiple sclerosis - the Short Maximum Speed Walk test. J Neuroeng Rehabil 2014;11:89 10.1186/1743-0003-11-89 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Vernon S, Paterson K, Bower K, et al. . Quantifying individual components of the timed up and go using the kinect in people living with stroke. Neurorehabil Neural Repair 2015;29:48–53. 10.1177/1545968314529475 [DOI] [PubMed] [Google Scholar]
- 17. Stone EE, Butler M, McRuer A. Evaluation of the Microsoft Kinect for screening ACL injury. 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE 2013:4152–5. [DOI] [PubMed] [Google Scholar]
- 18. Clark RA, Pua YH, Oliveira CC, et al. . Reliability and concurrent validity of the Microsoft Xbox One Kinect for assessment of standing balance and postural control. Gait Posture 2015;42:210–3. 10.1016/j.gaitpost.2015.03.005 [DOI] [PubMed] [Google Scholar]
- 19. Dolatabadi E, Taati B, Mihailidis A. Concurrent validity of the Microsoft Kinect for Windows v2 for measuring spatiotemporal gait parameters. Med Eng Phys 2016;38:952–8. 10.1016/j.medengphy.2016.06.015 [DOI] [PubMed] [Google Scholar]
- 20. Geerse DJ, Coolen BH, Roerdink M. Kinematic Validation of a Multi-Kinect v2 Instrumented 10-Meter Walkway for Quantitative Gait Assessments. PLoS One 2015;10:e0139913 10.1371/journal.pone.0139913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Fleiss JL. The design and analysis of clinical experiments. Wiley, 1999. [Google Scholar]
- 22. Perrott MA, Pizzari T, Cook J, et al. . Comparison of lower limb and trunk kinematics between markerless and marker-based motion capture systems. Gait Posture 2017;52:57–61. 10.1016/j.gaitpost.2016.10.020 [DOI] [PubMed] [Google Scholar]
- 23. Schmitz A, Ye M, Boggess G, et al. . The measurement of in vivo joint angles during a squat using a single camera markerless motion capture system as compared to a marker based system. Gait Posture 2015;41:694–8. 10.1016/j.gaitpost.2015.01.028 [DOI] [PubMed] [Google Scholar]
- 24. Beckerman H, Roebroeck ME, Lankhorst GJ, et al. . Smallest real difference, a link between reproducibility and responsiveness. Qual Life Res 2001;10:571–8. 10.1023/A:1013138911638 [DOI] [PubMed] [Google Scholar]
- 25. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1:307–10. [PubMed] [Google Scholar]
- 26. Portney LG, Watkins MP. Foundations of clinical research: applications to practice. [Google Scholar]
- 27. Eltoukhy M, Kelly A, Kim CY, et al. . Validation of the Microsoft Kinect® camera system for measurement of lower extremity jump landing and squatting kinematics. Sports Biomech 2016;15:89–102. 10.1080/14763141.2015.1123766 [DOI] [PubMed] [Google Scholar]
- 28. Hewett TE, Myer GD, Ford KR, et al. . Biomechanical measures of neuromuscular control and valgus loading of the knee predict anterior cruciate ligament injury risk in female athletes: a prospective study. Am J Sports Med 2005;33:492–501. 10.1177/0363546504269591 [DOI] [PubMed] [Google Scholar]
- 29. Kernozek TW, Torry MR, Iwasaki M. Gender differences in lower extremity landing mechanics caused by neuromuscular fatigue. Am J Sports Med 2008;36:554–65. 10.1177/0363546507308934 [DOI] [PubMed] [Google Scholar]
- 30. Liederbach M, Kremenic IJ, Orishimo KF, et al. . Comparison of landing biomechanics between male and female dancers and athletes, part 2: influence of fatigue and implications for anterior cruciate ligament injury. Am J Sports Med 2014;42:1089–95. 10.1177/0363546514524525 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
bmjsem-2018-000441supp001.docx (398.7KB, docx)