Abstract
Nonrandom mating based on phenotype has been observed in a number of organisms, but a very high proportion of these examples are of assortative mating. The strongest example of negative-assortative mating is for white-striped versus tan-striped crown in the white-throated sparrow, where about 98% of the observed pairings (mated pairs or social pairs) are between mates with different phenotypes and the correlation between mating types is −0.964. Although nonrandom mating has been explored theoretically for decades, these models have generally not focused on specific well-documented examples. Here we have developed a model to investigate the dynamics and equilibrium of this iconic example. The observed pattern of mating appears to be the result of 96% negative-assortative mating and a 17% advantage of W (white) male × T (tan) female matings compared to the reciprocal T male × W female matings. The equilibrium heterozygosity given these values is 0.500, very close to the 0.501 observed in our large sample of pairings, and this heterozygosity has been maintained for the 29 years from 1988 to 2016. In addition, the equilibrium frequency of 2m inversion determining the white-striped phenotype has been maintained at a frequency very close to its equilibrium frequency of 0.25. Overall, this model demonstrates how evolutionary genetic models can be used to understand negative-assortative mating.
Keywords: assortative mating, disassortative mating, equilibrium, heterozygosity, supergenes
In evolutionary genetic models, mating between individuals generally assumes that mating occurs randomly between individuals of different relatedness and phenotypes. Nonrandom mating based on phenotype occurs when there is positive-assortative mating (often termed just assortative mating), where mates are more similar phenotypically than expected at random, or negative-assortative mating (often termed disassortative mating), where mates are less similar phenotypically than expected at random. In general, positive-assortative mating can result in higher homozygosity and a decrease in genetic variation in a population whereas negative-assortative mating can result in higher heterozygosity and maintenance of genetic variation in a population. Nonrandom mating based on phenotypes only influences the genes that result in the phenotypic variation important in mating (and potentially those in linkage disequilibrium with these genes) whereas nonrandom mating based on relatedness has effects on all the genes in the genome.
For many decades, there has been an effort to explain the factors important in maintaining genetic variation in populations and it is generally accepted that some type of balancing selection could play a role in maintaining genetic variation. The exact form of this balancing selection appears elusive, or takes different forms in different populations, and it appears that heterozygote advantage, a longtime favorite type of balancing selection, is not as widespread as once suggested (Hedrick 2012). Negative-assortative mating is another form of balancing selection that could maintain genetic variation and detailed studies of the best documented cases of negative-assortative mating could provide insight into the general importance of this type of balancing selection in maintaining genetic variation.
A comprehensive review of 1116 assortative mating examples in animals (Jiang et al. 2013) documented many examples of positive-assortative mating but very few examples of negative-assortative mating, particularly in populations of vertebrates. For categorical (noncontinuous) traits in vertebrates, Jiang et al. (2013) found only 4 examples of statistically significant negative-assortative mating, 3 in birds (including crown color in white-throated sparrows) and one in fish (see discussion below). Hedrick et al. (2016) recently documented another example of significant negative-assortative mating for black and gray pelage color in wolves in Yellowstone National Park.
The highest level of negative-assortative mating observed in vertebrates was for the tan-striped and white-striped polymorphism on the median crown stripe in the white-throated sparrow (Zonotrichia albicollis) (Lowther 1961; Thorneycroft 1975; Tuttle et al. 2016; see perspective by Arnold 2016). Figure 1 gives photos of male white-throated sparrows from 2 perspectives to illustrate the color differences between the white-striped and tan-striped morphs. In all of these surveys, over 90% of the pairings (mated pairs or social pairs) were between different color morphs. In the largest and most recent survey of 1209 pairs (Tuttle et al. 2016 and our data here from 2015 and 2016), 98.2% of the pairings were between different color morphs and only 1.8% were between the same color morph.
Figure 1.
The white (left) and tan (right) forms of male white-crowned sparrows showing the color differences from both lateral and frontal views. The inset shows the genotypic differences for the metacentric inversion 2m as compared to the non-inverted chromosome 2 (photos and composition by E.M.T.).
The color differences in white-throated sparrows are associated with a chromosomal inversion (Thorneycroft 1966) (actually several adjacent inversions) greater than 100Mb in length that contains around 1000 genes and about 10% of the genome (Huynh et al. 2011). Tuttle et al. (2016) concluded that this inversion has resulted in a polymorphism for a tightly linked group of evolutionarily related genes, or a polymorphic supergene (Schwander et al. 2014). The recessive tan (T) variant is on the non-inverted form of chromosome 2, called 2 here, and T individuals have 2 copies of the non-inverted chromosome, identified here as genotype 22. The dominant white (W) variant is on the inverted chromosome 2m (m stands for metacentric and describes the position of the centromere on this chromosome) and W individuals are nearly all heterozygotes with the genotype 22m. Molecular analysis has shown that the 2 and 2m chromosomes are highly divergent within the inverted region of the chromosome (Tuttle et al. 2016). Mainly as a result of the strong negative-assortative mating associated with these color morphs and inversion types, homozygotes 2m2m for the inversion appear to be very rare. In addition, Tuttle et al. (2016) found that the frequency of 2m2m individuals appeared to be even further reduced by selection against these individuals who are homozygous for all the genes in the inversion.
Below we present a model of negative-assortative mating to use for an understanding of the dynamical changes and equilibrium proportions for this iconic and well-documented negative-assortative mating example in the white-throated sparrow. Here we compare the theoretical predictions from a model of negative-assortative mating designed for this example to the observed pairing frequencies found in a large natural population sample. This model provides a general framework for understanding the evolutionary factors and their magnitude that are likely present in this example and demonstrates how evolutionary genetic models can be used to describe and understand negative-assortative mating in nature.
Model
Nearly all of the individuals examined in white-throated sparrow populations are either tan (T) and homozygous for the non-inverted form, 22, or are white (W) and heterozygous for the inversion, 22m. Only 6 out of 3057 (0.2%) individuals surveyed by Tuttle et al. (2016) were found to be 2m2m homozygotes. Therefore, in the model below we will assume that the frequency of genotypes 22 and 22m are P and H, respectively, and that P + H = 1 (there are no 2m2m homozygotes). As a result, there are only the 4 mating types given in Table 1 for the different colors and genotypes. In the theoretical model below, we will refer to these mating types as “matings” rather than “pairings,” the term that is used here to describe the observed combination of mated pairs and social pairs.
Table 1.
The 4 different types of mating between the 2 genotypes and the frequency of matings given that A is the proportion of negative-assortative mating and s is the selective advantage of mating W male × T female relative to mating T male × W female
| Mating (male × female) | Frequency | |||
|---|---|---|---|---|
| Color | Genotype | Random | Negative-assortative | Total |
| Tan × Tan | 22 × 22 | — | ||
| Tan × White | 22 × 22m | |||
| White × Tan | 22m × 22 | |||
| White × White | 22m × 22m | — | ||
Assume that the proportion of negative-assortative mating is A and that 1−A is the proportion of random mating. As a result, the frequency of mating T × T is and the frequency of mating W × W is because all of the matings of these types are the result of random mating. The frequency of the mating type T male × W female (the first individual here and in other mating pairs is the male) is , where the first term is the contribution from random mating and the second term is the contribution from negative-assortative mating.
The frequency of the mating W male × T female has been observed to be higher than the reciprocal mating T male × W female (Lowther 1961; Thorneycroft 1975; Tuttle et al. 2016) (see discussion below). Therefore, we will assume a relative advantage s in the formation of W male × T female matings compared to the reciprocal matings of T male × W female. Therefore, the frequency of the mating type W male × T female is where the first term is the contribution from random mating and the second term is the contribution from negative-assortative mating.
Using these mating proportions, and assuming Mendelian segregation in the progeny as given in Table 2, the expected frequency of 22 and 22m offspring are the sums of their respective columns in Table 2 and are
Table 2.
The 4 different types of mating between the 2 genotypes and the proportions of progeny expected given that A is the proportion of negative-assortative mating and s is the selective advantage of mating W male × T female relative to mating T male × W female. Genotype 2m2m is very rare when A is large so this contribution is considered equal to 0 in this analysis
| Progeny | |||
|---|---|---|---|
| Mating | 22 | 22m | 2m2m |
| 22 × 22 | — | — | |
| 22 × 22m | — | ||
| 22m × 22 | — | ||
| 22m × 22m | |||
| Sum | 0 | ||
| (1) |
where
Note that genotype 2m2m is very rare when A is large (rightmost column of Table 2) so the contribution of this progeny genotype is considered equal to 0 in this analysis, an assumption that reflects the very low observed frequency of 2m2m. These equations can be iterated over time to determine the expected equilibrium frequencies for genotypes 22 and 22m of Pe and He.
The frequency of the inverted form of the supergene 2m is half the frequency of the heterozygotes or
Using these equilibrium genotypic frequencies, the expected equilibrium frequencies for the 4 mating types, where the first individual in the mating pair is the male, become
| (2) |
where
To find the values of A and s which are consistent with the observed mating frequencies, the range of A and s were explored to find the minimum summed squared deviation of the observed frequency to the expected equilibrium for the 4 mating types. When A = 1 for given years, that is, no homotypic matings were observed, then from Equation (1), H = P = 0.5. Then from Equation (2), assuming that WT is the frequency of W male × T female matings,
and
| (3) |
Results
Table 3 gives the observed numbers and frequencies of the 4 types of pairings for the Cranberry Lake, New York population from 1988 to 2016 (data through 2014 were given in Tuttle et al. 2016 and data for 2015 and 2016 are new here). The observed heterozygosity (and frequency of the W morph) in this sample of 1209 pairings was 0.501 (the observed homozygosity and the frequency of the T morph was 0.499) and the frequency of the inverted (2m) and the non-inverted (2) chromosomal forms were 0.250 and 0.750, respectively. The proportion of homotypic pairings is 1.8% and the proportion of heterotypic pairings was 98.2%, demonstrating the high proportion of pairings between different morphs. The negative correlation between mating types was −0.964, very near the maximum negative value. In addition, the observed proportion of W male × T female pairings was 0.528 compared to the somewhat smaller observed proportion of T male × W female pairings of 0.454.
Table 3.
The number and frequency observed of the 4 pairings from Cranberry Lake, New York from 1988 to 2016 (data through 2014 were given in Tuttle et al. 2016) in 1209 pairings. In the bottom row is the expected frequency of matings at equilibrium given that negative-assortative mating A = 0.961, an advantage favoring the W male × T female mating over the T male × W female mating of s = 0.166, and that 2m2m is absent
| Male × Female | Tan × Tan (22 × 22) | Tan × White (22 × 22m) | White × Tan (22m × 22) | White × White (22m × 22m) | Heterozygosity |
|---|---|---|---|---|---|
| Observed number | 10 | 549 | 638 | 12 | 1211 |
| Observed frequency | 0.008 | 0.454 | 0.528 | 0.010 | 0.501 |
| Expected frequency (A = 0.961, s = 0.166) | 0.009 | 0.454 | 0.528 | 0.009 | 0.500 |
First, the estimates in this population of A and s that are consistent with the observed proportions of the 4 mating types are A = 0.961 and s = 0.166. For these values of A and s, the observed and expected frequencies of heterotypic matings are identical and the observed and expected frequencies of 2 homotypic matings differ by only 0.001 from the observed frequencies (Table 3).
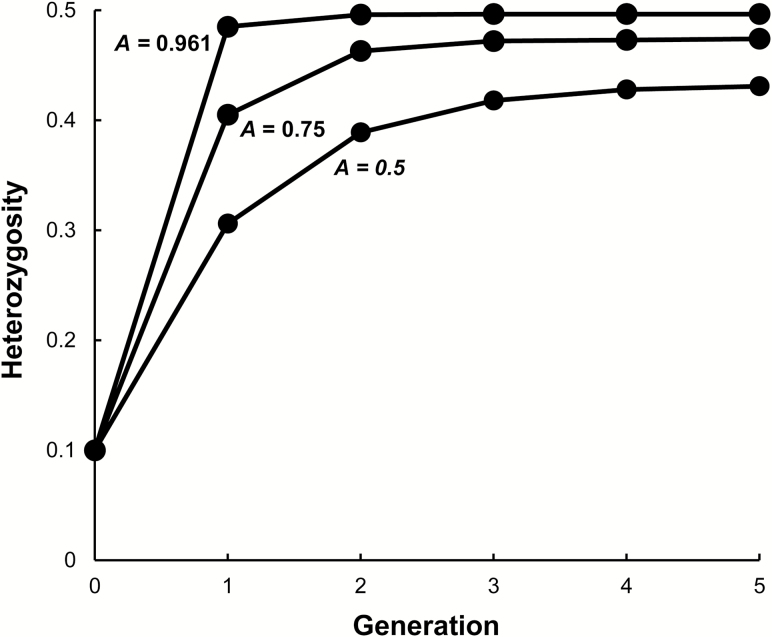
Let us now examine how fast the level of heterozygosity approaches its equilibrium frequency assuming that s is the estimated level of 0.166. Iterating expression (1), given that the initial frequency of heterozygosity is relatively low at 0.1 as might be expected from introduction by gene flow, the equilibrium heterozygosity is very quickly approached (Figure 2). For example, when A = 0.961, the estimate of the level of negative-assortative mating observed, the equilibrium heterozygosity is closely approached in just 2 generations. Even when A = 0.5, the equilibrium heterozygosity is closely approached in just 5 generations. As a result, it is reasonable to assume that the observed proportions of different pairings are close to the proportions expected at equilibrium from the actual amount of negative-assortative mating.
Figure 2.
The increase in frequency of heterozygosity over generations when initially H = 0.1, an advantage of W male × T female matings over other matings of s = 0.166, and negative-assortative mating of A = 0.961, 0.75, and 0.5.
The expected level of heterozygosity at equilibrium from equation (1) is mainly a function of A whereas s has a much smaller effect on this equilibrium. That is, as A increases from 0 to 1, the level of heterozygosity increases from 0 to 0.5. On the other hand, as s is increased from 0 to 0.4, given that A = 0.5, the heterozygosity only is increased from 0.428 to 0.438. Notice that when A = 0 that the heterozygosity is 0 because of the assumed selection against 2m2m individuals.
The Cranberry Lake population of white-throated sparrows has been surveyed annually since 1988 (except for 3 years in which complete censuses were not carried out, Table 4). One of the most striking observations from these long-term temporal data is that the heterozygosity is 0.5 in 22 of the 26 years sampled from 1988 to 2016 and averages 0.502 over the 26 years sampled. In other words, the population has been close to the equilibrium heterozygosity predicted by the model when there is high negative-assortative mating for nearly 30 years. Similarly, the population is also close to the equilibrium frequency of 0.25 predicted for the inversion 2m for this 29-year period.
Table 4.
The annual numbers of the 4 types of pairings and total annual number N in the white-throated sparrow population at Cranberry Lake, New York from 1988 to 2016 and the estimated values of H, s and A for each year (data from 1988 to 2014 were used in Tuttle et al. 2016 and data for years 2015 and 2016 are new here). In years 1993, 1996, and 1997, a complete census of pairings was not carried out
| Male × Female | ||||||||
|---|---|---|---|---|---|---|---|---|
| Year | T × T | T × W | W × T | W × W | N | H | S | A |
| 1988 | 0 | 1 | 3 | 0 | 4 | 0.5 | 2.00 | 1.0 |
| 1989 | 1 | 5 | 9 | 1 | 16 | 0.5 | 0.94 | 0.68 |
| 1990 | 0 | 5 | 6 | 0 | 11 | 0.5 | 0.20 | 1.0 |
| 1991 | 0 | 7 | 8 | 0 | 15 | 0.5 | 0.14 | 1.0 |
| 1992 | 0 | 7 | 8 | 0 | 15 | 0.5 | 0.14 | 1.0 |
| 1994 | 0 | 6 | 6 | 0 | 12 | 0.5 | 0.00 | 1.0 |
| 1995 | 0 | 10 | 9 | 0 | 19 | 0.5 | −0.10 | 1.0 |
| 1998 | 0 | 8 | 16 | 0 | 24 | 0.5 | 1.00 | 1.0 |
| 1999 | 0 | 14 | 22 | 1 | 37 | 0.514 | 0.59 | 0.94 |
| 2000 | 0 | 15 | 17 | 0 | 32 | 0.5 | 0.13 | 1.0 |
| 2001 | 0 | 19 | 19 | 0 | 38 | 0.5 | 0.00 | 1.0 |
| 2002 | 0 | 16 | 22 | 0 | 38 | 0.5 | 0.38 | 1.0 |
| 2003 | 0 | 23 | 19 | 1 | 43 | 0.512 | −0.17 | 1.0 |
| 2004 | 0 | 28 | 25 | 0 | 53 | 0.5 | −0.11 | 1.0 |
| 2005 | 0 | 22 | 34 | 0 | 56 | 0.5 | 0.54 | 1.0 |
| 2006 | 0 | 29 | 34 | 0 | 63 | 0.5 | 0.17 | 1.0 |
| 2007 | 0 | 49 | 59 | 0 | 108 | 0.5 | 0.20 | 1.0 |
| 2008 | 1 | 41 | 43 | 0 | 85 | 0.5 | 0.05 | 0.98 |
| 2009 | 1 | 41 | 48 | 1 | 91 | 0.5 | 0.18 | 0.95 |
| 2010 | 1 | 35 | 38 | 0 | 74 | 0.5 | 0.09 | 0.97 |
| 2011 | 2 | 32 | 37 | 4 | 75 | 0.514 | 0.17 | 0.83 |
| 2012 | 0 | 26 | 45 | 0 | 71 | 0.5 | 0.73 | 1.0 |
| 2013 | 1 | 29 | 41 | 0 | 71 | 0.5 | 0.42 | 0.96 |
| 2014 | 1 | 31 | 32 | 1 | 65 | 0.5 | 0.03 | 0.94 |
| 2015 | 1 | 21 | 14 | 0 | 36 | 0.5 | −0.33 | 0.95 |
| 2016 | 1 | 29 | 24 | 3 | 57 | 0.518 | −0.18 | 0.87 |
| Total or mean | 10 | 549 | 638 | 12 | 1209 | 0.502 | 0.166 | 0.961 |
In addition, there has been annual variation in the proportion of the 4 types of pairings in the Cranberry Lake population (Table 4). However, in all years the number of heterotypic pairings is much larger than the number of homotypic pairings and the estimate of negative-assortative mating A was 1.0 in 15 of 26 years and close to 1.0 in the other 11 years. Over the 26 years, the sample size weighted mean of A was 0.954 (±0.010). Similarly, the estimate of s, which reflects the relative proportions of the 2 heterotypic mating types, was positive in 21 out of 26 years and not very large negative levels in the other years. In this case, over the 26 years, the sample size weighted mean of s was 0.199 (±0.060).
Discussion
There are few well-documented examples of negative-assortative mating, particularly in vertebrates (Jiang et al. 2013). As a result, it is important to understand these examples and to provide models to predict both the expected dynamics and equilibria for them. Although theoretical models of negative-assortative mating have been explored for decades, most have been general models and not designed to understand specific examples of negative-assortative mating. It is essential to determine whether the observed factors in a particular negative-assortative mating example result in allele frequency change and maintenance of genetic variation as generally expected from models designed to reflect these factors.
Here a model of negative-assortative mating for variation in the median crown stripe in white-throated sparrows predicts very closely the proportions of the 4 types of pairings observed. That is, with 96.1% negative-assortative mating (3.9% random mating) and matings between W male × T female 16.6% more likely than the reciprocal T male × W female, the predicted proportions of the 4 mating types are very close to that observed. Also, given this value of negative-assortative mating and assuming that the inverted chromosome resulting in white crown stripe is introduced at a low frequency, the expected equilibrium heterozygosity of 0.5 is reached in only 2 generations.
Factors Influencing Mating Frequencies
What factors actually determine this high level of negative-assortative mating? First, the 2 phenotypic morphs differ in social behavior, including the level of parental care, aggression, and courtship (Knapton and Falls 1983; Tuttle 2003; Formica and Tuttle 2009). More specifically, W males are promiscuous at the expense of paternal care and T males contribute more to parental care (Tuttle 2003). Similarly, W females are also more aggressive and invest less in parental care than do T females (Tuttle 2003). Tuttle (1993) found that males of both morphs preferred W females and both Tuttle (1993) and Houtman and Falls (1994) found that both female morphs preferred T males. Because W females are more dominant, they outcompete T females for the preferred T males, resulting in heterotypic pairings. The remaining T females then pair with the less preferred W males.
As we mentioned above, the proportion of W male × T female pairings has been observed to be somewhat higher than the reciprocal pairings T male × W female (Lowther 1961; Thorneycroft 1975; Tuttle et al. 2016). In the 2 smaller, earlier samples from Algonquin Provincial Park from Lowther (1961) and Thorneycroft (1975) the proportion of W male × T female pairings was 73.7% and the reciprocal pairings T male × W female only 26.3%, statistically significantly different from that observed here and by Tuttle et al. (2016) (Table 5a). The estimate of A in the combined Algonquin sample was 0.990, similar to that in the Cranberry Lake population, whereas s was 2.40, much larger than in the Cranberry Lake population. In other words, it appears that other populations also have a high proportion of negative-assortative mating but that different populations might differ in both the proportions of the different mating types and the proportions of the 2 morphs in the 2 sexes (Table 5b) (a recent, large sample from the Algonquin Provincial Park would be necessary to examine this).
Table 5.
(a) The numbers of the 4 types of pairings and (b) the numbers of females and males of the different morphs in these pairings from the 2 samples from Algonquin Provincial Park, Ontario, Canada (Lowther 1961 and Thorneycroft 1975), and the sample from Cranberry Lake, New York, United States
| (a) Male × Female | Tan × Tan (22 × 22) | Tan × White (22 × 22m) | White × Tan (22m × 22) | White × White (22m × 22m) | Total |
|---|---|---|---|---|---|
| Lowther | 4 | 27 | 79 | 0 | 110 |
| Thorneycroft | 1 | 6 | 33 | 2 | 42 |
| Total | 5 (0.035) | 33 (0.217) | 112 (0.737) | 2 (0.013) | 152 |
| Tuttle et al. | 10 (0.008) | 549 (0.454) | 638 (0.528) | 12 (0.010) | 1209 |
| (b) | Females | Males | |||
| Tan (22) | White (22m) | Tan (22) | White (22m) | Total | |
| Lowther | 83 | 27 | 31 | 79 | 110 |
| Thorneycroft | 34 | 8 | 7 | 35 | 42 |
| Total | 117 (0.770) | 35 (0.230) | 38 (0.250) | 114 (0.750) | 152 |
| Tuttle et al. | 648 (0.536) | 561 (0.464) | 559 (0.462) | 650 (0.538) | 1209 |
The difference in the proportions of the 2 reciprocal matings might occur because the W males are more aggressive and more promiscuous than T males (Tuttle 2003). However, W male × T female pairings actually have lower reproductive success and extra pair fertilizations were more common in W male × T female nests than T male × W female nests (Tuttle 2003). In other words, the excess of these pairs in matings could potentially arise because of higher survivorship or territorial establishment of this morph mating type but this advantage appears to be subsequently reduced by lower reproductive success.
In addition, the proportion of W male × T female versus T male × W female in a given year is presumably influenced by the sex ratio within W versus within T birds. It is unlikely that the same sex ratio would always be present and the variation in the proportions of each pair type between years in the Cranberry Lake population is probably partly due to these changes in population composition. For instance, in 2016 there was a number of unpaired white males, possibly due to a deficit of tan females, and there were 3 incidences of secondary (during the second clutch) W × W pairings (Tuttle and Gonzer, unpublished data). This example illustrates that population composition can have a strong effect on the relative number of each pair type. For instance, if recruitment or mortality rates lead to fewer T males than W males, then this would limit the number of T male × W female pairs that can form. Potentially combining data across years could obscure some of these fluctuations and there have been 5 years out of the 26 surveyed with more T male × W female than W male × T female pairs.
Genotype 2m2m appears to be very rare for several reasons. First, there is a very high level of negative-assortative mating that results in a very low level of W × W homotypic pairings, the only mating from which 2m2m progeny can be produced. Overall in 1209 total pairings, only 12 (0.99%) were W × W (Table 2). From these pairings, ¼ of their progeny are expected to be genotype 2m2m so that the expected number of progeny from these pairings is (0.0099)(0.25)(1989) = 4.9 where the number of progeny genotyped in Tuttle et al. (2016) was 1989. In addition, 0.454 of the population pairs are T male × W female and in these pairings about 4% of the progeny are produced from extra-pair copulations with W males (Tuttle et al. 2016). From these pairings, the expected number of 2m2m progeny is (0.454)(0.04)(0.25)(1989) = 9.0, for a total of 13.9 expected 2m2m progeny. In fact, in the survey of Tuttle et al. (2016) only 3 out of 1989 were observed to be 2m2m (1 male and 2 females) and the male was much smaller than normal. Tuttle et al. (2016) also summarized the data from 4 other studies and in them only 3 of 1068 sparrows were 2m2m homozygotes.
There also appears to be some selection against homotypic W × W and T × T pairings because of both female-biased clutches and higher rates of extra pair paternity (Tuttle et al. 2016). However, there are very few homotypic matings because of the very high negative-assortative mating so this additional selection might not decrease the absolute number of progeny from these matings significantly. It is possible that this selection could have been present before the high level of negative-assortative mating and then become less important because of the low frequency of the homotypic matings.
Supergene Origin and Importance
One of the fascinating questions concerning the polymorphic supergene in the white-throated sparrow is the origin and order of incorporation of different mutants associated with the inversion. Tuttle et al. (2016) suggested that the inverted form is old because of its high divergence from the non-inverted form. They suggested that at some point this variant was introduced by hybridization into the ancestor of the white-throated sparrow and the resultant lineage became polymorphic for the supergene. They also suggested that some of mutational differences were already present at that point whereas other mutations were subsequently incorporated over time. However, the donor species for the 2m inversion has not been identified and might be extinct.
Another scenario is that first the inverted form 2m arose within the ancestor of the white-throated sparrow and became polymorphic. Because there is no successful recombination within the inverted region in chromosomal heterozygotes, mutations accumulated on the chromosome 2m. These mutations influenced behavior, the color of the median crown stripe, and viability. As a result, there was selection against 2m2m homozygotes and negative-assortative mating was advantageous because it resulted in a reduction of the frequency of 2m2m. It is noteworthy that the recently described inversions in the ruff (Philomachus pugnax) (Küpper et al. 2016; Lamichhaney et al. 2016) influencing male reproductive morphology although quite old (they appeared to have begun diverging nearly 4 million years ago) appear to have arisen within this species rather than ancestral to it.
An important aspect of the inversion and supergene to emphasize here, independent of the scenario of its origin, is that it has resulted in the strong association of a number of genes influencing behavior, morphology, physiology, and other traits related to fitness. As a result, the extent of selection influencing negative assortative mating in the white-throated sparrow is very large and this both results in strong selection for its maintenance and a fast approach to the polymorphic equilibrium if by chance it is moved away from it.
Other Examples of Negative-Assortative Mating
The mean correlation between mates was positive (0.28) in the review of 1116 examples of nonrandom mating in Jiang et al. (2013). Only 19.2% of the correlations between mates were negative and Jiang et al. (2013) suggested that that most or all of these cases of negative-assortative mating could be the result of a type I error because sampling error resulted in cases of negative-assortative mating when there was actually random or weak positive-assortative mating. As the basis for a more comprehensive understanding of negative-assortative mating in vertebrates, we discuss documented examples in vertebrates below.
Often cited examples of negative-assortative mating include mate selection based on MHC types but the overall support for MHC-based, negative-assortative mate choice in vertebrates is mixed and not strong (Kamiya et al. 2014). Using genomic data, 2 studies have examined the correlation of mates for MHC in humans compared to the correlation of genes in the rest of the genome. The first such study found a small but significant negative correlation at the MHC region of only −0.043 compared to the average in the rest of genome of no difference from zero (Chaix et al. 2008). However, a number of other genomic regions had more negative correlation than the MHC region and this level of association might not be significant biologically. In a following study, Derti et al. (2010) disagreed with the findings of Chaix et al. (2008) and they documented nonsignificant results in another sample. In comparison, the very high level of negative-assortative mating for crown color in white-throated sparrows is much, much higher than that found in these genomic studies for MHC markers in humans.
Jiang et al. (2013) documented 3 examples of significant negative-assortative mating in vertebrates (excluding crown color in white-throated sparrows), 2 in birds and one in fish, for categorical (noncontinuous) traits. First, Bengtson and Owen (1973) observed negative-assortative mating for light and dark color in the Arctic skua, Stercorarious parasiticus, where 20 of 28 (71.4%) of the matings were between dark and light birds and only 13.4 were expected (the correlation between mates was −0.49). In contrast, many subsequent much larger Arctic skua samples found either positive-assortative mating or random mating for color (Roulin 2004).
Second, Johnston and Johnson (1989) recorded plumage color and pattern phenotypes in matings of feral pigeons, Columba livia.These phenotypes were different from wild-type pigeons and originated from mutation and subsequent artificial selection in domesticated pigeons. Over 3 years, 90.5% of 116 observed matings were between different plumage types whereas only 71.4% were expected (the correlations between mates for the 3 years were all negative at −0.531, −0.414, and −0.347).
Third, matings in a scale-eating cichlid, Perissodis microlepis, which have different mouth orientations (left vs. right) were documented by Takahashi and Hori (2008). They observed overall that 21 out of the 25 matings (84.0%) were between fish with different mouth orientations whereas only 12.3 were expected (the correlations for 2 different years were −0.828 and −0.720). Subsequently, both Lee et al. (2015) and Kusche et al. (2012) provided data that they claimed were consistent with random mating between mouth orientations. Hori (1993) suggested that this morphological polymorphism was based on single-locus variation but Lee et al. (2015) provided observations they claimed showed polygenic inheritance and environmental influence.
Finally, the recently documented example of negative-assortative mating for color in wolves (Hedrick et al. 2016) is the only documented case in mammals. In this example, the negative-assortative mating between gray and black wolves was observed over 19 years (average correlation was −0.266) and the frequencies of these variants appears stable. This appears to be the only documented example of negative-assortative mating in vertebrates for a single gene, naturally occurring color polymorphism. The introduction of wolves into Yellowstone National Park and the subsequent close monitoring of this population provided an unusual situation for the detailed documentation of wolf behavior and consequently negative-assortative mating.
The negative assortative mating in white-throated sparrows appears considerably stronger than any of these other examples. In addition, the example in the skua has not been documented elsewhere and the example in feral pigeons was for variants introduced from mutation and artificial selection. The example in the scale-eating cichlid is also potentially different because their different mouth orientations are strongly associated with predatory differences and do not appear to be present in all samples.
Theoretical Treatments of Negative Assortative Mating
There is a long and rich history of theoretical models of negative-assortative mating with one of the first treatments in the classic paper by Wright (1921). A number of papers subsequently examined the importance of various theoretical negative-assortative mating models in maintaining genetic variation and generally found that it was a potent force (e.g., Watterson 1959; Naylor 1962; Workman 1964; Karlin and Feldman 1968; Falk and Li 1969; Li 1976). In general, negative-assortative mating was found to maintain genetic polymorphism using different model assumptions and mathematical approaches. In other words, theoretical modeling of nonrandom mating has been carried out for decades but not for specific well-documented examples of negative-assortative mating.
This changed when, as a result of 2 reports of negative-assortative mating for MHC in mice, Hedrick (1992) developed a specific model of female choice of mates different from themselves at the MHC. He found that this negative-assortative mating increased the proportions of heterozygotes, maintained genetic variation, influenced mating frequencies, and generated linkage disequilibrium, all observations of genetic variation at MHC loci. Recently, based on the finding of more matings between black and gray wolves than expected in Yellowstone National Park, Hedrick et al. (2016) developed another model of negative-assortative mating to understand the genetic variation for this polymorphism. This model also maintained genetic variation and gave a predicted level of polymorphism very close to that observed, suggesting that negative-assortative matting could be entirely responsible for this well-known color polymorphism.
Overall, there has been important and detailed theoretical examination of the impact of negative-assortative mating on genetic variation as well as some models that examine specific documented examples of negative-assortative mating. For many years, there were not detailed data on specific examples but this appears to be changing with the application of theoretical modelling for both the crown color in white-throated sparrows here and color polymorphism in Yellowstone wolves (Hedrick et al. 2014).
General Considerations of Negative-Assortative Mating
Negative-assortative mating is considered a potential form of balancing selection, that is, selection that maintains polymorphism in a population. Because of this evolutionary significance, it was surprising that Jiang et al. (2013) in their survey found that only 19.2% of the correlations between mates were negative. They then further suggested that it was plausible that most or all published cases of negative-assortative mating were the result of sampling error when there was actually random or weak positive-assortative mating. If negative-assortative mating is so rare, then its impact on maintaining genetic variation as a type of balancing selection is probably concentrated in the genetic regions influenced by the relatively few examples of strong negative-assortative mating, such as crown stripe variation in white-throated sparrows.
Assortative or disassortative mating could evolve because there is direct or indirect selection on phenotypic mate similarity (Jiang et al. 2013). That is, selection could act directly by favoring either phenotypically similar or dissimilar mates, or selection could act indirectly by influencing the fitness of offspring of the mating pair based on the phenotypic similarity of the parents. On the other hand, assortative mating could be “an incidental consequence of temporal, mechanical, and physiological constraints” (Jiang et al. 2013). For example, temporal segregation of mates that are phenotypically similar could result in positive-assortative mating.
The white-throated sparrow example does not appear incidental but it is also not clear that there is evidence of selection on phenotypic similarity of mates in the manner suggested by Jiang et al. (2013). Negative-assortative mating in this case does result in a reduced frequency of the low fitness inversion white homozygotes 2m2m, a factor that might contribute to the observed mating pattern. However, the main factors that appear to result in this negative-assortative mating are behavioral mating differences and interactions between T and W males with T and W females (see discussion above).
Why are there so few examples of negative-assortative mating? Because of the evolutionary implications of negative-assortative mating and the comprehensive nature of the survey of Jiang et al. (2013), it is unlikely that this conclusion is incorrect and the result of sampling or some other statistical anomaly. Perhaps negative-assortative mating is rare partly because the behavioral basis of mate selection favoring different types is complicated. For example, in general mating individuals would have to be able to determine their own phenotype and then determine that the phenotype of potential mates is the same or different from their own phenotype. For positive-assortative mating, either parents or siblings would likely share the same phenotype as the individual so that the comparison would be only between a parental or sib model and others.
Funding
P.W.H. acknowledges the Ullman Professorship for partial support. Funding sources included the School of Graduate and Professional Studies at Indiana State University, the National Science Foundation (grant DUE-0934648) and the National Institutes of Health (grant 1R01GM084229 to E.M.T. and R.A.G.), and ISU Unbounded Possibilities (to E.M.T. and R.A.G.).
Acknowledgments
We appreciate the comments on an earlier draft of the manuscript by M. Grunst, A. Grunst, and L. Forrette and comments by anonymous reviewers. We acknowledge the white-throated sparrow field crews, Cranberry Lake Biological Station, The Center for Genomic Advocacy at Indiana State University, the Tuttle and Gonser labs, C.A.T. Gonser, and Zonotrichia Zeke.
References
- Arnold C. 2016. The sparrow with four sexes. Nature. 539:482–484. [DOI] [PubMed] [Google Scholar]
- Bengtson S-A, Owen DF. 1973. Polymorphism in the Arctic Skua Stercorarius parasiticus in Iceland. Ibis. 115:87–92. [Google Scholar]
- Chaix R, Cao C, Donnelly P. 2008. Is mate choice in humans MHC-dependent?PLoS Genet. 4:e1000184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derti A, Cenik C, Kraft P, Roth FP. 2010. Absence of evidence for MHC-dependent mate selection within HapMap populations. PLoS Genet. 6:e1000925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falk CT, Li CC. 1969. Negative assortative mating: exact solution to simple model. Genetics. 62:215–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Formica VA, Tuttle EM. 2009. Examining the social landscapes of alternative reproductive strategies. J Evol Biol. 22:2395–2408. [DOI] [PubMed] [Google Scholar]
- Hedrick PW. 1992. Female choice and variation in the major histocompatibility complex. Genetics. 132:575–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedrick PW. 2012. What is the evidence for heterozygote advantage selection?Trends Ecol Evol. 27:698–704. [DOI] [PubMed] [Google Scholar]
- Hedrick PW, Smith DW, Stahler DR. 2016. Negative-assortative mating for color in wolves. Evolution. 70:757–766. [DOI] [PubMed] [Google Scholar]
- Hori M. 1993. Frequency-dependent natural selection in the handedness of scale-eating cichlid fish. Science. 260:216–219. [DOI] [PubMed] [Google Scholar]
- Houtman AM, Falls JB. 1994. Negative assortative mating in the white-throated sparrow, Zonotricia albicollis: the role of mate choice and intra-sexual competition. Anim Behav. 48:377–383. [Google Scholar]
- Huynh LY, Maney DL, Thomas JW. 2011. Chromosome-wide linkage disequilibrium caused by an inversion polymorphism in the white-throated sparrow (Zonotrichia albicollis). Heredity (Edinb). 106:537–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y, Bolnick DI, Kirkpatrick M. 2013. Assortative mating in animals. Am Nat. 181:E125–E138. [DOI] [PubMed] [Google Scholar]
- Johnston RF, Johnson SG. 1989. Nonrandom mating in feral pigeons. Condor. 91:23–29. [Google Scholar]
- Kamiya T, O’Dwyer K, Westerdahl H, Senior A, Nakagawa S. 2014. A quantitative review of MHC-based mating preference: the role of diversity and dissimilarity. Mol Ecol. 23:5151–5163. [DOI] [PubMed] [Google Scholar]
- Karlin S, Feldman MW. 1968. Further analysis of negative assortative mating. Genetics. 59:117–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapton RW, Falls JB. 1983. Differences in parental contribution among pair types in the polymorphic white-throated sparrow (Zonotrichia albicollis). Canad J Zool. 61:1288–1292. [Google Scholar]
- Küpper C, Stocks M, Risse JE, Dos Remedios N, Farrell LL, McRae SB, Morgan TC, Karlionova N, Pinchuk P, Verkuil YI et al. 2016. A supergene determines highly divergent male reproductive morphs in the ruff. Nat Genet. 48:79–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kusche H, Lee HJ, Meyer A. 2012. Mouth asymmetry in the textbook example of scale-eating cichlid fish is not a discrete dimorphism after all. Proc Biol Sci. 279:4715–4723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamichhaney S, Fan G, Widemo F, Gunnarsson U, Thalmann DS, Hoeppner MP, Kerje S, Gustafson U, Shi C, Zhang H et al. 2016. Structural genomic changes underlie alternative reproductive strategies in the ruff (Philomachus pugnax). Nat Genet. 48:84–88. [DOI] [PubMed] [Google Scholar]
- Lee HJ, Heim V, Meyer A. 2015. Genetic and environmental effects on the morphological asymmetry in the scale-eating cichlid fish, Perissodus microlepis. Ecol Evol. 5:4277–4286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li CC. 1976. First course in population genetics. Pacific Grove (CA): Boxwood Press. [Google Scholar]
- Lowther JK. 1961. Polymorphism in the white-throated sparrow, Zonontrichia albicollis. Canad. J Zool. 39:281–292. [Google Scholar]
- Naylor AF. 1962. Mating systems which could increase heterozygosity for a pair of alleles. Am Nat. 96:51–60. [Google Scholar]
- Roulin A. 2004. The evolution, maintenance and adaptive function of genetic colour polymorphism in birds. Biol Rev Camb Philos Soc. 79:815–848. [DOI] [PubMed] [Google Scholar]
- Schwander T, Libbrecht R, Keller L. 2014. Supergenes and complex phenotypes. Curr Biol. 24:R288–R294. [DOI] [PubMed] [Google Scholar]
- Takahashi T, Hori M. 2008. Evidence of disassortative mating in a Tanganyikan cichlid fish and its role in the maintenance of intrapopulation dimorphism. Biol Lett. 4:497–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorneycroft HB. 1966. Chromosomal polymorphism in the white-throated sparrow, Zonotrichia albicollis (Gmelin). Science. 154:1571–1572. [DOI] [PubMed] [Google Scholar]
- Thorneycroft HB. 1975. A cytogenetic study of the white-throated sparrow, Zonotrichia Albicollis (Gmelin). Evolution. 29:611–621. [DOI] [PubMed] [Google Scholar]
- Tuttle EM. 1993. Mate choice and stable polymorphism in the white-throated sparrow. Ph.D. Dissertation. Albany (NY): Department of Biological Sciences, State University of New York at Albany. [Google Scholar]
- Tuttle EM. 2003. Alternative reproductive strategies in the white-throated sparrow: behavioral and genetic evidence. Behav Ecol. 14:429–432. [Google Scholar]
- Tuttle EM, Bergland AO, Korody ML, Brewer MS, Newhouse DJ, Minx P, Stager M, Betuel A, Cheviron ZA, Warren WC et al. 2016. Divergence and functional degradation of a sex chromosome-like supergene. Curr Biol. 26:344–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson GA. 1959. Non-random mating, and its effect on the rate of approach to homozygosity. Ann Hum Genet. 23:204–220. [DOI] [PubMed] [Google Scholar]
- Workman PL. 1964. The maintenance of heterozygosity by partial negative assortative mating. Genetics. 50:1369–1382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. 1921. Systems of mating. III. Assortative mating based on somatic resemblance. Genetics. 6:144–161. [DOI] [PMC free article] [PubMed] [Google Scholar]