In silico labeling: Predicting fluorescent labels in unlabeled images

Summary

Microscopy is a central method in life sciences. Many popular methods, such as antibody labeling, are used to add physical fluorescent labels to specific cellular constituents. However, these approaches have significant drawbacks, including inconsistency, limitation in number of simultaneous labels due to spectral overlap, and necessary perturbations of the experiment, such as fixing the cells, to generate the measurement. Here we show a computational machine learning approach, which we call “in silico labeling" (ISL), reliably predicts some fluorescent labels from transmitted light images of unlabeled fixed or live biological samples. ISL predicts a range of labels, such as those for nuclei, cell-type (e.g., neural), and cell state (e.g., cell death). Because prediction happens in silico, the method is consistent, not limited by spectral overlap, and does not disturb the experiment. ISL generates biological measurements that would otherwise be problematic or impossible to acquire.

Graphicla abstract

Introduction

Microscopy offers a uniquely powerful way to observe cells and molecules across space and time. However, visualizing cellular structure is challenging, as biological samples are mostly water and poorly refractile. Optical and electronic techniques amplify contrast and make small signals visible to the human eye, but resolving certain structural features or functional characteristics requires different techniques. In particular, fluorescence labeling with dyes or dye-conjugated antibodies provides unprecedented opportunities to reveal macromolecular structures, metabolites, and other subcellular constituents.

Nevertheless, fluorescence labeling has limitations. Specificity varies, labeling is time consuming, specialized reagents are required, labeling protocols can kill cells, and even live cell protocols can be phototoxic. The reagents used for immunocytochemistry commonly produce non-specific signals due to antibody cross-reactivity, have significant batch-to-batch variability, and have limited time windows for image acquisition in which they maintain signal. Lastly, measuring the label requires an optical system that can reliably distinguish it from other signals in the sample while coping with fluorophore bleaching.

We hypothesized that microscopic images of unlabeled cells contain more information than is readily apparent, information which traditionally requires immunohistochemistry to reveal. To test this, we leveraged major advances in deep learning (DL), a type of machine learning that has resulted in deep neural networks capable of superhuman performance on specialized tasks (Schroff et al., 2015; Silver et al., 2016; Szegedy et al., 2016). Prior work using DL to analyze microscopy images has been limited, often relying on known cell locations (Held et al., 2010; Zhong et al., 2012) or the imposition of special and somewhat artificial sample preparation procedures, such as the requirement for low plating density (Held et al., 2010; Van Valen et al., 2016; Zhong et al., 2012). As such, it is unclear whether DL approaches would provide a significant and broad-based advance in image analysis and are capable of extracting useful, not readily apparent, information from unlabeled images.

Here, we sought to determine if computers can find and predict features in unlabeled images that normally only become visible with invasive labeling. We designed a deep neural network and trained it on paired sets of unlabeled and labeled images. Using additional unlabeled images of fixed or live cells never seen by the network, we show it can accurately predict the location and texture of cell nuclei, the health of a cell, the type of cell in a mixture, and the type of subcellular structure. We also show that the trained network exhibits transfer learning: once trained to predict a set of labels, it could learn new labels with a small number of additional data, resulting in a highly generalizable algorithm, adaptable across experiments.

Results

Training and testing data sets for supervised machine learning

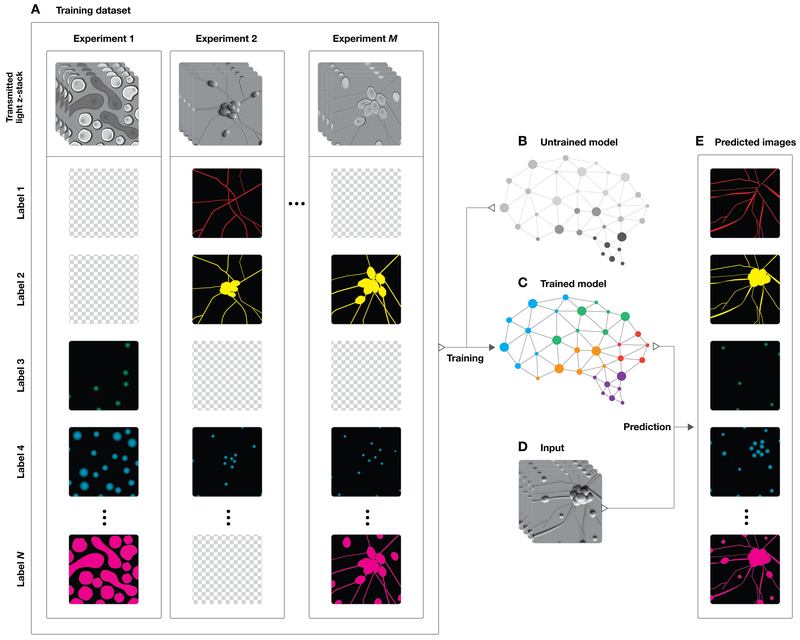
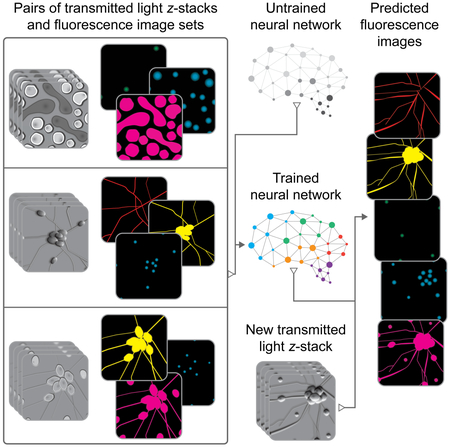
To train a deep neural network to predict fluorescence images from transmitted light images, we first created a dataset of training examples, consisting of pairs of transmitted light z-stack images and fluorescence images that are pixel registered. The training pairs come from numerous experiments across various labs, samples, imaging modalities, and fluorescent labels. This is a means to improve the network via multi-task learning: having it learn across several tasks (Fig. 1A). Multi-task learning can improve networks when the tasks are similar, because common features can be learned and refined across the tasks. We chose deep neural networks (Fig. 1B) as the statistical model to learn from the dataset because they can express many patterns and result in systems with substantially superhuman performance. We trained the network to learn the correspondence rule (Fig. 1C) - a function mapping from the set of z-stacks of transmitted light images to the set of images of all fluorescent labels in the training set. If our hypothesis is correct, the trained network would examine an unseen z-stack of transmitted light images (Fig. 1D) and generate images of corresponding fluorescent signals (Fig. 1E). Performance is measured by the similarity of the predicted fluorescence images and the true images for held-out examples.

Figure 1. Overview of a system to train a deep neural network to make predictions of fluorescent labels from unlabeled images.

(A) Dataset of training examples: pairs of transmitted light images from z-stacks of a scene with pixel-registered sets of fluorescence images of the same scene. The scenes contain varying numbers of cells; they are not crops of individual cells. The z-stacks of transmitted light microscopy images were acquired with different methods for enhancing contrast in unlabeled images. Several different fluorescent labels were used to generate fluorescence images and were varied between training examples; the checkerboard images indicate fluorescent labels which were not acquired for a given example. (B) An unfitted model comprising a deep neural network with untrained parameters was (C) trained by fitting the parameters in the untrained network to the data A. To test whether the system could make accurate predictions from novel images, a z-stack of images of a novel scene (D) were generated with one of the transmitted light microscopy methods used to produce the training data set, A. (E) The trained network, C, is used to predict fluorescence labels learned from A for each pixel in the novel images, D. The accuracy of the predictions is then evaluated by comparing them to the actual images of fluorescence labeling from D (not shown).

The training datasets (Table 1) include different cell types with different labels made by different laboratories. We used human motor neurons from induced pluripotent stem cells (iPSCs), primary murine cortical cultures, and a breast cancer cell line. Hoechst or DAPI was used to label cell nuclei, CellMask was used to label plasma membrane, and propidium iodide was used to label cells with compromised membranes. Some cells were immunolabeled with antibodies against the neuron-specific β-tubulin III (TuJ1) protein, the Islet1 protein for identifying motor neurons, the dendrite-localized microtubule associated protein-2 (MAP2), or pan-axonal neurofilaments.

Table 1.

Training data types and configurations

Condition designation	Cell type	Fixed	Transmitted light	Fluorescent label #1 and imaging modality	Fluorescent label #2 and imaging modality	Fluorescent label #3 and imaging modality	Training data (wells)	Testing data (wells)	Microscope field per well (μm)	Stitched image per well (pixels)‡	Pixel width before / after image processing (nm)	Laboratory
A (red*)	Human motor neurons**	Yes	Bright field	Hoechst (nuclei) widefield	Anti-TuJ1 (neurons) widefield	Anti-Islet1 (motor neurons) widefield	22	3	940 × 1300	1900 × 2600	250 / 500	Rubin
B (yellow*)	Human motor neurons**	Yes	Phase contrast	DAPI (nuclei) confocal	Anti-MAP2 (dendrites) confocal	Anti-neurofilament (axons) confocal	21	4	1400 × 1400	4600 × 4600	150 / 300	Finkbeiner
C (green*)	Primary rat cortical cultures	No	Phase contrast	Hoechst (nuclei) confocal	Propidium iodide (dead cells) confocal	-	72	8	720 × 720	2400 × 2400	150 / 300	Finkbeiner
D (blue*)	Primary rat cortical cultures	Yes	Phase contrast	DAPI (nuclei) confocal	Anti-MAP2 (dendrites) confocal	Anti-neurofilament (axons) confocal	2	1	1400 × 1400	4600 × 4600	150 / 300	Finkbeiner
E (violet*)	Human breast cancer line	Yes	DIC	DAPI (nuclei) confocal	CellMask (membrane) confocal	-	1†	1	1100 × 1100	3500 × 3500	160 / 320	Google

^*Color code: Border color in figures for enhanced readability.

^**Differentiated from induced pluripotent stem cells.

^‡Approximate size after preprocessing.

^†This condition purposely contains only a single well of training data to demonstrate that the model can learn new tasks from very little data through multitask learning.

To improve the accuracy of the network, we collected multiple transmitted light images with varying focal planes. Monolayer cultures are not strictly two dimensional, so any single image plane contains limited information about each cell. Translating the focal plane through the sample captures features that are in sharp focus in some images while out of focus in others (Methods S1 Fig. 1). Normally, out-of-focus features are undesirable, but we hypothesized the implicit three-dimensional information in these blurred features could be an additional source of information. We, thus, collected sets of images (z-stacks) of the same microscope field from several planes at equidistant intervals along the z-axis and centered at the plane that was most in-focus for the majority of the cell bodies.

During collection, the microscope stage was kept fixed in x and y while all images in a set were acquired, to preserve (x, y) registration of pixels between the transmitted light and fluorescence images (Fig. 2, Table 1).

Figure 2. Example images of unlabeled and labeled cells used to train the deep neural network.

Each row is a typical example of labeled and unlabeled images from datasets described in Table 1. The first column is the center image from the z-stack of unlabeled transmitted light images from which the network makes its predictions. Subsequent columns show fluorescence images of labels that the network will use to learn correspondences with the unlabeled images and eventually try to predict from unlabeled images. The numbered outsets show magnified views of subregions of images within a row. The training data are diverse: sourced from two independent laboratories using two different cell types, six fluorescent labels and both bright field and phase contrast methods to acquire transmitted light images of unlabeled cells. The scale bars are 40 μm.

Developing predictive algorithms with machine learning

With these training sets, we used supervised machine learning (ML) (Table S1) to determine if predictive relationships could be found between transmitted light and fluorescence images of the same cells. We used the unprocessed z-stack as input for ML algorithm development. The images were preprocessed to accommodate constraints imposed by the samples, data acquisition, and the network. For example, we normalized pixel values of the fluorescence images (Methods) as a way to make the pixel-prediction problem well defined. In addition, we aimed to predict the maximum projection of the fluorescence images in the z axis. This was to account for the fact that pairs of transmitted and fluorescence images were not perfectly registered along the z axis and exhibited differences in depth of field and optical sectioning.

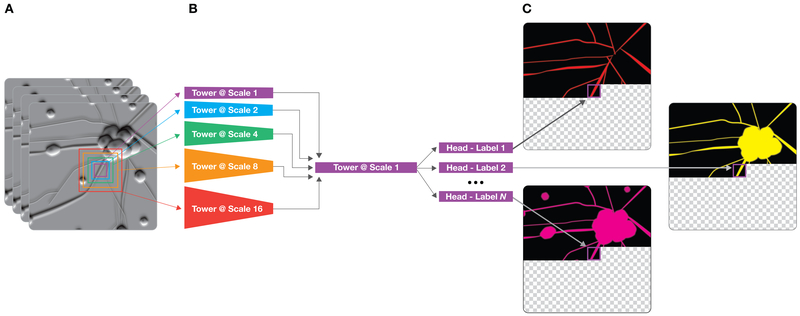
Our deep neural network performs the task of nonlinear pixel-wise classification. It has a multiscale input (Fig. 3). This endows it with five computational paths: a path for processing fine detail that operates on a small length-scale near the center of the network’s input, a path for processing coarse context that operates on a large length-scale in a broad region around the center of the network’s input, and three paths in between. Inspired by U-Net (Ronneberger et al., 2015) and shown in the leftmost path of Methods S1 Figure 3, the computational path with the finest detail stays at the original length-scale of the input so that local information can flow from the input to the output without being blurred. Multiscale architectures are common in animal vision systems and have been reported to be useful in vision networks (Farabet et al., 2013). We took a multiscale approach (Farabet et al., 2013), in which intermediate layers at multiple scales are aligned by resizing, but used transposed convolutions (Zeiler et al., 2010) to learn the resizing function rather than fixing it as in Farabet et al. This lets the network learn the spatial interpolation rule that best fits its task.

Figure 3. Machine learning workflow for network development.

(A) Example z-stack of transmitted light images with five colored squares showing the network’s multiscale input. The squares range in size, increasing approximately from 72×72 pixels to 250×250 pixels, and they are all centered at the same fixation point. Each square is cropped out of the transmitted light image from the z-stack and input to the network component of the same color in b. (B) Simplified network architecture. The network is composed of six serial sub-networks (towers) and one or more pixel-distribution-valued predictors (heads). The first five towers process information at one of five spatial scales and then, if needed, rescale to the native spatial scale. The sixth and last tower processes the information from the five scales. (C) Predicted images at an intermediate stage of image prediction. The network has already predicted pixels to the upper left of its fixation point, but hasn't yet predicted pixels for the lower right part of the image. The input and output fixation points are kept in lockstep and are scanned in raster order to produce the full predicted images.

The network is composed of repeated modules, as in the popular Inception network used in computer vision (Szegedy et al., 2015a), but with the Inception module optimized for performance (Methods, Methods S1 Fig. 2) using Google Hypertune (Golovin et al., 2017). Hypertune is an automatic function optimizer that tries to find a minimum of a function in a bounded space. We expressed module design choices as parameters and the prediction error as the function to be optimized, and used Hypertune to select the design, optimizing over the training dataset, with the test set withheld.

The learned part of the deep neural network is primarily made up of convolutional kernels - small filters that convolve over prior layers to compute the next layers. These kernels are restricted to the interiors of the input layers (i.e., the convolutions are valid or not zero-padded (Table S1) (Dumoulin and Visin, 2016)), making the network approximately translation invariant. As such, each predicted pixel of the network’s final output is computed by approximately the same function, but using different input data, improving the scalability and accuracy while minimizing boundary effects.

We implemented the network in TensorFlow (Abadi et al., 2015), a popular open-source library for deep learning. It was trained using the Adam optimizer (Kingma and Ba, 2014), a commonly used gradient-based function optimizer included in TensorFlow.

The final network (Methods) produces a discrete probability distribution over 256 intensity values (corresponding to 8-bit pixels) for each pixel of the output image. It reads z-stacks of transmitted light images collected with bright field, phase contrast, or differential interference contrast methods and outputs simultaneous predictions for every label kind that appeared in the training datasets. It achieves a lower loss on our data than other popular models while using fewer parameters (Methods, Fig. S4B).

Network predictions of cell nuclei

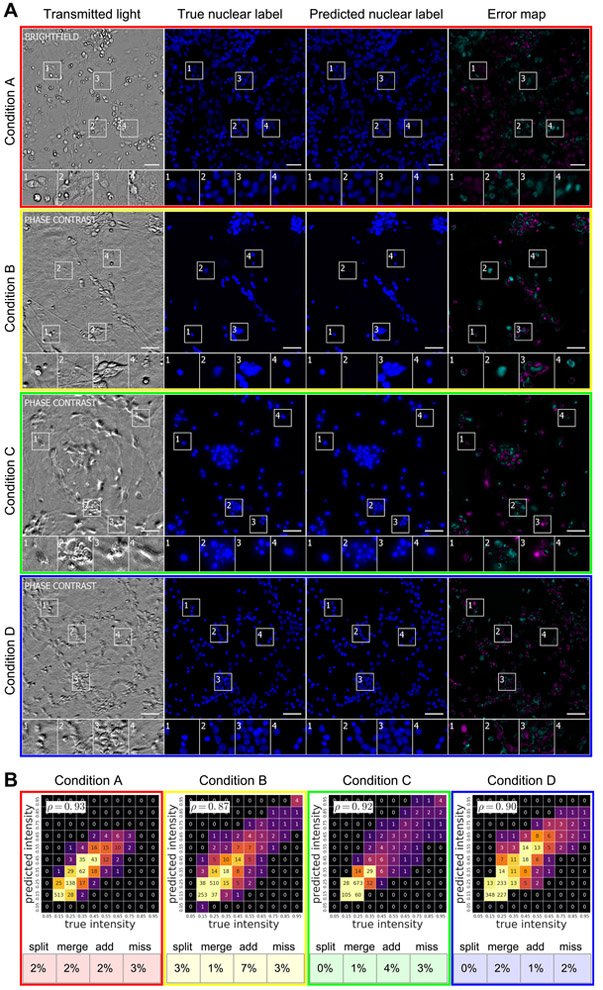
We asked whether we could train a network to predict the labeling of cell nuclei with Hoechst or DAPI in transmitted light images of fixed and live cells. With our trained network, we made predictions of nuclear labels (Fig. 4, Fig. S6) on the test images (Table 1) (i.e., images withheld during network development and training). Qualitatively, the true and predicted nuclear labels looked nearly identical, and the network’s few mistakes appeared to be special cases (e.g., cell-like debris lacking DNA). We created heat maps of true versus predicted pixel intensities and quantified the correlation. Pearson correlation (ρ) values of 0.87 or higher indicated that the network accurately predicted the extent and level of labeling and that the predicted pixel intensities reflect the true intensities on a per-pixel basis. The network learned features that could be generalized, given that these predictions were made using different cell types and image acquisition methods.

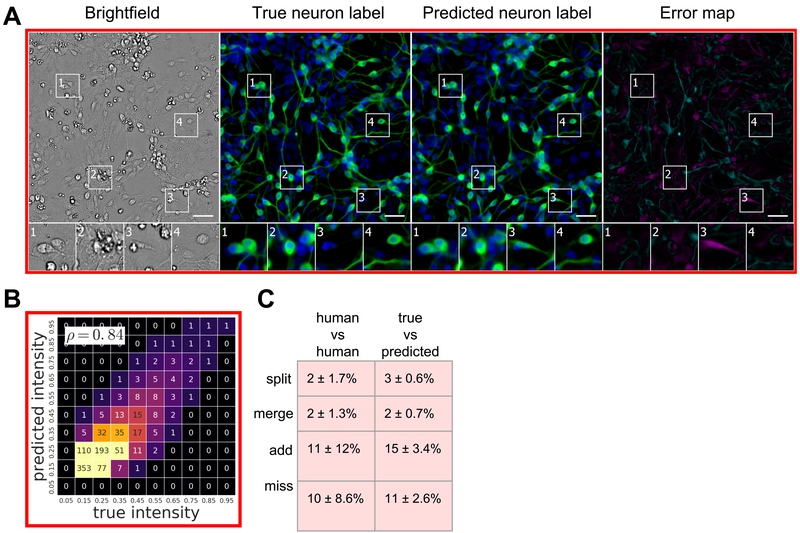
Figure 4. Predictions of nuclear labels (DAPI or Hoechst) from unlabeled images.

(A) Upper-left-corner crops of test images from datasets in Table 1; please note that images in all figures are small crops from much larger images and that the crops were not cherry-picked. The first column is the center transmitted image of the z-stack of images of unlabeled cells used by the network to make its prediction. The second and third columns are the true and predicted fluorescent labels, respectively. Predicted pixels that are too bright (false positives) are magenta and those too dim (false negatives) are shown in teal. Condition A Outset 4 and Condition B Outset 2 shows false negatives. Condition C Outset 3 and Condition D Outset 1 show false positives. Condition B Outsets 3 and 4 and Condition C Outset 2 show a common source of error, where the extent of the nuclear label is predicted imprecisely. Other outsets show correct predictions, though exact intensity is rarely predicted perfectly. Scale bars are 40 μm. (B) The heat maps compare the true fluorescence pixel intensity to the network’s predictions, with inset Pearson ρ values. The bin width is 0.1 on a scale of zero to one (Methods). The numbers in the bins are frequency counts per 1000. Under heat map plot is a further categorization of the errors and the percentage of time they occurred. Split is when the network mistakes one cell as two or more cells. Merged is when the network mistakes two or more cells as one. Added is when the network predicts a cell when there is none (i.e., a false positive), and missed is when the network fails to predict a cell when there is one (i.e., a false negative).

To assess the utility of the per-pixel predictions, we gave a team of biologists real and predicted nuclear label images and asked them to annotate the images with the locations of the cell centers. With annotations on real images as ground truth, we used the methodology of (Coelho et al., 2009) to classify the network's errors into four categories (Fig. 4B, Fig. S5A). Under conditions where the amount of cellular debris was high (e.g., Condition B) or distortions in image quality evident (e.g., Condition C), the network’s precision and recall drops to the mid-90 percent. In other cases, the network was nearly perfect, even with dense cell clumps (e.g., Condition D).

Network predictions of cell viability

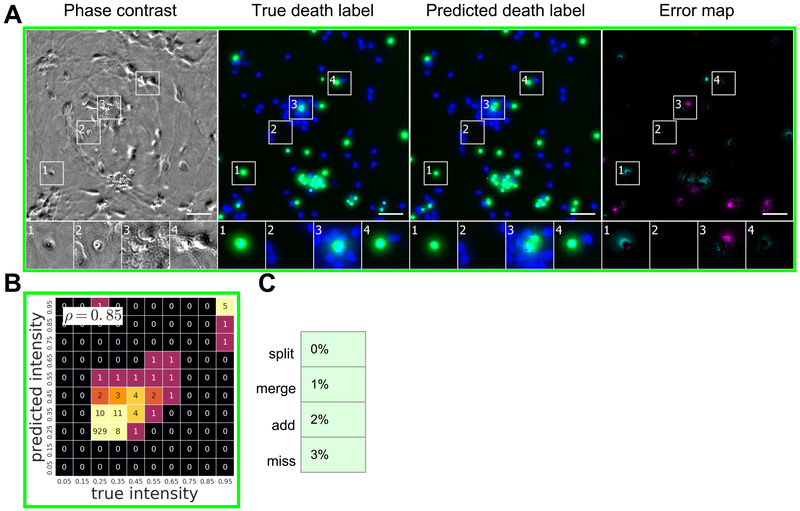
To determine if transmitted light images contain sufficient information to predict whether a cell is alive or dead, we trained the network with images of live cells treated with propidium iodide (PI), a dye that preferentially labels dead cells. We then made predictions on withheld images of live cells (Fig. 5A, Fig. S6). The network was remarkably accurate, though not as much as it was for nuclear prediction. For example, it correctly guessed that an entity (Fig. 5A, second magnified outset) is actually DNA-free cell debris and not a proper cell and picked out a single dead cell in a mass of live cells (third outset). To get a quantitative grasp of the network’s behavior, we created heat maps and calculated linear fits (Fig. 5B). The Pearson ρ value of 0.85 for propidium iodide indicated a strong linear relationship between the true and predicted labels.

Figure 5. Predictions of cell viability from unlabeled live images.

The trained network was tested for its ability to predict cell death, indicated by labeling with propidium iodide staining shown in green. (A) Upper-left-corner crops of cell death predictions on the datasets from Condition C (Table 1). Similarly to Figure 4, the first column is the center phase contrast image of the z-stack of images of unlabeled cells used by the network to make its prediction. The second and third columns are the true and predicted fluorescent labels, respectively, shown in green. Predicted pixels that are too bright (false positives) are magenta and those too dim (false negatives) are shown in teal. The true (Hoechst) and predicted nuclear labels have been added in blue to the true and predicted images for visual context. Outset 1 in A shows a misprediction of the extent of a dead cell, and Outset 3 in A shows a true positive adjacent to DNA-free debris which was predicted to be propidium iodide positive. The other outsets show correct predictions, though exact intensity is rarely predicted perfectly. The scale bars are 40 μm. (B) The heat map compares the true fluorescence pixel intensity to the network’s predictions, with an inset Pearson ρ value, on the full Condition C test set. The bin width is 0.1 on a scale of zero to one (Methods). The numbers in the bins are frequency counts per 1000. (C) A further categorization of the errors and the percentage of time they occurred. Split is when the network mistakes one cell as two or more cells. Merged is when the network mistakes two or more cells as one. Added is when the network predicts a cell when there is none (i.e. a false positive), and missed is when the network fails to predict a cell when there is one (i.e. a false negative).

To understand the network’s ability to recognize cell death and how it compared to a trained biologist, we had the real and predicted PI-labeled images annotated, following the same method as for the nuclear labels (Fig. 5C). A subset of the discrepancies between the two annotations in which a biologist inspecting the phase contrast images determined that an “added” error is a correct prediction of DNA-free cell debris was reclassified into a new category (Methods, Fig. S5B). The network has an empirical precision and recall of 98% at 97%, with a 1% chance that two dead cells will be predicted to be one dead cell.

To further evaluate the utility and biological significance of the quantitative pixel-wise predictions of the network, we wondered whether network predictions of DAPI/Hoechst labeling could be used to perform morphological analysis of nuclei and accurately detect and distinguish live cells from dead ones. We showed previously that neurons in vitro tend to die by apoptosis, a programmed cell death process that causes nuclei to shrink and round up (Arrasate et al., 2004). To perform the analysis, we used the transmitted light images above to make predictions of nuclear labels and then used those collections of pixel predictions to define nuclear objects and measured their dimensions. We then compared the dimensions of nuclei amongst cells determined to be dead or alive based on PI labeling. We found that the mean size of nuclei of live cells quantified from morphological analysis of pixel-wise predictions was very similar to that measured from actual labels (6.8±1.3 μm vs. 7.0±1.4 μm) (Fig. S7). Likewise, the nuclear sizes of dead cells from predicted labels was very similar to actual measurements (4.7±1.1 μm vs. 4.9±1.0 μm). Importantly, quantitative analysis of nuclear morphology based on pixel predictions sensitively and accurately identified and distinguished a subset of dead cells from neighboring live cells based on a change in the size of their nucleus. The result corroborates the predictions based on PI staining and demonstrates the utility of the network to make biologically meaningful quantitative morphological measurements based on pixel predictions.

Network predictions of cell type and subcellular process type

We tested the network’s ability to predict which cells were neurons in mixed cultures of cells containing neurons, astrocytes, and immature dividing cells (Fig. 6, Fig. S6). Four biologists independently annotated real and predicted TuJ1 labeling, an indication that the cell is a neuron. We compared the annotations of each biologist (Fig. 6) and assessed variability among biologists by conducting pairwise comparisons of their annotations on the real labels only.

Figure 6. Predictions of cell type from unlabeled images.

The network was tested for its ability to predict from unlabeled images which cells are neurons. The neurons come from cultures of induced pluripotent stem cells differentiated toward the motor neuron lineage but which contain mixtures of neurons, astrocytes, and immature dividing cells. (A) Upper-left-corner crops of neuron label (TuJ1) predictions, shown in green, on the Condition A data (Table 1). The unlabeled image that is the basis for the prediction and the images of the true and predicted fluorescent labels are organized similarly to Figure 4. Predicted pixels that are too bright (false positives) are magenta and those too dim (false negatives) are shown in teal. The true and predicted nuclear (Hoechst) labels have been added in blue to the true and predicted images for visual context. Outset 3 in A shows a false positive: a cell with a neuronal morphology that was not TuJ1 positive. The other outsets show correct predictions, though exact intensity is rarely predicted perfectly. The scale bars are 40 μm. (B) The heat map compares the true fluorescence pixel intensity to the network’s predictions, with inset Pearson ρ values, on the full Condition A test set. The bin width is 0.1 on a scale of zero to one (Methods). The numbers in the bins are frequency counts per 1000. (C) A further categorization of the errors and the percentage of time they occurred. The error categories of split, merged, added and missed are the same as in Figure 4. There is an additional "human vs human" column, showing the expected disagreement between expert humans predicting which cells were neurons from the true fluorescence image, treating a random expert"s annotations as ground truth.

With TuJ1 labels for the Condition A culture, the performance of biologists annotating whether an object is a neuron was highly variable, consistent with the prevailing view that determining cell type based on human judgment is difficult. We found humans disagree on whether an object is a neuron ~10% of the time, and ~2% of the time they disagree on whether an object is one cell or several cells. When a biologist was presented with true and predicted labels of the same sample, 11–15% of the time the type of cell is scored differently from one occasion to the next, and 2–3% of the time the number of cells is scored differently. Thus, the frequency of inconsistency introduced by using the predicted labels instead of the true labels is comparable to the frequency of inconsistency between biologists evaluating the same true labels.

Given the success of the network in predicting whether a cell is a neuron, we wondered whether it also could accurately predict whether a neurite extending from a cell was an axon or a dendrite. The task suffers from a global coherence problem (Methods), and it was also unclear to us a priori whether transmitted light images contained enough information to distinguish dendrites from axons. Surprisingly, the final network could predict independent dendrite and axon labels (Figs. S1, S6). It does well in predicting dendrites in conditions of low (Condition B) and high (Condition D) plating density, whereas the axon predictions are much better under conditions of low plating densities (Condition B).

Adapting the generic learned network to new datasets: Transfer learning

Does the network require large training data sets to learn to predict new things? Or does the generic model represented by a trained network enable it to learn new relationships in different data sets more quickly or with less training data than an untrained network? To address these questions, we used transfer learning to learn a label from a single well, demonstrating that the network can share learned features across tasks. To further emulate the experience of a new practitioner adapting this technique to their research, we chose data using a new label from a different cell type, imaged with a different transmitted light technology, produced by a laboratory other than those that provided the previous training data. In Condition E, differential interference contrast imaging was used to collect transmitted light data from unlabeled cancer cells, and CellMask, a membrane label, was used to collect foreground data (Table 1). With only the 1100 μm×1100 μm center of the one training well, regularized by simultaneously training on Conditions A, B, C, and D, the network learned to predict cell foreground with a Pearson ρ score of 0.95 (Figs. S2, S6). Though that metric was computed on a single test well, the test images of the well contain 12 million pixels each and hundreds of cells. This suggests that the generic model represented by the trained network could continue to improve its performance with additional training examples, and increase the ability and speed with which it learns to perform new tasks.

Discussion

Here we report a new approach: in silico labeling (ISL). This deep learning (DL) system can predict fluorescent labels from transmitted light images. The deep neural network we developed could be trained on unlabeled images to make accurate per pixel predictions of the location and intensity of nuclear labeling with DAPI or Hoechst dye and to indicate if cells were dead or alive by predicting propidium iodide labeling. We further show that the network could be trained to accurately distinguish neurons from other cells in mixed cultures and to predict whether a neurite is an axon or dendrite. These predictions showed a high correlation between the location and intensity of the actual and predicted pixels. They were accurate for live cells, enabling longitudinal fluorescence-like imaging with no additional sample preparation and minimal impact to cells. Thus, we conclude that unlabeled images contain substantial information that can be used to train deep neural networks to predict labels in both live and fixed cells that normally require invasive approaches to reveal, or which cannot be revealed using current methods.

DL has been applied to achieve useful advances in basic segmentation of microscopy images, an initial step in image analysis to distinguish foreground from background (Chen and Chefd’hotel, 2014; Dong et al., 2015; Mao et al., 2015; Ronneberger et al., 2015; Van Valen et al., 2016; Xu et al., 2016), and on segmented images of morphologically simple cells to classify cell shape (Zhong et al., 2012) and predict mitotic state (Held et al., 2010) and cell lineage (Buggenthin et al., 2017). (Long et al., 2010) applied DL methods to unlabeled and unsegmented images of low-density cultures with mixtures of three cell types and trained a network to classify cell types. (Sadanandan et al., 2017) used DL to segment cells from brightfield z-stacks, and also showed that cell nuclei can be segmented from non-nuclei fluorescent markers. Unfortunately, the task of predicting fluorescence images from transmitted light images is not well served by typical classification models such as Inception (Szegedy et al., 2015a) because they typically contain spatial reductions that destroy fine detail. In response, researchers developed specialized models for predicting images from images, including DeepLab (Chen et al., 2015) and U-Net (Ronneberger et al., 2015). However, we had limited success with these networks (Methods, Fig. S4B) and, thus, created a new one.

Our deep neural network comprises repeated modules, such as the reported Inception network, but the modules differ in important ways (Methods). Inspired by U-Net (Ronneberger et al., 2015), it is constructed so that fine-grain information can flow from the input to the output without being degraded by locality destroying transformations. It is multiscale to provide context, and it preserves approximate translation invariance by avoiding zero-padding in the convolutions (Methods), which minimizes boundary effects in the predicted images. Finally, it is specified as the repeated application of a single parameterized module, which simplifies the design space and makes it tractable to automatically search over network architectures.

We also gained insights into the strengths, limitations, and potential applications of DL for biologists. The accurate predictions at a per-pixel level indicate that direct correspondences exist between unlabeled images and at least some fluorescent labels. The high correlation coefficients for several labels indicate that the unlabeled images contain the information for a deep neural network to accurately predict the location and intensity of the fluorescent label. Importantly, we were able to show in at least one case (Fig. S7), that the predicted label could be used to accurately quantify the dimensions of the cellular structure it represented and thereby correctly classify the biological state of the cell, which we validated with independent direct measurements. This shows that labels predicted from a DL network may be useful for accurately inferring measurements of the underlying biological structures, concentrations, etc… that they are trained to represent. Lastly, the fact that successful predictions were made under differing conditions suggests that the approach is robust and may have wide applications.

ISL may offer, at negligible additional cost, a computational approach to reliably predict more labels than would be feasible to collect otherwise from an unlabeled image of a single sample. Also, because ISL works on unlabeled images of live cells, repeated predictions can be made for the same cell over time without invasive labeling or other perturbations. Many-label (multiplexed) methods exist that partially overcome the barrier imposed by spectral overlap, notably via iterative labeling or hyperspectral imaging. However, the iterative methods are lethal to cells, and the hyperspectral methods require a specialized setup and are limited by the distinctiveness of the fluorophores’ spectra.

That successful predictions could be made by a singly trained network on data from three laboratories suggests that the learned features are robust and generalizable. We showed that the trained network could learn a new fluorescent label from a very limited set of unlabeled data collected with a different microscopy method. This suggests that the trained network exhibited transfer learning. In transfer learning, the more a model has learned, the less data it needs to learn a new similar task. It applies previous lessons to new tasks. Thus, this network could improve with additional training data and might make accurate predictions on a broader set of data than we measured.

Nevertheless, we encountered clear limitations of the current network’s predictive ability. With supervised ML, the quality of predictions is limited by the information contained in the input data. For example, the network was less successful in identifying axons in high-density cultures. Although the network identified neurons in mixed cultures well, it was unsuccessful in predicting the motor neuron subtype (Fig. S3). The accuracy will be limited if there is little or no correspondence between pixels in the unlabeled image and those in the fluorescently labeled one, if the quality of labeling is severely affected due to contributions from nonspecific binding or variability, or if the data are insufficient. We found from error analysis that the performance of the network depended on the amount of information in the unlabeled images, as measured by the number of images in the z-stack (Fig. S4A), though we suspect transfer learning and better imaging protocols may reduce the need for a z-stack. One challenge is the empirical quality of DL approaches. Network architecture and training approaches can be optimized to perform at impressive levels, but it can be difficult to determine general principles of how the network made or failed to make predictions that might guide future improvements. This will be an important area for future research.

STAR Methods

Contact for reagent and resource sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Eric Christiansen (ericmc@google.com).

Experimental model and subject details

Cell preparation

Condition A.

The human iPSC line 1016A was differentiated as described in (Rigamonti et al., 2016). Briefly, iPSCs were grown to near confluency in adherent culture in mTesr media (StemCell Technologies) before being dissociated to single cells using Accutase (cat# 07920, StemCell Technologies). Single cells were seeded into a spinning bioreactor (Corning, 55 rpm) at 1×10⁶ cells/mL in mTesr with Rock Inhibitor (10 μM) and kept in 3D suspension culture for the duration of differentiation. The next day (day 1), dual SMAD inhibitors SB431542 (10 μM) and LDN 193189 (1 μM) were added. On day 2, the medium was switched to KSR media (15% knockout serum replacement, DMEM-F12, 1x Glutamax, 1x non-essential amino acids, 1x pen/strep, 1x beta-mercaptoethanol; all from Life Technologies) with SB and LDN. On day 3, the KSR medium was supplemented with SB, LDN, retinoic acid (Sigma, 1 μM), and BDNF (R&D, 10 ng/mL). Beginning on day 5 and ending on day 10, the culture was transitioned to NIM medium (DMEM-F12, 1x B-27, 1x N2, 1x Glutamax, 1x non-essential amino acids, 1x Pen/Strep, 0.2 mM ascorbic acid, 0.16% D-glucose; all from Life Technologies). On day 6, dual SMAD inhibition was removed, and Smoothen Agonist was added (1 μM). On day 10, DAPT was added (2.5 μM).

On day 15, the motor neuron spheres were dissociated using Accutase and DNAse. To dissociate the spheres, they were allowed to settle in a 15-mL tube, the medium was removed, they were washed with PBS and then approximately 2 mL of warmed Accutase (with 100 μL DNAse) was added to the settled pellet. Next, the tube containing the cells and Accutase was swirled by hand in a 37°C water bath for 5 minutes. Then, the cells were gently pipetted up and down using a 5-mL serological pipette. To quench and wash, 5 ml of NIM was added, and the cells were centrifuged at 800 rpm for 5 minutes. The pellet was then re-suspended in NB medium (Neurobasal, 1x B-27, 1x N2, 1x Glutamax, 1x non-essential amino acids, 1x pen/strep, 0.2 mM ascorbic acid, 0.16% D-glucose, 10 ng/mL BDNF, 10 ng/mL GDNF, 10 ng/mL CTNF) and passed through a 40-μm filter. The filter was washed with an additional 3 mL of NB medium, and the cells were counted using a BioRad automated cell counter.

For plating, the Greiner μclear 96-well plate was coated overnight at 37°C with 2.5 μg/mL laminin and 25 μg/mL poly-ornithine in water. The next day, the plate was washed with DPBS twice. The dissociated motor neurons were plated at 65,000 cells per well in 200 μL of NB medium and grown at 37°C with 5% CO ₂ for 48 hours to allow processes to form.

Condition B.

The human iPSC line KW-4, graciously provided by the Yamanaka lab, was differentiated to motor neurons via a modified version of the protocol in (Burkhardt et al., 2013). Briefly, iPSCs were grown to confluency on Matrigel, followed by neural induction via dual SMAD inhibition (1.5 μM Dorsomorphine + 10 μM SB431542) and WNT activation (3 μM CHIR99021) for 3 days (Du et al., 2015). Motor neuron specification began at day 4 by addition of 1.5 μM retinoic acid and sonic hedgehog activation (200 nM smoothened agonist and 1 μM purmorphamine). At day 22, cells were dissociated, split 1:2 and plated in the same medium supplemented with neurotrophic factors (2 ng/mL BDNF & GDNF). At day 27, neurons were dissociated to single cells using 0.05% Trypsin and plated into a 96-well plate at various cell densities (3.7K – 100K/well) for fixation and immunocytochemistry.

Conditions C and D.

Rat primary cultures of cortical neurons were dissected from rat pup cortices at embryonic days 20-21. Brain cortices were dissected in dissociation medium (DM) with kynurenic acid (1 mM final) (DM/KY). DM was made from 81.8 mM Na₂SO₄, 30 mM K₂SO₄, 5.8 mM MgCl₂, 0.25 mM CaCl₂, 1 mM HEPES, 20 mM glucose, 0.001% phenol red and 0.16 mM NaOH. The 10x KY solution, was made from 10 mM KY, 0.0025% phenol red, 5 mM HEPES and 100 mM MgCl₂. The cortices were treated with papain (100 U, Worthington Biochemical) for 10 minutes, followed by treatment with trypsin inhibitor solution (15 mg/mL trypsin inhibitor, Sigma) for 10 minutes. Both solutions were made up in DM/KY, sterile filtered and kept in a 37°C water bath. The cortices were th en gently triturated to dissociate single neurons in Opti-MEM (Thermo Fisher Scientific) and glucose medium (20 mM). Primary rodent cortical neurons were plated into 96-well plates at a density of 25,000 cells/mL. Two hours after plating, the plating medium was replaced with Neurobasal growth medium with 100X GlutaMAX, pen/strep and B27 supplement (NB medium).

Condition E.

The human breast cancer cell line MDA-MB-231 was obtained from ATCC (Catalog # HTB-26) and grown in Dulbecco’s modified Eagle medium (DMEM), supplemented with 10% fetal bovine sera (FBS). 15,000 cells in 150 μL of medium were used to seed each well of a 96-well plate. Cells were grown at 37°C for 2 days prior to labeling.

Method details

Fluorescent labeling

Condition A.

96 well plates were first fixed with a final concentration of 4% PFA by adding an equal volume as already present in each well of 8% PFA to each well. The plate was fixed for 15 minutes at room temperature. Next, the plate was washed with 200 μL/well of DPBS three times for 5 minutes each. To permeabilize the cells, they were incubated in 0.1% Triton in DPBS for 15 minutes. Again, the cells were washed with 200 μL/well of DPBS three times for 5 minutes each. The cells were then blocked with 1% BSA, 5% FBS in DPBS for 1 hour at room temperature. Primary antibodies were then added in blocking solution overnight at 4°C at the following concentrations: rbαIslet 1:1000 (Abcam cat#109517), msαTuj1 1:1000 (Biolegend cat# 801202). The next day, cells were washed with blocking solution three times for 5 minutes each. Secondary antibodies, gtαrb Alexa 488 and gtαms Alexa 546, were used at 1:1000 in blocking buffer and incubated for 45 minutes at room temperature protected from light. Next, Hoechst was added at 1:5000 in DPBS for 15 minutes at room temperature protected from light. The cells were then washed with 200 μL/well of DPBS, three times for 5 minutes each protected from light. The cells were imaged in at least 200 μL/well of clean DPBS to avoid evaporation during long scan times.

Condition B.

Day 27 iPSC-derived motor neurons were fixed in 4% Paraformaldehyde for 15 minutes and washed 3x in DPBS. Neurons were blocked and permeabilized using 0.1% Triton-X, 2% FBS and 4% BSA for 1 hour at room temperature, and then stained with MAP2 (Abcam ab5392, 1:10000) and NFH (Encor RPCA-NF-H, 1:1000) at 4°C overnight. Cells were then washed 3x with DPBS, and labeled with Alexa Fluor secondary antibodies (each 1:1000) for 1 hour at room temperature. Neurons were again washed 3x with DPBS, followed by nuclear labeling with 0.5 μg/mL DAPI.

Condition C.

Four-day in vitro primary rat cortical neurons were treated with a cell viability fluorescent reagent (ReadyProbes® Cell Viability (Blue/Green), Thermo Fisher Scientific). During treatment with the viability reagent, DMSO (1 in 1400) was added to a subset of the neurons to increase their risk of death. NucBlue® Live reagent (dilution of 1 in 72) and NucGreen® Dead (dilution of 1 in 144) were added to the neuronal media. The NucBlue® Live reagent stained the nuclei of all cells, and the NucGreen® Dead reagent stained the nuclei of only dead cells. The cells were then imaged.

Condition D.

Primary rat neurons were fixed in 96-well plates by adding 50 μL of 4% paraformaldehyde (PFA) with 4% sucrose to each well for 10 minutes at room temperature. PFA was removed and cells were washed three times with 200 μL of PBS. Blocking solution (0.1% Triton-x-100, 2% FBS, 4% BSA, in PBS) was added for 1 hour at room temperature. Blocking solution was removed and primary antibodies MAP2 (Abcam ab5392, 1:10000) and Anti-Neurofilament SMI-312 (BioLegend 837901, 1:500) were then added in blocking solution overnight at 4°C. The next day, cells were washed with 100 μL of PBS three times. Cells were then treated with Alexa Fluor secondary antibodies at 1:1000 in blocking solution for 1 hour at room temperature. Neurons were again washed three times with PBS, followed by nuclear labeling with 0.5 μg/mL DAPI.

Condition E.

Adherent MDA-MB-231 cells in wells of a 96-well plate were gently washed three times by aspirating and adding 150 μL of fresh medium to remove loosely attached cells. 150 μL of medium with 3× (0.5 μL) CellMask Deep Red membrane stain (Life Technologies, Catalog #: C10046) were added to each well for a final 1.5× final concentration and incubated for 7 minutes. Samples were washed twice with fresh medium. Then, samples were fixed by aspirating media and adding 100 μL of 4% PFA to each well, prepared previously from 16% PFA in PBS (Life Technologies, Catalog #: 28906). Samples were incubated for 15 minutes more and washed twice with PBS. PBS was aspirated and the wells were allowed to evaporate some moisture for a few of minutes. One drop of Prolong Diamond with DAPI mounting medium (Thermo Fisher, Catalog #: P36962) was added to each of the fixed wells, and the plate was gently agitated to allow the mounting medium to spread evenly. Samples were placed in the refrigerator and allowed to incubate for ≥ 30 minutes before imaging.

Imaging

Acquisition.

The Rubin lab (Condition A) acquired images with 40× high numerical aperture (0.95) objectives using the Operetta high-content imaging microscope (Perkin Elmer) running Harmony software version 3.5.2. The illumination system for fluorescence was a Cermax Xenon fiberoptic light source. The microscope acquires images with 14-bit precision CCD cameras then automatically scales the images to 16-bit. The plate used was a 96-well Greiner μclear plate. A total of 36 wells were acquired with 36 fields representing an enclosed 6×6 square region. For each field, 15 planes with a distance of 0.5 μm between each were acquired. Each field overlapped with adjacent fields by 34%. Four independent channels were acquired: Bright field (50-ms exposure), Hoechst (300-ms exposure, 360–400 excitation; 410–480 emission), TuJ1 (200-ms exposure, 560–580 excitation; 590–640 emission), and Islet1 (80-ms exposure, 460–490 excitation; 500–550 emission). A total of 77,760 images were collected.

The Finkbeiner lab (Conditions B, C, D) used a Nikon Ti-E with automated ASI MS-2500 stage equipped with a spinning disc confocal microscope (Yokogawa CSU-W1), phase contrast optics (Finkbeiner et al., 2015) (Nikon S Plan Fluor 40X 0.6NA) and controlled by a custom plugin for Micro-Manager 1.4.18. An Andor Zyla4.2 camera with 2048×2048 pixels, each 6.5 μm in size, was used to generate images. For each microscope field, 13–26 stacks of images were collected at equidistant intervals along the z-axis and centered in the middle plane of most of cell bodies in the field. Depending on the plate conditions, the planes in the stack were 0.3–1.53 μm apart, and the stack of images encompassed a total span of a 3.6–19.8 μm along the z-axis and centered around the midpoint of the sample. 96-well plates were used (PerkinElmer CCB). Each well was imaged with 9 to 36 tiles (3×3 to 6×6 patterns, respectively) with overlap of approximately 350 pixels. A total of 120,159 images were collected.

Google (Condition E) used a Nikon Ti-E microscope equipped with Physik Instrumente automated stage controlled by Micro-Manager 1.4.21. Images were acquired using a confocal microscope with 1-μm z-steps with a Plan Apo 40× NA 0.95 dry objective. In this condition, 26 z-steps were collected for each tile, but every other one was discarded to form 13-step z-stacks. An Andor Zyla sCMOS camera with 6.5-μm pixel size was used, generating images with 2048×2048 pixels. Two wells were imaged, with 16 tiles each in a 4×4 pattern with approximately 300 pixel overlap. A total of 2,496 images were collected.

Tiling overlap.

All the microscopes we used have a robotic stage for translation in the x and y dimensions, and a field of view substantially smaller than the size of the well, which provided unsatisfying spatial context. Thus, we acquired images in sets of tiles in square tiling patterns, using the microscope's stage to translate in x and/or y between successive shots in the same well. The patterns ranged from 3×3 tiles up to 6×6. In all cases, the tiles overlapped each other to enable robust visual features based stitching into larger images. The typical overlap was about 300 pixels.

The ability to stitch together a montage of tiled images depended on a variety of factors, including sample sparsity, imaging modality, number of z-depths and channels, and the overlap between adjacent tiles. On the data we worked with, we determined that a 300-pixel overlap was sufficient to get robust stitching across most datasets. This was determined empirically by cropping the tiles smaller and applying the stitching algorithm until it could no longer successfully stitch together a test set of images.

High dynamic range.

To increase the range of luminance in the image beyond the bit depth of the camera, we collected images in bursts of four 20-ms exposures in the fluorescence images from the Finkbeiner lab. We then summed the group of four images on a per pixel basis to resolve features closer to the noise floor. Summing allows simple creation of images with 20-, 40-, 60-, and 80-ms exposures. These group-summed images provide a higher dynamic range and can then be used to reconstruct the image plane with all features more clearly visible than could be seen with any one exposure. If a direct sum of all images is used, it is possible to generate an image of the acquired plane that exceeds the bit-depth of the camera. This increases the accessible information per image plane by achieving better dynamic range and adds flexibility to the analysis, allowing rescaling in bit-depth as needed.

Data preparation

Preprocessing pipeline.

The image datasets must be cleaned and canonized before they can be used to train or evaluate a ML system. To that end, they are fed through a preprocessing pipeline composed of the following stages:

1. Salt-and-pepper noise reduction in the fluorescence images by means of a median filter. The median filter is of size 5×5 and is applied successively until convergence, which occurs within 32 iterations.

2. Only needed for training. Dust artifact removal from fluorescence images, in which dust artifacts are estimated and then removed from the fluorescence images.

3. Downscaling, in which images are bilinearly downscaled by a factor of two in each dimension to reduce shot noise.

4. Flat field correction, in which the spatially varying sensitivity of the microscope is estimated and removed.

5. Dust artifact removal from transmitted light images.

6. Stitching, in which tiles with overlapping borders are montaged into a larger image, further reducing noise at the intersections while making it possible to see large parts of the well in one image.

7. Only needed for training. z-axis maximum projection, in which the target (fluorescence) images are projected along the z-axis by taking the 90^th percentile intensity as a robust estimate of the maximum. This step is necessary to make the prediction task well-defined, because some of our confocal images had insufficient voxel z size, and because we lack a mechanism for registering voxels in the z direction across all our datasets. If we had such a system we could attempt 3D (voxel) prediction, and indeed we've had some promising results, not reported here, on a small, z-registered, dataset.

8. Global intensity normalization, in which the per-image pixel intensity distributions are constrained to have a fixed mean and standard deviation. This step, which is aided by the previous stitching step, is necessary to make the ML task well defined, because our pixel intensities are not measured in comparable absolute units. Note this would not be necessary if our samples had been instrumented with standard candles (point sources of known brightness); we would like to see in-sample calibration objects become a standard part of in vitro biology.

9. Only needed for training. Quality control, in which low quality images are removed from the dataset. This makes ML more tractable, as otherwise the learning system would devote resources attempting to learn the unlearnable.

Dust artifact removal from fluorescence images.

A subset of the fluorescence images from the Finkbeiner Lab datasets contained the same additive intensity artifact likely due to excitation light scattering from dust. The artifact was located at the same location in each image, and appeared as a sparse pattern (< 10% of the pixels) of overlaid grey disks around 50 microns wide. The following procedure was used to estimate the shape and intensity of this artifact, and then to subtract it from all of the images, thereby removing the artifact. Given a collection of images all containing the artifact, the mean and minimum projections were taken across the images (i.e., for each (x, y) pixel coordinate, the mean and minimum across all images was evaluated). The sensor offset, an image sensor property, was then subtracted from the mean image, and an edge-preserving smoothing, followed by a thresholding operation, was used to produce a binary mask of the artifact location. The mask is used to replace artifact pixels in the mean image with the mean value of the non-artifact pixels, after which a Gaussian blur is applied to produce an estimate of the average background. Subtracting this average background from the average image yields the final estimate of the artifact, which is then subtracted from each of the images.

Flat field correction.

Flat field miscalibration can manifest as spatially-varying image brightness consistent from image to image. We assume the effect is multiplicative and slowly spatially varying. To estimate the flat field, we take a per-pixel median across a set of images assumed to have the same bright field and then blur the result using a Gaussian kernel. The kernel standard deviation in pixels is 1/16^th the image height for fluorescence images, and 1/32^nd the height for transmitted light images. To flat field correct a new image, we pixelwise divide it by the flat field image and then clip the result to capture most of the intensity variation.

Dust artifact removal from transmitted light images.

We treat dust in transmitted light images as a quickly spatially varying multiplicative artifact. To estimate the dust field, we take a per-pixel median across a set of images assumed to have the same dust pattern. We do not blur the images. To dust correct a new image, we pixelwise divide it by the dust field image and then clip the result to capture most of the intensity variation.

Image stitching.

To stitch a set of images, we first calculate approximate (x, y) offsets between neighboring tiles using normalized cross correlation. At this point, the set of offsets may not be internally consistent; there are many paths between any two images, and the accumulated offsets along two such paths may disagree. To make the offsets internally consistent and thus refine the solution, we use a spring system formulation and find the minimum energy configuration. In other words, for measured offsets $o_{ij}\in {\Re }^2$ we find the tile locations $l_i\in {\Re }^2$ which minimize ${\sum }_{i,j}{\Vert l_i-l_j-o_{ij}\Vert }_2^2$. With the set of refined (x, y) offsets, we then alpha composite the tiles into a shared canvas.

Global intensity normalization.

We globally affine normalize transmitted light pixel intensities to have mean 0.5 and standard deviation 0.125. We globally affine normalize fluorescence pixel intensities to have mean 0.25 and standard deviation 0.125. All pixels are clipped to fall within [0.0, 1.0]. These parameters capture most of the dynamic range. Previous versions of the system had used local normalization, but it wasn't found to make much of a difference in the final images, and it contained one more knob to tune (the size of the local neighborhood).

Quality control.

Of the five datasets considered in this paper, eleven wells were removed from Condition A for quality concerns due to an issue with the motorized stage. This yielded the 25 remaining wells listed in Table 1.

Machine learning

Inputs and outputs.

Our machine learning model is a deep neural network which takes, as input, sets of transmitted light images across 13 z-depths, and outputs fluorescence images. For each fluorescence image, the network outputs a discrete probability distribution (over 256 intensity values, corresponding to 8 bits of information) for each pixel. Note, this is in contrast to the more common foreground / background models which output a Bernoulli distribution for each pixel.

The input to the network is a z-stack of 13 250×250 images, where we treat the z-dimension as the feature dimension and we use a batch size of 16 for training. Thus, the input is a tensor of shape 16×250×250×13 of type float32 where the axes represent batch×row×column×feature. For the four towers with inputs smaller than 250×250, their inputs are center cropped from this tensor.

The outputs of the network (colloquially termed heads) are nine tensors: eight fluorescence tensors and an autoencoding tensor. The eight fluorescence tensors have shape 16×8×8×256 of type float32 where the axes are batch×row×column×pixel_intensity. The eight predicted labels are nuclear (DAPI or Hoechst) imaged in confocal, nuclear (DAPI or Hoechst) imaged in widefield, CellMask imaged in confocal, TuJ1 imaged in widefield, neurofilament imaged in confocal, MAP2 imaged in confocal, Islet1 imaged in widefield, and propidium iodide imaged in confocal. DAPI and Hoechst both label DNA and never co-occur in the same condition, so we treat them as one label. Nuclear widefield looks different from nuclear confocal, and they were treated as separate labels. Training on Islet1 resulted in unreliable predictions; see the Limitations section in Methods. Finally, note that no well in the data had more than three fluorescent labels, so at most three such heads would be updated for any given training example.

Autoencoding refers to training a model to predict the input from the input (i.e., learning the identity function). Our network has an autoencoding output in addition to the fluorescence outputs because it helps debug certain training pathologies. The autoencoding output tensor has shape 16×8×8×13×256 of type float32 where the axes are batchx×row×column×z×pixel_intensity. The model loss from this output is minimized when all the probability weight is assigned to the intensity values of the center crop of the input tensor.

The repeated module.

Inspired by Inception (Szegedy et al., 2015a), the full network comprises a number of repeated sub-networks (colloquially called modules). Methods S1 Figure 2 gives the architecture of the module. In the path on the right, information flows from the input, through a learned convolution that expands the feature dimension and then through a learned convolution that reduces the feature dimension. On the left, feature values are copied from the input, forming a residual connection (He et al., 2016). The features resulting from the two paths are added together, forming the input to the next module.

The convolutions are not zero-padded (i.e., the convolution kernels are restricted to the interiors of the layers where their supports are fully defined). This kind of convolution is colloquially called valid (e.g., by NumPy) (Walt et al., 2011). (Dumoulin and Visin, 2016) describes how convolutions are used in deep learning and what is meant by kernel size and stride in convolutions.

There are three possible configurations of the module: in-scale, down-scale, and up-scale. In the in-scale configuration, k = 3 and s = 1, meaning the convolution kernel size in the expand layer is 3×3 and the stride is one. This configuration does not change the length-scale of the features: translating the input in the row or column dimension would translate the output by the same amount. In the down-scale configuration, k = 4 and s = 2, meaning the expand convolution kernel is 4×4 and the stride is two. This configuration doubles the length scale of the features: translating the input in the row or column dimension would translate the output by half the amount. In the up-scale configuration, k = 4 and s = 2, the max pool is removed from the network, and the expand convolution is replaced with a convolution transpose (Zeiler et al., 2010), followed by a crop of all the features within two rows or columns of the border. This configuration halves the length scale of the features: translating the input in the row or column dimension would translate the output by double the amount.

Because the three configurations have different effects on the length-scales of the features, the residual connections must vary between the configurations. For the in-scale configuration, we trim off a size 1 border in the row and column dimensions, corresponding to a valid (non zero-padded) convolution with a kernel size of 3 and a stride of 1 (Dumoulin and Visin, 2016). For the down-scale configuration, we do the same trim, then downscale by a factor of 2 using average pooling with a kernel size of 2 and a stride of 2. For the up-scale configuration, we upscale by a factor of 2 using nearest neighbor interpolation.

Macro-level architecture.

The full network is composed of six sub-networks where computation proceeds serially (colloquially towers). There are five towers that take image pixels as input and operate on the pixels at different length-scales. The outputs of these five towers are concatenated in the feature dimension and input to a final tower which outputs predictions (Fig. 3).

Methods S1 Figure 3 is a more detailed view of the network, showing the sub-sub-networks (colloquially modules) that compose each tower. The modules were described in the previous section. The module is a function of its configuration (in-scale, down-scale, or up-scale), the number of features in its expand layer, the number of features in its reduce layer, and the shape of the input. These parameters are indicated by the shapes of and inset numbers in the boxes in Methods S1 Figure 3.

Each network output (colloquially head) is a linear function of the final layer in the network followed by a softmax nonlinearity (Wikipedia, 2017a) to make the predictions probability distributions over pixel intensities. The softmax function $\sigma :{\Re }^K\to {\Re }^K$ is a standard tool for transforming vectors into discrete probability distributions: $\sigma {(z)}_j=e^{z_j}∕{\sum }_{k=1}^K{e}^{z_k}$for j=1,2,...,K.

The in-scale and down-scale configurations of the module are translation invariant (i.e., they compute the same function for every value in the output); the only thing that changes is the input to the function as it translates in (x, y) over the network’s support. The up-scale configuration computes the same function for every 2×2 block in the output, so we say it is approximately translation invariant. The composition of translation invariant functions is translation invariant, so we say each tower, individually, is approximately translation invariant. The five lower towers are constructed so their outputs have the same numbers of rows and columns. These outputs are concatenated in the feature dimension at the midpoint of the network: the layer labeled “FEATURE CONCATENATION” in Methods S1 Figure 3. Because the concatenation (direct product) of translation invariant functions is translation invariant, we say the network is approximately translation invariant up to the midpoint of the network. Because the final tower is translation invariant, the full network is approximately translation invariant.

Approximate translational invariance is useful because it minimizes edge effects in predicted images. An edge effect is something which lets the viewer predict the location of a pixel in a model output from a neighborhood of the pixel, and often appears as a block structure in the resulting image. Because the edge effects are minimized, we can produce network predictions independently and in parallel.

The numbers of features in the modules were set such that each module would take roughly the same number of operations to evaluate, which means that modules get more features as their row and column size decreases. This also implies that every tower in the lower network takes roughly the same amount of time to evaluate, which is desirable for avoiding stragglers in environments that are not CPU limited. In other words, we assume each tower will be evaluated in parallel, and so to maximize the parameter count given a fixed latency, the towers should be designed to take the same time to evaluate.

Though absolute pixel sizes were available for all the data, they were not provided to the network. The network simply maps from pixels to pixels.

Training loss.

For each pixel in each predicted label, the network emits a discrete probability distribution over 256 discretized pixel intensity values. The model losses are calculated as the cross-entropy errors between the predicted distributions and the true discretized pixel intensity. These cross-entropy losses are scaled such that a uniform predictor will have an error of 1.0. Each loss is gated by a pixelwise mask associated with each output channel, where the mask indicates on a per-training-datum basis whether a particular label is provided. By gating the losses in this way, we can build a multihead network on a dataset created by aggregating all our datasets. The network takes any label-free modality as input and predicts all labels ever seen. The total loss is the weighted average of the gated losses.

We weighted the losses so 50% of the loss was attributed to error in predicting the fluorescence labels and 50% was attributed to error in autoencoding, in which we asked the network to predict its own inputs. We found it useful to additionally task the network with autoencoding because it can help in diagnosing training pathologies.

Training.

Training examples were generated by randomly selecting patches of size 250×250, the network input size, from the set of all the training images. The network is multi-task and was trained on all tasks simultaneously; no individual example contained labels for all the fluorescent channels, so gradient updates were only applied to the outputs for the existing channels.

The network was implemented in TensorFlow (Abadi et al., 2015) and trained using 64 worker replicas and eight parameter servers. Each worker replica had access to 32 virtual CPUs and about 20 GB of RAM. Note, GPUs would have been more efficient, but we lacked easy access to a large GPU cluster. We used the Adam (Kingma and Ba, 2014) optimizer with a batch size of 16 and a learning rate of 10⁻⁴ for 1 week, then reduced the learning rate to 10⁻⁵ for the second and final week. This would have cost about $7000 if trained from scratch in a public cloud, assuming a rate of $0.01 per CPU hour. Though training for 2 weeks (about 10 million steps) was necessary to get the full performance reported here, the network converges to good predictions within the first day.

Hyperparameter optimization.

Deep learning is somewhat notorious as an empirical endeavor, because of the importance of various design choices (colloquially hyperparameters), such as network architecture and optimization method, and the paucity of theory describing how these choices should be made (i.e., how the hyperparameters should be optimized over). A common way to deal with this uncertainty is to pose it as another learning problem, typically using a second learning system that is better understood than the original.

In designing our network, we used such a system: an early version of Google Hypertune (Golovin et al., 2017). Hypertune has two components: a learning component models the effect on network performance of various hyperparameters, and an optimization component suggests new hyperparameter settings to evaluate in an attempt to find the best setting. The two components take turns to advance the state of the design search: first, the learner builds a predictive model of how good new hyperparameter settings are likely to be given all the designs evaluated thus far; second, the optimizer evaluates designs that seem promising under the predictive model; third, the learner updates its model given the newly evaluated designs, etc.

For the learning component, Hypertune uses Gaussian process regression, a kind of regression that admits complex nonlinear models and that provides confidence bounds with its predictions. For the optimization component, Hypertune uses an algorithm that seeks to balance between refining existing good designs and searching for novel designs. Spearmint (Snoek et al., 2012) is a similar, open-source, system.

The network is comprised of repeated applications of the same module (Methods S1 Fig. 2), and we used Hypertune to optimize the design that module. To evaluate a design, we trained and evaluated four instances of the design via four fold cross validation. For efficiency, these instances were only trained for 12 hours, using 64 32-CPU machines as described in the previous section. We believe even 12 hours was enough to separate the terrible designs from the promising ones. In total, several hundred designs were evaluated.

Specifically, we optimized:

1. C_EXPAND, the ratio in the feature count between the EXPAND and REDUCE layers in the module (Methods S1 Fig. 2). We searched ratios between 0.1 and 10.0, and the best network had a ratio near 5.0. This is consistent with (Ramsundar et al., 2015) but appears to contradict the advice of (Szegedy et al., 2015b), in which it is argued the number of features in a layer should change gradually and monotonically.

2. The subset of activation functions (also called nonlinearities) to use. We searched all subsets of {RELU, TANH, MIRROR_RELU}. These are all scalar functions, where RELU is given by f(x) = max(0, x), TANH is given by f(x) = tanh(x), and MIRROR_RELU is given by f(x) = min(0, x). The best network used RELU and TANH but not MIRROR_RELU.

3. The minibatch size. We searched between 4 and 64, and the best network used a minibatch size of 16.

4. The optimizer. We tried Adam (Kingma and Ba, 2014) with the default TensorFlow parameters, Adagrad (Duchi et al., 2011) with the default TensorFlow parameters, and learning with momentum (where we also searched over the momentum values in [0.0, 1.0)), and the best network used Adam.

5. The learning rate. We tried learning rates between 10⁻³ to 10⁻⁶. However, because of the difference in training times between hyperparameter optimization (12 hours) and final training (2 weeks), this search was only useful to ensure the other hyperparameters were being fairly evaluated.

In this optimization, we attempted to keep the total number of network parameters constant, because we were interested in the best allocation of a fixed parameter budget, not whether more parameters would produce better performance.

Prediction.

The network is applied in a sliding-window fashion. So to predict (infer) a full image, the input images are broken into patches of size 250×250 with a stride of 8, the patches are fed to the network producing outputs of size 8×8, and the outputs are stitched together into the final image. Inferring all labels on a 1024×1024 image takes about 256 seconds using 32 CPUs, or about eight thousand CPU seconds, which currently costs about $0.02 in a public cloud. The process is parallelizable, so the inference latency can be very low, in the range of seconds. We do our own inference in parallel using Flume, a Google-internal system similar to Cloud Dataflow (https://cloud.google.com/dataflow/).

The network predicts a probability distribution for each output pixel, which is useful for analyzing uncertainty. To construct images we take the median of the predicted distribution for each pixel. We've also looked at the mode (too extreme) and mean (too blurry). The predicted images do not a priori have the same average brightness as the true images, so we run them through an additional global normalization step before declaring them final.

Performance dependence on z-stack size

In this work, we used the full set of 13 transmitted light images in each z-stack (Methods S1 Fig. 1). However, it wasn’t clear a priori whether the network needs all 13 z-depths. To test this, for each N_z in 1, 2, …, 13, we trained independent networks with N_z input z-depths. To specify which z-depths to provide the network, we used a fixed ordering of the z-stack images starting at the center plane where most of the cells should be in focus (z = 6 in a 0-indexed count) and expanding outward along the z axis in steps of two z-depths. For instance, with this strategy, to select three of the available 13 z-stacks, we would select z-depths 4, 6, and 8.

To measure the performance on a subset of N_z z-depths, we extracted N_z z-depths according to our fixed z-stack ordering and then trained an independent network on this image subset for four million steps. We then measured cross entropy loss for fluorescence image prediction on a validation set (Fig. S4A).

These experiments suggest that performance improves with the number of input z-depths, but that each additional image provides less benefit than the last. We do not find this surprising; each additional image provides additional information the network can learn to use, but eventually performance will saturate.

Limitations

Regardless of the power of the machine learning system, in silico labeling (ISL) will not work when the transmitted light z-stack lacks the information needed to predict the labels:

1. Neurites are hard to discern in Condition D, so the axon prediction was not very accurate (Fig. S1).

2. Nuclei are nearly invisible in Condition E, so the nuclear prediction was not very localized (Fig. S2).

3. Motor neurons look like regular neurons, so the predicted motor neuron label (Islet1) was not very specific to motor neurons (Fig. S3).

Thus, all applications of ISL should be validated on a characteristic sample before being trusted on a new dataset.

Global coherence

The current network uses an inexpensive approximation to the correct loss function, not the correct loss itself. The final output of ISL is an image, but the loss we use is over pixels, not images. Thus, the network will attempt to predict the most likely pixels, and will make each of those predictions independently. This means that predicted images may lack global coherence; instead of getting clear structures in images, predictions may produce erroneous averages over several structures. Practically speaking, the problem is most noticeable for long thin structures like neurites and explains why they’re not always predicted as continuous shapes (Fig. S1). The problem could be addressed with existing techniques from machine learning, e.g., sampling techniques (van den Oord et al., 2016) or adversarial models (Goodfellow et al., 2014).

Comparison to other deep neural networks

The proposed network outperformed the DeepLab network (Chen et al., 2015) and a modified U-Net network (Ronneberger et al., 2015) on these data. To determine this, we trained those networks and our proposed network on our training data. Our proposed network achieved a lower loss than the modified U-Net, which achieved a lower loss than DeepLab (Fig. S4B). Early comparisons of the same kind were what drove us to develop a new architecture, rather than rely on existing architectures.

For each learning rate in [1e-4, 3e-5, 1e-5, 3e-6], each network was trained for at least 10 million steps using Adam (Kingma and Ba, 2014), which took around 2 weeks each on a cluster of 64 machines. The proposed network and DeepLab were trained with a batch size of 16, and due to high memory usage the modified U-Net was trained with a batch size of 1. For each network, we selected the trained instance with the best error out of the four learning rates. For the proposed network, it was 3e-6. For DeepLab and U-Net it was 1e-5. These three trained instances had been continuously evaluated on the training and validation datasets, producing the training curves shown in the figure.

U-Net and DeepLab typically take 1 or 3 channel images as input (RGB), but our input has 13 channels from the 13 z-depths. To make these networks accept our data, we modified the input layers to have a feature depth of 13. To generate the fluorescence and autoencoding predictions, we similarly replaced the outputs (heads) of U-Net and DeepLab with the heads used by our network.

The DeepLab and U-Net implementations we used were provided by Kevin Murphy’s VALE team at Google, which maintains internal implementations of common networks, and which created DeepLab. No hyperparameter optimization was performed for DeepLab or U-Net, as we considered the DeepLab and U-Net designs to be fixed. However, we did shrink the input size of U-Net from 572×572 to 321×321 while keeping all the operations the same, because the 572×572 version used too much memory in our code. The proposed network had 27 million trainable parameters, DeepLab had 80 million, and the modified U-Net had 88 million.

A note on 3D prediction

The approach we describe can in principle be applied to predicting 3D confocal voxel grids, and an early version of this work did incorporate a 3D prediction task with modest results.

There are at least three problems which must be overcome to make 3D prediction work:

1. Representation of the z-dimension in the network (low difficulty): In this paper, we simply merged the z and feature dimensions, which works when the number of possible z values is small but doesn’t scale for a large number of possible z values. In that case, one would probably want to use 3D convolutions rather than 2D convolutions in the neural network.

2. Registration in z (higher difficulty): Independent pixel losses, such as the one we use, fail when input and target tensors are misaligned in an unpredictable manner. While we show it is possible to ensure registration in x and y across transmitted light and fluorescence images, we have not attempted to register in z.

3. Information (unknown difficulty): We suspect depth from blur in transmitted light will not be enough to recover 3D shape in multilayer cell cultures. It will take creative thinking to extract the information needed to reconstruct the 3D structure.

Image processing in figures

Images in this paper were transformed to make them easier to view. Transmitted light images were normalized to have a pixel intensity mean of 0.5 with standard deviation 0.125, where possible brightness values are in the range [0.0, 1.0]. Values falling outside [0.0, 1.0] were clipped. True and predicted fluorescence images were normalized to have a pixel intensity mean of 0.25 with standard deviation 0.125. These images were then affine rescaled and clipped so that 0.2 and below became 0.0 and 0.8 became 1.0 , using the function f(x) = max(0, min(1.0, (x – 0.2) / 0.6)). We sent 0.2 to zero because it is the apparent noise floor for much of our data, and we sent 0.8 to 1.0 to brighten the fluorescence images and make them easier to see in print. Error images were derived from fluorescence images normalized to have mean 0.25 and standard deviation 0.125. There were brightened in the same manner as the fluorescence images but were not clipped at the noise floor; the function was f (x) = min(1.0, x / 0.8). This means that errors predicting intensities below the noise floor can appear in the error images without appearing in the true or predicted fluorescence images. Figure S6 shows a larger dynamic range and color bars for calibration. Links to raw images can be found on GitHub at https://github.com/google/in-silico-labeling.

Quantification and statistical analysis

Statistical calculations

Pearson ρ values were computed via the pearsonr function in Python’s scipy.stats (Jones et al., 2001) from one million randomly selected pixel locations. The unbiased sample standard deviation was computed according to the definition on Wikipedia (Wikipedia, 2017b).

Manual identification of network errors

As a human interpretable metric of similarity between a pair of predicted and true nuclear label images, we compared manual annotations of cell positions on each label. First, a panel of three biologists viewed the true nuclear label and identified regions to be excluded where the cell density was too high to accurately determine the cell centers in the true fluorescence images, meaning we could not score predictions in those areas. This was only done for human assessment of nuclear predictions, only a small fraction of cells were excluded (Fig. S5A), and the network made plausible (though unscorable) predictions in those regions. Next, cell center coordinates were manually annotated in the remaining regions on each of the true and predicted nuclear labels. For each coordinate, a disc shape of fixed diameter approximately the size of a cell was assigned to each annotated cell center coordinate. We took the annotations on the true label to be the ground truth reference. Following (Coelho et al., 2009), one-directional correspondences between objects (disc shapes) in the true and predicted labels were determined by using maximum area of overlap and the errors were classified into four types: split, merged, added, and missing. Cells at the edges of the field of view were excluded from these metrics. We then take the accuracy to be the total number of objects in the true label, less the sum of the four types of errors, divided by the total number of objects in the true label (Fig. S5A).

The dead-cell-specific label (propidium iodide) was analyzed in a similar fashion as the nuclear labels, but as stated above we did not exclude high cell density regions nor annotations at the edges. We noted that the predicted dead-cell-specific label often included false positives that were not in the true label, but after closer inspection of the phase contrast images, many of these false positives were determined to be true cellular debris that perhaps did not have DNA to be marked by the true label. Hence, after the annotations on the true and predicted dead-cell-specific label were completed, a different biologist viewed the input phase contrast images and attempted to determine whether each added error (false positive) was a correct cellular debris prediction (Fig. S5B).

Finally, the TuJ1 label was analyzed in a similar fashion as the nuclear labels, but as stated above we did not exclude high cell density regions nor annotations at the edges. Here, not only did we repeat the within-person predicted and true label comparison across four independent biologists, but we also analyzed the consistency of their annotations on the true label to establish a baseline for human agreement. Their four annotations on the true labels yielded 12 unique pairwise comparisons for evaluating human consistency (for any two annotations, taking each to be the ground truth in turn yielded two comparisons). We report the mean error rates across both these 12 comparisons and the four predicted-versus-true comparisons, as well as the unbiased sample standard deviation (Fig. 6).

Noise and predictions near the noise floor

The proposed network cannot predict sensor noise, and so instead, it predicts a probability distribution that accounts for the typical variation in brightness caused by the noise it observed. Because we generate images by taking the median of that distribution for each pixel, the predicted images are typically less noisy than the ground truth images. For example, the predicted MAP2 image in Condition B of Figure S6 is less noisy than the ground truth. It also doesn’t contain the stitching artifact or disk-shaped dust artifact found in the ground truth, because the network could not predict from the transmitted light images that those artifacts would appear in the processed fluorescence image. The noise reduction is less clear in the other images because the ground truth images are less noisy to begin with. In regions without cells, the proposed network predicts a brightness approximately equal to the noise floor.

Live vs dead cell nuclear size

Dead neuronal nuclei in culture are often smaller than live nuclei, as one of the effects of apoptosis. We wondered if this holds true with our true fluorescent labels, and if so, whether it also holds true for the predicted labels. We considered the true and predicted DAPI images from the single test well in Condition C in which experts annotated dead cells. Using CellProfiler (Carpenter et al., 2006) to automatically segment the nuclei in these images, we measured the radius of each nucleus and partitioned the measurements via the live / dead annotations.

As expected, dead cell nuclei were smaller than live cell nuclei in the true DAPI image (Fig. S7A). This was also the case for the predicted DAPI image (Fig. S7B). The mean radii for live and dead cells were only slightly changed between the true and predicted images. Thus, ISL may be able to detect biologically relevant changes in nuclear size.

To segment nuclei, we used CellProfiler 2.2.0’s IdentifyPrimaryObjects routine with the Otsu thresholding method and default parameters. We labeled an auto-detected cell center as dead if it fell within 4.5 μm of a point marked as a dead cell by the expert annotators. Statistical distinctiveness was measured using the ks_2samp function in Python’s scipy.stats (Jones et al., 2001), which implements the two sample Kolmogorov-Smirnov test. All distributions were distinct, with the highest p values still less than 0.001.

Data and software availability

Code for running training and prediction (inference) is on GitHub at https://github.com/google/in-silico-labeling. It includes links to pre-trained network parameters, and all data, including training, test, and the predictions of our network. Users with basic Python skills can follow the README to run training and prediction on a single machine.

Supplementary Material

1

Figure S1 Predictions of neurite type from unlabeled images, related to Figures 4, 5, and 6

(A) Upper-left-corner crops of dendrite (MAP2) and axon (neurofilament) label predictions on the Conditions B and D datasets. The unlabeled image that is the basis for the prediction and the images of the true and predicted fluorescent labels are organized similarly to Figure 4. Predicted pixels that are too bright (false positives) are magenta and those too dim (false negatives) are shown in teal. The true and predicted nuclear (DAPI) labels have been added to the true and predicted images in blue for visual context. Outset 4 for the axon label prediction task in Condition B shows a false positive, where an axon label was predicted to be brighter than it actually was. Outset 1 for the dendrite label prediction task in Condition D shows a false negative, where a dendrite was predicted to be an axon. Outset 4 in the same row shows an error in which the network underestimates the extent and brightness of the dendrite label. Outsets 1,2 for the axon label prediction task in Condition D are false negatives, where the network underestimated the brightness of the axon labels. All outsets in this row show the network does a poor job predicting fine axonal structures in Condition D. All other outsets show basically correct predictions. Scale bars are 40 μm. (B) Pixel intensity heat maps and the calculated Pearson coefficients for the correlation between the intensity of the actual label for each pixel and the predicted label. See also Figures 4, 5, and 6.

2

Figure S2 An evaluation of the ability of the trained network to exhibit transfer learning, related to Figures 4, 5, and 6

(A) Upper-left-corner crops of nuclear (DAPI) and foreground (CellMask) label predictions on the Condition E dataset, representing 9% of the full image. The unlabeled image used for the prediction and the images of the true and predicted fluorescent labels are organized similarly to Figure 4. Predicted pixels that are too bright (false positives) are magenta and those too dim (false negatives) are shown in teal. In the second row, the true and predicted nuclear labels have been added to the true and predicted images in blue for visual context. Outset 2 for the nuclear label task shows a false negative in which the network entirely misses a nucleus below a false positive in which it overestimates the size of the nucleus. Outset 3 for the same row shows the network underestimate the sizes of nuclei. Outsets 3,4 for the foreground label task show prediction artifacts; Outset 3 is a false positive in a field that contains no cells, and Outset 4 is a false negative at a point that is clearly within a cell. All other outsets show correct predictions. The scale bars are 40 μm. (B) Pixel intensity heat maps and the calculated Pearson ρ coefficient for the correlation between the pixel intensities of the actual and predicted label. Although very good, the predictions have visual artifacts such as clusters of very dark or very bright pixels (e.g., boxes 3 and 4, second row). These may be a product of a paucity of training data. See also Figures 4, 5, and 6.

3

Figure S3 Predictions of neuron subtype from unlabeled images, related to Figures 4, 5, and 6

(A) Upper-left-corner crops of motor neuron label (Islet1) predictions for Condition A dataset. The unlabeled image that is the basis for the prediction and the images of the true and predicted fluorescent labels are organized similarly to Figure 4, but in the first row the true and predicted nuclear (DAPI) labels have been added to the true and predicted images in blue for visual context, and in the second row the true and predicted neuron (TuJ1) labels were added. Outset 1 shows a false positive, in which a neuron was wrongly predicted to be a motor neuron. Outset 4 shows a false negative above a false positive. The false negative is a motor neuron that was predicted to be a non-motor neuron, and the false positive is a non-motor neuron that was predicted to be a motor neuron. The two other outsets show correct predictions. The scale bars are 40 μm. (B) Pixel intensity heat map and the calculated Pearson coefficient for the correlation between the intensity of the actual label for each pixel and the predicted label. See also Figures 4, 5, and 6.

4

Figure S4 Dependence of network performance on z-stack size with comparison to other models, related to Figures 1 and 3 and Methods S1

(A) Dependence of network performance on the number of images in the transmitted light z-stack. The x-axis is the number of images in the network input. The y-axis is the cross entropy loss on fluorescence label prediction on a validation set. Each dot is the loss of a single network after training for 4 million steps with the optimal learning rate of 3e-6. Two networks were trained for each configuration, yielding 26 dots. The curve is the degree 5 polynomial which best fits the data under the least squares loss. The more distinct z-depths provided to the network, the better it performs. (B) Comparison of the proposed network to DeepLab and modified U-Net. The curves show combined cross entropy loss for prediction and auto-encoding on the training and validation data, as a function of the number of training steps. The proposed network achieved a lower loss than the modified U-Net, which achieved a lower loss than DeepLab. All networks were trained for at least 10 million steps, which took around 2 weeks per network training on a cluster of 64 machines. Note, A shows losses for prediction only, while B shows losses for the combined prediction of fluorescence labels and auto-encoding, which tends to be lower. See also Figures 1 and 3 and Methods S1.

5

Figure S5 Sample manual error annotations on the Condition C data, related to Figures 4 and 5

(A) Sample manual error annotations for the nuclear label (DAPI) prediction task on the Condition C data. The unlabeled image that is the basis for the prediction and the images of the true and predicted fluorescent labels are organized similarly to Figure 4, but the fourth column instead displays manual annotations. Merge errors are shown as red dots, add errors are shown as light blue dots, and miss errors are shown as pink dots. There are no split errors. All other dots indicate agreement between the true and predicted labels. Outset 1 shows an add error in the upper left, a miss error in the center, and six correct predictions. Outset 2 shows a merge error. Outset 4 shows an add error and four correct predictions. Outset 3 shows one correct prediction, and a cell clump excluded from consideration because the human annotators could not determine where the cells are in the true label image. The scale bars are 40 μm. (B) Sample manual error annotations for the cell death label (propidium iodide) prediction task on the Condition C data. The unlabeled image that is the basis for the prediction and the images of the true and predicted fluorescent labels are organized similarly to Figures 4 and 5, but the fourth column instead displays manual annotations, and the true and predicted nuclear (DAPI) labels have been added for visual context. Merge errors are shown as red dots, add errors are shown as light blue dots, miss errors are shown as pink dots, and add errors which were reclassified as correct debris predictions are shown as yellow dots. There are no split errors. Outset 2 shows an add error at the bottom and a reclassified add error shown at top. The top error was reclassified because of the visible debris in the phase contrast image. Outset 5 shows an add error at the top and a reclassified add error at the left. Outset 7 shows a reclassified add error. Outset 8 shows a merge error at the top and a reclassified add error at the bottom. All other dots in the outsets show correct predictions. Note, the dead cell on the left in Outset 3 is slightly positive for the true death label, though it is very dim. The scale bars are 40 μm. See also Figures 4 and 5.

6

Figure S6 Example predicted images showing the noise floor, related to Figures 4, 5, and 6

Unlike the images in all other figures, pixel intensities here were not cropped at the approximate noise floor; this is why background regions are not black. Each of the two blocks shows ground truth, predicted, and error images in the style of Figure 4. The color bars in the fluorescence images indicate the color of zero brightness at the bottom and color of full brightness at the top. The color bars in the error images indicate the color of a full false negative (true intensity 1.0, predicted 0.0) at the bottom and of a full false positive (true intensity 0.0, predicted 1.0) at the top. The inset text indicates the fluorescent labels, and the condition names at the sides indicate the source conditions. Unlike in Figures 5 and 6, nuclear labels are not provided as context for the predictions. In Condition B, the predicted MAP2 image lacks the stitching artifact (vertical boundary in the lower right) and the disk-shaped dust artifact present in the ground truth. It also contains dim neurites which are not visible above the noise in the ground truth. The scale bars are 40 μm. See also Figures 4, 5, and 6.

7

Figure S7 Histograms of nuclear radii of living vs dead cells in Condition C, related to Figure 5

(A) Radii predicted from the true DAPI label. The sample mean and standard deviation of the living and dead cells were 6.8±1.3 μm and 4.7± 1. 1 μm, respectively. (B) Radii predicted from the predicted DAPI label. The sample mean and standard deviation of the living and dead cells were 7.0±1.4 μm and 4.9±1.0 μm, respectively. For both true and predicted labels, dead cell nuclei are on average smaller than live cell nuclei. Cell debris was not excluded from these histograms, so the very small radii might be overcounted. All distributions are statistically distinct from one another; though the predicted distributions may be similar to their true counterparts, they are distinguishable using the two sample Kolmogorov-Smirnov test. See also Figure 5.

8

Methods S1 Data and model details, related to Figures 1,2, and 3

9

Table S1 Machine learning concepts, related to Figure 1

• Fluorescence microscopy images can be predicted from transmitted light z-stacks

• 7 fluorescent labels were validated across three labs, modalities, and cell types

• New labels can be predicted using minimal additional training data

ITI.

In silico labeling as a machine-learning approach to infer fluorescent measurements from transmitted light images of unlabeled fixed or live biological samples.