Abstract
Many cellular populations are tightly-packed, such as microbial colonies and biofilms, or tissues and tumors in multicellular organisms. Movement of one cell in those crowded assemblages requires motion of others, so that cell displacements are correlated over many cell diameters. Whenever movement is important for survival or growth, these correlated rearrangements could couple the evolutionary fate of different lineages. Yet, little is known about the interplay between mechanical forces and evolution in dense cellular populations. Here, by tracking slower-growing clones at the expanding edge of yeast colonies, we show that the collective motion of cells prevents costly mutations from being weeded out rapidly. Joint pushing by neighboring cells generates correlated movements that suppress the differential displacements required for selection to act. This mechanical screening of fitness differences allows slower-growing mutants to leave more descendants than expected under non-mechanical models, thereby increasing their chance for evolutionary rescue. Our work suggests that, in crowded populations, cells cooperate with surrounding neighbors through inevitable mechanical interactions. This effect has to be considered when predicting evolutionary outcomes, such as the emergence of drug resistance or cancer evolution.
The growth and division of non-motile cells tends to produce densely-packed assemblages. The tight packing of cells is the natural consequence of population growth against a visco-elastic extra-cellular environment, and can be further promoted by attractive cell-cell interactions [14, 6]. Common examples range from microbial communities, in the form of colonies or biofilms, to multi-cellular structures, such as developing tissues or tumors.
An important consequence of high packing density is that any cellular growth and division increases the spatial extent of the population. Statistical approaches to describe the ensuing growth dynamics have therefore been based predominantly on the framework of range expansions [13, 24, 30, 23]. This analogy is particularly apt when most of the growth occurs in a “growth layer” at the population margins [37, 19, 23, 45, 55, 15, 16]. In this case, “pioneer” cells near the periphery have a two-fold advantage: they enjoy high growth rates and place their offspring near the periphery so that those descendants can become the pioneer cells of the next generation.
The positional advantage of pioneer cells has important population genetic consequences. Mutant clones can reach high frequencies just by chance, when their descendants happen to keep up with the advancing edge of the expanding population. This process, termed “gene surfing”, is highly stochastic, but can be biased by mutations that increase or decrease the expansion velocity [31, 25]. Successfully surfing clones grow in well-segregated sectors, which have a spatial structure that reflects the competition between genetic drift and selection [24, 25, 23, 56]. These population genetic phenomena have been directly verified in microbial evolution experiments and shown to strongly influence evolutionary outcomes, including drug resistance [19, 4], the emergence of cheater types [48, 56], mutualism [46] or adaptation [50]. Even though spatially-resolved experiments in higher eukaryotic systems are much more challenging, hallmarks of gene surfing, including formation and coarsening of clonal sectors, were recently identified in cancer [36].
Despite this progress, we still lack an understanding of how evolutionary dynamics arise from the interactions between individual cells. In particular, conventional models of range expansions, based broadly on pulled or pushed reaction-diffusion waves, do not capture cell-cell forces resulting from the tight packings of growing cells. These forces have been seen to matter for the structure and function of biofilms [15, 53, 64, 3], and they might also influence natural selection. For example, slower-growing cells might be pushed along by the forces generated by faster-growing cells, leading to a form of mechanical cooperation.
To explore the interplay between mechanical forces and evolution, we tracked the evolutionary fate of slower-growing clones in dense colonies of the budding yeast S. cerevisiae. We find that high population density inherently results in a screening of fitness differences on small length scales due to the collective motion of nearby cells. Our results can be described in the framework of an effective surface tension originating from cumulative cell-cell forces.
Results
As a model system for crowded cellular populations, we focused on colonies of the budding yeast Saccharomyces cerevisiae [57]. Since yeast cells lack motility, colony expansion is fueled purely by the pushing forces generated by cellular growth in a peripheral growth layer (see Supplementary Fig. S7) [37, 45, 23]. To explore how these pushing forces affect the strength of natural selection, we competed a strain carrying a growth-rate deficit s with a faster-growing strain in expanding colonies (Fig. 1a) [23]. The behavior of the slower-growing strain is equivalent to that of a clone carrying a deleterious mutation, a ubiquitous scenario in population genetics. We therefore refer to the slower-growing strain as “mutant” and the faster-growing strain as “wild-type” throughout this work (see also Table 1). During colony expansion, mutant and wild-type cells remained in well-segregated monoclonal sectors separated by sharp boundaries [24].
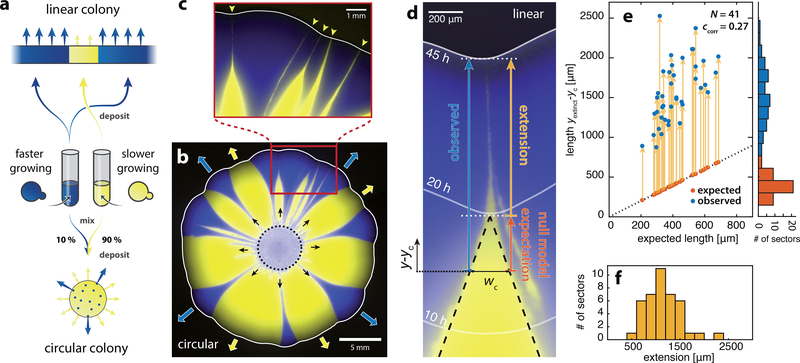
Figure 1: Slower-growing clones persist at the front of expanding yeast colonies.
a) Schematic of experimental setup. Competition experiments were conducted with a faster-growing (yMM9, false-color blue) and a slower-growing yeast strain (yJK22, yellow) with growth-rate deficit s = −0.06. Circular colonies were inoculated from a mixture of both strains (initial fraction of faster-growing cells was 10%). In linear colonies sectors expanded from flat fronts composed of extended regions with alternating cell types. b) Circular colony grown for 8 days from a mixture of both cell-types (dotted circle indicates area of cell deposition). Monoclonal “sectors” remain well-separated and expand outward at different rates (blue and red arrows). c) Sectors of the slower-growing strain form an inverted funnel shape with elongated tips (yellow arrowheads) that persist at the front before being completely expelled. d) Image of a mutant sector (yellow) being expelled from a linear colony (see movie S1 for a complete time lapse and Supplementary Fig. S1 for experimental setup). Same strains and colors as in a-c. Solid white lines mark the front position at the indicated times after inoculation. Dashed black lines delineate the sector shape predicted by the null model (local front speed only depends on cell type), and wc ≈ 230μm is the characteristic width below which observations deviate from null model predictions (see Supplementary Fig. S3 for assessment of wc). Sector extension (yellow arrow) is the difference between observed sector length (blue arrow) and the null model expectation (orange arrow). Positions along axis of sector expansion, y, are measured relative to yc, the position at which wc = w(yc). e) Observed clone lengths (blue dots) as a function of expected length (also indicated as orange dots) for N = 41 sectors. yextinct indicates the position of clone expulsion from the front. Yellow arrows indicate sector extension (see panel d). Histograms show binned distributions of expected and observed lengths. ccorr is the Pearson correlation coefficient of both lengths. f) Histogram of the sector length extensions (yellow arrows in panel e). Sectors are significantly (p-value < 10−29) extended by an average of 1150 ± 340μm.
Table 1:
S. cerevisiae strains used for this work.
| Name | Type | Color | Resistance | Genotype |
|---|---|---|---|---|
| yJK22 | mutant | yellow | hygromycin B | his3::prACT1-ymCitrine-tADH1:HygMX |
| yMM9 | wild-type | blue (false-color) | cycloheximide | his3::prACT1-ymCherry-tADH1:His3MX6 CYH2::cyh2-Q37E CYH2::cyh2-Q37E |
| yMM8 | wild-type | yellow | cycloheximide | his3::prACT1-ymCitrine-tADH1:His3MX6 CYH2::cyh2-Q37E CYH2::cyh2-Q37E |
| JHK111 | ancestor | - | - | his3::prACT1-ymCitrine-tADH1:His3MX6 |
| JHK102 | ancestor | - | - | W303 MATa bud4Δ::BUD4(S288C) can1–100 |
We could thus monitor the gradual decay of mutant clones by measuring the width w of mutant clones as a function of front propagation distance y.
We found that mutant clones were purged from the population front in two stages. In the first stage, the clone width decreased at a constant rate, dw/dy ≈ const. We observe this behavior both in circular (Fig. 1b, c) and linear (Fig. 1d) inoculations. To disentangle evolutionary dynamics from radial expansion effects we focus on linear inoculations in this work (see Supplementary Fig. S1 for example of linear front). The constant rate of mutant decline is in line with a minimal null model where local front expansion velocities depend only on the cell-type specific growth rates of the furthest forward pioneer cells at the leading edge, or “front cells” [25] (dashed black lines in Fig. 1d, see Supplementary Sec. 1 for model details). The null model predicts that the width of the mutant clone decreases at a constant rate until all mutant cells are expelled from the front. This form of abrupt clonal “extinction” is in agreement with commonly-used non-mechanical simulations (Supplementary Fig. S19 b-d). In contrast, we observed a second stage of mutant decline as the clone width fell below a characteristic width of wc ≈ 230μm (≈ 46 cell diameters). Then, clones progressively slow down narrowing, and gradually taper to form elongated streaks. As a result, clones persist at the growing front over distances that far exceed the null expectation (Fig. 1e, f). The consequences of this persistence become apparent on the colony-level: Even after 8 days of colony growth none of the slower-growing sectors shown in Fig. 1c, no matter how narrow initially, have been completely expelled from the front.
Thus, purifying selection is inefficient in removing small mutant clones in our experiments. In the following, we aim to show that a strongly reduced efficacy of selection is not specific to yeast colonies but, in fact, a predictable consequence of growth in crowded cellular populations, and that this effect can dramatically alter probabilities of important evolutionary outcomes.
The fate of clones in crowded populations fundamentally depends on the relative motion of mutant and wild-type front cells at clonal boundaries [23, 25, 58, 38, 31, 33]. In the null model the direction of cell motion abruptly changes at the wild-type/mutant boundary (Fig. 2a). A delay of the extinction of mutant clones could arise from a suppression of such discontinuities. Indeed, while front cells much further apart than wc can have substantially different velocity vectors, their direction of motion becomes highly correlated at smaller distances (Fig. 2b and c; Supplementary Videos S3 and S4). Front cells, including those at the mutant/wild-type boundary, tend to move perpendicular to the local front-line with very little lateral motion. This normal motion is also reflected in the trajectories of clone boundaries (Supplementary Fig. S4).
Figure 2: Delayed extinction can be described via an effective surface tension.
a) Schematic of a sector boundary (at steady state) in the null model exhibiting discontinuous front velocities (arrows). b) Tracks (blue/yellow arrows) of individual pioneer cells close to a clone boundary between a slower-growing (strain yJK22, yellow, s = −0.06) and a faster-growing sector (strain yMM9, false-color blue). White lines indicate the front position at shown times. Relative images positions are to scale. See movie S9 for complete time lapse series. c) Comparison of observed and expected clone-boundary and front behavior in a linear colony. Strains and colors as in b. Bottom and top panels are recorded at indicated times after inoculation and relative positions are to scale. Center: null model prediction. Blue/yellow arrows indicate the direction of motion of front cells perpendicular to the local front-line (white) as seen in panel b. Orange dashed lines and arrows delineate straight boundary trajectories as predicted by the null model. Dashed blue lines outline experimentally observed boundaries. d) Consecutive snapshots of a progressing wild-type front starting from cells deposited in a highly curved geometry. Arrows indicate different amounts of displacement of flat and curved regions. Time intervals are adjusted for constant displacement of flat regions (black arrows). e) Velocity v of cells at the front as a function of the local curvature κ (see movie S3 for cell tracking data). Fitting the linear relation v = v0(1 + Tκ) to the data results in v0 = 0.94μm/min and T = 27μm (dashed black line). f) Inset: Schematic of the surface tension model. v is the front velocity and vtype is the cell-type specific velocity of a flat front. The main graph shows the clone width w (average of N = 9 sectors shown in Supplementary Fig. S2) as a function of front position y with respect to yc = y(w = wc). The surface tension model is fitted to the experimental data, yielding a surface tension of T = 25μm. Gray shaded area indicates one standard deviation. The orange dotted line delineates the null model prediction. See panel g) for legend. g) Clone width-dependent effective fitness difference seff(w) calculated from the slope of w(y) (see Supplementary Sec. 1 and Fig. S9 for details).
Since the average motion of front cells is perpendicular to the local leading edge, directional alignment must be driven by a mechanism that suppresses high curvatures of the front-line. Indeed, while the null model predicts that the front-line develops a sharp kink (infinite curvature) as the mutant clone goes extinct, we find that the curvature of the front-line remains low in our experiments (Fig. 2c).
Curvature suppression is an active, growth-driven process: Fig. 2d shows how a region of high curvature in a purely wild-type front, deliberately formed by initial cell deposition, is smoothed out by subsequent growth. Cells in front regions exhibiting a higher degree of curvature move faster than those in flatter regions (Fig. 2e and Supplementary Videos S3 and S4).
Based on these observations we hypothesized that the dynamic suppression of high front curvatures, and thus the directional alignment of nearby cells, could be described by an effective surface tension [49, 39, 7, 59]. To test this, we set up a phenomenological “surface tension model” that represents the expanding population as a moving 1D front-line whose velocity depends not only on cell-type but also on local front curvature (Fig. 2f). The curvature dependence is controlled by an effective surface tension term that gives a velocity boost to indented divots in the front, as observed in our experiments (Fig. 2d, e). Mutant and wild-type lineages occupy contiguous portions of the front separated by sharp boundaries which move perpendicular to the front-line. This model corresponds to a multi-type extension of the KPZ model, a well-studied model of surface growth [27] (see Supplementary Sec. 3). The surface tension model reproduces the observed clone width dynamics very well upon tuning the surface tension, our single fitting parameter (see Fig. 2f). The condition that motion is perpendicular to the local front-line is an essential ingredient for the delayed extinction of the mutant clone. Even a small tilt results in abrupt extinction rather than extended clonal dynamics (Supplementary Fig. S17).
So far, we have shown that the delayed extinction of slower-growing clones can be traced back to the active suppression of high front curvature. This effective surface tension leads to the directional alignment of the motion of mutant front cells with that of the flanking wild-type population, thereby concealing the fitness difference between the two types. We can describe this screening effect by an effective fitness difference seff between mutant and wild-type that is sharply diminished for clones of small width (Fig. 2g).
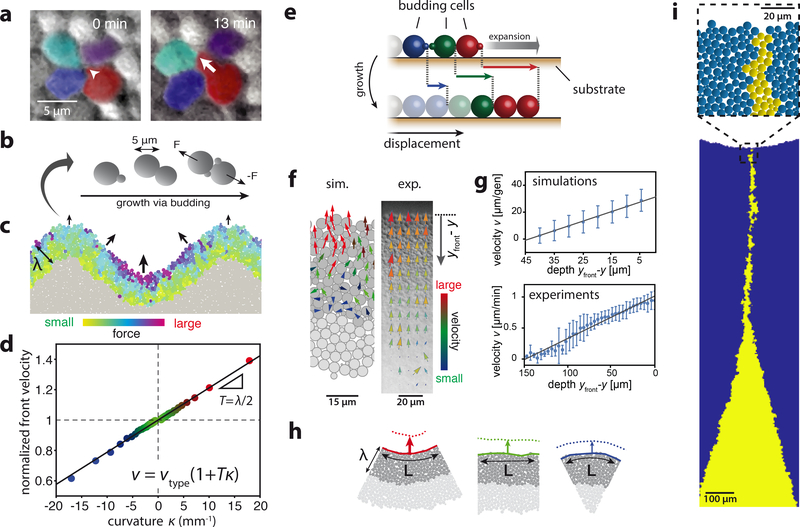
Which mechanism could generate an effective surface tension capable of driving the observed directional alignment? Expecting cell-cell pushing forces within a crowded growth layer to be the root cause for the collective cellular motion (see Fig. 3a), we tested in silico whether surface tension can be generated purely through the mechanical interactions between cells in a dense population. To this end, we simulated growing and dividing cells as proliferating elastic objects that move via over-damped dynamics (Fig. 3b). Similar to the expansion of yeast colonies (Supplementary Fig. S7), only cells within a peripheral growth layer grow and divide. In this simplified model we approximated the complex growth rate profile observed in experiments by assuming an effective growth layer of constant width λ and a uniform growth rate within the layer (see Methods for model parameterization and simplifying assumptions). These simulations allowed us to directly quantify the force exerted on each cell in the growth layer. Fig. 3c shows that cell-cell forces in an undulating monoclonal front are larger in divots than in flat regions or bulges. Consequently, front cells in divots move faster than those in bulges. The resulting velocities are consistent with a surface tension proportional to the growth layer depth (Fig. 3d).
Figure 3: Effective surface tension emerges in mechanical simulations from purely physical cell-cell interactions.
a) A budding cell (red, white arrow indicates bud growth) displaces neighboring cells. b) Schematic of cell-based simulations (see Methods and Supplementary Video S6 for simulation description). c) Total force on each cell from all intercellular contacts (colored cells) for cell-based simulations of a highly-curved growth layer (depth λ = 45μm, see Methods and Supplementary Fig. S14 for parameterization). Arrows indicate resulting front cell motion. d) Front velocity as a function of curvature κ, normalized to the velocity for a flat front (κ = 0). Curvature is defined as positive for inward divots and negative for outward bulges. The black line indicates v ∝ 1 + Tκ with T = λ/2 (see Supplementary Information Sec. 2 for derivation of relationship between T and λ ). Colors correspond to curvature as in h. e) Schematic of cumulative cell-cell pushing. Colors identify mother-daughter pairs with solid cells indicating the growth layer. Displacements of individual cells towards the front (right) upon growth are indicated by respective colored arrows. The gray arrow denotes resulting front expansion. f) Tracking cell movement inside the growth layer. Simulations: Arrows represent center-of-mass motion of budding cells (dark gray) with colors indicating total velocity magnitude. Experiments: Cell motion obtained via particle image velocimetry (see Methods). Arrows represent measured velocities with colors indicating arrow lengths for better visualization. g) Average forward velocities as a function of depth yfront −y (see panel f). Error bars indicate one standard deviation from the mean. Solid lines are calculated expected values (simulations) or a linear fit to the data (experiments). Experimental data is based on Supplementary Video S5 (2h after start, see Supplementary Fig. S7 for later time points). h) Depicted images are representative sections from simulated colonies with a constant front curvature. The number of growing and pushing cells (dark gray) per unit arc length L of the front depends on the curvature κ. Arrows indicate resulting front velocities (see panel d for quantification and color labeling). Front profiles (solid and dotted lines) are separated by 1/2 generation. i) Slower-growing clones in cell-based simulations (s = −0.06) exhibit a delay in extinction similar to experiments (see Supplementary Fig. S14 for comparison of simulations to experiments). The image is a snapshot of Video S2 at 35 generations.
In our cell-based simulations, the suppression of high curvatures can be rationalized from a mechanical connection between growth and motion in an incompressible cell packing. Consider first a linear chain of growing cells, as illustrated in Fig. 3e. To accommodate newly generated biomass, any growing cell must push forward the cells that are in front of it. Cell velocities in the growth layer are, therefore, directed towards the front and gradually increase from the bulk to the edge of the colony. These features can be seen both in simulations as well as in experiments (Fig. 3f and g).
In two dimensions, the picture subtly changes in that the front velocity also depends on the local curvature of the growth layer (Fig. 3d and h): If the front-line is indented and the growth layer depth is constant, there are more growing cells per unit length of curved front as compared to the flat front case. This leads to an increased rate of biomass production. Incompressibility of the cell packing requires that additional space needs to be made for the excess biomass. As a result the front advances at a slightly higher rate, which allows for the excess biomass to be added to the growth layer. Conversely, we observe a local slow-down if the front exhibits a bulge so that fewer cells per unit length of front contribute to pushing. Thus, a negative feedback on front curvature - which is equivalent to a surface tension - spontaneously arises from purely passive, mechanical effects generated by cell proliferation within a growth layer. Note that the link between excess biomass production and forward motion is based on the mechanical incompressibility constraint of the cell packing, which is a key feature of crowded cellular populations.
In addition to a sufficiently strong effective surface tension, our cell-based model produces two additional essential ingredient for fitness screening: sharp wild-type/mutant domain boundaries (Supplementary Fig. S21) that move perpendicular to the frontline (Supplementary Fig. S15). This condition also arises in a continuum description of colony growth which assumes that cell motion is driven by pressure gradients since the edge of the colony represents a constant pressure line [21]. It is violated, however, in commonly-used non-mechanical simulations of colony growth, such as diffusive waves, where domain boundaries are generically tilted with respect to the front-line (Supplementary Fig. S16). Our cell-based simulations thus generate all key ingredients of the surface tension model: a population front with a natural surface tension and sharp domain boundaries that move normal to that front. Consequently, upon simulating a slower-growing mutant clone in a wildtype background, we reproduce the experimentally observed funnel-like sector shapes with extended tips (Fig. 3i).
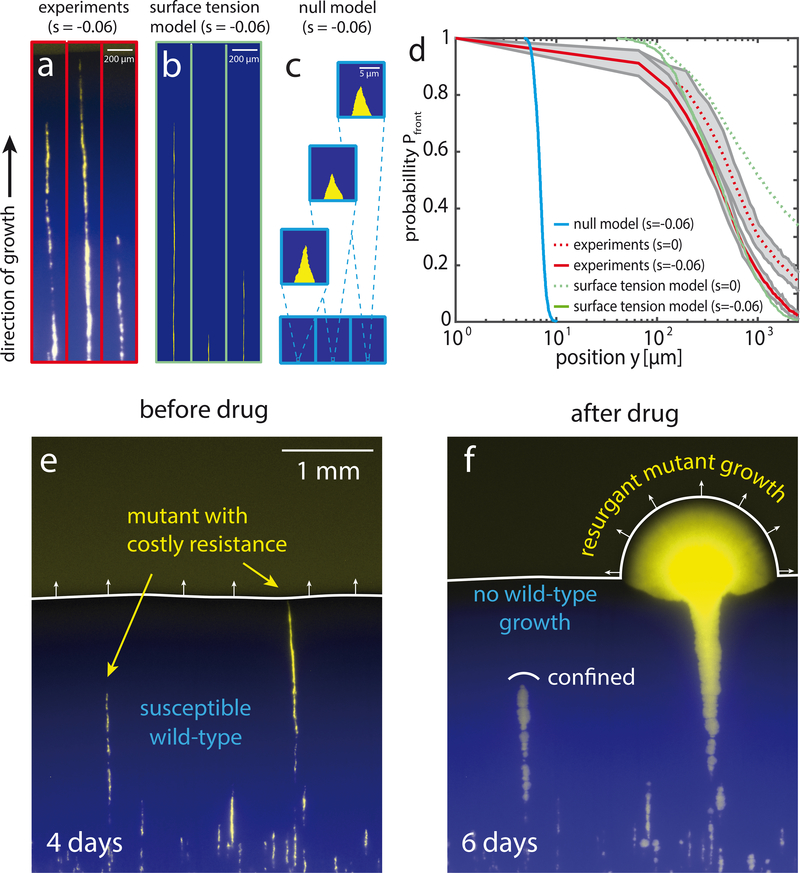
Our results so far suggest that slower-growing mutant clones at the advancing frontier are mechanically screened from the competition with wild-type cells, an effect that is strongest for clones of small width. Clones emanating from single mutant front-cells should therefore benefit the most and exhibit nearly neutral lineage dynamics. To test this prediction, we investigated the fate of clones originating from single mutant cells interspersed into a front of wild-type cells (see Supplementary Fig. S6). These experiments indeed show that mutant clones form elongated streaks (Fig. 4a) similar to a stochastic version of the surface tension model (Fig. 4b, see Methods). Even though slower growing mutant clones can still be expelled from the expanding front due to stochastic fluctuations in clone width, their probability to persist at the progressing front decays several orders of magnitude more slowly than the null model expectation (Fig. 4c,d). In addition, these extended lifetimes allow slower-growing mutant clones to produce a larger total number of offspring than expected from our null model (Supplementary Fig. S20).
Figure 4: Slow purging of costly drug-resistant mutations can lead to resurgent growth upon drug application.
a) Fluorescent micrographs of thin sectors originating from single mutant cells after 4 days of growth. Colonies were grown in a linear geometry from a mixture of strains yJK22 (5%, yellow, s = −0.06) and yMM9 (95%, false-color blue) (see Supplementary Fig. S6 for a wider field of view). b) Corresponding surface tension model simulations (s = −0.06 and T = 25μm, as in Fig. 2f) including stochastic boundary drift (see Methods for description and parameterization). c) Null model including boundary drift. d) Probability of a clone to persist at the front, Pfront, as a function of front position y relative to inoculation. Experimental data represents average of N = 12 fronts (≈ 3500 initial sectors, see Supplementary Fig. S6 for an example). Shaded gray area indicates one standard deviation. For neutral experiments (s = 0) mutant cells (strain yJK22) are substituted for cells with a growth rate identical to that of the wild-type (strain yMM8). Surface tension model and null model results are averages of N = 103 independent sectors for both models. e) Image of a persisting and an expelled mutant sector (yellow, yJK22, s = −0.06) in a wild-type background (blue, yMM9) after 4 days of growth. Mutant cells are resistant to the antimicrobial Hygromycin B while wild-type cells are susceptible. f) Application of Hygromycin B to the entire colony completely arrests wild-type growth. Mutant clones still present at the front at the time of drug application (right) expand quickly (see Video S8) while those inside the colony (left) remain confined.
The inefficient purging of slower-growing mutants can have crucial evolutionary consequences when the selection pressure suddenly shifts in favor of the mutants. For instance, costly drug-resistant mutants may persist long enough to trigger resurgent growth upon drug application [20, 2]. To test whether the screening of fitness effects promotes such an evolutionary rescue [5, 9], we first grew a colony interspersed with a small fraction of single mutant cells as described in Fig. 4a. These mutants are resistant to the antimicrobial Hygromycin B while having a fitness cost in the absence of the drug. Despite their growth disadvantage, some mutant clones persisted at the front even after 4 days of colony expansion (Fig. 4e). We then subjected the entire colony to high levels of Hygromycin B, completely stalling wild-type growth (see Methods). While mutant clones trapped inside the colony remained effectively confined by surrounding wild-type cells, those clones persisting at the leading edge radiated out, establishing an all-mutant population expansion (Fig. 4f).
Although our study focuses on deleterious mutations, the mechanism proposed here acts on less-fit and more-fit cells alike. Consequently, the screening of fitness differences also affects beneficial mutations: Sectors of faster-growing clones initially widen more slowly than predicted by non-mechanical models (Fig. 5a), a feature that had previously been noted in yeast colonies but not traced back to its mechanical origin [25, 31, 61]. As a result of this fitness screening, we expect faster-growing clones to take longer to establish thus slowing down adaptation [12, 23, 16].
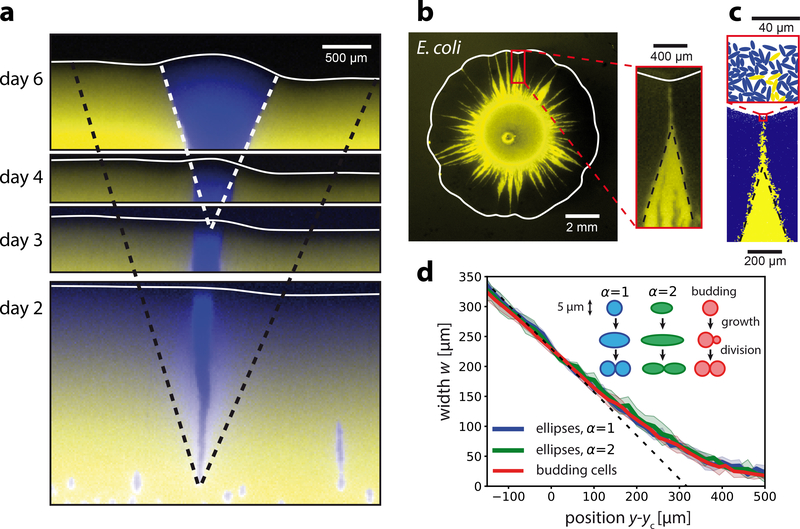
Figure 5: Fitness screening affects faster-growing mutants and is independent of cell morphology.
a) Sector originating from a single cell of a faster-growing strain (yMM9, false-color blue) in a slower-growing background (yJK22, yellow). Snapshots show the front position (white lines) and sector shape at the indicated times with relative image positions to scale. Black dashed lines show the null model prediction (s = 0.06). White dashed lines (same angle as black dashed lines) correspond to sector boundaries at day 6. b) A circular colony grown from two strains of E. coli bacteria with different growth rates (yellow strain SJ102, dark strain MG1655, s = −0.04) exhibits funnel-like sectors with extended tips similar to those observed in yeast. c) Cell-based simulations akin to those in Fig. 3i (s = −0.06 and λ = 45μm) but with symmetrically-dividing ellipsoidal cells that have an aspect ratio α = 2 at birth. d) Sector width w as a function of front progression y (widths aligned at w(yc) = wc = 230μm) for simulations of ellipsoidal cells with varying elongation (α = 2 and α = 4) and mode of cell duplication (symmetric division and budding). Solid lines show the average over 10 independent runs and shaded regions indicate one standard deviation. The black dashed line delineates the null model prediction for s = −0.06.
In addition to our findings in S. cerevisiae, we also observed fitness screening in colonies grown from the rod-shaped bacterium E. coli (Fig. 5b). E. coli differs from S. cerevisiae in a number of characteristics, such as cell size, shape, and modes of proliferation (budding vs. symmetric cell division).
The robustness of fitness screening is further demonstrated by cell-based simulations that model symmetrically-dividing ellipsoidal cells (Fig. 5c). All investigated cell shapes and division types exhibit the hallmarks of a crowding-mediated fitness screening. For a fixed growth layer depth even the magnitude of the effect is conserved in cell-based simulations (Fig. 5d). This finding corroborates our notion that the mesoscopic features of fitness screening are independent of microscopic cell properties.
Discussion
Our results demonstrate that evolutionary processes have a mechanical basis in crowded populations. Growth-induced pushing forces generate long-rang correlations in cell motion, thereby screening fitness differences. Consequently, selection is less efficient in weeding out less fit mutants from the expanding population front than predicted by non-mechanical models. Less fit mutant clones thereby produce many more offspring than expected. These persisting mutants can contribute to population resilience in the face of environmental deteriorations, such as the application of a drug. In addition, the larger total number of mutant offspring might increases the chance of mutant survival after a population bottleneck or acquisition of subsequent mutations compensating the fitness cost [62, 2].
Fitness screening has three necessary ingredients: the front has to exhibit an effective surface tension, the average motion of all cells has to be perpendicular to the local front-line, and domain boundaries have to be sharp in comparison to the characteristic length-scale of boundary interaction. Whereas conventional non-mechanical models fail to generate this combination of ingredients, all ingredients inherently result from the collective nature of mechanically-driven population expansion generated by growth and division of cells within a growth layer near the population frontier. In addition to the models presented in this work, fitness screening can also be described via overdamped continuum mechanics model. Using this approach, a parallel study by Giometto et al. corroborates our results and demonstrates their implications for adaptation in oscillating environments [21].
Fitness screening may be altered beyond the simple scenario presented in this paper. For example, a modulation of nutrient penetration into the colony could reduce the growth layer depth [43, 22, 29, 28, 16], decreasing the effective surface tension and the strength of fitness screening. An inherent surface tension can also arise in cellular populations independent of cell growth, originating from forces such as cell-cell adhesion [39, 17] and cell contractility [44, 41, 1].
Fitness screening can be viewed as a form of cooperation [18, 47, 56]: In crowded populations, faster-growing cells tend to push along nearby slower-growing cells, as dictated by the laws of mechanics. This mode of cooperation merely requires physical cell-cell forces and could therefore substantially affect the evolutionary dynamics in any crowded cellular population, such as biofilms, growing tissues or tumors [60, 32, 36, 34]. Potential implications range from the promoted accumulation of deleterious mutations [38, 50, 25, 8] to exacerbated clonal interference [26, 42] (see e.g. Supplementary Fig. S5) and an increased chance of evolutionary rescue [62, 2].
This study aims to demonstrate the fundamental features of fitness screening, which in more complex scenarios could act in conjunction with other processes such as nutrient depletion or the secretion of extracellular matrix [16, 63]. The presented results may therefore serve as a basis for future work integrating the described concepts into more involved scenarios, such as fluctuating environments or multistep adaptation [35, 21, 40, 62].
Methods
Strains.
Experiments in this work, using the nonmotile yeast Saccharomyces cerevisiae, were conducted with the strains yJK22 (“mutant”), yMM9 (“wild-type”), and yMM8 (“wild-type” with alternative color) with the common ancestor yJHK102 [31, 23] (see table 1). yMM9, yMM8, yJHK102 and yJHK111 were a kind gift of the lab of Andrew Murray (Harvard University). yMM8 and yMM9 both have a point mutation, CYH2::cyh2-Q37E, causing resistance to the translational inhibitor cycloheximide (Table 1). yJK22 is similar to yMM8 but featuring a HygMX-cassette, conveying resistance to the drug hygromycin B, instead of the CYH2 mutation. yJK22 was constructed from yJHK111 via integration of the HygMX-cassette from plasmid pAG32 (see https://www.addgene.org/35122/ for details). Note that the “mutant” (yJK22) and “wild-type” (yMM9) designations used in this paper refer to the mimicked scenario of a costly drug resistance mutation and not to the genotypes of the involved strains.
Yeast competition assays.
Unless otherwise specified, experiments are based on linear inoculations competing the strains yMM9 (“wild-type”) and yJK22 (“mutant”). Of these strains, only yJK22 is susceptible to the translational inhibitor cycloheximide, allowing us to impose a growth-rate deficit on yJK22 cells. All experiments were conducted in the presence of 90 nM cycloheximide, resulting in fitness difference of s = −0.06, as quantified previously [23].
s is defined via the ratio of strain-specific doubling rates k as s = kmutant/kwild-type −1. Neutral controls were conducted by substituting yJK22 with yMM8, with yMM8 exhibiting growth rates equal to that of yMM9 [23].
Linear colonies for the wide sector assays were inoculated by running a gravity-pulled droplet (10μL) of concentrated yJK22 culture (OD600 > 10) across an inclined agar plate (YPD, 1% (w/v) agar). Subsequent air drying produced a dense continuous layer of cells at the periphery of the wetted area (“coffee stain effect”). To produce mutant (yJK22) sectors flanked by wild-type (yMM9) regions (see Supplementary Fig. S1), sections of the linear yJK22 inoculum, several hundreds of micrometers apart, were removed by rolling a sterile glass bead across the front, lifting cells from the surface. The resulting gaps were filled by concentrated yMM9 culture. We conducted competitions assays in replicate on a total of 8 linear colonies on 4 plates, with each having an average number of 5 sectors. Generally, colonies were grown in an incubator and temporally transfered to the microscope for imaging. Time-lapse measurements with high spatial and temporal resolution were conducted in a temperature controlled chamber (Ibidi, Germany).
Imaging and analysis.
Sector boundaries serve as a record of past front compositions, allowing us to infer the spatio-temporal progression of a clone from a single fluorescence microscopy image [31, 23]. Mutant sectors were imaged on a Axio Zoom.V16 upright fluorescence microscope using the ZEN (2012, blue edition) acquisition software (Carl Zeiss, Germany). Depicted image use a non-linear intensity profile (gamma factor of 0.5) to allow for simultaneous visualization of all features. Image processing was performed using Fiji [51].
To quantify sector extension we first obtained the point of extinction anticipated from the null model by extending the linear trajectories exhibited by boundaries of clones wider than wc = 230μm (see below for details on the evaluation of wc). We then measured the experimentally observed extend of the sector by identifying the position of the most forward fluorescent signal, taking the major axis of the sector as definition for the direction of forward propagation. As a reference point for sector alignment and length calculations we used the front position yc = y(w = wc) := 0. Sector extension was then calculated as the difference between the extinction point expected from the null model and the experimentally observed sector lengths. For 9 sectors (shown in Supplementary Fig. S2 ) from 2 separate colonies we further evaluated the position dependent width w(y) as described below, yielding the results displayed in Fig. 2f, g.
Evaluation of w and wc.
The width of a sector w(y) is measured perpendicular to the axis of colony expansion and as a function of position y along the same axis. Measurements were taken from the complete sector at the end of the experiment by tracing the sector boundaries via a custom built, semiautomated algorithm developed in MATLAB (R2015a). To compare the lengths and widths of individual sectors it is necessary to align them to a common, globally defined reference width. Throughout this work, sectors in assays starting with wide section of the slower-growing cell type were aligned to the characteristic width wc below which the observed sector shape departed from its anticipated linear behavior. To evaluate wc we applied a linear fit to the initial straight boundary trajectory and calculated the difference δ(w) between the observed sector width and the linear fit for the sectors shown in Supplementary Fig. S2. This value is independent of sector alignment and can be averaged over all sectors (Supplementary Fig. S3 a). wc can then be defined as the width of a sector at which δ(w) exceeds a predefined threshold δc. Here, we chose δc = 5μm. The so obtained alignment of sectors is robust against variations of δc by a factor of 2 (Supplementary Fig. S3 b)
Single-cell sector assays.
Experiments tracking the fate of sectors originating from single cells (Fig. 4) were set up in a fashion similar to the wide-sector assays described above. Here, colonies were inoculated from a mixture of yMM9 containing a small fraction (5%) of yJK22. Cell separations was ensured by briefly sonicating the mixed culture prior to deposition. For the neutral control, we ran parallel experiments substituting yJK22 with yMM8. To verify neutrality we repeated these experiments, inverting the ratio of yMM8 to yMM9. We initially observed a total number of approx. 3500 sectors (in a total of 12 colonies) which, for s = −0.06, eventually decayed to 0 within the course of the experiment. Front-persistence probabilities (Pfront) were obtained by identifying fluorescent regions via a custom segmentation algorithm, based on local intensity gradient peaking, developed in MATLAB (R2015a).
Evolutionary rescue assays.
In a subset of colonies of the single-cell sector assay we halted wild-type growth by application of Hygromycin B. To this end, a line of 50mM Hygromycin B in medium (70μL total volume) was pipetted approximately 5 mm in front of the leading colony edge. The drug then dispersed via diffusion and local concentrations were sufficient to completely halt wildtype progression while allowing for continued growth of the mutant. The colony depicted in Fig. 4e and f exhibited a total of 8 sectors still at the front after 4 days of growth (the time point of Hygromycin B application), all of which exhibited resurgent growth at day 6.
High curvature inoculations.
Experiments with high initial curvature (see Fig. 2d) were initialized by first placing a small droplet (1μL) of culture on an agar substrate followed by air drying. A second droplet of equal volume and from the same culture was subsequently placed adjacent to the first droplet such that its peripheral ring of cell deposition intersects the one of the first droplet. This series of cell depositions created an initial front with a high radius of curvature at the intersection points.
Cell-tracking.
In single-cell scale time lapse movies, individual cells were tracked visually using custom MAT-LAB (R2015a) scripts. For images in Fig. 2b (and accompanying Supplementary movie S9), t = 0min is defined approximately 3 days after inoculation. To assess the relation between cell velocity and local curvature κ in curved inoculations, the instantaneous velocities were computed from individual cell tracks as a function of the local curvature, which was obtained from the smoothed front position y(x) of the colony as
| (1) |
Particle image velocimetry.
To find the local speed inside yeast colonies, Supplementary Video S5 of growing S. cerevisiae fronts were analyzed using particle image velocimetry (PIV) using the ImageJ PIV plugin [54]. Seven pairs of images, each pair taken one minute apart, were analyzed with a ∼8μm window size. To find the local speed as a function of distance from the (moving) colony front, images of the front at each time point were binarized to find the position of the front. Displacements in the growth direction were averaged along the direction perpendicular to the growth direction, shifted to account for the moving front position, and then averaged across image pairs to produce Fig. 3f. Supplementary Video S5 shows the expanding front after approximately 2h after start of expansion when the colony is still very thin. This allows for the tracking of features deep within the colony. Note that at this time point the growth layer has not yet reached its final profile. Refer to Supplementary Fig. S7 for data on the fully established growth layer.
E. coli colonies.
Colonies of E. coli were grown on plates of M9 minimal media containing 2% agar from a 1:1 mixture of strains MG1655 and the derivative SJ102 (fluorescently labeled; s = −0.04±0.03 as measured from N = 17 colony collision events [23]), which are non-motile under in the given conditions. Colonies were imaged after 5 days.
Verification of constant relative fitness.
The relative fitness between strains with the wild-type and resistant alleles of the CYH2 for the group of strains used in this study (with yJHK111 as the direct ancestor of yJK22) has been previously quantified as a function of cycloheximide concentration using liquid culture competition and colony collision assays[23]. The concentration of 90 nM used in this study corresponds to a fitness effect of s = kCYH2/kcyh2r − 1 = −0.06, with kCYH2 and kcyh2r indicating the doubling rates of the susceptible and resistant strains, respectively. To measure that the relative fitness remained constant over the course of our experiments, we measured the front velocities of colonies composed of the individual strains (as calculated from the width increase of linear monoclonal colonies). Fig. S8ac shows how front speeds generally decline over time as nutrients become depleted. However, the ratio of expansion velocities (Fig. S8d), the basis for competition, remains constant. While expansion speed assays might not be equivalent to measurements in liquid culture (see [31]), they here serve to verify the consistency of relative fitness in conditions equivalent to those applied in our competition assays.
Description of surface tension model.
Here we describe a phenomenological surface growth model, which we refer to as the “surface tension model”, where the population is modeled as a 1D surface with height h(x) that moves forward at velocities that are normal to the surface (Supplementary Fig. S11a). Each point on the surface moves at a velocity ν that is modulated by the local front curvature κ via an effective “surface tension” term T
| (2) |
where vtype is the cell type-specific velocity of a flat front.
Assuming that flat front velocities are proportional to the cellular growth rate of cells at the surface (Supplementary Fig. S11b), then forward velocities of a front composed purely of wild-type or mutant cells have separable selection (vtype = v0 for wild-type, vtype = (1+s)v0 for mutant) and surface tension (1 + Tκ) contributions
| (3) |
where v0 is the velocity of a flat front composed of wild-type cells. Eq. 3 describes the competition of adjacent phenotypes, in which case vtype changes discontinuously from vtype = v0 to vtype = (1 + s)v0 across the wild-type/mutant boundary. The wild-type/mutant boundary evolves in time, following the surface normal of the propagating front.
Parameterization of surface tension model.
To compare this surface tension model to S. cerevisiae experiments, we compare the decrease in width for initially-wide deleterious clone, shown in Fig. 1d for experiments. Initializing the surface tension model with a slanted front designed to be consistent with the null model (Supplementary Fig. S9), we find a funnel-like tapering of the deleterious clone as we found for experiments. The spatial extent of this deleterious tapering varies with surface tension T, and we find that the model best matches experiments with a surface tension of T = 25μm (Supplementary Fig. S13).
Stochasticity in interface models.
To incorporate stochasticity into the surface tension and null models, we have added diffusive boundary fluctuations along the front with a diffusion coefficient D. The mean-square displacement of boundaries is therefore Δx2 = DΔy in a neutral scenario on a flat front. Simulation results matched experimentally observed persistence probabilities best for D = 0.025μm (see Fig. 4d), which is significantly lower than what we had previously measured from single cell traces (D=0.3μm (calculated from a diffusive fit to the data in Fig. 3f of reference [23]). One potential reason for this difference is that the persistence times, the basis for our fit, are governed by the fluctuations of clone width rather than those of the individual boundary position in real space. It is conceivable that the assumption of independent diffusive behavior of the sector boundaries breaks down at small length scales due to the granularity of the system. Indeed, the single-cell traces shown in Fig. 2b suggest a certain degree of correlation in the positional noise of neighboring cells, resulting in a width dependence of sector width fluctuations.
Description of the cell-based model.
The cell-based model is based on simulations developed in [10] where budding cells are modeled as 2D frictionless disks (mother and bud) that are fused together. In this model, cells increase in area at rate γi by bud expansion (Eq. 17), move according to over-damped dynamics with mobility μ (Eqs. 18 and 19), and interact via repulsive spring forces with elastic modulus k (Eq. 20) as described in [52]
| (4) |
| (5) |
| (6) |
| (7) |
where is the area of cell i, σi,mother and σi,bud are the diameter of the mother and bud, ri is the cell position, θi is the cell orientation, mi is the cell mass, with Δi = σi,bud/σi,mother is the cell inertia, V is the total potential energy, Fi = −∇riV is the force on cell i, is the torque on cell i, is the overlap between lobes k of cell i and l of cell j, and Θ is the unit step function. Each mother lobe has diameter σi,mother = σ. Equations of motions are integrated using a 3rd order Gear Predictor-Corrector algorithm. Growth progresses while σi,bud < σ and culminates in division. After division, both new cells are oriented inward (axial division) with buds facing each other.
In this study, we further developed the simulations described in [10] so that cell populations growth in 2D colonies where only cells in a “growth layer” of depth λ near the edge actively grow. To calculate the growth layer depth, we first find all cells in the front. We then classify cells as being in the growth layer if they are within λ of any cell in the front. The resulting dynamics is shown in movie S6 for the neutral case (s = 0) and movie S2 for a deleterious clones (s = −0.06), both with λ = 45μm.
Boundary conditions in the cell-based model.
We utilize three different boundary conditions, illustrated in Supplementary Fig. S12. In Fig. 3h, we use open boundary conditions so that the colony grows radially in all directions. In Fig. 3c and f, we use periodic boundary conditions in the horizontal direction. In Fig. 3i, we use “wedge” boundary conditions, in which mutants occupy a large flat portion of the front and is bordered by regions composed of WT cells that are rotated at a tilt angle consistent with the non-mechanical model.
Parameterization of cell-based model.
To obtain a value for λ, we compare the decrease in width for initially-wide deleterious clone to S. cerevisiae experiments (shown in Fig. 1b). Initializing the cell-based model with a slanted front, we find a funnel-like tapering of the clone where the tapering length-scale increases with growth layer depth λ. Using a cell diameter of σ = 5μm, the cell-based model best matches experiments with λ = 45μm (Supplementary Fig. S14). To constrain the number of cells included in time-integration, we fix the position of cells further behind the front than 80μm. Note that the growth layer depth used for cell-based simulations refers to an idealized “effective” growth layer. It might therefore not directly reflect the depth up to which cell movement is observed in experimental colonies where additional factors, such as out-of-plane growth, nutrient absorption and diffusion or cell elasticity, influence the details of growth layer dynamics.
We use a mobility of μ = 4×103k−1γ and time-step of dt = 5×10–6γ−1 for time-integration. In Supplementary Fig. S14, we use a initial box width of 4mm and an initial clone mutant width of 2mm. The growth rates we use for mutant and wild-type cells are averaged growth rates, but we apply a variation on the growth rate of 20% in order to avoid synchronization in the cell cycle.
Description of Eden model.
In the Eden model [11] simulations, space is divided into a two-dimensional square grid, whose voxels can be empty, wild type, or mutant type. In general, each voxel represents a subpopulation, called deme, consisting of multiple individuals, and the lattice size a is a model parameter that characterizes the spatial extent of a deme.
The grid is initialized by either placing mutants and wild type at initial ratio 1:10 in a line at one end of the lattice (to measure extinction speed) or in a slanted half-space configuration (see Supplementary Fig. S9a), where the angle is chosen according to the non-mechanical expectation. In each step, we choose a voxel i that has at least one empty neighbor and one of its empty neighboring voxels j at random. The state of i is copied into j. The probability of choosing voxel of different types (wild-type vs. mutant) is proportional to their growth rate. A generation corresponds to a number of steps equal to the number of voxels that have at least one empty neighbor at the beginning of the generation.
Description of Stepping-stone model.
We perform individual-based, stepping stone simulations where both wild-type and mutants are modeled explicitly. The population is divided into demes with carrying capacity K = 10 on a two-dimensional lattice (10 individuals per deme). Each simulation step consists of a replication step and a migration step:
Replication Step. In this step, an individual located in a non-full deme is picked proportionally to its growth rate r (1 for wild-type and 1−s for mutants). A second “spot” among the K−1 in the same deme is picked at random, regardless of its type (wild-type, mutant or empty). The individual selected first is then copied in the “spot”. This process leads to logistic growth within deme.
Migration Step. Similarly to the replication step, an individual located in a non-full deme is picked according to a diffusion constant and copied in a random “spot” in a neighboring deme. Constraining the migration rate to be proportional to the replication rate takes into account that in a microbial colony movement is generated by growth.
The simulations are initialized with a slanted profile similar to that shown in Supplementary Fig. S9b. Mutants occupy a rectangular region with initial width w = 200 cells, while the wild-type fills the slanted surrounding regions. The angle α characterizing the slanted profile corresponds to the asymptotic angle predicted by the ETA argument.
Description of noise-less reaction-diffusion simulations
We numerically solve the following system of reaction-diffusion equations by discretizing space on a two-dimensional square grid and time:
where wt and m represent the wild-type and mutant concentrations, respectively, D is the diffusion constant, r is the replication rate of the wild-type and s is the selective coefficient associated with the mutant.
The simulations are initialized with a slanted profile as depicted in Fig. S9b. Boundary conditions are implemented in order to maintain the ETA angle α of the wild-type profile at the edge of the simulation box.
Supplementary Material
Acknowledgements
Research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award R01GM115851, by a National Science Foundation Career Award (#1555330), by a Simons Investigator award from the Simons Foundation (#327934), by the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02–05CH11231, and by the Berkeley Research Computing program at the University of California, Berkeley. JK acknowledges a Research Scholarship (KA 4486/1–1) awarded by the German Research Foundation (DFG). The authors thank Benjamin Good, Jayson Paulose, Marie-Cécilia Duvernoy, Stephen Martis for vital discussions and the lab of Jasper Rine for invaluable insights on yeast genetics.
Footnotes
Competing interests
The authors declare no competing interests.
Code availability.
Custom codes used in this study are available at https://github.com/Hallatscheklab/collectivemotion.
Data availability.
Imaging data used in this study is available at https://figshare.com/projects/Kayser2018_NatEE/55727.
References
- [1].Amack Jeffrey D. and Manning M. Lisa. Knowing the boundaries: Extending the differential adhesion hypothesis in embryonic cell sorting. Science, 338(6104):212–215, 2012. [DOI] [PubMed] [Google Scholar]
- [2].Andersson Dan I and Hughes Diarmaid. Antibiotic resistance and its cost: is it possible to reverse resistance? Nature Reviews Microbiology, 8(4):260–271, 2010. [DOI] [PubMed] [Google Scholar]
- [3].Asally Munehiro, Kittisopikul Mark, Rué Pau, Du Yingjie, Hu Zhenxing, ağatay Tolga C, Robinson Andra B, Lu Hongbing, Garcia-Ojalvo Jordi, and Süel Gürol M. Localized cell death focuses mechanical forces during 3d patterning in a biofilm. Proceedings of the National Academy of Sciences, 109(46):18891–18896, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Baym Michael, Lieberman Tami D, Kelsic Eric D, Chait Remy, Gross Rotem, Yelin Idan, and Kishony Roy. Spatiotemporal microbial evolution on antibiotic landscapes. Science, 353(6304):1147–1151, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Bell Graham and Gonzalez Andrew. Evolutionary rescue can prevent extinction following environmental change. Ecology letters, 12(9):942–948, 2009. [DOI] [PubMed] [Google Scholar]
- [6].Bertet Claire, Sulak Lawrence, and Lecuit Thomas. Myosin-dependent junction remodelling controls planar cell intercalation and axis elongation. Nature, 429(6992):667, 2004. [DOI] [PubMed] [Google Scholar]
- [7].Bidan Cécile M, Kommareddy Krishna P, Rumpler Monika, Kollmannsberger Philip, Bréchet Yves JM, Fratzl Peter, and Dunlop John WC. How linear tension converts to curvature: geometric control of bone tissue growth. PloS one, 7(5):e36336, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Bosshard Lars, Dupanloup Isabelle, Tenaillon Olivier, Bruggmann Rémy, Ackermann Martin, Peischl Stephan, and Excoffier Laurent. Accumulation of deleterious mutations during bacterial range expansions. Genetics, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Carlson Stephanie M, Cunningham Curry J, and Westley Peter AH. Evolutionary rescue in a changing world. Trends in Ecology & Evolution, 29(9):521–530, 2014. [DOI] [PubMed] [Google Scholar]
- [10].Delarue Morgan, Hartung Jörn, Schreck Carl, Gniewek Pawel, Hu Lucy, Herminghaus Stephan, and Hallatschek Oskar. Self-driven jamming in growing microbial populations. Nat Phys, 12(8):762–766, May 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Eden Murray. A two-dimensional growth process. Dynamics of fractal surfaces, 4:223–239, 1961. [Google Scholar]
- [12].Excoffier Laurent, Foll Matthieu, and Petit Rémy J. Genetic consequences of range expansions. Annual Review of Ecology, Evolution, and Systematics, 40:481–501, 2009. [Google Scholar]
- [13].Excoffier Laurent and Ray Nicolas. Surfing during population expansions promotes genetic revolutions and structuration. Trends in ecology & evolution, 23(7):347–351, 2008. [DOI] [PubMed] [Google Scholar]
- [14].Farhadifar Reza, Röper Jens-Christian, Aigouy Benoit, Eaton Suzanne, and Jülicher Frank. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Current Biology, 17(24):2095–2104, 2007. [DOI] [PubMed] [Google Scholar]
- [15].Farrell FDC, Hallatschek Oskar, Marenduzzo D, and Waclaw B. Mechanically driven growth of quasi-two-dimensional microbial colonies. Physical review letters, 111(16):168101, 2013. [DOI] [PubMed] [Google Scholar]
- [16].Farrell Fred D, Gralka Matti, Hallatschek Oskar, and Waclaw Bartlomiej. Mechanical interactions in bacterial colonies and the surfing probability of beneficial mutations. Journal of The Royal Society Interface, 14(131):20170073, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Foty Ramsey A. and Steinberg Malcolm S. The differential adhesion hypothesis: a direct evaluation. Developmental Biology, 6(1):255–263, 2005. [DOI] [PubMed] [Google Scholar]
- [18].Friedman Jonathan and Gore Jeff Ecological systems biology: The dynamics of interacting populations. Current Opinion in Systems Biology, 1:114–121, 2017. [Google Scholar]
- [19].Fusco Diana, Gralka Matti, Kayser Jona, Anderson Alex, and Hallatschek Oskar Excess of mutational jackpot events in expanding populations revealed by spatial luria-delbruck experiments. Nature communications, 7, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Gagneux Sebastien, Long Clara Davis, Small Peter M, Van Tran, Schoolnik Gary K, and Bohannan Brendan JM The competitive cost of antibiotic resistance in mycobacterium tuberculosis. Science, 312(5782):1944–1946, 2006. [DOI] [PubMed] [Google Scholar]
- [21].Giometto Andrea, Nelson David R, and Murray Andrew W Physical interactions reduce the power of natural selection in growing yeast colonies. bioRxiv, page 332700, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Golding Ido, Kozlovsky Yonathan, Cohen Inon, and Ben-Jacob Eshel . Studies of bacterial branching growth using reactiondiffusion models for colonial development. Physica A: Statistical Mechanics and its Applications, 260(3):510–554, 1998. [Google Scholar]
- [23].Gralka Matti, Stiewe Fabian, Farrell Fred, Moebius Wolfram, Waclaw Bartlomiej, and Hallatschek Oskar Allele surfing promotes microbial adaptation from standing variation. Ecology Letters, 19(8):889–898, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Hallatschek Oskar, Hersen Pascal, Ramanathan Sharad, and Nelson David R Genetic drift at expanding frontiers promotes gene segregation. Proceedings of the National Academy of Sciences, 104(50):19926–19930, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Hallatschek Oskar and Nelson David R Life at the front of an expanding population. Evolution, 64(1):193–206, 2010. [DOI] [PubMed] [Google Scholar]
- [26].Otwinowski J and Krug J Clonal interference and muller’s ratchet in spatial habitats. Physical Biology, 11(5):056003, 2014. [DOI] [PubMed] [Google Scholar]
- [27].Kardar Mehran, Parisi Giorgio, and Zhang Yi-Cheng Dynamic scaling of growing interfaces. Physical Review Letters, 56(9):889, 1986. [DOI] [PubMed] [Google Scholar]
- [28].Ke Wan-Ju, Hsueh Yi-Huang, Cheng Yu-Chieh, Wu Chih-Ching, and Liu Shih-Tung Water surface tension modulates the swarming mechanics of bacillus subtilis. Frontiers in Microbiology, 278(1017), 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Klapper I and Dockery J Finger formation in biofilm layers. SIAM Journal on Applied Mathematics, 62(3):853–869, 2002. [Google Scholar]
- [30].Kirill S Korolev, Avlund Mikkel, Hallatschek Oskar, and Nelson David R . Genetic demixing and evolution in linear stepping stone models. Reviews of modern physics, 82(2):1691, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Korolev Kirill S, Müller Melanie JI, Karahan Nilay, Murray Andrew W, Hallatschek Oskar, and Nelson David R Selective sweeps in growing microbial colonies. Physical biology, 9(2):026008, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Korolev Kirill S, Xavier Joao B, and Gore Jeff Turning ecology and evolution against cancer. Nature Reviews Cancer, 14(5):371–380, 2014. [DOI] [PubMed] [Google Scholar]
- [33].Korolev Kirill S., Xavier Joo B., Nelson David R., and Foster Kevin R. A quantitative test of population genetics using spatiogenetic patterns in bacterial colonies. The American Naturalist, 178(4):538–552, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Lambert Guillaume, Estévez-Salmeron Luis, Oh Steve, Liao David, Emerson Beverly M, Tlsty Thea D, and Austin Robert H An analogy between the evolution of drug resistance in bacterial communities and malignant tissues. Nature Reviews Cancer, 11(5):375, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Lambert Guillaume and Kussell Edo Memory and fitness optimization of bacteria under fluctuating environments. PLoS genetics, 10(9):e1004556, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Lamprecht Sebastian, Schmidt Eva Marina, Blaj Cristina, Hermeking Heiko, Jung Andreas, Kirchner Thomas, and Horst David Multicolor lineage tracing reveals clonal architecture and dynamics in colon cancer. Nature Communications, 8(1):1406, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Lavrentovich Maxim O, Korolev Kirill S, and Nelson David R Radial domany-kinzel models with mutation and selection. Physical Review E, 87(1):012103, 2013. [DOI] [PubMed] [Google Scholar]
- [38].Lavrentovich Maxim O, Wahl Mary E, Nelson David R, and Murray Andrew W Spatially constrained growth enhances conversional meltdown. Biophysical Journal, 110(12):2800–2808, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Lecuit Thomas and Lenne Pierre-Francois Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nature Reviews Molecular Cell Biology, 8(8):633, 2007. [DOI] [PubMed] [Google Scholar]
- [40].Lindsey Haley A, Gallie Jenna, Taylor Susan, and Kerr Benjamin Evolutionary rescue from extinction is contingent on a lower rate of environmental change. Nature, 494(7438):463, 2013. [DOI] [PubMed] [Google Scholar]
- [41].Lisa Manning M, Foty Ramsey A., Steinberg Malcolm S., and Schoetz Eva-Maria Coaction of intercellular adhesion and cortical tension specifies tissue surface tension. Proceedings of the National Academy of Sciences, 107(28):12517–12522, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Martens Erik A, Kostadinov Rumen, Maley Carlo C, and Hallatschek Oskar Spatial structure increases the waiting time for cancer. New journal of physics, 13(11):115014, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Matsushita Mitsugu and Fujikawa Hiroshi Diffusion-limited growth in bacterial colony formation. Physica A: Statistical Mechanics and its Applications, 168(1):498–506, 1990. [Google Scholar]
- [44].Mertz Aaron F., Banerjee Shiladitya, Che Yonglu, German Guy K., Xu Ye, Hyland Callen, Marchetti M. Cristina, Horsley Valerie, and Dufresne Eric R. Scaling of traction forces with the size of cohesive cell colonies. Phys. Rev. Lett, 108:198101, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Meunier Jean-Roch and Choder Mordechai Saccharomyces cerevisiae colony growth and ageing: biphasic growth accompanied by changes in gene expression. Yeast, 15(12):1159–1169, 1999. [DOI] [PubMed] [Google Scholar]
- [46].Muüller Melanie JI, Neugeboren Beverly I, Nelson David R, and Murray Andrew W Genetic drift opposes mutualism during spatial population expansion. Proceedings of the National Academy of Sciences, 111(3):1037–1042, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Nadell Carey D, Drescher Knut, and Foster Kevin R Spatial structure, cooperation and competition in biofilms. Nature Reviews Microbiology, 14(9):589, 2016. [DOI] [PubMed] [Google Scholar]
- [48].Nadell Carey D, Foster Kevin R, and Xavier Joao B Emergence of spatial structure in cell groups and the evolution of cooperation. PLoS computational biology, 6(3):e1000716, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Nguyen Baochi, Upadhyaya Arpita, Alexander van Oudenaarden, and Michael P Brenner. Elastic instability in growing yeast colonies. Biophysical journal, 86(5):2740–2747, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Peischl S, Dupanloup I, Kirkpatrick M, and Excoffier L On the accumulation of deleterious mutations during range expansions. Molecular Ecology, 22(24):5972–5982, 2013. [DOI] [PubMed] [Google Scholar]
- [51].Schindelin Johannes, Arganda-Carreras Ignacio, Frise Erwin, Kaynig Verena, Longair Mark, Pietzsch Tobias, Preibisch Stephan, Rueden Curtis, Saalfeld Stephan, Schmid Benjamin, et al. Fiji: an open-source platform for biological-image analysis. Nature methods, 9(7):676, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Schreck Carl F., Xu Ning, and O’Hern Corey S. A comparison of jamming behavior in systems composed of dimer- and ellipse-shaped particles. Soft Matter, 6:2960–2969, 2010. [Google Scholar]
- [53].Smith William PJ, Davit Yohan, Osborne James M, Kim Wook, Foster Kevin R, and Pitt-Francis Joe M Cell morphology drives spatial patterning in microbial communities. Proceedings of the National Academy of Sciences, page 201613007, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Tseng Qingzong, Duchemin-Pelletier Eve, Deshiere Alexandre, Balland Martial, Guillou Hervé, Filhol Odile, and Théry Manuel Spatial organization of the extracellular matrix regulates cell–cell junction positioning. Proceedings of the National Academy of Sciences, 109(5):1506–1511, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Váchová Libuše and Palková Zdena How structured yeast multicellular communities live, age and die? FEMS yeast research, 18(4):foy033, 2018. [DOI] [PubMed] [Google Scholar]
- [56].Dyken J David Van, Müller Melanie JI, Mack Keenan ML, and Desai Michael M Spatial population expansion promotes the evolution of cooperation in an experimental prisoners dilemma. Current Biology, 23(10):919–923, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Vopálenská Irena, Hůlková Marta, Janderová Blanka, and Palková Zdena The morphology of saccharomyces cerevisiae colonies is affected by cell adhesion and the budding pattern. Research in microbiology, 156(9):921–931, 2005. [DOI] [PubMed] [Google Scholar]
- [58].Wahl Mary E and Murray Andrew W Multicellularity makes somatic differentiation evolutionarily stable. Proceedings of the National Academy of Sciences, page 201608278, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Wang Xin, Stone Howard A, and Golestanian Ramin Shape of the growing front of biofilms. New Journal of Physics, 19(12):125007, 2017. [Google Scholar]
- [60].Waters Jonathan M, Fraser Ceridwen I, and Hewitt Godfrey M Founder takes all: density-dependent processes structure biodiversity. Trends in Ecology & Evolution, 28(2):78–85, 2013. [DOI] [PubMed] [Google Scholar]
- [61].Weinstein Bryan T, Lavrentovich Maxim O, Möbius Wolfram, Murray Andrew W, and Nelson David R Genetic drift and selection in many-allele range expansions. PLoS computational biology, 13(12):e1005866, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Weissman Daniel B, Desai Michael M, Fisher Daniel S, and Feldman Marcus W The rate at which asexual populations cross fitness valleys. Theoretical population biology, 75(4):286–300, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Yan Jing, Nadell Carey D, Stone Howard A, Wingreen Ned S, and Bassler Bonnie L Extracellular-matrix-mediated osmotic pressure drives vibrio cholerae biofilm expansion and cheater exclusion. Nature communications, 8(1):327, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Yan Jing, Sharo Andrew G, Stone Howard A, Wingreen Ned S, and Bassler Bonnie L Vibrio cholerae biofilm growth program and architecture revealed by single-cell live imaging. Proceedings of the National Academy of Sciences, 113(36):E5337–E5343, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.