Abstract
Plasma glucose in mammals is regulated by hormones secreted by the islets of Langerhans embedded in the exocrine pancreas. Islets consist of endocrine cells, primarily α, β, and δ cells, which secrete glucagon, insulin, and somatostatin, respectively. β cells form irregular locally connected clusters within islets that act in concert to secrete insulin upon glucose stimulation. Varying demands and available nutrients during development produce changes in the local connectivity of β cells in an islet. We showed in earlier work that graph theory provides a framework for the quantification of the seemingly stochastic cyto-architecture of β cells in an islet. To quantify the dynamics of endocrine connectivity during development requires a framework for characterizing changes in the probability distribution on the space of possible graphs, essentially a Fokker-Planck formalism on graphs. With large-scale imaging data for hundreds of thousands of islets containing millions of cells from human specimens, we show that this dynamics can be determined quantitatively. Requiring that rearrangement and cell addition processes match the observed dynamic developmental changes in quantitative topological graph characteristics strongly constrained possible processes. Our results suggest that there is atransient shift in preferred connectivity for β cells between 1–35 weeks and 12–24 months.
Keywords: pancreatic islets, beta cells, cyto-architecture
1. Introduction
Insulin, an essential hormone for cellular glucose uptake and hence, arguably, the key factor in the regulation of plasma blood glucose concentration, is produced by pancreatic islet β cells. Blood glucose homeostasis does not fall solely on the shoulders of β cells. Other pancreatic islet cells, such as glucagon-producing α cells and somatostatin-producing δ cells, play critical roles in its regulation. Although not electrically coupled, these cells can normally be found in the periphery around a core β-cell cluster in rodent and small (effective diameter <60 microns) human islets.
The architectural arrangement of cells in larger human islets differs from that of small islets in that α and δ cells intermingle with β cells. This cyto-architecture was first described as mantle-core subunits [1] or lobules [2]. Since then it has been described as a ribbon-like structure [3], a cloverleaf [4] and a trilaminar plate [5]. However, there is evidence for alternative structures [6] and the placement of endocrine cells in islets maybe random [7,8] or non-random [9,10].
The correct anatomical arrangement of β cells in their clusters and, possibly, of α and δ cells in relation to these clusters is essential for optimal production of insulin as β cells work more efficiently when in contact [11–13]. Clustering allows electrical coupling between neighboring cells, achieved through gap junction proteins (Cx36) [14,15] found on the cell surface, and this interaction leads to the observed 2-fold increase in insulin production when β cells are in a cluster compared to when they are isolated [16]. Gap junction coupling has not been proven in αα-αδ-, or δδ-cell interactions, though neighboring cells modulate activity through autocrine and paracrine interactions [17]. Given this, the optimal functional arrangement is controversial as islets are irregular in shape, sample sizes are typically quite small, and quantitative characterizations of their stochastic morphology have not been adequately developed.
β cell mass and its associated architecture is dynamic and adaptable to changes in energy needs, for example, during pregnancy [18], and changes in nutrient availability, as in obesity [19, 20]. During development, humans have changing energy needs and available nutrients, and this may also impact pancreatic islet cyto-architecture. We consider the following division of the stages of development: gestation, 1–35 weeks after birth, 12–24 months after birth and 28 months and after. During gestation most glucose is absorbed through the placenta from the mother along with endocrine hormones. After birth, during 1–35 weeks, infants are either breast- or formula-fed. In the period 12–24 months, children are eating solids, though a diet with liberal intake of unsaturated fat ensuring adequate intakes of omega-3 fatty acids is recommended [21]. In the last stage, the dietary difference between an adult and a child is minimal [21,22].
Stochastic graph theory, with its quantitative measures of neighborhood characteristics, provides an unbiased and mathematically rigorous framework for deciphering key architectural features found in islets. However, applications of graph theory to islet biology require data on the endocrine cell content and placement in a large number of islets, as the quantitative measures will display large fluctuations for small sample sizes. In previous work, with large-scale imaging data, this technique was used to quantify differences between human control and type 2 diabetic (T2D) β-cell cluster cyto-architecture. Surprisingly, the quantitative results suggested an increase in β-cell connectivity and number of β cells per cluster and a decrease in the number of clusters in T2D islets as compared to control islets. This could be an indication that the T2D environment needs higher connectivity for β cell survival compared to control. Graph theory was also used by Stozer et al [23] to analyze the small world activity of β cells in islets.
Given that β cell mass is dynamic, a natural question arises: How is optimal β cell function, as evidenced in islet cyto-architecture, regulated, given changes in energy needs and resources? Alternatively phrased, given a set of graphs representing β cell cyto-architecture, what stochastic processes acting on graphs, if any, can recapitulate changes in graph measures observed between developmental stages? The crux of this approach, proving the existence of such processes, was illustrated in [24] where an optimal stochastic model of vertex addition and deletion was found for maintaining the architecture observed in a large set of control and diabetic islet graphs. Using a simple analogy, the former descriptive quantification is akin to modeling a set of normally distributed random numbers by calculating their mean and standard deviation, and this latter dynamic view is similar to determining the Ornstein-Uhlenbeck process that would maintain the observed distribution.
Here, we have access to dynamic data in the form of islets from subjects with a wide range of ages. This is obviously not in the form of sequential time measurements, but can be grouped in four age intervals to preserve a balance between continuity in time and a sufficiency of data for each age interval. Thus, in the language of stochastic processes, we can roughly determine the non-equilibrium processes producing changes in the probability distribution on the space of graphs representing β cell cyto-architecture even though the partial time-derivative in the Fokker-Planck equation is replaced by the rough substitution of a discrete time step between age intervals. Therefore, we first use graph theory to shed light on the placement of α and δ cells relative to β cell clusters by quantifying the cyto-architecture found in β cell clusters, the non-β cells, and the interactions between the clusters and non-β cells at each developmental stage. With this quantification in hand, we go beyond the static equilibrium in islet graph architecture that we found in [24], to elucidate the dynamic processes underlying observed architectural differences between developmental stages. This, to our knowledge, is the first use of data to determine a time-dependent stochastic process on a space of graphs in the context of biology.
2. Methods
2.1. Data acquisition
Human pancreatic tissues were obtained from the University of Chicago Human Tissue Resource Center with an exemption from the Institutional Review Board. The two-dimensional sections were stained for insulin, glucagon, somatostatin and nuclei. Cells were labeled based on the hormone concentration surrounding each nucleus determining the cellular composition of each islet.
2.2. Graph creation
Graphs consist of vertices and edges. The vertices represent endocrine cells found in each individual islet (a representative islet is shown in figure 1(a)). To define edges between vertices, it is necessary to use the measured spatial separation between two cells to decide if the cells can interact, either by surface interactions or by intercellular signaling. If they can, based on a given neighborhood radius, an edge is added to the graph connecting the vertices corresponding to the two cells. The graphs of interest are (1) the β-cell cluster (ββ) graph (figure 1(b)) consisting of vertices representing β cells and edges between neighboring β cells, (2) the αδ graph (figure 1(c)) where vertices represent α and δ cells and edges are between nearby pairs of αα, αδ, and δδ cells, and (3) the αδ -β cell cluster interaction (αδ-β) graph (figure 1(d)) where vertices represent α, β and δ cells and edges are between αβ and βδ cell pairs.
Figure 1.
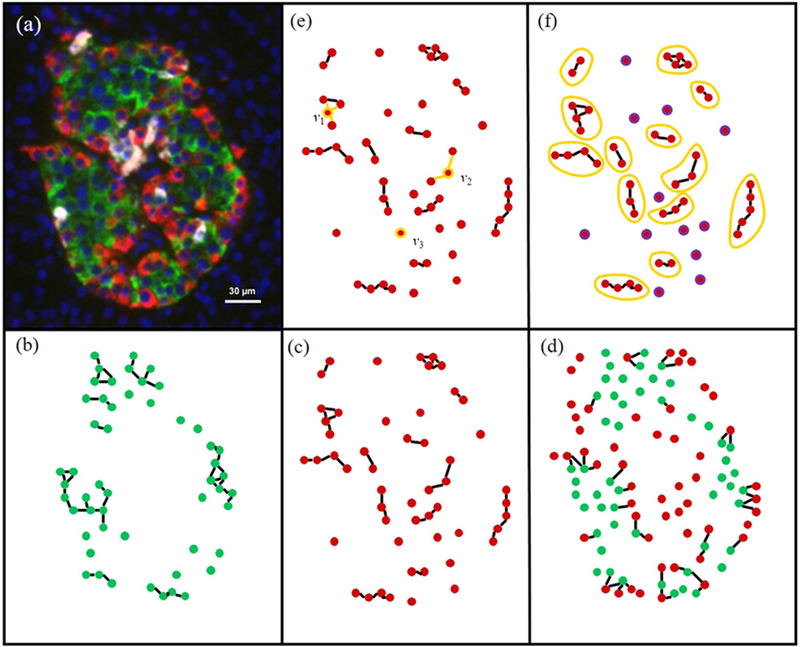
Creating graphs from islets and measure calculations, (a) Representative islet stained for insulin (green), glucagon (red) and nuclei (blue) (δ cells not shown). The three graphs of interest, the ββ (b), the αδ (c), and the αδ-β (d) graphs are shown for a representative large islet (a). The degree (e) and components (f) are two measures used to compute differences between graphs, (e) The degrees of vertices v1, v2, v3 are 3, 2, and 0, respectively, (f) Nonsingular components are enclosed in yellow circles, whereas singular components are in purple.
2.3. Pair correlation function
Knowing the range of intercellular distances that is sufficient and necessary for two cells to interact is critical for an accurate graph representation of surface interactions. Since this range is unknown in pancreatic islets, we determine the critical neighborhood radius based on the data. The pair correlation function, g(r), normalizes the number of cell pairs that are a given distance apart by the density of cells in the islet. For a given r0, if g(r0) is greater (less) than 1 then there are more (less) cell pairs within an intercell distance of r0 than would be expected if the cells were randomly distributed. Because the graphs here do not represent all cell interactions but rather inter- and/or intra- cell-type interactions, we use a slightly modified version of g(r), given by
for two sets, X and Y, where , rij is the distance between vertices i and j, and NX and NY are the number of vertices in sets X and Y, respectively, was used. For the ββ graph which captures interactions between β cells, X and Y both represent the β-cell vertices and NX and NY are the number of β cells. Since the αδ graph captures interactions between α and δ cells, X consists of the α- and δ-cell vertices and Y is the same. NX is the number of α and δ cells and NY is the same. The αδ-β graph represents interactions between the α and δ cells and β-cell clusters. Here X is the set of α- and δ-cell vertices, Yis the set of β-cell vertices, NX is the number of α and β cells and NY is the number of β cells.
2.4. Graph measures
The degree of a vertex (figure 1(e)) in a graph is the number of edges incident on the vertex. A component (figure 1 (f)) is a subgraph of the graph such that each vertex shares an edge with at least one other vertex in the subgraph and this subgraph cannot be decomposed into further subgraphs. Components can be either singular (S), i.e. containing only one vertex, or nonsingular (NS). We used these two measures to quantify islet architecture as viewed through the graphs we defined above. We used the degree averaged over all vertices in a given islet to calculate the mean degree. Component results are shown with respect to the mean number of components (NS + S and NS only) per islet, and the mean number of vertices per component (NS + S and NS only). Computational code was written in C++ using the Boost Graph Library [25].
Since the calculated measures are discrete values the Mann-Whitney test, a nonparametric test for the significance of the difference between the distributions of two independent samples, with a Bonferroni corrections were used to test for significance. The standard deviations of each data point (given in tables S1–S9) are large due to the fact that these values are discrete. The degree, number of components per islet and number of cells per component counts are given in tables S1–9.
2.5. ββ graph transition simulations
ββ graph measures change across developmental stages. Here, we model how the observed architectural alterations occur by taking the graphs corresponding to islets at an initial time and apply parameterized processes to these graphs to determine which process produces the architecture observed in the next developmental stage. The set of processes applied to the initial graphs should encompass (1) any rearrangements known to occur in islets, such as translocation [26–28], replication [29], and death [29], and (2) account for the increase in β cells per islet observed from developmental stage to developmental stage (figure 2(a)).
Figure 2.
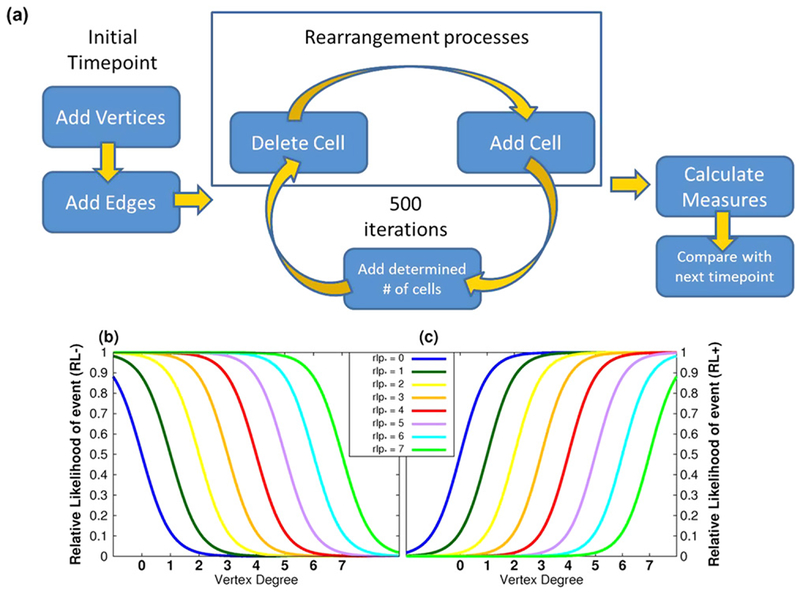
ββ Graph transition simulations determine which stochastic processes take islet graphs from one developmental stage and transform them to match the measures observed in the following developmental dataset, (a) Flowchart of an individual simulation, (b), (c) Relative likelihood functions for adding and deleting cells.
The rearrangement processes were discussed in detail in [24]. In short, these processes assume the deletion of a vertex or addition of a nearby vertex is dependent on the vertex’s degree (an alternate criterion, the size of a vertex’s associated component, was also tried with comparable results; results not shown). It is natural to assume these processes can take place in islets since connectivity and cluster size play a role in optimal insulin production. There is, at this time, no model system where such rearrangements can be observed in vivo. These simulation processes add and delete one vertex per graph during each iteration keeping the number of vertices constant per graph. We consider a number of possible models for the determinants of these rearrangements. In each model, the vertices that are chosen for either deletion or to have a vertex added nearby are chosen by a Monte Carlo approach based on their degree and a relative likelihood function. The first relative likelihood function is given by
where x is the degree of the vertex and rlp* is the given add or delete parameter for the process (see figure 2(b)). For this function higher-degreed vertices are less likely to be picked. The second relative likelihood function, given by
shows that higher-degreed vertices are more likely to be picked (see figure 2(c)). The relative likelihood parameter shifts the range of what is considered a higher-degreed vertex as shown in figures 2(b) and (c). There are two processes, addition and deletion, and two relative likelihood functions, RL− and RL+, resulting in four combinations of (Add, Delete), namely (RL+, RL+), (RL+, RL−), (RL−, RL+) and (RL−, RL−) which will be referred to as PP (plus,plus), PM (plus,minus), MP (minus,plus), and MM (minus, minus), respectively. Thus, the models we consider are defined by these relative likelihood functions and the parameters implicit in these functions.
Thus far we have addressed the rearrangement processes that leave the number of vertices unchanged. However, there is an increase in the number of β cells per islet observed between developmental stages, for which the stochastic process must account. The number of vertices to be added per iteration were calculated so that the resulting mean number of cells per islet matched that of the next developmental stage. For example, there are 199 197 total cells (38 281 total islets) and 176 463 total cells (29 174 total islets) in the gestational and 1–35 weeks datasets (tables 1–3), respectively. During the transition from gestation to 1–35 weeks, the number of cells per islet must increase from 5.20 to 6.05, resulting in the addition of 32 403 cells over a total of 500 iterations. Therefore there are 65 cells added per iteration. The placement of each cell in a chosen islet follows the given relative likelihood function.
Table 1.
Subject and islet count per developmental stage.
| Developmental Stage | #Subjects | #Large Islets | #Small Islets |
|---|---|---|---|
| Gestation | 36 | 8060 | 30 221 |
| 1–35 weeks | 20 | 6486 | 22 688 |
| 12–24 months | 21 | 5182 | 19 823 |
| 28 months+ | 62 | 13 428 | 38 928 |
Table 3.
Small Islet Composition.
| Developmental Stages |
α cells |
β cells |
δ cells |
||||||
|---|---|---|---|---|---|---|---|---|---|
| # cells | # cells/islet | Cell fraction | # cells | # cells/islet | Cell fraction | # cells | # cells/islet | Cell fraction | |
| Gestation | 40 130 | 1.33 | 0.33 | 44 924 | 1.49 | 0.37 | 34 962 | 1.16 | 0.29 |
| 1–35 weeks | 23 976 | 1.06 | 0.26 | 45 494 | 2.01 | 1.04 | 23 567 | 1.04 | 0.25 |
| 12–24 months | 10 904 | 0.55 | 0.13 | 60 134 | 3.03 | 0.70 | 15 315 | 0.77 | 0.18 |
| 28 months+ | 27 218 | 0.70 | 0.17 | 115 923 | 2.98 | 0.71 | 20 429 | 0.52 | 0.12 |
Choosing which islet graphs will have additional vertices is not straightforward. We reasoned that the observed differences in the islet size distributions between developmental stages (figures 3(a)–(c)) should determine the islets gaining cells. For each vertex added, the islet size distribution (Dist(s), where s is the number of vertices per islet) is calculated. The bin-size for the distribution is 1 vertex. Note that figure 3 is shown with respect to log (base 2) of the number of vertices per islet. The difference between this distribution and that of the next developmental stage is given by Diff (s) = Distt0 (s) − Distt1 (s) (figures 3(d)–(f)). This function gives a positive value for excess islets of a given islet size found in the simulated graphs. If an islet of a given size (sm) is chosen, Dist(sm) will decrease and Dist(sm+1) will increase when recalculated. To reduce islet sizes that have excess and to avoid adding to islet sizes that have excess the relative likelihood function RL (s) = Diff (s) − Diff (s + 1) is used for choosing which islet receives an additional vertex. Notice this relative likelihood function is different from those discussed for vertex placement and is updated after each vertex addition. Figures 3(g)–(i) illustrates the size of islets chosen for vertex additions for each transition. The size of the islets chosen correlates with the observed distribution differences for each transition.
Figure 3.
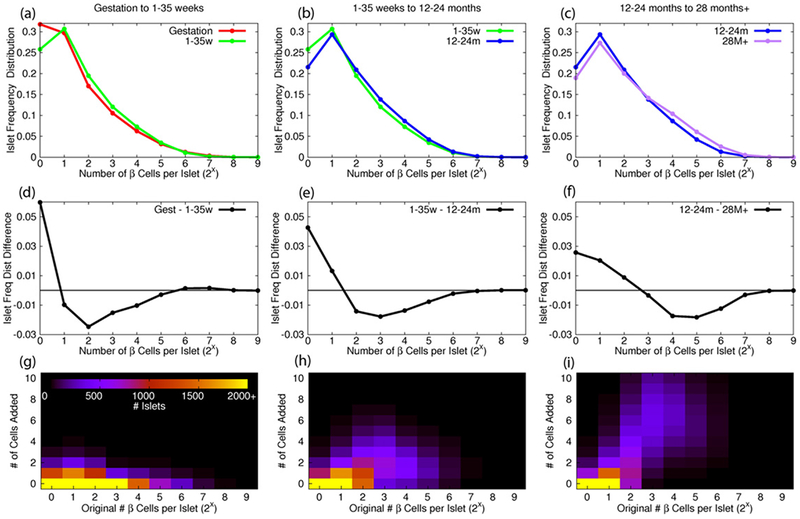
Simulation step representing increase in β cell count per islet observed between developmental stages. Islet graphs for vertex addition were chosen based on differences ((d)–(f)) in the distribution ((a)–(c)) of islets with respect to β cell count from developmental stage to stage. (g)–(i) After running all simulations, the number vertices added to islets of a given size were averaged over all simulations per transition.
In summary, the simulation process consists of 500 iterations, with each iteration consisting of steps where: (1) a vertex is removed from each islet chosen based on the given relative likelihood deletion function and parameter, (2) a vertex is added near a chosen vertex based on the given relative likelihood addition function and parameter, and (3) a determined number of vertices are added to the graph where the islet graph is chosen based on the difference in its islet size distribution and that of the next developmental stage and the placement of the vertex in the chosen islet is based on the given relative likelihood addition function. There are 500 simulations run for each combination of (Add, Delete) relative likelihood functions with relative likelihood addition (rlpa) parameter values ranging from 0 to 7 and relative likelihood death (rlpd) parameter values ranging from 0 to 7, resulting in a total of 128 000 simulations. As a test of convergence, the change in mean and standard deviation for each additional simulation was calculated.
3. Results
3.1. Islet composition
This dataset is comprised of 139 subjects ranging in age from gestation to 28 months and older. There are ~150 000 islets consisting of over 2,000,000 cells. The number of cells, average number of cells per islet and islet cell fraction are shown in table 1 for large and small islets. Over time the average number of β cells increases whereas the average number of δ cells decreases per islet.
3.2. Pair correlations
The pair correlation function was calculated for the three graphs described in Methods. In addition, it was calculated for pairs of the same cell type to see how cells are distributed with respect to the same cell type (supplementary figures S1(a)–(c)), for cell pairs of differing cell types to see how cells are distributed with respect to other cell types (supplementary figures S1(d)–(f)), and for all cell types together (supplementary figure S1(g)).
The pair correlation for the ββ graph (figure 4(a)) is greater than one (more intercell distance pairs than expected if the vertices were randomly distributed) between 7 and 27 microns for the gestation and 7 and 28 microns for the 1–35 weeks groups. There is a decrease in range observed in the 12–24 months and 28 months+ groups which had a range of 7–22 and 7–24 microns, respectively (figure 4(a)). However, all groups show a peak around 10 microns. Similar results are seen between same cell type pairs, such as αα and δδ (supplementary figures S1(a)–(c)). When comparing the pair correlation of β cells with respect to either α or δ cells, there is no peak which means that β cells are randomly distributed with respect to α and δ cells (supplementary figures S1(d) and (f)). However, when the pair correlation of α cells with respect to δ cells is calculated, there is a range of values greater than 1, less pronounced than that observed in the ββ graph (supplementary figure S1(e)).
Figure 4.
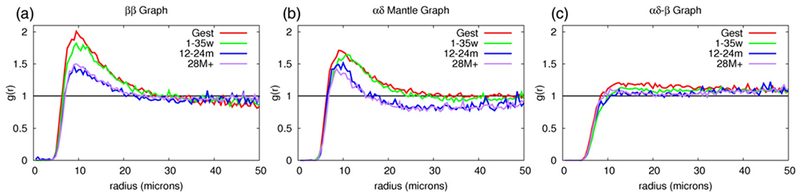
Nonrandom distribution of cells observed in ββ (a) and αδ (b) graphs, unlike the αδ-β graph (c).
The pair correlation for the αδ graph shows a non-random range of values with a peak around 10 microns (figure 4(b)), which is expected since it contains the cell pairs αα, αδ, and δδ, each of which individually showed correlation values greater than one and a peak around 10 microns. In contrast, the αδ-β graph does not have a peak (figure 4(c)) which is consistent with the correlation values seen for the cell pairs αβ and αδ.
3.3. Graph measure results
Since most pair correlation functions calculated here had a peak around 10 microns, this neighborhood radius was used to create all graphs for comparing measure results. The measure values themselves are strongly dependent on the neighborhood radius used (supplementary figures S2–S6). However, the statistical significance of the measure differences between developmental stages is relatively constant for neighborhood radii around 10 microns (supplementary figures S2–S6). Because of this, the focus here is not on the measure values per se but the statistically significant differences observed between developmental stages.
3.3.1. Mean degree
For the ββ graphs there is an increase in mean degree observed between 1–35 weeks and 12–24 months (figure 5(a)). The mean degree transitions between gestation and 1–35 weeks and between 12–24 months and 28 months+ remain rather constant, especially in the large islets between gestation and 1–35 weeks and the small islets between 12–24 months and 28 months+. The αδ graphs show mean degree differences between all developmental stages for all islet sizes (figure 6(a)). However, there is a pronounced decrease in mean degree between 12–24 months and 28 months+. For the αδ-β graphs the mean degree decreases for all islet sizes until 12–24 months (figure 6(d)). This is followed by a further decrease in mean degree in small islets and an increase in mean degree for large islets.
Figure 5.
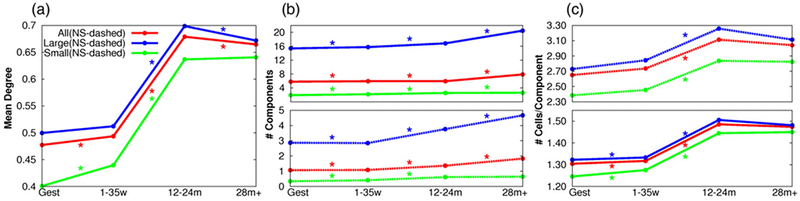
An increase in mean degree (a) and number of vertices per component (c) suggests increased connectivity and β-cell cluster size between 1–35 weeks and 12–24 months. Mean degree (a), number of components perislet (b) and number of vertices per component (c) are given for all (red), large (blue) and small (green) islets for each developmental stage. Component results are shown for S + NS (solid lines) and NS only (dashed lines). * indicates a statistically significant difference using the Mann-Whitney test and a Bonferroni correction (N = 27 (a) and N = 54 (b) and (c)). The standard deviation for each data point is given in tables S1–S3.
Figure 6.
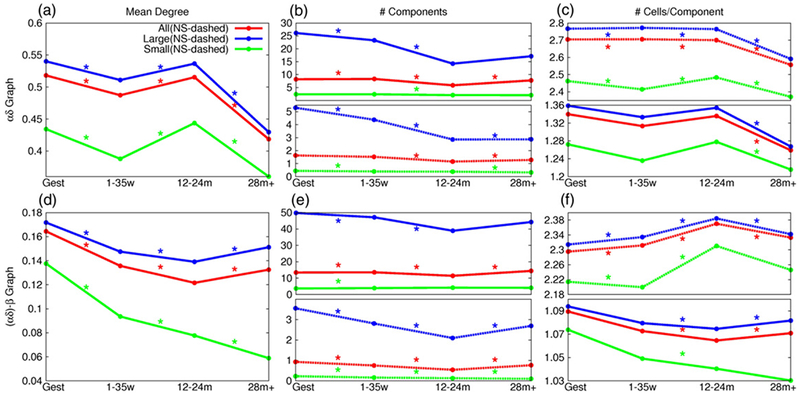
A decrease in mean degree (a) and number of cells per component (c) for the αδ graph suggests decreased connectivity and cluster size after 12–24 months. However, this is not observed in the αδ-β graphs (d), (f). Mean degree ((a) and (d)), number of components per islet (b) and (e) and number of vertices per component ((c) and (f)) for the αδ and αδ-β graphs, respectively, are given for all (red), large (blue) and small (green) islets for each developmental stage. Component results are shown for S + NS (solid lines) and NS only (dashed lines). * indicates a statistically significant difference using the Mann-Whitney test and a Bonferroni correction (N = 27 ((a) and (d)) and N = 54 ((b), (c), (e) and (f))). The standard deviation for each data point is given in tables S4–S9.
3.3.2. Number of components
The number of components (S + NS and NS only) per islet found in the ββ graphs increases with age (figure 5(b)). For αδ graphs (figure 6(b)) and αδ-β graphs (figure 6(e)), the number of components decreases until 12–24 months. This is followed by a statistically significant increase in the number of nonsingular components per large islet.
3.3.3. Number of vertices per component
For the ββ graphs the number of vertices per (S + NS and NS only) component increases for all islet sizes between 1–35 weeks and 12–24 months (figure 5(c)). The transitions between gestation and 1–35 weeks and between 12–24 months and 28 months+ shows little change for nonsingular components. There is a relatively small decrease in number of vertices per nonsingular component for the αδ graphs (figure 6(c)) up until 12–24 months as compared to the large decrease observed between 12–24 months and 28 months+. For the αδ-β graphs (figure 6(f)), the number of vertices per nonsingular component increases until 12–24 months followed by a decrease in vertices per nonsingular component between 12–24 months and 28 months+.
3.4. ββ graph transitions
The first simulated transition (T1) is between gestation and 1–35 weeks. The simulation process was as described in Methods with the initial and next developmental stage datasets given by the gestation and 1–35 weeks datasets, respectively. For each (rlpa, rlpd) combination (denoted by points on the difference plots in figure 7), the simulations were run and the measures of the resulting graphs were calculated. The resulting measures were subtracted from the measures observed in the next developmental stage, in this case 1–35 weeks, so that measure equilibrium can be easily detected (when difference values are zero) as shown in figure 7. The mean degree difference is shown in figure 7. The number of components per islet and the number of vertices per component differences can be found in supplementary figure S7. For PM (figure 7(b)) and MM (figure 7(d)), no measure equilibria are found. For MP (figure 7(c)), all rlpa values produce a measure equilibrium when rlpd was approximately 1.65 (intercept values range from 1.63–1.68). For PP (figure 7(a)), all rlpa produce a measure equilibrium but the rlpd value have a larger range, from 1.7 to 2.65.
Figure 7.
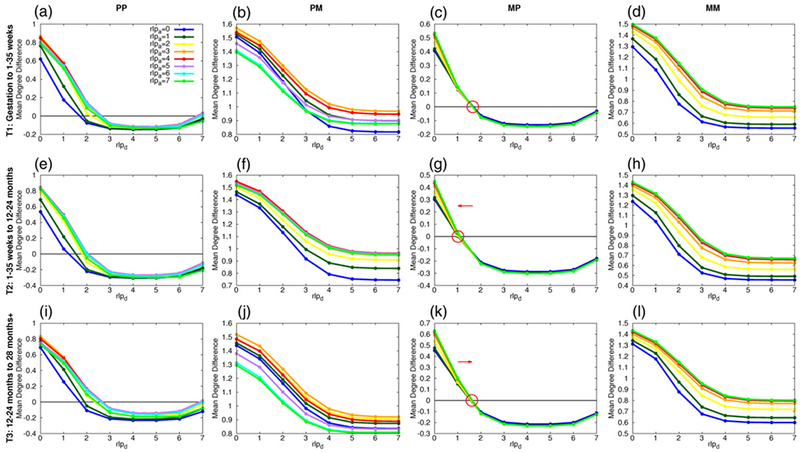
Results from ββ graph transition simulations illustrate possible (addition, deletion) processes for producing the next developmental stage’s architecture. (a)–(f) The difference in mean degree between the resulting ββ graph simulation and that of the next developmental stage for each process, (PP (column 1), PM (column 2), MP (column 3) and MM (column 4)) and each developmental transition (gestation to 1–35 weeks (row 1), 1–35 weeks to 12–24 months (row 2), 12–24 months to 28 months+ (row 3)). Each point represents a given (rlpa, rlpd) pair. Measure equilibria are found for each developmental transition for the PP an MP processes.
The second simulated transition (T2) is from 1–35 weeks to 12–24 months. The PM (figure 7(f)) and MM (figure 7(h)) processes produced no measure equilibria. For MP (figure 7(g)), all rlpa values produced a measure equilibrium when rlpd was approximately 1.08 (values ranged from 1.01 to 1.12)- a noticeable shift from the first transition’s rlpd values. The PP processes (figure 7(e)) produced measure equilibria for each rlpa with rlpd values ranging from 1.22 to 2.05. Similar results for the number of components per islet and number of vertices per component differences can be found in supplementary figure S8.
The third simulated transition (T3) is from 12–24 months to 28 months+. Again, the PM (figure 7(j)) and MM (figure 7(l)) processes produced no measure equilibria. For MP (figure 7(k)), all rlpa values produced a measure equilibrium when rlpd was approximately 1.61 (values ranged from 1.56 to 1.63), similar to what was observed in the first transition. For PP (figure 7(i)), the rlpd values that produced measure equilibria ranged from 1.7 to 2.67, also similar to what was observed in the first transition. Similar results for the number of components per islet and the number of vertices per component differences can be found in supplementary figure S9.
Bounds on the change in mean and standard deviation for each (rlpa, rlpd) combination can be found in supplementary figures S10–12.
4. Discussion
4.1. αδ graph measures
The measures calculated for the αδ and αδ-β graphs (figure 6) quantified key transitions in cyto-architecture over developmental stages. For instance, the mean degree of the αδ graphs decreased after 12–24 months probably due to the decrease in δ cells per islet. However, the αδ-β graph degree increased slightly after this developmental stage. Thus, surprisingly, even with the decrease in δ cells, the connectivity between β cells and the α and δ cells was maintained and actually increased slightly after 12–24 months.
For large islets, the mean number of nonsingular components per islet slightly increased (2.86 to 2.88) for the αδ graphs after 12–24 months, whereas for the αδ-β graphs the values increased from 2.10 to 2.70 after this developmental stage. The number of vertices per components decreased in both sets of graphs after 12–24 months, but there was a greater decrease observed in the αδ graphs (2.76 to 2.59) as compared to the αδ-β graphs (2.38–2.34). Therefore even with the decrease in number of components per islet and number of vertices per component found in the αδ graphs, only small differences in the αδ-β graphs are observed after 12–24 months.
4.2. ββ graph measures
The connectivity between β cells increases between 1–35 weeks and 12–24 months (figure 5). This is corroborated quantitatively by the increase in mean degree and the number of vertices per component (S + NS and NS only) for all islet sizes observed between the two developmental stages. The number of components (S + NS and NS only) per islet also increases overtime.
4.3. ββ graph transitions
4.3.1. Which add/delete process?
The PM (figures 7(b), (f), (j)) and MM (figures 7(d), (h), (l)) processes did not produce measure equilibria for any transition, implying that the deletion process must be of type P, where higher-degree vertices are removed. For the addition process, both MP (figures 7(c), (g), (k)) and PP (figures 7(a), (e), (i)) produced measure equilibria for each rlpa value. However, the range of rlpd values was greater in the PP process. Furthermore, the differences between the pair correlation functions of the simulations and that of the expected dataset are smaller for MP simulations than for PP simulations for each transition (supplementary figure S13 and supplementary table S10). We interpret this to mean that a measure equilibrium can be found for a fixed rlpd value when lower-degree vertices are chosen for addition. If higher-degree vertices are chosen, measure equilibrium can still be found when an adjustment is made to the deletion parameter.
Recent studies have shown that increased amounts of β cell coupling in islets protected cells from apoptosis [30, 31]. This is not contradicted by our findings that suggest highly-coupled vertices have a higher relative likelihood of being deleted, since the former is related to the amount of coupling, and the latter describes how they are coupled. For example, 4 cells can be arranged such that 3 cells are attached to a central cell (the graph would contain 3 edges) or arranged as a chain of cells (this graph would also contain 3 edges). The amount of connectivity, or coupling, in both graphs is the same but their vertex degree distributions differ. Our simulation results suggest that there is no preference for highly connected individual vertices in order to maintain the observed architecture.
4.3.2. Transitional shift
There is a significant shift in the equilibrium-producing rlpd value from 1.65 for T1 (figure 7(c)) to 1.08 for T2 (figure 7(g)) and then back to 1.61 for T3 (figure 7(k)) in the MP case. There is also a collective shift in the range of rlpd values producing measure equilibrium for PP processes for each transition. In figure 8, the associated relative likelihood functions for the addition process (rlpa = 3 is shown, however all rlpa values produced an equilibrium) and deletion processes for the MP case are shown for each transition. The T1 and T3 deletion parameter values are similar, which is interesting considering that there is little difference in the calculated mean degree and number of vertices per component between gestation and 1–35 weeks and between 12–24 months and 28 months+. Based on this, we suggest that the T1 and T3 rlpd values maintain a given initial architecture. Between 1–35 weeks and 12–24 months the mean degree and number of vertices per component increase. From the shift observed from T1 to T2, it appears this change in measures occurs from an increase in cells with lower connectivity, represented by lower-degree vertices, being chosen for deletion.
Figure 8.
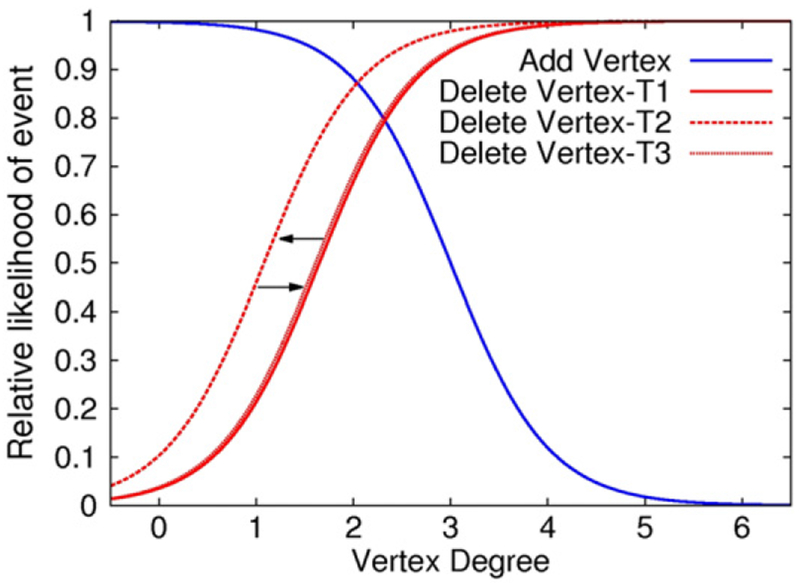
Relative likelihood curves for the equilibrium-producing values for each transition. Notice the leftward shift that occurs between T1 and T2, followed by a rightward shift for T3 back to a value closed to that observed for T1. T1-gestation to 1–35 weeks, T2–1-35 weeks to 12–24 months, and T3–12-24 months to 28 months+.
Chronic hyperglycemia induces morphological changes in islet structure, including large islet β-cell mass loss [9], hypertrophy in β cells [32] and islet amyloid plaque formations [33, 34]. Recently, Brereton et al [35] demonstrated that morphological changes observed in the islet structure are reversible once normoglycemia is attained. During development, humans have changing energy needs and available nutrients. The transitional equilibrium shifts observed between developmental stages possibly demonstrates how islet structure adapts to fluctuations in glycemia.
4.4. Future work
The simulations shown here are solely based on interactions between β cells. However, β cells may not be the sole determinants of islet architecture. Increased α-cell mass has been reported and distorted islet architectures have been observed in patients with T1D [36] and T2D [5]. Also, an increase in the proportion of α-δ and δ-δ cell contacts was observed in T2D subjects [9]. These results illustrate the importance of the number and placement of α and δ cells to islet function. An interesting extension of this work would be to include α and δ cells to the simulated graphs and determine whether β cell placement is dependent on the location of α and/or δ cells. This would further the understanding of the role of α and δ cells in islet architecture.
5. Conclusion
Our main deductive result from the simulations of stochastic processes on islet architectures is that it is indeed possible to find a time-dependent stochastic process that matches the developmental changes in graphical measures observed in human islets. We could rule out entire classes of stochastic rearrangement processes as implausible because of a failure to reproduce the observed dynamics of islet architectures during development. We used stochastic methods for our models because there is no evidence in correlation functions that there is a deterministic process underlying the observed development. Such a deterministic process would require a plethora of parameters for specification and it would be difficult to avoid the appearance of higher-order structures. We cannot, of course, rule out the possibility that the developmental process is deterministic.
Lineage tracing techniques may be able to test our prediction of the process parameters governing islet development in animal models. It is important to note that while our mathematical formulation of cell rearrangements is not based on experimental data, the model pair distribution captures the observed features of the pair distribution function observed in the data only at equilibrium (supplementary figure 13). This gives us some confidence that the simplicity of our approach did not introduce artifacts.
Among the limitations of our analysis, the most important is the lack of information on vasculature and on three-dimensional (3d) structure. The importance of vasculature in islets as endocrine organs needs no explanation, and the 3d structure may lead to aspects of connectivity that are not evident in the 2d sections. Our methods are, of course, general and can be applied to 3d data. The difficulty lies in the experimental acquisition of such data.
In conclusion, we have demonstrated that a developmental stochastic process of biologically complex organelles can be deduced from large-scale imaging data.
Supplementary Material
Table 2.
Large Islet Composition.
| Developmental Stages |
α cells |
β cells |
δ cells |
||||||
|---|---|---|---|---|---|---|---|---|---|
| # cells | # cells/islet | Cell fraction | # cells | # cells/islet | Cell fraction | # cells | # cells/islet | Cell fraction | |
| Gestation | 136 633 | 16.95 | 0.31 | 154 273 | 19.14 | 0.35 | 148 577 | 18.43 | 0.34 |
| 1–35weeks | 99 158 | 15.29 | 0.30 | 130 969 | 20.19 | 0.40 | 100 186 | 15.45 | 0.30 |
| 12–24 months | 45 828 | 8.84 | 0.21 | 128 848 | 24.86 | 0.59 | 42 166 | 8.14 | 0.19 |
| 28 months+ | 199 481 | 14.86 | 0.31 | 388 874 | 28.96 | 0.60 | 54 655 | 4.07 | 0.08 |
Acknowledgements
This research was supported by the Intramural Research Program of the National Institutes of Health, NIDDK. This study utilized the high-performance computational capabilities of the Biowulf Linux cluster at the National Institutes of Health (http://hpc.nih.gov).
Appendix
A.1. Graph Creation Algorithm
The ββ graph, used as an example, is created based on the anatomical locations of β cells in each islet. The vertices of the graph represent the β cells and edges are placed between cells within a given neighborhood radius (10 microns, unless otherwise stated). To ensure only nearest neighbors share edges, a shadow algorithm is applied (see [24]) where cells further away yet still within the given neighborhood radius of a given cell get an edge only if they are not blocked by, or in the shadow of, closer cells.
A.2. Graph Transition Simulation Algorithm
Each simulation consists of 500 iterations of 3 steps:
Deletion of one vertex per islet graph as determined by a given relative likelihood function as described in main text.
Addition of one vertex per islet graph as determined by a given relative likelihood function.
Addition of a predetermined number of vertices to increase the number of vertices per islet graph during the transition to that of the dataset at the next developmental stage (see example in main text). The islet graphs receiving additional vertices are chosen stochastically based on differences in the islet cell count distributions observed between stages. The placement of the vertex in the chosen islet graph is determined stochastically by the given relative likelihood function.
The process of deleting a vertex is straightforward. However, the process of adding a vertex, especially to a high-degreed vertex, is not as easy since the geometric integrity of the islet must be maintained. To work around this, when adding a new vertex, vnew, to an existing vertex, vold, the distance from vold to vnew is randomly chosen between 8 and 13 microns. This interval was chosen due to pair correlation distributions and to avoid regular triangles forming throughout the graphs (which are not observed in islets). The angle of placement was chosen randomly from angles not occupied by neighbors of vold. This placement, while trying to avoid neighboring vertices, can result in neighboring vertices of vold being too close to vnew (below the minimal distance observed between two vertices in the original islet graph dataset, dmin). When this occurs, two lists are created: (1) a list of ‘frozen’ vertices that are not to be moved; initially consists of vold and vnew; (2) a list of ‘problem’ vertices that are within dmin to vertices in the frozen list; this list is sorted by the distance from the vertex to the closest member of the frozen list. The algorithm goes as follows: The first vertex in the problem list is shifted radially outward from vold a random distance such that the distance between the newly-shifted vertex and the closest member of the frozen list is between dmin and 10 microns. Next, the newly-shifted vertex is removed from the problem list and added to the frozen list and all vertices that are too close the newly-shifted vertex are added to the problem list and the list is resorted. This is continued until there are no entries in the problem list and resembles a local wave travelling outward from vold. This algorithm for vertex addition was chosen because it minimized the amount of non-local perturbations and ensured that an endless loop would not occur, since movement is radially outward until the vertex is absorbed or the edge of the islet is reached. An alternative to this algorithm would be to employ stochastic graph layout relaxation techniques, however this would be computationally prohibitive to carry out for each addition/deletion.
A.3. Pair correlation functions of simulations
As described in A.2., simulations are meant to be driven by the dataset given. The effects of choices made for simulation setup can be viewed in the resulting pair correlation functions (figure S13). The placement of the new vertex in the graph is between 8 and 13 microns, which is observed as an increase in the pair correlation between these two radii. Another effect observed is the choice of dmin, the shortest distance between any two vertices in the dataset, as the smallest possible distance that any two vertices could possibly be when adjusting for vertex addition. For the three transitions, the dmin values for the initial datasets are 0.535 (gestation), 3.494 (1–35 weeks) and 0.065 (12–24 months) microns. These radial values correspond to local maximal values observed in the pair correlation functions.
Footnotes
Supplementary material for this article is available online
References
- [1].Orci L 1976. Microanatomy of islets of Langerhans Metabolism 25 1303–13 [DOI] [PubMed] [Google Scholar]
- [2].Bonner-Weir S, Sullivan BA and Weir GC 2015. Human islet morphology revisited: human and rodent islets are not so different after all J. Histochem. Cytochem 63 604–12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Grube D, Eckert I, Speck PT and Wagner HJ 1983. Immunohistochemistry and microanatomy of the islets of Langerhans Biomed. Res 4 25–36 [Google Scholar]
- [4].Bonner-Weir S and O’Brien TD 2008. Islets in type 2 diabetes: in honor of Dr Robert C Turner Diabetes 57 2899–904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Bosco D et al. 2010. Unique arrangement of α- and β-cells in human islets of Langerhans Diabetes 59 1202–10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Kharouta M et al. 2009. No mantle formation in rodent islets the prototype of islet revisited Diabetes Res. Clin. Pract 85 252–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Brissova M et al. 2005. Assessment of human pancreatic islet architecture and composition by laser scanning confocal microscopy J. Histochem. Cytochem 53 1087–97 [DOI] [PubMed] [Google Scholar]
- [8].Cabrera O, Berman DM, Kenyon NS, Ricordi C, Berggrern POand Caicedo A 2006. The unique cytoarchitecture of human pancreatic islets has implications for islet cell function Proc. Natl Acad. Sci. USA 103 2334–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Kilimnik G et al. 2011. Altered islet composition and disproportionate loss of large islets in patients with type 2 diabetes PLoS One 6 1–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Kilimnik G, Jo J, Periwal V, Zielinski MC and Hara M 2012. Quantification of islet size and architecture Islets 4 167–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Mears D, Sheppard NF, Atwater I and Rojas E 1995. Magnitude and modulation of pancreatic beta-cell gap junction electrical conductance in situ J. Membr. Biol 146 163–76 [DOI] [PubMed] [Google Scholar]
- [12].Halban PA, Wollheim CB, Blondel B, Meda P, Niesor ENand Mintz DH 1982. The possible importance of contact between pancreatic-islet cells for the control of insulin release Endocrinology 111 86–94 [DOI] [PubMed] [Google Scholar]
- [13].Jaques F et al. 2008. Dual effect of cell-cell contact disruption on cytosolic calcium and insulin secretion Endocrinology 149 2494–505 [DOI] [PubMed] [Google Scholar]
- [14].Bosco D, Haefliger J-A and Meda P 2011. Connexins: key mediators of endocrine function Physiol. Rev 91 1393–445 [DOI] [PubMed] [Google Scholar]
- [15].Ravier MA et al. 2005. Loss of connexin36 channels alters β-cell coupling, islet synchronization of glucose-induced Ca2+ and insulin oscillations, and basal insulin release Diabetes 54 1798–807 [DOI] [PubMed] [Google Scholar]
- [16].Bosco D, Orci L and Meda P 1989. Homologous but not heterologous contact increases the insulin-secretion of individual pancreatic B-cells Exp. Cell. Res 184 72–80 [DOI] [PubMed] [Google Scholar]
- [17].Koh DS, Cho JHand Chen LY 2012. Paracrine interactions within islets of Langerhans J. Mol. Neurosci 48 429–40 [DOI] [PubMed] [Google Scholar]
- [18].Sorenson RL and Brelje TC 1997. Adaptation of islets of Langerhans to pregnancy: β-cell growth, enhanced insulin secretion and the role of lactogenic hormones Horm. Metab. Res 29 301–7 [DOI] [PubMed] [Google Scholar]
- [19].Butler AE, Janson J, Bonner-Weir S, Ritzel R, Rizza RA and Butler PC 2003. Beta-cell deficit and increased beta-cell apoptosis in humans with type 2 diabetes Diabetes 52 102–10 [DOI] [PubMed] [Google Scholar]
- [20].Unger RHand Orci L 2001. Diseases of liporegulation: new perspective on obesity and related disorders Faseb Journal 15 312–21 [DOI] [PubMed] [Google Scholar]
- [21].Gidding SS et al. 2006. Dietary recommendations for children and adolescents: a guide for practitioners Pediatrics 117 544–59 [DOI] [PubMed] [Google Scholar]
- [22].US Department of Health and Human Services UDoA 2005. Dietary Guidelines for Americans 6th edn (Washington, DC: US Government Printing Office; ) [Google Scholar]
- [23].Stozer A. et al. Functional connectivity in islets of Langerhans from mouse pancreas tissue slices. PLoS Comput. Biol. 2013;9:12. doi: 10.1371/journal.pcbi.1002923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Striegel DA, Hara Mand Periwal V 2015. The beta cell in its cluster: stochastic graphs of beta cell connectivity in the islets of Langerhans PLoS Comput. Biol 11 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Siek J, Lee L-Q and Lumsdaine A 2001. Boost Graph Library: User Guide and Reference Manual (Boston: Addison-Wesley; ) [Google Scholar]
- [26].Cole L, Anderson M, Antin PB and Limesand SW 2009. One process for pancreatic β-cell coalescence into islets involves an epithelial-mesenchymal transition J. Endocrinol 203 19–31 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Pictet R and Rutter W 1972. Development of the embryonic endocrine pancreas ed Geiger S Handbook of Physiology Section 7: Endocrinology (Washington DC: American Physiological Society; )p25–66 [Google Scholar]
- [28].Sancho R, Gruber R, Gu GQ and Behrens A 2014. Loss of Fbw7 reprograms adult pancreatic ductal cells into α, δ, and β cells Cell Stem Cell 15 139–53 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Perl S et al. 2010. Significant human beta-cell turnover is limited to the first three decades of life as determined by in vivo thymidine analog incorporation and radiocarbon dating J. Clin. Endocrinol. Metab 95 E234–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Klee P et al. 2011. Connexins protect mouse pancreatic β cells against apoptosis J. Clin. Invest 121 4870–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Allagnat F, Klee P, Cardozo AK, Meda P and Haefliger JA 2013. Connexin36 contributes to INS-1E cells survival through modulation of cytokine-induced oxidative stress, ER stress and AMPK activity Cell Death Differ 20 1742–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Jonas JC et al. 1999. Chronic hyperglycemia triggers loss of pancreatic β cell differentiation in an animal model of diabetes J. Biol. Chem 274 14112–21 [DOI] [PubMed] [Google Scholar]
- [33].Jaikaran E and Clark A 2001. Islet amyloid and type 2 diabetes: from molecular misfolding to islet pathophysiology Biochim. Biophys. Acta 1537 179–203 [DOI] [PubMed] [Google Scholar]
- [34].Kahn SE, Andrikopoulos S and Verchere CB 1999. Islet amyloid: a long-recognized but underappreciated pathological feature of type 2 diabetes Diabetes 48 241–53 [DOI] [PubMed] [Google Scholar]
- [35].Brereton MF et al. 2014. Reversible changes in pancreatic islet structure and function produced by elevated blood glucose Nat. Commun 5 1–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Rahier J, Goebbels RMand Henquin JC 1983. Cellular composition of the human diabetic pancreas Diabetologia 24 366–71 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


