Using All Longitudinal Data to Define Time to Specified Percentages of Estimated GFR Decline: A Simulation Study

Abstract

Rationale & Objective:

The standard method to calculate time to the event of a specified percentage decline in estimated glomerular filtration rate (eGFR) uses two eGFR assessments, one at baseline and one at the event time. However, event times may be inaccurate due to eGFR variability and restriction of events to study visit times. We propose a novel method for calculating time to a specified percentage decline in eGFR that uses all available longitudinal eGFR assessments.

Study Design:

Simulation study and comparison of methods in two observational cohorts.

Settings & Participants:

Simulation data and study participants in the Nephrotic Syndrome Study Network (NEPTUNE) and Clinical Phenotyping and Resource Biobank Core (C-PROBE).

Exposure:

Analytical method for calculating time to a specified percentage decline in eGFR: standard two-point method versus a regression method incorporating all available longitudinally assessed eGFR assessments.

Outcome:

Time to percentage decline in eGFR.

Analytic Approach:

A two-point method only used the baseline eGFR and the first eGFR below the decline threshold. The comparison method used ordinary linear regression incorporating all longitudinal eGFR assessments to define the baseline measure and the 40% decline threshold. The time to a 40% decline in eGFR was defined as the time when the regression line crossed the decline threshold. The two outcome calculation methods were compared using simulations to assess accuracy of estimated event times and power to detect event time differences between groups. Comparison of event times calculated using each method was also implemented using data from NEPTUNE and C-PROBE.

Results:

The regression method incorporating all eGFR assessments was more accurate than the two-point method in estimating event times than the standard two-point method in simulation analyses, particularly when eGFR variability was high, there was a greater correlation among successive eGFR values, or there were more missing data. This method was also more powerful in detecting differences between groups. Using NEPTUNE and C-PROBE data, the standard method estimated a more rapid rate of events, some likely representing transient reductions in kidney function, and was less likely to give accurate estimates in the presence of non-linear eGFR trajectories.

Limitations:

Computation required for our proposed method currently limit its use to research rather than clinical applications.

Conclusions:

A regression method using all longitudinal eGFR values to estimate time to a percentage decline in eGFR increases the accuracy and power over traditional methods, representing a potential improvement in the ability to discover treatment or biomarker effects on kidney disease progression.

INTRODUCTION

In research studies of chronic kidney disease (CKD) progression, the outcome of interest is often time to kidney failure. Such a time-to-event outcome is frequently preferred over longitudinal analyses of change in kidney function, since it can better capture proportional exposure effects and can better handle informative missingness (i.e., missing data due to infrequent clinic visits or kidney failure events).^1,2 However, for studies with short follow-up, CKD subtypes with slow progression, or substantial dropout, few patients may reach kidney failure during the study period, limiting the ability to detect predictors of kidney failure.

Surrogate time-to-event outcomes have been proposed, including time to a percentage decline in estimated glomerular filtration rate (eGFR). While the U.S. Food and Drug Administration (FDA) had previously accepted a doubling of serum creatinine, or an approximately 57% decline in eGFR, as a surrogate end point in clinical trials, lesser changes in eGFR (e.g., 30, 40, or 50 percent decline) were more recently supported by a 2012 scientific workshop co-sponsored by the National Kidney Foundation and FDA.^2–4 Such surrogate outcomes have limitations, but they are easy to measure, can increase statistical power, have biological plausibility as surrogates, and are highly associated with subsequent kidney failure.^1,2,5 Furthermore, while these surrogate outcomes were originally proposed in the context of clinical trials, observational data were also provided to support their validity² and they have been used extensively as outcomes in many observational cohort studies.^6–9

To calculate time to, say 40%, decline in eGFR, researchers usually calculate (100– 40)%=60% of the first eGFR, which we term the decline threshold, and identify the first subsequent eGFR that is lower than this value (Figure 1). While simple and intuitive, this approach effectively uses the eGFR from only two assessments, one at baseline and the second as the assessment that first crosses the decline threshold. The estimated event time may be inaccurate due to variability in the eGFR assessment and because event times can only be measured when eGFR is assessed, usually at study visit times that may occur long after the eGFR has actually crossed the decline threshold. In addition, this definition of the decline threshold may not be appropriate for complex, non-monotone eGFR trajectories. Levey et al.² recommended the use of confirmatory assessments at baseline and after reaching the event, although guidelines on when the confirmatory measurements should be collected or how the values should be used are lacking. Although helpful, this strategy does not resolve the other drawbacks of the standard method and confirmatory measures are not always available in research studies. Thus, the standard method of calculating time to a percentage decline in eGFR may result in a noisy outcome for which small treatment effects are easy to miss.

Figure 1:

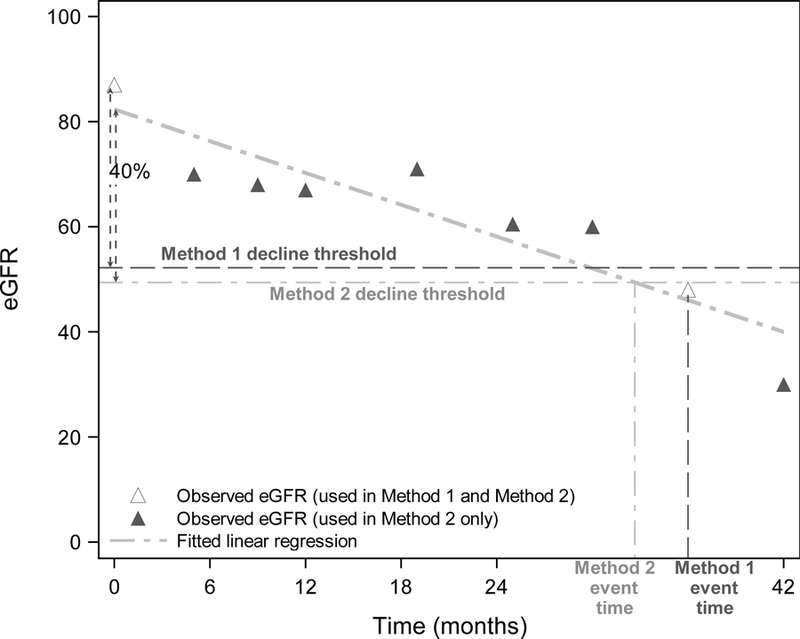
Example eGFR data to demonstrate estimated time to 40% decline using the standard two-point method (Method 1) and our proposed regression method (Method 2). Dashed horizontal lines represent 40% decline thresholds for each method. Hollow triangles represent the two eGFR measurements used for Method 1, whereas all eGFR assessments (hollow and solid) are used for Method 2.

In the current study, we propose to improve calculation of time to a percentage decline in eGFR by fitting a regression line using all longitudinal eGFRs. To our knowledge, while fitting a regression to eGFR values has been used in other contexts, e.g. to calculate eGFR slope or otherwise characterize CKD progression, it has not specifically been used to estimate event times for time to percentage eGFR decline outcomes. We first conducted a simulation study to compare the accuracy and power of our proposed regression method with the standard two-point method and to assess how the methods perform under different data structures. We then illustrated the effects of data characteristics on calculation of outcomes by each method using data from the Nephrotic Syndrome Study Network (NEPTUNE), part of the National Institutes of Health (NIH) Rare Disease Clinical Research Network (RDCRN), and the Clinical Phenotyping and Resource Biobank Core (C-PROBE) of the George M. O’Brien Michigan Kidney Translational Core Center.

METHODS

Proposed Method to Calculate Time 40% Decline in eGFR

For each individual patient, we used an ordinary linear regression to fit a line to all of that patient’s longitudinal eGFR assesments available (Method 2). We used the intercept of the line as the baseline measure and subtracted 40% to estimate the decline threshold. The time to 40% decline in eGFR was defined as the time when the regression line crossed the decline threshold (Figure 1), with censoring at the last observed eGFR. This method uses all eGFRs, whereas the standard two-point method only uses the baseline eGFR and the first eGFR below the decline threshold.

Simulation Study

To compare the performance of the standard method (Method 1) to our proposed method (Method 2), we conducted a series of simulations. Unlike in real data, we can assess a method’s accuracy because we can set true values of time to event in simulations and then compare each method’s estimated time to the true values. We can also imitate different data structures in simulations, thus allowing comparisons of methods across hypothetical CKD populations. Assuming a longitudinal study with eGFR collected about every four months, the following parameters were varied across simulations: A) the variability of eGFR, which could represent within-patient variability (e.g., transient medication effects or hydration status) or measurement error of eGFR, B) the correlation between an individual patient’s successive eGFR values over time, and C) the maximum percent of missing visits, which could represent missing eGFR values or less frequently assessed eGFR (Table 1). The range of parameter values was chosen to represent different study populations and to overlap with the parameters observed in our NEPTUNE or C-PROBE data examples (Item S1). We used simulations to compare the standard method to our proposed method, both for assessing event times in a single group and for detecting differences in event times between two groups. For comparing two groups, we also varied the difference in true event times, which could represent a group effect size. To determine each method’s accuracy, we calculated bias by subtracting the true event time from each method’s estimated median event time as determined by Kaplan-Meier curves. For comparing two groups, we also conducted a log-rank test and calculated the rejection rate, which reflects the Type I error (e.g., α=0.05) when there is truly no difference in event times between groups and reflects the power of the test when there is a true difference. Further details on simulation study methods can be found in Item S2.

Table 1:

Simulated Data parameters vs. NEPTUNE and C-PROBE Data Parameters

	eGFR Variability, SD or RMSE**	Percent Missing eGFR Follow-up Values	Correlation Between Successive eGFR Values*
Simulated Data	3, 5, 7, 9	0, 10, 20, 40, 60, 80	0, 0.2, 0.4, 0.6, 0.8
NEPTUNE	8.4 (4.3 – 13.6)	10 (0 – 25)	0.79
MN	8.7 (5.1 – 12.0)	0 (0 – 20)	0.80
MCD	11.3 (6.1 – 17.4)	14 (0 – 33)	0.56
FSGS	7.5 (4.0 – 13.7)	10 (0 – 25)	0.85
IgAN	5.5 (3.3 – 8.8)	0 (0 – 11)	0.93
C-PROBE	2.0 (0 – 6.4)	0 (0 – 29)	0.86
Diabetic nephropathy	0.5 (0 – 4.6)	0 (0 – 27)	0.90
CAKUT	0.3 (0 – 3.1)	0 (0 – 0)	0.82
Glomerular disease	3.5 (0 – 9.2)	0 (0 – 33)	0.83
Hypertensive nephropathy	2.1 (0 – 6.2)	0 (0 – 29)	0.85
Other/Unknown	1.7 (0 – 4.6)	0 (0 – 25)	0.89

Unless otherwise indicated, values shown are median (interquartile range).

^*For NEPTUNE and C-PROBE data: estimated from linear generalized estimating equation model

^**SD for simulations; RMSE for NEPTUNE data.

NEPTUNE, Nephrotic Syndrome Study Network; C-PROBE, Clinical Phenotyping and Resource Biobank Core; SD: standard deviation; RMSE: root mean squared error; MN: membranous nephropathy, MCD: minimal change disease, FSGS: focal segmental glomerularsclerosis, IgAN: immunoglobulin A nephropathy; CAKUT: congenital anomalies of the kidney and urinary tract.

NEPTUNE and C-PROBE Data

NEPTUNE is a multicenter prospective observational cohort study of patients with minimal change disease (MCD), focal segmental glomerulosclerosis (FSGS), or membranous nephropathy (MN).⁹ Although not one of the primary glomerular diseases of interest within NEPTUNE, immunoglobulin A nephropathy (IgAN) patients were also included in the present study. Children and adults are enrolled at the time of a clinically indicated biopsy, or initial presentation for children who do not get a biopsy, and followed every four months for the first year and every six months for four more years. eGFR is assessed at baseline and at each follow-up visit. C-PROBE contains phenotypic data and biological specimens from an ethnically diverse population of patients with a wide variety of chronic kidney diseases in stages 1–4, including non-glomerular disease.^9a eGFR is assessed at baseline and at annual follow-up visits. For the current study, all patients from either study with at least two eGFR assessments were included. Baseline demographic and clinical characteristics of each study sample were calculated using descriptive statistics. To assess linearity of eGFR trajectories, we also fit a quadratic regression to each patient’s longitudinal eGFRs and tested the quadratic term coefficient for statistical significance at level 0.05.

Using the standard two-point method and our proposed regression method, we calculated each patient’s time from study enrollment to 40% decline in eGFR. Those who ended follow-up before reaching the event were censored. In the (rare) event of kidney failure occurring prior to a 40% eGFR decline, we implemented a cause-specific hazard approach, which censors the data at the time of the competing event.¹⁰ We then compared the two methods descriptively using Kaplan-Meier estimates of the probability of 40% decline in eGFR and by calculating differences in estimated event times between methods for each patient. This was done for all patients and also stratified by disease etiology. In sensitivity analyses, we also calculated Kaplan-Meier estimates using a confirmatory measurement for the standard two-point method (Item S3) and using a weighted version of our proposed method (Item S4) with NEPTUNE data.

This study received a waiver for Institutional Review Board approval by Ethical & Independent Review Services, #16034–01. Patients in both studies provided informed consent, and the current study only used existing de-identified data.

RESULTS

Simulation Study

In all simulations, Method 2 was more accurate (i.e., had a smaller difference between the estimated event time and true event time, or smaller bias) and estimates of time to 40% decline had smaller standard deviations compared to Method 1 (Figure 2). As the variability of eGFR increased, the bias of Method 1 became more negative, implying underestimation of the median time to 40% decline in eGFR (Figure 2A). This result was expected, since higher eGFR variability implies a higher likelihood that a spuriously low eGFR is observed earlier. As the correlation between successive eGFR values increased, the bias of Method 1 became more positive, implying overestimation of the true event time (Figure 2B). With higher correlation, the eGFR trajectory is less volatile and therefore has fewer opportunities to reach the decline threshold. Finally, as the maximum percent of missing visits increased, the bias of Method 1 also became more positive (Figure 2C). This reflects the fact that event times can only occur when eGFR is observed and more missingness implies less frequently observed eGFR values. Therefore, if the first eGFR below the decline threshold is missing, the event time will be later according to Method 1. Since some parameters result in underestimation and others result in overestimation, Method 1 can also appear unbiased for a few specific combinations of parameters.

Figure 2:

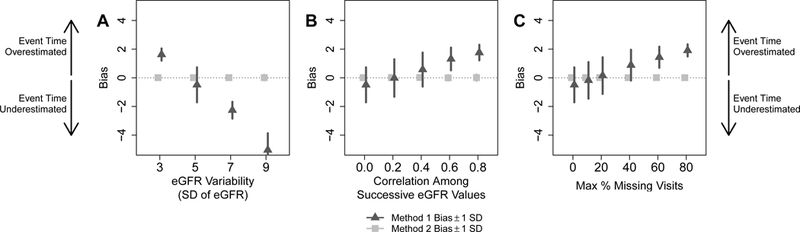
Mean bias and standard deviation across simulation repetitions of median survival times to 40% decline in eGFR estimated by the standard two-point method (Method 1) and our proposed regression method (Method 2). Positive bias implies that true event times were overestimated by each method, whereas negative bias indicates that true event times were underestimated. A) eGFR variability was varied, with correlation among successive eGFR values set at 0 and maximum missing visits set at 0%. B) Correlation among successive eGFR values were varied, with eGFR variability set at 5 and maximum missing visits set at 0%. C) The maximum percent of missing follow-up visits were varied, with eGFR variability set at 5 and correlation among successive eGFR values set at 0.

With two distinct groups of patients, e.g., representing two different disease subtypes with two different true times to 40% decline in eGFR, Method 1 consistently showed similar or greater bias compared to Method 2 (Fig S1, top row). With larger eGFR variability or more missing visits, Method 1 also had larger bias. Method 2 always had similar or greater power for detecting differences between groups compared to Method 1 (Fig S1, bottom row), and the increase in power was more pronounced as eGFR variability increased or as the maximum percent of missing visits increased. This result shows that the use of all longitudinal eGFRs in Method 2 increased the power to detect differences compared with Method 1. The amount of correlation between successive eGFRs had little effect on bias or power for either method.

NEPTUNE eGFR Data

Table 2 shows demographics and baseline clinical characteristics of NEPTUNE patients included in the current analysis. The 380 patients had a mean (SD) follow-up time of 33.6 (17.3) months and mean (SD, range) of 6.5 (2.7, 2–11) visits with eGFR assessments. Only 9.5% of patients had a statistically significant quadratic term in regressions, implying that the linear model fit well for most patients. Additional analyses in linear vs. non-linear subgroups is included in Item S5.

Table 2:

NEPTUNE and C-PROBE Patient Demographic and Baseline Clinical Characteristics

Variable	NEPTUNE	C-PROBE
No. of patients	380	938
Male sex	217 (59%)	419 (45%)
Age at baseline (years)	32 (14–52)	54 (33–65)
Under 18	125 (34%)	139 (15%)
Race
White	212 (57.6%)	528 (57%)
Black	86 (23.4%)	343 (37%)
Other	70 (19%)	50 (5%)
Hispanic/Latino	63 (17.1%)	71 (8%)
Baseline laboratory values
eGFR (mL/min/1.73m2)	85.4 (54.9–107.6)	52.7 (34.7–89.9)
UPCR	2.1 (0.6–4.5)
NEPTUNE Cohort
MN	68 (18.5%)
MCD	116 (31.5%)
FSGS	134 (36.4%)
IgAN	50 (13.6%)
C-PROBE Cohort
Diabetic nephropathy		152 (16%)
CAKUT		35 (4%)
Glomerular disease		389 (41 %)
Hypertensive nephropathy		95 (10%)
Other/Unknown		267 (28%)

Values shown are count (percentage) or median (interquartile range).

IQR=interquartile range, eGFR=estimated glomerular filtration rate, UPCR=urine protein creatinine ratio, MN= membranous nephropathy, MCD=minimal change disease, FSGS=focal segmental glomerularsclerosis, IgAN=immunoglobulin A nephropathy; CAKUT=congenital anomalies of the kidney and urinary tract; NEPTUNE, _______; C-PROBE, _______.

Figure 3A shows the distribution of patients’ times from baseline to 40% decline in eGFR using Kaplan-Meier curves. The lower estimates from Method 1 imply more and earlier outcomes compared to Method 2 (Fig S2). When analyses were stratified by diagnosis (MN, MCD, and FSGS), Method 1 consistently yielded earlier outcomes and therefore lower survival curve estimates compared to Method 2. Survival curves were similar among patients with IgAN diagnosis. When comparing patients below vs. above median age of 33.3 years, the log-rank test using Method 1 to estimate event times resulted in a p-value of 0.08 and using Method 2 resulted in a p-value of 0.02. Consistent with our simulation results, Method 1 was more conservative compared to Method 2.

Figure 3:

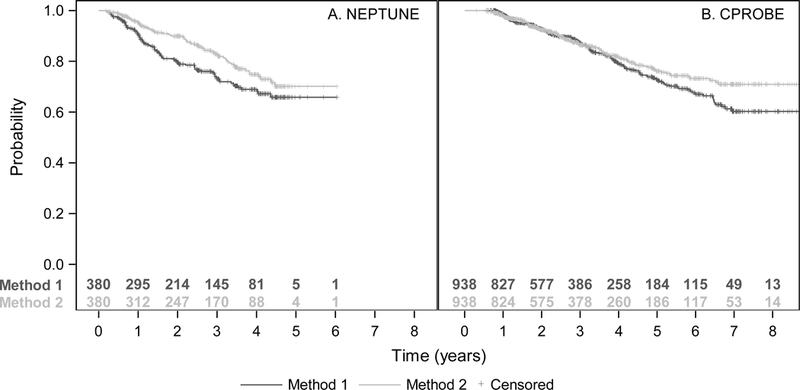
Kaplan-Meier estimates of the probability of a 40% decline in eGFR using NEPTUNE (A) and C-RPOBE (B) data and applying both the standard two-point method (Method 1) and our proposed regression method (Method 2).

Four eGFR trajectories from individual NEPTUNE patients are shown in Figure 4 to demonstrate the robustness of our proposed regression method. Figure 4A shows a patient whose eGFR dipped temporarily from its usual trajectory, possibly due to an acute kidney injury or measurement error. This patient’s eGFR trajectory crossed the Method 1 decline threshold at 12.7 months and would be unchanged even if using a confirmatory measurement since the next observed eGFR is also under the decline threshold. The patient’s eGFR trajectory crossed the Method 2 decline threshold 18.6 months later. Variability around the regression line, measured by root mean squared error (RMSE), was 8.1.

Figure 4:

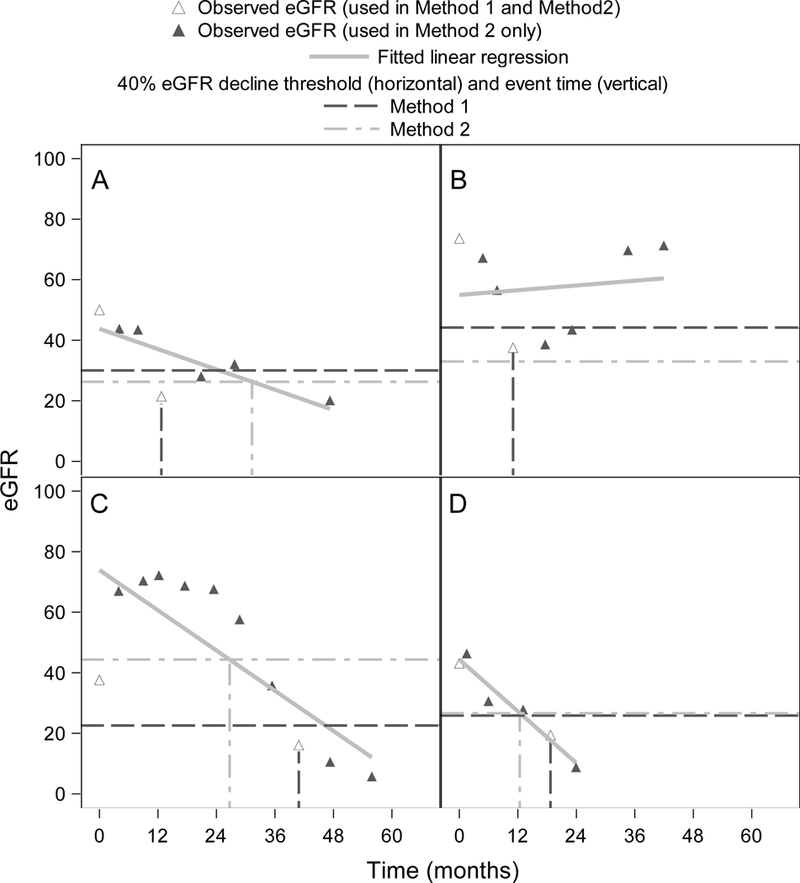
Four example eGFR trajectories from NEPTUNE cohort patients. Dashed horizontal lines represent 40% decline thresholds based on the standard two-point method (Method 1, dark gray) and our proposed regression method (Method 2, light gray). A) Patient with eGFR that dips temporarily from its usual trajectory; B) Patient with non-linear eGFR trajectory; C) Patient whose first eGFR measurement is very different from the regression line intercept; D) Patient with linear trajectory and similar decline thresholds between the two methods.

Figure 4B shows a patient whose eGFR over time was non-linear and highly variable, with RMSE of 16.4. Method 1 fails to capture this patient’s recovery and estimates their event time at 11 months. Despite the regression line of Method 2 not fitting the non-linear trajectory well, it is still able to capture the patient’s recovery and does not assign an outcome event to this patient. As in our simulation results, the large variability in eGFR may have caused the Method 1 event time to be too early.

Figure 4C shows a patient whose first eGFR assessment is very different from the regression line intercept from Method 2, resulting in a much lower decline threshold for Method 1. Since Method 1 ignores any eGFRs besides those at baseline and the event time, Method 1 estimates the event time to be much later compared to Method 2. Figure 4D shows a patient whose trajectory is relatively linear (RMSE 3.7) and whose baseline eGFR is close to the regression line intercept from Method 2. Thus, the decline threshold is similar for both methods. However, the Method 1 event time is 6.3 months after the Method 2 event time because Method 1 event times can only occur at visit times.

C-PROBE eGFR Data

The 938 C-PROBE patients included in the current study (Table 2) had a mean (SD) follow-up time of 38.4 (25.2) months and mean (SD, range) of 3.4 (1.6, 2–9) visits with eGFR assessments. Only 4.5% of patients had a statistically significant quadratic term in regressions. The Kaplan-Meier curves for Method 1 and Method 2 were similar for the first three years of follow-up, then diverged since Method 1 indicated more and earlier events (Figure 3B). C-PROBE patients had lower eGFR variability and less frequent eGFR assessments compared to NEPTUNE patients (Table 1). Our simulations showed this leads to more overestimation, or less underestimation, of event times using Method 1. Indeed, there were many more C-PROBE patients for which Method 1 likely overestimated event times, while some patients still had underestimated event times (Fig S2). Therefore, it was not surprising that the Kaplan-Meier curves in C-PROBE were closer together than they were in NEPTUNE. While patients with diabetic nephropathy had more events resulting in lower Kaplan-Meier curves, the comparison between methods was consistent across diagnoses and the shapes of subgroup curves were similar to the shape for the overall cohort.

DISCUSSION

Our simulation study demonstrated that the estimation of time to 40% decline in eGFR using our proposed method of fitting a regression line to all observed eGFR assessments was more accurate and led to greater power than the standard method, which only uses the baseline eGFR and the eGFR at the event time. Further, the disadvantage of the standard two-point method worsened as eGFR variability or missing visits increased, a common occurrence in observational research studies. Moreover, because event times using the standard two-point method can only occur at visit times but crossing the decline threshold may occur between visits, the standard method would estimate event times to be later with more missing visits. Because we used a wide variety of parameters in simulations, these results can be generalizable to a wide variety of data settings. For example, allowing visit dates to depart from exact scheduled dates and having high missingness (i.e., lower frequency of visits) may better mimic clinical administrative data.

Examples from the NEPTUNE and C-PROBE studies illustrated the shortcomings of the standard two-point method in real-data examples, including the lack of robustness compared to our proposed regression method in situations of high variability, non-linear eGFR trajectories, and the fact that events can only occur at visit times. The standard method therefore resulted in an outcome with substantial noise and gave conservative results compared to our proposed method. Our proposed regression method could therefore result in improved estimation of time to 40% decline in eGFR and, importantly, greater power to detect treatment or biomarkers predictive of clinical outcome.

The drawbacks of the standard two-point method may also be exacerbated under specific study designs. For example, studies that assess eGFR infrequently (e.g., with yearly visits) can only have event times during those visits. As we observed in Figure 4D, this can cause the standard method to overestimate the event time substantially. Using our proposed regression method, we are able to estimate event times between visits using interpolation. For studies focusing on specific CKD subtypes like children with proteinuria, there may be a large proportion of patients with non-linear eGFR trajectories. As we observed in Figures 4A and 4B, the standard method may often detect an outcome without taking into account the fact that later eGFRs show a slower progression or even a recovery. In contrast, our proposed method did not prematurely detect an event and was therefore more robust to non-linear eGFR trajectories. Finally, in studies targeting rare conditions like glomerular disease, the lower power of outcome comparisons based on the standard two-point method can be especially debilitating.

There are several limitations of our proposed regression method. First, it requires fitting a regression line to observed longitudinal eGFR data, which at present may be challenging to implement in clinical practice given the need for statistical software. The intended use of our proposed method is in research studies that collect serial eGFR assessments, including prospective or retrospective studies. With greater power to detect new biomarkers, however, its usefulness for clinical practice is imminent. Upon further validation, our proposed method could be automatically implemented within electronic patient records to aid clinicians in routine patient care. Second, for prospective studies that have not collected all longitudinal data at the time of analysis, refitting a regression line when data are updated can change patients’ event times and statuses as the slope can shift with new data points (Item S6). Although perhaps initially disconcerting, we contend that updating data to obtain more accurate outcome measures far outweighs the drawback of potentially changing some individual results as the study progresses. Third, our simulation study assumed truly linear trajectories and our proposed method fits a linear regression line to eGFR values. We did find that the linear regression fit well for most (90–95%) patients and that our proposed method was more robust than the standard method even when the linear regression did not fit well. However, future work will focus on simulating non-linear trajectories and extending our proposed methodology—for example, we can use polynomial regressions or linear splines to allow flexible functional forms for time, use orthogonal or median regression to mitigate the influence of outliers, or limit linear regressions to periods of eGFR decline to capture acute events.

Finally, measuring CKD progression with a percentage decline in eGFR is not always ideal, for example, when baseline eGFR is high or when treatment effects are uniform across eGFR levels.⁴ In the NEPTUNE data, for example, many patients had at least one eGFR>120 mL/min/1.73m². Patients who are hyperfiltering may have drops in eGFR that exceed the percentage decline of interest but that should actually be considered beneficial. For example, a patient whose eGFR is 200 at baseline and 100 at their next visit has a 50% decline that may not necessarily be an adverse outcome, no matter which method is used. Therefore, any study that utilizes a percentage decline in eGFR as an outcome must carefully consider patients with very high eGFR. In such cases, other outcomes, like change in eGFR over time as assessed by a mixed model or generalized estimating equation model, may be more efficient or serve as a better surrogate for kidney failure. Log-transformed eGFR values may also provide a better model fit. In addition, studies with many kidney failure events or deaths may benefit from using time to those hard clinical endpoints as the outcome of interest. However, in situations where time to a percentage decline in eGFR is the outcome of interest, we recommend our proposed regression method over the standard two-point method.

Our proposed method provides more accurate, powerful, and robust estimates of the time to a percentage decline in eGFR compared to the standard two-point method. While additional studies are warranted, this approach could also be applied to estimate the time to a percentage change in any serially measured data. In these situations, we recommend fitting a regression line using all longitudinal measurements to improve estimation of outcomes. We thus provide a new tool for studying kidney disease progression that can facilitate more accurate prediction models, treatment effect estimates, and ultimately, better-informed patient care.

Supplementary Material

Fig S1.

Mean bias and rejection rates of the difference in median times to 40% decline in eGFR between 2 groups, as estimated by the standard two-point method (Method 1) and our proposed regression method (Method 2).

Fig S2.

Individual comparisons of months to 40% decline in eGFR as estimated by the standard 2-point method (Method 1) and our proposed regression method (Method 2).

Item S1.

Methods for estimating simulation study parameters from real data.

Item S2.

Complete simulation study methods.

Item S3.

Standard 2-point method with confirmatory measures.

Item S4.

Weighted version of proposed method.

Item S5.

Analyses by linearity of eGFR trajectories.

Item S6.

Time-updated analyses using proposed method.