Tissue-Specific Compartmental Analysis for Dynamic Contrast-Enhanced MR Imaging of Complex Tumors

Abstract

Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) provides a noninvasive method for evaluating tumor vasculature patterns based on contrast accumulation and washout. However, due to limited imaging resolution and tumor tissue heterogeneity, tracer concentrations at many pixels often represent a mixture of more than one distinct compartment. This pixel-wise partial volume effect (PVE) would have profound impact on the accuracy of pharmacokinetics studies using existing compartmental modeling (CM) methods. We, therefore, propose a convex analysis of mixtures (CAM) algorithm to explicitly mitigate PVE by expressing the kinetics in each pixel as a nonnegative combination of underlying compartments and subsequently identifying pure volume pixels at the corners of the clustered pixel time series scatter plot simplex. The algorithm is supported theoretically by a well-grounded mathematical framework and practically by plug-in noise filtering and normalization preprocessing. We demonstrate the principle and feasibility of the CAM-CM approach on realistic synthetic data involving two functional tissue compartments, and compare the accuracy of parameter estimates obtained with and without PVE elimination using CAM or other relevant techniques. Experimental results show that CAM-CM achieves a significant improvement in the accuracy of kinetic parameter estimation. We apply the algorithm to real DCE-MRI breast cancer data and observe improved pharmacokinetic parameter estimation, separating tumor tissue into regions with differential tracer kinetics on a pixel-by-pixel basis and revealing biologically plausible tumor tissue heterogeneity patterns. This method combines the advantages of multivariate clustering, convex geometry analysis, and compartmental modeling approaches. The open-source MATLAB software of CAM-CM is publicly available from the Web.

I. Introduction

Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) provides a useful noninvasive tool for evaluating tumor vasculature patterns based on contrast accumulation and washout [1], [2]. DCE-MRI uses various molecular weight contrast agents to demonstrate tumor vasculature perfusion and permeability, thereby producing functionally relevant images of angiogenic status [3], [4]. For example, DCE-MRI can depict spatial heterogeneity of vascular permeability which reflects tumor angiogenic activity, and has potential utility in testing the alternative hypotheses for drug effects and predicting the efficacy of cancer treatment on the basis of functional vasculature changes observed over time [1], [5].

Compartmental modeling (CM) is a widely used mathematical tool to model dynamic imaging data and can provide accurate pharmacokinetics parameter estimates when delineated regions of interest (ROIs) are homogeneous and available a priori [6]-[8]. However, due to markedly tissue heterogeneity in malignant tumors and limited imaging resolution, tracer concentrations at many pixels often represent a complex mixture of more than one distinct vasculature compartment. This pixel-wise spatially-mixed partial volume effect (PVE), while often conveniently overlooked, would have a profound impact on the reliability of pharmacokinetics studies using existing CM methods [1], [3], [9]–[12].

To implicitly account for PVE, models with multiple parallel compartments on both ROI and pixel-wise scales have been used to fit to DEC-MRI data in previous pharmacokinetics studies [8], [13], [14]. However, many experimental results indicate that the use of commonly accepted multi-compartment models often leads to considerably biased and high-variance estimates of the pharmacokinetics parameters. Evidently, this is due to the existence of multiple local optima in the nonconvex parameter space, complex and nonlinear optimization procedures, and the lack of a theoretical identifiability proof [3], [9], [15]—[19]. To explicitly account for the PVE, a recent proof-of-principle study aimed to understand and evaluate PVE on pharmacokinetics parameter estimation using computer simulations and subsequently proposed a postprocessing technique for PVE compensation [10]. The major limitations of this pixel-by-pixel tissue heterogeneity evaluation include its high noise impact, high computational complexity, and limited applicability to normal tissues or static images [10],[20]. While time-concentration curve clustering using spatial prior knowledge has been exploited to improve pixel-by-pixel pharmacokinetics parameter estimation, this approach is both not intended and unable to mitigate pixel-wise PVE [13], [14], [16], [21].

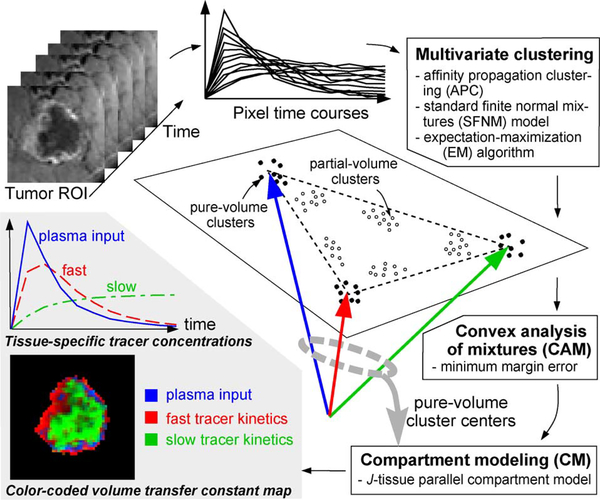
Motivated by the fact that the kinetics in each pixel can be expressed as a nonnegative combination of underlying compartments, we propose a convex analysis of mixtures (CAM) algorithm to explicitly eliminate PVE by identifying pure volume pixels at the corners of the clustered pixel time series scatter plot (Fig. 1). The algorithm is theoretically supported by a series of newly proved identifiability theorems and, practically by additional noise filtering and normalization preprocessing. We first isolate pixels that define tumor area using a standard masking technique and remove noise or outlier pixels using a vector-norm filtering [21]. By a perspective projection of pixel time series onto standard scatter simplex, we obtain normalized pixel temporal shape patterns independent of signal amplitude [22]. Subsequent multivariate pixel clustering, based on standard finite normal mixture (SFNM) distribution modeling, estimated using the affinity propagation clustering (APC) and the expectation-maximization (EM) algorithm, provides further noise and outlier reduced representations of the data set. CAM then effectively isolates pure volume pixels by identifying the corner cluster centers of the scatter plot convex hull, and accordingly eliminates the interior data points corresponding to partial volume pixels. The algorithm proceeds to accurately estimate tissue-specific pharmacokinetic parameter values by fitting the compartmental model to the data of the isolated pure volume pixels, based on which the pixel-by-pixel spatial distributions of these parameters can be readily obtained [8].

Fig. 1.

Roadmap of the CAM-CM method (illustrated on the special case of J = 3). A hybrid multivariate clustering first groups the normalized pixel time courses into “local” clusters that correspond to either pure-volume or partial-volume pixels. The CAM-CM then separates the pure-volume clusters from partial-volume clusters by detecting the corners of the clustered convex hull. The identified pure-volume cluster centers and their associated pixels are further used to estimate the tissue-specific kinetic parameters within the tumor site by compartment modeling globally and locally.

We demonstrate the principle and feasibility of the CAM-CM approach on realistic synthetic data involving two functional tissue compartments, and compare the accuracy of parameter estimates obtained with PVE elimination using CAM-CM to those obtained without PVE elimination using relevant techniques. Experimental results show a significant improvement in the accuracy of kinetic parameter estimation using the proposed PVE elimination approach, where we also report the comparative studies using other relevant techniques including classical CM, iterative quadratic maximum likelihood (IQML) estimation, and iterative maximum likelihood CM (IML-CM) [7], [13], [18]. We then apply the algorithm to real DCE-MRI breast cancer data and observe improved pharmacokinetics parameter estimation, separating tumor tissue into sub-regions with distinct tracer kinetics on a pixel-by-pixel basis and revealing biologically plausible tumor tissue heterogeneity patterns. Finally, extensions to the algorithm, and the relationships to previous approaches, are briefly discussed.

II. Background and Theory

A. Classical Compartment Model

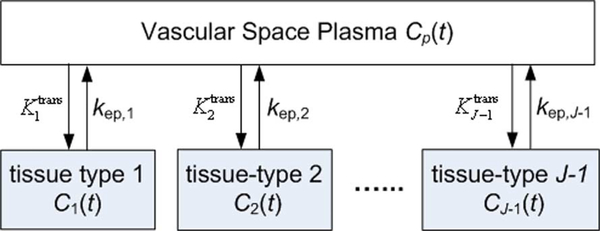
We first introduce an illustrative J-tissue compartment model of DCE-MRI time series (Fig. 2) (Jth tissue compartment corresponds to tracer plasma input indexed by p), whose tracer concentration kinetics are governed by a set of first-order differential equations [7], [8], [23], [24]

$$\begin{gathered} \frac{d{C}_1(t)}{dt}=K_1^{\text{trans}}{C}_p(t)-k_{\text{ep},1}{C}_1(t), \\ ⋮ \\ \frac{d{C}_{J-1}(t)}{dt}=K_{J-1}^{\text{trans}}{C}_p(t)-k_{\text{ep},J-1}{C}_{J-1}(t), \\ {C}_{\text{measured}}(t)=C_1(t)+\cdots +C_{J-1}(t)+K_p{C}_p(t) \end{gathered}$$ (1)

where C_j(t) is the tracer concentrations in the interstitial space weighted by the fractional interstitial volume in tissue-type j, at time t; C_p(t) is the tracer concentration in plasma (the input function); C_measured(t) is the measured tracer concentration in the ROI; $K_j^{\text{trans}}$ is the unidirectional volume transfer constant (/min) from plasma to tissue-type j; k_ep,j is the flux rate constants (/min) in tissue-type j; and K_p is the plasma volume in the ROI [13]. Equation (1) can be solved for C₁(t),…,C_J–1(t)in terms of the rate constants as

$$C_j(t)=K_j^{\text{trans}}{C}_p(t)\otimes \exp \left(-k_{\text{ep},j}t\right),j=1,\dots ,J-1$$ (2)

where ⊗ denotes the mathematical convolution operation.

Fig. 2.

Schematic diagram of parallel-mode J-tissue compartment model.

Letting $F_j(t)=C_p(t)\otimes \exp \left(-k_{\text{ep},j}t\right)\text{and}{F}_p(t)=C_p(t)$, the spatial-temporal patterns of tracer concentrations in DCE-MRI data can be expressed as [21]

$$\begin{gathered} \left[\begin{array}{c}{C}_{\text{measured}}\left(i,t_1\right)\\ C_{\text{measured}}\left(i,t_2\right)\\ ⋮\\ C_{\text{measured}}\left(i,t_L\right)\end{array}\right] \\ =\left[\begin{array}{cccc}{F}_1\left(t_1\right)& \cdots & F_{J-1}\left(t_1\right)& F_p\left(t_1\right)\\ F_1\left(t_2\right)& \cdots & F_{J-1}\left(t_2\right)& F_p\left(t_2\right)\\ ⋮& \dots & ⋮& ⋮\\ F_1\left(t_L\right)& \cdots & F_{J-1}\left(t_L\right)& F_p\left(t_L\right)\end{array}\right]\left[\begin{array}{c}{K}_1^{\mathrm{trans}}(i)\\ ⋮\\ K_{J-1}^{\mathrm{trans}}(i)\\ K_P(i)\end{array}\right] \end{gathered}$$ (3)

where C_measured (i,t_l) is the tracer concentration measured at time t_l at pixel i, L is the number of sampling time points $K_1^{\mathrm{trans}}(i),\dots ,K_{J-1}^{\mathrm{trans}}(i)$ are the local volume transfer constants of the tissue-types 1 to (J–1), at pixel i, respectively; and K_p(i) is the plasma volume at pixel i.

B. Convexity of Pixel Time Series Scatter Plot

Denote the measured dynamic tracer concentration curve vector by

$$\begin{gathered} {\mathbf{C}}_{\text{measured}}(i) \\ ={\left[C_{\text{measured}}\left(i,t_1\right),C_{\text{measured}}\left(i,t_2\right),\dots ,C_{\text{measured}}\left(i,t_L\right)\right]}^T \end{gathered}$$

the compartment time-concentration curves (TCs) by F_j = [F_j(t₁),F_j(t₂),…,F_j(t_L)]^T, and the local volume transfer constants along with the plasma volume by ${\mathbf{K}}^{\text{trans}}(i)={\left[K_1^{\text{trans}}(i),K_2^{\text{trans}}(i),\dots ,K_{J-1}^{\text{trans}}(i),K_p(i)\right]}^T$ where J is the number of latent compartments including plasma volume. We can then re-express (3) in its vector-matrix notation

$${\mathbf{C}}_{\text{measured}}(i)=\left[{\mathbf{F}}_1,\dots ,{\mathbf{F}}_J\right]{\mathbf{K}}^{\text{trans}}(i).$$ (4)

For ease of subsequent discussion, we normalize C_measured (i,t) and F_j(t) over their effective interval of L time samples, via a sum-based normalization that projects the scatter plot data points onto the standard simplex as follows:

$$x\left(i,t_l\right)=\frac{C_{\text{measured}}\left(i,t_l\right)}{\sum _{l^{\prime }=1}^L{C}_{\text{measured}}\left(i,t_{l^{\prime }}\right)},a_j\left(t_l\right)=\frac{F_j\left(t_l\right)}{\sum _{l^{\prime }=1}^L{F}_j\left(t_{l^{\prime }}\right)}$$ (5)

for l = 1,…,L, j = 1,…,J.

We can then re-express (4) as

$$\mathbf{x}(i)=\sum _{j=1}^J{K}_j(i){\mathbf{a}}_j$$ (6)

for i = 1,…,N, where K^trans(i) is accordingly normalized and denoted by K(i) with ${\sum }_{j=1}^J{K}_j(i)=1$, x(i) = [x(i,t₁),…,x(i,t_L)]^T, a_j = [a_j(t₁),…,a_j(t_L)]^T, and N is the number of pixels. Note that the physical meanings of the pharmacokinetics parameters remain the same after normalization while their values shall be interpreted as relatively “strength” at this stage. Furthermore, since these local volume transfer constants and plasma volume, entries in K^trans(i) or K(i), are non-negative, pixel time series model (6) indicates that the observed pixel time series x(i,t) is a non-negative linear combination of the compartment TCs, {a_j(t)}, weighted by their spatially-distributed local volume transfer constants, {K_j(i)}. This falls neatly within the definition of a convex set [25]. Specifically, the observed set of pixel time series $\mathcal{X}$ = {x(1),…,x(N)} forms a subset of the convex set readily defined by the set of compartment TCs $\mathcal{A}=\left\{{\mathbf{a}}_1,\dots ,{\mathbf{a}}_J\right\}$, i.e.,

$$\begin{gathered} \mathcal{X}=\{\sum _{j=1}^J{K}_j(i){\mathbf{a}}_j|{\mathbf{a}}_j\in \mathcal{A},K_j(i)\ge 0, \\ \sum _{j=1}^J{K}_j(i)=1,i=1,\dots ,N\}. \end{gathered}$$ (7)

C. Identifiability of Compartment Model

We now discuss the identifiability of the compartment model (6) and the required conditions via the following definitions and theorems (see formal proofs in Appendix A).

Definition 1: Given a set of compartment TCs $\mathcal{A}=\left\{{\mathbf{a}}_1,\dots ,{\mathbf{a}}_J\right\}$, we denote the convex set it specifies by

$$\mathcal{H}\{\mathcal{A}\}=\left\{\sum _{j=1}^J{\alpha }_j{\mathbf{a}}_j|{\mathbf{a}}_j\in \mathcal{A},{\alpha }_j\ge 0,\sum _{j=1}^J{\alpha }_j=1\right\}.$$ (8)

Definition 2: A compartment TC vector a_j is a corner point of the convex set $\mathcal{H}\left\{\mathcal{A}\right\}$ if it can only be expressed as a trivial convex combination of a₁,…,a_J.

Lemma 1 (Convex Envelope of Pixel Time Series): Suppose that the J compartment TCs a₁,…a_J are linearly independent, and $\mathbf{x}(i)={\sum }_{j=1}^J{K}_j(i){\mathbf{a}}_j$ where K₁(i),…, K_J(i) are the non-negative normalized spatially-distributed volume transfer constants. Then, the elements of $\mathcal{X}$ (the pixel time series) are confined within a convex set $\mathcal{H}\left\{\mathcal{A}\right\}$ whose corner points are the J compartment TCs a₁,…,a_J.

Definition 3: Any pixel whose associated normalized spatially-distributed volume transfer constants are in the form of K(i_WGP(j)) = e_j is called a well-grounded point (WGP) and corresponds to a pure-volume pixel, where {e_j} is the standard basis of J-dimensional real space (the axes of the first quadrant). In other words, we define pure volume pixels (or well-grounded pixels) as the pixels that are occupied by only a single compartment tissue type.

Theorem 1 (Convexity of Pixel Time Series): Suppose that the J compartment TCs a₁,…,a_J are linearly independent, and $\mathbf{x}(i)={\sum }_{j=1}^J{K}_j(i){\mathbf{a}}_j$ where non-negative normalized spatially-distributed volume transfer constants {K(i)} have at least one well-grounded point on each of the J coordinate axes (i.e., ∃i_WGP(j) such that K(i_WGP(j)) = e_j, ∀j), then, $\mathcal{X}$ uniquely specifies a convex set

$$\mathcal{H}\{\mathcal{X}\}=\left\{\sum _{i=1}^N{\alpha }_i\mathbf{x}(i)|\mathbf{x}(i)\in \mathcal{X},{\alpha }_i\ge 0,\sum _{i=1}^N{\alpha }_i=1\right\}$$

which is in fact the same as the convex set $\mathcal{H}\left\{\mathcal{A}\right\}$, whose corner points are the J compartment TCs a₁,…,a_J.

From Theorem 1, there appears to be a mathematical solution uniquely identifying the compartment model (6) based on the observed set of pixel time series $\mathcal{X}$ (identifiability): The corner points of the pixel time series convex set $\mathcal{H}\left\{\mathcal{X}\right\}$ are the compartment TCs {a_j} when pure-volume pixels exist for each of the compartments and for the plasma input function, That is, if pixel i is a pure volume pixel occupied by the jth compartment tissue type, mathematically, we will have K(i_WGP(j)) = e_j where e_j is the jth standard basis. Accordingly, for pure volume pixel i, since the corresponding pixel time series $\mathbf{x}(i)={\sum }_{j=1}^J{K}_j(i){\mathbf{a}}_j$ is now a trivial combination of {a_j}, it is the corner of the convex hull $\mathcal{H}\left\{\mathcal{A}\right\}$, and by Theorem 1, also the corner of the convex hull $\mathcal{H}\left\{\mathcal{X}\right\}$. This means that, in principle, under a noise-free scenario, we can directly estimate {a_j} by locating x(i_WGP(j)), ∀j. Note that there are computationally feasible algorithms for finding these corner points [27]–[29]. Moreover, Lemma 1 and Theorem 1 imply that the pure-volume pixels constitute the corner points of the observed pixel time series convex set and reflect the temporal patterns of the underlying compartments, while the partial-volume pixels constitute the interior points of the observed pixel time series convex set and, thus, can be readily identified and eliminated in the compartmental analysis (Fig. 1).

One important consideration with the present method is the existence of pure-volume pixels for each of the underlying compartments, and this reasonable assumption reflects only the ideal scenario and constitutes the necessary and sufficient condition for the mathematical identifiability of the tissue-specific CAM-CM model. Nevertheless, it is possible that in some datasets, no pixel is pure and it would be helpful to provide an accurate interpretation of the CAM-CM solution in such non-ideal scenarios. For the nonideal scenarios (accordingly with relaxed conditions), the following two theorems (see formal proofs in Appendix A) show that, if source-dominance or source-specific-dominance pixels exist for each of the underlying tissue compartments, CAM-CM will provide the optimal solution that captures maximum source information (i.e., with the identified corners of the pixel time series scatter simplex corresponding to maximum source-dominance or source-specific-dominance).

Theorem 2 (Source Dominance): Suppose that the non-negative normalized pixel-wise local volume transfer constants {K(c_j) = [K₁(c_j),…,K_m(c_j),…,K_J(c_j)]} are the corners of the pixel time series scatter simplex. Then the CAM-CM solution based on these corners {K(c_j)} achieves the maximum source dominance in the sense of K_m(c_j) = max_i=1,2,…N K_m(i).

Theorem 3 (Source-Specific Dominance): Suppose that the non-negative normalized pixel-wise local volume transfer constants {K(c_j) = [K₁(c_j),…,K_m(c_j),…,K_J(c_j)]} at the corners of the pixel time series scatter simplex are near well-grounded points and exist for each of the underlying tissue compartments (i.e., nearly-pure volume pixels that satisfy K_j(c_j) ≫ K_m(c_j) for m ≠ j reflecting source-specific dominance. Then the CAM-CM solution based on these corners {K(c_j)} achieves maximum source-specific dominance in the sense of the minimum Kullback-Leibler (KL) divergence between {e_j} and K(i).

III. Method and Algorithm

So far, we have developed a mathematical framework for partial volume elimination and tissue-specific compartmental analysis. In this section, we fully develop an associated practical algorithm, consisting of data preprocessing, clustering of pixel time series, convex analysis of mixtures, and compartment analysis (see the schematic flowchart of our algorithm in Fig. 1).

A. Data Preprocessing

For the identified tumor site, our algorithm begins with four data preprocessing steps. First, the tumor area is extracted by masking out the normal tissues surrounding the tumor site. This task can be fulfilled by either multivariate image segmentation or by a human expert as done in drawing conventional ROIs [9], [21]. Second, the first few image frames, for instance, four initial images in our experiments, are taken out, as they correspond to the time period before sufficient tracer uptake. This task is done with great care, in accordance with applied imaging protocols [18], [21]. Third, pixels whose temporal average signal intensity is lower than 5% of the maximum value or whose temporal dynamic variation is lower than 5% of the maximum value, are eliminated, as these noninformative pixels could have a negative impact on subsequent analyses. Fourth, the pixel time series is normalized over time using a sum-based normalization scheme specified by (5), as similarly done in [22]. This step focuses our analysis on the “shape” of pharmacokinetics rather than on absolute tracer concentration.

B. Clustering of Pixel Time Series

1). SFNM and EM Algorithm:

The purpose of multivariate clustering of normalized pixel time series is three-fold: 1) data clustering has proven to be an effective tool for reducing the impact of noise/outlier data points on model learning [21], [30], [31]; 2) aggregation of pixel time series into a few clusters improves the efficiency of subsequent convex analysis of mixtures, [31]; 3) the resultant clustered compartment model permits an automated determination of the number of underlying tissue compartments using the minimum description length (MDL) criterion [18], [32], [33].

There has been considerable success in using SFNMs to model clustered data sets such as DCE-MRI data, taking a sum of the following general form [21], [30], [34]:

$$\begin{gathered} p(\mathbf{K}(i))=\sum _{m=1}^J{\pi }_{m}g(\mathbf{K}(i)|{\mathbf{e}}_m,{\mathbf{\Sigma }}_{\mathbf{K},m}) \\ +\sum _{m=J+1}^M{\pi }_{m}g(\mathbf{K}(i)|{\mathit{\mu }}_{\mathbf{K},m},{\mathbf{\Sigma }}_{\mathbf{K},m}) \end{gathered}$$ (9)

where the first term corresponds to the clusters of pure volume pixels (m = 1,…,J), the second term corresponds to the clusters of partial volume pixels (m = J + 1,…,M), M is the total number of pixel clusters, 𝜋_m is the mixing factor, g(·) is the Gaussian kernel, e_m denotes the mth natural basis vector corresponding to the mean vector of the mth pure tissue compartment, and μ_K,m and Σ_K,m are the mean vector and covariance matrix of cluster m, respectively. It is worth noting that SFNMs are a flexible and powerful statistical modeling tool and can adequately model clustered structure with essentially arbitrary complexity by introducing a sufficient number of mixture components. Thus, strict adherence of the (in general, unknown) ground-truth data distribution to the form in (9) is not required in most real-world applications [30], [34]. By incorporating (7) into (9), the SFNM model for pixel time series becomes

$$\begin{gathered} p(\mathbf{x}(i))=\sum _{m=1}^J{\pi }_{m}g(\mathbf{x}(i)|{\mathbf{a}}_m,{\mathbf{\Sigma }}_{\mathbf{x},m}) \\ +\sum _{m=J+1}^M{\pi }_{m}g(\mathbf{x}(i)|{\mathbf{\mu }}_{\mathbf{x},m},{\mathbf{\Sigma }}_{\mathbf{x},m}) \end{gathered}$$ (10)

where Σ_x,m = AΣ_K,mA^T and μ_x,m = Aμ_K,m, with A = [a₁,…,a_J]. Accordingly, the first term of (10) represents the corner clusters and the second term of (10) represents the interior clusters (as shown in Fig. 1). From Theorem 1 and SFNM model (10), the clustered pixel time series set $\mathcal{X}$ is (approximately) confined within a convex set whose corner centers are the J compartment TCs a₁,…,a_J.

It has been shown that significant computational savings can be achieved by using the EM algorithm to allow a mixture of the form (10) to be fitted to the data [30], [34]. Determination of the parameters of the model (10) can be viewed as a “missing data” problem in which the missing information corresponds to pixel labels l_im = I(i,m) specifying which cluster generated each data point with I(i,m) denoting the indicator function. When no information about l_im is available, the log-likelihood for the model (10) takes the form

$$\log \mathcal{L}(\mathcal{X}|\mathbf{\Theta })=\sum _{i=1}^N\log \left\{\sum _{m=1}^M{\pi }_{m}g[\mathbf{x}(i)|{\mathit{\mu }}_{\mathbf{x},m},{\mathbf{\Sigma }}_{\mathbf{x},m}]\right\}$$ (11)

where $\mathcal{L}(\cdot )$ denotes the joint likelihood function of SFNM and Θ = {π_m,μ_x,m, Σ_x,m, ∀m}. If, however, we were given a set of already clustered data with specified pixel labels, then the log likelihood (known as the “complete” data log-likelihood) becomes

$$\log \mathcal{L}(\mathcal{X},\mathbf{L}|\mathbf{\Theta })=\sum _{i=1}^N\sum _{m=1}^M{l}_{im}\log \left\{{\pi }_{m}g[\mathbf{x}(i)|{\mathbf{\mu }}_{\mathbf{x},m},{\mathbf{\Sigma }}_{\mathbf{x},m}]\right\}$$ (12)

where L = {l_im|i = 1,…,N;m = 1,…,M}. Actually, we only have indirect, probabilistic, information in the form of the posterior responsibilities z_im for each model m having generated the pixel time series x(i). Taking the expectation of (12), we then obtain the complete data log likelihood in the form

$$\log \mathcal{L}(\mathcal{X},\mathbf{Z}|\mathbf{\Theta })=\sum _{i=1}^N\sum _{m=1}^M{z}_{im}\log \left\{{\pi }_{m}g[\mathbf{x}(i)|{\mu }_{\mathbf{x},m},{\mathbf{\Sigma }}_{\mathbf{x},m}]\right\}$$ (13)

in which the z_im = Pr(l_im = 1|x(i)) are constants, and Z = {z_im|i = 1,…,N;m = 1,…,M}.

Maximization of (13) can be performed using the two-stage form of the EM algorithm, where the pixel labels l_im are treated as missing data as aforementioned. At each complete cycle of the algorithm we commence with an “old” set of parameter values Θ. We first use these parameters in the E-step to evaluate the posterior probabilities z_im using Bayes theorem

$$\begin{gathered} z_{im}=\mathrm{Pr}\left(l_{im}=1|\mathbf{x}(i)\right) \\ =\frac{{\pi }_{m}g[\mathbf{x}(i)|{\mathit{\mu }}_{\mathbf{x},m},{\mathbf{\Sigma }}_{\mathbf{x},m}]}{\sum _{m^{\prime }=1}^M{\pi }_{m^{\prime }}g[\mathbf{x}(i)|{\mathit{\mu }}_{\mathbf{x},m^{\prime }},{\mathbf{\Sigma }}_{\mathbf{x},m^{\prime }}]},m\in \{1,\dots ,M\}. \end{gathered}$$ (14)

These posterior probabilities are then used in the M-step to obtain “new” values Θ using the following re-estimation formulas

$${\pi }_m=\frac{1}{N}\sum _{i=1}^N{z}_{im}$$ (15)

$${\mathit{\mu }}_{\mathbf{x},m}=\frac{\sum _{i=1}^N{z}_{im}\mathbf{x}(i)}{\sum _{i=1}^N{z}_{im}}$$ (16)

$${\mathbf{\Sigma }}_{\mathbf{x},m}=\frac{\sum _{i=1}^N{z}_{im}\left(\mathbf{x}(i)-{\mathit{\mu }}_{\mathbf{x},m}\right){\left(\mathbf{x}(i)-{\mathit{\mu }}_{\mathbf{x},m}\right)}^T}{\sum _{i=1}^N{z}_{im}}.$$ (17)

2). APC Initialization:

To reduce the likelihood of pixel time series clustering being trapped into local maxima, an effective and initialization-free affinity propagation clustering (APC) is attempted to initialize the parameter Θ for the EM algorithm and to estimate the number of obtainable clusters [35]. APC simultaneously considers all data points as potential exemplars (cluster centers) and recursively exchange real-valued messages between data points until a high-quality set of exemplars and corresponding clusters gradually emerges. Let the “similarity” s(i,m) = –‖x(i) – x(m)‖² indicate how well the data point x(m) is suited to be the exemplar for data point x(i); the “responsibility” r(i,m) reflects the accumulated evidence for how well-suited data point x(m) is to serve as the exemplar for data point x(i), and the “availability” a(i,m) reflects the accumulated evidence for how appropriate the data point x(i) chooses data point x(m) as its exemplar. Then, the responsibilities r(i,m) are computed based on

$$r(i,m)\leftarrow s(i,m)-\underset{{}_{m^{\prime }\ne m}}{\max }\left\{a\left(i,m^{\prime }\right)+s\left(i,m^{\prime }\right)\right\}$$ (18)

where the availabilities a(i,m) are initialized to zero and the competitive update rule (18) is purely data-driven. Whereas the responsibility update (18) allows all candidate exemplars to compete for ownership of a data point, the availability update rule

$$a(i,m)\leftarrow \min \left\{0,r(m,m)+\sum _{i^{\prime }\notin \{i,m\}}\max \left\{0,r\left(i^{\prime },m\right)\right\}\right\}$$ (19)

collects evidence from data points to support a good exemplar, where the “self-availability” is updated differently

$$a(m,m)\leftarrow \sum _{i^{\prime }\notin m}\max \left\{0,r\left(i^{\prime },m\right)\right\}.$$ (20)

Then, the availabilities and responsibilities are combined to identify exemplars; i.e., for a data point x(i), its exemplar is identified as x(m*) by

$$m^{*}=\arg \underset{{}_m}{\max }\{a(i,m)+r(i,m)\}.$$ (21)

If i = m*, x(i) itself is a exemplar; otherwise x(m*) is the exemplar of the data point x(i). The update rules (18)—(20) are repeated iteratively, and for each iteration, APC makes decisions on the exemplars based on (21). The iteration is terminated when these decisions do not change for 10 iterations [35].

One advantage of APC is that it does not need initialization for the exemplars, since the update rules are purely data-driven. A set of data points sharing the same exemplar can be considered as a cluster, with the exemplar being the cluster center. Therefore, the mean and the covariance matrix of this cluster can be estimated to initialize the parameter Θ for the EM algorithm. Another advantage of APC is that the number of clusters need not be specified a priori but emerges from the message-passing procedure and only depends on the density distribution of the data points. This enables automatic model selection at clustering stage [35].

C. Convex Analysis of Mixtures

At this point in our analysis procedure, each pixel time-course is represented by a group of cluster centers, where both the dimensionality and noise/outlier effect are significantly reduced. Given the obtained M cluster centers μ_x,1,…,μ_x,M, CAM is applied to separate pure-volume clusters from partial-volume clusters by detecting the “corners” of the convex hull containing all clusters of pixel TCs (theoretically supported by Lemma 1 and Theorem 1). Assuming the number of compartments J is known a priori, an exhaustive combinatorial search (with total $C_J^M$ combinations), based on a convex-hull-to-data fitting criterion, is performed to identify the most probable J corners. This explicitly maps partial-volume pixels to the corners and partial-volume pixels to the interior clusters of the convex hull.

Let $\{{\mathit{\mu }}_{\mathbf{x},m_1},\dots ,{\mathit{\mu }}_{\mathbf{x},m_J}\}$ be any size—J subset of {μ_x,1,…,μ_x,M}. Then, the margin (i.e., distance) between μ_x,m and the convex hull $\mathcal{H}\{{\mathit{\mu }}_{\mathbf{x},m_1},\dots ,{\mathit{\mu }}_{\mathbf{x},m_J}\}$ is computed by

$${\delta }_{m,\left(m_1,\dots ,m_J\right)}=\underset{{\alpha }_{m_1},\dots {\alpha }_{m_J}}{\min }{\Vert {\mathit{\mu }}_{\mathbf{x},m}-\sum _{j=1}^J{\alpha }_{m_j}{\mathit{\mu }}_{\mathbf{x},m_j}\Vert }_2$$ (22)

where ${\alpha }_{m_j}\ge 0,{\sum }_{j=1}^J{\alpha }_{m_j}=1$. It shall be noted that if μ_x,m is inside $\mathcal{H}\{{\mathit{\mu }}_{\mathbf{x},m_1},\dots ,{\mathit{\mu }}_{\mathbf{x},m_J}\}$ then ${\delta }_{m,(m_1,\dots ,m_J)}=0$. Next, we define the convex-hull-to-data fitting error as the sum of the margin between the convex hull and the “exterior” cluster centers and detect the most probably J corners with cluster indices $\left(m_1^{*},\dots m_J^{*}\right)$ when the criterion function reaches its minimum

$$\left(m_1^{*},\dots m_J^{*}\right)=\arg \underset{{}_{(m_1,\dots ,m_J)}}{\min }\sum _{m=1}^M{\delta }_{m,(m_1,\dots ,m_J)}.$$ (23)

The optimization problems of (22) and (23) can be solved by advanced convex optimization procedure described in [25] and an exhaustive combinatorial search (for realistic values of J and M, in practice), respectively.

One important issue concerning CAM-CM method is the detection of the structural parameter J in the model (the number of underlying tissue compartments or types), often called model selection [36]-[38]. This is indeed particularly critical in real- world applications where the true structure of the compartment models may be unknown a priori. We propose to use a widely- adopted and consistent information theoretic criterion, namely the minimum description length (MDL) [33], [36], [37], to guide model selection. The major thrust of this approach is the formulation of a model fitting procedure in which an optimal model is selected from several competing candidates, such that the selected model best fits the observed data. MDL formulates the problem explicitly as an information coding problem in which the best model fit is measured such that it assigns high probabilities to the observed data while at the same time the model itself is not too complex to describe.

However, when the number of pixels is large as in DCE-MRI application, direct use of MDL may underestimate the value of J, due to the lack of “structure” in classical compartment models (over-parameterization) [18], [32], [33]. We therefore propose to naturally adopt and extend the clustered compartment models into the MDL formulation [39]. The proposed clustered compartment model allows all pixels belonging to the same cluster to share a common K_m, thus greatly reducing model complexity for a given value of J (the number of convex hull corners). Specifically, a model is selected with J tissue compartments by minimizing the total description length defined by [32], [36]

$$\mathrm{MDL}(J)=-\log \left(\mathcal{L}\left({\mathbf{C}}_M|\mathbf{\Phi }(J)\right)\right)+\frac{5+J(M+1)}{2}\log (LM)$$ (24)

where $\mathcal{L}(\cdot )$ denotes the joint likelihood function of the clustered compartment model, C_M denotes the set of M cluster centers, and Φ(J) denotes the set of freely adjustable parameters in the clustered compartment model (see Appendix B for more detailed discussions).

D. Tissue-Specific Compartmental Analysis

Having determined the probabilistic pixel memberships associated with pure-volume compartments, $z_{ij}$ for j = 1,…, J, i = 1…., N, we can then estimate the tissue-specific compartmental parameters, namely $K_j^{\text{trans}}$ and k_ep,j, j = 1,…, J, directly from DCE-MRI pixel time series C_measured(i), in which various compartment modeling techniques can be readily applied.

To specify which “exterior” cluster is associated with which compartment, we investigate the temporal enhancement patterns of the “exterior” cluster centers. From (1) and (2), C_p is associated with the cluster of the fastest enhancement (reaching its peak most rapidly); C_j is associated with the cluster of jth tissue type. We then compute C_p and C_j via

$${\mathbf{C}}_p=\frac{\sum _{i=1}^N{z}_{iJ}{\mathbf{C}}_{\text{measured}}(i)}{\sum _{i=1}^N{z}_{iJ}},{\mathbf{C}}_j=\frac{\sum _{i=1}^N{z}_{ij}{\mathbf{C}}_{\text{measured}}(i)}{\sum _{i=1}^N{z}_{ij}}$$ (25)

For j = 1,…,J – 1.

We then recall the relationship $C_j(t)=K_j^{\text{trans}}{C}_p(t)\otimes \exp \left(-k_{\text{ep},j}t\right)$, and discretize the convolution (with discretization interval Δt (/min)) to the following vector-matrix notation

$${\mathbf{C}}_j=K_j^{\mathrm{trans}}\mathbf{H}\left(k_{\text{ep},j}\right){\mathbf{C}}_p,j=1,\dots ,J-1$$ (26)

by constructing a Toeplitz matrix

$$\begin{gathered} \mathbf{H}\left(k_{\text{ep},j}\right) \\ =\left[\begin{array}{ccccc}{e}^{-k_{\text{ep},j}{t}_1}& 0& 0& \dots & 0\\ e^{-k_{\text{ep},j}{t}_2}& e^{-k_{\text{ep},j}{t}_1}& 0& \dots & 0\\ \dots & \dots & \dots & \dots & \dots \\ e^{-k_{\text{ep},j}{t}_L}& e^{-k_{\text{ep},j}{t}_{L-1}}& e^{-k_{\text{ep},j}{t}_{L-2}}& \dots & e^{-k_{\text{ep},j}{t}_1}\end{array}\right]\mathrm{\Delta }t \end{gathered}$$ (27)

that is the sampled system impulse response. Then, the estimate of k_ep,j and $K_j^{\text{trans}}$ can be obtained by solving the following optimization problem:

$$\begin{gathered} \left\{{\widehat{k}}_{\text{ep},j},{\widehat{K}}_j^{\text{trans}}\right\}=\arg \underset{{}_{K_f^{\text{trans}},k_{\text{ep},f}}}{\min }{\Vert {\mathbf{C}}_j-K_j^{\mathrm{trans}}\mathbf{H}\left(k_{\text{ep},j}\right){\mathbf{C}}_p\Vert }_2 \\ s.t.K_j^{\text{trans}}>0,k_{\text{ep},j}>0 \end{gathered}$$ (28)

for j = 1…., J - 1. Finally, we can calculate the compartment TCs F $\left({\mathbf{C}}_p,{\widehat{k}}_{\text{ep},1},\dots ,{\widehat{k}}_{\text{ep},J-1}\right)$ based on C_p and ${\widehat{k}}_{\text{ep},1},\dots ,{\widehat{k}}_{\text{ep},J-1}$, and then estimate the local volume transfer constants ${\mathbf{K}}^{\text{trans}}(i)={\left[K_1^{\text{trans}}(i),\dots ,K_{J-1}^{\text{trans}}(i),K_p(i)\right]}^T$ based on (4) via

$$\begin{gathered} {\widehat{\mathbf{K}}}^{\mathrm{trans}}(i)= \\ \arg \underset{{\mathbf{K}}^{\text{trans}}\left(i\right)}{\min }\Vert {{\mathbf{C}}_{\text{measured}}(i)-\mathbf{F}\left({\mathbf{C}}_p,{\widehat{k}}_{\text{ep},1},\dots ,{\widehat{k}}_{\text{ep},J-1}\right){\mathbf{K}}^{\text{trans}}(i)\Vert }_2 \\ s.t.K_1^{\text{trans}}(i)\ge 0,\dots ,K_{J-1}^{\text{trans}}(i)\ge 0,K_p(i)\ge 0 \end{gathered}$$ (29)

that reflects the spatial heterogeneity of vascular permeability [8].

IV. Experiments and Results

In the absence of definitive ground truth about the volume transfer constants K^trans and flux rate constants k_ep in the tumor, the validation of a new method for tissue-specific compartment analysis of DCE-MRI data is always problematic. We propose therefore to first validate CAM-CM on realistic simulation data for the typical case of J = 3, where there are two tissue compartments: fast flow and slow flow, and the input function. The J = 3 case has been widely considered in previous studies [8], [18], [21], [40]. We then proceed to evaluate the method using real DCE-MRI data.

A. Experiment Design and Data Analysis

All the data sets were analyzed according to the algorithm described in Fig. 1. We tested CAM-CM on realistic simulation data, comparing the estimates of kinetic parameters produced by CAM-CM to the ground truth, both in terms of biases (accuracy) and variance (reproducibility) of the estimates, measured over 50 replicated data sets. For comparison purposes, we also evaluated three most relevant methods, including two ROI/subROI-based methods—classic CM and IQML [7], [13], and one pixel-based method—IML-CM [18], with randomized initialization of kinetic parameters within a pre-specific realistic range [13], [41]. We assess the performance of these peer methods using the same procedures as for CAM-CM. Specifically, classic CM and IQML require the input of predefined compartment ROIs that can often be acquired by winner-take-all classification of local volume transfer constants at each pixel [22]. To illustrate the impact of PVE elimination, we also report the reduction of relative bias achieved by CAM-CM over the peer methods, calculated as 1 - (Bias_cam/Bias_peer). To assess the accuracy of estimated local volume transfer constants ${\widehat{\mathbf{K}}}^{\mathrm{trans}}(i)$ produced by CAM-CM and IML-CM, we calculated the root mean-square fitting error (RMSE) defined by [16]

$${\text{RMSE}}_j=\frac{1}{K_j^{\text{trans*}}}\sqrt{\frac{1}{N}\sum _{i=1}^N{\left({\widehat{K}}_j^{\text{trans}}(i)-K_j^{\mathrm{trans}}(i)\right)}^2}$$ (30)

for j = 1,…,J, where $K_j^{\text{trans*}}$ is the ground truth compart- mental volume transfer constant for compartment j, $K_j^{\text{trans}}(i)$ is the ground truth local volume transfer constant for pixel i and compartment j, and ${\widehat{K}}_j^{\mathrm{trans}}(i)$ is the estimate of $K_j^{\text{trans}}(i)$.

We tested CAM-CM on four real DCE-MRI data sets acquired for breast cancer studies [1], [42]. We visually examined the convexity of projected pixel time series via the top two convexity-preserved projections. The convexity-preserved projections pursues two orthonormal bases that project the data points onto a 2-D space where the margin (i.e., distance) between the data points outside the convex hull and the convex hull [see (22)] is minimum.

In all four data sets, we observed that J = 3 compartments were sufficient to describe the scatter plots via a three-corner convex set. Additional compartments can be used to account for the noisy data points in the imperfect convex hull. However, these compartments become difficult to interpret [13], [16]. For comparison purposes, we analyzed the data using J = 4, 5, 6 and observed noise-like and biologically implausible TC patterns associated with these additional compartments. In addition, we also applied the proposed MDL criterion based on clustered compartment model to these four data sets (see (24) and Appendix B); where MDL achieves its minimum values when J = 3 for all cases. We, therefore, use J = 3 compartments in the CAM-CM analysis. The number of clusters M takes integer values between 12 and 18, determined automatically by the APC algorithm [35]. In addition to estimating kinetic parameters, we also plot the estimated compartment TCs, the local volume transfer constant maps, and the fitting error between the parametric compartment TCs F $\left({\widehat{k}}_{\text{ep},f},{\widehat{k}}_{\text{ep},s},{\mathbf{C}}_p\right)$ and non-parametric compartment TCs μ_x,f/s/p. To illustrate the existence of PVE and impact of partial-volume correction, we compared the dissected tissue-specific compartment TCs and overall ROI-based TCs.

B. Synthetic Data and Simulation Studies

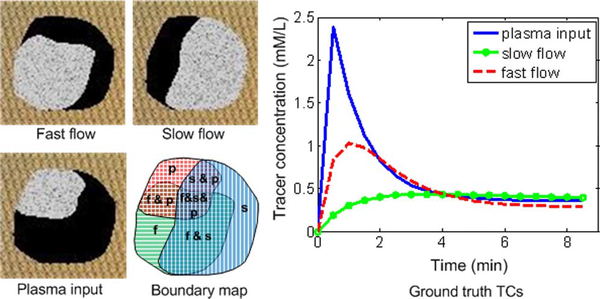
To validate CAM-CM, we reconstituted a large set of synthetic DCE-MRI time series by multiplying customized local volume transfer constant maps K^trans(i) by known compartment TCs F (k_ep,f,k_ep,s,C_p) (Fig. 3). Such mixtures mimic the common scenario in DCE-MRI of actual tumors [1], [8], [9], [21], [41]. Specifically, four sets of compartment TCs were synthesized according to the ground truth kinetic parameter values listed in Table I and were sampled at t_l = 0.5(l – 1) for l = 1, 2,…18 [41], The three customized local volume transfer constant maps K^trans(i) were synthesized based on the K(i) maps given in Fig. 3 multiplied by the compartment K^trans listed in Table I, where K(i) takes one of the vectors {[1,0,0], [0,1,0], [0,0,1]} for pure-volume pixels, one of the vectors {[0.5,0.5,0], [0.5,0,0.5], [0,0.5,0.5]} for two-tissue compartment partial-volume pixels, and equal-weight vector [1/3,1/3,1/3] for three-compartment partial-volume pixels. To account for object variability, we superimposed maximally 15% relative object variability to K(i) by introducing a zero-mean Gaussian perturbation term, where negative values were truncated to zero and K(i) was re-normalized. For highly unlikely pixels with all three negative values, we simply eliminated them from the synthetic data sets. To account for experimental noise, we introduced a zero-mean Gaussian term ε with covariance matrix $\mathrm{\Sigma }\left({\sigma }_{ij}={0.9}^{i-j}|{\sigma }^2\right)$ to each pixel kinetics C(i) = [F₁,…,F_J]K^trans(i) + ε, where the values of σ² were chosen according to the three signal-to-noise ratio (SNR) levels listed in Table I and defined by [29]

$$\text{SNR}=10{\log }_{10}\left[\frac{\sum _{l=1}^L{\left(C\left(i,t_l\right)-\frac{1}{L}\sum _{l^{\prime }=1}^{L}C\left(i,t_{l^{\prime }}\right)\right)}^2}{{\sigma }^{2}L}\right].$$ (31)

Fig. 3.

The spatial distributions of the compartments and TCs associated with the compartmental kinetic parameters used in the realistic DCE-MRI simulations. The nontumor background is denoted by “carpet texture” and the compartment pure-volume distributions are denoted by three partially-overlapped gray regions. The boundaries of the overlapping compartment pure-volume regions are also illustrated in “boundary map.”

Table I.

Kinetic Parameter Values Estimated by CAM-CM, Classic CM, and IQML Methods on the Simulation Data Sets, With Random Initialization

Ground truth parameter values		SNR=20dB			SNR=15dB			SNR=10dB
		CAM	CM	IQML	CAM	CM	IQML	CAM	CM	IQML
Scenario 1	$K_s^{\text{trans}}$= 0 03 /min	0.035±0.002	0.048±0.001	0.061±0.040	0.033±0.006	0.047±0.001	0.066±0.037	0.037±0.005	0.046±0.001	0.079±0.043
	kep,s = 0.1 /min	0.104±0.003	0.226±0.001	0.208±0.016	0.120±0.022	0.231±0.001	0.232±0.081	0.098±0.030	0.226±0.003	0.235±0.077
	$K_f^{\text{trans}}$= 0.03 /min	0.035±0.002	0.094±0.001	0.096±0.064	0.034±0.005	0.083±0.001	0.098±0.056	0.038±0.004	0.084±0.001	0.123±0.067
	kep,f= 0.5 /min	0.498±0.020	0.913±0.002	0.606±0.047	0.489±0.031	0.805±0.001	0.645±0.324	0.415±0.057	0.820±0.008	0.674±0.272
Scenario 2	$K_s^{\text{trans}}$= 0 03 /min	0.043±0.009	0.051±0.001	0.076±0.043	0.042±0.010	0.050±0.001	0.079±0.036	0.042±0.005	0.0049±0.001	0.076±0.036
	kep,s =0.1 /min	0.124±0.019	0.265±0.001	0.154±0.002	0.116±0.023	0.258±0.001	0.192±0.057	0.088±0.031	0.247±0.003	0.171±0.048
	$K_f^{\text{trans}}$= 0.05 /min	0.074±0.017	0.125±0.001	0.116±0.067	0.069±0.017	0.123±0.008	0.129±0.061	0.067±0.007	0.133±0.001	0.132±0.063
	kep,f =1.2 /min	1.286±0.058	1.587±0.005	0.508±0.007	1.232±0.074	1.545±0.006	0.654±0.229	1.003±0.182	1.708±0.019	0.648±0.235
Scenario 3	$K_s^{\text{trans}}$ = 0.06 /min	0.085±0.011	0.095±0.001	0.118±0.042	0.084±0.010	0.092±0.001	0.122±0.033	0.085±0.011	0.095±0.001	0.118±0.042
	kep,s =0.5 /min	0.516±0.014	0.758±0.001	0.728±0.133	0.510±0.030	0.743±0.002	0.735±0.106	0.516±0.014	0.758±0.001	0.728±0.133
	$K_f^{\text{trans}}$= 0.05 /min	0.071±0.010	0.134±0.001	0.149±0.054	0.071±0.009	0.132±0.001	0.158±0.043	0.071±0.010	0.134±0.001	0.149±0.054
	kep,f =1.2 /min	1.256±0.043	1.729±0.001	1.386±0.319	1.256±0.076	1.736±0.004	1.435±0.278	1.256±0.043	1.729±0.001	1.386±0.319
Scenario 4	$K_s^{\text{trans}}$= 0.05 /min	0.068±0.009	0.101±0.001	0.112±0.030	0.066±0.009	0.096±0.001	0.112±0.033	0.068±0.009	0.101±0.001	0.112±0.030
	kep,s =0.6 /min	0.625±0.011	1.047±0.001	0.795±0.201	0.627±0.038	1.000±0.002	0.784±0.179	0.625±0.011	1.047±0.001	0.795±0.201
	$K_f^{\text{trans}}$= 0.08/min	0.109±0.015	0.168±0.001	0.169±0.045	0.100±0.017	0.154±0.001	0.165±0.048	0.109±0.015	0.168±0.001	0.169±0.045
	kep,f =1.5 /min	1.582±0.040	2.104±0.004	1.335±0.401	1.425±0.183	1.957±0.006	1.309±0.371	1.582±0.040	2.104±0.004	1.335±0.401

We report the results of the analysis of total 600 (= 4×3×50) synthetic data sets, where 50 replicated data sets were generated for each of the 12 parameter settings. We compared the estimated tissue-specific compartmental kinetic parameter values by CAM-CM with the ground truth and observed consistent high estimation accuracy in terms of low estimation biases and variances (Table I). From these experimental assessments, the capability of CAM-CM approach is evident as the estimates of tissue-specific kinetic parameters are very close to the ground truth even with significant PVE present in a large number of pixels in the synthetic data sets.

Accurate correction of PVE enables the maximization of information obtainable from DCE-MRI of a heterogeneous tumor [1], [3], [9], [10]. To estimate the beneficial impact of eliminating PVE to tissue-specific compartment analysis, we analyzed the same data sets using two ROI-based methods: classic CM and IQML. The extensive experimental results show that CAM-CM significantly and consistently outperform the two peer methods on almost all data sets in terms of much lower estimation biases and variances (the most accurate estimates are marked as bold numbers for each scenario and noise level in Table I). Since classic CM and IQML do not explicitly correct PVE present in the overlapping areas of different compartments, large resulting biases in the tissue-specific kinetic parameter estimates are expected. On the other hand, the experimental results show the efficacy of CAM in eliminating the impact of PVE and reducing the estimation biases. Specifically, on $K_s^{\mathrm{trans}}$ estimation, CAM-CM achieved 25%−84% and 57%−92% reductions in relative bias over classic CM and IQML, respectively; on $K_f^{\mathrm{trans}}$ estimation, CAM-CM achieved 68%−93% and 64%−94% reductions in relative bias over classic CM and IQML, respectively; on k_ep,s estimation, CAM-CM achieved 85%−98% and 57%−92% reductions in relative bias over classic CM and IQML, respectively; on k_ep,f estimation, CAM-CM achieved 61%−99% and 50%−98% reductions in relative bias over classic CM and IQML, respectively.

To further illustrate the inevitable impact of PVE to the estimation bias of the tissue-specific kinetic parameters produced by classic CM and IQML, we used the true values of the kinetic parameters (ground truth) to initialize the classic CM and IQML algorithms. As expected (Table II), the experimental results show that the parameter estimates actually moved away from the initial, ground truth values, approaching the biased values similar to those summarized in Table I.

TABLE II.

Kinetic Parameter Values Estimated by Classic CM and IQML With Algorithms Being Initialized by the Ground Truth

Ground truth parameter values		SNR=20dB		SNR=15dB		SNR=10dB
		CM	IQML	CM	IQML	CM	IQML
Scenario 1	$K_s^{\text{trans}}$ = 0.03 /min	0.048	0.074	0.048	0.074	0.047	0.074
	kep,s =0.1 /min	0.227	0.170	0.231	0.193	0.228	0.186
	$K_f^{\text{trans}}$ = 0.03 /min	0.094	0.111	0.084	0.106	0.085	0.107
	kep,f =0.5 /min	0.920	0.496	0.810	0.515	0.827	0.509
Scenario 2	$K_s^{\text{trans}}$ = 0.03 /min	0.051	0.038	0.050	0.040	0.049	0.040
	kep,s =0.1 /min	0.266	0.154	0.257	0.163	0.253	0.156
	$K_f^{\text{trans}}$ = 0.05/min	0.125	0.058	0.124	0.063	0.134	0.067
	kep,f =1.2 /min	1.596	0.506	1.542	0.545	1.708	0.572
Scenario 3	$K_s^{\text{trans}}$ = 0.06/min	0.095	0.160	0.093	0.159	0.092	0.161
	kep,s =0.5 /min	0.758	0.631	0.745	0.624	0.756	0.633
	$K_f^{\text{trans}}$ = 0.05/min	0.134	0.200	0.132	0.200	0.130	0.200
	kep,f =l.2/min	1.729	1.144	1.730	1.144	1.724	1.143
Scenario 4	$K_s^{\text{trans}}$ = 0.05/min	0.101	0.119	0.097	0.128	0.098	0.128
	kep,s= 0.6 /min	1.045	0.849	0.998	0.849	1.001	0.850
	$K_f^{\text{trans}}$ = 0.08/min	0.168	0.181	0.155	0.191	0.157	0.189
	kep,f= 1.5 /min	2.106	1.418	1.960	1.422	1.965	1.422

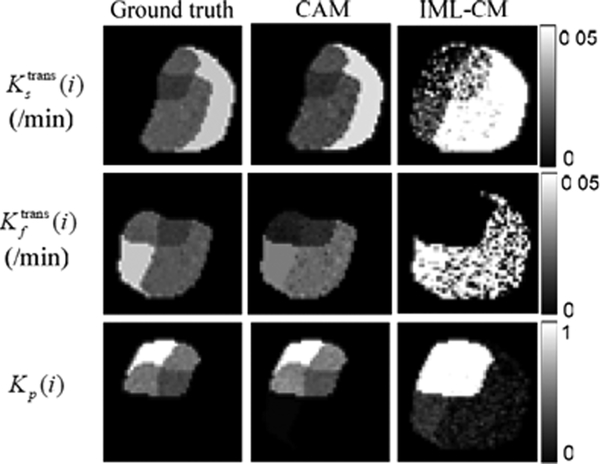
To validate CAM-CM in reconstructing local volume transfer constant maps K^trans(i) based on (27), we calculated the RMSE between the estimated tissue-specific compartmental kinetic parameter values ${\widehat{\mathbf{K}}}^{\mathrm{trans}}(i)$ by CAM-CM and the ground truth using (28) and observed consistent high estimation accuracy. Specifically, on data sets with scenario 1 parameter settings and 15 dB SNR, CAM-CM achieved quite low RMSE (mean ± standard deviation calculated over 50 replicated data sets), with RMSE_f = 0.163±0.032, RMSE_s = 0.145±0.042, and RMSE_P = 0.055 ± 0.021, respectively. We then analyzed the same data sets using the pixel-based method, IML-CM [18], and observed much higher RMSE, with RMSE_f = 0.529 ± 0.100, RMSE_s = 0.501 ± 0.095, and RMSE_p = 0.345 ± 0.040, respectively. Fig. 4 shows the local volume transfer constant maps estimated by CAM-CM and IML-CM, respectively. In addition, tested on the synthetic data sets with ground truth flux rate constants k_ep,s = 0.1 min⁻¹ and k_ep,f = 0.5 min⁻¹, CAM-CM produced more accurate and reliable estimates of ${\widehat{k}}_{\text{ep},s}=0.120\pm 0.022$ min⁻¹ and ${\widehat{k}}_{\text{ep},f}=0.489\pm 0.031$ min⁻¹ as compared to the highly biased and unstable estimates of ${\widehat{k}}_{\text{ep},s}=0.2773\pm 0.105$ min⁻¹ and ${\widehat{k}}_{\text{ep},f}=0.635\pm 0.278$ min⁻¹ produced by IML-CM.

Fig. 4.

Local volume transfer constants maps estimated by CAM-CM and IML-CM.

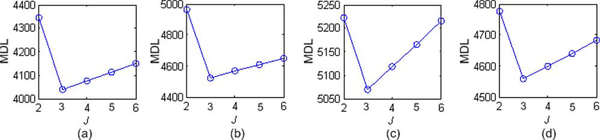
To determine whether the proposed MDL criterion (see (24) and Appendix B) selects the correct number of underlying tissue compartments (J = 3), we calculated the MDL values for J = 2, 3,…, 6 and found that MDL achieves its minimum values when J = 3, indicating the efficacy of the proposed MDL criterion in determining correct model structure. Fig. 5 displays the calculated MDL values (for scenarios 1–4) when SNR = 10 dB.

Fig. 5.

Model selection by MDL on different simulation data sets. MDL consistently indicates J = 3 as the optimum model order that is also consistent with the ground truth. (a) Scenario 1.SNR = 10dB (b) Scenario 2 SNR = 10 dB.(c) Scenario 3 SNR = 10 dB. (d) Scenario 4 SNR = 10 dB.

C. Real DCE-MRI Data Studies

As aforementioned, classic compartment modeling methods are oblivious to tissue heterogeneity. They can neither distinguish between variations in kinetic patterns resulting from actual physiological changes versus differences in tissue-type composition, nor identify the contributions of different compartments to the total measured tracer concentration. Therefore, their power to detect mechanistic change of kinetic patterns could be significantly confounded by tumor variations under different tissue-type compositions [1], [9].

We first considered a T1-weighted gadolinium-enhanced (Gd-DTPA) DCE-MRI data set (collected by P. L. Choyke, NIH Clinical Center) of an advanced breast cancer case [11], [12] (Fig. 1). The three-dimensional DCE-MRI scans were performed every 30 s for a total of 11 min after the injection, on a 1.5T magnet using three-dimensional spoiled gradient-echo sequences (TR < 7 ms, TE < 1.5 ms, flip angle = 30°, matrix = 192 × 256, 0.5 averages). Typically, 12–15 slices are obtained and 15–18 time frames are acquired for each case.

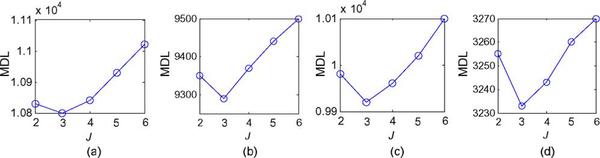
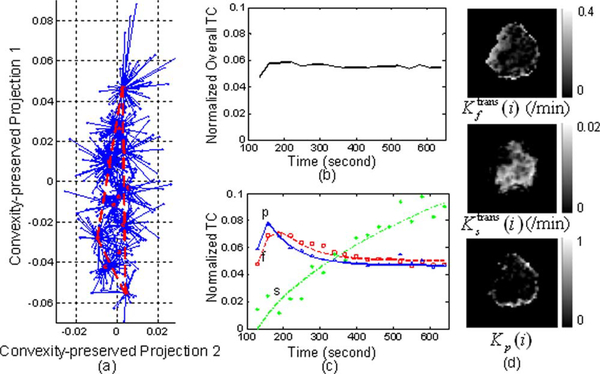
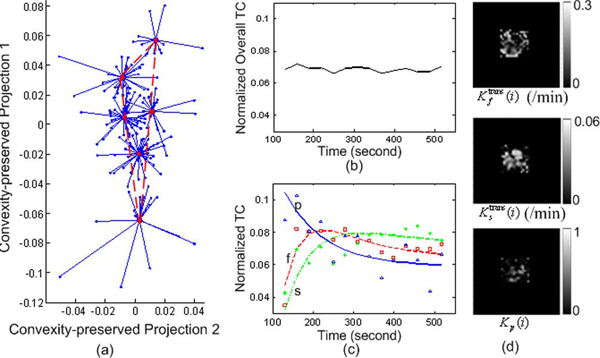
We applied the proposed MDL criterion together with clustered compartment model to detect the number of underlying tissue compartments, and observed that with J = 3, MDL achieves its minimum value [see Fig. 6(a)]. We therefore set J = 3 for this data set. Our CAM-CM analysis reveals two biologically interpretable compartments with distinct physiological kinetic patterns [Fig. 7(c)]: 1) Fast-flow: fast clearance rate of the tracer; 2) Slow-flow: very slow tracer kinetics. They are associated with local volume transfer constant maps with different spatial distributions [Fig. 7(d)]: 1) Fast-flow: peripheral “rim” region of the tumor; 2) Slow-flow: inner “core” region of the tumor. As can be expected, the overlap of regions (partial volume pixels) that was noticed on these maps cannot be obtained in the ROI studies. Our analysis indicates that the tumor site contains a significant fraction (84.3%) of partial volume pixels, which can be visually observed from and verified by the “filled” three-corner convex hull of the projected pixel time series scatter plot [Fig. 7(a)]. As shown by the dissected and overall TC dynamic patterns [Fig. 7(c) versus (b)], the values found for the kinetic parameters by CAM-CM demonstrate that the tumor site contains rapid and slow tracer clearance compartments and estimated K^trans(i) varies from pixel to pixel, which otherwise could not be seen if tissue heterogeneity was not taken into account [9].

Fig. 6.

Model selection by MDL on real DCE-MRI data sets. MDL consistently suggests J = 3 as the optimum model order. (a) Typical case. (b) Longitudinal 1. (c) Longitudinal 2. (d) Longitudinal 3.

Fig. 7.

The experimental results of CAM-CM on a typical breast cancer DCE-MRI data. The estimated kinetic parameters are $K_f^{\text{trans}}=0.382/\text{min}$, $K_s^{\text{trans}}=0.017/\text{min}$, k_ep,f = 3.063/min, k_ep,s = 0.293/min. (a) The identified convex hull of clustered pixel TCs (Blue dots: normalized pixel TCs; Red circles: cluster centers; Blue lines: cluster memberships). (b) Normalized overall TC calculated from the entire tumor ROI. (c) Normalized compartment TCs estimated by CAM-CM (the discrete curves show the normalized TCs directly estimated via CAM; while the smooth curves show the normalized TCs which are fitted by the kinetic parameters estimated via CAM-CM). (d) Local volume transfer constant maps estimated by CAM-CM.

The outcomes of CAM-CM analysis are plausibly consistent with the previously reported heterogeneity within tumors [1], [9], [11], [42]. Since angiogenesis is essential to tumor development, it has been widely observed that active angiogenesis in advanced breast tumors often occurs in the peripheral “rim” with co-occurrence of inner-core hypoxia [1], [43]. Defective endothelial barrier function due to vascular endothelial growth factor (VEGF) expression is one of the best-documented abnormalities of tumor vessels, resulting in spatially heterogeneous high microvascular permeability to macromolecules [1], [9], [11]. Specifically, tumor neovasculature is abnormal—leaky vessels, chaotic and tortuous structure, and dead ends, giving rise to a rapid enhancement and gradual washout pattern [11]. At the same time, as a tumor grows, it rapidly outgrows its blood supply and requires neovessel maturation, leaving an inner core of the tumor with regions where the blood flow and oxygen concentration are significantly lower than in normal tissues, gives rise to a much slower accumulation and minimum washout pattern [11], [44], In fact, the estimated K^trans(i) maps reveal regions of differential function that correlate with differential gene expression involved in angiogenesis [11], [42], Furthermore, the CAM-CM estimated values of k_ep,f = 3.06 min⁻¹ and k_ep,s = 0.29 min⁻¹ were generally consistent with the parameter values (k_ep,f = 2.95 min⁻¹ and k_ep,s = 0.16 min⁻¹) reported by the most relevant studies [41].

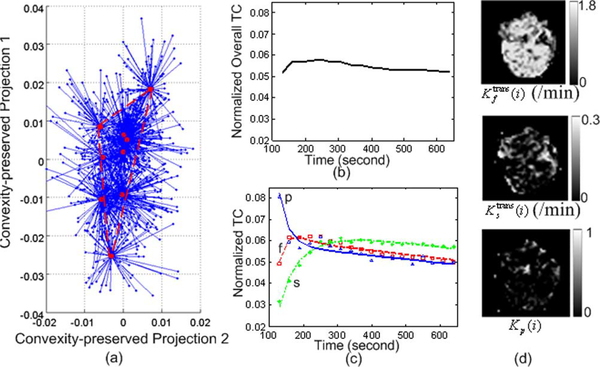
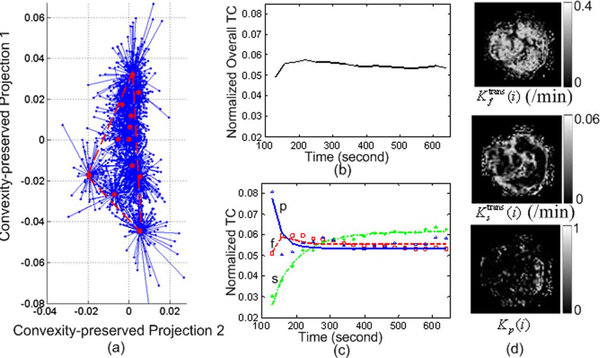
As an example of a more complex problem, we considered the data sets arising from a longitudinal study of tumor response to anti-angiogenic therapy using similar imaging protocols (Figs. 8–10) [1], [11], [42]. Three sets of DCE-MRI data were acquired before, during, and after the treatment period, each three months apart, serving as the potential endpoints in assessing the response to therapy. We calculated the MDL values based on (24) for J = 2,…, 6, and MDL suggests J = 3 for all these three data sets [see Fig. 6(b)-(d)]. On data set 1 (baseline), our CAM-CM analysis reveals two biologically interpretable compartments with distinct physiological kinetic patterns [Fig. 8(c)]. They are associated with local volume transfer constants maps with a significant fraction (72.4%) of partial volume pixels [Fig. 8(d)], which can be visually observed from the “filled” three-corner equal-lateral convex hull of the projected pixel time series scatter plot [Fig. 8(a)]. This represents a relatively less aggressive and early stage breast tumor with relatively higher permeability k_ep,f = 2.093 min⁻¹ in its fast-flow pool and relatively lower permeability k_ep,s = 0.695 min⁻¹ in its slow-flow pool (Table III). As expected, local volume transfer constants maps do not show any visible rim-shape region of aggressive angiogenesis or inner-core region of hypoxia but rather more uniform distributions of the two compartments.

Fig. 8.

The results of CAM-CM on DCE-MRI data set 1 of the breast cancer longitudinal study. (a) Identified convex hull of clustered pixel TCs (Blue dots: normalized pixel TCs; Red circles: cluster centers; Blue lines: cluster memberships). (b) Normalized overall TC calculated from the entire tumor ROI. (c) Normalized compartment TCs estimated by CAM-CM. (d) Local volume transfer constant maps estimated by CAM-CM.

Fig. 10.

The results of CAM-CM on DCE-MRI data set 3 of the breast cancer longitudinal study.

TABLE III.

Estimated Kinetic Parameters on Longitudinal Breast Cancer DCE-MRI Data Sets

	${\mathit{K}}_{\mathit{f}}^{\mathbf{trans}}$ (/min)	${\mathit{K}}_{\mathit{s}}^{\mathbf{trans}}$ (/min)	kep,f (/min)	kep,s (/min)
Longitudinal 1	1.780	0.270	2.093	0.695
Longitudinal 2	0.412	0.057	1.781	0.749
Longitudinal 3	0.289	0.055	1.068	0.582

On data set 2 (the same tumor, acquired during the treatment), our CAM-CM analysis reveals two biologically interpretable compartments with distinct, yet with much closer physiological kinetic patterns [Fig. 9(c)]. They are associated with local volume transfer constants maps with a significant fraction (61.8%) of partial volume pixels [Fig. 9(d)], which can be visually observed from the “filled” three-corner convex hull of the projected pixel time series scatter plot [Fig. 9(a)]. The CAM-CM estimated values of k_ep,f = 1.781 min⁻¹ and k_ep,s = 0.749 min⁻¹ indicated much reduced permeability in its fast-flow pool and slightly increased permeability in its slow-flow pool (Table III), while local volume transfer constant maps reveal disconnected and reduced regions of localized angiogenesis and connected and enlarged regions of normalized tissue [Fig. 9(d)]. On the data set 3 of the same tumor acquired after the treatment period, our CAM-CM analysis reveals two similar compartments with largely converged physiological kinetic patterns [Fig. 10(c)]. They are associated with local volume transfer constants maps with a significant fraction (59.4%) of partial volume pixels [Fig. 10(d)], which can be visually observed from the blended obtuse-isosceles triangle convex hull of the projected pixel time series scatter plot [Fig. 10(a)]. The CAM-CM estimated values of k_ep,f = 1.068 min⁻¹ and k_ep,s = 0.582 min⁻¹ indicate significantly reduced overall vascular permeability (Table III), while local volume transfer constant maps reveal globally reduced yet only isolated angio-genic activities [Fig. 10(d)].

Fig. 9.

The results of CAM-CM on DCE-MRI data set 2 of the breast cancer longitudinal study.

The outcomes of CAM-CM analysis here are plausibly consistent with the reported observations on tumor response to antiangiogenic therapy [1], [3], [5], [9], [11], [12], [43]. The interaction between angiogenic inhibitors and tumor vasculature is a complex process depending upon the doses and timing of the applied therapeutic agents [5], [9]. For example, controlled antiangiogenic therapies not only destroy aggressive angiogenesis but also transiently “normalize” the abnormal structure and function of surviving tumor vasculature to make it more efficient for oxygen and drug delivery. Initial results from trials of angiogenesis inhibitors monitored with DEC-MRI suggest that before therapy, the tumors are often highly and heterogeneously perfused and permeable, while soon after successful therapy begins, dramatically decreased perfusion and permeability can be detected [1], [11]. In breast cancer, a decrease in transendothelial permeability has been reported to accompany tumor response to therapy [9], [11]. We note that tumor induced vascular activities were significantly reduced as an early response to therapy, where most noticeable is the large and consistent drop in the relative fraction of the $K_f^{\text{trans}}(i)$ map and permeability rate k_ep,f (slower initial enhancement, decreased amplitude, slower wash-out) [11]. We note that the tumor vasculature is intrinsically heterogeneous and, as a result, the whole tumor region may not demonstrate responses to antiangiogenic therapy that occur in some parts of the tumor but not in other parts [12]. We also note that tumor islands of persistent enhancement have escaped the effects of therapy, representing previously reported foci of resistant and more aggressive clones within a tumor [3], [11], Once again, the CAM-CM estimated values of k_ep = 0.58 ~ 2.09 min⁻¹ were generally consistent with the parameter values of k_ep = 0.88 ~ 1.93 min⁻¹ reported by the most relevant studies [41].

V. Conclusion and Discussion

In this paper, we have addressed the critical yet subtle issue of spatially-mixed pixel-wise partial volume effect in multi-compartment modeling applied to kinetic parameter estimation using real DCE-MRI data [3], [9]-[12]. We have presented the CAM-CM approach to implement tissue-specific compartment modeling of DCE-MRI on complex tumors, which combines multivariate pixel time-series clustering, convex geometry analysis of the clustered scatter plot simplex, and PVE-free compartment modeling (Fig. 1). As illustrated both by extensive realistic simulations with significant PVE (more than 50% of pixels being spatially-mixed pixel-wise partial-volume pixels) and by real examples, CAM-CM can be very effective at revealing multi-compartment structure within the DCE-MRI data of highly heterogeneous tumors, eliminating partial-volume pixels, and estimating tissue-specific kinetic parameter values. The multiform summaries of Figs. 7–10 are visually simple to interpret, yet still convey considerable mathematical insights. While the effectiveness of many attempts on tissue-specific compartment modeling is often data-dependent given the challenging nature of the task, we would expect the CAM-CM method, with publicly available open-source software package, to be a very useful tool for the exploratory analysis in many research and clinical applications.

It is important to emphasize that in compartment modeling there is no absolute ground truth about the underlying physical model, and so it is difficult to validate the merits of a particular tissue-specific compartment modeling technique. This is one reason, clearly, why there are repeated discussions on the problems associated with tissue heterogeneity in compartment modeling [1], [3], [9]-[12], [21]. We note that we have opted for mathematical identifiability as opposed to large-scale assessment in designing our method. our primary goal was to demonstrate that convex analysis of the clustered pixel time-series scatter plot simplex is able to separate pure-volume pixels from spatially-mixed partial-volume pixels and to achieve PVE-free tissue-specific compartment modeling. our studies suggest that using a sufficient number of pure-volume pixels detected by clustered CAM as we do here combines the advantages of high-sNR sub-RoI based methods and less-PVE pixel-based methods [3], [9], [11], [12], [14], [22], [23], leading to a substantial improvement in the accuracy and reproducibility of multi-compartment kinetic parameter estimation. We have not explored the full flexibility that this method readily allows, with different numbers of clusters, M. Presumably, equal or better performance could be achieved with more clusters if more pixels were available. We may readily extend our method to incorporate spatial prior knowledge in place of the pixel time-series clustering in the current CAM-CM framework [16].

In relation to previous work, the concept of isolating sub- RoIs or single pixels for compartment or parametric analysis can be traced back to Zhu et al. [14], Hayes et al. [45], Li et al. [2], and Mayr et al. [46], and was further developed by Riabkov et al., [13], Yankeelov et al. [43], and Kelm et al. [16] by incorporating spatial prior knowledge (adjacent smoothness) or histogram analysis. As pointed out by Padhani and Leach [3], [19] and Cinotti et al. [22], pixel-based approaches attempt to visually appreciate tissue heterogeneity (thus being able to spatially match diagnostically-important tumor vascular characteristics) and remove the need to selectively place user-defined sub-RoIs, while at the cost of having poor sNR and less quantitative in- terpretability. It is important to emphasize that an additional limitation associated with these approaches is the inability to address spatially-mixed pixel-wise partial-volume effect, while the CAM-CM approach discussed in this paper permits robust identification of pure-volume pixels and subsequent PVE-free multi-compartment modeling. There is some similarity between the present method and our earlier work [18] which explicitly incorporates the PVE model (3) into a pixel-based maximum likelihood framework and so offers the potential for unbiased multi-compartment modeling. As well as again a key distinction is that the CAM-CM approach also allows to minimize the noise effect on modeling by aggregating pixels in a few clusters. Thus, it avoids a pixel by pixel compartmental analysis where noise would be maximum due to the lack of statistical accuracy [22].

A software implementation of the CAM-CM algorithm in open-source MATLAB is freely available online.¹

Appendix A

Proof of Lemma 1: By the definition of convex set [25], the fact that $\forall \{i,j\}{K}_j(i)\ge 0,{\sum }_{j=1}^J{K}_j(i)=1$, and $\mathbf{x}(i)={\sum }_{j=1}^J{K}_j(i){\mathbf{a}}_j$ readily yield $\mathbf{x}(i)\in \mathcal{H}\left\{\mathcal{A}\right\}$ where

$$\mathcal{H}\{\mathcal{A}\}=\left\{\sum _{j=1}^J{\alpha }_j{\mathbf{a}}_j|{\mathbf{a}}_j\in \mathcal{A},{\alpha }_j\ge 0,\sum _{j=1}^J{\alpha }_j=1\right\}.$$ (A1)

Since a₁,…a_J are linearly independent, it follows that

$$\sum _{j=1}^J{\alpha }_j{\mathbf{a}}_j=\mathbf{0}\text{iff}{\alpha }_j=0\forall j$$ (A2)

that also implies that ∀j

$${\mathbf{a}}_j=\sum _{j=1}^J{\alpha }_j^{\prime }{\mathbf{a}}_j\text{iff}{\left[{\alpha }_1^{\prime },\dots ,{\alpha }_J^{\prime }\right]}^T={\mathbf{e}}_j\forall j$$ (A3)

i.e., a_j can only be a trivial convex combination of a₁,…,a_J. Hence, by Definition 2, a₁,…,a_J are therefore the corner points of convex set $\mathcal{H}\left\{\mathcal{A}\right\}$.

Proof of Theorem 1: Since $\exists i_{\text{WGP}(j)},\mathbf{K}\left(i_{\text{WGP}(j)}\right)={\mathbf{e}}_j\forall j$, and $\mathbf{x}(i)={\sum }_{j=1}^J{K}_j(i){\mathbf{a}}_j$, we have

$$\mathbf{x}\left(i_{\text{WGP}(j)}\right)={\mathbf{a}}_j.$$ (A4)

Then, for any

$$\mathbf{z}\in \mathcal{H}\{\mathcal{A}\}=\left\{\sum _{j=1}^J{\alpha }_j{\mathbf{a}}_j|{\mathbf{a}}_j\in \mathcal{A},{\alpha }_j\ge 0,\sum _{j=1}^J{\alpha }_j=1\right\}$$

we have

$$\begin{gathered} \mathbf{z}=\sum _{j=1}^J{\alpha }_j{\mathbf{a}}_j=\sum _{j=1}^J{\alpha }_j\mathbf{x}\left(i_{\text{WGP}(j)}\right) \\ =\sum _{i=1}^N{\alpha }_i^{\prime }\mathbf{x}(i),\text{where}{\alpha }_i^{\prime }=\{\begin{array}{ll}{\alpha }_j,\hfill & i\in \left\{i_{\text{WGP}(j)}\right\}\hfill \\ 0,\hfill & i\notin \left\{i_{\text{WGP}(j)}\right\}\hfill \end{array} \end{gathered}$$ (A5)

that implies $\mathbf{z}\in \mathcal{H}\{\mathcal{X}\}=\left\{{\sum }_{i=1}^N{\alpha }_i^{\prime }\mathbf{x}(i)|\mathbf{x}(i)\in \mathcal{X},{\alpha }_i^{\prime }\ge 0,{\sum }_{i=1}^N{\alpha }_i^{\prime }=1\right\}$, i.e., $\mathcal{H}\left\{\mathcal{A}\right\}\subseteq \mathcal{H}\left\{\mathcal{X}\right\}$. On the other hand, for any $\mathbf{z}\in \mathcal{H}\{\mathcal{X}\}=\left\{{\sum }_{i=1}^N{\alpha }_i\mathbf{x}(i)|\mathbf{x}(i)\in \mathcal{X},{\alpha }_i\ge 0,{\sum }_{i=1}^N{\alpha }_i=1\right\}$, we have

$$\begin{gathered} \mathbf{z}=\sum _{i=1}^N{\alpha }_i\mathbf{x}(i)=\sum _{i=1}^N{\alpha }_i\sum _{j=1}^J{K}_j(i){\mathbf{a}}_j \\ =\sum _{j=1}^J\left[\sum _{i=1}^N{\alpha }_i{K}_j(i)\right]{\mathbf{a}}_j=\sum _{j=1}^J{\beta }_j{\mathbf{a}}_j \end{gathered}$$ (A6)

where ${\beta }_j=\sum _{i=1}^N{\alpha }_i{K}_j(i),\sum _{j=1}^J{\beta }_j=1$ that implies z ∈ $\mathcal{H}\{\mathcal{A}\}=\left\{{\sum }_{j=1}^J{\alpha }_j{\mathbf{a}}_j|{\mathbf{a}}_j\in \mathcal{A},{\alpha }_j\ge 0,{\sum }_{j=1}^J{\alpha }_j=1\right\}$, i.e., $\mathcal{H}\left\{\mathcal{X}\right\}\subseteq \mathcal{H}\left\{\mathcal{A}\right\}$. Combining $\mathcal{H}\left\{\mathcal{X}\right\}\supseteq \mathcal{H}\left\{\mathcal{A}\right\}$ and $\mathcal{H}\left\{\mathcal{X}\right\}\subseteq \mathcal{H}\left\{\mathcal{A}\right\}$ gives $\mathcal{H}\left\{\mathcal{X}\right\}=\mathcal{H}\left\{\mathcal{A}\right\}$, and together with Lemma 1 readily completes the proof of Theorem 1.

Proof of Theorem 2: Consider the pixel $\mathbf{K}\left(i^{*}\right)={\sum }_{j=1}^J{\alpha }_j\left(i^{*}\right)\mathbf{K}\left(c_j\right)$ of the convex hull defined by the corners {K(c_j)} whose mth entry is the largest among all pixels, i.e., $K_m\left(i^{*}\right)={\max }_{i=1,2,\dots N}{K}_m(i)$. Since ${\sum }_{j=1}^J{\alpha }_j\left(i^{*}\right)=1$, we may, therefore, write

$$K_m\left(i^{*}\right)=\left(\sum _{j=1}^J{\alpha }_j\left(i^{*}\right)\right)K_m\left(i^{*}\right)=\sum _{j=1}^J{\alpha }_j\left(i^{*}\right)K_m\left(i^{*}\right).$$ (A7)

Alternatively, the mth entry of K(i*) can be expressed as

$$K_m\left(i^{*}\right)=\sum _{j=1}^J{\alpha }_j\left(i^{*}\right)K_m\left(c_j\right).$$ (A8)

By the unique convex expression of K_m(i*), we have

$$\sum _{j=1}^J{\alpha }_j\left(i^{*}\right)\left(K_m\left(i^{*}\right)-K_m\left(c_j\right)\right)=0$$ (A9)

which, together with the fact αj·(i*) > 0 and K_m(i*) - K_m(c_j) ≥ 0, implies i* ∈ {c_j}. Q.E.D

Proof of Theorem 3: Since e_j represents the ideal source-specific dominance for the jth tissue compartment based on the definition of a pure-volume pixel, we can measure the degree of source-specific dominance in K(c_j) by the Kullback–Leibler (KL) divergence [47]

$$\text{KL}\left({\mathbf{e}}_j\Vert \mathbf{K}\left(c_j\right)\right)=\log \frac{1}{K_j\left(c_j\right)}.$$ (A10)

Similarly, we can evaluate the source-specific dominance in any interior pixel $\mathbf{K}(i)={\sum }_{j=1}^J{p}_{ij}\mathbf{K}\left(c_j\right)$ of the convex hull defined by the corners {K(c_j)}, which is sufficiently close to K(c_j) (i.e., p_ij ≫ p_im for m ≠ j with p_ij being the percentage of jth tissue compartment in pixel i), by the KL divergence

$$\begin{gathered} \text{KL}\left({\mathbf{e}}_j\Vert \mathbf{K}(i)\right) \\ =\log \left(\frac{1}{p_{i1}{K}_j\left(c_1\right)+\cdots +p_{ij}{K}_j\left(c_j\right)+\cdots +p_{iJ}{K}_j\left(c_J\right)}\right). \end{gathered}$$

Since K_j(c_j) ≫ K_m{c_j) and p_ij ≫ p_im for m ≠ j, ignoring the second-order terms {p_imK_j(c_m),m ≠ j} [48], we may, therefore, write

$$\text{KL}\left({\mathbf{e}}_j\Vert \mathbf{K}(i)\right)=\log \frac{1}{p_{ij}{K}_j\left(c_j\right)}.$$ (A11)

Combining (A10) and (A11), we have

$$\text{KL}\left({\mathbf{e}}_j\Vert \mathbf{K}\left(c_j\right)\right)-\text{KL}\left({\mathbf{e}}_j\Vert \mathbf{K}(i)\right)=\log p_{ij}\le 0$$ (A12)

which implies KL(e_j‖K(c_j)) ≤ KL(e_j‖K(i)) Q.E.D.

Appendix B

Our aim herein is to use MDL criterion [32], [36] and the CAM-CM estimates to select the best value of J automatically (the number of convex hull corners or tissue compartments). Since the number of pixels is large as in DCE-MRI application, direct use of MDL may underestimate J, due to the lack of “structure” in classical compartment models (over-parameterization) [18], [32], [33]. We, therefore, propose to naturally adopt and extend a clustered compartment model into the MDL formulation [39].

In the clustered J-tissue compartment model, we allow all pixels belonging to the same cluster [identified from SFNM, see (9) and (10)] to share a common local volume transfer constant, namely K_m with length J,m = 1,…,M. Letting C_m be the mth cluster center associated with K_m, from (4), we can express the clustered compartment model as follows:

$${\mathbf{C}}_m=\left[{\mathbf{F}}_1,\dots ,{\mathbf{F}}_J\right]{\mathbf{K}}_m+\mathbf{n}$$ (B1)

where n is the modeling residual noise assumed to follow zero-mean white Gaussian distribution n ~ N(0,σ²∙I) with variance σ². The corresponding minimum description length (MDL) [36] is then given by

$$\mathrm{MDL}(J)=-\log \left(\mathcal{L}\left({\mathbf{C}}_M|\mathbf{\Phi }(J)\right)\right)+\frac{|\mathbf{\Phi }(J)|}{2}\log (LM)$$ (B2)

where C_M = {C_m,m = 1,2,…,M}, $\mathcal{L}\left({\mathbf{C}}_M|\mathbf{\Phi }(J)\right)$ is the likelihood function for the clustered compartment model, Φ(J) is the set of freely-adjustable parameters in the clustered compartment model, Φ(J) is the cardinality of Φ(J), and L is the length of C_m.

We specify Φ(J) as follows. From (3)-(4), F₁,…,F_J−1 are parameterized by k_ep,j, j = 1,2,…,J−1. Furthermore, C_p is parameterized by {λ₁, λ₂, λ₃, α₂, α₃} based on the well-known exponential model [13], [18], Then, together with K₁,…,K_M and σ, we have

$$\begin{gathered} \mathbf{\Phi }(J)=\{{\lambda }_1,{\lambda }_2,{\lambda }_3,{\alpha }_2,{\alpha }_3,k_{\text{ep},1},k_{\text{ep},2}, \\ \cdots k_{\text{ep},J-1},{\mathbf{K}}_1,\dots ,{\mathbf{K}}_M,\sigma \} \end{gathered}$$

thus Φ(J)| = 5 + J + M ∙ J.

Based on CAM-CM estimated F₁,…,F_J determined by ${\widehat{\mathbf{C}}}_p$ and $\left\{{\widehat{k}}_{\text{ep},j},j=1,\dots ,J-1\right\}$, and K_m and σ obtained by the maximum-likelihood estimation

$$\begin{gathered} {\widehat{\mathbf{K}}}_m=\arg \underset{{}_{{\mathbf{K}}_m}}{\max }\left(\log \left(\mathcal{L}\left({\mathbf{C}}_M|\mathbf{\Phi }(J)\right)\right)\right) \\ =\arg \underset{{}_{{\mathbf{K}}_m}}{\min }\left({\Vert {\mathbf{C}}_m-\left[{\mathbf{F}}_1,\dots ,{\mathbf{F}}_J\right]{\mathbf{K}}_m\Vert }^2\right) \end{gathered}$$

s.t. K_m ≥ 0 ∀m

$$\begin{gathered} \widehat{\sigma }=\arg \underset{\sigma }{\max }\left(\log \left(\mathcal{L}\left({\mathbf{C}}_M|\mathbf{\Phi }(J)\right)\right)\right) \\ =\sqrt{\frac{1}{M\cdot L}\sum _{m=1}^M{\Vert {\mathbf{C}}_m-\left[{\mathbf{F}}_1,\dots ,{\mathbf{F}}_J\right]{\mathbf{K}}_m\Vert }^2} \end{gathered}$$

we can express the joint likelihood function in the MDL given by (B2) as

$$\begin{gathered} \mathcal{L}\left({\mathbf{C}}_M|\mathbf{\Phi }(J)\right) \\ =\prod _{m=1}^M{\left(2\pi {\sigma }^2\right)}^{-L/2}\exp \left(-\frac{{\Vert {\mathbf{C}}_m-\left[{\mathbf{F}}_1,\dots ,{\mathbf{F}}_J\right]{\mathbf{K}}_m\Vert }^2}{2{\sigma }^2}\right). \end{gathered}$$ (B3)