Abstract
We summarize unique aperture data on the degree of linear polarization observed for distant comets C/2010 S1, C/2010 R1, C/2011 KP36, C/2012 J1, C/2013 V4, and C/2014 A4 with heliocentric distances exceeding 3 AU. Observations have been carried out at the 6-m telescope of the Special Astrophysical Observatory of the Russian Academy of Sciences (Nizhnij Arkhyz, Russia) during the period from 2011 to 2016. The measured negative polarization proves to be significantly larger in absolute value than what is typically observed for comets close to the Sun. We compare the new observational data with the results of numerical modeling performed with the T-matrix and superposition T-matrix methods. In our computer simulations, we assume the cometary coma to be an optically thin cloud containing particles in the form of spheroids, fractal aggregates composed of spherical monomers, and mixtures of spheroids and aggregate particles. We obtain a good semi-quantitative agreement between all polarimetric data for the observed distant comets and the results of numerical modeling for the following models of the cometary dust: (i) a mixture of submicrometer water-ice oblate spheroids with aggregates composed of submicrometer silicate monomers; and (ii) a mixture of submicrometer water-ice oblate spheroids and aggregates consisting of both silicate and organic monomers. The michrophysical parameters of these models are presented and discussed.
Keywords: Distant comets, Polarization, Electromagnetic scattering, Aggregated particles, Numerical modeling
1. Introduction
Physical properties of cometary atmospheres are known primarily on the basis of observational data obtained for bright comets close to the Earth and the Sun (mostly at 1–2 AU). It was believed early that the nature of the particles forming cometary comas does not depend on the heliocentric distance [1]. However, more recent observations show the existence of differences between the activity of close-to-the-Sun comets and those located at large heliocentric distances (see, e.g., Refs. [2–5]). Therefore, it is reasonable to expect that the nature of particles in these two types of comets may be different as well. Since polarimetric observations of comets often allow one to obtain useful information about the properties of particles in their comas, such measurements have been carried out intensively for comets close to the Sun (see Refs. [6,7] and references therein). However, no ground-based polarimetric observations had been performed until quite recently for distant comets (i.e., those at heliocentric distances exceeding 3 AU). The first results of such observations have been published in Refs. [8,9]. In particular, they show a deeper branch of negative polarization at small phase angles in comparison with that observed for comets close to the Sun. Despite the limited statistics of these observations, one can assume that the particulate compositions of the atmospheres of these two types of comets can also be different.
The investigation of optical properties of cometary particles based on the results of polarimetric observations carried out for bright comets has been a hot topic over the past 15 years (see, e.g., Refs. [10–19]). Nevertheless, even though observational data have been obtained over wide ranges of phase angles and wavelengths, there is still no definitive conclusion as to the nature, morphology, and size of the particles in the atmospheres of these comets. Typically, analyses of polarimetric observations are largely focused on the reproduction of the negative branch of linear polarization at small phase angles. As the initial step, a model of the particle morphology is selected, for example aggregates [10–14], agglomerated debris [16,17], spheroids [10,18], or a mixture of aggregates and spheroids [15,19]. In Ref. [8], the first attempt was made to analyze the results of polatimetric measurements obtained for the distant comet C/2010 S1. It was found that the model of dust in the form of compact aggregates of an overall radius Rag ~ 1.3 μm composed of N = 1000 spherical monomers with a radius a = 0.1 μm and a refractive index m = 1.65 + i 0.05 allows one to obtain a satisfactory agreement between the results of polarimetric observations and computations.
The new polarimetric observations of distant comets remain sparse and cannot be used yet to derive individual models of dust for each comet. However, their systematic deviation from the results of previous polarimetric observations of comets at small heliocentric distances undoubtedly warrants an initial theoretical analysis. Hence the main objectives of this paper are as follows: (i) to summarize recent polarimetric data observed for six distant comets; (ii) to present the results of theoretical modeling of light scattering characteristics performed for different particle morphologies and to compare them with the observations; and (iii) based on the results of this comparison, to discuss the possible composition of particles in the atmospheres of distant comets. The final section summarizes our findings.
2. Results of polarimetric observations
Table 1 summarizes the results of aperture polarimetric observations carried out for distant comets during the period from 2011 to 2016. These observations have been performed using the 6m telescope of the Special Astrophysical Observatory (Nizhnij Arkhyz, Russia) with the multimode focal reducer SCORPIO-2 [20,21]. A detailed description of the procedure used to process polarimetric images is given in Refs. [9,22]. Table 1 provides the following information: the date of an observation (the mid-cycle time); the respective heliocentric, r, and geocentric, Δ, distances; the phase angle α; the spectral filter and its effective wavelength λeff; the total exposure time Texp; the degree of linear polarization P; and the name of the comet. It should be noted that because the tabulated values of polarization have been obtained from measurements with a circular projected diameter of the aperture ranging from 5000 up to 8000 km, they only represent average values of polarization for a cometary coma. This is explained by the fact that active comets have extended atmospheres of varying structure [8]. As a consequence, the measured values of polarization depend on the aperture used, and hence allow one to infer only “average” characteristics of cometary particles.
Table 1.
Log of polarimetric observations of distant comets
| UT Date |
r (AU) |
Δ (AU) |
α (deg) |
Filter |
λeff (μm) |
Texp (s) |
P (%) |
Object |
|---|---|---|---|---|---|---|---|---|
| Nov. 25.71, 2011 | 7.01 | 6.52 | 7.3 | V | 0.551 | 540 | −1.9 | C/2010S1 |
| Nov. 12.69, 2012 | 6.05 | 5.87 | 9.4 | g-sdss | 0.465 | 600 | −2.01 | C/2010S1 |
| Nov. 15.83, 2012 | 3.17 | 2.45 | 14.2 | V | 0.551 | 640 | −2.0 | C/2012J1 |
| Feb. 06.19, 2013 | 5.94 | 5.57 | 9.2 | r-sdss | 0.620 | 1260 | −3.0 | C/2010R1 |
| Nov. 05.89, 2015 | 4.21 | 3.28 | 4.9 | r-sdss | 0.620 | 450 | −1.9 | C/2014 A4 |
| Nov. 06.15, 2015 | 5.19 | 4.61 | 9.4 | R | 0.642 | 450 | −2.3 | C/2013 V4 |
| Nov. 25.82 2016 | 5.05 | 4.47 | 9.7 | r-sdss | 0.620 | 900 | −2.5 | 2011KP36 |
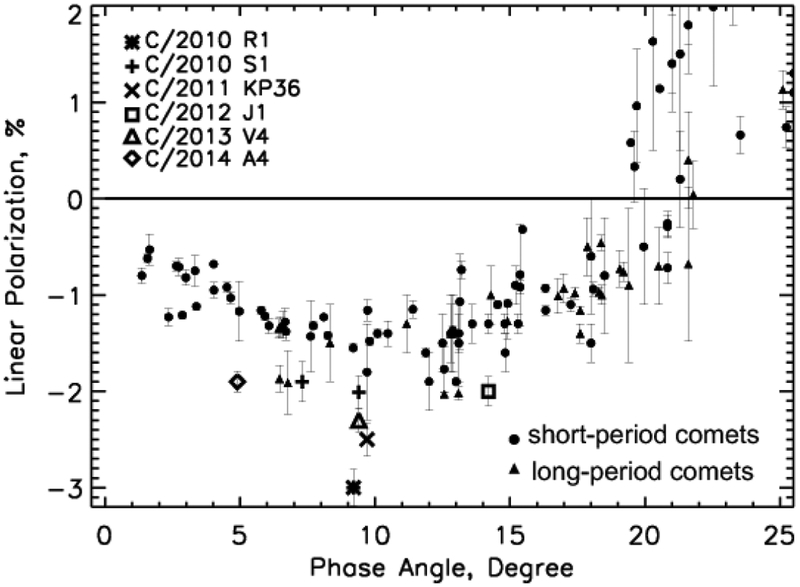
In Fig. 1, we depict the observed values of the degree of linear polarization for short- and long-period close-to-the-Sun comets at phase angles α ≤ 25° and in the spectral interval 0.5–0.7 μm [23], as well as our observational data obtained for the distant comets C/2010 S1, C/2010 R1, C/2011 KP36, C/2012 J1, C/2013 V4, and C/2014 A4. It is obvious that in the range of phase angles considered, all the distant comets exhibit larger absolute values of negative polarization compared to those observed for comets at small heliocentric distances.
Fig. 1.
Degree of linear polarization for comets at small heliocentric distances [21] and distant comets (this work).
3. Numerical modeling methodology
Theoretical modeling of the phenomenon of light scattering in the atmosphere of a comet is usually based on the assumption of a low volume concentration of the cometary particles. This assumption enables one to consider the cometary atmosphere as an optically thin cloud and thereby ignore the contribution of multiple scattering. For a macroscopically isotropic and mirror-symmetric particulate scattering medium, the far-field transformation of the Stokes parameters upon first-order scattering can be written in terms of the real-valued so-called normalized Stokes scattering matrix F(θ):
| (1) |
where θ ∊ [0°, 180°] is the angle between the incidence and scattering directions (i.e., θ = 180° − α, where α is the phase angle), and both sets of the Stokes parameters are defined with respect to the common scattering plane [24]. The element F11(θ) is called the phase function and satisfies the normalization condition
| (2) |
If the incident light (in our case, sunlight) is unpolarized then the element F11(θ) characterizes the angular distribution of the scattered intensity, while the ratio − F21(θ)/F11(θ) represents the corresponding degree of linear polarization.
In our numerical simulations, we have modeled cometary dust particles as oblate spheroids and fractal aggregates composed of identical homogeneous spherical monomers. The shape of an oblate spheroid is fully defined by its aspect ratio E, i.e., the ratio of the longest to the shortest spheroid axes, while the geometry of an aggregate is described by the conventional statisticalscaling raw [25]:
| (3) |
where rmon is the monomer radius, 1 ≤ Df ≤ 3 is the fractal dimension, k0 is the fractal prefactor, N is the number of monomers in the aggregate, and Rg, called the radius of gyration, provides a measure of the overall aggregate radius Ra. Both Df and k0 define the overall morphology of a fractal aggregate. Compact aggregates have Df values approaching 3, whereas the fractal dimension of fluffy clusters can be much smaller. The overall radius of an aggregate can be defined as [26]. In order to generate quasi-random coordinates of the monomers in a fractal cluster, we use the diffusion-limited aggregation (DLA) simulation procedure developed by D. W. Mackowski (personal communication; see also Ref. [27]), in which the generation procedure starts with a pair of spheres in contact for pre-set k0 and Df values and adds a single monomer at a time.
Our extensive computations of light scattering have been based on two numerical techniques. Specifically, in the case of spheroids, we have used the FORTRAN-77 T-matrix implementation [28] of the Waterman’s extended boundary condition method [29] coupled with quasi-analytical averaging over the uniform orientation distribution [30]. For aggregates, we have used the superposition T-matrix method developed for multisphere groups in random orientation [31] and implemented in the form of a FORTRAN-90 computer program designed for parallel computer clusters [32].
4. Modeling results and discussion
4.1. Spheroidal particles
The first step in our analysis of the polarimetric observational data was to parameterize the particle shape by selecting the simple model of randomly oriented homogeneous oblate spheroids, which can adequately reproduce the scattering properties of a variety of nonspherical particles (see, e.g., Ref. [24] and references therein). Particle polydispersity was modeled in terms of the simple power law distribution [33]:
| (4) |
in which the effective variance [33] was fixed at veff = 0.1.
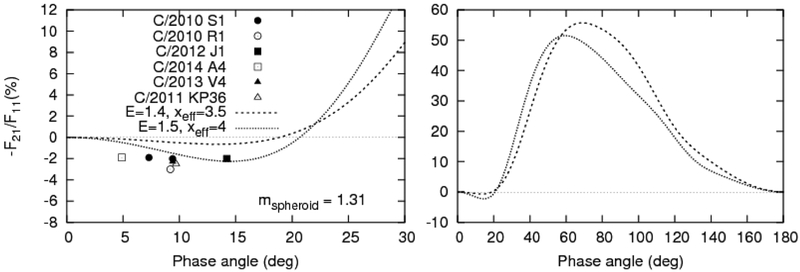
As a result of extensive computations of the degree of linear polarization for such particles with different effective size parameters xeff = 2πreff/λ (where reff is the effective radius [33]) and refractive indices in the range 1.25 ≤ m ≤ 1.65, we have concluded that the model of homogeneous oblate spheroids alone is not suitable for an adequate representation of the results of observations. Nevertheless, further analysis has shown that spheroids composed of water ice with m = 1.31, E = 1.4, and xeff = 3.5 (or E = 1.5 and xeff = 4) can be part of more complex models of particles in cometary atmospheres.
Fig. 2 depicts the computed phase-angle dependences of the degree of linear polarization for water-ice spheroids with E = 1.4, xeff = 3.5 and E = 1.5, xeff = 4.
Fig. 2.
Phase-angle dependence of the degree of linear polarization. Observational data for distant comets are compared with the results of computations for oblate spheroids.
4.2. Fractal aggregates
Needless to say, it is important to understand how much the specific aggregate structure can affect the resulting light-scattering characteristics. In some studies (see, e.g., Refs. [10,13,34]), it has been stated that the morphology of cometary grains has a weak influence on their optical properties. However, the computations reported in Refs. [11,35] show that the effect of morphology on the scattering characteristics of fractals can be quite significant.
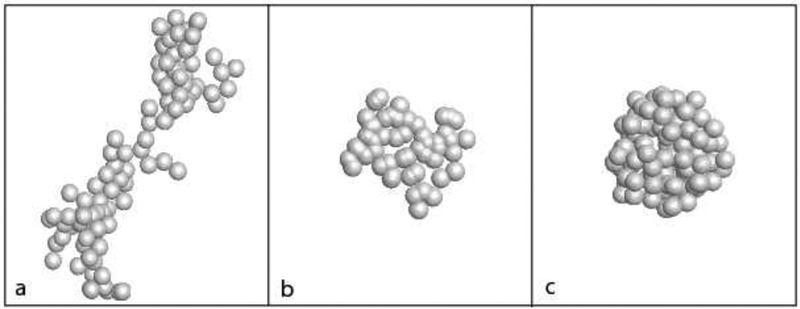
Given the importance of this problem, we have performed numerical modeling of light-scattering characteristics for three types of aggregates: (a) Df =1,8, k0= 1,2 (similar to those resulting from the so-called ballistic cluster–cluster aggregation, or BCCA); (b) Df =2,8, k0= 1,06; and (c) Df =3, k0= 1 (similar to those resulting from the ballistic particle–cluster aggregation, or BPCA). Fig. 3 illustrates fractal-like aggregates with these values of the fractal parameters Df and k0, assuming a fixed number of monomers N = 100. We believe that these three models of aggregates can be representative of the likely structure of particles in the comas of distant comets.
Fig. 3.
Examples of simulated aggregate particles: (a) Df =1.8, k0= 1.2; (b) Df =2.8, k0= 1.06; (c) Df =3, k0= 1. In all three cases, N = 100.
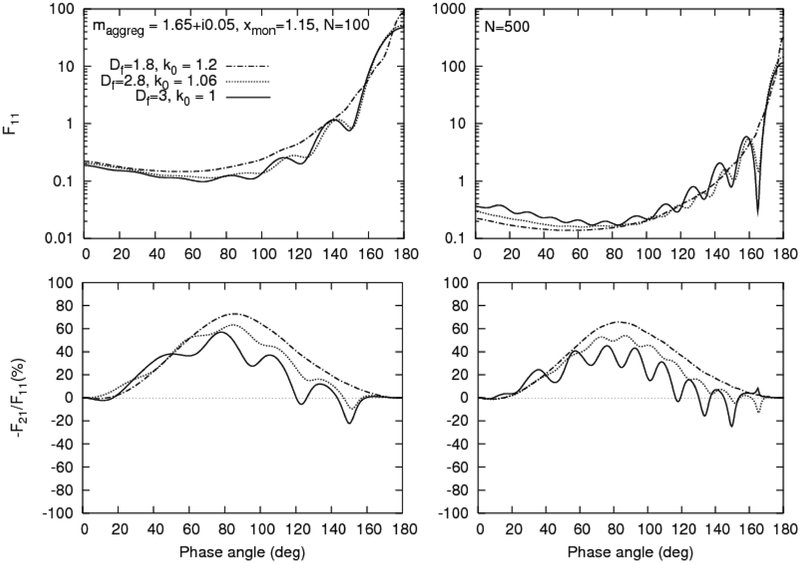
The computations have been performed for the refractive index of monomers m = 1.65 + i0.05, the monomer size parameter xmon = 2πrmon/λ = 1.15 (corresponding to the value of the monomer radius rmon = 0.1 μm at λ = 0.55 μm or rmon = 0.12 μm at λ = 0.642 μm), and the number of monomers N equal to 100 and 500. In Fig. 4, we depict the corresponding phase-angle dependences of the phase function F11 and the ratio –F21/F11. One can clearly see a significant dependence of both on the compactness of aggregates, wherein an increase in compactness results in the appearance and enhancement of interference features (oscillations) typical of large individual spherical particles [24]. Our modeling results (not shown here) demonstrate that the appearance of the oscillations depends also on the monomer size (a decrease in xmon necessitates an increase in the number of monomers N to cause oscillations) and does not depend on the refractive index. In order to smooth out the interference oscillations, it is necessary to perform ensemble averaging over aggregates with different overall sizes and/or different monomer sizes, but these procedure would require a substantial computational effort. It should be noted that the existence of interference waves in the phase-angle dependences of the elements of the Stokes scattering matrix for compact aggregates was previously discussed in Refs. [36,37].
Fig. 4.
Modeled phase-angle dependences of the phase function F11 (the upper panels) and the ratio –F21/F11 (the bottom panels) for different aggregate morphologies. The monomer size parameter is xmon = 1.15, their refractive index is m = 1.65 + i0.05, and the number of monomers is N = 100 (the left-hand panels) and N = 500 (the right-hand panels).
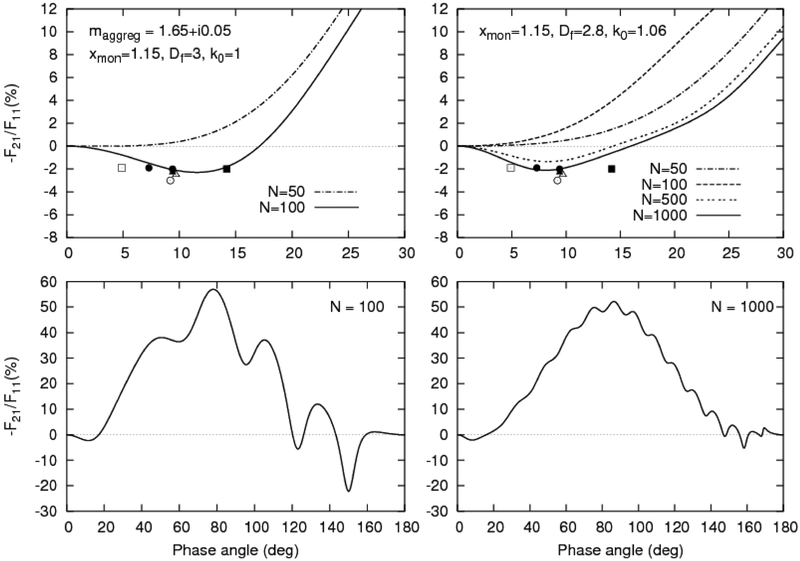
Extensive computations of light scattering by cometary dust particles of different size and chemical composition were performed in Ref. [8] by using the superposition T-matrix method [31,32]. In the upper row of Fig. 5, we demonstrate the phase-angle dependences of linear polarization computed in [8] using the single scattering approximation for a particulate medium composed of fractal aggregates with the monomer size parameter xmon = 1.15, the number of monomers N = 50 and 100, Df = 3, and k0 = 1 (the left-hand panels), as well as N = 50, 100, 500, 1000, Df = 2.8, and k0 =1.06 (the right-hand panels). These results were obtained for the monomer refractive index m = 1.65 + i0.05 typical of astronomical silicates in the visible spectral range [11]. It is seen that for N = 100 (Df = 3, k0 =1) and N = 1000 (Df = 2.8, k0 =1.06), there is a good agreement between the results of computations and the observational data for comet C/2010 S1. However, the strong oscillations of polarization at phase angles α > 50° in the case of N = 100 (the bottom left-hand panel) preclude the straightforward attribution of this model to cometary dust. For this reason in Ref. [8], only the model of aggregates with Df = 2.8 and k0 =1.06 (Fig. 2, type (b)) composed of N = 1000 silicate monomers was adopted as being plausible in the case of comet C/2010 S1.
Fig. 5.
Theoretical phase-angle dependences of the ratio –F21/F11 for different numbers of monomers in aggregates with Df = 3, k0 =1 (the left-hand panels), and Df = 2.8, k0 =1.06 (the righthand panels). The symbols show the results of observations according to Fig. 2.
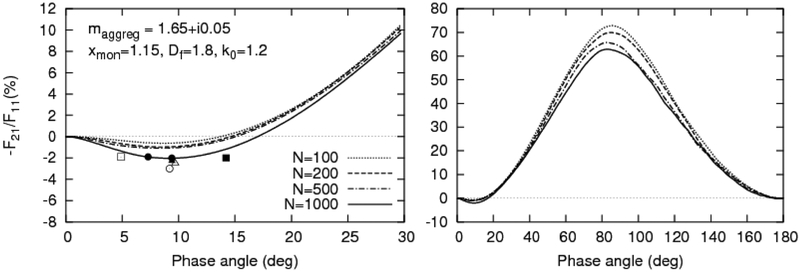
To discuss the behavior of linear polarization in the case of fluffy silicate aggregates of type (a) (Fig. 3), in Fig. 6 we depict the results of computations for clusters with Df = 1.8 and k0 =1.2 and the following monomer parameters: m = 1.65 + i0.05, xmon = 1.15, and N = 100, 200, 500, 1000. A weak branch of negative polarization is seen at phase angles α < 15° for N ≤ 500 which becomes much stronger for N = 1000. In this case, the modeled phase curve of polarization agrees with the results of observations for comet C/2010 S1. At α < 40° and α > 140°, one can see a very weak dependence of the degree of linear polarization on the number of monomers N. Also a strong maximum of positive polarization occurs at α = 80° which decreases with increasing N and shifts towards smaller phase angles.
Fig. 6.
As in Fig. 5, but for Df = 1.8 and k0 =1.2.
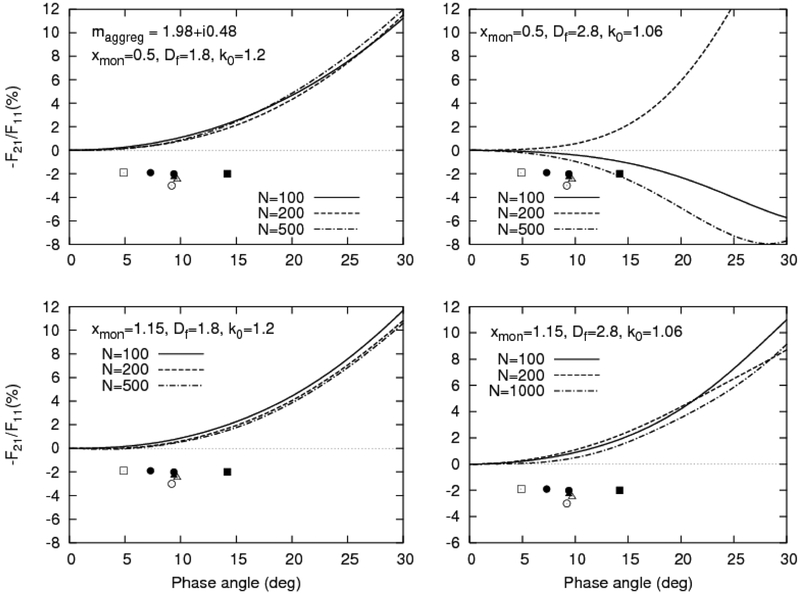
We have also considered aggregates with the composition consistent with that attributed to the dust in comet Halley (a mixture of 31.76% silicates, 2.56% iron, and 65.68% carbonaceous materials). This mixture was used in numerical modeling of polarization for dust in comets at small heliocentric distances (see, e.g., Refs. [10,34,38]). Specifically, the computations were based on the refractive index m = 1.88 + i0.47 (at λ = 0.45 μm) and m = 1.98 + i0.48 (at λ = 0.6 μm), as derived by using the Maxwell-Garnett mixing rule [39]. In our computations, we have adopted the value m = 1.98 + i0.48. The respective –F21/F11 results are depicted in Fig. 7. The upper row corresponds to the cases of xmon = 0.5, Df = 1.8, k0 =1.2 (the left-hand panels) and xmon = 0.5, Df = 2.8, k0 =1.06 (the right-hand panels); the bottom row corresponds to the case of xmon = 1.15. It is seen that neither theoretical angular dependence provides an adequate fit to the results of observations.
Fig. 7.
As in Fig. 5, but for the refractive index m = 1.98 + i0.48 and the monomer size parameter xmon = 0.5 (the upper panels) and xmon = 1.15 (the bottom panels). The left-hand panels correspond to Df = 1.8 and k0 = 1.2, while the right-hand panels correspond to Df = 2.8 and k0 = 1.06.
Interestingly, our numerical data contradict the results of Refs. [10,34,38] wherein a weak negative branch of polarization in the range of small phase angles was identified for BCCA and BPCA clusters composed of N = 256 monomers with m = 1.98 + i0.48 and rmon = 0.1 μm. Furthermore, applying the Maxwell-Garnett mixing rule to aggregates consisting of submicrometer monomers requires additional justification and can, in fact, be questionable. Indeed, in the case of heterogeneous scatterers, this effective-medium approximation is known to give numerically wrong results whenever the inclusion size parameter exceeds a few tenths [40,41]. A better approach would be to model the heterogeneity of aggregate particles explicitly and thereby avoid the use of a phenomenological effective-medium methodology.
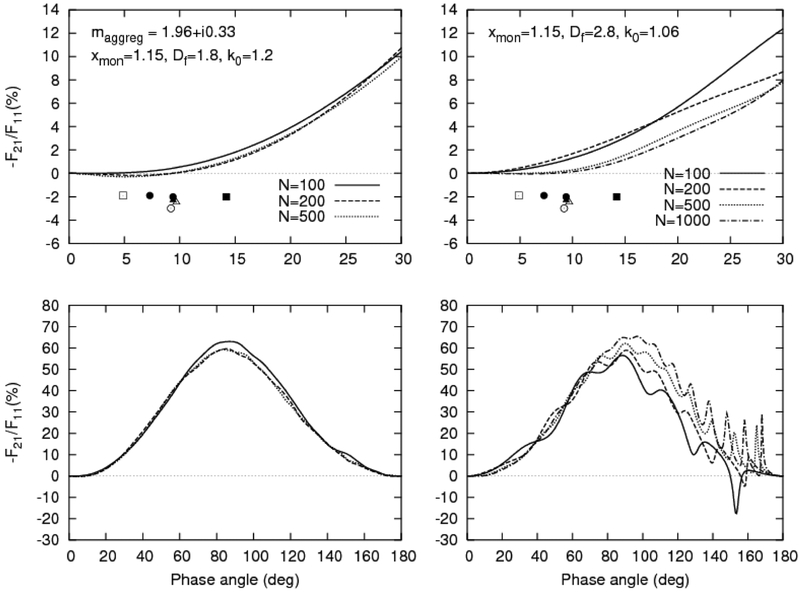
Also, we have considered the case of a cometary atmosphere composed of organic particles. The existence of such particles in bright comets has been discussed in a number of publications (see, e.g., Refs. [10,42,43]). Our computations are based on the refractive index m = 1.96 + i0.33 taken from Ref. [44], the monomer size parameter xmon = 1.15, two types of aggregate structure (Df = 1.8, k0 =1.2 and Df = 2.8, k0 =1.06), and different numbers of monomers. The results of computations presented in Fig. 8 reveal the absence of a negative branch of polarization at small phase angles and the (almost) complete absence of a dependence on N for N > 200 and Df = 1.8 and k0 =1.2. Furthermore, at large phase angles in the case of Df = 2.8 and k0 =1.06, one can see strong interference waves in the polarization curves which intensify with increasing N.
Fig. 8.
As in Fig. 5, but for the refractive index m = 1.96 + i0.33 and Df = 1.8, k0 =1.2 (the left-hand panels) and Df = 2.8, k0 =1.06 (the right-hand panes).
4.3. Morphological mixtures of particles
Finally, let us consider light scattering by a cometary atmosphere assuming that it consists of a mixture of different particle types. Note that similar scenarios have already been discussed previously (e.g., Refs. [15,18,19]). Let δn be the number fraction of the particles of the nth morphology, so that
| (5) |
where N is the total number of morphological types in the mixture. Then [22]
| (6) |
| (7) |
and
| (8) |
where Csca and Cext are the ensemble-averaged scattering and extinction cross sections per particle, respectively, ω is the resulting single-scattering albedo, and Csca,n and Cext,n are the scattering and extinction cross sections, respectively, for each particle of the nth morphological type. Furthermore, for the whole ensemble of cometary particles we have [24]
| (9) |
and
| (10) |
Eqs. (5)–(10) correct the methodology used in Refs. [15,18] wherein a simple average of the F11 and – F21/F11 values was computed.
We have analyzed several mixtures composed of ice spheroids + silicate aggregates and ice spheroids + silicate aggregates + organic aggregates. It should be noted that the possibility of the presence of ice grains in the comas of distant comets was discussed, for example, in Refs. [5,45,46].
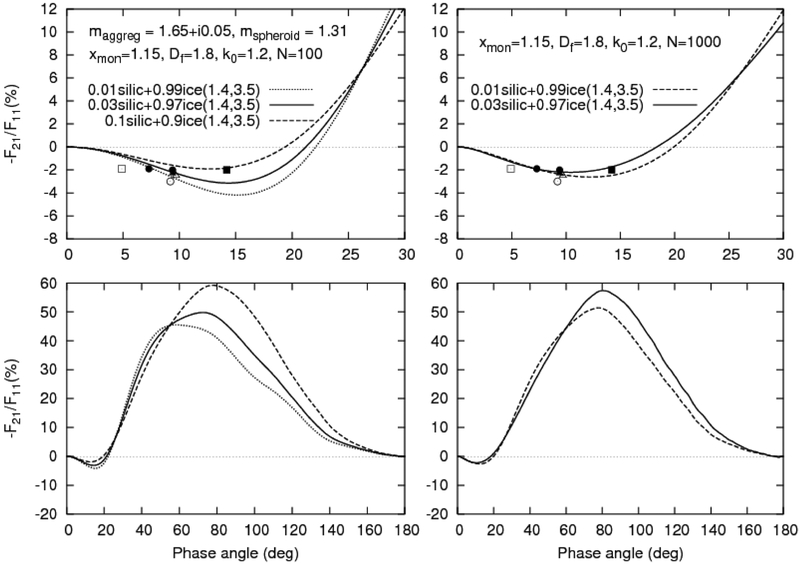
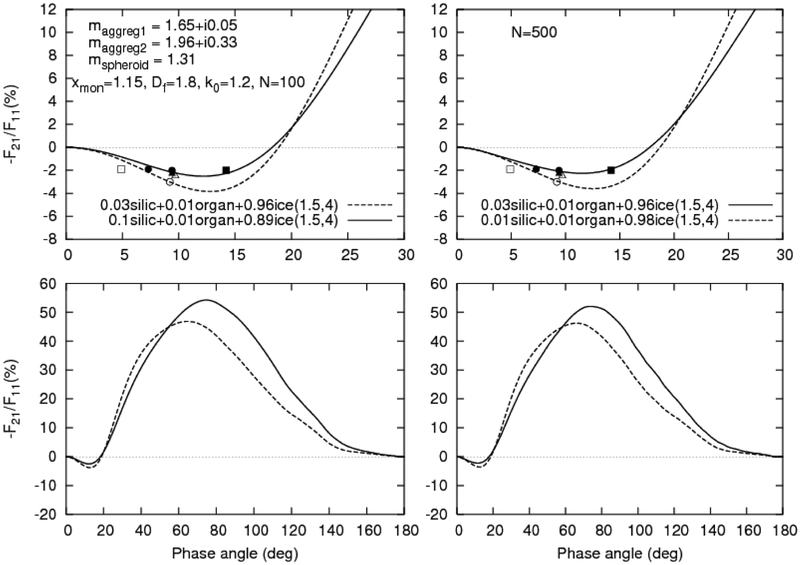
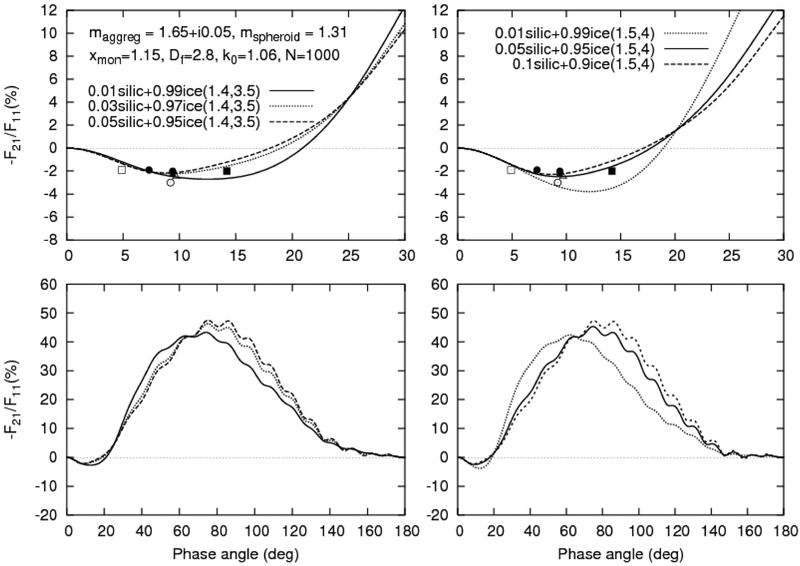
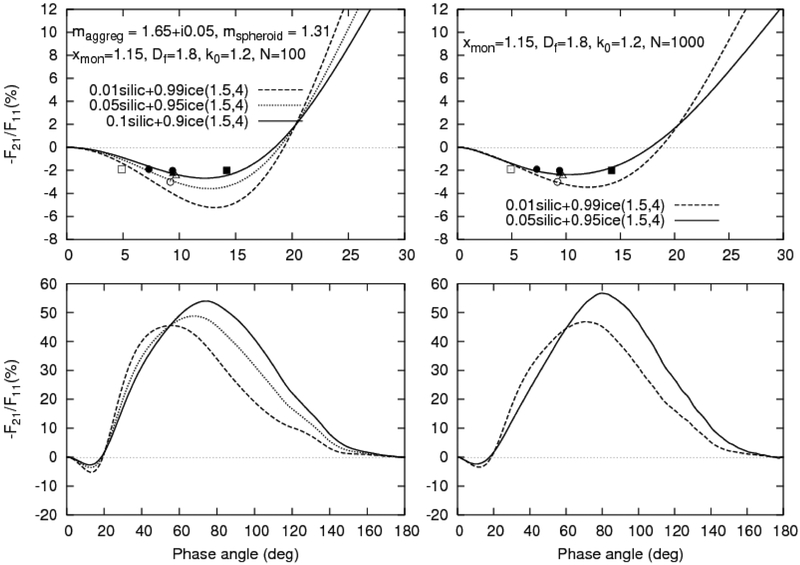
In Figs. 9–12, examples of the results of our numerous simulations are given. Figs. 9–11 correspond to the case of the mixture of ice spheroids and silicate aggregates with N = 100 and 1000 monomers. Fig. 12 pertains to the case of the mixture of three components, viz., ice spheroids and silicate and organic aggregates with N = 100 and 500 monomers. Note that we have considered silicate aggregates with Df = 1.8, k0 =1.2 and Df = 2.8, k0 =1.06, as well as organic aggregates with Df = 1.8 and k0 =1.2. In all these cases, the monomer size parameter xmon is equal to 1.15, while the spheroid component is specified by the parameters E = 1.4, xeff = 3.5 or E = 1.5, xeff = 4.
Fig. 9.
Theoretical phase-angle dependences of the ratio –F21/F11 for different mixtures of silicate aggregates with Df = 1.8 and k0 =1.2 and ice spheroids with E = 1.4, xeff = 3.5, and N = 100 (the left-hand panels) and N = 1000 (the right-hand panels). The symbols show the results of observations according to Fig. 2.
Fig. 12.
As in Fig. 9, but for different mixtures of silicate and organic aggregates with Df = 1.8 and k0 =1.2 and ice spheroids with E = 1.5, xeff = 4, N = 100 (the left-hand panels) and N = 500 (the right-hand panels).
Fig. 11.
As in Fig. 9, but for the mixture of silicate aggregates with Df = 2.8 and k0 =1.06 and ice spheroids with E = 1.4, xeff = 3.5 (the left-hand panels) and E = 1.5, xeff = 4 (the right-hand panels).
It is seen that no unique solution has been obtained in the form of a model of cometary particles that satisfies all available results of observations obtained for different distant comets. However, finding such a solution is impossible in principle because different comets at different heliocentric distances are unlikely to have exactly the same particulate composition. It can be concluded nonetheless that for some comets the use of a mixture of different particle morphologies and/or compositions can substantially improve the agreement between the modeling results and observational data.
Note that a mixture of compact silicate aggregates (Df = 2.8, k0 =1.06) and ice spheroids results in a smoothing of polarization curves (see Fig. 11), but the interference waves still persist. Therefore, in this case ensemble averaging appears to be warranted. It should be emphasized that our results imply the presence of a very large amount of ice in the atmospheres of the distant comets considered. This outcome is caused by the fact that the ice spheroids considered have much smaller scattering cross sections than the aggregated particles, so that a very large number of ice particles is required to make their effect on the total scattering matrix noticeable.
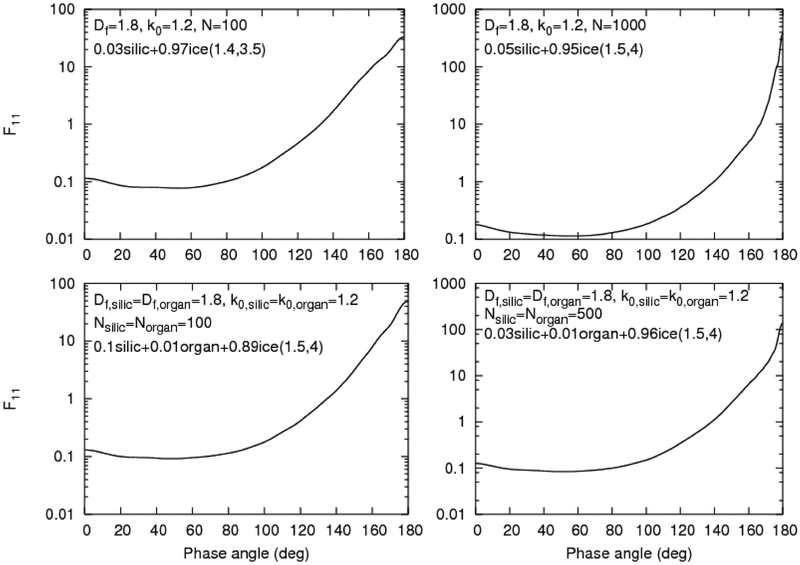
In Fig. 13, the theoretical phase-angle dependences of the phase function F11 are depicted for the values of model parameters that allow one to obtain the best agreement between the results of polarimetric observations and computations shown in Figs. 9–12. It is seen that all phase-function curves exhibit a strong diffraction peak at large phase angles (i.e., at small scattering angles) and a weak backscattering enhancement at α < 30°.
Fig. 13.
Modeled phase-angle dependences of the phase function F11.
5. Conclusions
The overall goal of this paper has been rather ambitious: to perform polarimetric observations of distant comets and use these data to infer the microphysical characteristics of the particles forming their atmospheres. All results of our observations carried out at phase angles α < 15° reveal the ubiquitous negative polarization branch to be significantly more pronounced than that typically observed for the whole coma of comets at small heliocentric distances. To simulate these observations theoretically, we have considered, in particular, aggregate particles (both very compact and very porous) composed of a large number (up to N = 1000) of submicrometer spherical monomers. The possibility of carrying out such calculations within reasonable computer time has demonstrated once again the very high efficiency of the superposition T-matrix program described in Ref. [32]. As a result of our extensive numerical modeling, we have obtained a reasonable semiquantitative agreement with all observational polarimetric data for the following two particulate models: a mixture of water-ice oblate spheroids (E = 1.4–1.5, xeff = 3.5–4) with porous aggregates (Df = 1.8, k0 = 1.2) composed of silicate monomers (N = 100, 500, 1000; xmon = 1.15) or compact aggregates (Df = 2.8, k0 = 1.06) composed of silicate monomers (N = 1000, xmon = 1.15); and a mixture of the same water-ice oblate spheroids with porous silicate and organic aggregates (Df = 1.8, k0 = 1.2, N = 100, 500). It should be noted that one of the main differences between our model and the ones used for comets close to the Sun (see, e.g., Ref. [19]) is the inclusion in the model of a large number of grains consisting of water ice. Comparison of the computed curves given in Figs. 6 and 8 with those presented in Figs. 9, 10 and 12 shows that the presence of ice particles (in this case in the form of oblate spheroids) results in a deepening of the negative branch of polarization, and thereby improves the agreement with the observational data for distant comets.
Fig. 10.
As in Fig. 9, but for ice spheroids with E = 1.5 and xeff = 4.
We are fully aware of the obvious fact that the derived models of particles in the atmospheres of distant comets are preliminary and highly approximate. Indeed, we have used extremely scarce observational data pertaining to no more than two phase angles per comet and only one wavelength per phase angle. Therefore, extensive additional photopolarimetric observations carried out at multiple phase angles and multiple wavelengths per comet are required for better understanding of the nature and morphology of particles in the atmospheres of distant comets.
Highlights.
The results of observations of the degree of linear polarization for distant comets C/2010 S1, C/2010 R1, C/2011 KP36, C/2012 J1, C/2013 V4, and C/2014 A4 are presented.
Numerical modeling of light scattering characteristics for different particle morphologies is performed by using the T-matrix and superposition T-matrix methods.
A comparison between the observational data and the results of computations is carried out.
The models of possible composition of particles in the atmospheres of distant comets are suggested.
Acknowledgments
We thank anonymous reviewers for constructive comments on the original manuscript. We appreciate Ludmilla Kolokolova for useful discussion. JMD recognizes the organizers of the ELS–XVI conference for providing full financial support and also acknowledges support from the National Academy of Sciences of Ukraine under the Main Astronomical Observatory GRAPE/GPU/GRID Computer Cluster Project. OVI acknowledgments supports from the European Union’s Seventh Framework Program (SASPRO) (grant agreement No. 609427) and the Slovak Academy of Sciences (grant Vega 2/0032/0014). This material is partly based upon work supported by the NASA Remote Sensing Theory Program managed by Lucia Tsaoussi.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Dollfus A, Bastien P, Le Borgne JF, Levasseur-Regourd AC, Mukai T. Optical polarimetry of P/Halley – synthesis of the measurements in the continuum. Astron Astrophys 1988; 206:348–56. [Google Scholar]
- [2].Epifani EM, Palumbo P, Capria MT, Cremonese G, Fulle M, Colangeli L. The distant activity of short-period comets – I. Mon Not R Astron Soc 2007;381:713–22. [Google Scholar]
- [3].Epifani EM, Palumbo P, Capria MT, Cremonese G, Fulle M, Colangeli L. The distant activity of short-period comets – II. Mon Not R Astron Soc 2008;390:265–80. [Google Scholar]
- [4].Korsun PP, Kulyk IV, Ivanova OV, Afanasiev VL, Kugel F, Rinner C, Ivashchenko Yu.N. Dust tail of the active distant comet C/2003 WT42 (LINEAR) studied with photometric and spectroscopic observations. Icarus 2010;210:916–29. [Google Scholar]
- [5].Korsun PP, Rousselot P, Kulyk IV, Ivanova OV. Distant activity of comet C/2002 VQ94 (LINEAR): optical spectrophotometric monitoring between 8.4 and 16.8 AU from the Sun. Icarus 2014;232:88–96. [Google Scholar]
- [6].Mishchenko MI, Rosenbush VK, Kiselev NN, Lupishko DF, Tishkovets VP, Kaydash VG, Belskaya IN, Efimov YS, Shakhovskoy NM. Polarimetric remote sensing of Solar system objects. Kyiv: Akademperiodyka; 2010. [Google Scholar]
- [7].Kiselev N, Rosenbush V, Levasseur-Regourd A-C, Kolokolova L. Comets In Kolokolova L, Hough J, Levasseur-Regourd A-C, editors. Polarimetry of stars and planetary systems. Cambridge, UK: Cambridge University Press; 2015, p. 379–404. [Google Scholar]
- [8].Ivanova OV, Dlugach JM, Afanasiev VL, Reshetnik VM, Korsun PP. CCD polarimetry of distant comets C/2010 S1 (LINEAR) and C/2010 R1 (LINEAR) at the 6-m telescope of the SAO RAS. Planet Space Sci 2015;118:199–210. [Google Scholar]
- [9].Ivanova O, Shubina O, Moiseev A, Afanasiev V. Polarimetric and spectroscopic observations of a dynamically new comet C/2012 J1 (Catalina). Astrophys Bull 2015;70:349–54. [Google Scholar]
- [10].Kolokolova L, Kimura H, Mann I. Characterization of dust particles using photopolarimetric data: example of cometary dust In Videen G, Yatskiv Ya, Mishchenko M, editors. Photopolarimetry in remote sensing. Dordrecht: The Netherlands: Kluwer; 2004. p. 431–53. [Google Scholar]
- [11].Petrova EV, Tishkovets VP, Jokers K. Polarization of light scattered by Solar system bodies and the aggregate model of dust particles. Solar Syst Res 2004;38:309–24. [Google Scholar]
- [12].Kimura H, Kolokolova L, Mann I. Light scattering by cometary dust numerically simulated with aggregate particles consisting of identical spheres. Astron Astrophys 2006;449:1243–54. [Google Scholar]
- [13].Das HS, Das SR002C Paul T, Suklabaidya A, Sen AK. Aggregate model of cometry dust: an application to comet Levy 1990XX. Mon Not R Astron Soc 2008;389:787–91. [Google Scholar]
- [14].Lumme K, Penttilä A. Model of light scattering by dust particles in the solar system: Applications to cometary comae and planetary regoliths. J Quant Spectrosc Radiat Transfer 2011;112:1658–70. [Google Scholar]
- [15].Kolokolova L, Kimura H. Comet dust as a mixture of aggregates and solid particles: model consistent with ground-based and space-mission results. Earth Planets Space 2010;62:17–21. [Google Scholar]
- [16].Zubko E, Furusho R, Kawabata K, Yamamoto T, Muinonen K, Videen G. Interpretation of photo-polarimetric observations of comet 17/PHolmes. J Quant Spectrosc Radiat Transfer 2011;112:1848–63. [Google Scholar]
- [17].Zubko E, Muinonen K, Videen G, Kiselev N. Dust in comet C/1975 V1 (West). Mon Not R Astron Soc 2014;440:2928–43. [Google Scholar]
- [18].Kolokolova L, Das HS, Dubovik O, Lapyonok T, Yang P. Polarization of cosmic dust simulated with the rough spheroid model. Planet Space Sci 2015;116:30–8. [Google Scholar]
- [19].Lasue J, Levasseur-Regourd AC, Hadamcik E, Alcouffe J. Cometary dust properties retrieved from polarization observations: Application to C/1995 O1 Hale-Bopp and 1P/Halley. Icarus 2009;199:129–44. [Google Scholar]
- [20].Afanasiev VL, Moiseev AV. Scorpio on the 6-m telescope: current state and perspectives for spectroscopy of galactic and extragalactic objects. Baltic Astron 2011;20:363–70. [Google Scholar]
- [21].Afanasiev VL, Amirkhanyan VR. Technique of polarimetric observations of faint objects at the 6-m BTA telescope. Astrophys Bull 2012;67:438–52. [Google Scholar]
- [22].Ivanova O, Rosenbush V, Afanasiev V, Kiselev N. Polarimetry, photometry, and spectroscopy of comet C/2009 P1 (Garradd). Icarus 2017;284:167–82. [Google Scholar]
- [23].Kiselev N, Shubina E, Velichko S, Jockers K, Rosenbush V, Kikuchi S. Compilation of comet polarimetry from published and unpublished sources, urn:nasa:pds:compilcomet:polarimetry::1.0, NASA Planetary Data System, 2017. <https://pdssbn.astro.umd.edu/holdings/pds4-compil-comet:poarimetry-v1.0/SUPPORT/dataset.html>
- [24].Mishchenko MI, Travis LD, Lacis AA. Scattering, absorption, and emission of light by small particles. Cambridge, UK: Cambridge University Press; 2002. <https://www.giss.nasa.gov/staff/mmishchenko/books.html> [Google Scholar]
- [25].Sorensen CM. Light scattering by fractal aggregates: a review. Aerosol Sci Technol 2001;35:648–87. [Google Scholar]
- [26].Kozasa T, Blum J, Mukai T. Optical properties of dust aggregates. I. Wavelength dependence. Astron Astrophys 1992;263:423–32. [Google Scholar]
- [27].Mackowski DW. Electrostatics analysis of radiative absorption by sphere clusters in the Rayleigh limit: application to soot particles. Appl Opt 1995;34:3535–45. [DOI] [PubMed] [Google Scholar]
- [28].Mishchenko MI, Travis LD. Capabilities and limitations of a current FORTRAN implementation of the T-matrix method for randomly oriented rotationally symmetric scatters. J Quant Spectrosc Radiat Transfer 1998;60:309–24. [Google Scholar]
- [29].Waterman PC. Symmetry, unitarity, and geometry in electromagnetic scattering. Phys Rev D 1971;3:825–39. [Google Scholar]
- [30].Mishchenko MI. Light scattering by randomly oriented axially symmetric particles. J Opt Soc Am A 1991;8:871–82. [DOI] [PubMed] [Google Scholar]
- [31].Mackowski DW, Mishchenko MI. Calculation of the T-matrix and the scattering matrix for ensembles of spheres. J Opt Soc Am A 1996;13:2266–78. [Google Scholar]
- [32].Mackowski DW, Mishchenko MI. A multiple sphere T-matrix Fortran code for use on parallel computer clusters. J Quant Spectrosc Radiat Transfer 2011;112:2182–92. [Google Scholar]
- [33].Hansen JE, Travis LD. Light scattering in planetary atmospheres. Space Sci Rev 1974;16:527–610. [Google Scholar]
- [34].Kimura H, Kolokolova L, Mann I. Optical properties of cometary dust. Constraints from numerical studies on light scattering by aggregate particles. Astron Astrophys 2003;407:L5–8. [Google Scholar]
- [35].Liu L, Mishchenko MI. Effects of aggregation on scattering and radiative properties of soot aerosols. J Geophys Res 2005;110:D11211. [Google Scholar]
- [36].Tishkovets VP, Petrova EV, Jokers K. Optical properties of aggregate particles comparable in size to the wavelength. J Quant Spectrosc Radiat Transfer 2004;86:241–65. [Google Scholar]
- [37].Kolokolova L, Mackowski D. Polarization of light scattered by large aggregates. J Quant Spectrosc Radiat Transfer 2012;113:2567–72. [Google Scholar]
- [38].Mann I, Kimura H, Kolokolova L. A comprehensive model to describe light scattering properties of cometary dust. J Quant Spectrosc Radiat Transfer 2004;89:291–301. [Google Scholar]
- [39].Chýlek P, Videen G, Geldart DJW, Dobbie JS, Tso HCW. Effective medium approximation for heterogeneous particles In Mishchenko MI, Hovenier JW, Travis LD, editors. Light scattering by nonspherical particles: theory, measurements, and applications. San Diego: Academic Press; 2000, p. 273–308. [Google Scholar]
- [40].Mishchenko MI, Dlugach JM, Liu L. Applicability of the effective-medium approximation to heterogeneous aerosol particles. J Quant Spectrosc Radiat Transfer 2016;178:284–94. [Google Scholar]
- [41].Mishchenko MI, Dlugach JM, Yurkin MA, Bi L, Cairns B, Liu L, et al. First-principles modeling of electromagnetic scattering by discrete and discretely heterogeneous random media. Phys Rep 2016;632:1–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Kissel J, Krueger FR, Siln J, Clark BC. The cometary and interstellar dust analyzer at comet 81P/Wild2. Science 2004;304:1774–6. [DOI] [PubMed] [Google Scholar]
- [43].Goesmann F, Rosenbauer H, Bredehöft JH, Cabane M, Ehrenfreund P, Gautier T, et al. Organic compounds on comet 67P/Churyumov–Gerasimenko revealed by COSAC mass spectrometry. Science 2015;349:aab0689. [DOI] [PubMed] [Google Scholar]
- [44].Li A, Greenberg JM. A unified model of interstellar dust. Astron Astrophys 1997;323:566–84. [Google Scholar]
- [45].Gunnarsson M Icy grains as a source of CO in comet 29P/Schwassmann–Wachmann 1. Astron Astrophys 2003;398:353–61. [Google Scholar]
- [46].Kawakita H, Watanabe J, Ootsubo T, Nakamura R, Fuse T, Takato N, et al. Evidence of icy grains in comet C/2002 T7 (LINEAR) at 3.52 AU. Astrophys J 2004;601:L191–4. [Google Scholar]