Joint Detection of Associations between DNA Methylation and Gene Expression from Multiple Cancers

Abstract

DNA methylation plays an important role in the development of various cancers mainly through the regulation on gene expression. Hence, the study on the relation between DNA methylation and gene expression is of particular interest to understand cancers. Recently, an increasing number of datasets are available from multiple cancers, which makes it possible to study both the similarity and difference of genomic alterations across multiple tumor types. However, most of the existing pan-cancer analysis methods perform simple aggregations, which may overlook the heterogeneity of the interactions. In this paper, we propose a novel method to jointly detect complex associations between DNA methylation and gene expression levels from multiple cancers. The main idea is to apply joint sparse canonical correlation analysis to detect a small set of methylated sites, which are associated with another set of genes either shared across cancers or specific to a particular group (group-specific) of cancers. These methylated sites and genes form a complex module with strong multivariate correlations. We further introduce a joint sparse precision matrix estimation method to identify driver methylation-gene pairs in the module. These pairs are characterised by significant partial correlations, which may imply high functional impacts and contribute to complementary information to the main step. We apply our method to The Cancer Genome Atlas(TCGA) datasets with 1166 samples from four cancers. The results reveal significant shared and group-specific interactions between DNA methylation and gene expression levels. To promote reproducible research, the Matlab code is available at https://sites.google.com/site/jianfang86/jointTCGA.

I. Introduction

CANCER is a complex disease that is caused by the abnormality of various molecule changes (e.g. genetic, epigenetic, transcription factors) and environmental influences. Identification of the alterations and interactions among different aspects is important for both understanding and prevention of cancers. DNA methylation is a major epigenetic factor, which was found to be relevant to almost every human cancer [1]. The DNA methylation plays an important role in the regulation of gene expression [2]. For example, DNA methylation in promoters is often negatively correlated with expression while methylation in gene-body has positive effects [3]. In this sense, conventional approaches first map the methylated site to a gene and then test the associations between paired methylation and gene expression levels [4] [5]. However, univariate methods are not able to detect complex regulatory relationships between genetic and epigenetic factors. To overcome this limitation, multivariate approaches, such as canonical correlation analysis [6], joint matrix decomposition [7] and reduced rank regression [8], were proposed to detect highly associated modules for multi-omics data.

In addition, an increasing number of tumor samples has attracted the attention in pan-cancer analysis [9]. It aims to find both similarities and differences across cancer types and organs. On one hand, the similarities allow the fusion of multiple datasets to increase statistical power and yield similar treatment. For example, in earlier studies [10] and [11], the samples from more than 10 types of cancers were pooled together to identify new cancer driver genes and somatic aberrations. On the other hand, the differences across multiple cancers could reveal group-specific patterns, which are crucial for the understanding and treatment of particular cancer types. Therefore, it is desirable to identify similarities and differences simultaneously. For example, a quantitative transcriptomics analysis method was applied to classify tissuespecific expression of genes across 27 different organs [12]. An integrative statistics method was developed to identify miRNA-gene interactions that are either shared or group-specific across cancers [13]. Moreover, in the studies of DNA methylation, it was concluded that some epigenetic changes are shared and some are cancer-type specific [14]. However, it is still challenging to explore the relationship between high-dimensional DNA methylation and gene expression data.

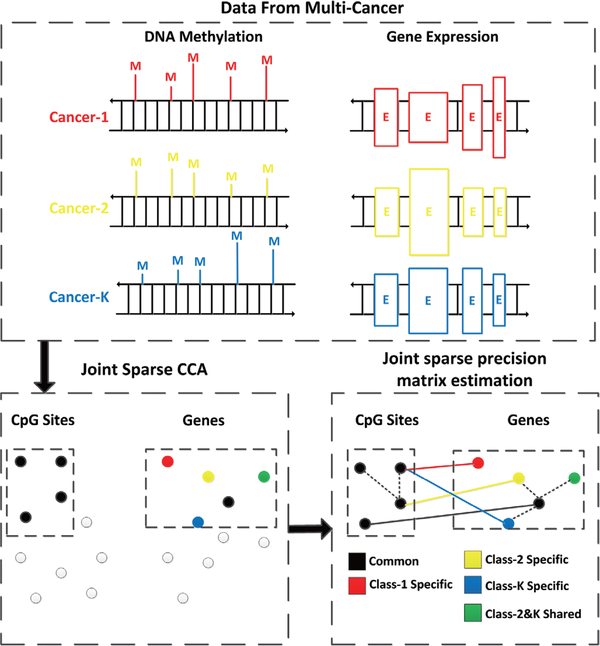
In this paper, we propose a multivariate method to detect associations between DNA methylation and gene expression from multiple cancers. Our main aim is to detect complex associations that are either shared or group specific. As shown in Fig. 1, we first apply joint sparse canonical correlation analysis(JSCCA) [15] to extract a densely correlated module that includes a common set of methylated sites and a set of genes that are shared or group-specific. Set enrichment analysis then can be applied to identify important biological processes, e.g. pathways, underlying the module. However, little work was done to further locate driver methylation-gene pairs in the module. A key challenge is that most of the interactions between methylated sites and genes are indirect due to complex gene regulations, co-expressions, co-methylations, and etc. To tackle this problem, we further adopt the method of joint sparse precision matrix estimation [16], which has the potential for the distinction between direct and indirect interactions [17]. The methylation-gene pairs with significant partial correlations are selected, which are expected to have high functional impacts in the detected module. We apply the method to TCGA data [9], [18] with samples from 4 cancers including breast invasive carcinoma(BRCA), lung squamous cell carcinoma(LUSC), colon adenocarcinoma(COAD), and ovarian serous cystadenocarcinoma(OV). A number of interesting correlated patterns between DNA methylation and gene expression are identified in tumors from different organs.

Fig. 1.

The flowchart of the proposed method. Given DNA methylation and gene expression profiles from multiple cancers, we first apply JSCCA to identify a set of methylation that affect a group of genes. These genes are classified into shared and group-specific ones. With this classification, we perform joint sparse precision matrix estimation to further identify driver methylation-gene pairs with significant partial correlations. The dash lines correspond to co-expressions or co-methylations.

The rest of the paper is organized as follows. Section II introduces our method for joint estimation of the methylation-expression interactions. The performance of the proposed method is evaluated through TCGA data analysis in Section III, followed by some discussions in the last section.

II. Background

During recent years, advances have been made for the detection of interactions between two sets of variables. Various methods have been developed in biomedical studies. For example, for genomic dataset consisting of single-nucleotide polymorphism (SNP) and expression data, the mapping of expression quantitative trait locus (eQTL) was widely studied [19]. Imaging genetics is also a hot topic, which aims to detect genetic variants that are related to brain activities [20]. Both applications involve with very high dimensional and heterogenous data, resulting in challenging analysis and inference. A straightforward approach is to fit all possible univariate pairs through correlation analysis, linear or nonlinear regressions. However, these methods may suffer from the problem of multiple testing due to massive number of pairs. Multivariate regression is another way to infer correlations. It takes into account the combination of multiple traits (e.g. the SNPs) by statistical methods, like the LASSO [21], but may overlook the relationships among multiple outcomes(expression levels or brain activities). Canonical correlation analysis can be viewed as a fully multivariate analysis method [22]. It aims at finding two linear combinations of each set of variables to maximize their correlation. In high dimensional problems, sparse CCA was developed to achieve feature selection and avoid over-fitting [6]. Similar approaches include sparse partial least squares regression, joint matrix decomposition, sparse reduced rank regression, which have been successfully applied in genomic and imaging studies [23]. More recently, Zhang et al. [7] proposed a modular analysis approach based on joint non-negative matrix decomposition to detect associations among multi-platforms of genomic profiling, including DNA methylation and gene expression. An extension was proposed in [24], which further captures homogeneous and heterogeneous effects. In addition, Wang et al. [8] proposed a network guided reduced rank regression method to detect the associations between DNA methylation and gene expression. All of the above methods are not restricted to the cis-effects of methylations, but focus on multi-dimensional modules, whose members are from both genes and methylations. A more general approach to group correlated features is variable clustering, which has been widely applied in genomic data [25] [26]. The main idea is to cluster variables into homogeneous subsets, in which the variables are similar to each other [27]. A variety of methods were proposed based on different similarity measures, including the Pearson’s correlation [28], mutual information [29], nonlinear coupling [27], and etc.

On the other hand, multiple tissue analysis is also an emerging topic. It aims to combine samples from multiple sources, and detect interactions that are shared by multiple tissues, or specific to certain ones. Many methods were built based on a post-hoc approach [30] [31]. The interactions are estimated separately for each tissue, and then combined with statistical methods to determine whether a connection is shared or group-specific. Joint estimation is an alternative approach [16] [15], which analyzes all the samples together, and detects homogeneity and/or heterogeneity by enforcing a similarity regularization. The estimation is always more flexible, which can be applied to methods like sparse CCA [32], whose post-hoc testing statistics are not well studied.

Recently, partial correlations have been widely studied for exploration of multivariate dependence patterns [17]. The partial correlation quantifies the dependency of two variables, conditioning on all the others. Hence, as compared to the marginal correlation, e.g. Pearson’s correlation, the partial correlation is able to distinguish direct associations from indirect ones. To calculate the partial correlation, several methods have been proposed, including regularized precision matrix estimation [33], node-wise regression [34] [35], and etc. When the data belong to different classes, Danaher et. al. proposed the joint graphical lasso approach, which borrows strength across the classes to estimate multiple graphical models simutaneuously [16].

In addition, set enrichment and pair-wise association are two common strategies to analyze biological data. In practice, they are complementary to each other for interpreting the results. For example, in gene co-expression network analysis [36], the correlations between all pairs of genes were computed to construct the network, and then highly correlated genes are clustered into modules, resulting in a number of subnetworks. However, for some specific correlation measures, such as the partial correlation, the computational cost increases rapidly as the number of features grows. As an alternative, we try to detect the module first and then calculate the partial correlation on a small set of variables, which is computationally more efficient. Moreover, the detection based on the modules derived from sparse CCA can make best use of two types of data information.

III. Methods

Let $X_k\in {\mathcal{R}}^{n_k\times p},Y_k\in {\mathcal{R}}^{n_k\times q},k=1,\dots ,K$ denote DNA methylation and gene expression profiles respectively from K > 1 cancers, where n_k is the number of observations in the k-th cancer, p is the number of CpG sites and q is the number of genes. Assuming that the data have been standardized with zero mean and unit variance according to samples from each cancer, we develop a multivariate method to infer both shared and group-specific methylation-expression interactions. In this section, we will describe the estimation and statistical inference models for the proposed method.

A. Joint Module Detection via JSCCA

Canonical correlation analysis(CCA) [22] is a well-known method for investigating the relationships between two sets of variables. The main idea is to find linear combinations of the variables in both sets to maximize their correlation. However, the conventional CCA is subject to overfitting in high-dimension and is difficult to detect heterogeneity among multi-class data, so it is not suitable for multi-cancer data analysis described above.

To this end, we extend CCA to extract both shared and group-specific associations between methylated sites and genes. We develop a joint sparse CCA model based on our previous model [15]. The main idea is to jointly estimate sparse CCA models belonging to multiple cancers with one common canonical vector for DNA methylation and K related sparse canonical vectors for gene expression. In this way, we expect to identify methylation important for all cancers in association with shared or group-specific genes that are affected by these methylated sites. The JSCCA can increase the power of detection as compared to standard SCCA (details can be found in [15]). The basic model used here is described

$$\begin{gathered} \underset{{}_{w,V}}{\min }-\sum _{k=1}^K\frac{1}{n_k}{w}^T{X}_k^T{Y}_k{v}_k+{\lambda }_1\Vert w{\Vert }_1^1 \\ +\sum _{k=1}^K{\lambda }_2{\Vert v_k\Vert }_1^1+\tau \sum _{i=1}^q{d}_i{\Vert v^i\Vert }_{\infty } \\ s.t.\Vert w{\Vert }_2^2=\Vert V{\Vert }_F^2=1 \end{gathered}$$ (1)

where $w\in {\mathcal{R}}^{p\times 1}$ and V = [v₁,...,v_K] = [v¹,...,v^q]^T ∈ ${\mathcal{R}}^{q\times K}$ are the canonical vectors of X_k and Y_k respectively, λ₁,λ₂,τ are the regularization parameters. The Frobenius and L_∞ norms are defined as $\Vert V{\Vert }_F^2={\sum }_k{\Vert v_k\Vert }_2^2,{\Vert v^i\Vert }_{\infty }={\max }_k\left|v_k^i\right|$. The L₁ penalties ${\Vert w\Vert }_1^1$ and ${\Vert v_k\Vert }_1^1,k=1,\dots K$ encourage sparsity over each canonical vector, which can overcome the problem of overfitting while achieve feature selection. The group L_∞ norm, which is a widely used structure sparsity penalty [37], is imposed on each gene so that the corresponding canonical vectors from different cancers share a similar structure. The weight vector d_i = ‖vⁱ‖₀ (the number of non-zero coefficient in vⁱ) is introduced to encourage the selection of group-specific genes, since they contribute less covariance than shared ones.

To solve (1), the block coordinate decent algorithm is applied. The main idea is to alternatively update w, V and d until their convergence. We outline the implementation as follows while discuss the details in Appendix:

1. Initialize the canonical vectors. In particular, w is initialized as the first left-singular vector of ${\sum }_k\frac{1}{n_k}{X}_k^T{Y}_k$.

2. Update w, V, d using block coordinate descent until they converge.

   1. Update V by first solving

      $$\begin{gathered} V=\arg \underset{{}_V}{\min }\sum _{k=1}^K\Vert v_k-\frac{1}{n_k}{Y}_k^T{X}_{k}w\Vert \\ +\sum _{k=1}^K{\lambda }_2{\Vert v_k\Vert }_1^1+\tau \sum _{i=1}^q{d}_i{\Vert v^i\Vert }_{\infty }, \end{gathered}$$ (2)

      which can be efficiently acquired using the algorithm proposed in [37]. Then normalization is applied as V/‖V‖_F;
   2. Update $w={\sum }_{k=1}^K\frac{1}{n_k}{X}_k^T{Y}_k{v}_k$; Then normalization is applied as w = w/‖w‖₂;
   3. Update d by calculating d_i = ‖vⁱ‖₀.

3. Get the next L pairs of canonical vectors. Calculate $X_k=X_k-X_{k}w{w}^T,Y_k=Y_k-\frac{Y_k{v}_k{v}_k^T}{{\Vert v_k\Vert }_2^2}$; return to Step 2.

In (1), there are three tuning parameters λ₁,λ₂,τ. To determine them, we apply 10-fold cross validation with a stability criterion similar to [38]. More specifically, the data are partitioned into 10 subsets $X_k^{(b)},Y_k^{(b)},b=1,\dots ,10$, where the portion of samples in different subsets is kept the same for each cancer. For each subset, the JSCCA is fitted on $X_k^{\left(b^C\right)},Y_k^{\left(b^C\right)}$, and the canonical vectors $w^{(b)},v_k^{(b)}$ are obtained. Define

$$\begin{gathered} m=\sum _b\sum _k\frac{1}{n_k^{(b)}}{(X_k^{(b)}{w}_b)}^T{Y}_k^{(b)}{v}_k^{(b)} \\ T=\sum _b{(\sum _k\frac{1}{n_k^{(b)}}{(X_k^{(b)}{w}_b)}^T{Y}_k^{(b)}{v}_k^{(b)}-m)}^2 \end{gathered}$$

Then the parameters are selected by maximizing $\frac{m}{\sqrt{T}}$. In real data analysis, we found that the stability criterion described above can result in a more reasonable and stable module size than other available criteria.

Finally, the JSCCA is fitted on full data with selected parameters. The variables in w,v_k with non-zeros entries are selected as correlated modules:

$${\mathrm{\Gamma }}_w=\left\{j\left|\right|w_j|>0\right\},{\mathrm{\Gamma }}_v=\left\{i\right|{\Vert v^i\Vert }_{\infty }>0\},$$ (3)

Moreover, one interesting property of the group L_∞ optimization (2) [37] is that the algorithm tends to obtain a solution, where the nonzero canonical coefficients for each gene across different cancers are exactly the same (see Fig. S1 in the appendix). Accordingly, we assign each gene to a certain group of cancers as follows:

$$C_i=\left\{k\left|\right|v_k^i\left|=ma{x}_k\right|v_k^i|\right\},i=1,\dots ,q.$$ (4)

That means, for any cancer in C_i, the ith gene is detected to be affected by the selected methylated sites. Specifically, if |C_i| = K, the gene is shared by all studied cancers. In the following, we call the cancers in C_i as inside-group cancers for the ith gene, and that out of C_i as outside-group cancers.

A major difference of formulation (1) from our previous work is that we replace the fused lasso penalty by group L_∞ penalty. There are mainly two reasons for this change. First, as compared to group L₂ norm, which is the most popular similarity penalty, the use of both group L_∞ and fused lasso penalty has the exclusive advantage of encouraging similar features to have the same coefficient, which is desirable for the identification of group-specific genes. Second, as compared to imaging genetics data studied in our previous work [15], the DNA methylation and gene expression profiles used here have larger sample size, lower dimension, and higher pairwise correlation. In our application, we found that the fused lasso penalty is too strong to derive a desirable result. Instead, a weaker penalty like L_∞ is preferable. In fact, the solution of fused lasso encourages all the variables in the same group to be the same, while group L_∞ norm enforces the similarity of nonzero coefficients only. Therefore, we choose group L_∞ penalty instead.

B. Joint Partial Correlation Detection

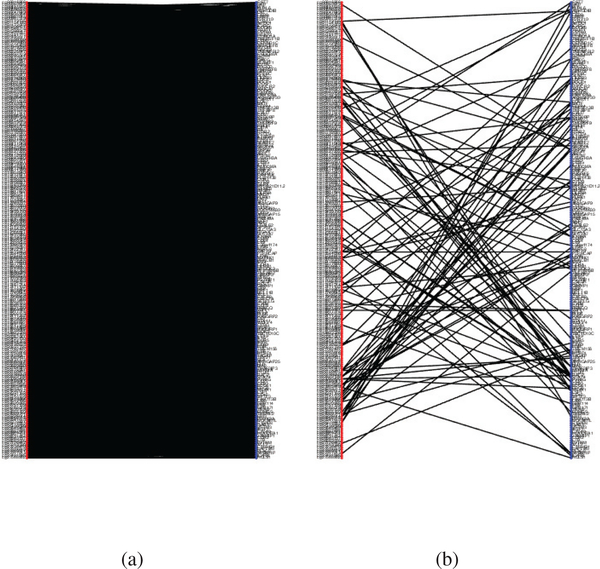
In the previous section, we presented the joint sparse CCA, which can identify complex associations between two data types in the form of a module. Given a detected module, we can apply biological pathway-based analysis and look for potential interactions between pathways enriched by methylation and genes. A question is then how a single pair of methylation and gene interacts in the module. For example, one may be interested in whether and where the cis effects impact the module, or more generally, in locating driver methylation-gene pairs that have high functional impacts. This goal can not be directly achieved by CCA analysis, and an additional step is therefore required to distinguish driver pairs from the module. However, the challenge is that the network always contains a lot of indirect correlations(see Fig. 6 as an example), due to co-expression and co-methylation. To this end, we introduce a joint sparse precision matrix estimation model and show how it can detect driver methylation-gene pairs from a module derived from joint sparse CCA.

Fig. 6.

The bipartite network of DNA methylation and gene expression network with a p-value threshold of 0.01. (a) Constructed by the mean Pearson’s correlation over the four cancers. The number of connected edges is 28347. (b) Constructed by the estimated joint precision matrix Ω. The number of connected edges is 102.

Gaussian graphical model (GGM) is a widely used method to infer dependency relationships among multiple variables. The GGM can be represented by an undirected graph, where each edge measures the dependency of two variables conditioned on all the other variables. The GGM is closely related to partial correlation network, and can be obtained through the estimation of the inverse covariance matrix, also known as the precision matrix. Specifically, assuming the data samples are drawn from a multivariate normal distribution N(0,Σ) with covariance matrix Σ, the goal of GGMs is to estimate the inverse covariance matrix $\mathrm{\Omega }={\mathrm{\Sigma }}^{-1}=\left({\omega }_{ij}\right)$. The precision matrix can be converted to the partial correlation matrix R where:

$$r_{ij}=\frac{-{\omega }_{ij}}{\sqrt{{\omega }_{ii}{\omega }_{jj}}}$$ (5)

However, in high-dimensional problems, the inverse of the empirical covariance matrix is not well-defined. To overcome this limitation and apply to multiple cancer data with the same features, the joint sparse penalized precision matrix estimation method is an ideal approach [16]. In general, the method is based on a penalized log-likelihood approach, where the penalty encourages different networks to share a similar structure:

$$\underset{{}_{\mathrm{\Omega }\succ 0}}{\max }\sum _{k=1}^K\log \det \left({\mathrm{\Omega }}_k\right)-tr\left(S_k{\mathrm{\Omega }}_k\right)-{\lambda }_1{p}_1\left({\mathrm{\Omega }}_k\right)-{\lambda }_2{p}_2\left({\mathrm{\Omega }}_1,\dots {\mathrm{\Omega }}_K\right)$$ (6)

In (6), S_k is the empirical covariance matrix for the kth class of data samples, Ω_k is the precision matrix to be estimated for the kth class, p₁ is a sparse penalty term (e.g., L₁ norm, SCAD) that leads to sparse solution, p₂ is a similarity penalty (e.g. fused lasso, group L₂) that encourages the similarity among the K precision matrices. However, the optimization does not scale well to high-dimensional data and the finding of two tuning parameters λ₁,λ₂ will further increase computational costs.

Here, we instead consider joint estimation of partial correlations only among the methylated sites and genes selected by JSCCA, i.e., Γ_w and Γ_v. The aim of this estimation is to further extract significant pairwise associations between DNA methylation and gene expression levels that can infer more specific functions related to the cancer process. In addition, instead of imposing a similarity penalization p₂, the information in (4) obtained in the first stage is used, leading to a more efficient algorithm and more interpretable results. More specifically, we first pool DNA methylation data and gene expression data to calculate the empirical covariance matrix S_k:

$$S_k=\frac{1}{n_k-1}{\left[Y_{k,{\mathrm{\Gamma }}_v},X_{k,{\mathrm{\Gamma }}_w}\right]}^T\left[Y_{k,{\mathrm{\Gamma }}_v},X_{k,{\mathrm{\Gamma }}_w}\right].$$ (7)

Then, we assume the partial correlation network to be the same across cancers except the edges belonging to outsidegroup cancers for each gene. More specifically, we assume the precision matrices for each cancer Ω_k,k = 1,..,K to have the following form:

$${\mathrm{\Omega }}_k=\mathrm{\Omega }\cdot {\mathrm{\Theta }}_k,$$

where Ω is the joint precision matrix and · denotes the elementwise multiplication, and the element in Θ_k is defined that θ_ijk = 0(I ≠ j) if k ∉ C_i and θ_ijk = 1 otherwise.

Finally, we can formulate the joint sparse precision matrix estimation model as the following:

$$\underset{{}_{{\mathrm{\Omega }}_k\succ 0}}{\max }\sum _{k=1}^K\log \det \left({\mathrm{\Omega }}_k\right)-tr\left(S_k{\mathrm{\Omega }}_k\right)-{\lambda }_3{p}_{mcp}\left({\mathrm{\Omega }}_k\right)$$ (8)

in which the Ω_ks are constrained to be positive definite. We choose mini-max concave penalty(MCP) [39] as the sparse constraint. The derivative function of MCP is defined as $p_{mcp,{\lambda }_3}^{\prime }(t)=\left({\lambda }_3-\frac{t}{a}\right)$, where a was suggested to be 2 [39]. To solve (8), we used the local linear approximation algorithm with quadratic inverse covariance estimation [40] [41], which is an efficient algorithm capable of achieving strong oracle optimality under certain conditions (see Appendix for more details). In addition, to determine the parameter λ₃, we apply 10-fold cross validation by maximizing the testing likelihood.

Through the above procedures, we can obtain a joint precision matrix Ω, where each edge ω_ij is shared by cancers in C_i. Then, the partial correlation matrix R can be calculated according to (5). To address the statistical testing problem of non-zero partial correlation, we followed the estimation in [42]

$$\sqrt{l_i{\left(1-r_{ij}\right)}^{-2}}{r}_{ij}\to N(0,1)$$ (9)

under the null hypothesis that the true partial correlation $r_{ij}^{*}=0$, where $l_i={\sum }_{k\in C_i}{n}_k$ is the effective sample size for edge r_ij. Therefore, the p-values can be acquired according to

$$p_{ij}=2(1-\mathrm{\Phi }(\sqrt{l_i{(1-r_{ij})}^{-2}}\left|r_{ij}\right|))$$ (10)

where Φ(x) is the standard normal cumulative distribution function. Finally, we control the proportion of false positives by calculating the false discovery rate (FDR) using the Benjamini-Hochberg procedure [43].

In summary, this step provides additional information complementary to the one derived from joint sparse CCA, leading to a more comprehensive analysis of two data types.

IV. Results

In this section, we applied the proposed method to a paired dataset from The Cancer Genome Atlas(http://cancergenome.nih.gov/). The data were downloaded using the toolbox TCGA2STAT [44]. The samples containing both DNA methylation and gene expression profiles were kept. Then, the cancer types with sample size higher than 100 were selected, including BRCA, COAD, LUSC, OV, and Glioblastoma Multiforme(GBM). Finally, we selected the first four cancers which are more related to each other. The data left were from 1166 tumor samples, among them 311, 151, 133, 571 samples were from BRCA, COAD, LUSC, and OV, respectively. DNA methylation profiles were obtained from level-3 data by HumanMethylation27 BeadChip. The gene expression data were level-3 gene-level expression data from Agilent G450. The DNA methylation and gene expression levels with missing rate higher than 5% in any cancer type were deleted and the remaining missing values were imputed by the k-nearest neighborhood method. Then, the methylation levels with standard variance below 0.01, which are almost unchanged among samples, were removed from the data. Finally, to find the epigenetic effects only related to cancers, for each cancer, a two sample t-test was applied to the methylation levels between the tumor samples and normal samples, and BH procedure with target FDR= 0.05 was applied. The methylated sites were kept if the t test showed significance in any cancer types. All these procedures resulted in 14023 methylated sites and 17766 genes.

A. A Comparison of Different Penalties for Joint Sparse CCA

In this section, we will show group L_∞ penalty is a good choice for JSCCA in multi-class problems. To do this, we designed a simple simulation and compared the power and false discover rate between group L_∞ and fused lasso penalties.

The simulated data were generated using a latent variable model similar to [32]. Suppose we have two types of data, e.g. the methylation and gene expression, which belong to 4 classes. For each class, we generated 200 samples, and the correlated data were simulated based on predefined canonical vectors. More specifically, we first generated one methylation canonical vector α with p = 2000 features and 100 non-zero entries. We then generated 4 gene expression canonical vectors β_k with q = 2000 features and 200 non-zero entries. Among the 200 gene canonical variables, 100 of them had the same value across classes while 25 of them were only present in one class. Each non-zero variable in α and β_k was drawn independently from U[−1,−0.5] or U[0.5,1] with equal probability.

Given a sample belonging to the k-th(k = 1,2,3,4) class, we drew a random number h from normal distribution N(0,σ_h), where σ_h is the signal to noise level. Then the methylation levels and gene expression profiles were simulated using αh + ϵ_m and β_kh 𝜖_g respectively, where ϵ_m and ϵ_g are random noise with distribution N(0, I_p) and N(0, I_q). In this way, the methylation and gene expression are correlated through the latent variable h. In each simulation, the statistics were averaged over 20 replications. The parameters were tuned by 10-fold cross-validation with the stability selection criterion.

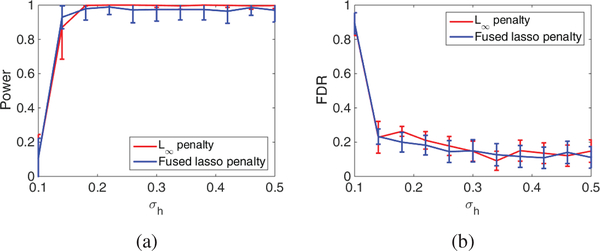
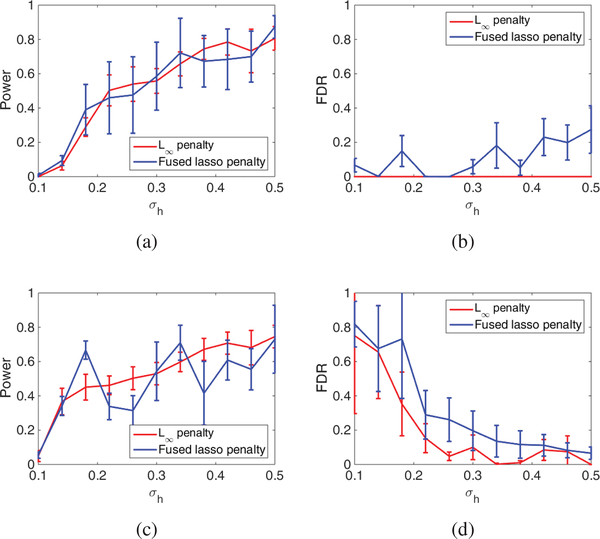
Fig. 2 and 3 evaluate the success in detecting correlated methylation and gene with varying noise level σ_h. The figures imply that both penalties work well for the detection of methylation and genes. Fig. 3 also implies that the power for gene detection is limited, but the FDR can be well controlled. It should be noted that the low FDR may not be guaranteed in real data with much more complex structures. Nevertheless, we can still expect that our method can achieve decent FDR control. Moreover, as compared with the fused lasso penalty, the group L_∞ penalty can achieve similar power but much lower FDR. This fact supports our selection of group L_∞ in pan cancer analysis.

Fig. 2.

A comparison of the power and FDR between Group L_∞ penalty and Fused Lasso penalty (a) Power for methylation (b) FDR for methylation.

Fig. 3.

A comparison of the power and FDR between Group L_∞ penalty and Fused Lasso penalty (a) Power for common genes (b) FDR for common genes. (c) Power for cancer specific genes (d) FDR for cancer specific genes.

B. Canonical Correlated methylated sites and genes

We firstly applied the JSCCA method described in Section 2 to the cancer data. The parameters were tuned by 10-fold cross-validation with the stability selection criterion. Using the selected parameters, we obtained a set of 220 methylated sites and 211 genes, which were listed in the table in the supporting document. We calculated C_i for each selected gene and found that 112 of them are shared by all 4 cancers while 28,26,45 genes are specific to a single, two, and three cancers, respectively. The CpG sites were annotated to the nearest genes, and 14 of them are among the detected genes. Through a permutation test, we find the number of overlaps is significant(p < 1e − 6), which proves that cis-effect plays an important role in methylation regulation.

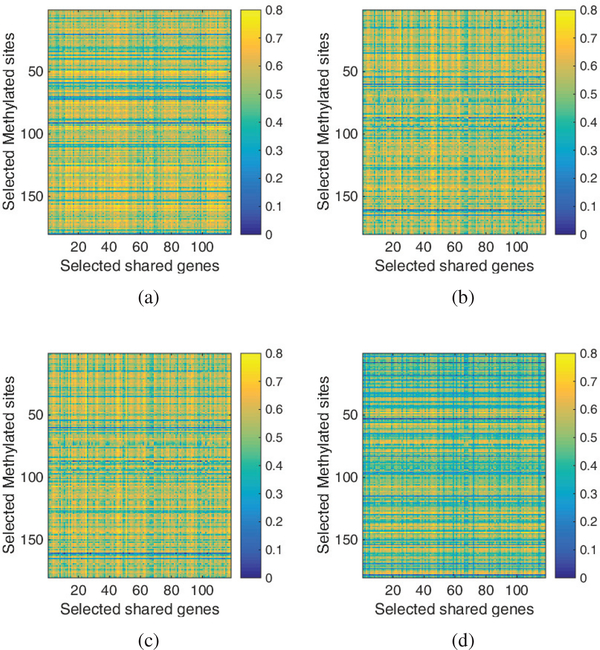
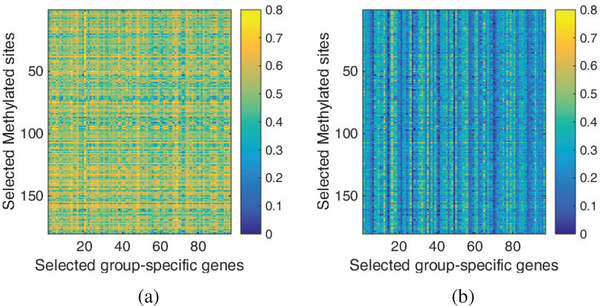
In Fig. 4, we plotted the detailed correlations between the selected methylated sites and shared genes for each cancer. As shown in the figure, the correlated pairs are dense in all four cancers. In contrast, we also plotted the correlations between methylation and group-specific genes in Fig. 5. Specifically, for each gene, we plotted the mean correlation over inside-group cancers in Fig. 3(a) and that over outside-group cancers in Fig. 3(b). As seen in the figure, the correlations corresponding to inside-group cancers are constantly higher than outside-group ones. Overall, we can find that JSCCA is able to detect correlated DNA methylation and gene expression, and well classify both shared and group specific interactions.

Fig. 4.

Heatmap of the correlation between methylation and shared genes for (a) BRCA (b) COAD (c) LUSC and (d) OV.

Fig. 5.

The heatmap of the mean correlation between methylation and genes on (a) inside-group cancers and (b) outside-group cancers.

To study the biological implications of the results, we began with the testing on the selected methylated sites. To do this, we mapped them to the nearest genes and then performed gene set over-representation analysis using ConsensusPathDB [45]. The pathways enriched with p-value less than 0.01 and by at least three methylated sites were summarized in Table I. There were mainly 8 pathways enriched. Furthermore, we investigated the potential functions of selected genes. We also performed the gene set over-representation analysis on the shared genes and cancer-specific genes separately (the groupspecific genes corresponding to two or three cancers were not considered here). We listed some selected pathways in Table II, including 5 shared pathways and one COAD specific pathway.

TABLE I.

The selected enriched pathways by selected methylation sites.

Pathways	p-value
GRB7 events in ERBB2 signaling	8.62e-06
Bladder cancer	6.32e-04
α6β1 and α6β4 integrin signaling	1.15e-03
EGFRI	1.49e-03
ErbB Signaling Pathway	1.92e-03
Constitutive Signaling by Aberrant P13K in Cancer	3.52e-03
Signaling by PTK6	3.95e-03
Oncostatin M	6.20e-03

TABLE II.

The selected enriched pathways by identified genes.

Pathways	p-value	Type
TCR Signaling	2.37e-11	Shared
Primary immunodeficiency	3.15e-09	shared
Cytokine-cytokine receptor interaction	1.85e-08	Shared
Class I P13K signaling events	2.38e-04	Shared
NF-κB signaling	3.90e-04	Shared
Jak-STAT signaling	3.98e-03	Shared
Pathways in cancer	1.06e-04	COAD

C. Significant partial correlated pairs

Then, we applied the joint sparse precision matrix estimation method to the 431 features selected by JSCCA. Fig. 6 compared the bipartite networks constructed by the joint partial correlation matrix (Ω estimated) with those constructed by the mean Pearson’s correlation over four cancers. The p-value threshold was set as 0.01 for both networks. As shown in the figure, with the Pearson’s(marginal) correlation, most of the methylation-expression correlations are strong. In contrast, with the partial correlation, the overall network is much sparser. On one hand, Fig. 6 shows that the associations between DNA methylation and gene expression are involved with a complex system and contain many indirect connections. On the other hand, since the precision matrix can fully describe the marginal correlation network, Fig. 6 also implies that a few pairs of methylation-gene interactions can spread over the whole system. All these facts motivated us to perform partial correlation analysis to detect the methylations and the closely related genes.

With a FDR threshold of 0.05, we detected 22 methylation-gene pairs with significant partial correlations. Table III listed all the pairs with p-value estimated from (10) as well as from the data of each single cancer using FastGGM [42]. Among these pairs, 18 are shared by all studied cancers. As shown in the table, the p-value estimated from pan-cancer analysis is much lower than that from any single cancer. In addition, 3 pairs (cg15518883 and SIT1, cg10590292 and BIN2, cg16068833 and cd52) were found to be cis-effect, where both pan-cancer and single cancer p-value are much lower than the average. Unlike trans-effect, which is still debatable, the cis-effect of methylation is widely accepted. So we are quite interested in the three genes. SIT1 (signaling threshold regulating transmembrane adaptor 1) is a protein coding gene. It plays an important role in the TCR signaling, and influences the outcome of thymic selection [46]. BIN2 (Bridging Integrator 2) is related to innate immune system. Differential expression and methylation BIN2 were found in head and neck squamous cell carcinoma [47]. CD52(CD52 molecule) is a glycoprotein expressed on the all lymphocytes [48], which is closely related to the activity and treatment of lymphocytic leukemia [49]. We further look into the clinical relevance of the three genes. To this end, the gene expression data (Level 3 RNA-Sequencing data) and the corresponding clinical data were downloaded from the TCGA, including 1200, 314, 544, and 307 samples for BRCA, COAD, LUSC, OV, respectively. For each gene and each cancer, the samples were separated into a high-expression group and low-expression group by the median expression level. Then, the log rank test was performed to test the difference of the survival curves of the two groups and the p-values were listed in Table IV (The Kaplan Meier plots were included in the supplementary material). From the table we can see that all the three genes are related to the survival time of breast cancer, and SIT1, BIN2 were weakly associated with the survival time of OV and LUSC, respectively. All these evidences demonstrated the important roles of the three genes played in cancers, especially in the aspect of immunity. However, little knowledge was known about how the methylations regulate them in these cancers. Our results suggested strong associations between the methylation and gene expression levels of these three genes.

TABLE III.

The significant partial correlations between the selected DNA methylation and gene expression.

CpG site	Gene	p.joint	p.brca	p.coad	p.lusc	p.ov
cg16068833	CD52	7.83E-12*	1.65E-04*	1.67E-01*	2.07E-03*	4.20E-18*
cg17518965	RAC2	9.80E-08*	2.07E-01*	1.19E-01*	4.54E-01*	1.52E-04*
cg23093496	EDG6	1.33E-07*	1.62E-01*	2.07E-08*	3.25E-01*	9.44E-01*
cg09307264	Rgr	1.83E-06*	5.77E-01*	1.41E-03*	5.59E-03*	4.30E-03*
cg18536148	WIPF1	1.32E-05*	3.83E-03*	3.41E-01*	7.59E-02*	1.95E-01*
cg10590292	BIN2	1.62E-05*	5.94E-19	5.58E-01*	1.52E-02*	2.12E-01*
cg23093496	RAC2	1.91E-05*	3.24E-02*	7.83E-01*	2.64E-03*	4.34E-01*
cg24855780	LCK	2.12E-05*	9.70E-01*	1.29E-02*	1.82E-01*	5.49E-02*
cg13797282	RAC2	2.74E-05*	4.39E-03*	5.59E-01*	1.89E-03*	4.41E-03*
cg10981541	C20orf174	6.64E-05*	4.24E-02*	1.18E-01*	1.48E-01*	8.40E-04*
cg20792833	SP140	9.08E-05*	2.72E-01*	4.09E-01*	1.69E-01*	3.04E-02*
cg24453664	RP5–821D11.2	9.29E-05*	6.68E-01*	8.73E-03*	5.20E-01*	6.25E-01*
cg22820108	ABI3	1.05E-04*	6.68E-02*	1.08E-01*	1.28E-02*	1.82E-01*
cg22820108	CCR7	1.16E-04*	5.26E-01*	5.45E-04*	1.35E-01*	7.48E-05*
cg17740645	LCK	1.17E-04*	2.94E-01*	7.40E-03*	2.25E-03*	1.44E-02*
cg15518883	SIT1	1.63E-04*	8.20E-04	1.40E-41*	6.80E-10*	5.48E-18*
cg04008913	RAC2	1.70E-04*	9.39E-01*	8.31E-01*	8.75E-06*	1.49E-07*
cg01119135	ARHGDIB	1.98E-04	9.26E-01	8.62E-01*	3.94E-02*	1.18E-01*
cg17078393	LILRB3	2.77E-04*	6.04E-03*	1.27E-02*	3.93E-02*	2.12E-02*
cg08361238	LILRB1	2.84E-04*	7.31E-02*	8.37E-01*	6.77E-01*	2.13E-02*
cg17471102	LILRB1	3.58E-04*	1.36E-01*	7.78E-01*	1.27E-02*	8.12E-01*
cg03776060	IL16	3.93E-04*	5.38E-02*	1.86E-01*	1.69E-01*	1.98E-01*

^*cancers share the corresponding partial correlation.

TABLE IV.

Log-rank p values from analysis of correlation between mRNA expression level and patient survival.

	BRCA	COAD	LUSC	OV
SITI	7.76e-3	9.13e-1	8.62e-1	1.03e-1
BIN2	1.73e-2	6.71e-1	9.17e-2	9.47e-1
CD52	3.25e-4	5.3e-1	4.07e-1	6.2e-1

V. Discussions and Conclusions

In this paper, we have put forward an approach for discovering associations between DNA methylation and gene expression profiles from multiple cancers. The approach is able to detect both shared and group-specific interactions. Different from the single variate methylation-gene correlation analysis, we focus on the interactions from any loci and multivariate effects. To realize the goal, we first applied joint sparse CCA to detect a correlated module and then estimated the partial correlations in this module to further detect significant pairwise interactions.

We have analyzed the data consisting of DNA methylation and gene expression profiles from 4 types of cancers. The method with complementary two stages has shown to be effective in extracting interactions from different aspects.

From joint sparse CCA analysis, many interesting pathways have been enriched by both methylated sites and genes. On one hand, overexpression of ERBB2 is shared by several types of human carcinomas [50], while differentially methylated region was identified in ERBB2 in non-small cell lung cancer [51] and breast cancer [52]. EGFR hypermethylation was found in breast cancer, lung tumors, and etc. [53]. The integrin α6β4 was shown to be related to the demethylation of selected promoters in cancer through the cooperation with growth factor receptors including EGFR, ERBB2 [54]. Promoter methylation mediated silencing of Oncostatin M receptor-beta was found in the progression in colon cancer and was recognized as a novel therapeutic marker [55]. PTK6 was identified to be hypermethylated in ovarian cancer cells, and treatment with the demethylation can restore the expression [56]. All these findings demonstrate the biological significance of the selected methylated sites.

On the other hand, several pathways enriched by genes are closely related to epigenetic dysregulation in one or more cancers. With pathways enriched by shared genes, PI3K signaling plays a crucial role in the growth and survival of cancer cells [57], and was shown to be related to epigenetic alterations [58]. Epigenetic dysregulation of the Jak/STAT pathway was identified in various cancers [59] [60] [61]. Abnormal NF-κB activity was found in most cancers, and several aberrant methylation sites of NF-κB were identified to be related to cancers [62]. Findings further validate that the selected genes are affected by aberrant methylation in cancer progress.

From joint partial correlation analysis, we have detected some significant pair-wise interactions. Among these genes, WIPF1, ABI3, RAC2, CCR7, ARHGDIB, were found to be related to abnormal methylation in one or more types of cancers. Of particular note, the methylation of ARHGDIB was identified to be related to squamous cell lung carcinoma [63] and ovarian cancer [64].

Moreover, although the strength of methylation-expression interactions depends on the distance, they may also involve some complex interactions and functions that perhaps have stronger associations. In fact, close interactions were found between the pathways listed in Table I and Table II, which were enriched by selected DNA methylation sites and genes respectively. For example, altered DNA methylation of ERBB2 was found to be related to PI3K pathway in breast cancer [52]. The integrin α6β4 was found to amplify the pathway PI3K, and upregulate key tumor-promoting transcription factor including NF-κB [65]. Therefore, the proposed multivariate method can potentially provide a cluster view of the complex interactions.

There are still some potential limitations of the proposed method. First, we assume that the standardized methylation level follows the multivariate Gaussian distribution. It is not always true in real data. We will test transformations [66] that can better fit to the requirement for GGMs. Second, parameter selection for joint sparse CCA is still a challenging problem. In this paper, we have proposed a criterion that combines stability and prediction, which well controls the FDR, but the power is limited. Therefore, we will consider the improvement of power in the future. Third, the methylation in our analysis is measured by microarray, which has much less CpG sites than the NGS-based profiling. By controlling the number of CpG sites to be similar to the number of genes, we can have a moderate ratio between the number of features and samples in our pan cancer analysis, which is helpful for reliable inferences. However, it will be very interesting to consider the NGS-based methylation data, which may contain more fruitful information. Fourth, our current method did not include the clinical outcome in the analysis. To improve the clinical relevance of the finding, the prediction of clinical data could be included in our model. Fifth, in our application, we extracted only variables associated to the first canonical vectors. Further canonical vectors could been extracted following the procedure described in [15]. Finally, although we have classified the interactions into shared and group-specific ones, more biological evidences are needed to support the results.

As a final note, the proposed method can be applicable to a broad spectrum of data and diseases, where the detection of associations between two high-dimensional data from multiple classes is ubiquitous. Such examples include the interactions between miRNA and gene expression from multiple cancers, and the interactions between genetic variation and brain activity from various age groups.