Abstract
Irradiation of aqueous [AuCl4]− with 532 nm nanosecond (ns) laser pulses produces monodisperse (PDI = 0.04) 5-nm Au nanoparticles (AuNPs) without any additives or capping agents via a plasmon-enhanced photothermal autocatalytic mechanism. Compared with 800 nm femtosecond (fs) laser pulses, the AuNP growth kinetics under ns laser irradiation follow the same autocatalytic rate law, but with a significantly lower sensitivity to laser pulse energy. The results are explained using a simple model for simulating heat transfer in liquid water and at the interface with AuNPs. While the extent of water superheating with the ns laser is smaller compared to the fs laser, its significantly longer duration can provide sufficient energy to dissociate a small fraction of the [AuCl4]− present, resulting in the formation of AuNPs by coalescence of the resulting Au atoms. Irradiation of initially formed AuNPs at 532 nm results in plasmon-enhanced superheating of water, which greatly accelerates the rate of thermal dissociation of [AuCl4]− and accounts for the observed autocatalytic kinetics. The plasmon-enhanced heating under ns laser irradiation fragments the AuNPs and results in nearly uniform 5-nm particles, while the lack of particles’ heating under fs laser irradiation results in the growth of the particles as large as 40 nm.
1. Introduction
Laser-assisted synthesis has attracted much attention as a versatile route to many types of nanoparticles and composite materials that has the advantage of meeting “green chemistry” objectives by eliminating the need for toxic chemical reducing agents and surfactants to control nanoparticle shape and size.1–3 In particular, “naked” Au nanoparticles (AuNPs) with no surface capping agents constitute one of the most widely studied targets of laser-assisted synthesis due to their suitability for catalysis,4 plasmonic sensing,5 and bioconjugation.6 Uncapped AuNPs with varied sizes and shapes have been synthesized through pulsed laser ablation of an Au target in solution4–16 and photochemical reduction of the tetrachloroaurate complex, [AuCl4]− .17–27
Laser-mediated photochemical reduction of aqueous [AuCl4]− is predominantly performed with intense laser pulses of picosecond (ps) or femtosecond (fs) duration at the Ti:Sapphire wavelength of 800 nm.19–29 Such intense pulses can induce ionization and decomposition of water through multiphoton absorption to form hydrated electrons and hydroxyl radicals30–32
| (1) |
Multiple investigations have established that the resulting hydrated electrons26–29 and hydrogen peroxide formed by recombination of hydroxyl radicals21–26 drive the conversion of [AuCl4]− to AuNPs. At sufficiently high laser peak intensities where the laser beam is tightly focused, water decomposition proceeds through optical breakdown (OB) to produce a dense plasma with electron densities exceeding 1020 cm−3,30–32 while adopting a loose focusing geometry produces a low-density plasma (LDP) with electron densities on the order of 1018 cm−3 33 through self-focusing and filamentation.34–36 The latter LDP conditions have been likened to those produced upon the interaction of water with densely ionizing radiation,27,28 and have been adopted for [AuCl4]− reduction.27–29
In contrast to the well-established ps and fs laser-induced photochemical conversion of aqueous [AuCl4]− to AuNPs, the use of ns lasers has required the addition of support materials such as graphene oxide,37,38 biopolymer films39 or silicon surfaces40–42 to aid in the reduction of [AuCl4]− . A recent study reported that no [AuCl4]− reduction occurred under irradiation with 1040 nm, 120 ns pulses at intensities up to 2.2×109 W cm−2 in the absence of the silicon surface.42 This circumstance likely arises because extremely high pulse energies and tight focusing conditions are required for OB with ns lasers in water, and the dominance of cascade ionization (as opposed to photoionization) with ns pulses precludes the formation of LDP at intensities below the OB threshold.30,31 In this work, we demonstrate that irradiation with 532 nm, 8 ns pulses at intensities well below the OB threshold can produce AuNPs from aqueous [AuCl4]− in the absence of a support material or additional chemical reducing or capping agents. Analysis of the AuNP growth kinetics and comparison to the results using fs pulses under LDP conditions indicates that the ns laser induces AuNP formation through a plasmon-enhanced photothermal autocatalytic mechanism.
2. Experimental
2.1. Materials
Potassium tetrachloroaurate (III) (Strem Chemicals), HPLC-grade water (Fisher Scientific), and potassium hydroxide (Fisher Scientific) were used as obtained. From stock solutions of KAuCl4 (25 mM) and KOH (500 mM), a working solution for experimental runs was prepared containing 0.1 mM KAuCl4 and 0.35 mM KOH (pH 5.3 ± 0.2). The working solution was prepared 24 hours in advance, and stored at 6° C. Prior to laser irradiation, 3.0 mL of the working solution was brought to room temperature, and transferred to a 10 × 10 × 40 mm quartz cuvette.
Citrate-capped AuNPs were used for experiments testing the effect of fs and ns laser irradiation on spherical AuNPs. These were prepared by the standard citrate reduction method according to the previously reported procedure.43 A 100 mL aqueous 1 mM HAuCl4 solution was heated under stirring until boiling, and then 10 mL of a trisodium citrate solution (granular U.S.P., Mallinckrodt Chemical Works) was added followed by stirring for an additional 15 minutes. This solution was stored at 6° C, and brought to room temperature prior to laser irradiation.
Quantification of H2O2 produced during laser irradiation was performed with a spectroscopic assay adapted from Ref.44 and reported in our previous publications.26,45 Briefly, samples of deionized water were irradiated for 30 minutes at the laser conditions described below, after which 400 μL of titanium(IV) sulfate (25 mM) was added to the cuvettes. The titanium(IV) sulfate (Ti4+) reacts with H2O2 to form pertitanic acid (eq 2), resulting in a yellow solution. The intensity of the yellow color is directly related to the amount of H2O2 present, and is quantified by measuring the absorbance at 407 nm.
| (2) |
2.2. Instrumentation
Nanosecond laser irradiation was performed using a pulsed Nd:YAG laser (Lab 170–30, Spectra Physics) operated at the 2nd harmonic, producing 532 nm, 8 ns, pulses at a 30 Hz repetition rate. The fundamental 1064 nm wavelength was also used for comparison. The pulse energy was varied from 50 mJ to 100 mJ by adjusting the output energy of the flash lamps that pump the Nd:YAG crystal. The output beam was down-collimated to a diameter of 7.0 mm using a pair of fused silica lenses with f = 15 mm and f = −7.5 mm. Femtosecond laser irradiation was carried out with a Ti:Sapphire regenerative amplifier (Astrella, Coherent, Inc.) delivering 7 mJ, 30 fs pulses with bandwidth centered at 800 nm at a 1 kHz repetition rate. The pulse energy was varied between 2.4 mJ and 3.6 mJ with a zero-order λ/2 waveplate (ThorLabs, Inc.) and a broadband thin-film polarizer (Altechna). The 11 mm (1/e2) diameter beam out of the laser was down-collimated to a diameter of 5.8 mm using a pair of f = 20 cm and f = −10 cm spherical mirrors. Both ns and fs beam diameters were measured using the knife-edge method. The shortest pulse duration in our fs experiments was previously reported to be 30 fs based on Frequency Resolved Optical Gating (FROG) measurements.26 To obtain this short pulse duration inside the cuvette, the grating position in the compressor was adjusted to maximize the intensity and spectral width of the supercontinuum emission generated in a cuvette containing water.
Under the collimated beam conditions, the calculated peak intensities were I0 = 3 × 107 W cm−2 for 100 mJ, 8 ns pulses and I0 = 4 × 1011 W cm−2 for 3 mJ, 30 fs pulses. However, the actual peak intensities in both laser beams are expected to be significantly higher due to nonlinear self-focusing and filamentation effects.34,35,46,47 For the ns laser, the peak power reaches P0 = 12.5 MW for 100 mJ pulses, exceeding the self-focusing threshold of Pcrit = 1.7 MW at 532 nm in water by a factor of 7.36,48 Under these conditions, the peak intensity enhancement factor I/I0 is roughly proportional or slightly higher than the excess power ratio P0/Pcrit35,47 and can be further enhanced when the pulse duration is compressed inside a filament.46 Thus, the actual peak intensity is likely to be at least an order of magnitude higher, or above I = 3 × 108 W cm−2. The peak power in the fs experiments exceeds the self-focusing threshold of 4.2 MW49 by more than 104, and therefore likely produces peak intensities in the range of I = 1012 − 1013 W cm−2.33
All laser irradiation experiments were carried out in a home-built UV-vis spectrometer consisting of a stabilized deuterium-tungsten light source (Ocean Optics, DH2000-BAL), optical fibers, two pairs of off-axis parabolic mirrors, and a compact spectrometer (Ocean Optics, HR4000).25,26 In each experiment, 3.0 mL of the working solution (0.1 mM KAuCl4 and 0.35 mM KOH in water) was placed in a 10 × 10 × 40 mm cuvette and irradiated with either the ns or fs laser under magnetic stirring for sufficient time to convert all [AuCl4]− to AuNPs. The water temperature increase in all experiments was measured using a thermocouple. For the laser fragmentation experiments, 3.0 mL of a 0.1 mM solution of colloidal citrate-capped AuNPs was irradiated under stirring for 10 minutes and a UV-vis spectrum of the solution was obtained after laser irradiation.
2.3. Characterization
Transmission Electron Microscopy (TEM).
The AuNPs were visualized using TEM (JEOL JEM-1400 TEM). A small volume of the post-irradiated solution was drop-cast onto a carbon-coated grid (Ted Pella, Inc.) and left to dry for at least 24 hours. The size distributions of the AuNPs were measured from at least three different areas of the TEM grid using ImageJ software.
UV-vis Spectroscopy.
An Agilent 8453 UV-vis Spectrometer with Agilent ChemStation software was used to measure the plasmon peaks of the post-irradiated citrate-capped AuNPs.
X-ray Photoelectron Spectroscopy (XPS).
XPS spectra were collected on a Thermofisher ESCALab 250 with a AlKα X-ray source (1486.6 eV). The colloidal samples were dried at 60°C, and the resulting powder was deposited on indium foil (ACROS Organics). Spectra were analyzed and deconvoluted using the Thermo Scientific Avantage Software; Au4f peaks were referenced to the C1s peak, which was adjusted to center at 284.8 eV.
3. Results
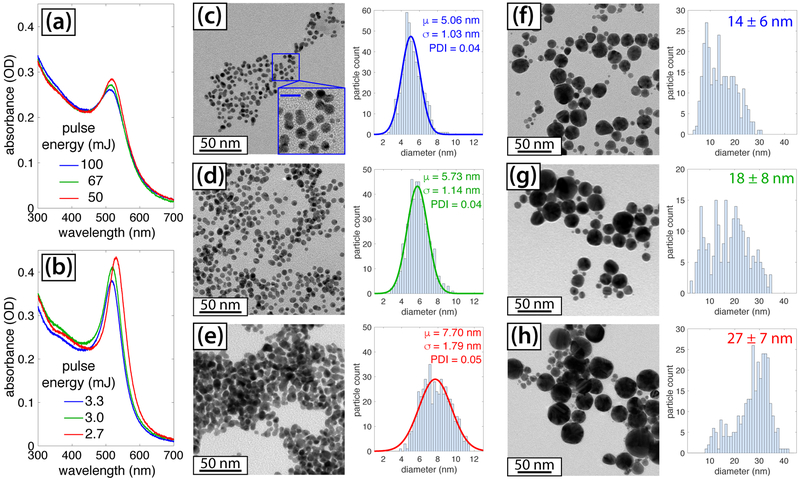
Irradiation of [AuCl4]− resulted in its complete conversion to AuNPs upon 10–40 minutes of irradiation with 532 nm ns pulses and 800 nm fs pulses, depending on the pulse energy and which laser was used. Irradiation with 1064 nm ns pulses at 100 mJ did not induce any conversion of [AuCl4]− to AuNPs after 30 minutes of irradiation based on the lack of any changes observable in the UV-vis spectrum. Figures 1(a) and (b) display the UV-vis spectra taken following irradiation of [AuCl4]− at different pulse energies with the ns (a) and fs (b) lasers. The spectra show the characteristic AuNP surface plasmon resonance (SPR) feature centered at 515 nm and 525 nm in the ns and fs cases, respectively. For both lasers, increasing the pulse energy results in a decrease in the AuNP size, as evident by the blue-shift of the SPR feature.50 The formation of smaller AuNPs at higher pulse energies (equivalently, peak intensities) is consistent with a number of earlier results using fs pulses.22,26,28 However, the most striking observation is that the ns laser produces significantly smaller AuNPs, as confirmed by TEM analysis (Figures 1(c)–(h)). The size distributions in the ns experiments could be fit well to a Gaussian function (solid curves, Figures 1(c)-(e)), which enabled computation of the mean particle size μ and standard deviation σ. Using these values, the polydispersity index (PDI) was calculated as σ2/μ2 as in Ref.14. The AuNPs produced with 100 mJ and 67 mJ ns pulses (Figure 1(c)–(d); ESI†, Figures S1 and S2) have an exceptionally tight size distribution with PDI 0.04 and are uniformly spherical, as shown in the magnified inset in Figure 1(c). These AuNPs are even smaller and more monodisperse than surfactant-free AuNPs synthesized by a two-step ns laser ablation-fragmentation process in water (8.2 ± 1.6 nm)12 and are similar to those synthesized by ns laser ablation in the presence of 0.1 − 1 mM sodium phosphate buffer that reported PDI of 0.05 and mean diameter of 5 nm.14 Thus, our results show that 532 nm ns laser-induced photochemical conversion of [AuCl4]− can produce monodisperse, surfactant-free AuNPs.
Fig. 1.
Characterization of AuNPs synthesized with 532 nm, 8 ns pulses (a; c-e) and 800 nm, 30 fs pulses (b; f-h). (a), (b): UV-vis spectra of final AuNP products synthesized with different pulse energies. (c)-(h) TEM images and size distributions: (c) ns, 100 mJ; (d) ns, 67 mJ; (e) ns, 50 mJ; (f) fs, 3.3 mJ; (g) fs, 3.0 mJ; (h) fs, 2.7 mJ. The scale bar of the inset in (c) is 10 nm.
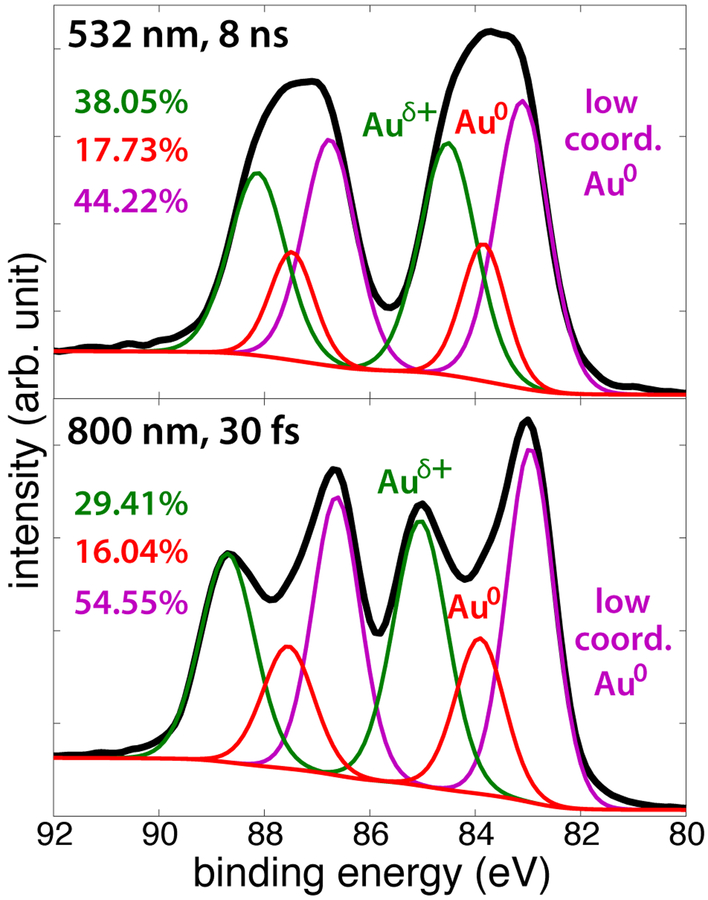
The AuNP products synthesized at an average power of 3 W (100 mJ ns pulses and 3 mJ fs pulses, Figures 1(c) and 1(g)) were also characterized with XPS to determine the oxidation states of Au present. Figure 2 shows the Au4f spectra (with 7/2 and 5/2 spin-orbit splitting), with three species deconvoluted in the samples. The peak at 83.9 eV corresponds to bulk Au0 atoms,7,51 while the peak at 83.1 eV corresponds to low-coordinated Au0 atoms,52–54 and the peak around 85 eV corresponds to oxidized or partially oxidized Au atoms, indicated as Auδ+.7,52 Low-coordinated Au0 atoms have been reported to have slightly lower binding energies relative to bulk Au0 atoms.52–54 These species are present in both fs- and ns-generated AuNPs, with a slightly higher fraction in the fs-sample. The binding energy of the Auδ+ peaks are slightly lower than the reported Au1+ atoms (85.6 eV), which could be due to low-coordinated Au1+ or partially oxidized Auδ+.52,53 The fs-generated AuNPs had a slightly higher binding energy of the Auδ+ peak (85.0 eV) relative to the ns-generated AuNPs (84.5 eV), while a somewhat higher fraction of the Au atoms are partially oxidized in the ns sample. The presence of both partially oxidized and low-coordinated Au atoms and small sizes of our ns-generated AuNPs may make them well-suited for catalytic CO oxidation.54
Fig. 2.
XPS spectra of AuNPs formed with 100 mJ ns pulses (top) and 3 mJ fs pulses (bottom) with deconvoluted peaks and atomic percentages.
To understand the origin of the different AuNP size distributions, we examined the effects of solution heating. The temperature changes of the bulk solution measured with a thermocouple during irradiation with 100 mJ ns pulses and 3 mJ fs pulses are shown in Figure 3. Both lasers have an average power of 3 W, so the total energy input as a function of time is the same (Figure 3, top axis). For the ns pulses, the solution temperature significantly rises with time when [AuCl4]− is present, but barely changes in pure water (Figure 3(a)). In contrast, the temperature rise for fs pulses is the same in the presence and absence of [AuCl4]− (Figure 3(b)), suggesting that a photothermal effect is operating in the ns case. In particular, the delayed temperature increase after ~4 minutes of ns irradiation in the presence of [AuCl4]− suggests that its conversion to AuNPs with a high absorption efficiency at 532 nm drives the temperature increase. To confirm that the presence of AuNPs induces photothermal solution heating, the temperature was measured during irradiation of a 0.1 mM solution of 15 nm citrate-capped AuNPs. The immediate temperature increase under ns irradiation in the presence of citrate-AuNPs as compared to the delayed response in the presence of [AuCl4]− (Figure 3(a)) confirms that AuNPs cause the temperature increase. In contrast, the lower temperature increase under fs irradiation in the presence of citrate-AuNPs is likely due to light scattering off of the AuNPs that prevents effective self-focusing of the beam.
Fig. 3.
Temperature change during irradiation with ns pulses (a) and fs pulses (b) in pure water (blue triangles), 0.1 mM AuCl4 (red squares), and 0.1 mM citrate-AuNPs (green diamonds). Error bars denote standard deviation over two measurements.
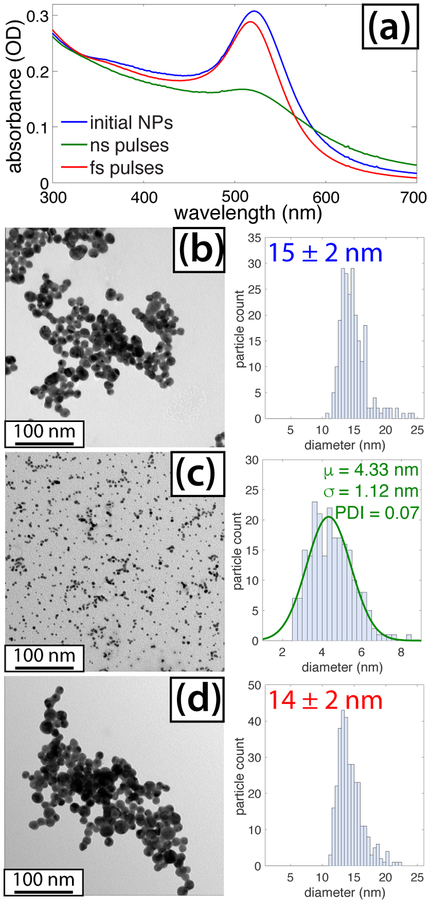
Irradiation of the citrate-capped AuNPs resulted in significant fragmentation with ns pulses but not with fs pulses (Figure 4). The lowering and blue-shifting of the SPR feature for AuNPs irradiated by the ns pulses when compared with spectrum of the initial NPs (Figure 4(a)) indicates that smaller AuNPs were formed.50 In contrast, only a small blue-shift and reduction in SPR intensity were observed for fs pulses. The as-prepared citrate-capped AuNPs are 15 nm in size and spherical in shape based on TEM analysis (Figure 4(b)). Following ns and fs laser irradiation, TEM analysis (Figures 4(c) and (d)) shows that the average particle sizes are 4.3 and 14 nm, respectively. The size distribution of the AuNPs following ns irradiation was fit to a Gaussian function, producing a PDI of 0.07. The similarity between the AuNP size distributions for the ns experiments in Figures 1(c) and 4(c) explains the 5-nm AuNPs produced by ns laser reduction of [AuCl4]−. In contrast, the lack of fragmentation of the citrate-capped AuNPs in the fs experiments (Figure 4(d)) explains why significantly larger AuNPs were formed in the corresponding [AuCl4]− reduction experiment (Figure 1(f)). These results are consistent with the widely observed AuNP fragmentation upon irradiation with wavelengths resonant with the SPR frequency55–58 and limited changes in AuNP size upon irradiation with fs lasers at non-resonant wavelengths.58,59 While the citrate-AuNPs irradiated with the ns laser have a slightly lower mean size than the NPs in Figure 1(c), they exhibit a larger PDI and a significant number of melted, fused, and agglomerated NPs (ESI†, Figure S3). The lower-quality size distribution is similar to previous studies of AuNP fragmentation55–58 and may result from the “top-down” procedure beginning with larger NPs as compared to the “bottom-up” synthesis producing the AuNPs in Figure 1.
Fig. 4.
(a) UV-vis spectra of citrate-capped AuNPs before (blue) and after irradiation with ns (green) and fs (red) pulses. (b) TEM and size distribution of initial NPs. (c) TEM and size distribution of NPs following ns irradiation. (d) TEM and size distribution of NPs following fs irradiation.
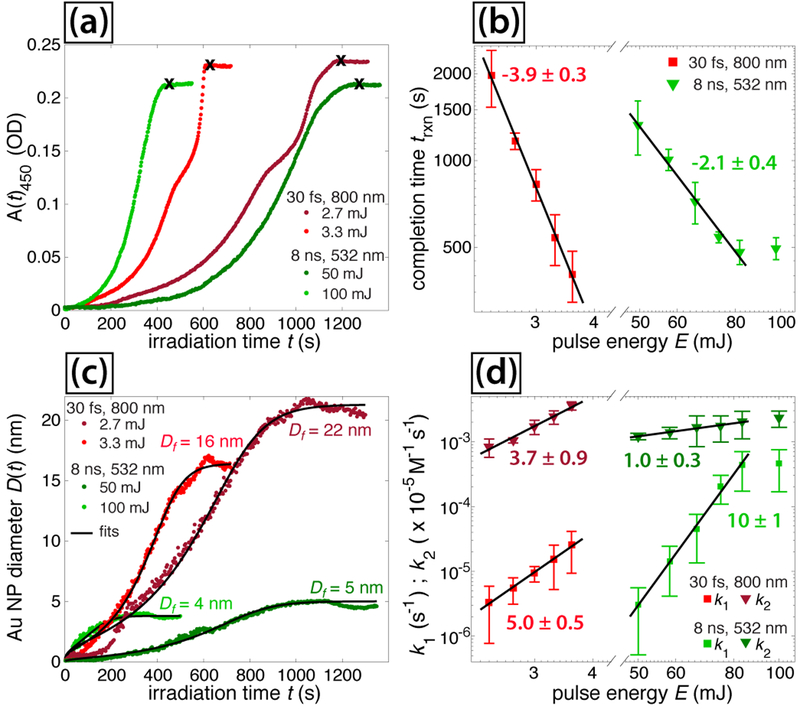
Further insight into the AuNP growth mechanisms in the ns and fs laser experiments may be gained through analysis of UV-vis spectra measured during irradiation. The absorbance at 450 nm as a function of irradiation time, A450(t), indicates the time-dependent Au(0) concentration,50 and is shown for representative experiments in Figure 5(a). Complete conversion to AuNPs occurs when A450(t) stops increasing (black x, Figure 5(a)), indicating the completion time trxn. A strong inverse correlation can be seen between the pulse energy E and trxn for both fs and ns pulses (Figure 5(b)), as quantified by fits to a power law: trxn ~ E−4 for fs and trxn ~ E−2 for ns experiments. For the ns experiments, trxn saturates at energies above 83 mJ. From these trxn values, we may calculate the AuNP throughput rate assuming 100% Au mass conversion to AuNPs. The most efficient AuNP production rate is 0.003 mg W−1 min−1 for 2.5 W (83 mJ) ns pulses, which take ~8 minutes to convert the 0.0591 mg of Au present in the cuvette. While this production rate is a factor of ~30 lower than for laser ablation syntheses reporting up to 0.094 mg W−1 min−1,13 future optimization of the reaction conditions and adoption of a flow setup like in Refs.13,14 could improve the production rate.
Fig. 5.
Absorbance at 450 nm selected pulse energies for fs (dark and light red) and ns (dark and light green) lasers. (b) Reaction completion times vs. pulse energy. (c) Fits to eq (5) for selected experiments. (d) Extracted rate constants from eq (5). Error bars in (b) and (d) denote standard deviations over four measurements at each pulse energy.
The origin of the different scaling of trxn with E in the ns and fs experiments was determined by quantification of the reaction kinetics for conversion of [AuCl4]− to AuNPs. A number of previous investigations with fs lasers25–28 have quantified the [AuCl4]− reduction kinetics using the two-step Finke-Watsky autocatalytic rate law60
| (3) |
where [A] is the [AuCl4]− concentration, [B] is the AuNP concentration, k1 is the first-order rate constant corresponding to metal-cluster nucleation and and k2 is the second-order rate constant corresponding to autocatalytic growth of the nanoparticles. In order to apply this rate equation to the UV-vis spectral data obtained in our experiments, the AuNP diameter as a function of irradiation time, D(t), was estimated using the empirical formula of Haiss et al.50
| (4) |
where ASPR(t) denotes the time-dependent absorbance at the SPR wavelength (obtained from each spectrum by cubic spline fitting of the SPR feature). The constants B1 = 3.0 and B2 = 2.2 were set based on previously determined empirical quantities.50 The experimentally obtained D(t) values were fit to the integrated Finke-Watsky rate law describing the time-dependent AuNP diameter, which may be written as27,28
| (5) |
where [A(0)] is the initial [AuCl4]− concentration and Df is the final AuNP diameter.
The D(t) values obtained from the experiments shown in Figure 5(a) using eq (4) are shown in Figure 5(c) (dots). These data were fit to eq (5) (black lines, Figure 5(c)) using nonlinear least squares optimization in MATLAB with free parameters k1, k2, and Df. Tabulated values of the rate constants k1 and k2 extracted from curve fitting to eq (5) are given in Tables 1 and 2, along with the estimated Df values and comparison to the AuNP diameters obtained with TEM (Figure 1). The estimated uncertainties are obtained from the standard deviation of each fitting parameter over four experiments performed at the same laser conditions. The predicted Df values qualitatively agree with the size distributions obtained from TEM, which validates the use of eqs (4) and(5) in characterizing the AuNP nucleation and growth kinetics.
Table 1.
Rate constants and AuNP diameters for ns experiments.
| E (mJ) | ki (×10−6s−1) | k2 (M−1 s−1) | Df (nm) | DTEM (nm) |
|---|---|---|---|---|
| 50 | 3.0 ± 2.5 | 121 ± 14 | 5.2 ± 0.5 | 7.7 ± 1.8 |
| 58 | 14 ± 10 | 138 ± 29 | 4.3 ± 0.8 | |
| 67 | 45 ± 31 | 167 ± 83 | 4.1 ± 1.2 | 5.7 ± 1.1 |
| 75 | 200 ± 90 | 173 ± 75 | 5.0 ± 0.5 | |
| 83 | 440 ± 260 | 202 ± 91 | 4.6 ± 0.3 | |
| 100 | 460 ± 290 | 230 ± 64 | 3.7 ± 0.4 | 5.1 ± 1.0 |
Table 2.
Rate constants and AuNP diameters for fs experiments.
| E (mJ) | k1 (×10−6 s−1) | k2 (M−1 s−1) | Df (nm) | DTEM (nm) |
|---|---|---|---|---|
| 2.4 | 3.3 ± 2.6 | 83 ± 26 | 20 ± l | |
| 2.7 | 7.2 ± 5.5 | 104 ± 9 | 23 ± 7 | 27 ± 7 |
| 3.0 | 9.4 ± 2.5 | 171 ± 43 | 20 ± 2 | 18 ± 8 |
| 3.3 | 15 ± 10 | 242 ± 57 | 16 ± 2 | 14 ± 6 |
| 3.6 | 25 ± 16 | 358 ± 50 | 16 ± 1 |
The rate constants k1 and k2 are plotted as a function of pulse energy E in Figure 5(d), along with nonlinear least squares curve fitting to a linear function in log-log space. The slopes of these lines denote the dependence of each rate constant on E, where the uncertainty reflects the 95% confidence interval. The energy dependences k1 ~ E5 and k2 ~E4 are similar for fs pulses, and correlate well with the observed dependence trxn ~ E4 (Figure 5(b)). In contrast, for the ns laser, the energy dependence k1 ~ E10 is much higher than k2 ~ E1, and the observed dependence trxn ~ E2 appears to be mostly driven by the k2 dependence. These significant differences between the pulse energy scaling of the rate constants for the ns and fs lasers suggest that distinct reaction mechanisms drive the AuNP nucleation and growth kinetics for each type of laser.
A summary of the quantified results for ns and fs laser experiments shown in Table 3 indicates three significant differences between the two lasers. Irradiation with ns pulses produces (1) smaller AuNP sizes, whether from directly synthesized or preexisting NPs; (2) a greater solution temperature increase; and (3) a lower pulse energy dependence for trxn and the second-order rate constant k2. In the following section, we explore the origins of these differences.
Table 3.
Summary of experimental results.
| Property | 532 nm, 8 ns | 800 nm, 30 fs |
|---|---|---|
| NP diameter | 5–8 nm | 14–27nm |
| ΔT, [AuCl4]−a | 5.7 ± 0.6°C | 0.7 ± 0.4 °C |
| ΔT, citrate AuNPb | 10.5 ± 0.1 °C | 2.0 ± 0.1 °C |
| Citrate-AuNP diameterc | 4.5 ± 1.1 nm | 14 ± 2 nm |
| E power law, trxn | −2.1 ± 0.4 | −3.9 ± 0.3 |
| E power law, k1 | 10 ± l | 5.0 ± 0.5 |
| E power law, k2 | 1.0 ± 0.3 | 3.7 ± 0.9 |
: Temperature increase after 9 minutes irradiation, relative to pure water.
: Temperature increase after 10 minutes irradiation.
: After 10 minutes irradiation.
4. Discussion
To explain the differences in AuNP growth kinetics and sizes using ns and fs lasers, we consider the general reaction mechanism for the photochemical conversion of Au3+ ions to AuNPs61–65
| (6) |
| (7) |
| (8) |
| (9) |
where reducing species R* can involve UV photons to excite the Au complex and organic radicals to induce dissociation,61–63 or hydrated electrons resulting from water ionization to reduce the Au ions.63–65 The specific intermediates and side-products of the above mechanism differ depending on the Au salt, reducing agents, and additives such as alcohols.61–65 The solution pH also determines the Au3+ reduction rate due to speciation of the [AuCl4]− complex, where the Cl− ligands are exchanged for OH− ligands as the pH increases.66 In wet-chemical syntheses, the reduction rate is slower at high pH due to the lower redox potential of [Au(OH)4]− as compared to [AuCl4]− ,67,68 while a higher reduction rate with increasing pH is seen in fs laser photochemical reduction experiments due to the greater availability of reducing species.25 Our experiments were conducted at a fixed pH of 5.2 that was previously found to be suitable for fs-laser photochemical reduction experiments25 to ensure no pH influence on the observed kinetics in the ns and fs experiments.
Across different synthetic methods, it is generally observed that eq (8) is the rate-limiting step in Au3+ reduction that defines the nucleation rate k1, and eqs (8) and (9) both contribute to the observed autocatalytic growth rate.62,64,65 However, complete reduction of Au3+ to Au0 atoms is not necessary to produce stable colloidal NPs, as electrostatic stabilization of positively-charged Au surfaces14 and surface oxidation of AuNPs7,11 help stabilize the colloids. Thus, the apparent incomplete Au3+ reduction in our experiments due to presence of oxidized Au species based on the XPS spectra in Figure 2 may be expected and does not preclude analysis of the reduction mechanisms.
In our fs experiments, the formation of LDP with electron density of ~1018 cm−3 provides hydrated electrons that can act as the reducing agent R* in the above mechanism to reduce [AuCl4]− through the net reaction
| (10) |
Recent work with fs pulses has shown that the nucleation rate constant k1 in eq (5) is directly proportional to the volume of the OB plasma in a tight focusing geometry26 and to the hydrated electron formation rate under LDP conditions.28 The pulse energy dependence k1 ~ E5 in our fs experiments suggests that the availability of hydrated electrons grows as the 5th power of laser intensity, consistent with the requirement of 5 photons to ionize water at 800 nm.30
The hydroxyl radicals present in the LDP can react with Cl− ions in solution to form reactive species such as ClOH·− and Cl2·− 69,70 or recombine to form hydrogen peroxide. Because the rate constant for OH· recombination (0.5 − 3 × 1010 M−1 s−1)71 is somewhat higher than for the initial reaction between Cl– and OH· (4.3 ± 0.4 × 109 M−1 s−1),69,70 it is expected at least half of the OH· radicals form H2O2 through recombination. H2O2 is known to catalyze the reduction of [AuCl4]− in the presence of AuNPs through the reaction72
| (11) |
The production rate of H2O2 in pure water under tight-focusing conditions where a high-density OB plasma is formed has been quantified in a number of studies,21,25,26,45 and is correlated to the rate constant k2 in eq (5) as k2 ~ [H2O2]0.5·26 While the auto-catalytic growth under OB conditions can be entirely attributed to hydrogen peroxide, hydrated electrons have also been proposed to contribute to k2 under LDP conditions due to the predicted lower rate of H2O2 formation.27
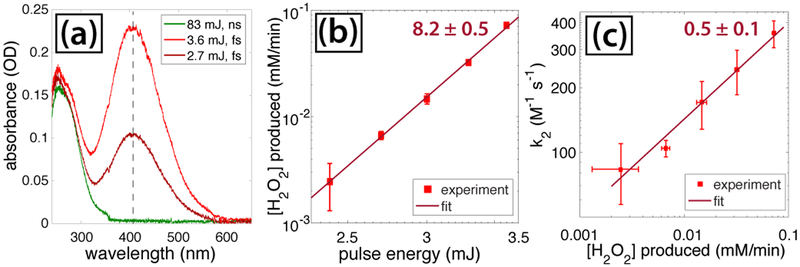
To determine the relation between H2O2 and k2 in our LDP fs experiments, we measured the amount of H2O2 formed in pure water after 30 minutes of fs laser irradiation at each pulse energy using the spectrophotometric assay of pertitanic acid formed upon addition of titanium (IV) sulfate to H2O2 (c.f., Section 2.1). Representative spectra of irradiated water with added titanium(IV) sulfate are shown in Figure 6(a), where the peak at 407 nm (indicated by the dashed line) corresponds to the absorbance of pertitanic acid. The extracted H2O2 formation rate from the assay is plotted as a function of pulse energy in Figure 6(b), showing that the peroxide yield increases as [H2O2]~ E8. This sensitivity of H2O2 formation on pulse energy is significantly higher than the linear scaling observed under OB conditions26 and is consistent with the predicted low peroxide yields under LDP conditions.27 Even with these limited peroxide yields, comparison of the H2O2 formation rates with k2 values (Figure 6(c)) reveals the same dependence of k2 ~ [H2O2]0.5 as observed previously.26 Additionally, the modest solution pH drop of 0.1 ± 0.04 units following fs irradiation is consistent with the formation of HCl via eq (11), so we conclude that H2O2 is the primary driver of k2 in our fs experiments.
Fig. 6.
(a) Spectra of irradiated water following addition of titanium (IV) sulfate. The dashed line denotes pertitanic acid absorption at 407 nm. (b) Rate of H2O2 production as a function of pulse energy for fs pulses. (c) Relation between rate constant k2 and H2O2 formation rate for fs pulses.
While the fs laser reduction kinetics of [AuCl4]− are readily explained by the formation of hydrated electrons and H2O2, this mechanism is unlikely to operate in our ns laser experiments because no H2O2 is formed during irradiation of water (Figure 6(a), green spectrum). While we cannot rule out some H2O2 formation in the [AuCl4]− experiments based on recent reports of H2 and O2 generation (implying concomitant H2O2 formation) by laser-induced AuNP fragmentation,73,74 this process cannot account for the initial AuNP formation in our experiments. An alternative mechanism is direct excitation of the [AuCl4]− ligand-metal charge transfer (LMCT) transitions at 215 and 300 nm, which can result in [AuCl4]– conversion to AuNPs in the presence of ethylene glycol.61 However, this mechanism would require at least two- or three-photon excitation at 532 nm, which is unlikely at the modest laser intensities below 109 W cm−2 used in the ns experiments. To rationalize the observed [AuCl4]– reduction kinetics in our ns experiments, we consider the possibility that the ns laser can induce thermal dissociation of [AuCl4]– to initiate reduction in eq (6) and that resonant SPR absorption of initially formed AuNPs can induce photothermal heating that drives auto-catalytic growth kinetics.
Assessing the plausibility of this mechanism requires simulating laser-induced heat transfer in water and AuNPs, which is a challenging problem due to the involvement of nonlinear processes including evaporation, hydrodynamic expansion, and molecular dissociation.75 Here, we consider a simple model for heat transfer in water that neglects the above nonlinear processes. We model the time-dependent temperature T averaged over the length of a cylindrical region of the laser beam solution as shown in Figure 7(a) using the classical thermal conductivity equation76
| (12) |
where λw is the heat conductivity of water, ρ and c are water density and specific heat capacity, respectively, and Q(t) is the heat source due to absorption of the laser radiation. Integrating eq(12) over a cylindrical volume with the radius Rb equal to the radius of the laser beam in solution and assuming an instantaneous heat source Q(t) = I, where I is the peak laser intensity, yields the following expression for the average temperature T inside the laser beam,
| (13) |
where k is the wavelength-dependent absorption coefficient of water, σ = 0.5 is the Stefan-Boltzmann constant using the approximation of gray substance, and Tm = 300 K is the temperature of the solution outside of the laser beam. The density of the medium is not expected to change on the short timescale of the laser pulses, so the product of ρc may be taken as constant. The absorption coefficient values k = 1.32 × 10−9 at 532 nm and k = 1.25 × 10−7 at 800 nm were taken from the literature.77
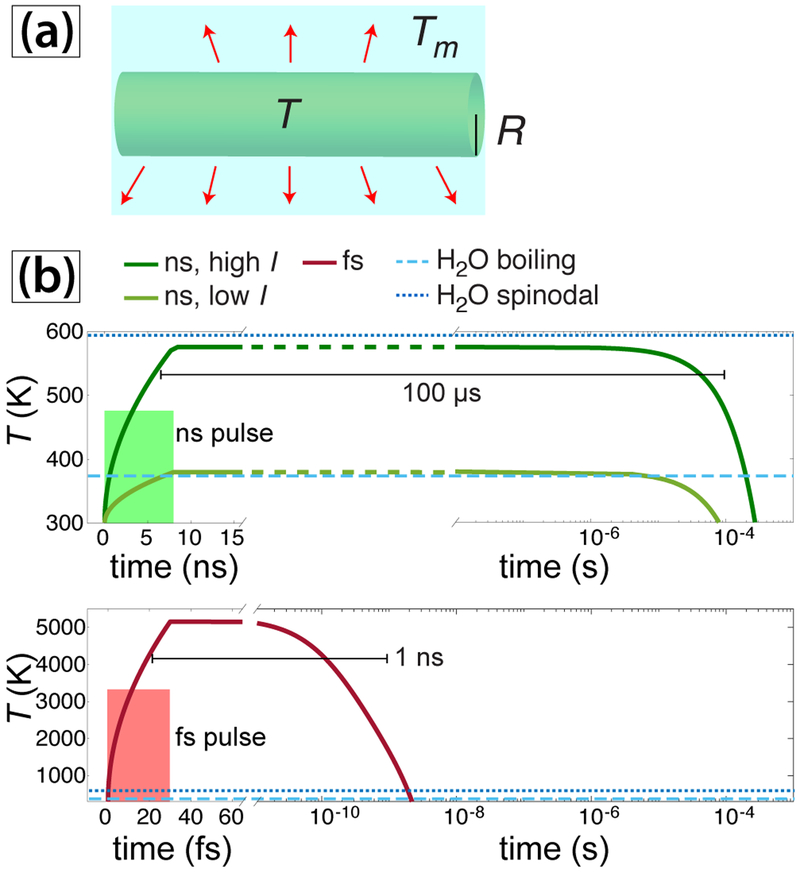
Fig. 7.
(a) Schematic of heat-transfer model. Red arrows denote heat transfer to the surrounding water with temperature Tm. (b) Heating and cooling profiles of water for ns (top) and fs (bottom) pulses using eq (13).
The peak intensity I in the experiments was estimated to be at least I = 3 × 108 W cm−2 and I = 1012 W cm−2 for the ns and fs pulses, respectively (c.f. Section 2.2). Simulation results using eq (13) for ns pulses with I = 3 × 108 W cm−2 show that the average water temperature reaches 380 K, just above the boiling point of water (Figure 7(b), light green curve). Using a higher intensity of 9 × 108 W cm−2, which may be accessible with strong self-focusing, results in a maximum temperature of 580 K (Figure 7(b), dark green curve). For comparison, simulations were performed with a fs pulse with the intensity I = 109 W cm−2 (Figure 7(b), red curve), which reaches a temperature exceeding 5000 K. Although 109 W cm−2 is significantly below the intensities in our fs experiments, we use this value in the simulation because nonlinear heating effects cannot be neglected at 1012 W cm−2.75 Both the ns and fs lasers can induce superheating of liquid water above the boiling point (light blue dashed lines, Figure 7(b)) and can approach or exceed the spinodal temperature limit of 594 K (dark blue dotted lines, Figure 7(b)). Beyond the spinodal limit, metastable liquid water spontaneously forms bubbles via phase explosion.78,79 While the extent of superheating with the ns laser is considerably smaller, the duration of heating exceeding the boiling point of water is much longer by five orders of magnitude (100 μs as opposed to 1 ns). This long duration of superheating, along with the possibility of phase explosion effects, could provide sufficient energy to dissociate a small fraction of the [AuCl4]– complex present. The extremely high sensitivity of the k1 value to the laser intensity in the ns experiments (k1 ~ I10, Figure 5(d)) is consistent with the probability of [AuCl4]– dissociation being extremely low and its having a significant dependence on the maximum temperature reached by laser heating.
Assuming that even a small fraction of the [AuCl4]– can dissociate upon ns laser irradiation, the initial reduction to Au0 atoms may proceed by a similar mechanism to that proposed in UV irradiation experiments,61–63
| (14) |
| (15) |
| (16) |
where the disproportionation in eq (16) constitutes the rate-limiting step.62
In the presence of AuNPs, irradiation at the resonant SPR wavelength of 532 nm results in plasmon-enhanced superheating of water to the spinodal temperature limit and beyond.80–82 For instance, the spinodal temperature limit of water at the interface with 27 nm AuNPs can be reached at an intensity of only 106 W cm−2 at 532 nm,80 well below the intensities used in our ns experiments. Thus, extremely high local temperatures are expected in our ns experiments once AuNPs are present, which is consistent with the observed bulk temperature rise (Figure 3(a)). Such high temperatures should greatly accelerate the rate of thermal [AuCl4]– dissociation and drive autocatalytic AuNP growth.
To estimate the effects of AuNP presence on the local temperatures reached the ns experiments, we model heat transfer to AuNPs with the ns and fs lasers for different AuNP sizes (Figure 8(a)). While this simple model only provides a qualitative estimate of the local AuNP temperature since it neglects the effects including Kapitza resistance, bubble formation, and transient SPR bleaching,83–86 the results can account for both the observed acceleration of [AuCl4]– reduction once a small amount of AuNPs are present and the small AuNP sizes. In the presence of AuNPs, diffraction leads to the absorbance coefficient k(R,λ) becoming dependent on the radius of nanoparticle RNP, where the absorbance coefficient grows with RNP.87 The time-dependent temperature of AuNPs with radius RNP before substantial evaporation can written as75,87
| (17) |
where ρg is the gold density, cg is heat capacity of gold, and T is the nanoparticle temperature. In our numerical estimations we use the following approximation for RNP << λ87
| (18) |
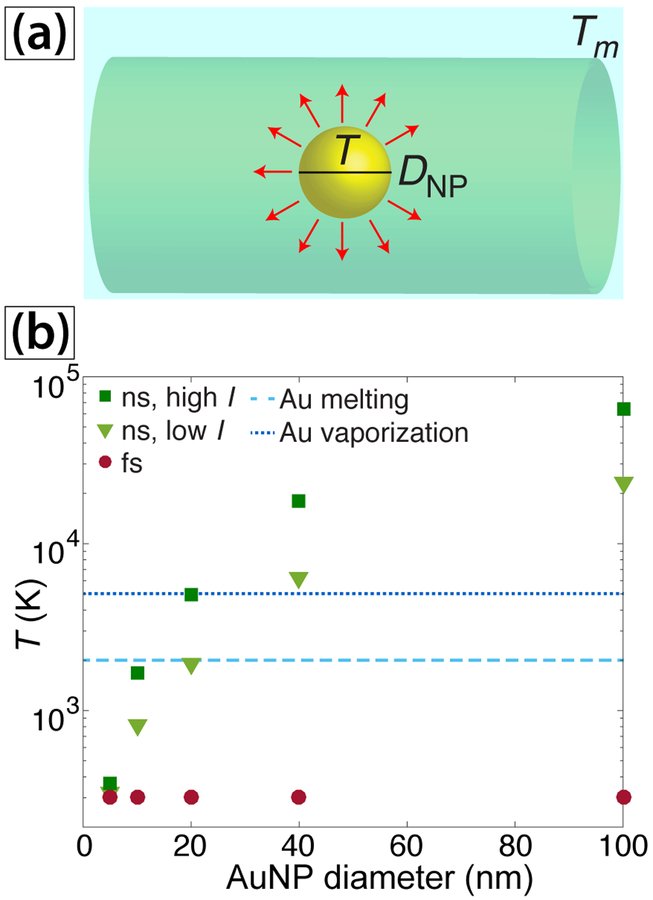
where kg(λ) is the absorbance of bulk gold. For this linear approximation, absorbance is equal to 0 for RNP = 0 and reaches the macroscopic value for RNP = λ/2. The simulated AuNP peak temperatures following exposure to one laser pulse are shown in Figure 8(b). For ns irradiation at 532 nm, temperatures near the Au melting threshold of 1300 K are reached for AuNPs as small as 10 nm, and AuNPs larger than 20 nm reach the vaporization temperature of 5000 K. In contrast, the AuNPs of all sizes are barely heated with the fs laser. These results can explain both the observed autocatalytic growth kinetics in the ns experiments and the different size distributions of AuNPs obtained with the ns and fs lasers.
Fig. 8.
(a) Schematic of heat transfer model in AuNPs. (b) Maximum AuNP temperature reached from interaction with a single laser pulse versus particle size.
First, we consider the autocatalytic growth kinetics in the ns experiments. SPR-enhanced AuNP heating will significantly raise the local solution temperature beyond that attained in water alone. For instance, the local temperature achieved after interaction with one ns pulse at I = 3×108 W cm−2 is 820 K for 10 nm AuNPs (Figure 8(b)), as compared to 380 K in pure water (Figure 7(b)). This high AuNP temperature will further heat the water, thereby significantly increasing the rate of the [AuCl4]– dissociation reactions proposed in eqs (14) and (16). As the AuNP concentration grows, the solution heating rate will further accelerate, which is consistent with the observed nonlinear growth in the bulk temperature of aqueous [AuCl4]– (Figure 3(a), red squares). Collectively, these conditions can lead to the observed autocatalytic AuNP growth kinetics. The observed linear dependence of k2 on the pulse energy (Figure 5(d)) is consistent with the autocatalytic rate depending on a linear optical process, in this case SPR absorption, as opposed to a multiphoton process. Additionally, we expect that the conversion of [AuCl4]– to AuNPs in our ns experiments requires resonant SPR absorption because ns irradiation at 1040 nm and intensities at least an order of magnitude higher than ours report no AuNP formation in aqueous [AuCl4]– .42
Second, we consider the effects of AuNP heating on the observed size distributions of AuNPs in the ns and fs experiments. The simulation results in Figure 8(b) indicate that sufficiently large AuNPs will be melted or vaporized during irradiation with 532 nm ns pulses, which explains the observed small AuNPs in the ns experiments and is consistent with previous reports of AuNP fragmentation upon irradiation at 532 nm55–59 and our results that 15 nm citrate-AuNPs fragment upon exposure to the ns laser. The lack of AuNP heating under 800 nm fs irradiation allows them to agglomerate and form large particles due to the lack of capping agents present. While filamentation of fs laser pulses in water can form sufficient spectral intensity at the AuNP SPR wavelength ~520 nm to fragment AuNPs to sizes below 5 nm,10 the spectral intensity after laser passage through the cuvette at 520 nm (0.2% relative to 800 nm, Figure S4) is too small to induce any SPR-induced AuNP fragmentation in our fs experiments. The formation of large AuNPs up to 40 nm is consistent with a recent report of large AuNPs formed under similar LDP conditions.27
5. Conclusions
We have investigated the photochemical reduction of [AuCl4]– to form AuNPs using ns and fs lasers at wavelengths of 532 nm and 800 nm, respectively. While fs laser-induced conversion of [AuCl4]– to AuNPs has been well-studied by multiple groups,19–29 the potential of ns lasers to induce this reaction had not been previously explored. This work demonstrated that near-monodisperse 5-nm Au NPs with a PDI as low as 0.04 can be formed upon irradiation with 532 nm ns laser pulses at modest intensities. Such a high-quality AuNP size distribution is rare using laser-based synthetic methods.14 We also identified a photothermal autocatalytic mechanism for the conversion of [AuCl4]– to AuNPs using ns laser pulses resonant with the SPR frequency of AuNPs. This mechanism relies on local photothermal heating of the solution driven by resonant SPR absorption, making it distinct from the radical-mediated [AuCl4]– reduction mechanism induced with fs laser pulses and consistent with the lack of [AuCl4]– conversion with 1064 nm ns pulses. Both the ns photothermal and fs radical-mediated mechanisms follow the Finke-Watsky autocatalytic rate law,60 suggesting that autocatalytic conversion of [AuCl4]– to AuNPs is a generalizable process of AuNP formation, independent of the specific mechanism. The SPR-enhanced photothermal heating of AuNPs produced from ns laser reduction of [AuCl4]– prevents their growth beyond a size of 5 – 7 nm, which makes this method potentially suitable to produce small uncapped Au nanoclusters that may subsequently be functionalized for various applications. Additionally, the high fraction of low-coordinated and oxidized Au atoms in the AuNPs may make them suitable for catalytic CO oxidation.54 Finally, this facile synthesis procedure opens up the possibility of developing additional plasmon-mediated photothermal synthetic methods to produce Au-containing nanostructures.
Supplementary Material
Acknowledgements
This work was supported by the National Science Foundation (CHE-1463989) (MSE) and the American Chemical Society Petroleum Research Fund (57799-DNI10) (KMT). Microscopy was performed at the VCU Department of Anatomy and Neurobiology Microscopy Facility, supported, in part, by funding from NIH-NCI Cancer Center Support Grant P30 CA016059.
Footnotes
Electronic Supplementary Information (ESI) available: Additional TEM images of AuNPs synthesized with the ns laser. See DOI: 10.1039/b000000x/
Conflict of interest
There are no conflicts to declare.
References
- 1.Zeng H, Du X-W, Singh SC, Kulinich SA, Yang S, He J and Cai W, Adv. Funct. Mater, 2012, 22, 1333–1353. [Google Scholar]
- 2.Barcikowski S and Compagnini G, Phys. Chem. Chem. Phys, 2013, 15, 3022–3026. [DOI] [PubMed] [Google Scholar]
- 3.Zhang D, Gökce B and Barcikowski S, Chem. Rev, 2017, 117, 3990–4103. [DOI] [PubMed] [Google Scholar]
- 4.Gu S, Kaiser J, Marzun G, Ott A, Lu Y, Ballauff M, Zac-cone A, Barcikowski S and Wagener P, Catalysis Letters, 2015, 145, 1105–1112. [Google Scholar]
- 5.Amendola V, Meneghetti M, Fiameni S, Polizzi S, Fracasso G, Boscaini A and Colombatti M, Anal. Methods, 2011, 3, 849–856. [Google Scholar]
- 6.Petersen S and Barcikowski S, J. Phys. Chem. C, 2009, 113, 19830–19835. [Google Scholar]
- 7.Sylvestre J-P, Poulin S, Kabashin AV, Sacher E, Meunier M and Luong JHT, J. Phys. Chem. B, 2004, 108, 16864–16869. [Google Scholar]
- 8.Besner S, Kabashin AV and Meunier M, Appl. Phys. Lett, 2006, 89, 233122. [Google Scholar]
- 9.Besner S, Kabashin A and Meunier M, Appl. Phys. A Mater. Sci. Process, 2007, 88, 269–272. [Google Scholar]
- 10.Besner S, Kabashin AV, Winnik FM and Meunier M, J. Phys. Chem. C, 2009, 113, 9526–9531. [Google Scholar]
- 11.Muto H, Yamada K, Miyajima K and Mafuné F, J. Phys. Chem. C, 2007, 111, 17221–17226. [Google Scholar]
- 12.Fong Y-Y, Gascooke JR, Visser BR, Metha GF and Buntine MA, J. Phys. Chem. C, 2010, 114, 15931–15940. [Google Scholar]
- 13.Barcikowski S, Menéndez-Manjón A, Chichkov B, Brikas M and Račiukaitis G, Applied Physics Letters, 2007, 91, 083113. [Google Scholar]
- 14.Rehbock C, Merk V, Gamrad L, Streubel R and Barcikowski S, Phys. Chem. Chem. Phys, 2013, 15, 3057–3067. [DOI] [PubMed] [Google Scholar]
- 15.Resano-Garcia A, Champmartin S, Battie Y, Koch A,En Naciri A, Ambari A and Chaoui N, Phys. Chem. Chem. Phys, 2016, 18, 32868–32875. [DOI] [PubMed] [Google Scholar]
- 16.Scaramuzza S, Zerbetto M and Amendola V, J. Phys. Chem. C, 2016, 120, 9453–9463. [Google Scholar]
- 17.Inasawa S, Sugiyama M and Koda S, Jpn. J. Appl. Phys, 2003, 42, 6705. [Google Scholar]
- 18.Inasawa S, Sugiyama M and Yamaguchi Y, J. Phys. Chem. B, 2005, 109, 9404–9410. [DOI] [PubMed] [Google Scholar]
- 19.Nakamura T, Mochidzuki Y and Sato S, J. Mater. Res, 2008, 23, 968–974. [Google Scholar]
- 20.Nakamura T, Herbani Y, Ursescu D, Banici R, Dabu RV and Sato S, AIP Adv, 2013, 3, 082101. [Google Scholar]
- 21.Tangeysh B, Moore Tibbetts K, Odhner JH, Wayland BB and Levis RJ, J. Phys. Chem. C, 2013, 117, 18719–18727. [Google Scholar]
- 22.Odhner JH, Moore Tibbetts K, Tangeysh B, Wayland BB and Levis RJ, J. Phys. Chem. C, 2014, 118, 23986–23995. [Google Scholar]
- 23.Tangeysh B, Moore Tibbetts K, Odhner JH, Wayland BB and Levis RJ, Nano Lett, 2015, 15, 3377–3382. [DOI] [PubMed] [Google Scholar]
- 24.Tangeysh B, Tibbetts KM, Odhner JH, Wayland BB andLevis RJ, Langmuir, 2017, 33, 243–252. [DOI] [PubMed] [Google Scholar]
- 25.Tibbetts KM, Tangeysh B, Odhner JH and Levis RJ, J. Phys. Chem. A, 2016, 120, 3562–3569. [DOI] [PubMed] [Google Scholar]
- 26.Meader VK, John MG, Rodrigues CJ and Tibbetts KM, J. Phys. Chem. A, 2017, 121, 6742–6754. [DOI] [PubMed] [Google Scholar]
- 27.Belmouaddine H, Shi M, Karsenti P-L, Meesat R, Sanche L and Houde D, Phys. Chem. Chem. Phys, 2017, 19, 7897–7909. [DOI] [PubMed] [Google Scholar]
- 28.Belmouaddine H, Shi M, Sanche L and Houde D, Phys. Chem. Chem. Phys, 2018, DOI: 10.1039/C8CP02054J. [DOI] [PubMed] [Google Scholar]
- 29.Nakashima N, Yamanaka K, Saeki M, Ohba H, Taniguchi S and Yatsuhashi T, J. Photochem. Photobiol. A, 2016, 319–320, 70–77. [Google Scholar]
- 30.Noack J and Vogel A, IEEE J. Quant. Electron, 1999, 35, 1156–1167. [Google Scholar]
- 31.Vogel A, Nahen K, Theisen-Kunde D and Noack J, IEEE J. Sel. Top. Quantum Electron, 1997, 2, 847–860. [Google Scholar]
- 32.Vogel A, Noack J, Hüttman G and Paltauf G, Appl. Phys. B, 2005, 81, 1015–1047. [Google Scholar]
- 33.Minardi S, Gopal A, Tatarakis M, Couairon A, Tamošauskas G, Piskarskas R, Dubietis A and Trapani PD, Opt. Lett, 2008, 33, 86–88. [DOI] [PubMed] [Google Scholar]
- 34.Marburger J, Prog. Quantum Electron, 1975, 4, 35–110. [Google Scholar]
- 35.Shen Y, Prog. Quantum Electron, 1975, 4, 1–34. [Google Scholar]
- 36.Shen YR, The Principles of Nonlinear Optics, Wiley, New York, 1984. [Google Scholar]
- 37.Moussa S, Atkinson G, El-Shall M, Shehata A, AbouZeid KM and Mohamed MB, J. Mater. Chem, 2011, 21, 9608–9619. [Google Scholar]
- 38.Sygletou M, Tzourmpakis P, Petridis C, Konios D, Fotakis C,Kymakis E and Stratakis E, J. Mater. Chem. A, 2016, 4, 1020–1027. [Google Scholar]
- 39.Mescola A, Canale C, Fragouli D and Athanassiou A, Nanotechnology, 2017, 28, 415601. [DOI] [PubMed] [Google Scholar]
- 40.Jiménez E, Abderrafi K, Abargues R, Valdés JL and Martínez-Pastor JP, Langmuir, 2010, 26, 7458–7463. [DOI] [PubMed] [Google Scholar]
- 41.Liu P, Chen H, Wang H, Yan J, Lin Z and Yang G, J. Phys. Chem. C, 2015, 119, 1234–1246. [Google Scholar]
- 42.Saraeva IN, Luong NV, Kudryashov SI, Rudenko AA,Khmelnitskiy RA, Shakhmin AL, Kharin AY, Ionin AA,Zayarny DA, Tung DH, Duong PV and Minh PH, J. Photochem. Photobiol., A, 2018, 360, 125–131. [Google Scholar]
- 43.Zedan AF, Moussa S, Terner J, Atkinson G and El-Shall MS, ACS Nano, 2013, 7, 627–636. [DOI] [PubMed] [Google Scholar]
- 44.Eisenberg G, Industrial & Engineering Chemistry Analytical Edition, 1943, 15, 327–328. [Google Scholar]
- 45.Meader VK, John MG, Frias Batista LM, Ahsan S andTibbetts KM, Molecules, 2018, 23, 532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Loy MMT and Shen Y, IEEE J. Quant. Electron, 1973, 9, 409–422. [Google Scholar]
- 47.McAllister GL, Marburger JH and DeShazer LG, Phys. Rev. Lett, 1968, 21, 1648–1649. [Google Scholar]
- 48.Helle MH, Jones TG, Peñano JR, Kaganovich D and Ting A, Appl. Phys. Lett, 2013, 103, 121101. [Google Scholar]
- 49.Kandidov V, Kosareva O, Golubtsov I, Liu W, Becker A, Akozbek N, Bowden C and Chin S, Appl. Phys. B, 2003, 77, 149–165. [Google Scholar]
- 50.Haiss W, Thanh NTK, Aveyard J and Fernig DG, Anal. Chem, 2007, 79, 4215–4221. [DOI] [PubMed] [Google Scholar]
- 51.Radnik J, Mohr C and Claus P, Phys. Chem. Chem. Phys, 2003, 5, 172–177. [Google Scholar]
- 52.Heimann P, van der Veen J and Eastman D, Sol. Stat. Commun, 1981, 38, 595–598. [Google Scholar]
- 53.Weststrate C, Lundgren E, Andersen J, Rienks E, Gluhoi A,Bakker J, Groot I and Nieuwenhuys B, Surface Science, 2009, 603, 2152–2157. [Google Scholar]
- 54.Klyushin AY, Rocha TCR, Hävecker M, Knop-Gericke A and Schlögl R, Phys. Chem. Chem. Phys, 2014, 16, 7881–7886. [DOI] [PubMed] [Google Scholar]
- 55.Takami A, Kurita H and Koda S, J. Phys. Chem. B, 1999, 103, 1226–1232. [Google Scholar]
- 56.Pyatenko A, Yamaguchi M and Suzuki M, J. Phys. Chem. C, 2009, 113, 9078–9085. [Google Scholar]
- 57.Werner D, Hashimoto S and Uwada T, Langmuir, 2010, 26, 9956–9963. [DOI] [PubMed] [Google Scholar]
- 58.González-Rubio G, Guerrero-Martínez A and Liz-Marzán LM, Acc. Chem. Res, 2016, 49, 678–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Baffou G and Rigneault H, Phys. Rev. B, 2011, 84, 035415. [Google Scholar]
- 60.Watzky MA and Finke RG, J. Am. Chem. Soc, 1997, 119, 10382–10400. [Google Scholar]
- 61.Eustis S, Hsu H-Y and El-Sayed MA, J. Phys. Chem. B, 2005, 109, 4811–4815. [DOI] [PubMed] [Google Scholar]
- 62.Harada M and Kizaki S, Crystal Growth & Design, 2016, 16, 1200–1212. [Google Scholar]
- 63.Kurihara K, Kizling J, Stenius P and Fendler JH, J. Am. Chem. Soc, 1983, 105, 2574–2579. [Google Scholar]
- 64.Henglein A, Langmuir, 1999, 15, 6738–6744. [Google Scholar]
- 65.Dey GR, El Omar AK, Jacob JA, Mostafavi M and Belloni J, J. Phys. Chem. A, 2011, 115, 383–391. [DOI] [PubMed] [Google Scholar]
- 66.Peck JA, Tait CD, Swanson BI and Brown GE, Geochim. Cosmochim. Acta, 1991, 55, 671–676. [Google Scholar]
- 67.Ji X, Song X, Li J, Bai Y, Yang W and Peng X, J. Am. Chem. Soc, 2007, 129, 13939–13948. [DOI] [PubMed] [Google Scholar]
- 68.Wang S, Qian K, Bi X and Huang W, J. Phys. Chem. C, 2009, 113, 6505–6510. [Google Scholar]
- 69.Yu X-Y and Barker JR, J. Phys. Chem. A, 2003, 107, 1313–1324. [Google Scholar]
- 70.Yu X-Y and Barker JR, J. Phys. Chem. A, 2003, 107, 1325–1332. [Google Scholar]
- 71.Nikogosyan DN, Oraevsky AA and Rupasov VI, Chemical Physics, 1983, 77, 131–143. [Google Scholar]
- 72.Zayats M, Baron R, Popov I and Willner I, Nano Lett, 2005, 5, 21–25. [DOI] [PubMed] [Google Scholar]
- 73.Barmina E, Simakin A and Shafeev G, Chemical Physics Letters, 2016, 655–656, 35–38. [Google Scholar]
- 74.Kalus M-R, Reimer V, Barcikowski S and Gökce B, Applied Surface Science, 2019, 465, 1096–1102. [Google Scholar]
- 75.Gerasimov VS, Ershov AE, Karpov SV, Gavrilyuk AP,Zakomirnyi VI, Rasskazov IL, Ågren H and Polyutov SP, Opt. Mater. Express, 2017, 7, 555–568. [Google Scholar]
- 76.Yener Y and Kakac S, Heat Conduction (4th edition), Taylor & Francis, 2008. [Google Scholar]
- 77.Hale GM and Querry MR, Appl. Opt, 1973, 12, 555–563. [DOI] [PubMed] [Google Scholar]
- 78.aus der Wiesche S, Rembe C and Hofer EP, Heat Mass Transf, 1999, 35, 25–31. [Google Scholar]
- 79.aus der Wiesche S, Rembe C and Hofer EP, Heat Mass Transf, 1999, 35, 143–147. [Google Scholar]
- 80.Carlson MT, Green AJ and Richardson HH, Nano Lett, 2012, 12, 1534–1537. [DOI] [PubMed] [Google Scholar]
- 81.Hu M and Hartland GV, J. Phys. Chem. B, 2002, 106, 7029–7033. [Google Scholar]
- 82.Lukianova-Hleb E, Hu Y, Latterini L, Tarpani L, Lee S, Drezek RA, Hafner JH and Lapotko DO, ACS Nano, 2010, 4, 2109–2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Fujiwara H, Yanagida S and Kamat PV, The Journal of Physical Chemistry B, 1999, 103, 2589–2591. [Google Scholar]
- 84.Baffou G and Quidant R, Laser & Photonics Reviews, 2013, 7, 171–187. [Google Scholar]
- 85.Baffou G, Polleux J, Rigneault H and Monneret S, The Journal of Physical Chemistry C, 2014, 118, 4890–4898. [Google Scholar]
- 86.Plech A, Ibrahimkutty S, Reich S and Newby G, Nanoscale, 2017, 9, 17284–17292. [DOI] [PubMed] [Google Scholar]
- 87.Bohren CF and Huffman DR, Absorption and Scattering of Light by Small Particles, WILEY-VCH Verlag, 1983. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.