Does Proton Conduction in the Voltage-Gated H⁺ Channel hHv1 Involve Grotthuss-like Hopping via Acidic Residues?

Abstract

Hv1 are ubiquitous highly selective voltage-gated proton channels involved in male fertility, immunology and the invasiveness of certain forms of breast cancer. The mechanism of proton extrusion in Hv1 is not yet understood while it constitutes the first step towards the design of high-affinity drugs aimed at this important pharmacological target. In this contribution, we explore the details of the mechanism via an integrative approach, using classical and QM/MM molecular dynamics simulations of a monomeric hHv1 model. We propose that protons localize in three binding sites along the channel lumen, formed by three pairs of conserved negatively charged residues lining the pore: D174/E153, D112/D185 and E119/D123. Local rearrangements, involving notably a dihedral transition of F150, a conserved phenylalanine lining the permeation pathway, appear to allow protons to hop from one acidic residue to the next through a bridging water molecule. These results constitute a first attempt at rationalizing hHv1 selectivity for H+ and the role of D112 in this process. They pave the way for further quantitative characterization of H⁺ transport in hHv1.

Graphical Abstract

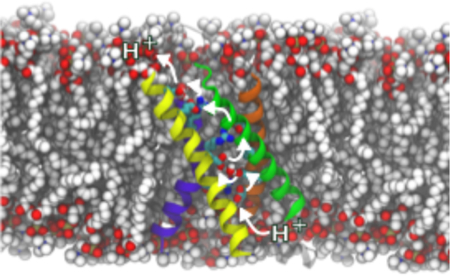
Introduction

Voltage-gated proton channels (Hv1s) play a role in many processes relevant to human physiology¹ such as sperm capacitation² and various aspects of the immune response.^3–5 Malfunctioning of this protein is implicated in the pathology and invasiveness of, for instance, certain types of breast cancers⁶ and the propagation of ischemic strokes.⁷ In other species Hv1’s roles can be extremely diverse, such as bioluminescence of dinoflagellates⁸ and the biocalcification of coccolithophores.⁹

Hv1 channels are gated mainly by two stimuli: a change in the transmembrane (TM) potential (∆V) or a change in the TM difference in pH (∆pH).^10,11 While there is a consensus on the general aspects of the ∆V-dependent gating mechanism, the ∆pH-one is not well understood. Because of the 40–70 nM proton concentration in most mammalian cells, to achieve its physiological role, a proton selective channel must have developed a highly effective selectivity mechanism.¹² Indeed, other cations are ~10⁶ times more abundant, such that the selectivity for protons of Hv1 has to be higher than 10⁶ to ensure that other ions are rarely transported. The experimentally measured selectivity, even though hard to gauge, ranges from 10^{7 10} to quasi-perfect.⁸ Beyond the intriguing question of its selectivity, understanding the details of proton conduction constitutes the first step towards designing high-affinity molecules that modulate this pharmacological target.

The TM portion of Hv1 channels is made of a four helix bundle that shares a high sequence homology with the voltage-sensor domains (VSDs) of voltage-gated ion channels and voltage-sensitive phosphatases (Figure 1.A).^13,14 A unique property of its fourth TM segment (S4) is the presence of three basic residues (arginines) that confer to the protein its transmembrane voltage sensitivity. The consensus activation model of other VSDs involves an S4 motion along the normal to the membrane upon membrane polarization.^15–17 The remaining segments (S1–S3) carry acidic residues that serve as counter-charges, whose role is to stabilize the S4 basic residues in a TM position. The activation mechanism of the channel involves a ratchet-like movement of the S4 arginines during which each of the arginines jumps from one binding partner to the next. In Hv1, when S4 reaches its outermost position, the channel is believed to open and allow proton conduction.¹⁸ Under physiological conditions, in most species, Hv1 is a dimer, made of two homologous four helical bundles joined via an intracellular C-terminal coiled-coil domain.^19–21 However, also the monomeric form is able to transport protons with biophysical characteristics similar to the dimer, albeit with a hastened activation kinetics and a conductance/voltage relationship slightly shifted towards depolarized potentials.^20,21

Figure 1:

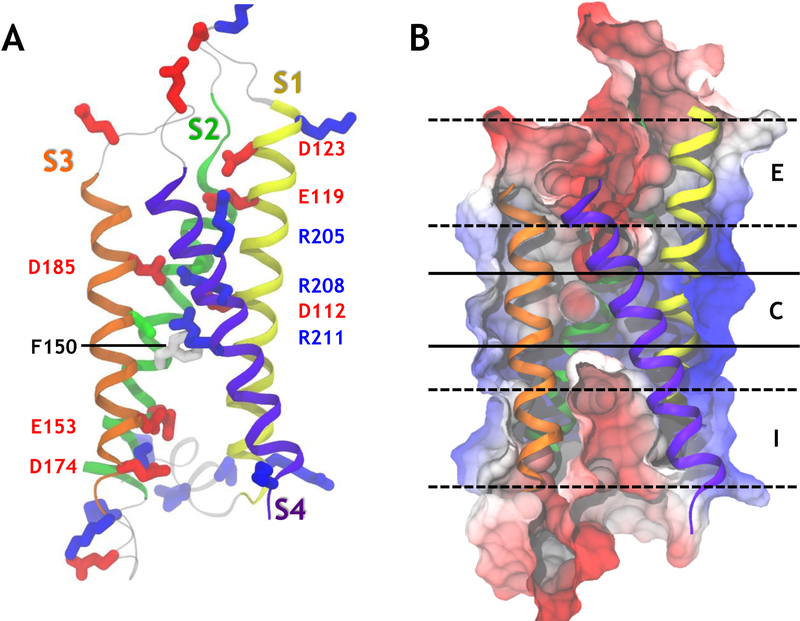
Topology of the human voltage gated proton channel hHv1. (A) A representative snapshot of the open activated state of the human Hv1 protein is presented. The four helices of the helical bundle are represented as ribbons of different colors. The side chains of important residues are represented as sticks. Acidic residues are shown in red, basic ones in blue, polar ones in green and non-polar ones in white. (B) The electrostatic potential calculated over the last 100 ns of simulation #1 (Table S1) is projected onto a cut-through of the protein surface. Negative potentials are shown in red and positive potentials are represented in blue. The color scale ranges from −385 mV to 128 mV. The three main binding sites along the central pore (red patches) are labeled I, C and E, from the most intracellular to the most extracellular region.

Although the residues involved in the activation mechanism have been identified, the proton transport mechanism itself is still debated. Because of their chemical nature, protons do not need to travel bound to one or more water molecules in the form of H₃O⁺ or H₅O₂+ ions. Instead, they can hop as bare protons from one protonatable species to the next, giving rise to many challenges when devising a simulation strategy (see Methods).²² In Hv1, the permeation pathway has been proposed to involve Grotthuss hopping of a proton along a file of preordered water molecules.²³ Open state models have thus been selected on the basis of the presence of a hydrated pathway along the bundle.^24–26 This view has the clear limitation of neglecting the significant structural rearrangements caused by the proton itself. It has been shown, for instance, that the presence of a proton can promote solvation of hydrophobic cavities.²⁷

Like other voltage sensor domains, S1, S2 and S3 bear several acidic residues lining the permeation pore. Their extensive conservation along evolution suggests an important role in their physiological function.⁹ Whereas in other voltage sensor domains acidic residues serve as counter charges for the state-dependent binding of S4 basic residues, their involvement in the proton permeation mechanism in Hv1 remains to be clarified. Although the individual mutation of every acidic residue appears to yield fully functional and selective channels,²⁸ these results were later disputed when a more extensive study showed that among them, the mutation of D112 (S1) to any residue other than a glutamate rendered the channel also anion-permeable.²⁹ As such, D112 has been labeled as the selectivity filter of the channel. On the other hand, quite unexpectedly, mutation of E119, D123, E153, D174 or D185 does not seem to alter Hv1’s selectivity substantially.^29,30 The effect of these mutations on the conductivity itself, however, has not yet been investigated in details.

Previous homology models have placed D112 in an extracellular crevice, but the first crystal structure of a hHv1 (human Hv1) homolog, murine Hv1 (mHv1), indicates that D112 is located right in the center of the four-helix bundle, in a region that is buried within the membrane and engaged in an electrostatic interaction with R211 on S4 (Figure 1.A).¹⁸ Given D112’s location, protons being transported across the membrane could transiently protonate this residue, thus challenging the Grotthuss hopping model of proton transport along a water wire. Supporting this theory, Dudev et al. have explained selectivity in the channel using quantum mechanics (QM) calculations of a reduced model of the putative selectivity filter made of one Asp and one Arg residues tethered to a hydrocarbon ring in the presence of a permeating ion.³¹ In this model, a hydronium ion is able to break the salt bridge formed between the arginine and the aspartate residues by protonating the aspartate and thus opening the permeation pathway. Any other cationic or anionic species, on the other hand, remains trapped by the selectivity filter’s salt bridge and thus leaves the selectivity filter closed. In the context of the entire channel, the mechanism by which the proton approaches the D112/R208 salt bridge has not yet been investigated. According to the crystal structure of mHv1, D185 is located close to D112. In the open state of the channel, R208 and R211 are hypothesized to be in contact with these two aspartate residues, complicating the simple picture sketched by Dudev et al. The other acidic residues (E119, D123, E153, D174) are located in the intra and extracellular crevices, rationalizing why their mutation does not alter selectivity.^28,29

Here, we have carried out a first exploratory study of the proton permeation pathway along the human Hv1 (hHv1) by running simulations of an open state model of a monomeric hHv1 in the presence of one or more protons. The model of the open/activated state channel was built using the crystal structure of mHv1 as a template (see Methods), and its stability and validity was extensively characterized previously.³² All systems are simulated in an explicit palmitoyl-oleoyl-phosphatidyl-choline (POPC) membrane and in an explicit solvent considering a 150 mM NaCl solution. Because the simulation of the entire proton transport using quantum calculations is beyond our reach, we have adopted an integrative approach (see Methods). Most simulations of the long time-scale conformational rearrangements were performed using a classical force field (Tables S1–S5). On the other hand, key steps of the mechanism, which involved covalent (un)binding of the proton, were investigated using mixed quantum mechanics/molecular mechanics (QM/MM) molecular dynamics (MD) simulations (Table S6). The simulations suggest that the proton transport mechanism occurs as a series of jumps between consecutive acidic residues lining the pore. According to our results, the transport involves structural rearrangements that enable the proton to travel from one acidic residue to the next by hopping on a single water molecule.

Theoretical Methods

Modeling of the activated open state of hHv1

No crystal structure exists of the hHv1 channel in its open state. The closest relative for which a crystal structure exists is a mHv1-chimera¹⁸ (PDB ID:3WKV), solved in an intermediate-resting state. To produce models of a fully activated state of hHv1, we used a procedure similar to the one described in Wood et al.²⁴ and Kulleperuma et al.²⁵ Building an alignment in which S4 is manually shifted by three residues toward the C-terminus (corresponding to one helical turn, Figure S1) enabled to build a homology model of hHv1 in the fully activated state using a standard MODELLER routine.³³ The protonation state of the different protonatable residues was determined using pKa estimates from propKa (Table S7). An extensive validation of the model has been presented elsewhere.³²

Simulations

All performed simulations are summarized in Tables S1–S6. Throughout the paper, the simulations are referred to by their number as listed in these tables. The simulations were performed on the CRAY XE/XK BlueWaters system from NCSA, USA and on the Cray XC30 Piz Daint from CSCS, Switzerland.

Classical molecular dynamics simulations

The procedure used to equilibrate the hHv1 model is described extensively elsewhere.³² In brief, the homology model of hHv1 was then inserted in a fully hydrated (150 mM NaCl) 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine bilayer. For equilibration, the membrane was equilibrated during the first nanosecond, restraining the position of the protein, lipid head groups, water molecules, and ions to their initial position with a strong harmonic potential. To ensure correct reorganization of the lipids and solution, the positions of all the atoms of the channel were then restrained for 2 ns. The side chains were then allowed to reorganize while the backbone was kept restrained for 8 ns.

Several simulations were conducted, as reported in Tables S1–S5. In some, one or two hydronium ions were added to the solution. In others, the effect of a 100 mV TM potential was mimicked by applying an external electric field in the form of a force acting on all charged particles of the system. All systems were simulated under normal constant temperature and pressure conditions (298 K, 1 atm.).

The molecular dynamics (MD) simulations were performed using the NAMD2 program.³⁴ Langevin dynamics were applied to keep the temperature (298 K) fixed. The equations of motion were integrated using a multiple time-step algorithm.³⁵ Short- and long-range forces were calculated every one and two time steps, respectively, with a time step of 2.0 fs. Chemical bonds between hydrogen and heavy atoms were constrained to their equilibrium value. Long-range electrostatic forces were taken into account using the particle mesh Ewald approach.³⁶ The water molecules were described using the TIP3P model.³⁷ The simulation used the CHARMM27-CMAP force field with torsional cross-terms for the protein³⁸ and CHARMM36 for the phospholipids.³⁹

Force field parameterization of the hydronium ion

We parameterized an all-atom force field for the hydronium ion (H₃O⁺) to perform classical MD simulations using the existing CHARMM general force field.⁴⁰ First, we determined interaction energies and geometries of a complex. between a hydronium ion and a water molecule placed in a pair of distinct locations using the HF/6–31G** level of theory and the NWCHEM program.⁴¹ We adjusted the hydronium charges to reproduce interaction energies obtained by quantum chemical calculations (QM) in a classical calculation based on the TIP3P water model. We used bond lengths and angles obtained from the quantum geometry optimization and treated the hydronium as a rigid moiety. The hydronium force field parameters used to performed the MD are provided in Table S8.

Molecular dynamics simulations with the Proton mimicked by a Gaussian charge distribution

We also performed all-atom MD simulations in which the proton was mimicked by the presence of an electrostatic potential resulting from a Gaussian charge density located at a fixed position in space. In doing this, we attempted to ascertain the robustness of the mechanism proposed and its substantial independence from the particular choices made to model hydronium species. Indeed, each charged chemical group induces a peculiar orientational ordering in the first shell of waters (and thus at short range) due to the anisotropic nature of H-bonding (protonated water species) or to the value of the van der Waals radius (Na+ ion). While this ordering should be considered part of the physical phenomenon to be described, it depends crucially on the chosen models and model parameters; however, a common feature of all the cations is their ability to induce a long range reorientation of waters entailed by dipolar screening of the bare positive charge. Therefore, we used the Gaussian distribution as a probe in lieu of a point charge.

In practice, the isotropic Gaussian charge density was modeled using:

$$\rho (r)=\frac{Q}{{\sigma }^3{\left(2\pi \right)}^{3/2}}{e}^{\raisebox{1ex}{$-r^2$}\!\left/ \!\raisebox{-1ex}{$2{\sigma }^2$}\right.},$$

where Q is the total charge. The solution of Poisson’s equation reads:

$$\phi \left(r\right)=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r}erf\left(\frac{r}{\sqrt{2\sigma }}\right)$$

where erf(x) is the error function and σ is set to 1.2 Å. Forces resulting from the electrostatic potential were added to the equations of motions.

QM/MM molecular dynamics simulations

Hybrid quantum mechanical/molecular mechanical (QM/MM) MD simulations of the Hv1 bundle embedded in a lipid bilayer were performed with the CPMD software package.⁴² The QM region was defined to contain the hydronium, the acidic residue(s) in contact with it and the first shell of water molecules (see Table S6). The total system consisted of the protein embedded in a POPC bilayer. Periodic boundary conditions were applied to the MM system to avoid boundary effects (see Table S6 for the box size). The total system (QM+MM combined) amounted to ~75,000 atoms.

The QM region was treated at the DFT level of theory in combination with a plane wave basis set. The BLYP functional^43–45 and Martins-Troullier pseudopotentials were used.⁴⁶ Monovalent pseudopotentials were used to cap the residues at the C$\alpha$ atoms to saturate the electronic density at the C β atom.⁴⁷ An energy cutoff of 70 Ry was employed in the plane wave representation of the Kohn-Sham orbitals. A Hockney poisson solver was used.⁴⁸ The AMBER force field was used to account for interactions among the atoms of the MM region. The electrostatic interactions of the total QM/MM system were treated with the P3M method with a real space cutoff of 10 Å.⁴⁹ The same cutoff was used for the Lennard-Jones interactions. Electrostatic interactions between QM and MM regions were taken into account by means of a fully Hamiltonian hierarchical coupling scheme,^50–52 whereas bonded and van der Waals interactions between both subsystems were described at the force field level. The simulations were performed with Car-Parrinello-MD (CPMD),⁵³ using a time step of 0.12 fs and a fictitious electronic mass of the CP Lagrangian of 700 au. The 300 K temperature was maintained using a Nosé-Hoover chains thermostat. The QM and the MM subsystem were coupled separately, with a thermostat frequency of 2000 and 1000 cm−1, respectively.

Metadynamics simulations

A history dependent repulsive potential was added along a set of collective variables s(x) in the shape of a sum of Gaussians of the form:⁵⁴

$$V\left(s,t\right)={\sum }_{t\text{'}={\tau }_G,2,\mathrm{3...}}^{t<t\text{'}}W\exp \left(-{\sum }_{i=1}^d\frac{{\left(s_i(x)-s_i(x(t^{\prime }))\right)}^2}{2{\sigma }_i^2}\right),$$

where W is the height of the Gaussian at its center, and σ is its width at half maximum height.

Here, we use the position of one or two hydronium ions along the long axis of the channel as a collective variable. W was set to 0.001 kcal/mol and σ to 0.25. The Gaussians were added every 1000 MD step, i.e. every 2 ps. The metadynamics simulations were performed using the collective variables module of NAMD.⁵⁵

Free energy perturbation calculations

To calculate the free energy difference between the hydronium-bound and sodium-bound states, the hydronium ion was slowly morphed into a sodium ion (λ=0 to 1) and back (λ=1 to 0), using 19 windows of dλ=0.05 each. In order to avoid end-point catastrophes, the electrostatic interactions were switched on from λ=0.5 and onward. Each window was equilibrated for 192,000 classical MD steps, and the first 25,000 steps were discarded during free energy estimation. The ions were constrained to the binding site by using distance restraints, using a force constant of 100 kcal/mol/Ų. The free energy difference between adjacent windows was estimated according to the Zwanzig relation ΔG(A→B)= −k_BT ln <exp (−(E_B–E_A)/k_BT)>_A.⁵⁶ The Simple Overlap Sampling (SOS) scheme⁵⁷ was used for free energy estimation, as implemented in the VMD ParseFEP analysis tool.⁵⁸

The total free energy difference was estimated using the following relationship: $\Delta G_{H_3{O}^{+}\to N{a}^{+}=}\Delta G_{H_3{O}^{+}\to {Na}^{+}}^{app}-\Delta G_{H_3{O}^{+}\to N{a}^{+}}^{wat}+\Delta G_{H_3{O}^{+}}^{cst}-\Delta G_{N{a}^{+}}^{cst}$ where ∆G_app is the apparent relative affinity for hydronium over sodium in the binding site as calculated by FEP calculations, ∆Gwat is the reference free energy difference in water, and the two last terms compensate for the free energy loss from enforcing distance restraints in the FEP calculations. The errors on these terms are estimated using the difference in the free energy obtained during the forward and backward transitions (switching the harmonic restraints off and on).

Electrostatic potential calculations

The three-dimensional maps of the electrostatic potential were generated by solving numerically the Poisson equation on a grid with a 1.5 × 1.5 × 1.5 Å3 mesh: ${\nabla }^2{\Phi }_j\left(r\right)=-4\pi \sum _i{\rho }_i\left(r\right)$, where ρ_i is the point charge approximated by a spherical Gaussian of inverse width σ (0.25 Å⁻¹) and the sum running over all protein atoms. An average was obtained from 100 equally spaced frames from the last 100 ns of the simulations. The implementation of the PMEPot module of the visualization program VMD was used.⁵⁹

Correlation analyses

The Pearson correlation coefficients between a set variables were calculated as:

$$r_{12}=\frac{\sum \left(y_{i1}-{\overline{y}}_1\right)\left(y_{i2}-{\overline{y}}_2\right)}{\sqrt{\sum {\left(y_{i1}-{\overline{y}}_1\right)}^2{\left(y_{i2}-{\overline{y}}_2\right)}^2.}}$$

Results

Three negatively charged binding sites line the proton permeation pore of hHv1.

The TM portion of the hHv1 channel consists of four TM helices (S1–S4) linked by short intracellular and extracellular loops. After equilibration of the fully activated structure (Sim. #1), our classical molecular dynamics (MD) simulations revealed that its overall topology is similar to that of other voltage sensor domains, with a few marked differences.^15,16,32,60 Segments S1, S2 and S3 bear six acidic residues, D174, E153, D112, E185, E119 and D123, from the most intracellular to the most extracellular region. Segment S4 contains three basic residues: R211 (R3), R208 (R2) and R205 (R1), from the most intracellular to the most extracellular region. The activated state of hHv1 is stabilized by interactions between acidic and basic residues, i.e. salt bridges. The most characteristic ones are R211 and D112, R208 and D185, and R205 interacting either with D119 or with a neighboring lipid headgroup. Water molecules permeate from the intra- and extracellular media to define an hourglass-like solvent-accessible volume that is reminiscent of the voltage-sensor domains of ion channels and of the voltage-sensing phosphatase. The other voltage-sensor domains of known structure feature salt bridges either in the intra- or the extracellular crevices.^15,61–63 Homology models of Hv1 channels are built using these VSDs as templates, and therefore also share these similarities.^24–26,28 In the crystal structure of mHv1 and in our model, on the other hand, hHv1’s R211/R208/D112/D185 cluster is located right in its core (Figure 1.A). This difference raises the possibility that this central region is crucial for the conduction mechanism and the selectivity mechanism of the channel. The electrostatic potential map computed along the last 100 ns of the equilibrium simulation (Sim. #1) of the activated state of hHv1 reveals three main regions along the long axis of the four-helical bundle that would favor binding of a positively charged species (Figure 1.B). The innermost one (I) comprises acidic residues E153 and D174, the central one (C) includes D185 and D112 while the outermost one (E) contains E119 and D124 (Figure 1.B). The electrostatic potential map calculated from the contributions of the protein also reveals a large dipole oriented along the normal to the membrane (Fig. S2), which interestingly enough is completely screened by the contributions of the lipids and the solution (Fig. 1.B and S2,D).

To characterize the proton permeation pathway, we considered systems in which one or two protons are present in the channel. Because of the elusive chemical nature of the proton, we considered three classical MD simulation protocols in which the proton is: (1) bound to a water molecule in the form of a hydronium, (2) bound to an acidic residue in the form of an aspartic acid or a glutamic acid, and (3) represented as a positive Gaussian charge distribution. We also considered QM/MM simulations whenever a (de)protonation step was possible.

In the three identified binding sites, protons localize between acidic residues lining the pore.

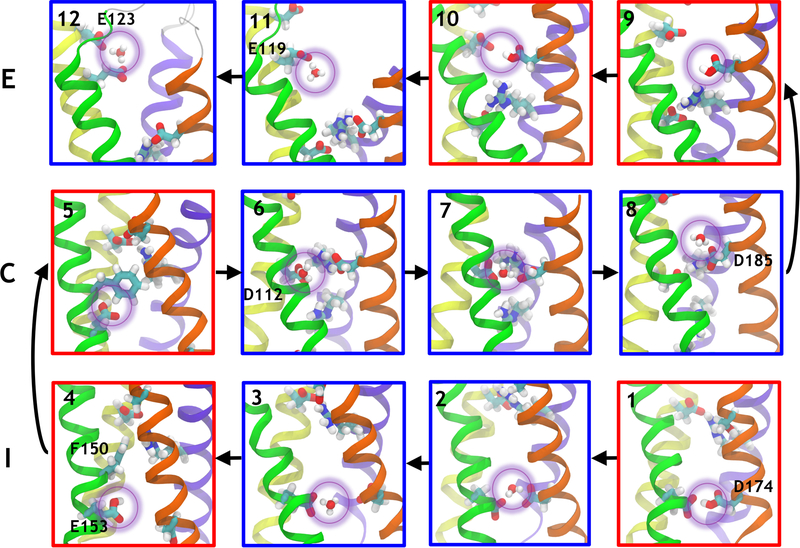
When a hydronium ion was placed at random in the intra- or the extracellular hydrated cavity of hHv1 (Sim. #3, #6 and #13), classical MD simulations revealed that it locates spontaneously in one of the three sites (I, C, E), indicating the presence of local free energy minima for hydronium localization (Figure 2). Specifically, within the intracellular site I, the hydronium can interact either with E153 (Figure 2.3), or bridge E153 and D174 (Figure 2.2). The situation is similar in the core (C), in which the H₃O⁺ molecule can interact with D112 (Figure 2.6), D185 (Figure 2.8) or both residues at once (Figure 2.7). The same features were observed in two separate metadynamics simulations using the position of a single H₃O⁺ molecule along the channel axis as reaction coordinate (Sim. #18 and #19). Note however that the metadynamics simulations remained unconverged due to the choice of the proton model and the inability of the classical MD simulations to account for bond breaking and forming, presumably leading to artificially high free energy barriers. We therefore used these calculations not for free energy estimation but only to generate configurations otherwise scarcely visited during regular MD simulations.

Figure 2:

Proton transport along hHv1. Outward transport (vignettes 1 to 12) involves the sequential binding to D174, E153, D112, D185, E119 and D123. Each proton transfer from one residue to the next involves conformational rearrangements that bring the two acidic residues closer together. The helices are shown in the same representation as in Figure 1. The acidic and basic residues and the conserved F150 are shown as sticks, oxygen atoms are shown in red, carbons in cyan, nitrogens in blue and hydrogens in white. The proton being transported is highlighted by a purple circle. Configurations in which the proton is bound to a protein residue are framed by a red box whereas configurations in which the proton is bound to a water molecule are framed in blue.

To uncover the precise preferred location of the proton within the three different binding sites, we conducted four QM/MM MD simulations (Table S6), using snapshots extracted from the classical molecular dynamics simulations as starting structures. We considered the region around the hydronium at the QM level (including the acidic residue(s) in contact with the hydronium and the first shell of water molecules, see Methods) while the rest of the system is treated classically. One of the configurations extracted from the classical molecular dynamics run (Figure 2.3) had the H₃O⁺ moiety located in I, in close proximity to E153 (Sim. #Q1). During initial annealing, the proton, which was first bound to a water molecule (in the form of a hydronium ion), spontaneously transferred to the negatively charged E153 to yield a water molecule and a protonated form of the aspartic acid (Figure 2.4). It then remained bound to the aspartic acid during the heating phase and the rest of the 14.4 ps of the 300K, NVT simulation. Next, two separate QM/MM simulations initiated in configurations in which the hydronium is located in C interacting with both D112 and D185 (Sim. #Q2,3) (Figure 2.7) showed that the proton spontaneously transfers to D185 to form a water molecule and a protonated D185 (Figure 2.9). Finally, in a similar manner, when H₃O⁺ is placed in E, it spontaneously binds to E119, in spite of the fact that D185 is also present in the QM box and remains stably bound for 9.0 ps (#Q4). Hence, all QM/MM simulations indicated that whenever a H₃O⁺ molecule approaches one of the aspartate or glutamate residues, the proton is spontaneously transferred to the charged residue resulting in a water molecule and an aspartic or glutamic acid residue, in agreement with the pKa difference between a water molecule and the carboxylate moiety of an aspartate or glutamate residue.

Protonating acidic residues causes major structural rearrangements.

In order to explore the structural rearrangements entailed by protonation of the different glutamate and aspartate residues, we collected classical MD trajectories of systems in which E153, D174, D112 and D185 were individually protonated.

The simulations with the two I residues individually protonated was started from a configuration in which D174 and E153 are within hydrogen-bond distance. The protonated D174 (#17) remained involved in a hydrogen bond with E153 for 128 ns (Figure 2.1), before reorienting towards the space between S3 and S4 for the remainder of the 320.5 ns simulation. Notably, the addition of a 100 mV TM potential to the same initial configuration (#18) yielded similar results: the hydrogen bond to E153 remains stable for the initial 194 ns of the 279 ns simulation. Protonating E153, on the other hand, results in a completely different outcome (#19). The hydrogen bond between the protonated E153 and D174 breaks immediately and D174 orients towards the channel lumen, or the space between S3 and S4. E153 remains oriented towards the channel lumen for 215 ns, just below F150, which is blocking the access to the next binding site C (Figure 2.4). After these initial 215 ns, a series of five opening events occur, during which F150 reorients towards the S2/S3 interface (Figure 2.5 and Figure S3) and the protonated E153 changes configuration, orienting the protonated OH group upward, towards C. This opening event lasts from 2 to 6 nanoseconds and out of the 325 ns simulation, the open state represents 6% of the configurations. This conformational rearrangement is potentially necessary to enable proton transition between I and C. However, in a 278 ns simulation initiated in same conditions but in which the system is exposed to a 100 mV TM potential, F150 remains in the closed position (#20), thus highlighting the need for a future quantitative analysis of the conformational ensemble visited by this residue.

We then ran two simulations of systems in which D112 was protonated. In the first one, D112 was initially pointing downward towards E153 (#25), featuring F150 pointing outward, i.e. in the open position. In the second simulation, D112 was initially oriented horizontally, pointing towards D185 (#26), with F150 assuming a closed configuration. In the first scenario, D112 remained pointing downward for ~18 ns, before rapidly reorienting towards D185 where it remained separated by two water molecules from D185 for the next ~26 ns. A second rearrangement then occurs in which D112 becomes separated from D185 by one water molecule only. This state is only short-lived (~20 ns), before the interaction between D185 and the protonated D112 is broken. The rest of the 184 ns simulation reveals a very swollen and hydrated hHv1 structure that does not seem compatible with proton selectivity. The second simulation, initiated with D112 pointing towards D185 reveals a similar phenomenon: while the first few nanoseconds correspond to rearrangements leading to D112 pointing downward, a sharp transition occurs at 22 ns simulation time where the interactions within the core are disrupted, the Hv1 channel loses its hourglass structure while the lumen is filled with a large number of water molecules. In both simulations, it is noteworthy that the initial configuration of F150 remains unchanged (open in #25 and closed in #26). These results demonstrate that when D112 remains protonated for an extended period of time, due to the loss of electrostatic interactions in the C site, the channel cannot retain an hourglass structure due to a large influx of water molecules. The wide hydrophilic pore resulting from this swelling is unlikely to sustain proton selectivity. This may indicate that during proton extrusion, D112 can only be transiently protonated.

Simulations of protonated D185 on the other hand (#21–#24), showed that this residue can take part in three main conformations without disrupting the integrity of the channel structure: D185’s protonated OH group can be oriented towards D112 (Figure 2.9) or the hydroxyl group of D185 is oriented upwards in the channel, facing E119 (Figure 2.10) or is in direct contact with H140, a residue located on S2 and facing the lumen of the channel. Both outward facing positions represent configurations in which the proton could be delivered to the E binding site. Interestingly, despite these significant rearrangements occurring during proton transport, the overall dipole remains unchanged, as shown by the electrostatic potential calculated over 100 ns of simulations #17 and #21 (Figure S2).

An independent proton model reproduces the same features.

In a final attempt at characterizing the preferred location of the proton and the conformational rearrangements occurring upon proton insertion in the channel, we considered a third proton model. In order to preclude the proton from being covalently bound to a water molecule, we represented it as a Gaussian density of positive charge (see Methods).

We considered first an equilibrated snapshot of the activated Hv1 system in which we placed the charge density at a fixed position in the intracellular site (Sim. #13). Initially (Figure S4.A), the charge is centrally located along the channel’s z-axis, halfway between E153 (S2 helix) and D174 (S3 helix) (Figure S7.A, Figure S4.B). F150 (S2 helix) initially points towards the channel lumen, thus blocking the permeation pathway. Both E153 and D174 move towards the lumen closer to the charge (Figure S7.B). Interestingly, after the first 40 ns and for the rest of the 185 ns simulation, we observe a preference of the charge for being stabilized by E153 (Figure S7.C-D), as a consequence of the attractive interactions established between D174 and K211, the D174 side-chain turns away from the charge (Figure S4.C). This is reminiscent of simulation #17 with a protonated D174, which had a tendency to orient its proton towards E153. Note also that, as in the case of the protonated E153 simulations (Sim. #19), in this configuration, F150 orients its side chain to adopt an open configuration that will allow the proton to be transferred to the C site (Figure S4.B, Figure S7.C-D). In the second configuration we considered, the charge is located in the C site, approximately halfway between D112 and D185 (Sim. #14, Figure S5). At the beginning of the simulated time, the charge interacts with surrounding water molecules and approaches alternatively either residue D112 or D185 at interacting distances (Figure S7.E). As the simulation progresses, the charge shows a preference for being stabilized by the carboxylic oxygen of D112, an event that occurs within the first 30 ns of simulation (Figure 2–S5 and Figure S7.F). The preferred charge stabilization on D112 is partnered by D185 engaging in an attractive interaction with R208 (Figure S5 and Figure S7.F-H). While all these rearrangements occur in the core site, R211 is pushed away from the C-site to interact with E153 in the I-site (Figure S5 and Figure S7.H). As a consequence, F150 is released from a cation-pi interaction, resulting in a significant enhancement of its flexibility. Movement of F150 ultimately plays a role in driving the system towards a configuration with the positive Gaussian charge stabilized by D112 (Figure S7.G). Notably, this phenomenon of pushing R211 away from C occurs in all the simulations where a proton is present in any form (hydronium ion, protonated aspartate or Gaussian potential) in the C site.

Finally, the Gaussian density was placed in the extracellular site, with the charge placed halfway between E119 and D123 (Sim. #16, Figure S7.I, Figure S6.A, B and C). One histidine residue (H193), located on the loop connecting S3 to S4, faces the extracellular site at similar distances from the two negatively charged residues. During the first 40 ns of simulation, the charge bridges between E119 and H193 (Figure S7.J). After 40 ns of simulation (Figure S6.B-C, Figure S7.K), H193 adopts a configuration in which the side chain is turned towards the lipid headgroups and D123 and E119 compete for the stabilization of the Gaussian charge. Finally, when E119 gets closer to H193 (Figure S6.B, Figure S7.L), the charge localizes in the vicinity of D123 and this configuration remains unchanged for the remaining 120 ns simulation time. These results indicate that when in the extracellular funnel, the proton is driven outwards, similarly to what is observed with the classical hydronium model simulations.

Increasing the proton concentration facilitates proton transfer.

The ensemble of these classical MD simulations has sampled a subset of the configurations visited during the proposed proton transport mechanism. In order to characterize the proton conduction pathway completely, we have mimicked the effect of a decreased intracellular pH by raising the local proton concentration. The electrostatic potential calculations reveal that even in the presence of one protonated residue in different TM positions, the channel lumen remains attractive for positive charges (Figure S2), rationalizing this choice. Therefore, we consider two hydronium molecules in the channel (Sim. #27). To enhance the sampling of the conformational space, and possibly characterize the rest of the configurational ensemble, we performed a two-dimensional classical metadynamics simulation of the fully deprotonated system using the position of two H₃O⁺ molecules along the channel axis as collective variables (Sim. #28, Figure 3.A and methods).

Figure 3:

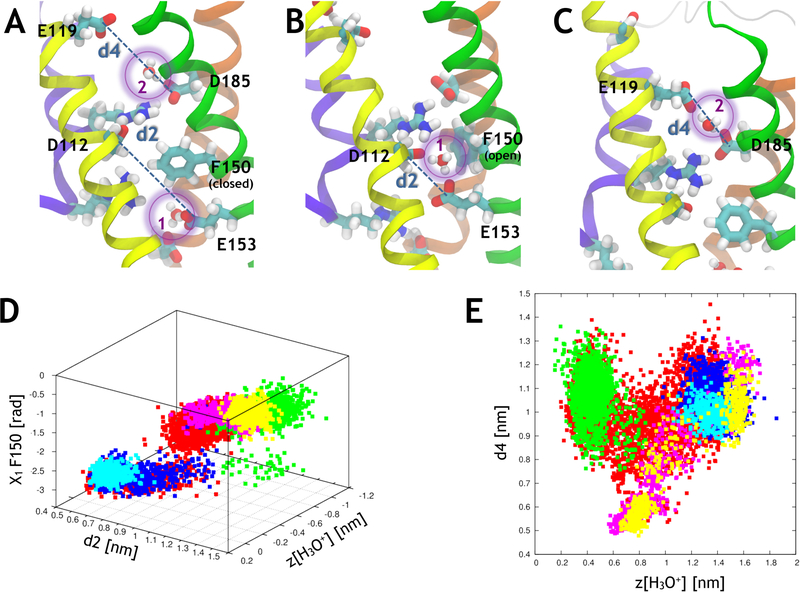
Correlations between various variables during proton transport through hHv1. (A) Simulation setup with 2 H₃O⁺ molecules located in the channel, H₃O⁺(1) is in I and H₃O⁺(2) is in C. F150 is in its closed conformation and prevents H₃O⁺(1) from transferring to C. The representations are the same as in Figure 2. The distances found in panels D and E are represented for clarity. (B) F150 reorients outwards and H₃O⁺(1) is found in a bridging position between E153 and D112. (C) H₃O⁺(2) is found in a bridging position between D185 and E119. (D) The position of the H₃O⁺(1) ion (the origin is located at the center of the helical bundle) of the channel is correlated with the distance between E153 and D112 (d2) and with the X₁ dihedral angle of F150. (E) The position of the H₃O⁺(2) is correlated with the distance between D185 and E119 (d4). The data points come from five separate simulations (#28 in red, #30 in green, #31 in blue, #32 in cyan and #33 in yellow, see Table S5).

By employing this scheme, in contrast to the one-hydronium metadynamics simulations, in which the free energy barriers were too high to allow proton transport, we were able to observe the transfer of one of the hydronium ions between I and C and of the other between C and E. As was hinted at during our previous simulations, charge transport involves significant conformational rearrangements: during the transport between I and C, E153 moves upward while D112 moves slightly downward, resulting in a shortening of the distance between the two residues (d2, Table 1, Figure 3B,D). This allows the hydronium ion to bridge between these two residues.

Table 1:

Correlations between variables involved in proton transport. Pearson correlation coefficients were calculated for a set of collective variables. The z-position of hydroniums #1 and #2, R205 (R1), R208 (R2), R211 (R3) and S143, the distances between D174 and E153 (d1), between E153 and D112 (d2), D112 and D185 (d3) and D185 and E119 (d4) and the X₁ and X₂ dihedral angles of F150 are considered. The upper triangular matrix represents the coefficients calculated over simulations #28, #30, #31, #32 and #33. The lower triangular matrix represents the coefficients calculated over simulations #28 only. Coefficients > 0.7 are highlighted in red, > 0.6 in orange, >0.5 in yellow, >0.4 in green and >0.3 in light blue. The low correlation coefficient highlighted in bright blue is due to a V-shape correlation (see Fig. 3). Note that the number of strongly correlated variables is low.

	H3O+(1)	H3O+(2)	ZR1	ZR2	ZR3	ZS143	d1	d2	d3	d4	X1 FI50	X2 F150
H3O+(1)		0.52	−0.4	−0.38	−0.38	0.44	0.33	−0.85	0.64	0.09	−0.61	−0.04
H3O+(2)	0.21		−0.38	−0.46	−0.29	0.44	0.04	−0.55	0.75	0.06	−0.38	−0.07
ZR1	−0.41	−0.52		0.7	0.49	−0.51	−0.13	0.37	−0.55	0.31	0.24	0.04
ZR2	−0.16	−0.42	0.58		0.54	−0.4	−0.27	0.45	−0.57	0.32	0.25	0.05
ZR3	−0.05	0.07	0.29	0.24		−0.45	−0.09	0.4	−0.21	0.39	0.21	0.08
ZS143	−0.21	0.41	−0.49	−0.38	−0.32		0.08	−0.47	0.44	−0.28	−0.3	−0.09
d1	0.3	−0.28	0.4	0.22	0.11	−0.15		−0.52	0.15	0.32	−0.51	0.01
d2	−0.74	−0.19	0.33	0.28	0.16	−0.29	−0.37		−0.65	−0.08	0.72	0.08
d3	0.3	0.68	−0.53	−0.37	0.34	0.23	−0.32	−0.26		−0.04	−0.44	−0.06
d4	0.25	0.1	0.17	0.17	0.42	−0.19	0.4	−0.1	0.7		−0.23	−0.06
X1 F150	−0.65	−0.06	0.18	0.1	0.05	−0.12	−0.45	0.71	−0.13	−0.28		0.11
X2 F150	−0.1	−0.01	0.02	0.02	0.09	−0.08	−0.03	0.15	−0.04	−0.09	0.19

Similarly to what was observed in simulation #29, this new hydronium conformation involves the rearrangement of F150, which needs to pivot towards S4 to leave space for the transfer of H₃O⁺, as shown by the high Pearson correlation coefficient between z_H3O+1, d2 and X_{1 F150} (Figure 3.D and Table 1). R211 (R3), which is free from the interaction with R211, favors the approach of E153 and D112. During the transport from C to E, D185 initially comes closer to E119, enabling H₃O⁺ to bridge between these two negatively charged residues (Figure 3.C). Once H₃O⁺ is transferred to E119, D185 and E119 can move apart, leading to a V-shape correlation between d4 and z_H3O+2 (Figure 3.E).

Protons can hop between binding sites I and C, and C and E.

Because metadynamics enables to explore regions of the configurational space of high free energy, we monitored the stability of snapshots generated by metadynamics that represented important conformations along the proton transport mechanism (Figure 3.B,C). This was investigated by equilibrating the conformations using plain classical MD. The first configuration in which H₃O⁺ is bridging between E153 and D112 remained stable over a 140 ns simulation (Sim. #30). The second snapshot in which H₃O⁺ is bridging between D185 and E119 remained stable over a 96 ns simulation (Sim. #32). This indicates that these configurations represent transiently stable states that can be confidently considered as part of the proton transfer mechanism. Finally, within these two configurations, we allowed the protons to bind to their preferred location by equilibrating them using QM/MM MD simulations (Sim. #Q5,Q6). These simulations also serve the purpose of investigating whether the protons would be preferentially transported towards one or the other bridging residues, i.e. in the outward or inward direction. Similarly and in line with what was observed in the other QM/MM MD simulations, in both cases, the protons spontaneously transferred from the hydronium ion to one of the negatively charged residues to yield a water molecule and a protonated residue. Quite interestingly, in both cases, the proton relocated to the residue nearest to the extracellular medium, i.e. to D112 and E119, respectively.

Discussion

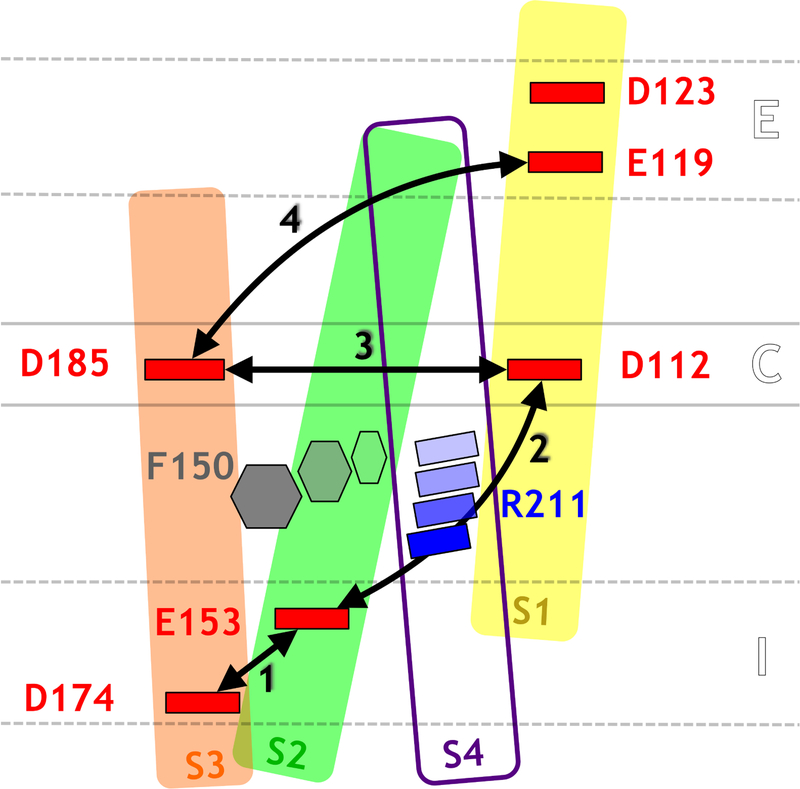
Overall, these simulations reveal a proton permeation mechanism that involves side chain rearrangements (Figure 4): H+ protonates the negatively charged aspartate and glutamate residues lining the pathway in a sequential manner by hopping through a bridging water molecule. The transport involves the sequential protonation of E174, E153, D112, D185, E119 and D123. Each time the proton jumps from one residue to the other, the distance between these residues reduces in such a way as that only one water molecule bridges them and the proton can be transported from an acidic residue to the next by jumping on a water molecule (Figure S8).

Figure 4:

Schematic representation of the conformational rearrangements occurring during proton transport through hHv1. Colors are the same as in Figure 1. The distances for which the Pearson correlation coefficients were calculated are represented as black arrows. As the proton hops outwards, pairs of acidic residues (1, 2, 3 and 4) come in closer contact in a sequential manner. During step 2, the proton hops from E153 to D112 through a water molecule. This is made possible by the reorientation of the F150 and R211 side chains.

Protons pose several challenges for simulations.

Ideally, the quantum properties of the system should be fully described but this is currently beyond the reach of present-day computer resources. Mixed QM/MM calculations have been proposed as a means to reduce the computational cost while still allowing to describe the regions of interest of the system at a quantum mechanical level. The length scales that can be reached through such methodology, on the other hand, are usually too short to observe significant conformational rearrangements. Reactive force fields, such as MS-EVB have been developed as a means to enable chemical bond breaking and formation while allowing simulations to reach longer time scales. Originally only used in the field of proton transport in the context of Grotthuss hopping along water chains,²² recent developments enable to now model proton transfer to and from aspartates and glutamates.⁶⁴ The parametrization of the force field through force matching to QM/MM simulations is then crucial and unfortunately, this type of force field is not well suited for cases that involves large environment changes of the protonatable residues and where the system would need to be reparametrized every time a significant conformational change occurs. Finally, classical MD simulations have the clear drawback of precluding bond breaking and formation, but allow sampling much larger time scales. To try and address the problem to its fullest extent, we have here adopted an integrative approach. Most simulations of the long time-scale conformational rearrangements are performed using a classical force field in which the proton is modeled in three different ways: bound to a water molecule in the form of a hydronium, bound to an acidic residue in the form of an aspartic acid or a glutamic acid, and represented as a positive Gaussian charge distribution. On the other hand, key steps of the mechanism, which involved covalent (un)binding of the proton, are investigated using mixed quantum mechanics/molecular mechanics (QM/MM) molecular dynamics (MD) simulations.

Acidic residues in hHv1 tend to protonate in the presence of H⁺.

Aspartic and glutamic acids are weak acids; the pKa of their side chain in water is 3.86 and 4.07, respectively. While their precise pKa in the hHv1 channel are not known, rough propKa estimates (Table S7) indicate that they also tend to be in majority in their charged form in this system. As such, when the local proton concentration increases, as is the case when a proton is transported along hHv1, the protons will tend to spontaneously bind to the negatively charged form of the acidic residue, at least transiently. The spontaneous binding of protons to these species has been reported by several groups, in water⁶⁴ and in other environments closer to the one found in the proton channel.^31,65,66

Sites E, C and I seem selective for H₃O⁺ over Na⁺.

The conservation of the acidic residues lining the pore tends to indicate their important role in the physiological function of the channel.⁹ So far, mutagenesis experiments have yielded conflicting conclusions. In the present work, we conducted classical FEP calculations to estimate the selectivity of the binding sites: all three of them were found to be more favorable for hydronium than for sodium ions (Table 2). Two notable differences exist between the two chemical species: the difference in their first coordination shell and in the reactive capabilities of the ions. While we observe that Na+ is able to interact with the two negatively charged residues in each site (I, C, and E), the hydronium ion can interact with the negative species as well as react with these residues. The reactive nature of the hydronium ion enables the proton to move upwards in the channel by hopping from the hydronium ion to the aspartate/glutamate. In contrast, Na+ is trapped between both negatively charged species and is unable to change environment. Note however that only resorting to a model allowing protonation and deprotonation will allow accurate estimates of the selectivity of each site.

Table 2:

Relative affinities for hydronium/sodium binding in the three binding sites of hHv1, estimated from free energy perturbation (FEP) calculations. The total free energy difference was estimated using the following relationship : $\Delta G_{H_3{O}^{+}\to N{a}^{+}=}\Delta G_{H_3{O}^{+}\to {Na}^{+}}^{app}-\Delta G_{H_3{O}^{+}\to N{a}^{+}}^{wat}+\Delta G_{H_3{O}^{+}}^{cst}-\Delta G_{N{a}^{+}}^{cst}$ where ∆G_app is the apparent relative affinity for hydronium over sodium in the binding site as calculated by FEP calculations, ∆G_wat is the reference free energy difference in water, and the two last terms compensate for the free energy loss from enforcing distance restraints in the FEP calculations.

[kcal/mol]	${{\text{ΔG}}_{\text{H3O+>Na+}}}^{\text{app}}$	${{\text{ΔG}}_{\text{H3O+>Na+}}}^{\text{wat}}$	${{\text{ΔG}}_{\text{H30+}}}^{\text{cst}}$	${{\text{ΔG}}_{\text{Na+}}}^{\text{cst}}$	${\text{ΔG}}_{\text{H30+>Na+}}$
Ext	8.1±0.6	3.6±0.4	0.9±1.0	1.5±1.0	4.0±2.0
Core	14.0±0.6	3.6±0.4	1.1±1.0	2.7±1.0	8.8±2.0
Int	8.5±0.6	3.6±0.4	1.2±1.0	2.0±1.0	4.1±2.0

F150 plays a major role in proton transport.

Our simulations have revealed the crucial role of F150 in the proton transfer from I to C. F150 adopts preferentially a closed conformation in which the intracellular crevice is slightly dehydrated and acts as a steric hindrance for ion transport. Under specific conditions (protonation of E153 or presence of a solvated proton in the core), F150 can adopt a conformation in which it is oriented towards S3 and where the channel can be open. The next natural step will be to characterize quantitatively the propensity of F150 to open under different conditions using enhanced sampling techniques in the near future. Interestingly, F150 is extremely conserved, not only in the Hv1 family but also in other VSDs.⁶⁷ In VSDs, it has been described as the gating charge transfer center since its role is to enable the state dependent transfer of S4 arginines during the activation mechanism.⁶⁸ Hence, it is interesting to note that a nonpolar phenylalanine at this location is involved in the transport of the charged species, whether it is a proton in Hv1 or the guanidinium group of an arginine in other VSDs. In addition, F150 has been implicated in the binding of positively charged guanidinium derivatives that act as intracellular blockers for Hv1.⁶⁹

Why is D112 crucial for selectivity?

Their selectivity reveals that sites I and E have the capability to preselect H₃O⁺ over Na+ before the ion reaches the core. However, mutagenesis experiments have indicated that only the mutation of D112 changes the selectivity of hHv1. All binding sites contain two acidic residues, thus the mutation of a single one may not be enough to modify selectivity in the sites in which the two residues can be considered as accessible from the solution. The C binding-site, however, is rather specific because of its position in a constrained, rather dehydrated environment. Our study has revealed that out of the two residues in the core, D112 is the first residue to which a proton binds when coming from the I-site. We also show that D112 cannot remain protonated for too long because it leads to the abnormal swelling of the channel. The protonation of D185, on the other hand, does not change the overall topology of the channel. This points to the fact that D112’s role is crucial in delivering the proton to the next aspartate in a fast manner. In order to transfer the proton from I to C, F150 has to open as well, which constitutes a significant rearrangement. Stabilizing the proton after this presumably slow step is therefore crucial, rationalizing the sensitivity of D112 mutation. Interestingly, experiments by Morgan et al. show that in a D112V mutant, a substitution to D at position V116 allows to recover proton selectivity,⁷⁰ indicating either that the position of aspartate residues can be slightly modified to still allow for proton conduction, or that the double mutant induces local conformational rearrangements that end up placing 116D in the position of D112. We propose that key elements of the proton-transfer mechanism in Hv1 suggested here, such as the sequential protonation of acidic residues could be generalized for other H+-channels, and that the presence of several protonatable residues in various protein environments could induce the presence of various degenerate pathways along a single channel.

An increased proton concentration enhances hHv1 conduction.

Despite the low concentration of protons under physiological conditions, the local environment of a channel can favor binding of protons and, through successive protonation events, store multiple positive charges. This was demonstrated in the case of the influenza A M2 channel.⁷¹ In Hv1, we noticed that the presence of a protonated glutamate/aspartate residue in the channel did not change the attractive nature of the channel lumen for positively charged ions (Figure S2). Hence we investigated the effect of increasing the proton concentration in the channel lumen.

Our correlation analyses indicate that when two protons are located in the channel, their position is not directly correlated (Table 1). Because some of the simulations were conducted out of equilibrium, however, we cannot exclude that under physiological conditions, protons would only be transported if an incoming proton would push forward the one present in the core, in a knock-on manner. What could be observed from our simulations, however, is that F150 reorientation away from the channel lumen and proton hop from E153 to D112 seems to be facilitated by the presence of a proton in the core. Indeed, when no proton is present in the core, F150 seems to be mostly locked in a closed state configuration because it interacts strongly with R211. When a positive charge is present in the core on the other hand, R211 appears to be pushed away, and F150 seems more likely to assume an open conformation, thus reducing the free energy barrier for proton hop from E153 to D112. Although further investigations will be needed to determine the free energy of F150 opening under both conditions, we propose that increasing the proton concentration leads to more efficient conduction through an enhanced F150 outward reorientation.

Conclusion

This study reports an initial attempt at characterizing the proton transfer pathway along the human voltage-gated proton channel hHv1, as well as represents a first step towards elucidating its function at the atomistic level. Because no crystal structure of the open activated state of hHv1 exists, we have built a model using the crystal structure of the chimeric murine homolog, mHv1.³² To take into account major conformational rearrangements while still enabling proton binding and unbinding to the different chemical species in the conduction pathway, we have adopted an integrative approach in which some simulations are conducted using classical MD simulations and others using a mixed QM/MM scheme.

In this study, we show that three main cation binding sites line the pore: an intracellular one encompassing D174 and E153, a central one made of D112 and D185 and an extracellular one involving E119 and D123. Our investigation indicates that rather than a Grotthuss hopping mechanism along a pre-oriented water wire, proton conduction may involve sequential binding of the proton to the six conserved acidic residues lining the pore: D174, E153, D112, D185, E119 and D123. Structural rearrangements accompany the proton jumps: at each step, two acidic residues come in close contact, enabling transfer from one to the next residue by hopping via a water molecule. The rate-limiting step is presumably the one bringing the proton from the intracellular binding site to the core, from E153 to D112, because it involves the flipping of the F150 side chain in an open conformation. These observations help to rationalize the role of D112 as a selectivity filter. We suggest that the presence of a second proton in the core of the channel favors F150 reorientation because it repels R211, which releases F150 from a strong cation-pi interaction with R211.

While this is a first attempt at investigating the proton transport along hHv1, it provides hypotheses that can be tested by experiments, resorting, for example, to mutagenesis of the residues involved in the conduction pathway to non-natural amino-acids (Aspartate to nitrohomoalanine (Nha), for instance). It also serves as the basis for further computational work to study the energetics and kinetics of the different steps and to rationalize the selectivity mechanism.