Activationless Multiple-Site Concerted Proton-Electron Tunneling

Abstract

The transfer of protons and electrons is key to energy conversion and storage, from photosynthesis to fuel cells. Increased understanding and control of these processes are needed. Anew anthracene–phenol–pyridine molecular triad was designed to undergo fast photo-induced multiple-site concerted proton–electron transfer (MS-CPET), with the phenol moiety transferring an electron to the photoexcited anthracene and a proton to the pyridine. Fluorescence quenching and transient absorption experiments in solutions and glasses show rapid MS-CPET (3.2 × 10¹⁰ s⁻¹ at 298 K). From 5.5 to 90 K, the reaction rate and kinetic isotope effect (KIE) are independent of temperature, with zero Arrhenius activation energy. From 145 to 350 K, there are only slight changes with temperature. This MS-CPET reaction thus occurs by tunneling of both the proton and electron, in different directions. Since the reaction proceeds without significant thermal activation energy, the rate constant indicates the magnitude of the electron/proton double tunneling probability.

The coupled movement of electrons and protons drives biological processes such as photosynthesis and cellular respiration. Understanding and mimicking this proton–electron transfer reactivity is valuable for the development of new energy technologies. In some cases, the electron and proton transfer to or from separated sites in the same chemical step. This type of proton–coupled electron transfer (PCET) is termed multiple-site concerted proton electron transfer (MS-CPET) or orthogonal PCET.^1–6 An exemplar of MS-CPET is the oxidation of Tyr_Z in photosystem II, with electron transfer (ET) to the oxidized chlorophyll and proton transfer (PT) to the hydrogen bonded histidine.⁵ Experimental studies of MS-CPET in hydrogen-bonded phenol-base systems have shown that MS-CPET rates vary with the driving force, Marcus-type intrinsic barriers, and electron and proton donor–acceptor distances.^3,4,7–25

Theoretical descriptions of PCET reactions usually involve both electron and proton tunneling. This can be described by an overlap of vibronic wave functions, or (in the Born–Oppenheimer limit) as the product of an electronic coupling term and a sum of vibrational wave function overlap integrals.^26,27 Some MS-CPET reactions exhibit experimental hallmarks of proton tunneling, such as significant rates at cryogenic temperatures.^28–32 For instance, MS-CPET was implicated in the photo-oxidation of a phenol–benzimidazole unit at 13 K.¹⁹ Reported here is a study of MS-CPET using a unimolecular anthracene–phenol–pyridine system that undergoes rapid photoinduced MS-CPET via electron and proton tunneling, with little or no thermal activation energy. The system mimics MS-CPET reactivity in biology and provides new insights into this class of reactions.

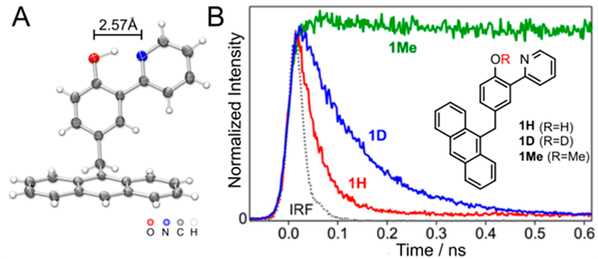
The anthracene–phenol–pyridine triad 1H (Figure 1) was designed to undergo favorable and rapid photoinduced MS-CPET. The photoexcited anthracene is a strong oxidant,⁷ and the conjugated phenol–pyridine has a low intrinsic barrier to MS-CPET.^11,12 Our prior studies of phenol–base MS-CPET oxidations involved bimolecular reactions; their rates therefore could not exceed the diffusion limit.⁷ The unimolecular system 1H removes this limitation. A methylene spacer was included between the anthracene and phenol–pyridine to keep them electronically distinct at a short distance. The spacer prevents π–π stacking of the phenol–pyridine and anthracene, as shown by the X-ray crystal structure of solid 1H (Figure 1A). The phenol-pyridine unit has the typical planar structure with a short OH⋯N hydrogen bond [d(O⋯N) = 2.566(5) Å].^12,14

Figure 1.

(A) X-ray crystal structure of 1H. (B) Time evolution of fluorescence from 1H (red), 1D (blue), and 1Me (green) in acetonitrile at 298 K after excitation at 362 nm. Dotted line = instrument response function.

Solutions of compound 1H, along with O-deuterated and O-methylated analogs 1D and 1Me, were studied by time-resolved fluorescence using a photon-counting streak camera (Figure 1B). Irradiation with 362 nm laser pulses selectively excited the anthracene portion of the triads (Figure S12). The emission spectra of 1H, 1D, and 1Me in MeCN at room temperature are similar to the spectrum of free anthracene (Figure S12). The control compound 1Me, which cannot undergo MS-CPET, has an emission lifetime (5 ns) similar to that of free anthracene.³³ In contrast, 1H exhibited fast quenching of the anthracene emission. The decay of the emission in MeCN was dominated by a fast component (τ = 31 ps) and showed a minor slow component (≤2%, τ = 8 ns). Fast quenching was also observed in less polar media: fluorescence lifetimes were 56 and 86 ps in 2-methyl-THF (2-MeTHF) or methylcyclohexane (MeCy) solutions, respectively, and 92 ps in poly(methylmethacrlylate) (PMMA) films. Triad 1D showed a fast quenching component in MeCN (τ = 116 ps) that is longer than that of 1H, corresponding to a primary kinetic isotope effect (KIE) of 3.7 ± 0.4.

UV–vis transient absorption (TA) spectroscopy corroborated the lifetimes measured by fluorescence quenching and indicated an electronically isolated anthracene moiety (Figures 2A, S20–23). For 1H and 1Me, the TA data after 365 nm excitation showed spectral features and decay time constants (4 ps) characteristic of formation and vibrational energy redistribution of the S₁ anthracene excited state (S₁-anth*).^34,35 Thus, both the fluorescence and TA show that the CH₂–phenol–pyridine substituent does not affect the S₁-anth*.

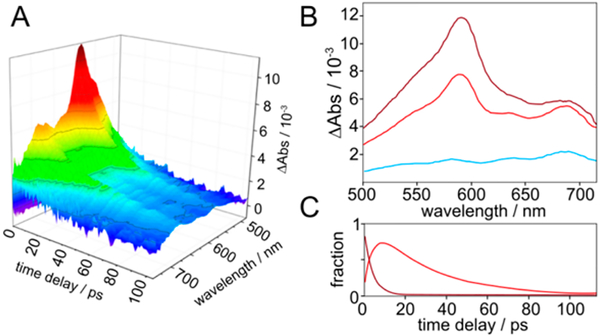
Figure 2.

(A) TA spectra of 1H in MeCN up to 100 ps after photoexcitation. (B) Component transient absorption spectra from global analysis of spectra from 0 to 100 ps: initial excited state (maroon), vibrationally cooled S₁-anth* state (red), and long-lived photoproduct (cyan). (C) Mole fractions of initial and cooled anth* states.

The S₁-anth* in 1Me persists for more than 1 ns, while the corresponding state in 1H decays with τ = 28 ps. These values are in agreement with the 5 ns and 31 ps decays measured by fluorescence quenching. The decay of the 1H excited state is slower than vibrational cooling, so quenching occurs predominantly from the thermally equilibrated anthracene local excited state.

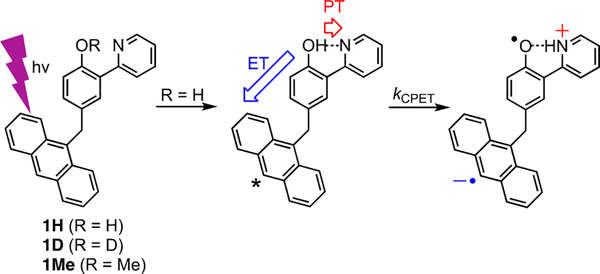
The rate constants and isotope effects implicate an MS-CPET mechanism for the quenching in 1H and 1D. This mechanism involves ET from the phenol–pyridine to the S₁-anth* local excited state in concert with PT across the OH⋯py hydrogen bond (Scheme 1). The quenching rate constant for 1H, k =3.2 × 10¹⁰ s⁻¹ in MeCN must correspond to a unimolecular process because it is faster than diffusional collisions between dilute solutes. The primary KIE of 3.7 between 1H and 1D implies that the hydrogen/deuterium nucleus is involved in the process. Förster and Dexter energy transfer are unlikely quenching mechanisms. The anthracene emission and the phenol–pyridine absorption show negligible spectral overlap (Figure S12) and indicate that energy transfer would be energetically uphill (FMO analysis, Supporting Information). The driving force for MS-CPET can be roughly estimated as −9 kcal mol⁻¹, the value for the related bimolecular reaction.⁷ The unlikelihood of Förster and Dexter energy transfer is further supported by the unperturbed nature of the initially formed S₁-anth* state and by 1Me exhibiting nearly identical photophysical behavior to free anthracene. Additionally, phenol–imine excited states often exhibit emission in the visible range,³⁶ but photoexcited samples of 1H showed emission only from anthracene, suggesting that phenol–imine excited states were not present and energy transfer did not occur. The data presented here, together with published results on bimolecular oxidations of similar phenol–base compounds (including with excited anthracene),^3,4,7–25 all indicate the MS-CPET mechanism in Scheme 1.

Scheme 1.

MS-CPET Mechanism for Excited State Quenching in 1H

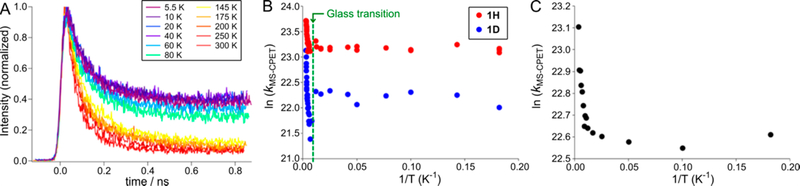
The photoinduced fluorescence of 1H was measured over a large temperature range (Figure 3A). The fast decay rates are insensitive to temperature: they vary only by a factor of 2 over the temperature range 5.5–350 K in 2-MeTHF. Emission from 1Me has a nearly constant long lifetime over the entire temperature range. The quenching rate for 1H at 5.5 K is unaffected by the incident laser power over a range from 0.1 to 1.4 mW, so local heating and multiphoton effects are not significant. The long-lived minor slow component of the fluorescence decay becomes more pronounced at lower temperatures, to a degree that depends on the medium (up to ~40% in 2-MeTHF, up to ~20% in PMMA at 5.5 K). This long-lived component could correspond to a different conformer of 1H and could relate to the weak long-lived signal seen in the TA spectra (Figure 2B), which we have been unable to assign with confidence. The MS-CPET zwitterionic photoproduct (Scheme 1) is expected to be difficult to observe because it would likely rapidly convert back to the 1H ground state, due to a driving force for decay that can be roughly estimated as −64 kcal mol⁻¹. This driving force corresponds approximately to the 0–0 transition energy (~390 nm/73 kcal mol⁻¹) less the MS-CPET driving force (~ −9 kcal mol⁻¹).

Figure 3.

(A) Time dependence of the fluorescence decay of 1H in 2-MeTHF from 5.5 to 300 K. (B) Arrhenius plots for 1H (red) and 1D (blue) in 2-MeTHF. (C) Arrhenius plot for 1H in a PMMA film. For (B) and (C), the experimental uncertainties in ln(k_MS-CPET) and 1/T are smaller than the size of the data points.

The Arrhenius plot of MS-CPET rate constants for 1H in 2-MeTHF (Figure 3B) has unusual features. First, the range of temperatures is large, from 5.5 to 350 K, a factor of 64 in temperature. Second, the range of rate constants is extremely small: the k_MS-CPET for 1H are all within less than one In unit. Within this scale, the Arrhenius plot has two distinct regimes. In the low-temperature regime (5.5 to 85 K), k_MS-CPET is constant at [1.2 ± 0.1] × 10¹⁰ s⁻¹. The best fit to the Arrhenius equation gives zero activation energy (E_a = 0.0 ± 0.01 kcal mol⁻¹) and a small pre-exponential factor (A = [1.2 ± 0.1] × 10¹⁰ s⁻¹). At higher temperatures, 145 to 350 K, k_MS-PET increases only slightly, by a factor of 2. The Arrhenius plot in this regime is slightly curved, and the approximate parameters extracted from it are unusually small: A = 2.9 × 10¹⁰ s⁻¹ and E_a = 0.33 kcal mol⁻¹.

The MS-CPET rate constants were measured for 1H in PMMA, which is a glass at all temperatures studied. The same distinct temperature regimes were observed as in 2-MeTHF, but without the discontinuity (Figure 3C). Thus, the change in E_a with temperature is a property of 1H and is not caused by the glass transition in 2-MeTHF, while the small discontinuity observed in 2-MeTHF may be an effect of the glass transition.

The fluorescence lifetimes for the major fast component varied slightly in different glasses at 5.5 K, with values of 88 ps (MeCy), 94 ps (2-MeTHF), and 151 ps (PMMA). The slower component became more pronounced at low temperatures, perhaps reflecting a temperature- and solvent-dependent distribution of conformers of 1H that do not interconvert on the time scale of the MS-CPET reaction. The mechanistic conclusions below are for the predominant fast component.

The temperature dependence of k_MS-CPET for 1D in 2-MeTHF is similar to that for 1H (Figure 3B). It has an Arrhenius slope of zero in the low-temperature regime, and a small E_a(D) = 0.48 kcal mol⁻¹ between 145 and 350 K. The KIE is constant at 2.7 ± 0.3 from 5.5 to 85 K and varies from ± 0.5 at 175 K to 1.8 ± 0.2 at 350 K (E_a(D) − E_a(H) = 0.2 kcal mol⁻¹). The room-temperature KIE values support an MS-CPET mechanism because they are similar to values measured for thermal bimolecular MS-CPET reactions of related phenol–pyridines (~2.7 in MeCN).¹²

Overall, MS-CPET in 1H has unusual kinetic features. The reactions are fast even at 5.5 K, with zero Arrhenius activation energy up to 80 K, and small sensitivity to the surrounding medium. The temperature independence of the KIE at low temperatures is a marker for proton tunneling.³⁷ Together, these results indicate that the electron and proton both transfer by tunneling from a thermodynamic minimum configuration, with essentially no nuclear reorganization. At higher temperatures, MS-CPET in 1H has a very small Arrhenius activation energy of 0.33 kcal mol⁻¹ (115 cm⁻¹) in 2-MeTHF. Given this small value and the insensitivity of k_MS-CPET to the medium, this energy may reflect thermal excitation of a vibration modulating the proton donor–acceptor (O⋯N) distance.²⁶ In a simple tunneling model, the fast rates and small KIE’s observed would correspond to a short O⋯N distance and a narrow barrier. A much more complete theoretical treatment of the system is needed to include, for instance, the role of vibrational excited states.^13,26

Since MS-CPET in 1H below 85 K proceeds without thermal activation, its rate constant is limited only by the probability of the proton/electron double tunneling event. The theoretical maximum rate constant for electron or proton transfer is on the order of 10¹³ s⁻¹, based on the maximum rate of activationless electron transfer and the period of skeletal vibrations.^10,38,39 Thus, the k_MS-CPET for 1H of ~10¹⁰ s⁻¹ implies that the probability of the concerted electron/proton tunneling process is about 10⁻³. The probability corresponds to a prefactor for an exponential, like κ in transition state theory, and is consistent with a nonadiabatic process. It represents a rare direct experimental determination of a reaction probability for a proton-coupled electron transfer process.

In conclusion, photoexcited 1H undergoes fast intramolecular electron and proton transfer in different directions in a single kinetic step, even at 5.5 K. The temperature insensitivity of the reaction rate indicates an important limiting case in which the charge separation reaction is not thermally activated and proceeds via simultaneous tunneling of the electron and proton. The measured rates allow direct experimental determination of the approximate probability of proton–electron tunneling (~10⁻³). The simple molecular system examined here shows how to achieve rapid and barrierless MS-CPET, which could be relevant to biological processes and new energy technologies.