Effective design principles for leakless strand displacement systems

Significance

The modern information age was enabled by encoding, transmitting, and manipulating information in a way that is robust to error. However, synthetic biology and molecular programming, fields that aim to recapitulate the successes of electronics within biochemistry, still struggle with error tolerance. The ability to create “smart” molecular systems capable of robust information processing and decision making would enable important applications in biomaterial production, biosensing, and therapeutics. Based on DNA strand displacement building blocks, we demonstrate de novo engineered molecular cascades robust to spurious interactions using an error correction scheme based on redundancy. In principle, arbitrary levels of error reduction could be attained. The information propagation cascades form a foundation for more complex, resilient, and faster programmable reaction networks.

Abstract

Artificially designed molecular systems with programmable behaviors have become a valuable tool in chemistry, biology, material science, and medicine. Although information processing in biological regulatory pathways is remarkably robust to error, it remains a challenge to design molecular systems that are similarly robust. With functionality determined entirely by secondary structure of DNA, strand displacement has emerged as a uniquely versatile building block for cell-free biochemical networks. Here, we experimentally investigate a design principle to reduce undesired triggering in the absence of input (leak), a side reaction that critically reduces sensitivity and disrupts the behavior of strand displacement cascades. Inspired by error correction methods exploiting redundancy in electrical engineering, we ensure a higher-energy penalty to leak via logical redundancy. Our design strategy is, in principle, capable of reducing leak to arbitrarily low levels, and we experimentally test two levels of leak reduction for a core “translator” component that converts a signal of one sequence into that of another. We show that the leak was not measurable in the high-redundancy scheme, even for concentrations that are up to 100 times larger than typical. Beyond a single translator, we constructed a fast and low-leak translator cascade of nine strand displacement steps and a logic OR gate circuit consisting of 10 translators, showing that our design principle can be used to effectively reduce leak in more complex chemical systems.

Naturally evolved molecular machines are capable of conducting reliable computation from signal transduction to information storage and processing (1). The development of robust artificial molecular machinery could, in turn, enable the systematic construction of molecular computing circuitry embedded within living cells or cell-free molecular technologies.

The natural property of Watson–Crick base pairing makes DNA a powerful and unique engineering material to be rationally programmed and easily predicted at the nanoscale. In contrast to synthetic biology, which adapts naturally evolved molecular machines for new purposes (2), DNA nanotechnology aims to build up functionality from first principles (3). With a quantitative understanding of the kinetics and thermodynamics of DNA hybridization, the toehold-mediated strand displacement reaction (4) has emerged as a uniquely versatile building block (5). Strand displacement reactions underlie molecular motors (4, 6), robots (7, 8), logic circuits capable of signal restoration, amplification, digital (9, 10) and neural network-like computation (11), and controllers that implement prescribed time-varying dynamics (12, 13) based on a systematic theory (14, 15). Strand displacement-based molecular amplifiers (16–19) are not only an essential component for signal restoration in digital circuits but also, useful for diagnostic applications (20, 21). The successful implementation of synthetic cell-free systems also leads to additional applications at the interface with biology: nucleic acid-based nanodevices have been delivered in vivo (22) as imaging probes (23) or to perform logical computation (24, 25). Inspired by DNA nanotechnology, RNA strand displacement can be engineered to regulate gene expression in response to specific target RNA inputs (26, 27).

Although DNA strand displacement systems have shown remarkable promise, experimental demonstrations of more complicated tasks and practical applications are still limited in large part due to a lack of robustness in large systems. A general strategy used in electrical engineering and computer science to generate error-tolerant systems is to introduce various levels of redundancy and ensure that multiple low-probability events need to occur to cause error. For example, error-correcting codes are universally used in telecommunications (28). At the cost of sending more data, messages can be recovered unless many bits are corrupted. Von Neumann multiplexing achieves reliable computation in the presence of error-prone logic gates: each computing stage contains redundant blocks, and majority gates select the more likely correct result (29). In DNA nanotechnology as well, redundancy-based proofreading significantly reduces the error rate in algorithmic self-assembly by requiring a sequence of unfavorable mismatched binding events (30). Given the programmability of strand displacement systems, can we incorporate redundancy to curtail the error reaction pathways to an arbitrary chosen degree?

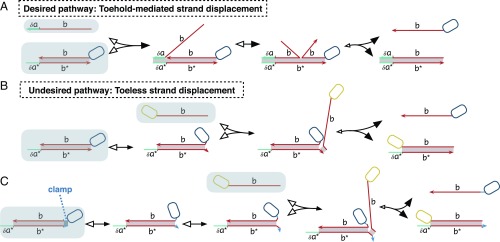
In the toehold-mediated strand displacement mechanism shown in Fig. 1A, an invader input strand displaces an output strand from a multistranded complex after initially binding at a short single-stranded “toehold” region (five to seven bases). The input and output strands carry information between multistranded complexes; thus, chaining multiple strand displacement reactions together makes complicated cascades possible. Even in the absence of the correct invader strand, DNA strand displacement systems are vulnerable to the undesired release of output, called leak (31). Although the initially present complexes are designed not to have interacting toeholds, leak is thought to be caused by undesired “toeless” strand displacement between them. The basic toeless strand displacement reaction is shown in Fig. 1B. It can spuriously produce output strands, critically disrupting desired system behavior (9, 10) and reducing sensitivity by making it difficult to distinguish positive signal and system background (17). In addition, prior experimental and modeling studies found that problems with leak are exacerbated at high concentration (10, 11). Consequently, the reacting species in strand displacement circuits are typically kept at low concentrations, which limits the speed. It often takes hours for existing systems to reach completion.

Fig. 1.

Desired and leak strand displacement reactions. Letter labels represent domains, which are contiguous bases that logically act as a unit. The domains with complementary sequences are labeled with asterisks. The black arrowheads show the direction of forward reactions, and the white arrowheads show the direction of backward reactions relative to the illustrated reaction pathway. Small arrowheads indicate reactions that are expected to be slow relative to other steps. Shaded background indicates molecular species that are initially present. Toehold domains are labeled by the symbol $\delta$ and a thicker strand line. (A) Intended strand displacement reactions are initiated by binding of a toehold (domain $\delta a$) followed by the displacement of the incumbent strand by the matching portion of the invader strand (domain $b$). The participating strands can have other domains on either side of the involved displacing region; for example, the dark blue rounded rectangle box represents the part of the released strand on the 5′ end not involved in this interaction. (B) Leak is hypothesized to be caused by toeless strand displacement reactions, which start from the fraying of the end of a DNA helix where no neighboring base pairs can help stabilize the structure. (Here, both ends of the helix could fray. The figure only shows one scenario.) After they are frayed, the opened nucleotides can be the initiation point for the undesired strand displacement. The invading strand can be a part of a larger complex, which is indicated by the yellow rounded rectangle box. (C) Short clamp domains (indicated by a darker shaded helix) help to reduce leak. The toeless displacement on the right side of the helix now requires larger fraying as shown. (Note that the clamp shown does not inhibit toeless displacement on the left side of the helix.)

A number of leak reduction methods have been proposed. At the sequence level, terminating helices with C–G bonds helps to prevent fraying (32). Furthermore, mismatches at the fraying region have been shown to hinder toeless displacement (33–35). Another widely used technique introduces modifications at the end of helices called “clamps,” which are smaller than a toehold (typically one to three bases) (9, 10, 13). Clamps require a larger fraying event to cause toeless displacement, introducing an energetic barrier (Fig. 1C). The programmable hairpin assembly and disassembly architecture of Yin et al. (18) included longer padding domains that inhibited spurious hairpin interactions. However, these techniques can be used only in a limited number of contexts, and none of the above sequence-level techniques seem sufficient to eliminate leak entirely and in a systematic way.

Beyond the sequence design level, system-level leak reduction strategies have been proposed. Physically separating components that have cross-talk using solid support or on DNA origami can decrease leak (36–39) at the cost of greater experimental complexity. In well-mixed systems, threshold gates are sometimes used for digital signal restoration (9, 10). However, thresholding cannot be used when we want to preserve the exact amount of output for analog computation (40) or dynamical systems (13). Some implementations of thresholding, which rely on preferentially consuming leaked strands before they are able to interact downstream, require slowing down the competing downstream reactions, thereby slowing the intended pathway (10). Recent work proposed using multiarm junction structures to create multiple high-energy barrier steps to leak (19). However, the desired reaction slows down as well, and leak cannot be systematically reduced to arbitrarily low levels. Moreover, the design principle is more complex, and it cannot easily be used as a building block for strand displacement systems.

Inspired by logical error correction schemes in computer science that improve robustness by encoding redundant information, a new system-level method that can systematically reduce leak by using different levels of redundancy was introduced, and the correctness was theoretically proved (41). This design method has the key property that, at level $N$ redundancy, $N$ initial species need to bind together to produce leaked signal. In contrast to clamping techniques that introduce an energy barrier to overall thermodynamically favorable reactions, forming such large complexes here incurs a thermodynamic (entropic) penalty, making leak unfavorable. In principle, this method could offer a systematic way to reduce leak to an arbitrarily low level by increasing $N$ and reducing concentration. In related prior experimental works, the cell surface automata by Rudchenko et al. (24) included components with effectively $N=2$ redundancy, but leak reduction was not the aim. However, a systematic method to achieve leak reduction was still lacking before our work.

Here, we experimentally implement the previously proposed error reduction scheme (41) and demonstrate a dramatic reduction in leak. (Our scheme is compatible with the clamping technique described above. For a fair comparison with standard design methods, we use clamps throughout our design to show leak reduction beyond clamp-only schemes.) Going beyond the previous theoretical analysis (41), which required a low concentration and therefore, kinetically slow regime, here we demonstrate leak reduction for highly concentrated, fast systems. We experimentally characterize the systems from both thermodynamic and kinetic perspectives. In terms of thermodynamics, we demonstrate that it is possible to increase the free energy penalty to leak by increasing system redundancy, thus reducing the total amount of leak. We also develop a kinetic model that quantitatively captures the leak dynamics at high concentrations, including two distinct timescales of leak that we observed.

To investigate this leak reduction method, we start with the simplest nontrivial strand displacement cascade, a “translator,” which converts an input into an output of independent sequence. At the high concentrations permitted by the “leakless” design, the desired strand displacement reaction in the presence of input is very fast: the output signal reaches $>80\%$ completion within 3 min of addition of input, while by increasing redundancy, leak could be reduced to the limit of detection in our experimental setting. At $N=3$ redundancy, no leak was observed in a 10-h experiment, even if the concentration was increased up to $10\hspace{0.17em}\mathrm{\mu }$M, which is on the order of 100 times higher than typical concentrations (50–400 nM) in strand displacement systems (9–11, 13, 16, 17, 20). In addition to showing that no measurable leak was produced in the duration of our experiment, we indirectly confirm that no significant leak would be generated even with longer incubation by measuring leak at thermodynamic equilibrium. Beyond a single translator, we also engineered a four-layer linear translator cascade consisting of 9 multistranded complexes and a three-layer digital circuit of five OR gates consisting of 21 multistranded complexes. The fast (order of minutes) and low-leak (less than $5\%$ over 10 h) performance of these circuits shows that leak reduction generalizes to more complex settings.

Leakless Design

The Single-Long Domain and the Double-Long Domain Designs.

To understand the leak mechanism in strand displacement systems, we begin by studying the simplest translator gate $X\to Y$, which consumes input signal strand $X$ to release output signal strand $Y$ of independent sequence to $X$. After it is released, the output strand can then react with a downstream component. The multistranded complexes are named fuels, since the net free energy of hybridization of complementary strands between signal strands and fuels drives the series of strand displacement reactions. Translators can be used to build logic OR gate functionality by having multiple translators translate different input signals to the same output. Recent work demonstrated probabilistic switching circuits composed of translators, which can generate output signals with programmed concentration ratios (42). A catalytic molecular amplifier can be engineered if the output signal produced by the translator cascade is the same as the input signal. The simplicity of translator systems makes them amenable to biological applications: for example, as the molecular automata to target specific cellular surface markers (24). Translators are also closely related to seesaw gates, which have diverse functionalities, including arbitrary Boolean and linear threshold computation (10, 11).

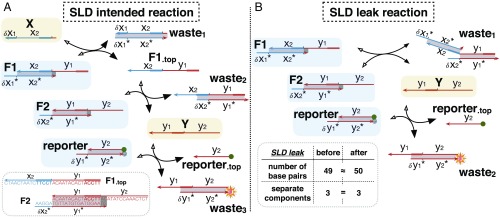
A typical translator gate consists of two fuel complexes ($F1$, $F2$) (Fig. 2A). In our schemes, we use four different domain types: full domains, almost full domains (with the symbol $\mathrm{\Delta }$), toehold domains (with the symbol $\delta$), and clamp domains. Unless otherwise specified, full domains are 15 bases, $\mathrm{\Delta }$ domains are 10 bases, $\delta$ domains are 5 bases, and clamp domains are 2 bases. Since we assume that domains with length longer than a toehold do not spontaneously dissociate, both the full domains and the $\mathrm{\Delta }$ domains are called long domains. In Fig. 2A, since every fuel species is bound by one long domain, we refer to this scheme as the single-long domain (SLD) design.

Fig. 2.

The typical SLD translator system. The symbol $\delta$ denotes a toehold-size subsection of a long domain (e.g., $\delta x_2*$ is the toehold-size 5′ end of $x_2*$). The faint blue background indicates the fuel and reporter species; the faint yellow background indicates the signal species. Domains that logically belong to input $X$ and output $Y$ are colored blue and red, respectively. (A) The intended pathway of the translator $X\to Y$ that translates strand $X$ to strand $Y$. Per standard practice, every fuel complex contains a clamp domain to help reduce leak. The input strand $X$ first interacts with the fuel complex F1, displacing an intermediate strand F1_.top with the toehold domain $\delta x_2$ and the long domain $y_1$ exposed, which then reacts with F2 releasing the output strand $Y$. The output strand $Y$ can be detected by a downstream reporter. (Inset) The sequences of F1_.top and fuel F2 used in our experiments. (B) The leak reaction of the translator in the absence of the input strand $X$. After the clamp in F2 opens, the unbound domain $y_1$ in the fuel complex F1 can interact with the sequestered domain $y_1*$ in F2 through toeless strand displacement and then, produce the output strand $Y$. (Inset) Thermodynamic analysis suggests that there is very little energy difference between the leaked and unleaked states. Each full long domain is 15 bases, domains with the symbol $\delta$ and toehold domains are 5 bases, and clamp domains are 2 bases. The change in the number of base pairs due to the net leak reaction is equal to $\left\{\text{toehold size}\right\}-2\times \left\{\text{clamp size}\right\}=1$. As long as this number is small, it does not play an important role in the thermodynamics of the system. There is no difference in the number of separate components.

The intended reaction pathway is a cascade of events in which each top strand of a fuel, after it is released, will subsequently react with a downstream fuel (or reporter) by toehold-mediated strand displacement. Critically, the toehold needed for the downstream reaction is initially sequestered within the upstream fuel complex (e.g., thick blue region of the top strand of $F1$ in Fig. 2), only becoming exposed and thus, active after the top strand is released. The output strand $Y$ is initially sequestered on $F2$ and is expected to be released only after a cascade triggered by the input $X$. In our experiments, we measure the amount of $Y$ released via a reporter complex as the downstream component. The two strands of the reporter complex are labeled by a fluorophore and a quencher. The output strand $Y$ hybridizes with the fluorophore-labeled reporter strand, displacing its quencher-labeled binding partner and thus, separating the fluorophore and quencher. The increased fluorescence is measured by a spectrofluorometer. The overall reaction results in the formation of one additionally bound toehold, which provides the thermodynamic driving force (clamps introduce slight reversibility in the desired reaction) (SI Appendix, section S1.1 has more details).

The leak pathway in the absence of input strand is thought to be caused by toeless strand displacement between the unbound long domain $y_1$ in $F1$ and the bound long domain in $F2$ (Fig. 2B) (10). The output strand $Y$ is thus released and can then react with a downstream component or be measured through the reporter.

To reduce leak without interfering with the desired reaction pathway, the SLD scheme can be modified to prevent the release of the output strand in the case of toeless displacement (41). As shown in Fig. 3B, the unbound domain $y_1$ in fuel $F1$ can only partially displace the top strand (output strand) in fuel $F2$. Since the output strand remains bound by a long domain $\mathrm{\Delta }{x}_2$, it cannot easily dissociate. The resulting $Y_{complex}$ is then likely to quickly revert back into the two original fuel species. For leak to occur, $Y_{complex}$ must react with the downstream complex (e.g., reporter) before this reverse reaction. The intended pathway of the translator in this design is the same as that of the SLD translator: the input strand $X$ initiates a cascade of two strand displacement reactions to produce the output strand $Y$ (Fig. 3A). Since here, every fuel species is bound by two long domains, it is called the double-long domain (DLD) scheme.

Fig. 3.

The DLD translator system. The symbol $\mathrm{\Delta }$ denotes an almost full domain, which is a 10-base subsection of a full domain. The faint yellow background indicates the signal species in the intended pathway (input $X$ and output $Y$) and the species that can trigger the reporter in the leak pathway ($Y_{complex}$). (A) The intended pathway of the translator $X\to Y$ that translates strand $X$ to strand $Y$, which is similar to that of the SLD translator. (B) The proposed leak pathway of the DLD translator in the absence of the input strand $X$. After the clamp domain in F2 is open, the unbound domain $y_1$ in fuel F1 displaces the $y_1$ domain in fuel F2 through toeless strand displacement (the intermediate is shown in the pathway above the arrow), resulting in a short-lived species ($Y_{complex}$). Since the $\mathrm{\Delta }{x}_2$ domain is still bound, $Y_{complex}$ can quickly revert back to F1 and F2 via a unimolecular reaction (green). False-positive signal requires $Y_{complex}$ to react with the downstream reporter before dissociating. Note that $Y_{complex}$ can also isomerize to other configurations (SI Appendix, Fig. S7). (Inset) Thermodynamic analysis suggests that the leaked state has higher thermodynamic energy (one unit of entropic penalty) than the unleaked state. The change in the number of base pairs due to the net leak reactions is equal to $\left\{\text{toehold size}\right\}-2\times \left\{\text{clamp size}\right\}=1$. The number of separate components decreases by one after leak. Under experimental conditions, one entropy penalty is worth roughly 8 bp (in the text), and therefore, the thermodynamics is dominated by the entropic cost of leak.

The underlying leak reduction can be understood via a thermodynamic analysis. As simple metrics, we consider the number of base pairs and the change of the stoichiometry coefficients of reactants and products. We use “one unit of entropy” to indicate the entropic penalty due to the joining of two separate molecules. Quantitatively, one unit of entropy at concentration $c$ M is $\mathrm{\Delta }{G°}_{\text{assoc}}+RT\ln \left(1/c\right)\approx 1.96+0.6\ln \left(1/c\right)$ kcal/mol at 37 °C (43). The entropic penalty is significant—at roughly 250 nM concentration and 37 °C, overcoming one unit of entropy penalty requires forming roughly 8 bp [the average free energy of forming 1 bp is 1.4 kcal/mol at 37 °C (43)]. Although the entropic penalty becomes smaller at higher concentrations, our results below demonstrate that it can still meaningfully prevent leak.

Based on these metrics, leak in the SLD design is expected to be roughly thermodynamically neutral. Comparing the two states “before leak” and “after leak,” the leak reaction is driven forward by the energy of forming 1 bp, and there is no difference in the number of separate molecules (Fig. 2B). In the DLD design, leak also results in gaining the energy of binding 1 bp; however, since the output strand $Y$ cannot be fully released in the leaked state, the after leak state has one less separate component than that of the reactants in the before leak state (Fig. 3B). Thus, compared with the SLD design, the DLD design has a higher-energy penalty (one unit of entropic penalty) to leak. [Our choice of toehold and clamp lengths is typical of translator systems (10); different choices of toehold and clamp lengths would have resulted in a slightly larger gain or a slight loss of base pairs in the leak state, affecting the SLD and the DLD leak similarly.] Note that the leak reduction in the DLD design is not simply a result of the increased length of the double-stranded region of the fuels that stabilizes the complexes; DLD gives an order of magnitude greater reduction in leak. (Results and SI Appendix, section S5 have more information.)

The Triple-Long Domain Design.

Beyond the DLD design, we ask if leak can be reduced further by increasing redundancy level to $N=3$. The redundancy level $N⩾2$ determines the number of bound long domains in fuels, the number of long domains in signal strands, the number of fuels in a single-translator system, the number of strand displacement steps in the desired reaction pathway to release the output, and most importantly, the number of fuels that must come together as a single complex before leak can occur. (Note that $N=1$ is not a valid design; see SI Appendix, Fig. S11.) In the triple-long domain (TLD) scheme (Fig. 4), the sequestered output strand is bound by three long domains ($\mathrm{\Delta }{x}_3$, $y_1$, and $y_2$) in $F3$. All of the fuel complexes contain three bound long domains in the double-stranded region and one long domain unbound. The TLD translator contains three fuels species, and it takes three strand displacement steps to displace the output signal strand $Y$ (Fig. 4A). Producing a leaked signal in the absence of input strand in the TLD translator system requires forming a complex with $F1$, $F2$, and $F3$ bound together. Leak in the TLD design is more unfavorable compared with other designs in terms of both kinetics and thermodynamics. In terms of kinetics, Fig. 4B provides a plausible leak pathway: to produce a leaked signal, $F1$ and $F2$ start by forming the four-stranded complex, which could quickly reverse to the original configuration. Then, $F3$ reacts with this complex, forming a six-stranded complex, which could also quickly reverse to the unreacted configuration. The downstream reporter needs to capture this six-stranded complex before the complex reverses to separate species. The leak pathway has more fast reverse steps compared with the DLD scheme, which reduces the probability of the reporter reacting with $Y_{complex}$ even further. In terms of thermodynamics, leak results in two units of entropic penalty (and 1-bp penalty) comparing the before leak and after leak states. In principle, leak could be reduced through a systematic process to an arbitrary low level by increasing redundancy level $N$ even further. Specifically, based on the fact that translator top strands have $N+1$ long domains while bottom strands have $N$ long domains, a counting argument shows that separating the two strands of the reporter in the absence of input (leak) requires forming a large complex of size $2N$ strands (41).

Fig. 4.

The TLD translator system. (A) The intended pathway of the translator $X\to Y$ that translates strand $X$ to strand $Y$. (B) One possible leak pathway of the TLD translator in the absence of the input strand $X$. After the clamp domain in F2 is open, the unbound domain $y_1$ in fuel F1 displaces the $y_1$ domain in fuel F2 through toeless strand displacement, resulting in a short-lived four-stranded complex, which could quickly reverse (unimolecular reaction; green) to the original configuration. Then, after the clamp domain in F3 is open, F3 reacts with this four-stranded complex and forms a six-stranded species $Y_{complex}$, which can similarly quickly reverse. Finally, the downstream reporter needs to capture this transient six-stranded complex before the reverse reaction occurs. This pathway suggests that the leak rate in the TLD translator should be even slower than that in the DLD translator, since this leak pathway requires a longer series of slow reactions to occur, and each transient in the leak pathway is more likely to quickly reverse toward the nonleak state. (Inset) Thermodynamic analysis shows that leak has an energy penalty of two units of entropy, which is one unit of entropy more than in the DLD design. The change in the number of base pairs due to the net leak reactions is equal to $\left\{\text{toehold size}\right\}-3\times \left\{\text{clamp size}\right\}=-1$. The number of separate components decreases by two after leak.

While both our design and the technique of adding clamps insert additional double-stranded domains into fuel complexes, the long domains added in our scheme can be opened via displacement rather than spontaneous dissociation as in the case of clamps. Therefore, our leakless design methodology is complementary to the technique of adding clamps, and both can be used simultaneously (as we do here). Note in particular that maximum size (toehold size) clamp schemes were recently shown to have strong thermodynamic guarantees of robustness not based on the association penalty and could in principle also lead to arbitrary leak reduction (44). However, the intended reaction in these schemes has a smaller thermodynamic driving force and necessarily does not reach full completion.

The DLD, TLD, and higher-redundancy schemes introduced in previous theoretical work (41) are motivated by the low-concentration regime in which the entropic penalty is largest and equivalently, the reverse (unimolecular) reactions along the leak pathway are much faster than the forward (bimolecular) reactions. In contrast, we demonstrate significant leak reduction with the DLD and TLD schemes even at concentrations of up to two orders of magnitude higher than the typical 50- to 400-nM regime.

Results

Leak Reduction for a Single Translator.

To experimentally investigate the leak reduction method, we first need to generate the DNA sequences. Since the translators have the property that all domains have well-defined neighboring domains, the sequence space can be represented by one contiguous sequence (i.e., $x_1{x}_2{y}_1{y}_2$ for the SLD and DLD designs). We generated sequence candidates randomly and eliminated the ones with excessively long repeats. Self-complementarity was avoided by using the ATG alphabet for the bottom strands and ATC for the top strands. (SI Appendix has additional constraints and more information.) The DNA sequences were then chemically synthesized and PAGE purified, and each duplex was annealed in TAE/Mg²⁺ buffer (0.04 M Tris, 1 mM EDTA, 12.5 mM Mg²⁺, pH balanced to 8.0 by acetate). To remove unhybridized single strands or misfolded duplexes, the annealed duplexes were purified through nondenaturing PAGE. After elution and quantification, different reacting species were mixed together to initiate the experiment. Reporter fluorescence was read out on a plate reader in 18 $\mathrm{\mu }$L solution volume.

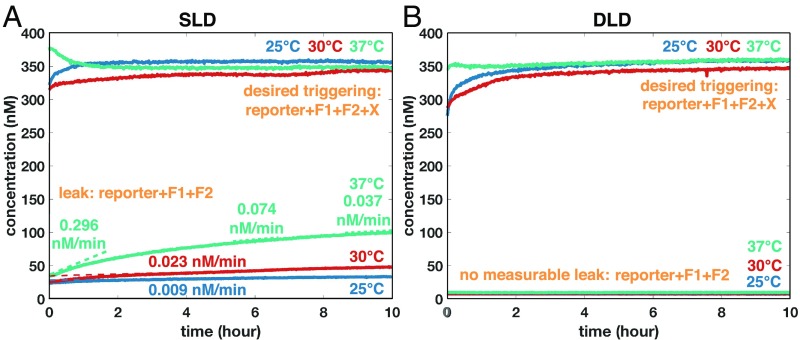
We first compare the single-translator system using the SLD and the DLD design principles. Fig. 5 shows the kinetic behavior of the SLD and DLD translators. The desired triggering signals of these two translators show similar kinetics (i.e., larger than $75\%$ completion within a few minutes).

Fig. 5.

Kinetics of (A) the SLD translator and (B) the DLD translator with/without the input $X$. The leak rate in the SLD design increases with larger temperature (at 37 °C, leak rates were measured at three different time windows), while the leak in the DLD design was not measurable in this experimental setup. The desired triggering signal with the input strand $X$ reaches more than $75\%$ completion before the first measurable data point. [Because the samples are otherwise identical, we assume that, before addition of the trigger, the triggered samples had initial fluorescence levels no higher than the untriggered samples. A slight decrease in the SLD signal with input at 37 °C during the first hour appears in some experiments (SI Appendix, Fig. S1A).] Species concentration: [reporter] = 400 nM; [fuels] = 350 nM; [input $X$] = 350 nM. Time 0 represents the moment that the first data point was measured; the inputs are added no more than 3 min before measurement at 25 °C and no more than 13 min before measurement at 30 °C and 37 °C.

For the SLD translator, when increasing the temperature from 25 °C to 37 °C, the leak rates significantly increase (from 0.009 to 0.296 nM/min in the first hour), which is likely due to increased fraying. In contrast, the leak rate in the DLD design is too slow to be measurable in this experiment setup. To demonstrate the generality of the DLD design, these results are successfully replicated on a different set of sequences (SI Appendix, Fig. S1).

Note that the baseline of the leak is higher in the SLD experiments. This so-called “initial leak” (13) is thought to be due to some small fraction of truncated complexes caused by imperfect sequence synthesis or misfolded complexes. Because of the redundancy, it is less likely that a short truncation would result in leak in the DLD design (SI Appendix, Fig. S2).

We would like a robust strand displacement system that is not prone to leak even at high concentration, which enables fast kinetics. Going beyond the low-concentration regime that underlies previous theoretical work (41), we increased the concentration of each fuel species to 10 $\mathrm{\mu }$M, which is up to two orders of magnitude higher than the usual concentration used previously. We also increased temperatures, since higher temperature incurs a greater probability for fraying and thus, provides a more stringent test. Fig. 6A compares the leak kinetics of the SLD and the DLD translator in the absence of input strand at 37 °C. At 10 $\mathrm{\mu }$M initial concentration of fuels, leak of the SLD translator saturates after 4 h, and it reaches one-half of the maximum within 30 min. Note that the reaction of $Y$ with the reporter is reversible, despite being strongly biased forward, and therefore, after the initial kinetic phase of the leak, the system reaches thermodynamic equilibrium where the reporter molecules are not fully triggered. The leak fraction ([leak]/[initial fuel]) of the SLD translator after 10 h ranges from 24 to 41%, while that of the DLD translator is below 2% for all different initial fuel concentrations over all 10 h.

Fig. 6.

Kinetics of the leak for (A) the SLD, (A and B) the DLD, and (B) the TLD translator in the absence of input at high concentration. In the timeframe of 10 h, the leak fraction in the DLD translator remains below 2%. (B) The DLD leak kinetics is the results zoomed in from A. Although the DLD leak kinetics is still measurable, the TLD translator did not show apparent leak even when the concentration is 10 $\mathrm{\mu }$M. The negative values are numerical artifacts that arise due to differences of small noisy values during normalization. The dotted lines show simulation traces of the kinetic model (SI Appendix, Table S1) of the leak in the DLD translator. The first phase reflects $Y_{complex}$ reacting with reporter and emits leak signal. The second phase reflects $Y_{complex}$ slowly isomerizing to other possible configurations, which can also react with reporter and emit leak signal. Initial leak is accounted for by fitted concentration offsets. Species concentration: (light blue) [fuels] = 10 $\mathrm{\mu }$M, [reporter] = 11 $\mathrm{\mu }$M; (red) [fuels] = 5 $\mathrm{\mu }$M, [reporter] = 6 $\mathrm{\mu }$M; (dark blue) [fuels] = 2 $\mathrm{\mu }$M, [reporter] = 3 $\mathrm{\mu }$M; and (yellow) [fuels] = 1 $\mathrm{\mu }$M, [reporter] = 1.2 $\mathrm{\mu }$M. These experiments were conducted at 37 °C. The inputs are added no more than 13 min before measurement.

Our theoretical framework argues that the leak reduction of the DLD design is due to the entropy penalty manifested as unimolecular reverse reactions that undo leak intermediates rather than a result of the increased length of the double-stranded region stabilizing the fuel complexes. The results shown in SI Appendix, section S5 confirm that increasing the size of the bound domains in SLD fuel complexes to be the same as in the DLD scheme (the Long SLD scheme) does not decrease leak as much as the DLD scheme—the leak concentration after 10 h of the DLD scheme is still an order of magnitude smaller than that of the Long SLD scheme. Note that the Long SLD scheme requires longer strands than the DLD scheme, which is more expensive, especially for larger systems.

The leak kinetics of the DLD translator is compared with the TLD translator in Fig. 6B. The DLD leak shows two-phase behavior, which we discuss in Quantitative Model of Leak Reduction. As expected, the TLD translator shows an even greater degree of leak reduction, with no apparent leak even at high concentration (10 $\mathrm{\mu }$M) for 10 h.

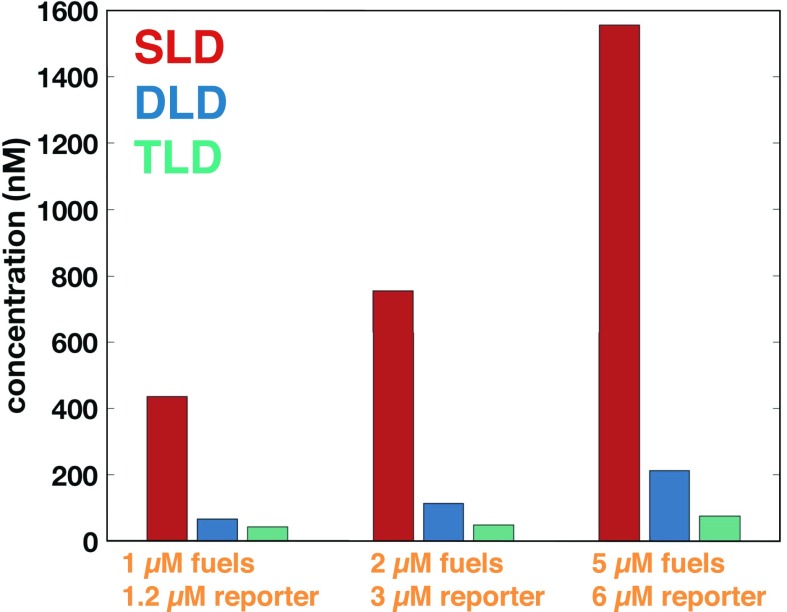
We further confirmed the theoretical prediction that the total amount of leak in a single-translator plus reporter system at thermodynamic equilibrium is lower in the DLD or the TLD schemes compared with the SLD scheme (Fig. 7). Leak concentration at thermodynamic equilibrium is an upper bound on the total leak that would ever be observed in the system. To reach thermodynamic equilibrium, the fuels and the reporter are slowly annealed for 18 h, and the fluorescence is subsequently measured. The annealed leak signal of the DLD design is approximately six times less than that of the SLD design. The TLD design has the least amount of total leak: when the fuel concentration is $5\hspace{0.17em}\mathrm{\mu }$M, the TLD leak concentration is 20 times less than that of the SLD design. It is interesting that the kinetic decrease in leak seems more significant than the leak reduction at thermodynamic equilibrium.

Fig. 7.

Leak concentration of a single translator at thermodynamic equilibrium, which sets an upper bound on the leak producible in the corresponding kinetic experiment. We drive the system to thermodynamic equilibrium by slowly annealing (0.06 °C/min) the fuels and the reporter for 18 h from 90 °C to 25 °C.

Although the design principles demonstrated in this paper were effective in reducing leak, we did observe an undesirable property in the TLD scheme: the amount of output released was less than the amount of input provided [e.g., about 75% when fuels were initially 5 $\mathrm{\mu }$M (SI Appendix, Fig. S9)]. A possible mechanism that could explain the decrease of the completion level, and which could only occur in designs with redundancy $N\ge 3$, is presented in the SI Appendix, Fig. S10.

Quantitative Model of Leak Reduction.

The thermodynamic analysis of the previous section can be quantitatively calculated by NUPACK (45) for the specific sequences that we used. The NUPACK energy model takes into account both the free energy of binding as well as the free energy of association. The predicted concentration of the leak products at equilibrium for the SLD translator is close to experimental data (SI Appendix, Fig. S3). For the DLD translator, however, NUPACK predicts an order of magnitude less leak than experimentally observed (SI Appendix, Fig. S4). This discrepancy could be because (i) NUPACK ignores coaxial stacking and only roughly approximates the dangle energies of nucleic acids or because (ii) NUPACK disregards strand configurations with pseudoknots, which could also be stable at equilibrium.

Apart from the thermodynamic property, we studied the mechanism of the kinetic behavior. Consistent with the leak mechanism shown in Fig. 3, most of the leak involves the interaction between both of the fuels and the reporter (SI Appendix, Fig. S5). We observed that there is an unexpected two-phase kinetic behavior in the DLD translator (Fig. 6B). During the first 15 min, the leak signal quickly increases with saturating kinetics (first phase) and then continues to slowly increase at a roughly constant rate over the next 10 h (second phase). (Note that the first-phase kinetics is different from the initial leak discussed above.) To investigate the source of the second phase, we found that the leak rate of that phase does not depend on the reporter concentration (SI Appendix, Fig. S6). Considering the structure of $Y_{complex}$, it is possible that it can reconfigure to other isomers through four-way branch migration (SI Appendix, Fig. S7), which could also be detected by the reporter. Since initiation of four-way branch migration is slow ($\sim 10^{-3}$ s⁻¹) (46), this may be the rate-limiting step and may explain why the overall leak rate of the second phase does not depend on reporter concentration.

The kinetic model that we proposed based on this analysis (SI Appendix, section S1.6 and Table S1) fits the kinetic data well (Fig. 6B) and captures the timescales of the two-phase kinetics. In the model, the leak pathway is that the fuel species $F1$ and $F2$ react through toeless strand displacement and form $Y_{complex}$, which can quickly dissociate back or slowly isomerize to other configurations. Both the $Y_{complex}$ and its isomers can be detected by the reporter. The quantitative model is consistent with the intuitive picture of leak reduction in the DLD scheme in that $Y_{complex}$ is much more likely to dissociate back before interacting with the reporter, even at 1 mM concentrations. Note that there may exist other leak pathways (e.g., $F2$ reacts with reporter first, and they form a complex; then, $F1$ invades, producing leak signal), and the real leak could be caused by a combination of all possible leak pathways. The model provided here shows one possible pathway and suggests that, although the species $Y_{complex}$ could quickly reverse back to the original fuel species, it can also be trapped in the leaked state through reconfiguration. Designing a leakless system with no trapped leaked state remains an open problem.

Our model of leak described in the previous section associates leak with the formation of certain large DNA complexes. Indeed, PAGE analysis (SI Appendix, Fig. S12) shows that, to produce a leaked signal, a complex with large molecular weight is formed in the DLD design of size consistent with the leak products in our model.

Cascade and OR Circuit.

We applied the DLD leakless design to a translator cascade containing eight fuel species (four translators), which translates the input strand $A$ to the output strand $E$ via a sequence of intermediate output strands (Fig. 8A). Fig. 8B shows the desired triggering kinetics as well as the leak of the system. We adjusted the depth of the translator cascade by including different length portions of the cascade (e.g., $F5,\dots ,F8$ can translate signal strand $C$ to $E$ through intermediate signal $D$, and this system has two layers of translation). The reporter reacting with the final output signal $E$ is set as a positive control. At 25 °C, for all cascade depths, the desired triggering is fast and reaches half-completion within 3 min from the time that inputs are added (Fig. 8B). Leak increases with the depth of the cascade, but after 100 min (as plotted), the leak fraction ([leak]/[initial fuel]) of even the longest cascade is less than 4%. After 10 h, the leak fraction is only 5% (Fig. 8B, Inset). To show the robustness of the system, we also conducted experiments at 37 °C with twice the initial concentration of fuel and input compared with that at 25 °C: the desired triggering signals reach half-completion at the first measured data point. While leak becomes more apparent, the leak fraction is still smaller than 9% even after 10 h (SI Appendix, Fig. S15). These results suggest that we can construct complex circuits with reduced leak and that their robustness will allow us to successfully operate at high concentrations and achieve fast kinetics.

Fig. 8.

DLD linear translator cascade. (A) Scheme of a four-layer translator cascade with nine steps of strand displacement implemented with eight fuel complexes and a reporter. (B) Kinetics of the desired reactions in the presence of input and the leak reactions in the absence of input. We tested different depths of the cascade by including a different subset of fuels. In each case, the desired reaction reached half-completion at the first measured data point. In the timeframe of 100 min, the leak fraction ([leak]/[initial fuel]) is less than 4%. (Inset) Leak of the translator cascade over 10 h. The largest leak fraction is roughly 5%: [reporter] = [fuels] = 500 nM, [input] = 250 nM, 25 °C. The inputs are added no more than 3 min before measurement.

To demonstrate the potential for reducing leak in more complex computation, we used the DLD leakless design to engineer a circuit composed of OR gates. Since one contiguous sequence could not represent the sequence space, we generated the individual signal sequences one by one (SI Appendix has more information on sequence design). A two-input logic OR gate produces output signal if at least one input signal appears. An OR gate can be constructed by putting two translators in parallel: two translators translating two independent input signals to the same output signal. Fig. 9A shows the construction of a three-layer OR circuit consisting of 10 translators (20 DLD fuel complexes) that can accept six independent input signals. The produced output signal is detected by a downstream reporter. In digital circuits, signal restoration methods are used to decide whether a logic gate outputs logic zero or one; analogously, here we cap the output signal by using a smaller concentration of the reporter than of fuels and inputs. Fig. 9B shows the kinetics of the positive triggered signals and nontriggered signal, where output value one represents fully triggering the reporter. Five of six triggered signals reach half-completion at the first data point. It takes at most 10 min for all of the triggered signals to reach 80% completion. In the 100-min timeframe, leak is less than 5% of the output signal. The same experiments with a lower concentration of the fuels and the input species were conducted (SI Appendix, Fig. S16). Even after 10 h, leak maintains a low level (less than 4%). In this timeframe, leak is mainly composed of the initial leak, and the total leak amount is around 2.8% of the concentration of fuels. These results suggest that the DLD design can be used for constructing fast, robust, and large-scale logic circuits.

Fig. 9.

DLD OR circuit. (A) Scheme of a three-layer DLD translator cascade with seven layers of strand displacement implemented with 20 fuels and a reporter, accepting six independent inputs. (B) Kinetics of the OR circuit with and without input signals. Output value 1 corresponds to fully triggering the reporter. Five of six desired triggering signals reach half-completion at the first measured data point, and all of six desired triggering signals reach 90% completion within 15 min (vertical dashed line). Leak is less than 1.5% in the first 15 min [input] = [fuels] = 1 $\mathrm{\mu }$M, [reporter] = 500 nM, 25 °C. The inputs are added no more than 3 min before measurement.

Discussion

DNA strand displacement cascades have enabled the bottom-up construction of sophisticated interacting molecular machines (3–11, 13, 16–18, 20, 22–25, 47, 48). Emergent from the programed interactions of DNA complexes are functionalities, such as signal amplification, oscillation, digital and analog computation, distributed computation, control of self-assembly processes, and performing robotic tasks. However, the operation of DNA strand displacement is still hindered by system errors. In the applications of computer science and electrical communication, error correction paradigms based on redundancy include error correction codes for communication (28), Von Neumann multiplexing to perform accurate computation despite logic gate errors (29), and various error reduction methods based on repeated execution of probabilistic algorithms (49). Closer to our work, redundancy-based proofreading significantly reduces the error rate in algorithmic self-assembly by requiring multiple erroneous steps to occur in sequence (30).

Inspired by the error reduction methods exploiting redundancy, we have developed a systematic method capable of reducing leak to arbitrary low levels and experimentally tested the chemical error correction method. Strand displacement systems designed by the leakless method in this paper have shown remarkable behaviors combating errors: at concentrations as high as 10 $\mathrm{\mu }$M (up to 100 times higher than the concentrations of current strand displacement systems), the leakless design could decrease leak to a level that was not apparently measurable, even at temperatures at which leak in standard designs becomes unmanageable. Moreover, the systems using the leakless design are not only kinetically robust but also, less prone to leak even after remaining inactive for as long as possible—the thermodynamic leak concentration, which is the upper bound of the system (leak reaches equilibrium), is significantly less than that of the traditional design. Beyond the simple translator system, we successfully engineered a linear translator cascade and an OR circuit with negligible leak and fast desired kinetics. The underlying leakless mechanism, which could be explained in terms of both thermodynamics and kinetics, provides an insight for the future development of the design of strand displacement systems. It is still a challenge to apply the leakless mechanism for systems other than translators, such as AND gates, which require a gate to take two signal strands simultaneously as inputs.

Apart from leak, other problems, such as imperfect DNA synthesis or the difficulty of ensuring matching stoichiometry between complementary strands, could also contribute to the lack of robustness in strand displacement systems. Errors during chemical synthesis (50) are thought to contribute to initial leak (5), and excess unpaired fuel strands are likely to cause undesired reactions with other species. Mobility-based purification protocols currently used cannot completely eliminate these issues, but more advanced purification methods (51, 52) and synthesis by enzymes (53) might improve performance. Despite these remaining challenges, which are especially important for certain applications of enzyme-free strand displacement circuits, such as the detection of minute quantities of a known target sequence by exponential feedback amplification, our solution of the leak problem already overcomes the main barrier to feedforward circuits with order of magnitude improved performance.

Specifically, our results suggest that, through this design principle, it is possible to achieve more complicated, more robust, more intelligent, and faster molecular systems with the capability of decision making or changing its state according to the outside environment. Currently, the largest strand displacement circuits were executed at 50 nM and complete on the order of 10 h (10). It is possible that the same computation could complete within a few minutes if the design of the strand displacement system is robust to leak and the reactants are safely kept at high concentration, such as 1 $\mathrm{\mu }$M.

Recent advances in molecular programing have shown that enzyme-free strand displacement systems can be adapted to low-cost and point-of-care diagnostics, but the background noise caused by leak limits the sensitivity of nucleic acid detection (20). Our method could offer an approach for designing enzyme-free nucleic acid amplifiers for biological sequences with less background and thus, achieve a rapid and sensitive molecular detection alternative to PCR. However, the sequences that we used are short and unstructured, while biological sequences usually have significant intrinsic secondary structures, which could affect desired kinetic behavior (54) or impose sequence constraints and limit the design space. Despite these challenges, there is a body of work demonstrating strand displacement cascades with natural DNA and RNA inputs, including logic computation both in vitro (9) and in vivo (25), a molecular multigene classifier (21), regulation of cellular gene expression (26, 27), and in situ fluorescence imaging of mRNA expression (55). Destabilizing organic solvents (56) and the hybridization probe method (21) can be generally adopted to overcome secondary structure in strand displacement. We envision that, with these techniques, leakless architectures could be used to interface with biological sequences.

A variety of error correction strategies not based on redundancy have been identified in biology. For example, biological regulatory networks are usually robust to kinetic parameters, which are often attributed to feedback loops [e.g., in chemotaxis (57) and the circadian clock (58)]. Biological reactions are also often remarkably specific, with low rates of side reactions. In the kinetic proofreading model introduced by Hopfield (59), incorrect reaction products preferentially exit the reaction pathway, which increases the specificity. (Note that, in contrast to our strategy, kinetic proofreading relies on kinetics alone for error correction without affecting the thermodynamic equilibrium.) Understanding the full variety of design principles for robust molecular systems, including redundancy-based methods, provides testable hypotheses for analyzing natural regulatory networks and methods for systematically engineering complex reaction networks. It is possible to envision a near future where artificially designed molecular programs can achieve the robustness and complexity of natural systems (60).

Materials and Methods

All DNA sequences are listed in SI Appendix. DNA oligonucleotides were purchased PAGE purified from Integrated DNA Technologies. All fuel and reporter species were annealed at $40\hspace{0.17em}\mathrm{\mu }$M in $1\times$ TAE/Mg²⁺ buffer with 12.5 mM Mg²⁺. After annealing, the fuel species were purified using $12\%$ PAGE. Fluorescence kinetics experiments were performed after mixing all of the species.