Combined molecular dynamics and neural network method for predicting protein antifreeze activity

Significance

Antifreeze proteins offer a technologically underutilized approach for controlling the freezing of water, a process intrinsically important in broad areas, such as medicine, agriculture, and food engineering, among others. To harness this capability, a better understanding of the measurable properties involved and their quantitative contribution to the observed antifreeze effect is needed. Here, we present a physically motivated method for the prediction of antifreeze activity purely from simulation, opening routes for the design of computationally optimized antifreeze materials.

Abstract

Antifreeze proteins (AFPs) are a diverse class of proteins that depress the kinetically observable freezing point of water. AFPs have been of scientific interest for decades, but the lack of an accurate model for predicting AFP activity has hindered the logical design of novel antifreeze systems. To address this, we perform molecular dynamics simulation for a collection of well-studied AFPs. By analyzing both the dynamic behavior of water near the protein surface and the geometric structure of the protein, we introduce a method that automatically detects the ice binding face of AFPs. From these data, we construct a simple neural network that is capable of quantitatively predicting experimentally observed thermal hysteresis from a trio of relevant physical variables. The model’s accuracy is tested against data for 17 known AFPs and 5 non-AFP controls.

Antifreeze proteins (AFPs) have been identified from a variety of sources, including fish, insects, bacteria, plants, and fungi (1). The antifreeze activity of these proteins is characterized by the difference between the nonequilibrium melting and freezing points, referred to as thermal hysteresis ($\mathrm{\Delta }T$) (2). $\mathrm{\Delta }T$ values span a wide range from $<$1 K for most alanine-rich $\alpha$-helical AFPs in fish (3, 4) to more than 6 K in hyperactive threonine-rich $\beta$-helical proteins found in insects (5). At lower concentrations ($<$0.5 g/L), hyperactive AFPs greatly outperform more traditional antifreeze agents, making them of potential interest for use in medicine, agriculture, food processing, and surface protection (6).

The most widely accepted theory for the origin of $\mathrm{\Delta }T$ was put forward by Raymond and DeVries (7) in 1977. They postulated that AFPs first bind irreversibly to the surface of a nascent ice crystal. The ice surface is then forced to adopt an increased curvature as a cap grows between the bound AFPs. This increased surface curvature then depresses the freezing point through the Gibbs–Thomson (Kelvin) effect (8, 9):

$$\mathrm{\Delta }T={\alpha }_p\left(\frac{{\gamma }_{sl}{T}_m\nu }{\mathrm{\Delta }{H}_m}\right)\cos \theta /d.$$ [1]

Here, ${\alpha }_p$ is a geometric constant (two for cylindrical ice cap, four for spherical), ${\gamma }_{sl}$ is the ice–liquid surface tension, $T_m$ is the bulk freezing point, $\nu$ is the molar volume of ice, $\mathrm{\Delta }{H}_m$ is the molar latent heat of fusion, $\theta$ is the ice cap contact angle, and $d$ is distance between adsorbed AFPs. This theory has recently been supported via molecular simulation work by Naullage et al. (9), who accurately calculated $\mathrm{\Delta }T$ from $\theta$ and $d$ for a model system. Additionally, Kuiper et al. (10) confirmed that the binding of an AFP to the ice front is nearly irreversible in microsecond-long simulations, agreeing with earlier experimental evidence (11).

However, how does the AFP first recognize and bind to a small quantity of solid water in a vast reservoir of liquid water? Nutt and Smith (12) suggested that AFPs accomplish this feat by preorganizing a “quasi ice-like layer” of water on the ice binding surface (IBS) of the protein. This layer can then be easily incorporated into the growing ice crystal, binding the protein to the solid–liquid interface (12). Recent work by Hudait et al. (13) has shown that water near the IBS is not truly ice like, since its structural order is much lower than ice, but simulations do show that water near the IBS displays exceptionally slower hydrogen bond reorientation dynamics compared with other protein surfaces (14). The presence of slow hydrogen bond dynamics near the IBS was also confirmed experimentally by Meister et al. (15).

Despite a growing body of literature on the topic of AFPs, there has been little progress in successfully engineering new AFPs. Many studies have shown that single mutations often lead to decreased antifreeze activity, with the best-performing mutants often showing little to no advantage over the naturally occurring protein (16–19). In contrast, Marshall et al. (20) showed that the antifreeze activity of a commonly studied AFP, isolated from the spruce budworm beetle, could be enhanced by the addition of coils already found in the AFP. While encouraging, this technique relies on copying an existing structure, and therefore is not a viable route for designing improved antifreeze functionality. Similar efforts have been made by linking two AFPs together, but on a per mass basis, this showed very little improvement (21).

Development of nonbiological thermal hysteresis molecules has been similarly challenging. Synthetic polymers, while often good ice recrystallization inhibition agents, possess a $\mathrm{\Delta }T$ less than 1 K at relevant concentrations (22). Thermal hysteresis has also recently been observed with a red synthetic dye, Safranin, but its activity was found to be considerably smaller than the best naturally occurring AFPs (23).

Given the growing use of computation in materials design, the availability of a quantitative method for predicting AFP activity in silico would clearly be of interest. Since ice nucleation and freezing occur on time scales much too long for efficient simulation of molecular models of water, this task must be done in an indirect way. More than 15 y ago, Graether et al. (17) attempted to predict the antifreeze activity resulting from single mutations using a neural network (NN) approach. While the strategy was sound, their analysis was limited to the static properties of a single protein, yielding results that were not particularly accurate. A more general approach was undertaken by Doxey et al. (24), who managed to successfully separate AFP structures from non-AFP structures using the fraction of ordered surface carbons, but their method was only intended for classification and actually “scored” rather low-activity AFPs much higher than hyperactive AFPs.

To address this lack of an accurate and transferable method for predicting AFP activity in silico, we use molecular dynamics simulations to analyze the geometric properties of AFPs and the dynamics of the surrounding water. From these data, we construct both a linear model (LM) and an NN, and we demonstrate that the NN is able to accurately predict the activity of a wide variety of AFPs. Our results identify key parameters necessary for antifreeze activity and should be of use in designing antifreeze materials.

Results and Discussion

Experimental Data.

For this study, we attempt to include all available nonmutant AFPs that have both a structure deposited in the Protein Data Bank (PDB) (www.rcsb.org) and a published thermal hysteresis curve as a function of concentration. We also avoid any multisubunit or linked AFPs. As a result, we selected 17 proteins with a spectrum of antifreeze activities along with 3 non-AFPs containing exposed planar faces and 2 homologs (proteins with similar structure to AFPs but no known antifreeze activity) to be used as a control. The AFPs come from a wide variety of organisms (fish, insects, plants, bacteria, and fungi) and cover all basic classes of AFP (e.g., types I–III and hyperactive) (22).

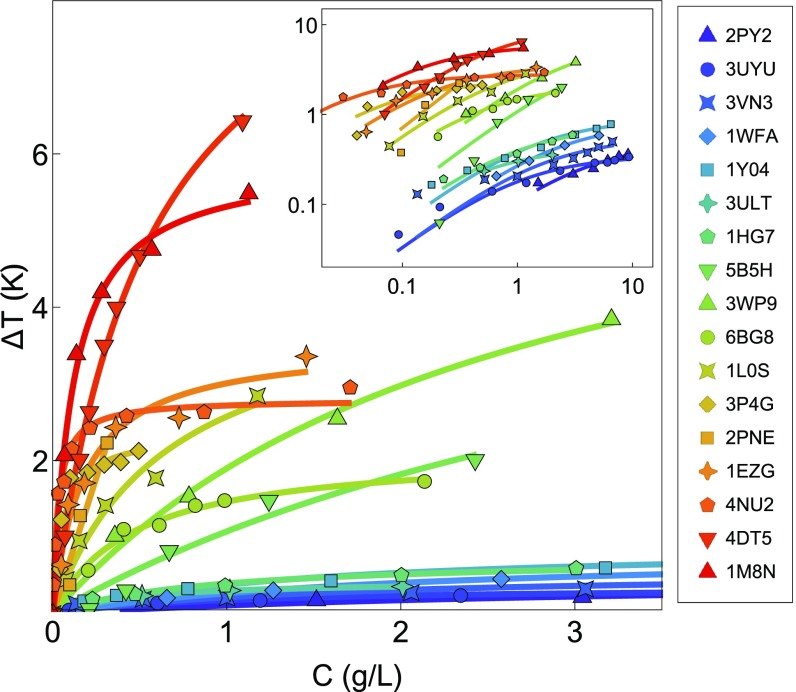
To avoid confusion with different isoforms, we reference the proteins by their PDB ID codes. Experimental data for $\mathrm{\Delta }T$ were collected from the literature and are shown in Fig. 1. We plot $\mathrm{\Delta }T$ as a function of mass concentration to ensure equal treatment between AFPs of different sizes.

Fig. 1.

Experimental thermal hysteresis ($\mathrm{\Delta }T$) as a function of mass concentration for 17 selected AFPs collected from the literature. Proteins are referred to by their PDB ID codes: 2PY2 from ref. 25; 3UYU from ref. 26; 3VN3 and 5B5H from ref. 18; 1Y04, 1WFA, 1HG7, and 3P4G from ref. 27; 3ULT from ref. 28; 3WP9 from ref. 29; 6BG8 from ref. 30; 1L0S from ref. 31; 2PNE from ref. 32; 1EZG from ref. 20; 4NU2 from ref. 33; 4DT5 from ref. 5; and 1M8N from ref. 34. Solid lines are fits to the data. Inset shows the full dataset in log–log representation.

Assuming a square lattice of adsorbed AFPs, Raymond and DeVries (7) suggested that the data could be fit with a function of the form

$$\mathrm{\Delta }T=\alpha C^{1/2},$$ [2]

where $\alpha$ is a constant and $C$ is the bulk concentration of AFP. While this form is acceptable for low-activity AFPs, it fits the data rather poorly for hyperactive AFPs. The same is true for the kinetic pinning model suggested by Sander and Tkachenko (35). Since a fitting function is still desired to avoid statistical error in the experimental data, we use an expression based on the Langmuir adsorption model (36):

$$\mathrm{\Delta }T=\alpha \left(\frac{KC}{1+KC}\right),$$ [3]

where $K$ is a constant. This model fits the data for all AFPs much better (solid lines in Fig. 1), but we emphasize that this is a phenomenological choice, not a rigorous derivation in this context. Additionally, our treatment (as well as Eq. 2) ignores the interesting sigmoidal behavior of AFP activity noted at extremely low concentrations (37). We consider this approximation quantitatively sufficient for all relevant concentrations and use it to compare $\mathrm{\Delta }T$ at a selected concentration.

Which Properties Characterize Antifreeze Activity?

To construct a predictive model, input variables must first be selected. We begin by assuming that a given AFP is characterized by two surfaces: the planar IBS, which faces into the ice crystal after binding, and the nonplanar, nonice-binding surface (NBS), which faces into liquid water and prevents additional ice growth. A detailed justification for this assumption is given by Knight and Wierzbicki (38). Next, we quantify the slow hydrogen bond dynamics (mentioned above) using a hydrogen bond lifetime, $L$ (defined below). Three variables were then chosen for our analysis.

• i)$A$: the area of the predicted IBS.
• ii)$L_B$: $L$ measured near the IBS.
• iii)$L_N$: $L$ measured near the NBS.

The logic for selecting each parameter is as follows. (i) The larger the area of the IBS, the more likely that contact with the ice will lead to binding and the greater the surface coverage will be. (ii) Slow hydrogen bond dynamics near the IBS has long been recognized as a signature of AFPs, and therefore, we hypothesize that AFPs with larger $L_B$ will be better able to recognize/bind ice. (iii) By the same argument, if $L_N$ is large, this indicates that the protein will be more susceptible to ice overgrowth on the NBS, destroying the antifreeze effect. Therefore, we expect $\mathrm{\Delta }T$ to be positively correlated with $A$ and $L_B$ and negatively correlated with $L_N$.

Work by Naullage et al. (9) suggests that bulkier AFPs should display increased $\mathrm{\Delta }T$. We, therefore, also tested the inclusion of the following variables: protein height, $H$; distance across the binding plane, $D$; molecular mass of the protein, $M_p$; and radius of gyration, $R_g$. The inclusion of these variables in the models discussed below did not significantly increase prediction accuracy and led to overfitting. As such, they are not considered in the following work. This is not to say that the bulkiness of the protein is irrelevant to antifreeze activity. It could be that $A$ captures this property appropriately or that bulkiness is less important at fixed mass concentration. Nevertheless, we provide the values of the variables in Table 1 in case this information could prove helpful to the reader.

Table 1.

Data for all 22 proteins used in this work

PDB ID code	Source	$M_p$ (kDa)	$N$	$N_B$	$H$ (nm)	$D$ (nm)	$R_g$ (nm)	$A$ (${\mathrm{n}\mathrm{m}}^2$)	$L_B$ (ps)	$L_N$ (ps)	LM $\mathrm{\Delta }{T}_C$ (K)	NN $\mathrm{\Delta }{T}_C$ (K)	Exp. $\mathrm{\Delta }{T}_C$ (K)
3CM4*	Non-AFP	7.50	60	8.00 $\pm$ 0.00	1.79 $\pm$ 0.16	1.84 $\pm$ 0.41	1.08 $\pm$ 0.01	2.05 $\pm$ 0.66	97.6 $\pm$ 5.55	98.1 $\pm$ 1.82	−0.08 $\pm$ 0.22	0.06 $\pm$ 0.12	0.00
3WHD†	Non-AFP	18.3	137	8.57 $\pm$ 0.53	3.03 $\pm$ 0.18	1.28 $\pm$ 0.21	1.48 $\pm$ 0.01	2.63 $\pm$ 0.35	111. $\pm$ 6.08	112. $\pm$ 2.42	−0.02 $\pm$ 0.13	0.00 $\pm$ 0.00	0.00
1AKI	Non-AFP	14.3	129	8.43 $\pm$ 0.53	2.82 $\pm$ 0.05	2.36 $\pm$ 0.29	1.42 $\pm$ 0.01	2.68 $\pm$ 0.25	103. $\pm$ 4.17	98.8 $\pm$ 1.52	0.30 $\pm$ 0.13	0.11 $\pm$ 0.06	0.00
1UBQ	Non-AFP	8.58	76	9.43 $\pm$ 1.51	2.01 $\pm$ 0.06	2.07 $\pm$ 0.45	1.17 $\pm$ 0.01	2.53 $\pm$ 0.65	117. $\pm$ 5.89	108. $\pm$ 2.76	0.27 $\pm$ 0.21	−0.00 $\pm$ 0.00	0.00
3Q6L	Non-AFP	16.9	131	9.57 $\pm$ 1.81	2.73 $\pm$ 0.34	2.17 $\pm$ 0.84	1.42 $\pm$ 0.00	2.98 $\pm$ 0.86	117. $\pm$ 2.61	126. $\pm$ 4.85	−0.25 $\pm$ 0.42	0.04 $\pm$ 0.02	0.00
2PY2	Fish	15.5	127	9.67 $\pm$ 1.63	2.70 $\pm$ 0.14	2.16 $\pm$ 0.27	1.36 $\pm$ 0.00	3.68 $\pm$ 0.86	125. $\pm$ 9.94	122. $\pm$ 2.40	0.49 $\pm$ 0.60	0.05 $\pm$ 0.10	0.03
3UYU	Fungus	25.2	231	9.14 $\pm$ 0.90	4.44 $\pm$ 0.70	2.28 $\pm$ 0.40	1.73 $\pm$ 0.01	2.62 $\pm$ 0.48	122. $\pm$ 2.40	122. $\pm$ 2.07	−0.08 $\pm$ 0.23	0.07 $\pm$ 0.03	0.08
3VN3	Fungus	22.5	222	12.4 $\pm$ 4.50	3.26 $\pm$ 0.45	1.60 $\pm$ 0.91	1.69 $\pm$ 0.00	2.82 $\pm$ 1.58	135. $\pm$ 5.79	125. $\pm$ 1.78	0.28 $\pm$ 0.69	0.34 $\pm$ 0.07	0.08
1WFA	Fish	3.24	37	12.7 $\pm$ 1.50	0.65 $\pm$ 0.13	1.05 $\pm$ 0.32	1.66 $\pm$ 0.01	3.23 $\pm$ 0.44	125. $\pm$ 6.67	115. $\pm$ 3.04	0.58 $\pm$ 0.29	0.09 $\pm$ 0.13	0.10
1Y04	Fish	3.09	35	11.7 $\pm$ 2.07	0.79 $\pm$ 0.23	1.05 $\pm$ 0.17	1.56 $\pm$ 0.04	3.14 $\pm$ 0.52	126. $\pm$ 8.88	105. $\pm$ 3.60	0.98 $\pm$ 0.42	0.32 $\pm$ 0.36	0.16
3ULT	Plant	27.6	114	12.4 $\pm$ 3.10	1.72 $\pm$ 0.02	1.68 $\pm$ 0.41	1.36 $\pm$ 0.00	3.37 $\pm$ 1.21	121. $\pm$ 11.3	92.6 $\pm$ 1.46	1.44 $\pm$ 0.24	0.98 $\pm$ 0.15	0.17
1HG7	Fish	7.14	66	8.14 $\pm$ 0.37	2.23 $\pm$ 0.16	1.67 $\pm$ 0.22	1.09 $\pm$ 0.01	1.96 $\pm$ 0.35	137. $\pm$ 18.8	122. $\pm$ 6.10	0.09 $\pm$ 0.68	0.33 $\pm$ 0.14	0.18
5B5H	Fungus	22.4	223	9.57 $\pm$ 2.51	3.32 $\pm$ 0.62	1.91 $\pm$ 0.58	1.70 $\pm$ 0.00	2.74 $\pm$ 0.92	138. $\pm$ 5.25	122. $\pm$ 1.90	0.47 $\pm$ 0.44	0.40 $\pm$ 0.10	0.36
3WP9	Bacteria	23.5	224	15.7 $\pm$ 1.60	3.32 $\pm$ 0.10	3.32 $\pm$ 0.20	1.67 $\pm$ 0.00	4.37 $\pm$ 0.38	145. $\pm$ 4.48	120. $\pm$ 3.00	1.54 $\pm$ 0.29	0.94 $\pm$ 0.30	0.70
6BG8	Bacteria	26.3	239	8.86 $\pm$ 1.07	3.52 $\pm$ 0.07	1.41 $\pm$ 0.22	1.75 $\pm$ 0.00	2.11 $\pm$ 0.26	140. $\pm$ 4.77	128. $\pm$ 2.29	0.00 $\pm$ 0.25	0.52 $\pm$ 0.07	0.84
1L0S	Insect	9.07	88	12.0 $\pm$ 1.73	2.16 $\pm$ 0.04	1.57 $\pm$ 0.26	1.14 $\pm$ 0.00	3.07 $\pm$ 0.56	133. $\pm$ 3.30	101. $\pm$ 1.58	1.36 $\pm$ 0.19	1.18 $\pm$ 0.25	1.34
3P4G	Bacteria	33.9	301	21.0 $\pm$ 3.61	2.86 $\pm$ 0.07	1.53 $\pm$ 0.41	2.40 $\pm$ 0.01	5.29 $\pm$ 1.44	163. $\pm$ 7.75	127. $\pm$ 1.83	2.26 $\pm$ 0.45	1.77 $\pm$ 0.32	1.98
2PNE	Insect	6.49	81	15.3 $\pm$ 2.75	1.05 $\pm$ 0.09	1.54 $\pm$ 0.26	1.38 $\pm$ 0.01	4.38 $\pm$ 0.65	149. $\pm$ 6.23	106. $\pm$ 4.58	2.24 $\pm$ 0.57	2.36 $\pm$ 0.85	2.13
1EZG	Insect	8.39	82	15.0 $\pm$ 2.08	1.46 $\pm$ 0.02	1.57 $\pm$ 0.28	1.17 $\pm$ 0.00	3.73 $\pm$ 0.48	107. $\pm$ 3.57	89.8 $\pm$ 1.51	1.28 $\pm$ 0.27	1.77 $\pm$ 0.24	2.22
4NU2	Bacteria	25.5	216	17.7 $\pm$ 1.50	3.16 $\pm$ 0.07	2.97 $\pm$ 0.56	1.65 $\pm$ 0.00	5.24 $\pm$ 0.35	136. $\pm$ 4.68	114. $\pm$ 1.59	1.91 $\pm$ 0.15	2.19 $\pm$ 0.13	2.54
4DT5	Insect	14.5	143	21.7 $\pm$ 2.63	1.43 $\pm$ 0.05	3.78 $\pm$ 0.44	1.56 $\pm$ 0.01	6.48 $\pm$ 0.75	136. $\pm$ 6.39	108. $\pm$ 3.06	2.71 $\pm$ 0.38	3.37 $\pm$ 0.49	3.43
1M8N	Insect	12.5	120	15.3 $\pm$ 0.75	2.18 $\pm$ 0.02	2.24 $\pm$ 0.32	1.34 $\pm$ 0.00	5.04 $\pm$ 0.54	150. $\pm$ 4.82	96.6 $\pm$ 1.13	2.96 $\pm$ 0.20	4.06 $\pm$ 0.23	4.28

M_p is the molecular mass of the protein. N is the number of solvent-accessible residues in the protein (defined in Materials and Methods), and N_B is the number of residues in the IBS. Height, H, is the maximum distance from the ice binding plane S (defined in the text) to the geometric center of any residue in the protein measured in the direction normal to S. The width of the IBS, D, is the minimum edge length of a rectangle that bounds all coordinates in S. R_g is the radius of gyration measured using the GROMACS 2016.4 tool gmx polystat. A, L_B, and L_N (defined in the text) are computed from molecular simulation. LM ΔT_C and NN ΔT_C are predicted values using the LM and the NN, respectively. Exp. ΔT_C at 0.3 g/L was interpolated from experimental data using Eq. 3. All errors are one SD.

^*Only the C-terminal domain of 3CM4 was used for the study.

^†Residue numbers 61–68 were excluded from PDB ID code 3WHD, as they are not part of the main backbone.

Automated Detection of the IBS.

The determination of the IBS is critical to our analysis. Since we intend our method for materials design, we keep this calculation as general as possible, selecting the IBS based on geometric requirements and the optimization of our three physical variables as described next.

For each protein, standard molecular dynamics simulations were performed as described in Materials and Methods. From the simulation data, an average protein structure composed of residue coordinates is generated, and a water–water hydrogen bond lifetime, $L_i$, is assigned to each residue (the procedure is described in Materials and Methods). The residues are then grouped into planes using the following procedure.

• i)Using any three noncollinear residues, define a plane $P$.
• ii)Identify a set $S$ of all residues within 0.11 nm of $P$.
• iii)If $S$ contains eight or more residues and all residues have at least two neighbors in $S$ within 1 nm, continue. Otherwise, discard the set. This ensures a connected set with a relevant number of residues.
• iv)Calculate the number of residues not in $S$ found above or below $P$, defined as $n_1$ and $n_2$. If $\text{min}\left(n_1,n_2\right)=0$, continue. Otherwise, discard the set. This effectively eliminates all planes “inside” the protein structure.
• v)Add set $S$ to the set of possible IBSs, $S_{all}$.
• vi)Repeat for all possible sets of three noncollinear residues.

For each $S$ in $S_{all}$, we then calculate $L_{S,B}$, the average of $L_i$ for all residues in $S$ weighted by the solvent-accessible surface area (SASA) of each residue, and $L_{S,N}$, being the same as $L_{S,B}$ but for all residues not in $S$. We also calculate $A_S$, which is defined as the area enclosed by the convex envelope containing the projection of all of the solvent-accessible atoms corresponding to the points in $S$ onto plane $P$—essentially the planar area of the IBS.

Since the scoring function is not known a priori, we choose the IBS simply as the $S$ that maximizes the expression

$$A_S^{*}+{\left(L_{S,B}-L_{S,N}\right)}^{*}.$$ [4]

Here, the asterisks denote that the value was normalized by the maximum of the respective quantity observed in $S_{all}$ so that all values can be compared on a one-to-one basis. $A_S$, $L_{S,B}$, and $L_{S,N}$ of the $S$ selected as the IBS then become $A$, $L_B$, and $L_N$, respectively, for the scoring functions described below. If no $S$ is found during evaluation (i.e., $S_{all}$ is an empty set), the protein can be considered a non-AFP and scored as having a $\mathrm{\Delta }T$ of zero. A schematic of this process is included in SI Appendix, Fig. S1.

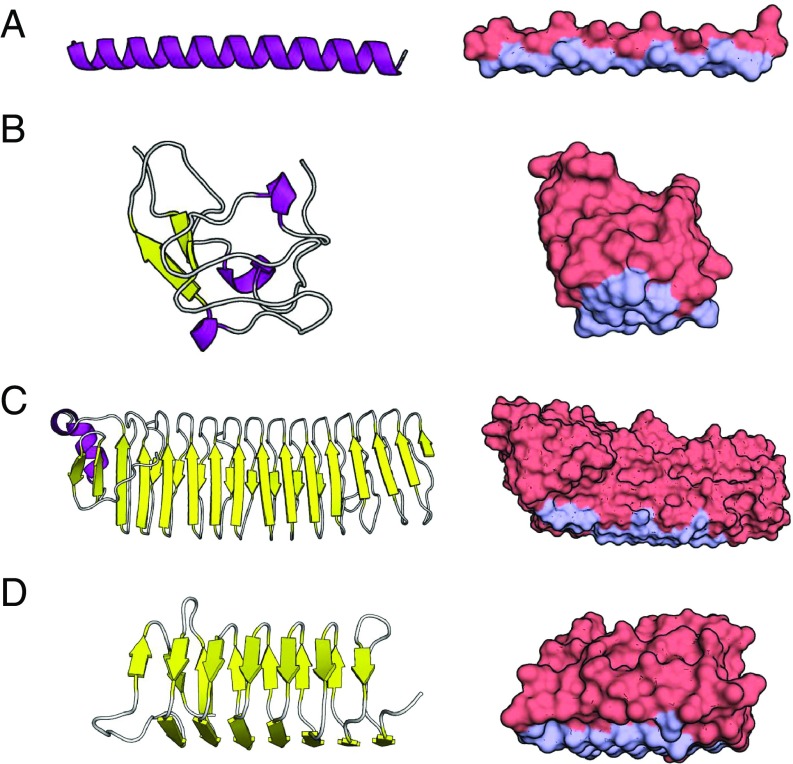
We note that the IBS predicted by our method shows excellent agreement with the IBS suggested by experiment and computationally by Doxey et al. (24). Fig. 2 shows a graphical display of the IBS for selected AFPs and additional details. This automated method successfully identifies the IBS based on geometry, and on the dynamic properties of water near the protein.

Fig. 2.

Secondary/tertiary structure (Left) and surface structure with the IBS shown in light blue (Right). (A) Protein ID code 1WFA. Type I $\alpha$-helical fish protein. Predicted IBS matches that identified by ref. 3. (B) Protein ID code 1HG7. Type III globular fish protein. Predicted IBS matches that identified by ref. 16. (C) Protein ID code 3P4G. Ca²⁺-dependent bacterial protein. Predicted IBS matches that identified by ref. 39. (D) Protein ID code 1M8N. Hyperactive AFP from the spruce budworm beetle. Predicted IBS matches that determined by ref. 40. Visualization done with PyMOL (41).

Predicting Antifreeze Activity Using an NN.

We measured our selected variables for each protein using 10-ns blocks from 30 to 100 ns for a total of 7 measurements per protein and 154 measurements overall. Averages are shown in Table 1. We first fit the data (excluding the two homologs) to the simplest possible equation, a linear combination:

$$\mathrm{\Delta }{T}_C=a_0+a_{1}A+a_2{L}_B+a_3{L}_N.$$ [5]

Here, $a_0$ through $a_3$ are fitted constants, and $\mathrm{\Delta }{T}_C$ is the experimental $\mathrm{\Delta }T$ evaluated at a concentration of 0.3 g/L using Eq. 3. This concentration was selected to avoid saturation effects (where $\mathrm{\Delta }T$ is nearly constant with increasing concentration) and extrapolating the data. While this treatment is somewhat biased against AFPs like PDB ID code 4DT5 that show better performance at higher concentrations, some compromise is necessary, since an accurate single-variable equation for $\mathrm{\Delta }T$ as a function of concentration is not available.

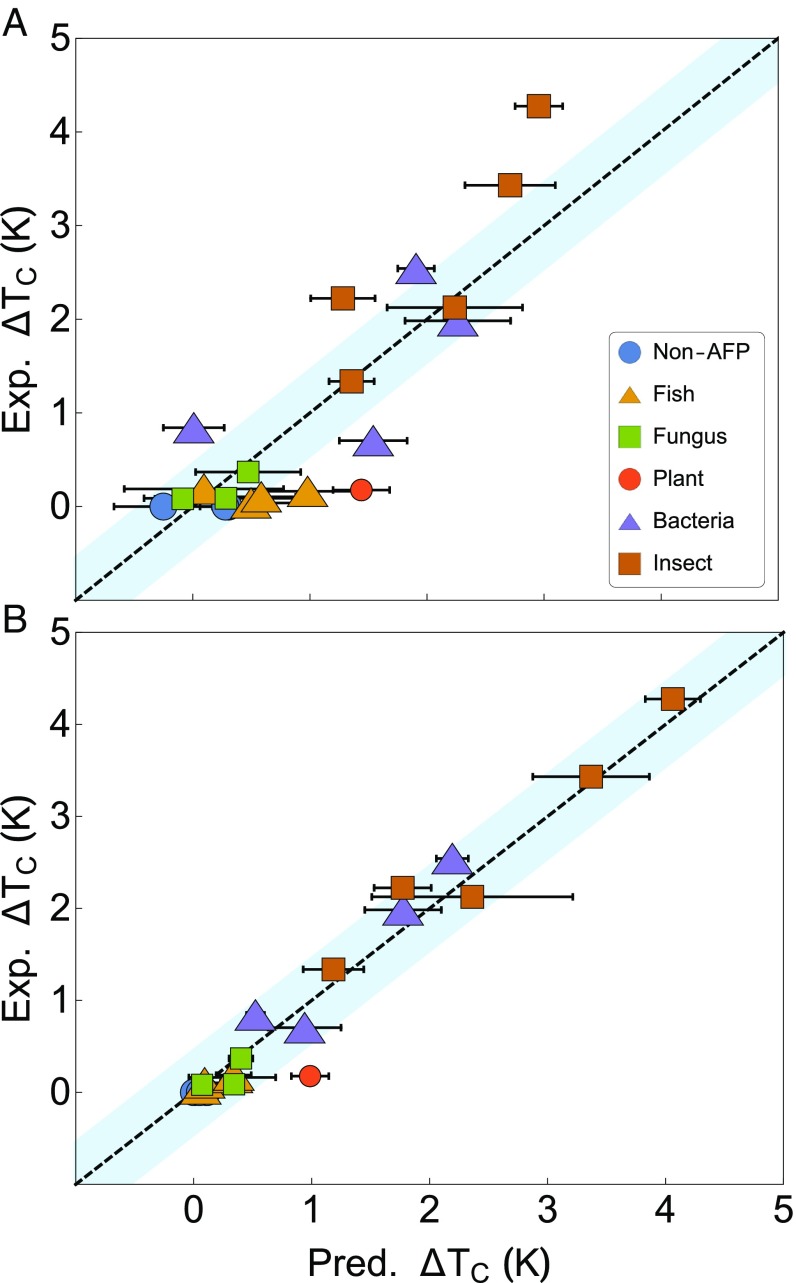
The results of this LM are shown in Fig. 3A, and the values of the fitted coefficients in Eq. 5 are as follows: $a_0$ = −0.167 K, $a_1$ = 0.456 K/nm², $a_2$ = 0.032 K/ps, $a_3$ = −0.0411 K/ps. The performance of the LM is quite mediocre, with a mean error from experiment of 0.51 K and a correlation coefficient of $R^2=$ 0.80. Clearly, Eq. 5 is not complex enough to accurately capture $\mathrm{\Delta }{T}_C$. We show it here, however, as it does exhibit an important qualitative insight: our coefficients match the physical intuition discussed earlier. $A$ and $L_B$ are positively correlated with $\mathrm{\Delta }{T}_C$, and $L_N$ is negatively correlated with $\mathrm{\Delta }{T}_C$.

Fig. 3.

$\mathrm{\Delta }{T}_C$ values predicted (Pred.) by (A) LM and (B) NN compared with values from experimental (Exp.) data in Table 1. Dashed lines are y = x, and the blue regions represent an error of $\pm 0.5$ K. Error bars represent one SD in the predicted value. Error is a result of uncertainty in the measured variables due to thermal motion.

Given the quantitative shortcomings of the LM, we turn to a non-LM in the form of an NN. The NN is trained on the same 154 data points as the LM. To minimize overfitting, we use a validation holdout set along with L2 regularization (42) and model averaging (43). Details are given in Materials and Methods. Fivefold cross-validation for the NN shows a mean deviation from experiment of 0.36 K, suggesting that the NN is quite robust. When trained on 70$\%$ of the data, the NN shows a mean error from experiment of 0.19 K and an $R^2$ of 0.97, a significant improvement compared with the LM. Results are given in Fig. 3 and Table 1. This NN is remarkable in its accuracy given the diversity of the proteins in the dataset and that it only requires three variables ($A$, $L_B$, and $L_N$) as input.

While the NN performs extremely well for almost all proteins in the dataset, it does struggle to accurately predict our one plant AFP, PDB ID code 3ULT (also known as Lolium perenne ice-binding protein, LpIBP), isolated from ryegrass. This error may be due to the lack of other plant AFP samples in the model, but interestingly, this is not the first instance where the ryegrass AFP has underperformed expectation. Work by Middleton et al. (44) showed that, while PDB ID codes 3ULT and 1EZG (an insect AFP; also known as Tenebrio molitor antifreeze protein, TmAFP) are very similar in structure, PDB ID code 1EZG exhibits a $\mathrm{\Delta }T$ more than 10 times that of PDB ID code 3ULT. Importantly, ice growth experiments in the same study showed that PDB ID code 1EZG binds to all ice faces, while PDB ID code 3ULT binds almost exclusively to the basal plane. This difference would not be captured by our model given that we make no distinction regarding which ice face the AFP prefers. Incorporating this information may lead to increased accuracy in future work.

As an additional test of the NN, we also score the two homologs in our dataset that were not included in any of the training procedures. The selected homologs are (i) the C-terminal domain of sialic acid synthase (PDB ID code 3CM4), which is a homolog of type III AFPs like PDB ID code 1HG7, and (ii) a C-type lectin (PDB ID code 3WHD), which is a homolog of type II AFPs like PDB ID code 2PY2. Both homologs were evaluated in the same manner as the rest of the AFPs and received $T_C$ scores of nearly zero (Table 1), confirming that the NN can discriminate even against AFP homologs.

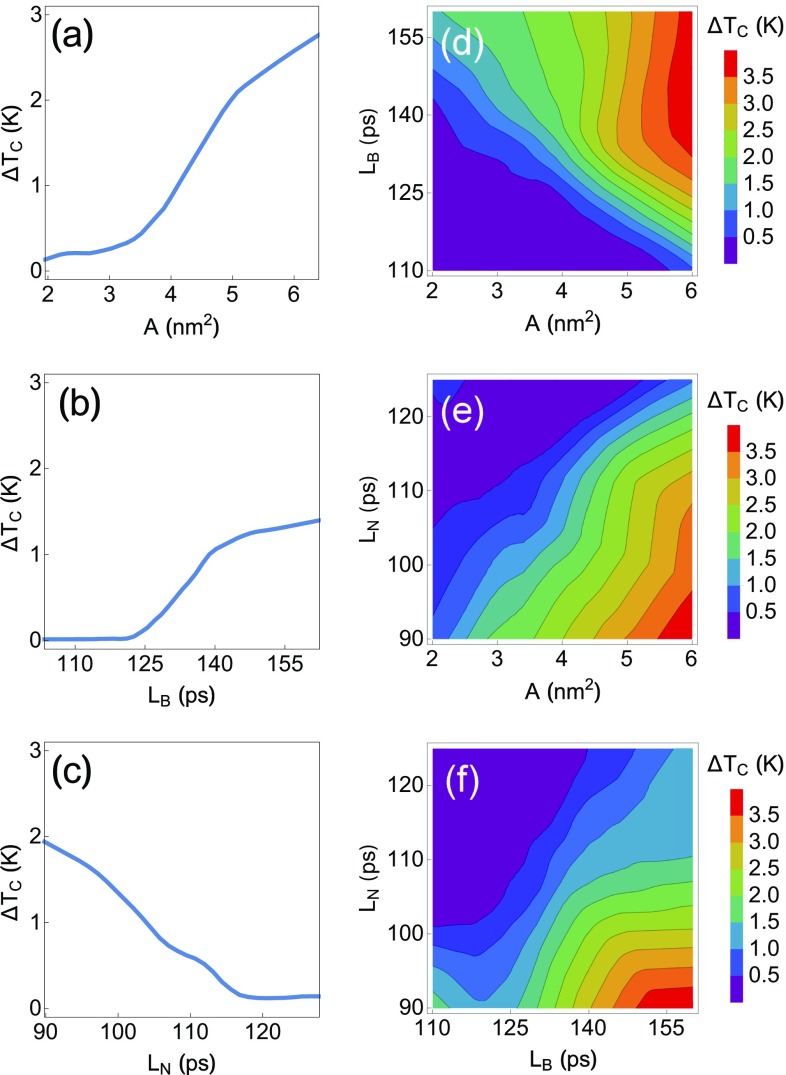
For a better understanding how the NN scores AFPs, we hold two of three variables constant at their average values in the dataset and vary the third. An effective trend for each variable is, therefore, calculated as shown in Fig. 4. Overall, the curves in Fig. 4 are very clear: $\mathrm{\Delta }{T}_C$ is positively correlated with $A$ and $L_B$ and negatively correlated with $L_N$, in agreement with the LM.

Fig. 4.

Average behavior of the NN: (A–C) holding two variables at their average value and (D–F) holding one variable at its average value ($⟨A⟩$ = 3.57 nm², $⟨L_B⟩$ = 131 ps, $⟨L_N⟩$ = 113 ps).

Importantly, the NN additionally shows that there are certain thresholds at which $\mathrm{\Delta }{T}_C$ changes dramatically with respect to the input variables. Moving from $A$ = 2 to 3.5 ${\mathrm{n}\mathrm{m}}^2$ results in very little change, but moving from $A$ = 3.5 to 5 ${\mathrm{n}\mathrm{m}}^2$ results in a nearly fourfold increase in $\mathrm{\Delta }{T}_C$. Similarly, for $L_B$ between 110 and 125 ps, $\mathrm{\Delta }{T}_C$ is roughly zero, but for $L_B$ between 125 and 140 ps, there is a significant gain in activity, which then slows after 140 ps. With respect to $L_N$, there is a nearly linear drop in activity with increasing $L_N$ until $\mathrm{\Delta }{T}_H$ is nearly zero at $L_N>115$ ps. We imagine that this information might be of use when deciding how to construct, run, and attain convergence of a computational design process. We also include the behavior of the NN as a function of two variables (holding the third constant at its average value in the dataset) in Fig. 4.

Conclusions

This work presents a straightforward and physically motivated method for predicting the antifreeze activity of AFPs from molecular simulation. The method supports current understanding that AFPs recognize and bind ice with a water layer defined by long hydrogen bond lifetimes near the IBS. We show that a simple NN produces quantitatively accurate predictions of thermal hysteresis. Furthermore, the NN suggests that short hydrogen bond lifetimes on the NBS are also quite important for producing high-activity AFPs. We hope that this information will aid in the development of advanced antifreeze materials.

Materials and Methods

Molecular Dynamics.

All molecular dynamics simulations were performed using GROMACS 2016.4 (45–48). Protein structures were obtained from the Research Collaboratory for Structural Bioinformatics (RCSB) PDB and solvated in at least 1.5 nm of water in all directions using periodic boundary conditions for a protein–protein self-image distance of at least 3 nm. Water was modeled using the Transferable Intermolecular Potential, 4-point, Ice (TIP4P/Ice) model (49) for its realistic melting temperature of $\sim$270 K (50), and proteins were modeled by the Amber03w force field (51) for its compatibility with four-site water models (52, 53). Additional details and comments on computational efficiency are included in SI Appendix.

Protein Structure Coordinates.

An average protein structure was first generated by averaging over atomic coordinates for the simulation window. This structure was then reduced to a set of $N$ residue coordinates using the geometric center of all atoms with an SASA $\ge$0.01 ${\mathrm{n}\mathrm{m}}^2$ in each residue. If a residue has no atoms with SASA $\ge$ 0.01 ${\mathrm{n}\mathrm{m}}^2$, it is eliminated. SASA is determined using GROMACS 2016.4 following the method of Eisenhaber et al. (54).

Hydrogen Bond Lifetimes.

We define a hydrogen bond lifetime, $L_i$, as the average time that it takes for the hydrogen bond autocorrelation function (${\mathrm{H}\mathrm{B}\mathrm{A}\mathrm{F}}_i$) to decay to 0.1. ${\mathrm{H}\mathrm{B}\mathrm{A}\mathrm{F}}_i$ was defined for water–water hydrogen bonds occurring between water molecules within 0.8 nm of any atom in residue $i$. HBAFs were calculated over 1-ns blocks and averaged over the sample simulation window. Calculations were performed using the Python package MDAnalysis (55, 56), which uses the definition provided by Rapaport (57). For a select few partially buried residues, there exist trapped water molecules that do not influence ice binding but nevertheless, drive $L_i\to \infty$. We, therefore, ignore any $L_i$ longer than 1 ns by setting it to zero.

NN.

The NN was trained using the machine learning suite in Mathematica 11.3 (58). It was composed of one three-node batch normalization layer, four fully connected hidden layers with six nodes each, and a final single-node output layer. Linear, Ramp, Linear, Ramp activation functions, respectively, were used for the hidden layers. A minimum of 10,000 training rounds using the ADAM algorithm (59) were used to minimize a mean squared error loss function. L2 regularization coefficient 0.01 was used for all training. Standard fivefold cross-validation was used to check performance (60). The final NN is an average of five separately trained NNs using different random samplings of 70$\%$ of the data, with the remaining 30$\%$ of the data acting as a validation holdout set to reduce the overfitting and error from outliers. Experimentation with larger/deeper NNs and more complex activation functions lead to worse cross-validation scores. A grid of points scored by the NN is included in Dataset S1.