Experimental accuracy in protein structure refinement via molecular dynamics simulations

Significance

Protein structures in atomistic detail are essential for a full understanding of biological mechanisms, yet high-resolution structural information remains unavailable for many proteins. Computational structure prediction aims to fill the gap but does not routinely provide models that reach experimental resolution. This study explores the conformational landscape between imperfect structure predictions and correct native experimental structures via molecular dynamics computer simulations. The results presented here demonstrate that structure refinement to experimental accuracy via simulation is indeed possible, but significant challenges are revealed that have to be overcome in practical refinement protocols.

Abstract

Refinement is the last step in protein structure prediction pipelines to convert approximate homology models to experimental accuracy. Protocols based on molecular dynamics (MD) simulations have shown promise, but current methods are limited to moderate levels of consistent refinement. To explore the energy landscape between homology models and native structures and analyze the challenges of MD-based refinement, eight test cases were studied via extensive simulations followed by Markov state modeling. In all cases, native states were found very close to the experimental structures and at the lowest free energies, but refinement was hindered by a rough energy landscape. Transitions from the homology model to the native states require the crossing of significant kinetic barriers on at least microsecond time scales. A significant energetic driving force toward the native state was lacking until its immediate vicinity, and there was significant sampling of off-pathway states competing for productive refinement. The role of recent force field improvements is discussed and transition paths are analyzed in detail to inform which key transitions have to be overcome to achieve successful refinement.

Modern biochemistry relies on the detailed understanding of molecular processes provided by the successes of structural biology. Except for membrane proteins, structural coverage of the majority of protein classes is comprehensive, at least in terms of the fold space utilized by nature (1, 2). On the other hand, apart from a few viruses, complete structural resolution of the proteins in any specific organism is still a distant goal. For extensively studied systems, a good number of structures are available in the Protein Data Bank (PDB) (3), but the vast majority of organisms have very sparse structural coverage. This situation is unlikely to change, as experiments are limited by challenges in sample preparation, data collection, and structure determination.

Computational protein structure prediction is an alternative to experimental structure determination. A conceptually simple approach is ab initio folding from extended chains to follow the folding process based on physical laws (4). This is feasible for the smallest proteins but at significant computational expense (5–8). A more practical method is homology modeling (9), where known structures with related sequence are used as templates to generate models for sequences without known structure (10). This approach works best when the sequence similarity between the template and target is high (10), but advanced methods can generate good models when there are only distant homologs (11, 12). Homology models typically capture the topology of a given protein but retain deviations from experimental structures with Cα coordinate root-mean-square deviations (RMSD) of 2 Å to 5 Å (13). This level of accuracy is only sufficient for some applications, e.g., to identify candidates for mutations in biochemical experiments. A higher level of accuracy is needed when structures are used as starting points for computational studies (14), for solving X-ray structures via molecular replacement (15), or for fitting cryo-EM densities (16).

Structure refinement methods aim at improving the accuracy of homology models toward experimental quality (17). A common approach is to initiate extensive conformational sampling from a given homology model to search for structures that are closer to the true native state and identify those via suitable scoring functions (18–26). Refinement is achieved when the sampling generates conformations closer to the native state and when the scoring protocol can discriminate such conformations (19). In practice, such a protocol works best when selected ensemble subsets are averaged to match the nature of experimental structures and reduce scoring function noise (27, 28).

Conformational sampling via molecular dynamics (MD) simulations based on atomistic force fields is an obvious choice for structure refinement (19, 28). The resolution of the atomistic model matches the resolution of experimental structures, and the general physics-based nature of the underlying force fields provides, at least in principle, universal applicability to any protein structure. First reports of the successful refinement of homology models via MD simulations emerged about a decade ago (29–31). Model refinement methods have been evaluated in blind tests during CASP (Critical Assessment of protein Structure Prediction) since CASP8, held in 2008 (32). Initially, refinement success was limited to a few cases, and there was a lack of consistency. In fact, in most submissions at that time, the quality of models deteriorated as a result of “refinement” (17). Since CASP10, MD-based refinement protocols have started to achieve more consistent structural improvements (33, 34), and such methods have become a key element in structure refinement protocols (20, 21, 23, 28, 35–41). Despite the progress, the overall degree of refinement, even with the best methods, has remained modest (17, 42). The structural accuracy of predictions is commonly assessed via GDT (global distance test) scores (43) in addition to Cα RMSDs. The GDT-HA (high accuracy) variant captures the average percentage of Cα atoms that can be superimposed within RMSD distance cutoffs of 0.5, 1, 2, and 4 Å. Current protocols can reliably improve initial models by a few GDT-HA units, and the refined models rarely decrease in RMSD by more than 1 Å (33). To achieve consistency, MD-based refinement protocols commonly apply positional restraints with respect to the initial homology models (28). Without such restraints, initial models tend to move away from the native state (44) without returning, even during simulations over 100 μs (40) and with enhanced sampling methods (24). However, the restraints also limit progress toward the native state.

Given that atomistic MD simulations can successfully fold proteins ab initio (7), it is puzzling that refinement of a model that is already close to the native state would be so difficult. It has remained unclear whether the MD simulations are limited by sampling and/or inadequate force fields when applied to the refinement problem or whether the refinement of homology modeling is inherently difficult due to the nature of the energy landscape between homology models and the native state.

Here, we describe results from extensive MD simulations followed by Markov state modeling (MSM) to reconstruct the conformational energy and kinetic landscapes between initial homology models and native states for targets from previous rounds of CASP to examine whether native states correspond to global free energy minima. Further analysis focused on the nature of the refinement paths and key kinetic barriers along such paths. The relation to folding transition pathways is discussed, and how the insight gained here informs the development of more successful refinement protocols.

Results

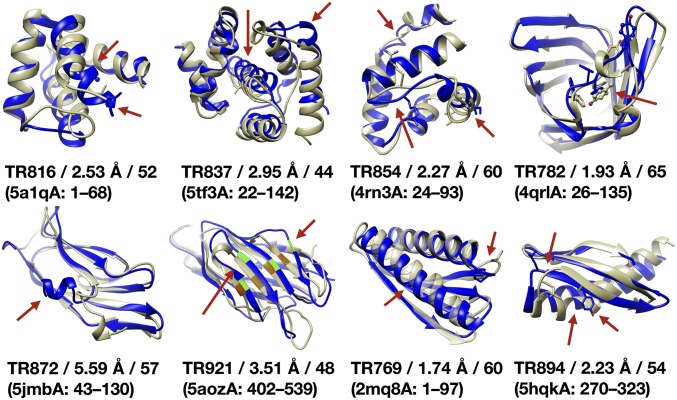
MD simulations were applied in combination with MSM analysis to explore refinement pathways from initial homology models to native states for eight small proteins that were refinement targets in previous rounds of CASP with moderate initial deviations and a variety of different fold types and modeling errors (Fig. 1 and SI Appendix, Table S1). The initial models deviated from the native structures by 1.7 Å to 5.6 Å Cα RMSD or GDT-HA scores of 44 to 65. For each system, unbiased simulations were started from the homology model and the experimental structure and then iterated by restarting from intermediate states until a single MSM connecting the native state and homology model was obtained (see Methods and SI Appendix, Table S2). While many types of conformational transitions have been studied via many different methods (45, 46), we chose the iterative sampling protocol based on unbiased simulations to study the refinement transition without having to make any presumptions about the pathway(s) or suitable progress variables.

Fig. 1.

Protein test set. Experimental structures (yellow) and homology models (blue) with CASP ID, PDB ID of the experimental structure, residue ranges, and deviations in Cα-RMSD and GDT-HA. Red arrows and stick representations identify modeling errors and key residues. For TR921, the highlighted residues M66, N75, D40, and E119 indicate alignment errors.

Markov State Model Generation.

Final Markov state models were built based on the total combined sampling for each system (between 15 μs and 56 μs). The conformational sampling was initially clustered into 40 to 200 microstates that were lumped into 11 to 50 macrostates based on lag times of 5 ns to 10 ns (SI Appendix, Fig. S1 and Table S3). On average, the pairwise similarity between macrostates was 2 Å to 3 Å RMSD. Uncertainties in the free energies of the macrostates were evaluated by 20-fold cross-validation from subsets of the MD trajectories to validate the MSM models (SI Appendix, Fig. S2). The majority of macrostates displayed little uncertainty in their free energies, implying that the Markov state models were converged and not biased by specific trajectories.

Initial and Native States.

The macrostates closest to the initial homology model and the experimental structure were considered as the MD-based “initial” and “native” states, respectively. The initial states deviated by about 2 Å RMSD from the homology models for the majority of systems (SI Appendix, Table S4). Larger deviations of 3 Å (TR854) and 5 Å (TR872) were due to significant rearrangements of the termini at the beginning of the simulations. Although restraints were not applied here, the initial states reflect largely what a restraint-based MD refinement protocol would achieve. The initial states deviated between 1.5 Å and 4 Å RMSD from the experimental structures, and, on average, the RMSD values were decreased by 0.1 Å and GDT-HA scores increased by 2.6 units over the initial homology models. There was no significant improvement in sidechain accuracy measured by global distance cutoff-side chain (GDC-SC) scores, which is analogous to GDT-HA but based on sidechain atoms (Table 1).

Table 1.

Energetics, kinetics, and structures from Markov state models of refinement landscapes

Target	Initial model*	Initial state* (MD†)	Native state* (MD†)	ΔΔG (native − initial),‡ kcal/mol	MFPT§/slowest transition, μs	Number of transitions¶
TR816	2.53/51.8/22.0	2.79/50.0/24.6	0.80/86.8/52.8	−2.46 (±0.02)	1.7/3.7 (5.1#)	5
TR837	2.95/43.8/21.1	3.93/36.0/16.7	0.88/80.2/55.1	−2.60 (±0.06)	43.4/33.1	7
TR854	2.27/60.4/28.2	2.69/66.8/31.8	1.04/80.0/45.7	−1.59 (±0.02)	1.5/1.0	3
TR782	1.93/65.2/37.1	1.99/66.8/36.2	0.94/86.4/55.4	−0.65 (±0.06)	39.6/31.0	5
TR872	5.59/56.8/38.1	2.98/67.9/43.1	1.97/79.8/55.8	−0.83 (±0.02)	2.9/2.2	2
TR921	3.51/48.4/27.1	3.32/54.2/30.4	0.90/87.3/57.8	−0.85 (±0.06)	637.9/623.0	15
TR769	1.74/59.8/33.0	1.47/65.5/35.2	1.14/72.4/41.2	−1.10 (±0.01)	0.8/0.5	2
TR894	2.23/54.2/23.6	2.49/54.2/24.8	0.85/95.4/54.2	−1.71 (±0.04)	6.0/3.9	5

^*Structure similarity between structures in Cα RMSD, GDT-HA, and GDC-SC.

^†Ensemble-averaged structures based on conformations for a given state sampled in the MD simulations.

^‡Free energy difference between the native and the initial state with SEs evaluated from 20 MSM iterations with 95% trajectory subsets.

^§Mean first passage time between initial and native state.

^¶Between initial and native states.

^#Alternate transition path.

The native states were about 1 Å RMSD from the respective experimental structures, with GDT-HA scores of 72 to 95 for all but one system (Table 1). For TR872, the native state was about 2 Å RMSD from the experimental structure, with a GDT-HA score close to 80. Given that the systems involve truncated structures and there is a possibility of crystal artifacts and other experimental uncertainties, it may be reasonable to consider models within 1 Å RMSD from the experimental structures or with GDT-HA scores of 80 or more to approach experimental accuracy. Moreover, sidechain accuracies were also improved as GDC-SC scores reached values of 41 to 56, reflecting almost native-like sidechain packing at the protein cores. This was achieved for all of the systems tested here. On average, the MD-based native states were improved over the initial homology models by 1.8 Å in RMSD, by 28.5 GDT-HA units, and by 23.5 GDC-SC units with respect to the experimental structures (Table 1).

Free Energy Landscapes.

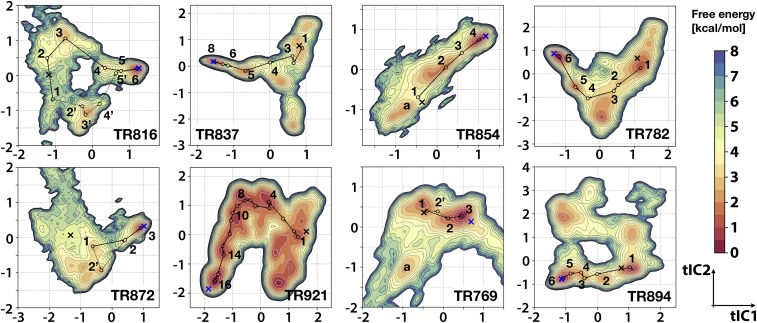
The free energy landscapes for each system, projected onto the first two principal components from time structure independent component analysis (tICA), are shown in Fig. 2. In all cases, there are a number of favorable states within 1 kcal/mol to 2 kcal/mol of each other (see SI Appendix, Fig. S2). The experimental structures are close to a major minimum in all of the systems. In contrast, the initial models are generally in regions with elevated energies, and, even when a favorable state is found near the initial model (e.g., for TR769, TR782, TR894), those minima have higher energies than the native state. Indeed, the native state was favored over the initial state in all systems by 0.65 kcal/mol to 2.60 kcal/mol (Table 1). Moreover, the native state was always found at the global free energy minimum relative to all other states (SI Appendix, Fig. S2). In half of the cases, there is a significant free energy gap of 0.5 kcal/mol or more to the state with the next highest energy (SI Appendix, Fig. S2).

Fig. 2.

Free energy landscapes and refinement pathways. Potentials of mean force projected onto the first two tIC principal coordinates according to the color bar. Contour lines are drawn for every 0.5 kcal/mol up to 8.0 kcal/mol. For TR816, TR872, and TR769, the maps focus on the major regions relevant for refinement. The entire maps for these systems are shown in SI Appendix, Fig. S3. Projections of the experimental structures and initial homology models are indicated with blue and black Xs, respectively. Refinement pathways and intermediate states identified from the MSM analysis are marked with arrows and numbered circles. Alternative pathways are indicated with dashed lines, and additional off-pathway states discussed in Free Energy Landscapes are labeled with lowercase letters.

Closer inspection of Fig. 2 suggests pathways between the initial and native states via a number of intermediate states. The intermediate states are energetically similar to the initial state or even higher in free energy in some cases (e.g., in TR816 and TR894). This indicates a rough energy surface where the transition from the initial homology model to the native state is not guided strongly by a downhill gradient. Furthermore, there are a number of off-pathway states with energies comparable to on-pathway intermediate states. These states are expected to distract sampling away from the native state in refinement applications where the experimental structure is not known.

Kinetics of Transitions from Initial to Native States.

The Markov state models allow the construction of transition paths and the extraction of kinetic rates between states. We focused the analysis on transitions from the initial to the native state to understand the kinetic factors of successful refinement. In all systems, multiple transitions were necessary to reach the native state from the initial state (Fig. 2 and Table 1 and detailed pathways in Fig. 3 and SI Appendix, Figs. S5–S20). Individual transition rates across the associated kinetic barriers and mean first passage times were generally on the order of microseconds, but the slowest transitions reached tens of microseconds for two systems (TR837 and TR782) and hundreds of microseconds for TR921 (Table 1). Most individual steps during the refinement transitions involve continuous increases in GDT-HA scores, but the largest increase in GDT scores often occur during the last transition to the native state (such as from states 5/5′ to 6 in TR816; Fig. 3). RMSD values generally decrease more gradually as the native state is approached (SI Appendix, Fig. S4). On the other hand, free energies do not decrease continuously for most systems, and, in many cases, an intermediate state with higher free energy than the initial state (e.g., 5′ in TR816) is visited along the path.

Fig. 3.

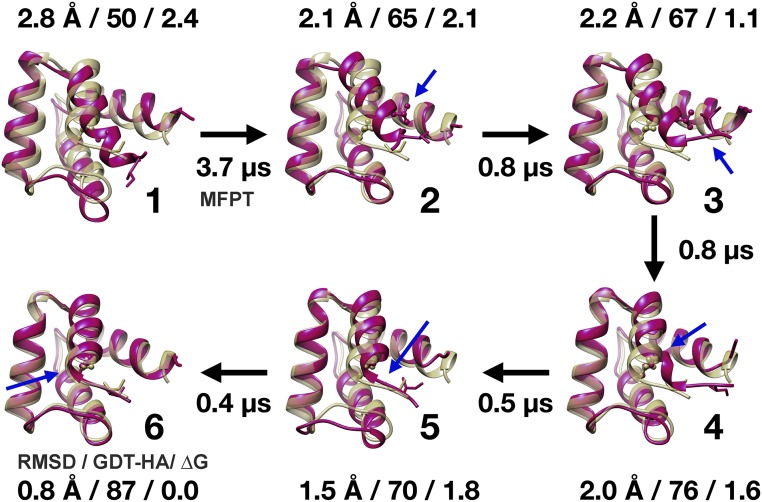
Refinement path transition in TR816. Ensemble-averaged structures for MSM states during refinement transitions (magenta) are compared with experimental structures (yellow) for one of two paths. The alternative path is shown in SI Appendix, Fig. S6. The numbering of states corresponds to the states identified in Fig. 2. Cα-RMSD values, GDT-HA scores, and free energies in kilocalories per mole are given for each state, and mean first passage times (MFPT) refer to transitions toward the native state. Blue arrows indicate key structural changes after each transition.

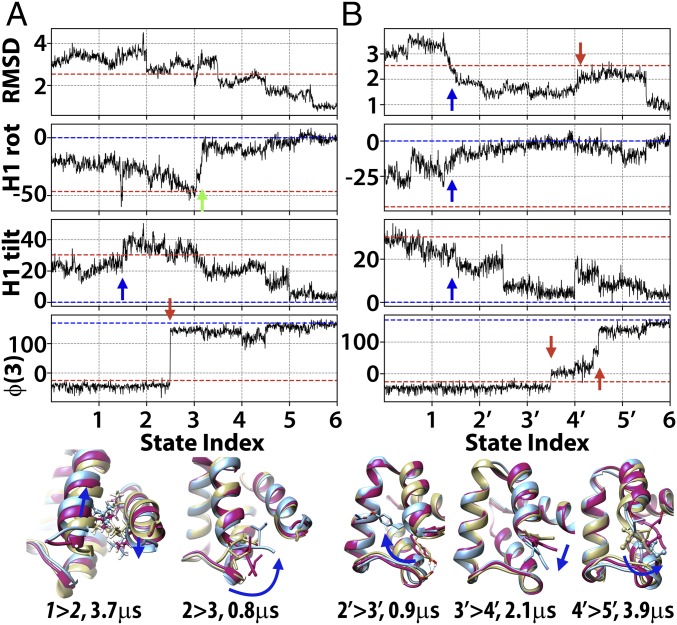
TR816 is discussed as a representative example (Figs. 3 and 4 and SI Appendix, Fig. S6). There are two significant errors in the initial model: (i) The N terminus helix is misoriented with incorrect hydrophobic interactions, and (ii) the helix at the N terminus extends too far. We found two major paths to address these errors via a number of conformational transitions. Along the first path (Figs. 3 and 4A), the N-terminal helix H1 first loses unfavorable incorrect hydrophobic interactions by tilting (1→2, blue arrow in Fig. 4A and Movie S1), the overpredicted part of H1 unwinds (2→3, red arrow in Fig. 4A and Movie S2), helix H1 rotates along the helix axis (3→4, green arrow in Fig. 4A), and subsequent relaxation repacks residues to the native state (4→6). The first transition takes the longest time because sidechains encounter steric hindrance when passing each other. The second transition requires a backbone torsion change but is less sterically hindered because the structure is partially opened up. In the alternative path (Fig. 4B and SI Appendix, Fig. S6), helix H1 finds its correct orientation first via a number of transitions (1→2′→3′, blue arrows in Fig. 4B and Movie S3), and the overpredicted helix then unwinds to a coil (3′→6, red arrows in Fig. 4B and Movie S4). The last transition incurs slow kinetics because multiple residues between H1 and the rest of the structure have to be rearranged. The coil region is interacting with a loop, and the loop hinders transitions. Therefore, it partially unfolds (to state 5′ where RMSD is increased, Fig. 4B) before refolding to overcome the energy barrier. The other systems followed similar sets of transitions (SI Appendix, Figs. S5–S20). Generally, the structural transitions necessary to refine the initial homology models can be classified as helix movements, α-helix and β-sheet extensions and dissolutions, loop and terminal reconfigurations of the backbone, sidechain flips, and overall relaxation involving simultaneous adjustments of several residues (SI Appendix, Fig. S21 and Table S6).

Fig. 4.

Structural transitions during refinement of TR816. Progress in terms of Cα-RMSD, rotation, and tilt angles of the N-terminal helix (H1, residues 4 to 15) with respect to the experimental structure, and φ backbone torsion for residue 3 along subsampled refinement trajectories. Two alternative paths are shown in A and B along states numbered as in Figs. 2 and 3. Key transitions are indicated with arrows. Dashed lines show values in the experimental structure (blue) and the initial homology model (red). Selected transition states are shown in molecular detail (magenta) with structures before (yellow) and after (blue). Colored arrows are referred to in Kinetics of Transitions from Initial to Native States. Additional details are shown in SI Appendix, Fig. S13.

Alternative Initial States.

Alternative initial models submitted for each of the targets during CASP (see Methods) were projected onto the free energy landscape diagrams (SI Appendix, Fig. S32). Most of the alternative models map onto the original energy landscape, but, in a few cases, models lie outside the originally generated landscapes. Outliers analyzed in detail (SI Appendix, Fig. S33) show deviations in secondary structure elements that may be due to sequence alignment errors. Since the reconfiguration of secondary structure elements incurs significant kinetic barriers (SI Appendix, Fig. S21), it is not surprising that these states were not reached in our simulations. On the other hand, these outliers are located farther away from the native state in the energy landscapes and are therefore not likely intermediates on the refinement pathways described in Kinetics of Transitions from Initial to Native States. A few initial models appear close to the native state when projected onto the tIC coordinates (SI Appendix, Fig. S32). The analysis of two such examples (SI Appendix, Fig. S33) suggests that the modeling errors present in the original initial models were largely absent in these models, but other modeling errors were present instead. Therefore, these models would require orthogonal refinement paths rather than being alternate states that could be reached easily from the original initial models.

Three alternative initial models were selected for each target to carry out additional simulations (see Methods). The resulting sampling largely overlapped with the previously generated free energy landscapes (SI Appendix, Fig. S34), and it resembled the first iteration started from the original initial model (SI Appendix, Fig. S35). In the cases where there was significant sampling outside the original free energy landscapes (e.g., TR769 and TR854), those conformations became unstable and unfolded partially. A combined Markov state model was constructed from the sampling with different initial models. This allowed us to estimate the relative free energies including the additional sampling (SI Appendix, Fig. S36). As before, the native state remained at the lowest free energy for all targets.

Refinement vs. (Un)folding Transition.

Additional sampling was also generated via high-temperature unfolding starting from the native state (see Methods). Interestingly, the initial unfolding pathways partially overlap with the refinement pathways, and, for most targets, sampling projected onto the tIC coordinates remained within the already sampled energy landscapes (SI Appendix, Fig. S37). In some cases, we find more significant deviations due to substantial unfolding, but the initial homology models were never reached. This suggests that the initial homology models are off-pathway with respect to the folding transition, although the final parts of the refinement pathways may overlap with folding pathways.

Discussion and Conclusions

Free Energy Landscapes During Refinement.

For small, single-domain proteins, protein folding transitions from extended to native states are believed to be guided by cooperative transitions involving few or no barriers on funnel-like landscapes (47). In contrast, the conversion of near-native homology models to native states appears to take place on rough energy landscapes where multiple native-like minima and significant kinetic barriers hinder conformational sampling. The presence of a significant number of native-like states with energies similar to the true native state has been described in earlier studies (48). In that work, the argument has been made that crystallization and/or ligand binding focuses native-like conformations onto the experimentally observed conformation. While that may also apply here, we found that unfolding trajectories beginning from the native states overlap only with part of the refinement landscape. Therefore, the rough energy landscape encountered during refinement may be away from the main folding funnel.

The sampling described here was focused on the space between the homology models and experimental structures. Therefore, the extent of a largely flat rugged energy landscape around the homology model could be even greater. However, at least with respect to possible alternative initial models for the targets studied here, the presented energy landscapes seem to cover the majority of accessible states. Alternative initial models were largely found to map onto the energy landscapes, and additional sampling from selected alternative models also largely overlapped with the already generated landscapes. Therefore, the presented energy landscapes are believed to be representative not just for the chosen initial model but also for likely alternative models.

In computational structure refinement, a rough landscape presents significant challenges. The existence of many competing off-pathway states explains why simulations started from homology models are often seen to deviate significantly away from the native state when restraints are not applied. Moreover, the time scales of the kinetic barriers even on the most direct path to the native state exceed the length of typical MD simulations applied during structure refinement for most of the systems studied here.

Importance of the Force Field and Rescoring with Other Functions.

A central question has been whether MD simulations would reach the native state if simulations are long enough to overcome the kinetic barriers. In other words, does the native state correspond to the lowest free energy with a given force field? For the systems studied here, this appears to be the case. To assess the importance of the force field, we compared free energies of the MSM states with reweighted energies based on older versions of the Chemistry at Harvard Macromolecular Mechanics (CHARMM) force field [c22/CMAP (49) and c36 (50)]. This analysis assumes that the overall conformational sampling remains the same with different force fields, and only the relative weights of different conformations are altered. We found that, with reweighted energies based on c36 (SI Appendix, Fig. S22), the native state remained energetically lower than the initial states but, for four systems (TR837, TR782, TR769, and TR894), the native state was not found at the global free energy minimum anymore. With c22/CMAP, the situation became worse. The native state also did not correspond to the lowest free energy for four systems (TR816, TR837, TR854, and TR872), and, in two of these cases (TR816 and TR837), the native state had a higher free energy than the initial state. While a more comprehensive test may be necessary to come to full conclusions, this analysis suggests that the quality of the force field is important and that the latest CHARMM force field, c36m (51), performs best among the CHARMM force fields. This is consistent with previous findings that improvements in force fields benefit protein structure refinement (35, 38).

Although the native state was found at the free energy minimum for the systems studied here, this may not always be the case, even with the best force fields. Moreover, reliable free energy estimates require multiple transitions to and from the native state (and other states), while it may be difficult enough to reach the native state just once in blind refinement applications. Therefore, we tested whether scoring functions could also identify the native state without having to rely on free energies estimated directly from the MD sampling. We applied molecular mechanics generalized born/surface area (MMGB/SA)-type scoring functions based on CHARMM (c36m, c36, and c22/CMAP) and Amber (ff14sb) force fields as well as the statistical potentials random walk plus (RWplus) (52) and dipolar distance-scaled, finite ideal-gas reference (dDFIRE) (53). For most targets, the lowest scores correlate indeed with the lowest RMSD structures (SI Appendix, Figs. S23–S30), so that native-like structures could be identified just based on scoring. As alternative initial models have higher relative free energies, the sampled conformations also have higher RWplus scores (SI Appendix, Fig. S38). The MMGB/SA and statistical potentials perform similarly well, but the statistical potentials generate a more pronounced energy gradient away from the native state that would be helpful during refinement to guide progress toward the native state. We did, however, find only moderate correlation between scores averaged over MSM states and the MD-based free energies with correlation coefficients of 0.32 to 0.37 for the force field-based MMGB/SA scores and 0.24 with the statistical potentials (SI Appendix, Table S5). The correlation was highest with the recent CHARMM c36m and Amber ff14sb force fields, again indicating the benefit of recent force field improvements.

Implications for Practical Refinement Applications.

It appears that protein structure refinement of homology models to experimental accuracy via MD simulations is indeed possible. For all of the systems studied here, we found direct paths from initial homology models to states close to the experimental structures, and those states corresponded to the lowest free energies. Therefore, it appears to be simply a matter of time before regular MD simulations can reach sufficiently long time scales to refine homology models to experimental accuracy. In the meantime, the practical question is whether one can develop more effective refinement protocols with more moderate computer resources, based on the insights gained here.

Restraints have been used in previous protocols to limit the sampling of states that are farther away from the experimental structure than the initial model. It is clear that, in most cases, such restraints do not allow refinement all of the way to the native state, simply because the native state is too far and would incur a significant energetic penalty from the restraint potential. In past protocols, weak harmonic restraints were applied, with the idea that any significant deviation from the initial state likely leads away from the native state. A better choice may be a flat-bottom potential that is just wide enough to allow the native state and transition intermediates to be reached while still limiting off-pathway states that are farther away. An analysis of RMSD deviations from the initial model for the states along the refinement pathways (SI Appendix, Fig. S31) suggests that flat-bottom widths of 2 Å to 4 Å appear to be enough to provide such a balance for the systems studied here. It would be interesting to test such a restraint potential with established refinement protocols.

Even if conformational sampling is limited to just the refinement pathway, it is clear that significant kinetic barriers have to be overcome. In principle, enhanced sampling techniques (54) could be applied to specific barriers, e.g., to facilitate helix movements or the crossing of backbone and sidechain torsion barriers. Moreover, sidechain adjustments hindered by steric interactions could be facilitated by soft Lennard-Jones interactions. However, the practical success of such refinement protocols depends on being able to identify which residues are most likely in need of refinement, for example, via quality assessment methods (55). One could also imagine nonequilibrium methods to rapidly generate new conformations in specific directions of conformational space. In such a case, the application of scoring functions as discussed in Importance of the Force Field and Rescoring with Other Functions would be especially valuable for identifying which of the generated states are closest to the native state.

Summary.

Structure refinement from homology models to experimental accuracy is the missing piece for generating high-resolution protein structures for sequences where no structural information is available from experiment. This study indicates that this is becoming possible with MD-based methods. The next step is the development of practical protocols that can deliver such structure refinement routinely with moderate computational resources followed by testing on blind predictions within CASP.

Methods

Multiple rounds of unrestrained MD simulations were employed to build Markov state models covering the conformational space between a given homology model and the experimental structure. In the first round of the simulations, 10 100-ns-long MD simulations were started each from the homology model and the experimental structure. Residues present in only one of the structures were removed in the other to match systems. The resulting conformations were classified via tICA from Cα−Cα distance matrices and clustered based on Euclidian distances in tICA space as the distance metric. New clusters that were located between the native and homology structures were then preferentially used as starting points for subsequent simulations. Several simulation trajectories were generated for each starting structure at the next iteration, and the procedure was repeated until there was sufficient overlap between the sampling initiated from the experimental structure and the homology model to build a single combined Markov state model. Further details of the simulation methodology, MSM construction, and scoring and reweighting protocols are given in SI Appendix.