Continuous-range tunable multilayer frequency-selective surfaces using origami and inkjet printing

Significance

Conventional reconfigurable electrical and radio frequency (RF) structures commonly used in applications involving real-time reconfigurability in response to fast varying operational scenarios require specialized substrates or complex electrical circuits. Origami-based RF reconfigurable components and modules offer a solution featuring unique properties. First, they enable reconfigurability over continuous-state ranges (as opposed to discrete states). Second, they do not require specialized mechanical support for multilayer frequency-selective surface structures. Moreover, deployable origami-based RF structures can achieve large surface reconfigurability ratios from folded to unfolded states. Finally, these structures allow for independent control of multiple figures of merit: bandwidth, frequency of operation, and angle of incidence.

Abstract

The tremendous increase in the number of components in typical electrical and communication modules requires low-cost, flexible and multifunctional sensing, energy harvesting, and communication modules that can readily reconfigure, depending on changes in their environment. Current subtractive manufacturing-based reconfigurable systems offer limited flexibility (limited finite number of discrete reconfiguration states) and have high fabrication cost and time requirements. Thus, this paper introduces an approach to solve the problem by combining additive manufacturing and origami principles to realize tunable electrical components that can be reconfigured over continuous-state ranges from folded (compact) to unfolded (large surface) configurations. Special “bridge-like” structures are introduced along the traces that increase their flexibility, thereby avoiding breakage during folding. These techniques allow creating truly flexible conductive traces that can maintain high conductivity even for large bending angles, further enhancing the states of reconfigurability. To demonstrate the idea, a Miura-Ori pattern is used to fabricate spatial filters—frequency-selective surfaces (FSSs) with dipole resonant elements placed along the fold lines. The electrical length of the dipole elements in these structures changes when the Miura-Ori is folded, which facilitates tunable frequency response for the proposed shape-reconfigurable FSS structure. Higher-order spatial filters are realized by creating multilayer Miura-FSS configurations, which further increase the overall bandwidth of the structure. Such multilayer Miura-FSS structures feature the unprecedented capability of on-the-fly reconfigurability to different specifications (multiple bands, broadband/narrowband bandwidth, wide angle of incidence rejection), requiring neither specialized substrates nor highly complex electronics, holding frames, or fabrication processes.

Frequency-selective surfaces (FSSs) have found many applications, ranging from design of radomes, reflectors, and spatial filters to reduction of antenna radar cross-section and realization of artificial electromagnetic bandgap materials (1–3). FSS structures typically consist of periodic arrangement of resonant elements on a thin sheet of substrate that reflect, absorb, or allow certain electromagnetic waves to pass through them based on their frequency, thus exhibiting either bandpass or band-reject characteristics (4–6). These characteristics have made them a subject of extensive research for the past five decades, resulting in the evolution of their design from a simple planar array of 2D resonant structures to complex 3D resonant elements printed/etched on thin sheets of substrates (1, 7–10).

The electromagnetic behavior of a single-layer FSS is primarily determined by the shape, size, and type of resonant elements as well as their interelement distances (1). Moreover, the effects of the dielectric substrate can be ignored if its thickness is less than $\lambda$/100, where $\lambda$ is the wavelength. Typically, single-layer FSS structures suffer from poor selectivity and narrow bandwidth (1). These characteristics are improved by using multilayer configurations that are traditionally realized by either placing the resonant element on both sides of a thick substrate or using specialized frames to separate the FSS layer by the required distance (1, 11, 12); especially at higher frequencies, both techniques drastically limit the effective realization of the optimum frequency response in terms of tunable frequency range, suppression level, angle of incidence rejection range, and other common performance parameters.

Traditional FSS structures are unable to tune their response according to the environmental changes over an almost continuous multitude of states. Typically, tunable FSS structures are realized by incorporating electronic components such as varactor diodes (13) and micro-electro-mechanical systems switches (14) or by changing the electrical properties (15, 16) or geometric configuration (17) of the substrate. However, these approaches become extremely expensive, laborious, and impractical as the size of the FSS is increased. To address this problem, origami-based structures have been proposed as a solution to create deployable continuous-state tunable structures, in which an origami pattern enables the change in the overall shape of the structure, thereby realizing on-demand reconfigurability (18–27). These properties make them a good candidate for terrestrial, outer-space, and electromagnetic cloaking applications over tunable frequency ranges, as well as in morphing devices (SI Appendix, section 8).

However, previous work in origami-based FSS (20, 28, 29) has been dedicated to single-layer structures in which the resonating elements were realized by etching copper tape and manually placing them over the flat panels or the fold lines of the Miura-Ori pattern. Nevertheless, copper tape is prone to peel off with humidity and high temperature, and the manual placement of the resonant elements is a laborious, inefficient, and nonrepeatable procedure, which limits its use for practical applications. Because the unique “continuous-state” reconfigurability feature of a (origami-based) shape-shifting structure can be fully exploited only if the used resonators are highly flexible and their shape changes along with the underlying origami structure, then a repeatable and accurately controlled manufacturing technology is required. Along that line of reasoning, a preliminary single-layer prototype of a Miura-FSS has been realized by inkjet printing (30), in which the flexible conductive lines are printed using silver nanoparticle ink (31).

The folding-induced reduction of the electrical length of the dipole resonators in the FSS structures implies that, without changing the physical length of the dipoles, the folding introduces an additional degree of continuous-state reconfigurability through an increase in effective capacitance to the bandstop Miura-FSS structure, resulting in a resonant frequency shift to higher values. In addition, because the Miura-Ori has a negative in-plane Poisson’s ratio (32, 33), it proportionally reduces the resonators’ electrical length as well as their interelement spacing to enable a continuous-state tunability without the use of any electronic component. Furthermore, it is also a developable pattern (that is, it can be developed from a single 2D sheet) that enables the realization of a full 3D-FSS from a 2D-FSS structure, thereby enhancing the portability while significantly reducing the metalization complexity and the cost typically required by the conventional 3D-FSS structures.

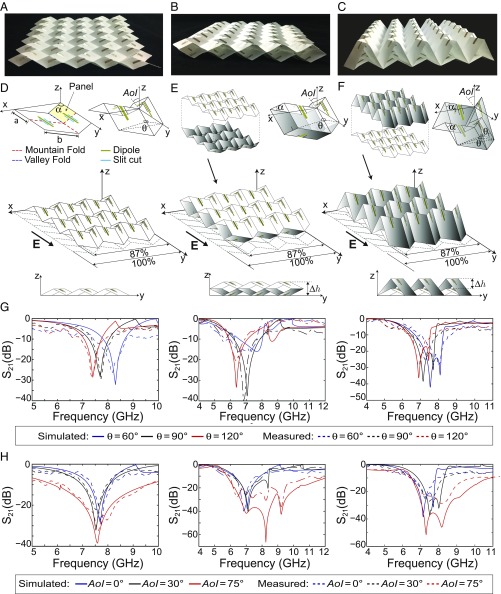
However, single-layer Miura-FSS implementations typically result in narrow bandstop frequency responses, which severely limits their use in practical applications. Thus, this paper introduces two multilayer Miura-FSS configurations (Movie S1 and Fig. 1), the mirror stacking and the inline stacking, that feature “on-demand” broad bandwidth with a wide angle of incidence stability (Movies S2 and S3 and Figs. 1 and 2). These configurations eliminate the need for a holding frame or a thick dielectric substrate to maintain an accurately controlled interlayer distance as required by conventional multilayer FSS structures (1). Each layer consists of a cellulose paper with inkjet-printed dipole elements folded in the Miura-Ori pattern (Fig. 1 A–F). Fully inkjet-printed multilayer tunable Miura-FSS structures are demonstrated and compared with the limited performance of the single-layer Miura-FSS structure.

Fig. 1.

Design, assembly, and response of a proof-of-concept origami FSS assemblage with dipole elements of dimension 20 × 2 mm. Shown are prototypes of (A) Miura-FSS, (B) mirror-stacked Miura-FSS, and (C) inline-stacked Miura-FSS. (D) Miura-FSS unit cell with $a=b=20$ mm, $\alpha =45°$, and its folded configuration with folding angle $\theta$. (E) Assembly of two identical Miura-Ori layers into a mirror-stacked configuration and its unit cell. (F) Assembly of two Miura-Ori layers into an inline-stacked configuration and its unit cell, where the intrinsic geometry for the “white” unit cell is defined as $a=b=20$ mm, $\alpha =45°$, and for the “shaded” unit cell as $a=23.3\hspace{0.17em}\text{mm}$, $b=20\hspace{0.17em}\text{mm}$, $\alpha =52°$ (see SI Appendix for details). (G) Frequency response in terms of transmission coefficient ${\mathrm{S}}_{21}$ for the single-layer, mirror-stacked, and inline-stacked Miura-Ori assemblages for folding angles $\theta =60°,90°,120°$ corresponding to panel extensions of 50%, 71%, 87%, respectively, and considering a normal angle of incidence (AoI) with a linearly polarized electric field E that is oriented along the length of the dipole elements. (H) Frequency response in terms of transmission coefficient ${\mathrm{S}}_{21}$ for the single-layer, mirror-stacked, and inline-stacked Miura-Ori assemblages for folding angle $\theta =90°$ (i.e., 71% extension) and AoI = $0°,30°,75°$.

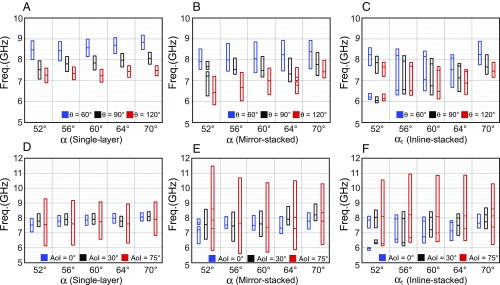
Fig. 2.

Simulated response of the Miura-Ori–based FSS, in which the internal lines represent the resonant frequency, and the top and bottom lines represent the cutoff frequencies at −10 dB. Shown is the response of the FSS structures with distinct panel angles $\alpha =52°,56°,60°,64°,70°$ (in the case of inline stacking, $\alpha ={\alpha }_t$, i.e., the angle $\alpha$ for the top layer). (A–C) For a specific AoI$\hspace{0.17em}=\hspace{0.17em}0°$ and distinct folding angles $\theta =60°,90°,120°$ for single-layer, mirror-stacked, and inline-stacked Miura-FSS, respectively. (D–F) For a specific folding angle $\theta =90°$ and distinct AoI = $0°,30°,75°$ considering single-layer, mirror-stacked, inline-stacked Miura-FSS, respectively.

The remainder of this paper is organized as follows. First, we introduce the geometry of the Miura-FSS unit cell for single- and multilayer configurations. Next, we present and discuss the frequency response of these structures obtained from an integrated experimental and simulation-based investigation. In addition, we correlate the response of the proposed structures with the intrinsic geometry of the unit cell to provide a systematic methodology for using this approach in applications with arbitrary reconfigurability requirements over a continuous range. We conclude with some final remarks.

Miura-Ori–Based FSS Assemblages

The Miura-Ori pattern has been extensively studied (32, 33) and has found many applications in engineering (21, 22, 34–36). Thus, it has been selected as the basis for our origami-based FSS investigation. The Miura-Ori is a rigid origami defined by the geometry of the unit-cell rhombic-shaped panels, which are characterized by two lengths, $a$ and $b$, and the panel angle $\alpha$ (Fig. 1D). This pattern features 1 df, meaning that we can fully describe its kinematics using the unit-cell intrinsic geometry and one of the dihedral angles between panels, here defined as the folding angle $\theta$.

A typical single-layer Miura-FSS consists of a single sheet of the Miura-Ori pattern with two dipole elements per unit cell (Fig. 1 A and D). In this paper, the dipole elements are inkjet printed over the mountain fold such that they are centered along length $b$ to demonstrate the realization of highly flexible conductive traces that is a key requirement for origami-inspired tunable electrical/radio frequency structures over a continuous range of states. Dipoles are fundamental electromagnetic structures, which would help to fully understand the frequency behavior of a Miura-FSS with folding.

By stacking two Miura-FSS sheets, we realized two multilayer configurations: the mirror multilayer stacking (Fig. 1 B and E) and the inline multilayer stacking (Fig. 1 C and F). The former consists of two identical Miura-FSS layers connected along the valleys in a mirror fashion, and the latter consists of distinct and kinematic compatible layers (33) connected along the valley folds. Both stacking types preserve the flat-foldability and in-plane kinematics of the Miura-Ori (SI Appendix, section 1), which are described as a function of the intrinsic geometry and dihedral angle $\theta$ (shown in Fig. 1 D–F).

Results and Discussion

The single-layer Miura-FSS structure and its two multilayer configurations were designed and simulated in ANSYS High Frequency Structure Simulator (HFSS). To exploit the periodic nature of the Miura-FSS structure while saving computational time and resources, only the unit cell of each configuration (shown in Fig. 1 D–F) was simulated using master/slave boundary conditions and Floquet port excitation (SI Appendix, section 4). The simulation results were verified by a bistatic measurement setup consisting of two broadband horn antennas placed in the line of sight to each other with the fabricated Miura-FSS structure placed in the middle. To ensure uniform folding angle throughout the Miura-Ori–based FSS structure and minimize measurement errors, specialized 3D-printed frames were fabricated that hold the FSS structures at different folding angles. As shown in Fig. 1G, the simulated and measured insertion losses (${\mathrm{S}}_{21}$) for the single and the two multilayer Miura-FSS configurations display good agreement with each other.

The structures presented in this paper are designed such that they operate within the so-called no grating-lobe regime (1) by limiting interelement periodicity to be less than the wavelength of the first high-order Floquet harmonic ${\lambda }_g^{{ϵ}_r}=D_{\ell }\left(\sqrt{{ϵ}_r}+\sin \left(\text{AoI}\right)\right)$, where ${ϵ}_r$ represents the effective dielectric constant of the substrate and $D_{\ell }$ is the interelement distance along the y axis. Since the structures resonate at wavelengths longer than ${\lambda }_g$, the fundamental propagating mode dominates. The higher-order modes are evanescent and decay exponentially as we move away from the FSS structure. Note that the grating-lobe wavelength is equal to the interelement distance ($D_{\ell }$) for normal incidence (AoI $=0^o$). The sudden null in the insertion loss diagrams indicates the onset of the grating-lobe region. The location of the grating-lobe region also changes as the interelement distance varies with change in folding angle $\theta$, as shown in Fig. 1G.

The simulated frequency response for the three Miura-FSS configurations with respect to different folding angle ($\theta$) and panel angle ($\alpha$) is shown in Fig. 2. All Miura-FSS structures resonate at a higher frequency as the folding angle ($\theta$) is decreased. This is due to reduction in the effective electrical length of the dipole elements as they morph from a flat configuration to a V-shape structure as the Miura-FSS structure is folded. It is also interesting to note here that while the single-layer Miura-FSS structure has a single resonant frequency with narrow bandwidth ($\le 15\%$), the two multilayer Miura-FSS structures feature multiple-resonance behavior to realize much broader bandwidth. The frequency response of a typical Miura-FSS can be easily changed on demand by varying the folding angle ($\theta$) for a given panel angle ($\alpha$).

Fig. 1G shows that the inline-stacked Miura-FSS configuration features two operating frequencies (modes). The lower frequency is mainly determined by the coupling between the two layers (coupling mode) while the higher frequency is determined by the size of the resonant dipole element and the folding angle (resonant mode). At lower values of the panel angle (${\alpha }_t$), the change in effective interlayer distance is negligible compared with the wavelength of the resonant mode frequency, which results in same coupling mode frequency for different folding angles. Moreover, the overall electrical length of the dipole element is reduced by decreasing the folding angle ($\theta$), thereby causing a shift in resonant mode frequency to higher values. However, the coupling mode frequency also changes with different folding angles for higher values of ${\alpha }_t$ since the change in interlayer distance becomes comparable to the resonant mode frequency. The two resonant frequencies merge at ${\alpha }_t=70^{○}$, which indicates strong coupling between the two layers as shown in Fig. 2C. Furthermore, it can be seen that the resonant frequency shift for different values of ${\alpha }_t$ for a given $\theta$ in this multilayer Miura-FSS configuration is negligible. Finally, the inline-stacked Miura-FSS structure features a very stable angle of incidence (AoI) frequency response as shown in Fig. 2F. That is, the change in resonant frequency is relatively small that can be compensated by larger filter bandwidth at higher AoI (1). An exception occurs at panel angles that feature weak coupling between the two layers (e.g., $\alpha =52°$).

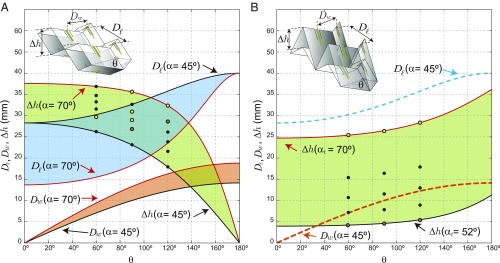
In contrast to the inline-stacked Miura-FSS, the interlayer distance for mirror-stacked Miura-FSS increases as folding angle $\theta$ decreases. This behavior is illustrated in Fig. 3, which shows how the distances between the resonant elements change, depending on panel angle $\alpha$ and folding angle $\theta$ (SI Appendix, section 1 and Fig. S1). By comparing the interlayer distance ($\mathrm{\Delta }h$) plots for the two multilayer configurations, we see that mirror stacking offers a relatively higher variation in $\mathrm{\Delta }h$. This causes the frequency response of the structure to be more sensitive to the folding angle as opposed to the inline-stacking configuration. However, the optimum interlayer distance for a given $\alpha$ is difficult to achieve in the mirror configuration for all folding angles $\theta$. Typically, the structure would have a strong resonance with wide bandwidth when $\mathrm{\Delta }h\le n\lambda /2$, where $n$ is a positive integer. In contrast to in-line stacking configuration, mirror-stacked Miura-FSS has good AoI rejection only at lower values of $\alpha$ ($\le 60°$). Due to poor interlayer coupling at higher values of $\alpha$, we get unstable AoI rejection as shown in Fig. 2E.

Fig. 3.

Relation between folding angle $\theta$ and dipole distances $D_w$, $D_{\ell }$, and $\mathrm{\Delta }h$ for the mirror stack and inline stack of the Miura-FSS. (A) For the mirror stacking of identical layers, the shades represent the range of the curves for panel angles $\alpha$ between $\mathrm{45}°$ and $\mathrm{70}°$. The green, blue, and orange shades represent how $\mathrm{\Delta }h$, $D_{\ell }$, and $D_w$, respectively, vary with respect to $\alpha$. (B) For the inline stacking, the green shade represents the variation of $\mathrm{\Delta }h$ for panel angles ${\alpha }_t$ (subscript $t$ refers to the top layer) between $\mathrm{52}°$ and $\mathrm{70}°$. The blue and orange dashed lines represent the distances $D_{\ell }$ and $D_w$ between the dipoles of the top and bottom layers. In both A and B, the yellow circles represent the configurations in which percentage bandwidth is $\le 15\%$ (comparable to single-layer Miura-FSS) while black circles represent configurations which can realize broader bandwidth ($>15\%$), and brown circles represent configurations with multiband and multiresonant frequency.

Concluding Remarks

In this work, we created Miura-Ori–based FSS multilayer structures that feature the unprecedented capability of on-the-fly reconfigurability to different specifications (multiple bands, broadband/narrowband bandwidth, wide angle of incidence rejection). By combining additive manufacturing and origami principles, we achieve tunable electrical components that can be reconfigured over continuous-state ranges from folded (compact) to unfolded (large surface) configurations on cellulose paper. The use of a highly porous substrate along with the “bridge-like” structures allows realization of truly flexible resonant elements that maintain high conductivity even for large bending angles, further enhancing the states of reconfigurability. The electrical length of the dipole elements in these structures changes when the Miura-Ori is folded, which is the tuning mechanism for shape-reconfigurable response of the FSS structure.

We remark that the present approach is applicable to other developable and nondevelopable tessellations. Furthermore, a multilayer origami-based FSS can be developed from layers of tessellations with compatible in-plane kinematics (37), such as Miura-Ori derivatives (38, 39) and kirigami patterns (40, 41). In addition, the mirror-stacking FSS could be explored by considering layers with distinct intrinsic geometry, in which the maximum distance between resonant elements could be better controlled, such that the distance among the resonant elements is finite (no interpenetration) as the stacked configuration unfolds.

Materials and Methods

Sample Fabrication.

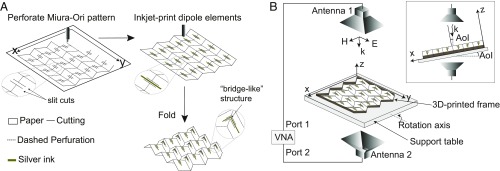
We fabricated each layer of the Miura-FSS by perforating the Miura pattern on 110-$\mathrm{\mu }\text{m}$ cellulose paper with a perforation machine that perforates and cuts the origami pattern on the paper. The pattern had $6\times 5$ unit cells in the $x$ and $y$ directions, respectively. These cells were a modified version of the Miura-Ori unit cell, in which we included slit cuts with no perforation between them to realize bridge-like structures that would allow the inkjet-printed dipoles to smoothly bend over the fold lines, thereby avoiding cracks or breakage in the conductive trace during folding (Fig. 4A).

Fig. 4.

Schematics of the general fabrication process and experimental setup. (A) Schematics of the fabrication process of each Miura-FSS layer, which consists of the perforation of the modified Miura-Ori pattern, inkjet printing of the dipole elements, and manual folding of the pattern. (B) Schematics of the experimental characterization setup. Top box shows a side (“plane of incidence”) view of the setup, where angle of incidence (AoI) represents how much we tilted the support table, reflecting the relative angle between the incident waves and the normal to the FSS structure plane.

Experimental Testing.

We tested each prototype in three geometric configurations. For accuracy, we used 3D-printed frames to shape the prototype into the desired folding angles ($\theta =60°,90°$, and $120°$). Each test consisted of placing the prototype with the 3D-printed frame between two horn antennas in the line of sight. We attached the horn antennas to a vector network analyzer (VNA), to measure the ${\mathrm{S}}_{21}$ (transmission coefficient) values of the three Miura-FSS configurations. The frequency response of the structures with respect to folding angle was measured for only normal incidence (AoI$\hspace{0.17em}=\hspace{0.17em}0°$), while the angle of incidence rejection capability of the structures was measured by keeping the folding angle fixed ($\theta =90°$) and rotating the support table about the rotation axis (Fig. 4B and SI Appendix, Fig. S5).