Significance
Allosteric processes are ubiquitous in macromolecules and regulate biochemical information transfer between spatially distant sites. Despite decades of study, allosteric processes remain generally poorly understood at the molecular level. Here, we introduce the eigenvector centrality measure of mutual information to disentangle the complex interplay of amino acid interactions giving rise to allosteric signaling. The analysis of eigenvector centrality is tested in imidazole glycerol phosphate synthase (IGPS), a prototypical V-type allosteric enzyme. The resulting insights allow us to pinpoint key amino acids in terms of their relevance in the allosteric process, suggesting protein-engineering strategies for control of enzymatic activity.
Keywords: allostery, graph theory, eigenvector centrality, information theory, IGPS
Abstract
Determining the principal energy-transfer pathways responsible for allosteric communication in biomolecules remains challenging, partially due to the intrinsic complexity of the systems and the lack of effective characterization methods. In this work, we introduce the eigenvector centrality metric based on mutual information to elucidate allosteric mechanisms that regulate enzymatic activity. Moreover, we propose a strategy to characterize the range of correlations that underlie the allosteric processes. We use the V-type allosteric enzyme imidazole glycerol phosphate synthase (IGPS) to test the proposed methodology. The eigenvector centrality method identifies key amino acid residues of IGPS with high susceptibility to effector binding. The findings are validated by solution NMR measurements yielding important biological insights, including direct experimental evidence for interdomain motion, the central role played by helix h, and the short-range nature of correlations responsible for the allosteric mechanism. Beyond insights on IGPS allosteric pathways and the nature of residues that could be targeted by therapeutic drugs or site-directed mutagenesis, the reported findings demonstrate the eigenvector centrality analysis as a general cost-effective methodology to gain fundamental understanding of allosteric mechanisms at the molecular level.
Allostery establishes a wide range of regulatory processes in biological macromolecules. The primary step in the allosteric regulation often involves binding of a ligand effector that regulates catalytic activity far away from its biding site. The mechanisms of energy transfer between the allosteric and catalytic sites are essential for design of selective therapeutic methods. However, they are typically poorly understood due to the intrinsic complexity of the systems and the lack of effective characterization methods. Thus, establishing methodologies for understanding communication pathways between physically distant sites in allosteric enzymes remains an important outstanding challenge. Such methods could expedite the design of innovative drug therapies (1, 2) as well as protein engineering strategies (3–5).
Significant efforts have been recently reported in the development of computational tools to support, interpret, and/or predict experiments focused on the elucidation of allosteric pathways (2, 6–12). Network analysis has been extensively used in this context by incorporating concepts and approaches from graph theory in the realm of molecular dynamics (MD) simulations (9, 13–22). For instance, community network analysis (CNA) has emerged as a powerful and increasingly popular approach to analyze the dynamics of enzymes and protein/DNA (and/or RNA) complexes in studies of allosteric mechanisms (23–29).
Graph theory represents proteins as networks of nodes corresponding to amino acid residues or DNA/RNA bases, linked by edges. The length of the edges corresponds to the magnitude of a physical property correlating the nodes, such as the dynamical correlation (9, 30, 31), coupling strength (32), or distance between residues (33). For a network of nodes, the corresponding graph is described by an adjacency matrix with elements defining the strength of the physical correlation between nodes and .
One of the cornerstones of network analysis is the concept of centrality—that is, the relative importance of an individual member in a group. Measures of centrality are crucial to identify the more influential nodes in a network. There are many measures of centrality characterizing slightly different aspects of the network. Probably the simplest of all is the degree centrality (DC), , providing a measure of the relative connectivity of node in the network, as follows:
| [1] |
where defines the strength of the physical correlation between nodes and . A node that is well connected is expected to have a large “influence” on the graph. While the DC can provide useful information, it is not a true “node centrality” as defined by Ruhnau (34) and thus does not give a measure of centrality based on a fixed scale that allows comparisons between different graphs.
An alternative definition is the betweenness centrality (BC), , which provides a measure of how information can flow between nodes (or edges) in a network. The BC can be quantified as the number of times a node acts as a bridge along the geodesic (shortest) path between two other nodes,
| [2] |
where is the number of shortest paths between nodes and that pass through node , and is the total number of shortest paths between nodes and . The nodes with high BC have a large influence on the overall information passing by flow, and, hence, the removal of such nodes may disrupt the communication in the network. However, communication does not always take the shortest path, and, hence, the BC may provide only partial information on the relevance of each amino acid in the functional dynamics of a protein.
Somehow, in between these two definitions of centrality (i.e., degree and betweenness centralities), the eigenvector centrality (EC) emerges as an alternative that takes into account both the number of connections of a given node and its relevance in terms of information flow. The EC of a node, , is defined as the weighted sum of the centralities of all nodes that are connected to it by an edge, ,
| [3] |
where is the eigenvector associated to the eigenvalue of . The EC is a measure of how well connected a node is to other well-connected nodes in the network. Importantly, the EC serves as a measure of the connectivity against a fixed scale when normalized, so it can be used to reliably compare different networks (34). For example, the normalization becomes essential when analyzing differences between graphs, for example, to study the pattern of centrality variation between the apo and holo states of a protein.
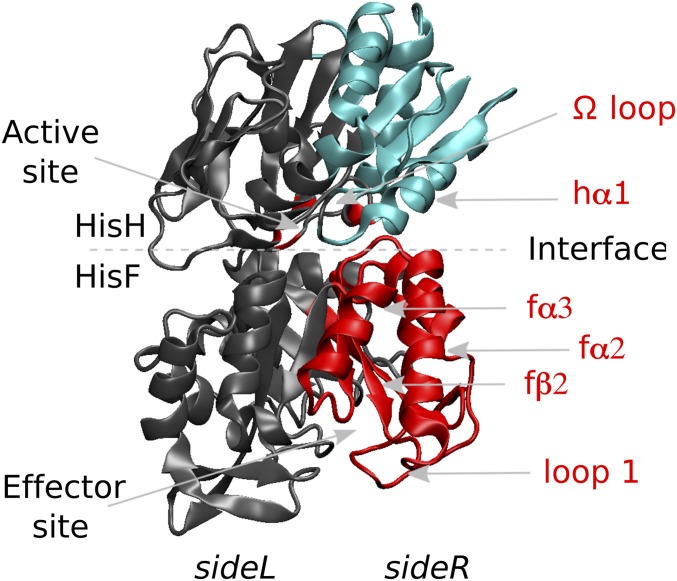
In the present work, we illustrate the potential of the EC measure to provide a molecular-level characterization of the allosteric mechanism of enzymes. In particular, we focus on the prototypical case of the imidazole glycerol phosphate synthase (IGPS), a bacterial enzyme present in the amino acid and purine biosynthetic pathways of most microorganisms, making it an attractive target for antibiotic, pesticide, and herbicide development (35). Structurally, IGPS is a tightly associated heterodimer (Fig. 1) in which each monomer catalyzes a different reaction: The HisH enzyme promotes the hydrolysis of glutamine (Gln) to produce ammonia, which diffuses to the HisF subunit and reacts with the effector N-[(5-phosphoribulosyl)formimino]-5-aminoimidazole-4-carboxamide ribonucleotide (PRFAR) to form imidazole glycerol phosphate and AICAR. While Gln binding is unaffected by the presence of PRFAR, the hydrolysis of Gln is accelerated 5,000-fold upon PRFAR binding through a mechanism that, for many years, has remained elusive (36). IGPS is thus a V-type enzyme and a model system to study noncooperative allostery involving conformational changes.
Fig. 1.
Molecular representation of IGPS. Red labels indicate secondary structure elements that are directly involved in the allosteric regulation. Communities h2 (cyan) and f3 (red) in the sideR of IGPS are also depicted.
In a recent study (9), we carried out a BC-based CNA by optimizing the modularity function to explore the underlying allosteric mechanism of this enzyme. We now present an alternative strategy, exploring the description of allostery provided by the EC compared with the CNA based on optimal modularity (the connection between CNA and the EC is analyzed in detail in SI Appendix). This approach identifies the most important amino acids for the allosteric signaling, providing an ideal route for the identification of mutation targets to inhibit or enhance the IGPS catalytic activity and opening the doors to a plethora of combined theoretical–experimental studies oriented to increase the control of its function and develop new alternatives for drug discovery. Additionally, the strategy introduced in this work allows us to capture long-range contributions to the correlation pattern beyond our previous CNA study and fundamental aspects of the allosteric behavior of IGPS. In particular, we show that while the correlation between residues is enhanced by a conformational breathing motion, the allosteric pathway is dominated by short-range contacts (9).
The present paper is organized as follows: We first summarize the method of CNA and results for ref. 9. Next, the method of EC is introduced and applied to the IGPS systems. Results are discussed and compared with CNA. Correlation matrices are obtained from the same trajectories and following the same protocol as in ref. 9.
CNA
Consider a protein residue network where each node represents the -carbon of an amino acid in the protein, and each edge represents the dynamical correlation between the two residues (nodes) it connects. The latter can be quantified by using the generalized correlation coefficients, based on the mutual information (MI) between two residues (30):
| [4] |
where the fluctuation or atomic displacements vectors are computed from MD simulations. For clarity, we have kept the original notation used in refs. 9 and 30, where a detailed explanation on the calculation of the generalized correlation coefficients can be found.
The MI between the two residues is computed as:
| [5] |
where
| [6] |
| [7] |
are the marginal and joint Shannon entropies, respectively, obtained as ensemble averages over the atomic displacements , with marginal and joint probability distributions and computed over thermal fluctuations sampled by MD simulations of the system at equilibrium. The coefficient ranges from zero for uncorrelated variables to 1 for fully correlated variables.
The protein graph connectivity is then built, excluding direct connections of first neighbors (in amino acid sequence) and according to two cutoffs: Two nodes are considered connected if the distance between their -carbons is within a distance cutoff (generally 4–6 Å) for a certain percentage of the MD trajectories (percentage cutoff, usually 65–85%). The distances between all of the connected nodes () in the graph topology define a matrix of elements obtained from , according to:
| [8] |
setting the distance to infinity (in practice to extremely large values) when two nodes are not connected, as defined by the connectivity rules. The Floyd–Warshall algorithm (37) is then used to determine the matrix of minimum distance (maximum correlation), , considering direct distances as well as up to N possible intermediate residues mediating indirect communication pathways (where N is the total number of residues in the system). The total number of residues for the IGPS case is N = 454.
The edge-betweenness matrix with elements is defined as the number of shortest paths that include edge () as one of its communication segments. In other words, the edge-betweenness matrix is an estimation of the information “traffic” passing through the edge connecting residues and in the network. The edge-betweenness matrix is then used for partitioning the network into communities according to the Girvan–Newman algorithm, which is based on maximizing the modularity measure (38, 39). Details of the computation of the community structure based in the maximum modularity from the generalized correlation matrix can be found in ref. 9.
Fig. 1 shows the two most important communities h2 (cyan) and f3 (red) projected onto the residue space of IGPS in the apo state as determined in ref. 9. Secondary structural elements of h2 involve h, h, h, h, h, h, h, and -loop. Secondary structural elements of f3 instead involve f, f, f, h, h, f, f, f, h, and Loop1.
We have previously shown that the correlation between communities h2 and f3 is enhanced (with larger interbetweenness) after PRFAR binding. Furthermore, it was shown that the explanation for this enhancement relies on the increase in the frequency of an interdomain motion at the dimeric interface (HisH–HisF) upon binding of PRFAR. This was described as a low-frequency interdomain breathing motion that allows for fluctuations between two states (open and closed IGPS heterodimer) that are accessible at thermal equilibrium in both the apo and PRFAR complexes. Disruption of this breathing mode with drug-like compounds was recently suggested as a method for inhibiting the allosteric mechanism (20).
The recognition of the local interactions that determine variations in the breathing motion (and, thus, in the h2–f3 intercommunities correlations) has been performed by detailed comparative analysis of chemical interactions along the MD trajectories of apo and PRFAR-bound IGPS complexes (9). In particular, it was observed that PRFAR binding affects specific hydrophobic interactions in Loop1 and f2 (in HisF), altering salt-bridge formations at the surface-exposed f2, f, and h helices (at the HisF/HisH interface) that, in turn, determine modification of the breathing motion and of the hydrogen-bonding network between the Omega loop and the oxyanion strand nearby the HisH active site. Thus, among the secondary structure elements of communities h2 and f3, the following elements have been retained as allosteric pathways: Loop1, f, f, f, h, and -loop (indicated with red labels in Fig. 1). The active allosteric role of some of these residues has been recently proved by single-site mutation experiments (40).
The CNA provides an introspection tool for visualizing the most important transformations induced by the allosteric effector in a coarse-grained fashion, allowing easy detection of effector-driven changes in the overall intercommunities information flows. However, we have shown that to recover direct information on allosteric pathways, a detailed analysis of the MD trajectory is still necessary (9). Therefore, CNA can successfully assist the tedious allosteric pathway detection by indicating major network changes due to the effector binding, but it cannot provide an easy detection and immediate visualization of the sequence of amino acids involved in the allosteric-to-active-site signal propagation. Here, we show that a comparative EC approach, on the other hand, can provide fast detection of allosteric nodes and easy interpretation of the signal pathways “activated” by the effector binding.
EC Analysis
Let us define the adjacency matrix as follows:
| [9] |
Just as in the CNA approach, here, each node of the graph corresponds to the -carbon of an amino acid residue, and the off-diagonal elements of are the weights associated with every edge. Additionally, an exponential damping factor with a length parameter has been introduced to Eq. 9. This parameter can be adjusted to control the locality of the correlations under consideration based on the average distance between residues (). This means that if is short enough, the correlation between residues that are far away from one another will be disregarded, and the effect of the locality in the allosteric pathway will be revealed. On the other hand, if is set to a very large value, all correlations, including those between residues separated by long distances, will be accounted for (i.e., , ). By adopting such damping factor, we obtain a twofold benefit for the EC analysis: (i) By setting reasonably small damping values, we could mimic the distance cutoff used in the CNA, and we can then fairly compare EC and CNA results; and (ii) comparison of EC values at various damping distances provides direct information on the role of long-range correlations in allosteric pathways. This will be discussed in further detail in The Locality Factor.
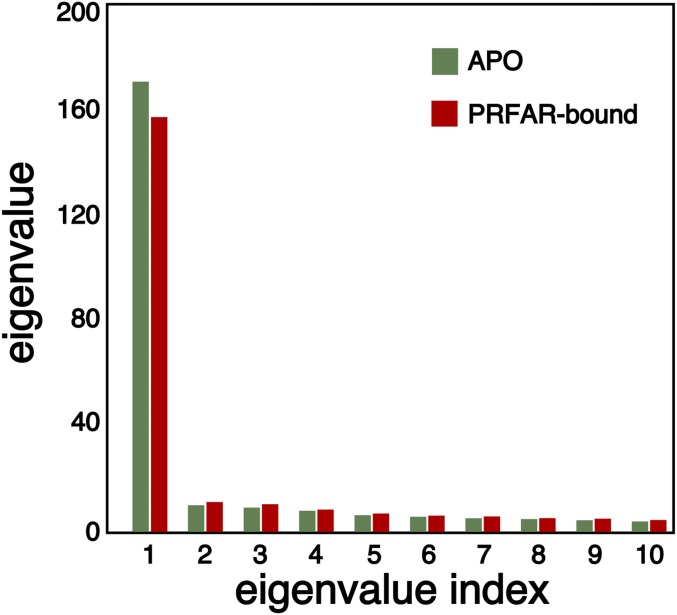
As mentioned in the introduction, the EC arises from an eigendecomposition of the adjacency matrix, , where is the vector containing the centralities for each node and is the associated eigenvalue. Therefore, there is a set of solutions to this eigenvalue problem, with being the number of -carbon atoms in the protein. However, we will rely here on the assumption that the functional dynamics of the protein can be assigned to the major collective mode of correlation. Consequently, the eigenvectors associated with the remaining eigenvalues will be neglected. The election of this leading eigenvector as the principal component of the correlation pattern can be formally justified, considering that the adjacency matrix defined by Eq. 9 has the following mathematical properties: (i) ; and (ii) . Hence, uniqueness of the definition of the EC is ensured by the Perron–Frobenius theorem, which states that any symmetric matrix (property i) with nonnegative entries (property ii) has a unique largest real eigenvalue. Fig. 2 shows that the highest eigenvalue exceeds the others by almost two orders of magnitude, illustrating the Frobenius theorem in practice for apo and PRFAR-bound IGPS.
Fig. 2.
Largest 10 eigenvalues obtained from the adjacency matrix (as defined by 9 in the limit of ) for the apo (green) and PRFAR-bound (red) IGPS.
The EC values are computed by diagonalizing A and keeping the eigenvector c corresponding to the maximum eigenvalue. The power method (41) is an alternative to matrix diagonalization that is computationally more efficient and would be more appropriate for large systems. The information encoded on the resulting eigenvector reveals the importance of the nodes for the whole connectivity of the network. The nodes with the highest centralities will act as the principal “channels” for momentum transmission across the protein. This strategy has been applied as a means of visualizing dynamical phenomena in other domains of science (42). The eigenvalue , in turn, gives a measure of the network degree of connectivity. At (no exponential damping), the values of are 166.8 and 154.0 for apo and PRFAR-bound, respectively. This indicates that the system experiences an overall decrease of correlation as a consequence of PRFAR binding as suggested by inspecting the correlation matrix (9). Moreover, our solution NMR spectroscopic measures characterizing the conformational exchange () for numerous amino acids in the HisF domain indicate that nearly every residue increases its flexibility upon PRFAR binding (21). This increase in flexibility is translated into an effective reduction of the intermolecular connectivities and, hence, results fully consistent with the predicted drop in the overall correlation.
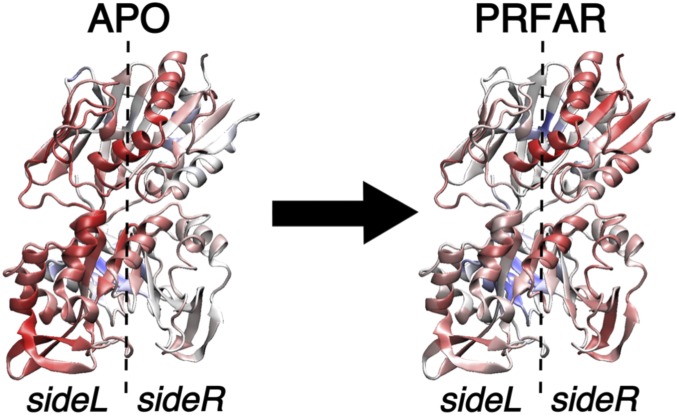
The EC values for each node can be easily visualized in the protein structure (Fig. 3), displaying the coefficients for each amino acid with a color scale from blue (zero centrality) to red (maximum centrality). In all of the cases, a renormalization of the centrality values was applied for plotting purposes (SI Appendix). Fig. 3 shows the values of for both apo and PRFAR-bound IGPS proteins, as computed by setting the damping distance to infinity. Importantly, the subgraph composed by the most important nodes in the network changes dramatically with the effector binding, highlighting the connection between the EC distribution and the momentum transport pathway. As indicated in Fig. 3, the highest EC values shift collectively from sideL to sideR in IGPS upon PRFAR binding. This variation of the relative EC distribution evidences a change in the correlation pattern that is in agreement with our previous analysis and consistent with the enhancement in the betweenness of h2–f3 pair of communities (9).
Fig. 3.
Computed centrality values for both apo and PRFAR-bound IGPS. The color scale goes from blue () to red (maximum values of ).
The methodology introduced above resembles the well-known essential dynamics (ED) scheme in which the global trajectory of a system is analyzed in terms of its major collective modes of fluctuation. (43–46) These modes—usually called essential modes—are obtained by diagonalizing the covariance matrix, defined as
| [10] |
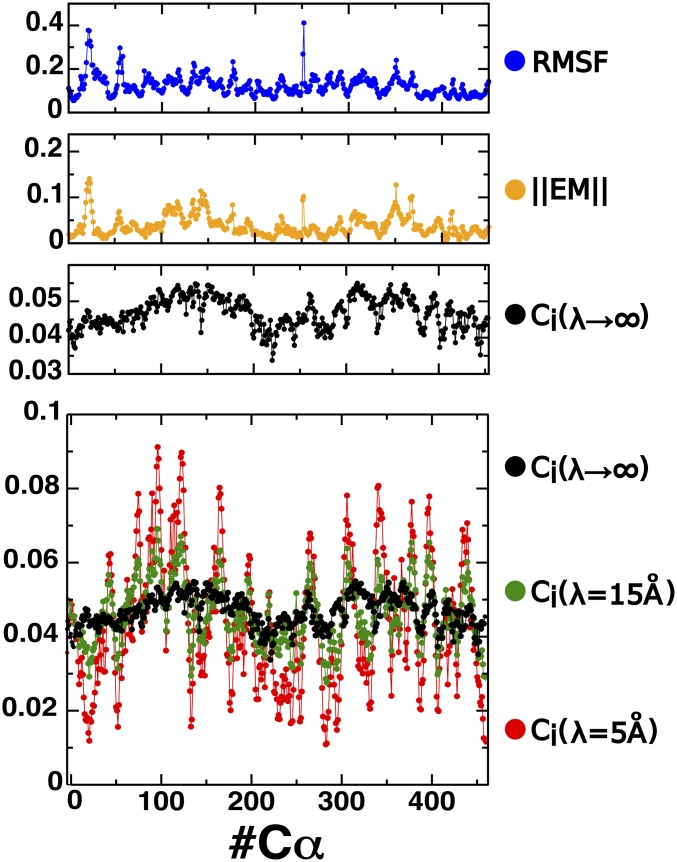
Normally, despite not being formally guaranteed, it is observed that the protein dynamics is dominated by a few essential modes. Therefore, this scheme also provides a way to obtain eigenvector coefficients that reveal the relevance of each node in the overall behavior of the network. Nevertheless, the measure of relevance can have several meanings; in particular, Fig. 4, Upper shows that the nature of the eigenvector coefficients obtained from the first essential mode (the one associated to the highest eigenvalue) is qualitatively different from that of the EC coefficients. There are two main reasons that justify this difference: (i) While in the latter case, the generalized MI matrix is only a measure of the dynamical correlation between pairs of nodes, in the former case, the covariance matrix is both a measure of correlation and the amount of fluctuation. (ii) On the other hand, the covariance measure fails to account for noncolinear correlations. The first observation is consistent with the fact that the behavior of the essential mode coefficients (orange line, Fig. 4, Upper) is quite similar to the root-mean-square fluctuation per residue (blue curve, Fig. 4, Upper). Therefore, this analysis illustrates that the ED and the EC extracted from the MI are two complementary methodologies that provide different insight on the system’s dynamics. In particular, the technique presented in this work constitutes a powerful alternative to analyze allosterism because it isolates the principal component in terms of the correlation and not in terms of flexibility, as in the case of ED.
Fig. 4.
(Upper) Comparison between the Euclidean norm of the elements of the first essential mode associated with each (orange line), the centrality coefficients obtained from the first eigenvector of the adjacency matrix defined in Eq. 9 with (black line), and root-mean-square fluctuation per residue (RMSF; blue line). (Lower) Effect of the length parameter in the exponential damping factor of the adjacency matrix defined in Eq. 9. Values of Å Å, and are depicted in red, green, and black, respectively.
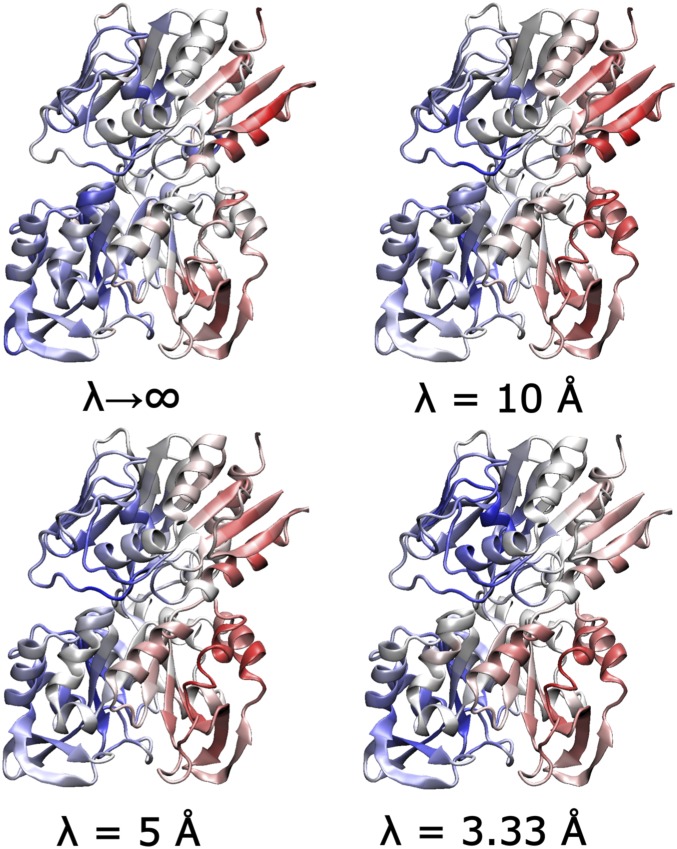
Fig. 4, Lower shows the effect of the length parameter defined in Eq. 9. In the limit of , the off-diagonal elements of the adjacency matrix become equivalent to the generalized correlation function for each pair of nodes. The centrality coefficients obtained in this way exhibit a smooth variation. In contrast, when is short enough, only the local components of the correlations survive, and the centrality coefficients reveal the relevance of each residue in terms of its dynamical correlation with neighboring amino acids. In this context, the exponential damping filters out long-range correlations, thus providing a strategy to elucidate the allosteric paths triggered by short-range molecular correlations.
Centrality Variation Triggered by Effector Binding
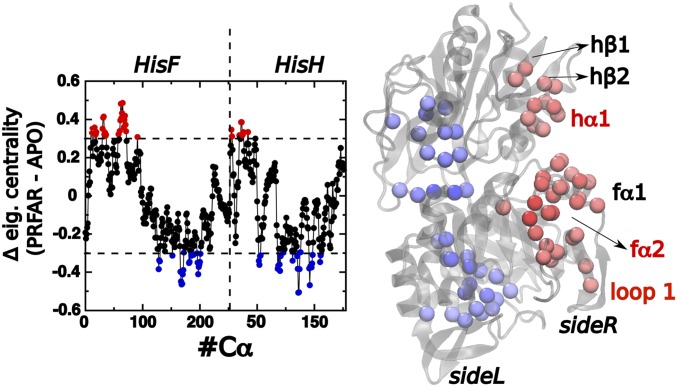
We have examined the EC differences associated with PRFAR binding () for each residue to analyze changes in the EC distribution caused by binding of the effector PRFAR (Fig. 3). Fig. 5 shows that there is significant redistribution of the EC values upon PRFAR binding. Two protein regions feature increased centralities, namely, residues around fL10–fG80: loop1 (HisF: 16–31), f1 (HisF: 31–43), f2 (HisF: 59–72), and hM1-hQ36: h1 (HisH: 1–5), h1 (HisH: 12–25), and h2 in HisH. Connections between the loop1 and -loop are hence established after PRFAR is bound to IGPS, as depicted in the centrality-differences analysis presented in Fig. 5.
Fig. 5.
Centrality differences (PRFAR-bound – APO) for an exponential damping Å as a function of the residue index (Left) and plotted on top of the protein representation (Right). Red and blue values are regions that, respectively, gain and lose centrality upon PRFAR binding. The domains with higher PRFAR-induced centrality increase are loop1 (HisF: 16–31), f1 (HisF: 31–43), f2 (HisF: 59–72), h1 (HisH: 1–5), h1 (HisH: 12–25), and h2 (HisH: 30–35).
Previous studies have postulated the existence of two dynamically differentiated sides in IGPS—that is, left and right or sideL and sideR, respectively (9, 20) (Fig. 5). Detailed inspection of MD trajectories have suggested that the allosteric signal propagates through sideR. Importantly, in agreement with that observation, Fig. 5 shows that binding of the effector PRFAR causes an increase in the centrality values of sideR amino acids. Moreover, the pattern shown by the centrality distribution allows clear identification of the two sides of IGPS, confirming our previous hypothesis.
The identified residues, including 10–80 (in HisF) and 1–36 (in HisH) (Fig. 5, highlighted in red), represent promising targets for site-directed mutagenesis studies since they exhibit the highest increase in centrality upon PRFAR binding. Importantly, we identify helix h1 as one of the domains with higher centrality increase upon PRFAR binding. We anticipate that these findings should stimulate significant interest for site-directed mutagenesis studies or the use of small allosteric drugs targeting helix h1. Therefore, the reported results provide biological insights that are potentially useful for therapeutic applications that could aim at disrupting IGPS functionality by targeting the h1 dynamics.
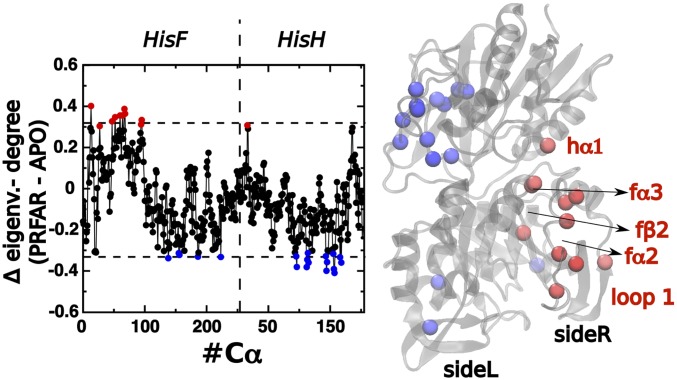
In addition, instead of focusing on the nodes that are important per se, another criteria that can be relevant to guide mutagenesis efforts is to focus on the “neighborhood” of those nodes. This sort of modification may play a more subtle role in altering the protein activity, which can be potentially relevant for applications like drug discovery in which the desired effect comes from disrupting the environment of key residues in the protein. Given that the difference between DC (Eq. 1) and the EC is the fact that the former weights the correlation by the centrality of the neighbors, a strategy to obtain this neighborhood-centrality measure is to subtract the DC coefficients from the original EC values:
| [11] |
Fig. 6 illustrates the coefficients associated with the transition between the apo and PRFAR-bound states [i.e., ]. This analysis highlights residues fN14, fV48, fR59, fT61, fL65, fQ67, fV69, fR95, fG96, and hN14 as the ones neighboring the amino acids with a large increase of centrality upon PRFAR binding. With the exception of residues fT61, fL65, and fV69, all of the amino acids pointed out by this analysis coincide with those that have large PRFAR-induced EC variation. Remarkably, single-point mutation of residues fV48 and fN98 (in the vicinity fG96) have a dramatic effect on the PRFAR-induced activation of IGPS catalytic activity (40). On the other hand, the relevance of fV48 as part of the hydrophobic cluster in f2 and fE67 and fR95 as part of the surface salt-bridge network at f2/f3 have been suggested by tedious inspection of MD trajectories, while here they are rapidly detected by the comparative EC analysis.
Fig. 6.
Difference between EC and DC, , for the PRFAR-binding process (PRFAR-bound – apo) for an exponential damping of Å as a function or the residue index (Left) and plotted on top of the protein representation (Right). Red and blue values are regions that, respectively, gain and lose correlation with central amino acids upon PRFAR binding. The domains with higher PRFAR-induced increase are labeled.
Interestingly, the amplitude of the distribution increases with the reduction of the locality factor (SI Appendix, Fig. S2, Upper). This result shows that the difference between EC and DC arise mainly from short-range correlations, which is fully consistent with the neighborhood-centrality interpretation (Eq. 11).
The Locality Factor
Fig. 7 shows the calculated EC coefficients at different values of to further analyze the impact of the locality factor in the overall centrality distribution. We note that reducing the damping parameter down to Å does not significantly affect the overall EC differences between apo and PRFAR-bound IGPS. The same allosteric pathway for IGPS is revealed whether or not we include the correlations between residues separated by long distances. Moreover, the sideL/sideR structure is maintained at all ’s. These results imply that the allosteric pathway is dominated by short-range correlations. We note that the locality factor decays with the average distance between residues along the entire MD trajectory. Thus, the locality factor filters long-range correlations and also infrequent short-range correlations ( i.e., short-lived local interactions). Since no qualitative changes are observed for a broad range of damping factors (Fig. 7), we conclude that the flow of allosteric communication does not include infrequent contacts or long-range conformational motions. These findings point to a very fundamental aspect of IGPS allosterism with implications for design of therapeutic agents.
Fig. 7.
Centrality differences (PRFAR-bound – APO) for different values of . Regions in red and blue correspond to gains and lose of centrality, respectively.
The average distance is 3.8 Å. Therefore, the correlation matrix becomes almost diagonal (SI Appendix) when Å, and the key EC trend is most likely masked by numerical errors.
As discussed above, it is possible to select the correlations whose range is below a certain distance threshold from the overall motion of the system simply by introducing the locality factor . On the other hand, it is possible to analyze the nature of long-range contributions, even though short-range components dominate the overall correlation pattern. Fig. 8 shows variations in the EC coefficients due to the long-range component of correlations, computed as follows:
| [12] |
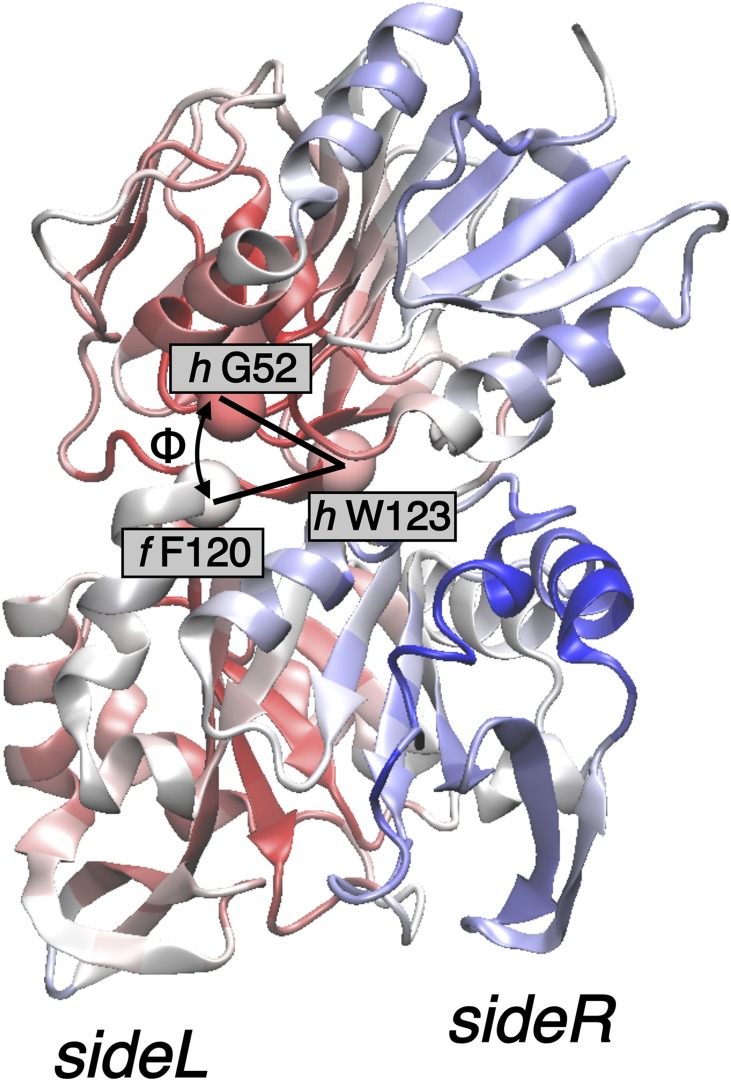
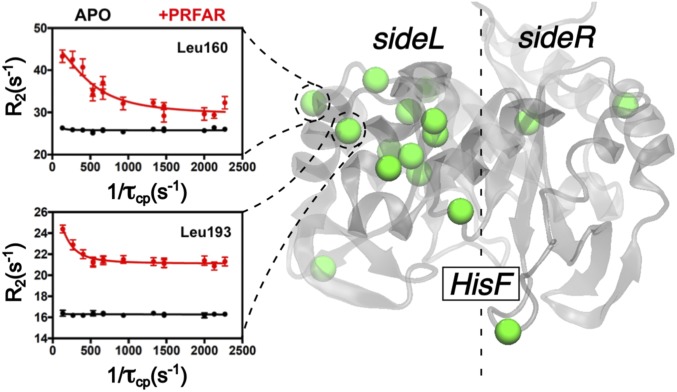
for = 5 Å. Remarkably, the long-range distribution also preserves the qualitative sideL/sideR structure, although the trends are inverted with respect to the short-range picture, and the largest increase in the long-range centrality coefficients upon PRFAR binding is mainly located on sideL. These results are consistent with the presence of an interdomain “breathing” motion, as reported (9, 20) (Fig. 8, dashed black lines forming an angle ). The large structural (long-range) rearrangement associated with this motion increases its frequency upon PRFAR binding almost fourfold (20). Consequently, the highest gain of long-range correlation that occurs mainly in sideL can be assigned to this low-frequency motion. In agreement with this, our solution NMR relaxation dispersion experiments show that the PRFAR-induced millisecond motions are primarily located on sideL (Fig. 9), which supports the existence of a large motion with maximum amplitude on sideL, as determined by the long-range centrality analysis. Furthermore, effectors weaker than PRFAR induce weaker perturbations on sideL of HisF (21), suggesting that the breathing motion influences the allosteric activation of IGPS. Remarkably, Fig. 9 shows experimental evidence of the suggested breathing motion (47).
Fig. 8.
Variation in the PRFAR-induced centrality coefficients caused by the application of the locality factor ( Å). Red to blue scale characterizes a gain or loss of centrality, respectively, upon the application of the locality factor.
Fig. 9.
NMR relaxation dispersion experiments characterizing the PRFAR-induced millisecond motions in the HisF subunit of IGPS. Right highlights the residues that show the highest variation on their relaxation-dispersion profile upon PRFAR binding. Left shows two representative relaxation dispersion curves for residues Leu160 (Upper) and Leu193 (Lower) in the apo and PRFAR-bound states (black and red, respectively).
The NMR study presented in Fig. 9 also provides an experimental proof for the presence of the sideL/sideR structure predicted by the EC analysis, in which the two sides of IGPS display clear differences in terms of their dynamical features. Interestingly, the overall difference between sideR and sideL values is considerably reduced when going from 5 to 10 Å, and for Å the distribution becomes almost uniform. This indicates that the characteristic correlation distances involved in the breathing mode are within the range of 5–20 Å (SI Appendix).
Conclusions
We have introduced a methodology based on the EC of MI to elucidate allosteric pathways at an atomistic level. The method allows for identification of amino acid residues that are critical for allosteric signaling and characterization of the correlation distances that determine allosterism. Furthermore, the analysis of DC allows us to identify key residues neighboring amino acids with a large increase in centrality, consistent with recent site-directed mutagenesis experiments (40).
The EC scheme introduced in this work provides a valuable approach to obtain the main mode of collective correlation responsible for the allosteric signal, beyond the capabilities of standard principal component methods. The analysis is based on the generalized MI which correctly captures noncollinear correlations beyond the well-known limitations of methods based on the Pearson correlation coefficients.
We have applied the EC method to the IGPS enzyme to demonstrate the capabilities of our approach to identify the most important amino acid residues involved in the allosteric mechanism triggered upon effector binding. The EC results show excellent agreement with our solution NMR relaxation experiments, providing experimental evidence of the previously hypothesized interdomain breathing motion (9, 20, 40, 47).
The locality-based centrality analysis shows that the allosteric pathway is established by short-range correlations. Nevertheless, as observed (20), the resulting breathing motion enhances the allosteric signal. Furthermore, the EC method identifies helix h1 (HisH: 12–25) as one of the domains with higher centrality increase upon PRFAR binding. We anticipate that site-directed mutagenesis or the use of allosteric drugs could target helix h to control enzymatic activity. The reported results should motivate a wide range of studies to control IGPS activity by disrupting h dynamics, considering that IGPS is a potential therapeutic target that is found in bacteria as well as in some plants and fungi, but not in mammals.
Supplementary Material
Acknowledgments
J.P.L. and V.S.B. were supported by NIH Grant GM106121. V.S.B. also acknowledges supercomputer time from the National Energy Research Scientific Computing Center, XSEDE, and the Yale University Faculty of Arts and Sciences High Performance Computing Center, partially funded by National Science Foundation (NSF) Grant CNS 08–21132. I.R. was supported by École Normale Supérieure de Lyon (ENS-Lyon) “Fonds Recherche, MI-LOURD-FR15” and “Institut Rhônalpin des Systèmes Complexes (IXXI)” and the use of high-performance computing resources of the “Pôle Scientifique de Modélization Numérique” at the ENS-Lyon, France. J.P.L. was supported by NSF Grant MCB 1615415.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1810452115/-/DCSupplemental.
References
- 1.Csermely P, Korcsmáros T, Kiss HJM, London G, Nussinov R. Structure and dynamics of molecular networks: A novel paradigm of drug discovery: A comprehensive review. Pharmacol Ther. 2013;138:333–408. doi: 10.1016/j.pharmthera.2013.01.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wagner JR, et al. Emerging computational methods for the rational discovery of allosteric drugs. Chem Rev. 2016;116:6370–6390. doi: 10.1021/acs.chemrev.5b00631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Goodey NM, Benkovic SJ. Allosteric regulation and catalysis emerge via a common route. Nat Chem Biol. 2008;4:478–482. doi: 10.1038/nchembio.98. [DOI] [PubMed] [Google Scholar]
- 4.Reetz MT, Soni P, Acevedo JP, Sanchis J. Creation of an amino acid network of structurally coupled residues in the directed evolution of a thermostable enzyme. Angew Chem. 2009;121:8268–8272. doi: 10.1002/anie.200904209. [DOI] [PubMed] [Google Scholar]
- 5.Ozbil M, Barman A, Bora RP, Prabhakar R. Computational insights into dynamics of protein aggregation and enzyme–substrate interactions. J Phys Chem Lett. 2012;3:3460–3469. doi: 10.1021/jz301597k. [DOI] [PubMed] [Google Scholar]
- 6.Hawkins RJ, McLeish TCB. Coarse-grained model of entropic allostery. Phys Rev Lett. 2004;93:98104–98108. doi: 10.1103/PhysRevLett.93.098104. [DOI] [PubMed] [Google Scholar]
- 7.Ming D, Wall ME. Allostery in a coarse-grained model of protein dynamics. Phys Rev Lett. 2005;95:198103–198107. doi: 10.1103/PhysRevLett.95.198103. [DOI] [PubMed] [Google Scholar]
- 8.Palumbo M, Farina L, Colosimo A, Tun K, Dhar PK. Networks everywhere? Some general implications of an emergent metaphor. Curr Bioinformatics. 2006;1:219–234. [Google Scholar]
- 9.Rivalta I, et al. Allosteric pathways in imidazole glycerol phosphate synthase. Proc Natl Acad Sci USA. 2012;109:E1428–E 1436. doi: 10.1073/pnas.1120536109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vanwart AT, Eargle J, Luthey-Schulten Z, Amaro RE. Exploring residue component contributions to dynamical network models of allostery. J Chem Theor Comput. 2012;8:2949–2961. doi: 10.1021/ct300377a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ribeiro AAST, Ortiz V. A chemical perspective on allostery. Chem Rev. 2016;116:6488–6502. doi: 10.1021/acs.chemrev.5b00543. [DOI] [PubMed] [Google Scholar]
- 12.Blacklock K, Verkhivker GM. Computational modeling of allosteric regulation in the Hsp90 chaperones: A statistical ensemble analysis of protein structure networks and allosteric communications. PLoS Comput Biol. 2014;10:1–21. doi: 10.1371/journal.pcbi.1003679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sun X, Ågren H, Tu Y. Microsecond molecular dynamics simulations provide insight into the allosteric mechanism of the Gs protein uncoupling from the β2 adrenergic receptor. J Phys Chem B. 2014;118:14737–14744. doi: 10.1021/jp506579a. [DOI] [PubMed] [Google Scholar]
- 14.Zhu Y, Ma B, Qi R, Nussinov R, Zhang Q. Temperature-dependent conformational properties of human neuronal calcium sensor-1 protein revealed by all-atom simulations. J Phys Chem B. 2016;120:3551–3559. doi: 10.1021/acs.jpcb.5b12299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Appadurai R, Senapati S. Dynamical network of HIV-1 protease mutants reveals the mechanism of drug resistance and unhindered activity. Biochemistry. 2016;55:1529–1540. doi: 10.1021/acs.biochem.5b00946. [DOI] [PubMed] [Google Scholar]
- 16.Xu L, et al. Recognition mechanism between lac repressor and DNA with correlation network analysis. J Phys Chem B. 2015;119:2844–2856. doi: 10.1021/jp510940w. [DOI] [PubMed] [Google Scholar]
- 17.VanWart AT, Eargle J, Luthey-Schulten Z, Amaro RE. Exploring residue component contributions to dynamical network models of allostery. J Chem Theor Comput. 2012;8:2949–2961. doi: 10.1021/ct300377a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Palermo G, et al. Protospacer adjacent motif-induced allostery activates CRISPR-Cas9. J Am Chem Soc. 2017;139:16028–16031. doi: 10.1021/jacs.7b05313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Guo J, Zhou HX. Protein allostery and conformational dynamics. Chem Rev. 2016;116:6503–6515. doi: 10.1021/acs.chemrev.5b00590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rivalta I, et al. Allosteric communication disrupted by a small molecule binding to the imidazole glycerol phosphate synthase protein–protein interface. Biochemistry. 2016;55:6484–6494. doi: 10.1021/acs.biochem.6b00859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lisi G, et al. Dissecting dynamic allosteric pathways using chemically related small-molecule activators. Structure. 2016;24:1155–1166. doi: 10.1016/j.str.2016.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Palermo G, et al. Key role of the rec lobe during CRISPR–Cas9 activation by sensing, regulating, and locking the catalytic HNH domain. Q Rev Biophys. 2018;51:e9. doi: 10.1017/S0033583518000070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Li S, et al. The mechanism of allosteric inhibition of protein tyrosine phosphatase 1B. PLoS ONE. 2014;9:1–10. doi: 10.1371/journal.pone.0097668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sethi A, Eargle J, Black AA, Luthey-Schulten Z. Dynamical networks in tRNA:protein complexes. Proc Natl Acad Sci USA. 2009;106:6620–6625. doi: 10.1073/pnas.0810961106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ricci CG, Silveira RL, Rivalta I, Batista VS, Skaf MS. Allosteric pathways in the ppar-rxr nuclear receptor complex. Sci Rep. 2016;6:19940. doi: 10.1038/srep19940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Papaleo E, Lindorff-Larsen K, De Gioia L. Paths of long-range communication in the e2 enzymes of family 3: A molecular dynamics investigation. Phys Chem Chem Phys. 2012;14:12515–12525. doi: 10.1039/c2cp41224a. [DOI] [PubMed] [Google Scholar]
- 27.David-Eden H, Mandel-Gufreund Y. Revealing unique properties of the ribosome using a network based analysis. Nucleic Acid Res. 2008;36:4641–4652. doi: 10.1093/nar/gkn433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jiang X, Chen C, Xiao Y. Improvements of network approach for analysis of the folding free-energy surface of peptides and proteins. J Comput Chem. 2010;31:2502–2509. doi: 10.1002/jcc.21544. [DOI] [PubMed] [Google Scholar]
- 29.Szilagyi A, Nussinov R, Csermely P. Allo-network drugs: Extension of the allosteric drug concept to protein-protein interaction and signaling networks. Curr Top Med Chem. 2013;13:64–77. doi: 10.2174/1568026611313010007. [DOI] [PubMed] [Google Scholar]
- 30.Lange OF, Grubmüller H. Generalized correlation for biomolecular dynamics. Proteins: Struct Funct Bioinformatics. 2006;62:1053–1061. doi: 10.1002/prot.20784. [DOI] [PubMed] [Google Scholar]
- 31.Lange OF, Grubmüller H. Full correlation analysis of conformational protein dynamics. Proteins: Struct Funct Bioinformatics. 2008;70:1294–1312. doi: 10.1002/prot.21618. [DOI] [PubMed] [Google Scholar]
- 32.Savoie BM, et al. Mesoscale molecular network formation in amorphous organic materials. Proc Natl Acad Sci USA. 2014;111:10055–10060. doi: 10.1073/pnas.1409514111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Doshi U, Holliday MJ, Eisenmesser EZ, Hamelberg D. Dynamical network of residue–residue contacts reveals coupled allosteric effects in recognition, catalysis, and mutation. Proc Natl Acad Sci USA. 2016;113:4735–4740. doi: 10.1073/pnas.1523573113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ruhnau B. Eigenvector-centrality - A node-centrality? Soc Networks. 2000;22:357–365. [Google Scholar]
- 35.Chaudhuri BN, et al. Crystal structure of imidazole glycerol phosphate synthase. Structure. 2001;9:987–997. [PubMed] [Google Scholar]
- 36.Myers RS, Jensen JR, Deras IL, Smith JL, Davisson VJ. Substrate-induced changes in the ammonia channel for imidazole glycerol phosphate synthase. Biochemistry. 2003;42:7013–7022. doi: 10.1021/bi034314l. [DOI] [PubMed] [Google Scholar]
- 37.Floyd RW. Algorithm 97: Shortest path. Commun ACM. 1962;5:345. [Google Scholar]
- 38.Girvan M, Newman MEJ. Community structure in social and biological networks. Proc Natl Acad Sci USA. 2002;99:7821–7826. doi: 10.1073/pnas.122653799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Newman MEJ. Modularity and community structure in networks. Proc Natl Acad Sci USA. 2006;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lisi GP, East KW, Batista VS, Loria JP. Altering the allosteric pathway in IGPS suppresses millisecond motions and catalytic activity. Proc Natl Acad Sci USA. 2017;114:E3414–E3423. doi: 10.1073/pnas.1700448114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Watkins DS. Fundamentals of Matrix Computations. 3rd Ed John Wiley & Sons; New York: 2010. [Google Scholar]
- 42.Jimenez-Martinez J, Negre CFA. Eigenvector centrality for geometric and topological characterization of porous media. Phys Rev E. 2017;96:013310. doi: 10.1103/PhysRevE.96.013310. [DOI] [PubMed] [Google Scholar]
- 43.Amadei A, Linssen ABM, Berendsen HJC. Essential dynamics of proteins. Proteins: Struct Funct Bioinformatics. 1993;17:412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- 44.Hayward S, de Groot BL. Normal Modes and Essential Dynamics. Humana Press; Totowa, NJ: 2008. [DOI] [PubMed] [Google Scholar]
- 45.Meyer T, et al. Essential dynamics: A tool for efficient trajectory compression and management. J Chem Theor Comput. 2006;2:251–258. doi: 10.1021/ct050285b. [DOI] [PubMed] [Google Scholar]
- 46.Morzan UN, Capece L, Marti MA, Estrin DA. Quaternary structure effects on the hexacoordination equilibrium in rice hemoglobin rHb1: Insights from molecular dynamics simulations. Proteins: Struct Funct Bioinformatics. 2013;81:863–873. doi: 10.1002/prot.24245. [DOI] [PubMed] [Google Scholar]
- 47.Amaro RE, Sethi A, Myers RS, Davisson VJ, Luthey-Schulten ZA. A network of conserved interactions regulates the allosteric signal in a glutamine amidotransferase. Biochemistry. 2007;46:2156–2173. doi: 10.1021/bi061708e. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.