A Systematic Evaluation of Effect of Adherence Patterns on the Sample Size and Power of a Clinical Study

Abstract

The objective of our study was to evaluate the effect of adherence patterns on the sample size and power of a clinical trial. Simulations from a population pharmacokinetic/pharmacodynamic (PK/PD) model linked to an adherence model were used. Four types of drug characteristics, such as long (~35 hours) and short (~12 hours) half‐life in combination with earlier or delayed time to reach steady‐state PD end points were studied. Adherence patterns were simulated using Markov chains. Our results clearly demonstrate the significant impact of varying levels and patterns of nonadherence on the sample size and power of a study. For drugs with short half‐lives the evidence to support efficacy could be diluted by various patterns of nonadherence that would make its efficacy indistinguishable from the response to placebo. Prospectively utilizing clinical trial simulations with thorough incorporation of various adherence patterns would provide valuable information when designing a trial.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Although the importance of adherence is well recognized in the clinical pharmacology community, its incorporation and utility in clinical trial simulations is suboptimal. Considering adherence as a static or summary variable based on pill counts may not be sufficient to predict the impact of nonadherence in trials designed to determine the efficacy of a drug. We show that it is important to incorporate the magnitude and patterns of nonadherence in clinical trial simulations.

• WHAT QUESTION DID THIS STUDY ADDRESS?

This study quantifies the impact of adherence patterns on the sample size and power of a hypothetical trial, giving careful consideration to its PK/PD properties of the compound under study. Using Monte Carlo simulations, we clearly demonstrate the impact of various patterns of nonadherence in conjunction with the PK/PD properties of the compound on sample size requirements.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

This study provides compelling evidence for integrating adherence patterns along with population PK/PD models in clinical trial simulations. It particularly illustrates the impact of different scenarios for the PK/PD characteristics, including a compound with a long half‐life that rapidly attains steady‐state PD effects. In combination with full adherence, this scenario required the smallest sample size and had optimal power. At the other extreme, a compound with a short half‐life, a delayed onset of its PD effect, onset, and combined with poor adherence may result in a trial outcome that fails to demonstrate a significant difference compared to the placebo group, resulting in a type II statistical error, unless sample sizes are very large. Adherence patterns in conjunction with PK/PD characteristics of compound can greatly affect the outcome of a clinical study and, therefore, require careful consideration in the design of a study.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

Thoughtful simulations of clinical trials using population PK/PD models linked with quantitative adherence models provide valuable information on study design aspects. There are a number of clinical trial simulation programs available that could be used for such simulations. Collecting data on adherence patterns in specific populations early in the drug development programs would greatly assist in informing clinical trial simulations.

Medication adherence has been defined as a process by which a patient takes their medications as prescribed and is comprised of three components: initiation, which indicates that the first dose has been taken; implementation, a measure of the fidelity of the individual's dosing regimen compared with the prescribed regimen; and persistence, which is the time from the initiation to the cessation of drug therapy.1 For a more thorough treatment of this concept, readers are referred to Vrijens et al., Vrijens and Urquhart,1, 2 and Blaschke et al.3 Nonadherence to prescribed medications is a well‐known phenomenon in the medical community dating back to the days of Hippocrates. Much of the older literature on this subject referred to this phenomenon as “compliance.” The Ascertaining Barriers for Compliance (the ABC project) proposed new terminology and has recommended the use of the term “adherence” rather than “compliance” because of the negative connotation associated with the term “compliance,” implying that patients are subservient to prescribers. Nonadherence to medications is a worldwide phenomenon and it has been found that in developed countries, adherence rate, expressed as a percent of prescribed doses taken, averages around 50% for chronic illnesses.4 Recent divergent results of several large phase III clinical trials of pre‐exposure prophylaxis to prevent acquisition of human immunodeficiency virus5, 6, 7, 8, 9, 10, 11 serves as a wakeup call for drug developers to take action on the most relevant covariate that determines therapeutic efficacy—whether or not the participant in a clinical trial actually takes the drug under study as required by the protocol. Several thought‐provoking commentaries have been published on the need for collecting and monitoring adherence in clinical trials.3, 12 In a progressive move, regulatory bodies have realized the importance of adherence and have updated recommendations to improve adherence in clinical trials. In the draft guidance on “Enrichment strategies for clinical trials to support approval of human drugs and biological products,” the US Food and Drug Administration (FDA) recommends practices that encourage adherence by making participants aware of the conditions and demands of clinical trials, and using adherence prompts and alert systems, such as “smart bottles,” to monitor study drug use.13 A recent addendum to the International Conference on Harmonization E9 guidance recognizes adherence as an important intercurrent event that can offer important information on treatment effect.14 This addendum proposes to precisely define the treatment effects (estimands) in a clinical trial considering the intercurrent events.15 This can be considered a major improvement over the standard “intent to treat” approach currently used in the majority of randomized clinical trials. In another innovative move, the FDA approved the first‐ever “digital pill” for tracking and monitoring adherence in patients diagnosed with schizophrenia, an encouraging development for drug developers, medical practitioners, and patients to appropriately address adherence issues. Encouraging and monitoring adherence can help drug developers to separate the true efficacy and toxicity signals from noise by ensuring that trial participants take the drug(s) under study as required by the protocol. The improved reliability of early proof‐of‐principle and proof‐of‐concept studies due to significantly better adherence fits well with the paradigm of “Learn‐Confirm” for drug development proposed by Lewis Sheiner.16

As the pharmaceutical industry and regulatory agencies continue to adopt the model‐informed drug development philosophy,17 clinical trial simulation (CTS) is increasingly being used as a tool for designing clinical trials.18, 19, 20 The models most used in CTS are population pharmacokinetic (PK), pharmacodynamic (PD) models along with the important intercurrent behaviors, such as adherence and dropout models that are very likely to influence the outcome. However, in most CTSs, adherence is not modeled with the granularity that is necessary, and traditional measures of adherence in actual clinical trials, such as pill counts and patient diaries, are generally biased toward adherence and do not provide the fine granularity necessary in a quantitative framework to inform the analysis of the trial data. Adherence to medications is often reported as a summary variable, such as total number of doses taken or missed using pill counts. However, it is very likely that specific patterns of dose‐taking result in particular therapeutic outcomes and different patterns of adherence may lead to a wide distribution of outcomes. Markov chain models of adherence have been proposed to inform CTSs by providing discrete time series of dose‐taking behavior.18, 21

In this study, we have incorporated various adherence patterns along with the PK/PD properties of drug molecules that are commonly encountered in drug development into a model framework. Our goal was to evaluate the effect of varying adherence patterns on the sample size and power of clinical studies using CTS in particular to avoid a type I error for drugs that are efficacious.

Methods

The approach was to simulate the attainment of a PD end point from linked adherence, PK and PD submodels, as shown in Figure 1. Various PK and PD parameters of the “drug” or “compound” under investigation were systematically altered to allow the findings of the simulations to mimic results that would apply to actual clinical trials. Within each combination of differing drug properties, varying adherence patterns were evaluated by systematically altering the adherence model input parameters. Details of the PK, PD, and adherence submodels are provided in the following sections.

Figure 1.

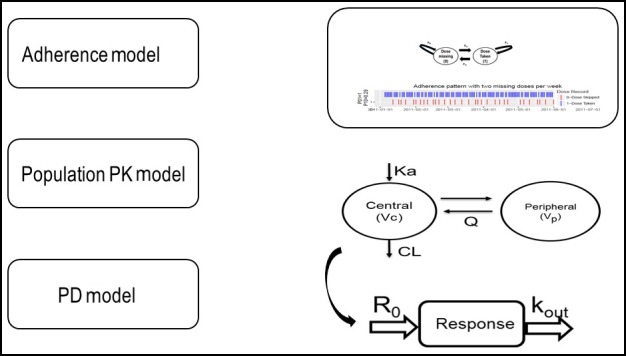
Linked adherence, population pharmacokinetic (PK) and pharmacodynamic (PD) models used in simulations. Adherence model: two‐state (dose taken = 1, dose missed = 0), discrete time, Markov Chain model with transition probabilities (P01, P00, P10, and P11) to simulate adherence patterns. Population PK model: two‐compartment model with first order absorption and elimination parameterized as clearance (CL), central volume (V _c), peripheral volume (V _p), intercompartmental clearance (Q), and absorption rate constant (K _a). PD model: indirect (inhibitory) response model, where drug concentration inhibits the production rate (R ₀) and response is cleared by a turnover rate constant of k _out.

Population PK model

A two‐compartment open model with first order absorption and elimination was used as a structural model. The stochastic model included an exponential error (30% coefficient of variance (CV)) for the between‐subject variability in the parameters of clearance and volume of distribution. A proportional error model (30% CV) was used as the residual variability model. Two PK scenarios were simulated by altering clearance: Scenario A = a long half‐life compound (~35 hours); and Scenario B = a short half‐life compound (~12 hours). The PK parameters used in simulations are shown in Table 1.

Table 1.

PK/PD characteristics of simulated scenarios

PK/PD parameters [units]	AC (long half‐life and rapid onset)	AD (long half‐life and delayed onset)	BC (short half‐life and rapid onset)	BD (short half‐life and delayed onset)
Absorption rate constant (K a) [h−1]	1	1	1	1
Central volume (V c) [L]	534	534	534	534
Peripheral volume (V p) [L]	1,530	1,530	1,530	1,530
Clearance (CL) [L/h]	50a	50a	150b	150b
Intercompartmental clearance (Q) [L]	144	144	144	144
Rate of production (K in) [h−1]	1	1	1	1
Turnover rate (Kout) [h−1]	0.0165c	0.01d	0.0165c	0.01d
Inhibitory concentration‐50 (IC50) [ng/mL]	1	1	1	1

PK/PD, pharmacokinetic/pharmacodynamic.

^aLong half‐life characteristic. ^bShort half‐life characteristic. ^cRapid PD onset characteristic. ^dDelayed onset of PD characteristic.

Population PD model

An indirect response model in which the “drug” acts by inhibiting a biomarker related to the efficacy of the drug was used as the structural PD model. Inhibition of the biomarker for PD was assumed to be reversible with discontinuation of drug. An exponential error model (40% CV) was used for between‐subject variability on half‐maximal inhibitory concentration, K _in, and K _out parameters. A proportional error model (40% CV) was used as the residual variability model. Two PD scenarios were simulated by altering K _in: Scenario C = faster onset of action (~2 weeks to reach steady‐state); and Scenario D = slower onset of action (~4 weeks to reach steady‐state). The PD parameters used in simulations are shown in Table 1.

Adherence model

A first order, homogenous, two‐state Markov chain model was used for simulating adherence patterns. Two states of the Markov model were dose taken = 1 and dose missed = 0. The Markov model was parameterized using the following transition probability matrix, as shown below:

$\left[\begin{array}{cc}P00& P01\\ P10& P11\end{array}\right]$

Where P is the probability of transition from one state to another (e.g., 0–1) or staying within the same state (e.g., 0–0) in fixed discrete time steps (1 day in this case). Using this transition matrix structure above, 200 adherence patterns were generated. The full adherence dataset had no missing doses. By varying P00 and P01 from 0.5 to 1, varying adherence patterns ranging from 50−100% of adherence were generated. Simulated Markov chains were summarized by two metrics, drug holidays per month, and nontherapeutic time (NTT). Drug holidays per month were calculated as the sum of missing doses in a 30‐day period. Given the once‐daily dosing in the simulation study, the duration of action for each dose was assumed to be 24 hours. The NTT was calculated as the cumulative time (in days) that a sequential dose was missed in a Markov chain. As NTT is a cumulative measure of the entire Markov chain it is a pattern indicator, unlike the number of holidays per month. The Markov chains were simulated using the R software package version 3.3.2.22

Simulation of clinical trials

Four representative clinical trial scenarios were created by combining different properties of PK and PD parameters, as described above:

1. Long half‐life drug with rapid onset of action (designated AC in Table 1).

2. Long half‐life drug with delayed onset of action (designated AD in Table 1).

3. Short half‐life drug with rapid onset of action (designated BC in Table 1).

4. Short half‐life drug with delayed onset of action (designated BD in Table 1).

For each representative combined PK/PD property, the effect of adherence patterns (50%, 60%, 70%, 80%, 90%, and 100%) was evaluated in a simulated clinical trial. Thus, a total of 24 clinical trials were simulated representing 6 adherence patterns for each of the 4 representative drug properties. Each clinical trial included 200 virtual subjects. This number was based on the size of a typical phase II study. A once‐daily dosing regimen was used. The duration of the trial was set at 6 months (24 weeks). PK samples were simulated at 0, 2, 4, 6, 8, 10, 12, and 24 hours on day 10 at steady‐state. The PD variable was simulated every day for the entire study period in 24‐hour intervals for further processing. The R code used for dataset preparation is provided in the Data S1. Simulations were conducted using NONMEM, version 7.3 (ICON, Ellicott City, MD) in conjunction with a g95 (64‐bit) compiler using Perl‐Speaks NONMEM, version 4.6.0 (PSN) as an interface to run NONMEM.

Sample size and power calculations

Calculation of sample size

Sample size and power was calculated using the two‐sample, continuous outcome, two‐tailed t test approach, with type I and type II errors fixed at 5% and 10%, respectively.23

A type I error is the incorrect rejection of a true null hypothesis (the error of rejecting a null hypothesis when it is actually true), whereas a type II error is incorrectly retaining a false null hypothesis. Sample size was calculated as follows:

$$\mathrm{Sample}\mathrm{size}(N)=2{(Z_{\mathrm{\alpha }}+Z_{\mathrm{\beta }})}^2{\left(\frac{\mathrm{\sigma }}{\mathrm{\Delta }}\right)}^2$$

Where Z _α is a type I error (1.96 for two‐tailed test at 5%), Z _β is a type II error (1.28 for two‐tailed test at 10%), delta (Δ) is the absolute mean difference between test (${\mathrm{\mu }}_1$) and placebo (${\mathrm{\mu }}_2$) groups, and σ is the pooled SD calculated as follows:

$\mathrm{\sigma }=\sqrt{\frac{S{1}^2+S{2}^2}{2}}$

Where S1 and S2 are SDs of test and placebo groups, respectively. The simulated PD data point at the last day of the 24th week was used for calculation of ${\mathrm{\mu }}_1$ and S1. For the placebo response (${\mathrm{\mu }}_2$) and SD (S2), PD data at baseline (time = 0) was utilized. Mean values of the placebo group were empirically fixed at a particular value to achieve various effect sizes. The placebo response was assumed to follow proportional error and S2 was scaled at each empirical placebo mean value.

Calculation of power

$\mathrm{Beta}=\mathrm{\Phi }\left[\left(\frac{\mathrm{\Delta }}{\mathrm{\sigma }}\right)\left(\sqrt{\frac{N}{2}}\right)-Z_{\mathrm{\alpha }}\right]$

Φ is a function to convert beta to Z values and N is the sample size. Estimates of (1−beta) are converted to percentage power. Power was calculated, fixing sample size to 100. This number was selected to give the optimal power for a group with the most favorable variables, like long half‐life and rapid onset with full adherence and a Δ of 0.2.

Both sample size and power were estimated at various Δ values ranging from 0.1−1 with increments of 0.1. Comparison of results was made at Δ of 0.2, 90% power, and adherence scenarios of 50–100% for sample size calculations. For calculation of power, comparisons were made at Δ of 0.2, sample size of 100, and adherence scenarios of 50–100%.

Relation between adherence patterns and NTT

To understand the relation between various adherence patterns and NTT, five simulated subjects from 70% adherence rate with differing NTTs were selected. Their PK profile is simulated for a period of 1 month. The simulated PK profile is overlaid with their adherence pattern for the same period in a plot for comparison.

Results

The results from this CTS study clearly demonstrate the impact of various scenarios of nonadherence on the sample sizes needed to achieve a statistically significant outcome for forgiving (long terminal half‐life) and nonforgiving (short terminal half‐life) drugs. Depending on the pattern of nonadherence, the calculated mean drug holidays per month ranged from 3−15 days. As expected, the calculated NTT exhibited an increasing trend with increasing nonadherence rates (Table S1).

As noted earlier the sample size was calculated using the two‐sample, continuous outcome, two‐tailed, t test approach, with type I and type II errors fixed at 5% and 10%, respectively. Power was calculated by fixing type I errors at 5% and sample sizes as 100. Comparisons were made at Δ of 0.2. When the impact of PK/PD characteristics on the sample size and power were evaluated, the drug feature of long half‐life and rapid onset of effect (AC) had the most forgiveness to nonadherence when compared with other scenarios. Adherence levels indicated here are summary adherence measures derived from varying adherence patterns and expressed as average adherence rate. Simulated PK profiles of 5 subjects with an average 70% adherence, but with different NTTs, were generated and are shown in Figure 2. Note that the differences in adherence patterns led to different NTTs and consequently different PK profiles, sample sizes, and power of a study.

Figure 2.

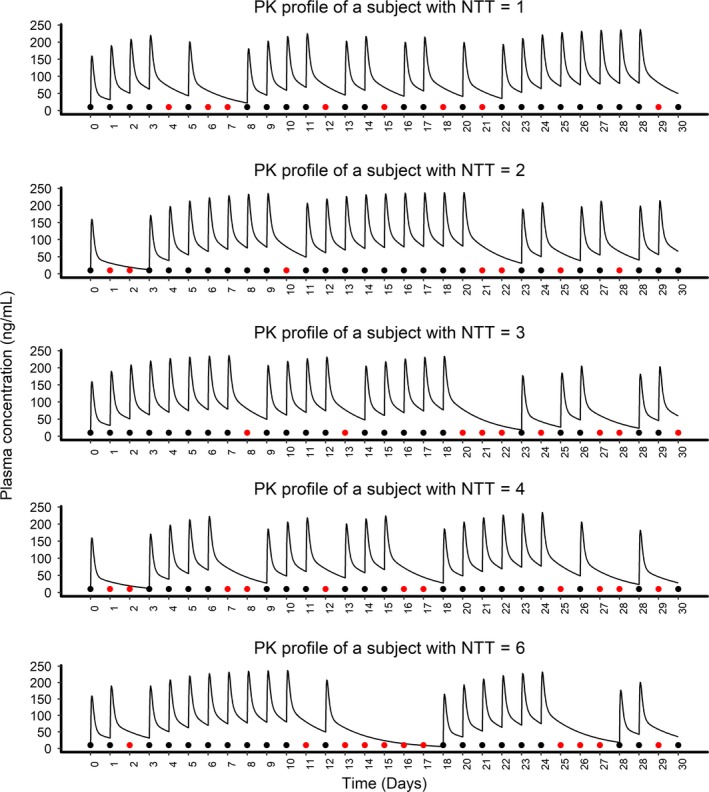
The plot illustrates plasma concentration profile of five subjects for 30 days, with an average adherence of 70% and nontherapeutic times (NTTs in days) ranging from 1−6. Solid black points represent doses taken and red points represent missed doses. Two sequential missing of doses were considered as one unit of NTT. Variation in NTTs are due to the difference in adherence patterns even though all of them had an aggregate adherence rate around 70%. PK, pharmacokinetic.

With full (100%) adherence, the sample size required for this group was 100. When the adherence patterns resulted in an overall adherence of about 50%, the required sample size increased to 202 (a twofold increase). The sample size for long half‐life and delayed PD onset group (AD) with full adherence was 105, which increased to 351(3.5‐fold increase) for the 50% adherence category. The drug feature of short half‐life and delayed onset of PD (BD) had the most unfavorable profile. The sample size in this group for the full adherence scenario was 249, which was 2.5 times higher than the comparable group of AC category. In this group (BD), when adherence levels reached 80%, the mean value of the test group reached the levels of the placebo group; therefore, sample size was not calculated below this adherence level. The effect of various adherence patterns (50–100%) on the sample size for the four PK/PD characteristics studied is shown in Figure 3. Sample sizes for the full adherence scenarios were much lower than the various poor adherence scenarios across various PK/PD characteristics studied by CTS. A comprehensive plot of delta vs. sample size for all delta sizes and adherence rate is presented in Figure 4. The effect of various adherence patterns on the PD outcome of placebo and test groups in four PK/PD characteristics are also presented in a comprehensive plot (Figure S1).

Figure 3.

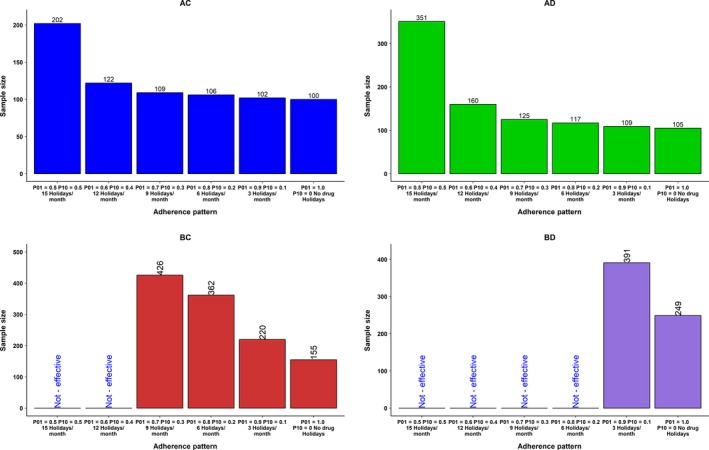
Effect of adherence pattern on the sample size for drug characteristics AC, AD, BC, and BD at the delta level 0.2. Markov model was used to produce various adherence patterns with average adherence rates (summarized as percentage of missed doses) from 50−100%. Specific combinations of transition probabilities (P01 and P10) produce a characteristic adherence pattern with an average adherence rate. Sum of missed doses in a month represented as drug holidays/month for another perspective on adherence pattern. For example, the median drug holidays per month for the 50% adherence group were 15. Holidays/month reduced as adherence rate increased. AC, long half‐life and rapid onset of pharmacodynamics (PDs); AD, long half‐life and delayed onset of PDs; BC, short half‐life and rapid onset of PDs; BD, short half‐life and delayed onset of PDs. In the groups labeled as “Not‐Effective,” the mean value of the test drug overlapped with the mean values of the placebo group. Because the clinical simulation scenarios are with a drug that is active, not effective would represent a type II error, incorrectly retaining a false null hypothesis (also known as a “false‐negative” finding).

Figure 4.

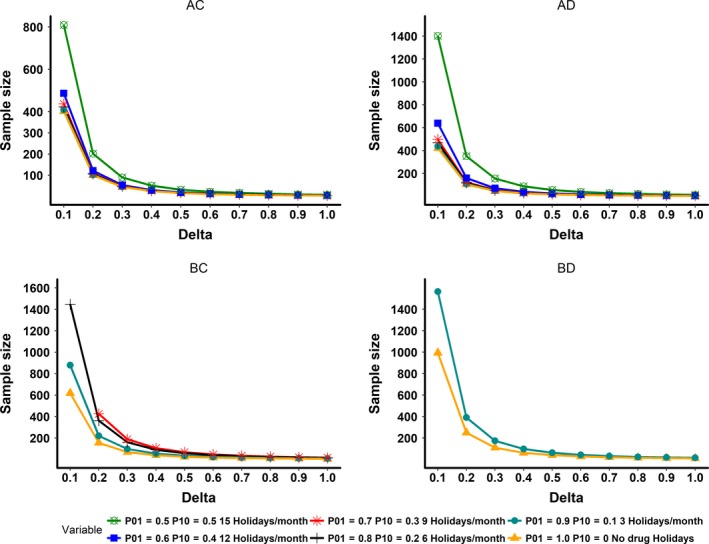
This plot illustrates delta (absolute mean difference value between test and placebo) vs. sample size for all simulated pharmacokinetic/pharmacodynamic (PK/PD) characteristics. AC, long half‐life and rapid onset of PDs; AD, long half‐life and delayed onset of PDs; BC, short half‐life and rapid onset of PDs; BD, short half‐life and delayed onset of PDs. In the groups AC and AD, all adherence rates are represented. In the groups BC and BD, ineffective adherence rates, which resulted in similar mean values for the test group compared to the placebo group were dropped.

The statistical power for the long half‐life and rapid onset of the PD group (AC) was 90% at the full adherence rate and, as expected, gradually decreased along with the drop in adherence. At adherence rates in the range of 50%, the power decreased to 63%. For the long half‐life and delayed onset of the PD group (AD), the power was 88% even with full adherence and decreased to 41% with adherence patterns near 50%. Short half‐life and delayed onset of the PD group (BD) had a power of only 54% even at full adherence. As the overall adherence rate declined in this group (BD), the study power decreased further. At nominal adherence rates of 80% and below in this group (BD), the CTS showed that the mean values of the test and placebo groups were not different and, therefore, power was not calculated. The results demonstrated that favorable PK/PD profiles of long half‐life and rapid PD onset along with full adherence provided adequate statistical power, whereas groups lacking one or more of these characteristics did not attain adequate power. The effect of various adherence patterns (50–100%) on the statistical power for the four PK/PD characteristics at Δ of 0.2 is shown in Figure 5. A comprehensive plot of delta vs. power for all delta sizes and adherence rate is presented in Figure 6.

Figure 5.

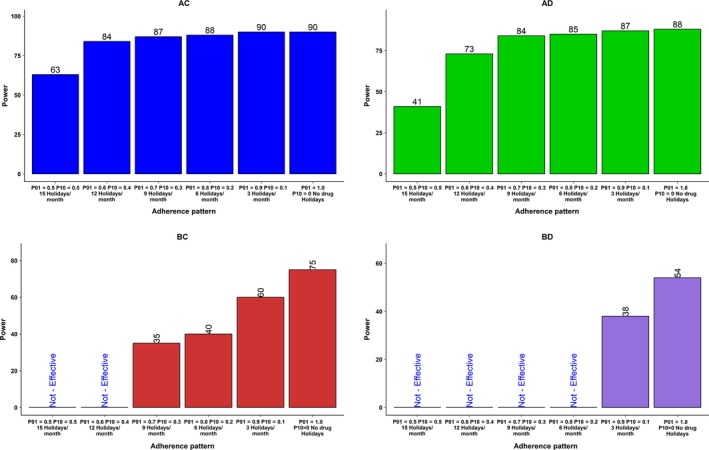
Effect of adherence pattern on the power for drug characteristics AC, AD, BC, and BD at the delta level 0.2. The Markov model was used to produce various adherence patterns with average adherence rates (summarized as percentage of missed doses) from 50−100%. Specific combinations of transition probabilities (P01 and P10) produce a characteristic adherence pattern with an average adherence rate. The sum of missed doses in a month was represented as drug holidays/month for another perspective on adherence pattern. For example, the median drug holidays per month for 50% adherence group were 15. Holidays/month reduced as adherence rate increased. AC, long half‐life and rapid onset of pharmacodynamics (PDs); AD, long half‐life and delayed onset of PDs; BC, short half‐life and rapid onset of PD; BD, short half‐life and delayed onset of PDs. In the groups labeled as “Not‐Effective,” the mean value of the test drug overlapped with the mean values of the placebo group. Because the clinical simulation scenarios are with a drug that is active, not effective would represent a type II error, incorrectly retaining a false null hypothesis (also known as a “false‐negative” finding).

Figure 6.

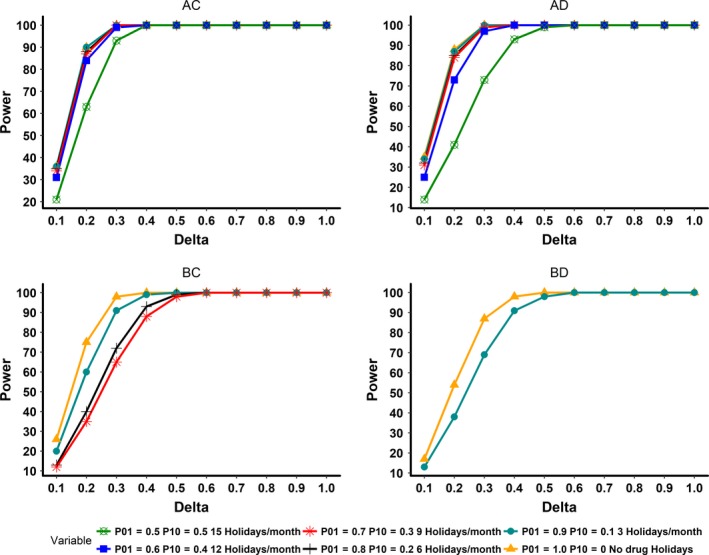
This plot illustrates delta (absolute mean difference value between test and placebo) vs. power for all simulated pharmacokinetic/pharmacodynamic (PK/PD) characteristics. AC, long half‐life and rapid onset of PDs; AD, long half‐life and delayed onset of PDs; BC, short half‐life and rapid onset of PDs; BD, short half‐life and delayed onset of PDs. In the groups AC and AD, all adherence rates are represented. In the groups BC and BD, ineffective adherence rates, which resulted in similar mean values for the test group compared to the placebo group were dropped.

Discussion

In a recent review of 218 failed phase II and III studies, “lack of efficacy” was reported as the reason for failure in 52% of the studies.24 This underscores the need to investigate the underlying causes for the “lack of efficacy,” which might be the correct result but also might not be correct, due to any number of reasons, one of which is poor adherence of clinical trial subjects to the protocol‐specified drug regimen. Harter and Peck25 described the effect of different sources of variability on therapeutic outcomes using data from theophylline. They identified drug formulation, adherence to therapy, PK and PD as sources of variability, and used “propagation of error” techniques to explain the combined effect of these sources on the clinical responses to theophylline. Together, all of these sources described 79% of the variability, with PK and adherence accounting for 67% of the total variability. In their analysis, the authors showed the importance of reducing the major sources of variability in response, in particular “compliance,” in order to reduce variability in therapeutic outcomes. It has been emphasized that adherence monitoring should be considered an important component of drug development and with the advent of new advances in ways to measure adherence26 it is possible to quantify and enhance adherence in clinical trials.

Next, we discuss three clinical examples that we believe would have been predictable using the framework of the prospective use of CTS. In a weight loss study of DOV21947, there was a clear benefit of therapy in adherent vs. nonadherent subjects. In this study, plasma concentrations of DOV21947 were used to classify adherence behavior as a dichotomous variable.27 This was a twice‐daily dosing study with an 8‐week duration. This example fits well into our scenario of short half‐life (given b.i.d. dosing) drug category (BD), in which adherence had a large impact on the PD measure, in this case, weight loss. Although this study was not powered adequately before implementation, it could nevertheless retrospectively differentiate outcomes based on the monitoring of adherence using concentration measurements of the study medication. The second example is a study of imatinib in patients with myeloid leukemia, in which there was a strong correlation between adherence determined by electronic monitoring (MEMS‐based) and a major molecular response that was measured.28 Imatinib has a half‐life of ~18 hours, but its active metabolite has a half‐life of ~40 hours.29 Based on parent drug half‐life, it could be considered closer to the BD scenario in our simulations. The third example is the striking dependence of adherence to the antiretroviral drug, tenofovir, to prevent human immunodeficiency virus 1 infection, known as pre‐exposure prophylaxis.3 Tenofovir and its active intracellular metabolite tenofovir diphosphate have ~18 and 60‐hour half‐lives, respectively. Based on the metabolite half‐life and slower buildup of active metabolite, tenofovir is closer to the AD scenario in our simulations. However, multiple failures in large pre‐exposure prophylaxis clinical trials indicate that forgiveness is low in this particular therapeutic area. Adherence patterns are particularly important in this indication, as it is important to maintain tenofovir concentrations above protection threshold levels at all times of potential viral insult. In addition, tissue‐specific metabolism of tenofovir has been reported,30 which results in variable concentrations at different tissue sites, like rectal and vaginal tissues, which are sites of possible viral insult. Such variability calls for optimal adherence as a key component to ensure prophylaxis.

Although the simulations presented in this article are theoretical in nature, they incorporate commonly encountered PK/PD characteristics and their variability and also incorporated various adherence patterns into the PK/PD model. Scenarios with higher than 40% CV in between‐subject variability in PK/PD parameters and effect of nonadherence were not evaluated in our report. It is recommended to consult literature in specific therapeutic areas and use appropriate parameters to get more realistic assessment of the impact of nonadherence on sample size. The current CTS framework recommended here is not common practice in the pharmacometric community nor has it had a place in classical statistical power or sample size calculations. Nonadherence is known to impact clinical trial outcomes by affecting the statistical power of the study and methods to handle nonadherence using CTS21 and during data analysis have been explored.31 Inclusion of adherence patterns along with various PK/PD characteristics in the current simulations has revealed the impact of these variables on sample size and power. The availability of such information could have helped investigators of the above examples to come up with better study designs, potentially increasing chances of an informative trial, whether positive or negative. We strongly recommend including adherence patterns into a CTS framework to provide more realistic phase II/III outcome predictions.

Effect size (E) is also an important determinant of sample size. Effect size is the absolute mean difference ($\mathrm{Delta}\mathrm{or}\mathrm{\Delta }$) between groups normalized by the SD $(\mathrm{\sigma })$.

$E=\frac{|{\mathrm{\mu }}_1-{\mathrm{\mu }}_2|}{\mathrm{\sigma }}$

In the present study, the impact of adherence patterns on sample size and power was illustrated at $\mathrm{\Delta }$ of 0.2. This represents E values ranging from 0.2−0.4 for the current simulations, given varying $\mathrm{\sigma }$ due to the effect of a particular adherence pattern. This effect size range is considered to be small32 and, therefore, this $\mathrm{\Delta }$ value was chosen for a conservative evaluation. Fukunaga et al.33 studied the effect sizes in 145 trials from 90 test drugs for indications, including schizophrenia, asthma, hypertension, and diabetes. Effect sizes ranged from −0.64 to 1.94 in their study with the average of 0.19. The mean effect sizes in diabetes were much larger (0.48) compared with other indications (0.04−0.17). Our decision to use the range of 0.2–0.4 as effect size is in line with these findings.

Our current analysis provides a justification for quantitatively considering adherence in CTS to understand the impact of adherence patterns on outcomes. The CTS framework is relevant for phase II, phase III, and potentially even in the postmarketing stages of drug development, in which population PK/PD models are available. The current framework can be utilized to explore various possible scenarios with different levels of variability in PK and PD models, drugs with nonlinear PKs, variability in maximal response, and prolonged offset of PD effects. Patient dropout scenarios, variations in time of medicine intake (dose time errors), and nonadherence in the presence of drug‐induced adverse effects can also be explored with the current framework for more granular CTS. A recent report elegantly considers the interaction between poor response and dropout rates in obesity trials in a pharmacometric model framework to predict the outcomes.34 In addition, the input model to describe adherence could be varied depending on the source and type of nonadherence of interest (variation in dose timing, longer holidays, and nonpersistence, etc.). A particular type of scenario of interest to consider as an input model is when adherence declines due to drug‐induced side effects or impact of other aspects of quality of life (e.g., weight gain). In the current simulation, the PD component was a reversible process and the impact of nonadherence could be reversed by enhancing adherence. However, in the case of irreversible PD outcomes, like rejection post organ transplant and development of resistance to anti‐infectives, suboptimal adherence and unfavorable patterns of adherence could result in the complete failure of therapy. These kinds of outcomes could be studied and possibly predicted using a pharmacometric framework that includes a consideration of medication adherence. An important question, which should be asked by anyone contemplating simulating adherence as part of the development of a clinical trial, is “What level of nonadherence should I use for my simulations?” Without prior knowledge on potential adherence patterns, it is difficult to specify a particular level or pattern of nonadherence, and it might be argued that several patterns of nonadherence should be explored in clinical trial simulations to anticipate potential effects of poor adherence. This also points out the importance of collecting adherence profiles for specific study population(s) using an appropriate measure of adherence monitoring, and to potentially prospectively stratify the results based on adherence when seeking regulatory approval. This is one of the recommendations from the FDA guidance on enrichment strategies for clinical trials.13 A precedent of prerandomization screens of adherence to enroll adherent participants has been reported. In an early trial, the Veterans Affairs Cooperative Hypertension studies utilized placebo pills of riboflavin during prerandomization visits. Only subjects who showed florescence in their urine were subsequently randomized to treatments.35 Similarly, The Physician's Health study utilized a prerandomized placebo run‐in to identify subjects with optimal adherence before beginning actual study visits.36 With the technological advances and availability of several adherence monitoring tools,37 prerandomization periods in clinical trials could be a way to collect adherence patterns before and within‐study during phase I and II and even in some phase III trials. This approach could also inform subsequent trials using CTS combined with realistic information about potential adherence and also gauging the potential impact of real‐world adherence behavior on drug efficacy. Improving adherence in clinical trials may enhance the probability of showing drug efficacy (method‐effectiveness). In the postmarketing environment, adherence‐related problems will impact the efficacy of the therapy (also termed use‐effectiveness), if proper plans are not in place to support better adherence, which might include adherence monitoring and interventions in certain diseases and settings. Such analyses may also be supportive of decisions on recommending adherence interventions or monitoring in drug labeling.

Conclusion

Our study assessed the impact of different patterns of adherence and various PK/PD scenarios on the sample size and power of clinical trials. The PK/PD characteristics of long half‐life and rapid onset of action offer some therapeutic forgiveness and tolerance to poor adherence. Drugs with a short half‐life and delayed onset of action may require a higher sample size and have reduced power when adherence is suboptimal. In fact, the low adherence scenarios in this PK/PD group may seem to be ineffective when compared to placebo, possibly resulting in type II errors during clinical development. A decrease in the adherence rate from 100% to 50% led to large increases in sample size in order to attain statistical significance across all the PK/PD scenarios studied. The findings support the value of incorporating realistic adherence patterns in CTS prior to the finalization of the study design by providing accurate estimates of the sample size and power of the proposed study.

Funding

No funding was received for this work.

Conflict of Interest

The authors declared no competing interests for this work.

Author Contributions

S.M., A.C., T.B., and M.J.F. wrote the manuscript. A.C. and S.M. designed the research. S.M. and A.C. performed the research. S.M. and A.C. analyzed the data.

Supporting information

Figure S1. Effect of adherence patterns on the PD profile of drug characteristics of AC, AD, BC, and BD.

Table S1. Drug holiday per month and NTT for various adherence rates.

Data S1. Model code file