Quantitative Understanding of SHAPE Mechanism from RNA Structure and Dynamics Analysis

Abstract

The selective 2’-hydroxyl acylation analyzed by primer extension (SHAPE) method probes RNA local structural and dynamic information at single nucleotide resolution. To gain quantitative insights into the relationship between nucleotide flexibility, RNA 3D structure, and SHAPE reactivity, we develop a 3D Structure-SHAPE Relationship model (3DSSR) to rebuild SHAPE profiles from 3D structures. The model starts from RNA structures and combines nucleotide interaction strength and conformational propensity, ligand (SHAPE reagent) accessibility, and base-pairing pattern through a composite function to quantify the correlation between SHAPE reactivity and nucleotide conformational stability. The 3DSSR model shows the relationship between SHAPE reactivity and RNA structure and energetics. Comparisons between the 3DSSR-predicted SHAPE profile and the experimental SHAPE data show correlation, suggesting that the extracted analytical function may have captured the key factors that determine SHAPE reactivity profile. Furthermore, the theory offers an effective method to sieve RNA 3D models and exclude models that are incompatible with experimental SHAPE data.

Abstract Graphical

INTRODUCTION

RNA plays crucial roles in cellular functions at the level of gene expression and regulation. Recent discoveries concerning new functions of non-coding RNAs have led to an unprecedented rise in demand for the determination of RNA 3D structures.^{1, 2} However, computational prediction of RNA 3D structures from the sequence remains a significant unsolved problem.^1–3 One of the principal challenges arises from the conformational flexibility, especially in the loop and junction regions, and the resultant rugged energy landscape of RNA. The dynamic structures of RNA lead to the diverse catalytic and regulatory roles of RNA in cellular functions^{4, 5} such as transcription, mRNA splicing, and translation.^{6, 7} RNA nucleotides contain a ribose sugar on the backbone chain with a base attached to the 1’ position of the sugar ring. Phosphodiester backbone rotation facilitates large conformational flexibility of RNA.⁸ Hence, base configurations can sample a large portion of the conformational space. RNA bases form a variety of strong base-base and base-backbone interactions,^9–11 which can cause a multitude of stable and metastable RNA conformations. The distribution of the collection of heterogeneous conformations determines RNA structure and stability.

In general, RNA structures contain both rigid and flexible structural elements. The rigid structural elements such as RNA helices and structured loops are primarily stabilized by base-base interactions, such as base pairing and stacking in secondary structures and other noncanonical and long-range interactions in tertiary structures. Both global structural features, such as helix orientations, and local structural features are essential for the interpretation of RNA structural changes in function, such as gene regulation through ligand-induced RNA conformational switches and protein-induced structural changes at active sites.

From an energetics point of view, a flexible RNA can adopt multiple low-energy states from sampling a variety of global folds and local conformations.^12–14 Low-energy state multiplicity results in great difficulties for predicting and modeling RNA 3D structures. For instance, because of the diversity and sequence-sensitivity of loop/junction structures, 3D structure predictions often rely on fragment/template assembly for highly homologous sequences.^15–21 However, given the limited number of known RNA structures, structural motif templates with the required high sequence identity are difficult to attain. As of February 2018, about 3800 structures containing RNA are in the PDB database: approximately 1855 of these are high-resolution crystal structures (< 3Å ). The lack of reliable structural templates for loops and junctions greatly hampers accurate structure prediction.

Inspired by the recent progress in RNA chemical probing methods, researchers have proposed and developed several data-facilitated experimental modeling approaches to complement established template and physics based methods.^22–26 Selective 2’-hydroxyl acylation analyzed by primer extension (SHAPE) is an RNA structure probing technology that provides significant insights into local nucleotide structure and dynamics.^{27, 28} SHAPE reagents are small ligands: 1-methyl-7-nitroisatoic anhydride (1M7), 1-methyl-6-nitroisatoic anhydride (1M6), N-methylisotoic anhydride (NMIA), benzoyl cyanide (BzCN), 2-methyl-3-furoic acid imidazolide (FAI), and 2-methylnicotinic acid imidazolide (NAI) that form a 2’-O-adduct with the nucleotide 2’-hydroxyl group.²⁹ Previous studies^30–32 suggested that unconstrained nucleotides that sample more flexible conformations have greater probability to adopt the SHAPE-reactive conformations and, thus, show higher SHAPE reactivity. In contrast, nucleotides that are constrained by base pairing and stacking interactions are much less reactive. This quantitative measurement of local nucleotide dynamics makes SHAPE an effective tool to probe whether a nucleotide forms a base pair (either in a helix or in a structured loop) or remains unpaired in a flexible loop/junction. In comparison to modeling without experimental data, SHAPE data places effective constraints on RNA conformational search space and can significantly improve the efficiency of conformational sampling. SHAPE-directed RNA structure prediction substantially increases the accuracy of RNA secondary structure modeling,^33–37 where SHAPE reactivity/nucleotide dynamics provides additional structural constraints for the free-energy based predictions.³⁸ Moreover, combined with other strategies, such as differential SHAPE reactivity, mutate-and-map, and time-resolved SHAPE chemistry, SHAPE probing provides highly useful information for the in vitro and in vivo determination of non-canonical tertiary interactions and RNA kinetics.^39–45

Although SHAPE technology is widely applied and is a highly valuable tool to RNA modeling and (2D) structure prediction, the mechanism of the SHAPE reaction is not fully understood. A variety of conformations render a nucleotide reactive by SHAPE.^{33, 34} Specific RNA structural features correspond to high SHAPE reactivity, including a long PO-to-2’-OH distance, short 2’-OH to O2/N3 distance, and short 2’-OH to non-bridging O distance. These conclusions³² were mainly derived from SHAPE mapping data for 16S rRNA in ribosome crystals and focused on the conformations that tend to increase SHAPE reactivity. Low SHAPE reactivities are known to correlate with positions in helices and rigidly structured loops, but the full mechanisms by which nucleotides can be conformationally constrained, and rendered inert, are not fully understood. Additionally, the accuracy of SHAPE experiments relies on carefully chosen experimental and data processing methods.^{35, 37} While SHAPE data may suggest that an unreactive nucleotide forms an interaction with another member of the system, SHAPE cannot give us information about who is interacting with the nucleotide or what kind of interaction is formed.³⁵ These limitations mean that SHAPE-directed structures should not be considered absolutely determined, but SHAPE can give us useful structural hypotheses.³⁵ Although SHAPE has limitations, prediction of 2D structure using SHAPE has reached a level of accuracy on par with comparative sequence analysis.³³ Conversely, by calculating the effective stability determined by O2’-P-O5’ angle fluctuations and optimizing the native structure-based potential using MD simulations, SHAPE profiles have been rebuilt.⁴⁶ In this study, we focused on developing analytical function for quantitative prediction of the SHAPE profile from individual RNA 3D structures, and applying our function to exclude SHAPE-incompatible structures.

To analyze SHAPE reactivity, we used conformational ensembles generated by MD simulations to investigate the correlation between the SHAPE reactivity and the nucleotide conformational propensity. Then, by combining multiple key factors, such as the nucleotide interaction strength, SHAPE reagent accessibility, and base-pairing pattern, we built an analytical function—the three-Dimensional Structure-SHAPE Relationship (3DSSR) function—to characterize the conformational flexibility and SHAPE reactivity based on the conformational and energetics information. Finally, we showed how the 3DSSR function can be used to exclude some 3D structures based on experimental SHAPE data.

METHODS

Interaction intensity for base pairs and base stacks

Each base pairing interaction between two RNA nucleotides can be divided into 12 families based on the geometric conformations involving three nucleotide edges: Watson-Crick, Hoogsteen, and Sugar.⁹ Based on statistical frequencies derived from 41 RNA structures in the PDB database,⁹ we assigned pseudo-free energy potentials to each base pair interaction class according to the quasi-chemical approximation:⁴⁷

$$E_{\text{bp}}^{(t)}(i,j)=-k_{B}T\text{\hspace{0.17em}ln}(N_{\text{obs}}^{(t)}(i,j)/N_{\text{exp}}^{(t)}(i,j))$$ (1)

for type-t base pair (t = 1, 2, · · ·, 12). Here, i and j refer to the base types (A,U,G,C), and $E_{\text{obs}}^{(t)}(i,j)\text{\hspace{0.17em}and\hspace{0.17em}}{N}_{\text{exp}}^{(t)}(i,j)$ are the observed number and the expected number, respectively, of type-t base pair (i, j) in the database.$N{N}_{\text{exp}}^{(t)}(i,j)$ is computed as

$$N_{\text{exp}}^{(t)}(i,j)=N_{\text{obs}}^{(t)}{x}_i{x}_j,$$ (2)

where $N_{\text{obs}}^{(t)}$ is the total observed number of type-t base pair and x_i and x_j are the mole fractions of the nucleotide types i and j in the entire database, respectively. The database for the 12 types of RNA base-pairing families contained 3917 entries.⁹ The canonical cis Watson-Crick/Watson-Crick conformation (abbreviated as WWc) occurs much more frequently (762 for WWc C-G, 771 for WWc G-C, 205 for WWc A-U and 238 for WWc U-A) than the occurrences (mostly less than 50) of the other non-canonical base pairs. We identified the base pair types with RNAview software.⁹

The above interaction intensities are intended to be used as a (crude) measure for the relative depths of the potentials of mean forces for the different base pairs. These parameters are not real physical free energies, which are determined by the Boltzmann-averaged (nonadditive) energies for the whole structure. Therefore, rigorously speaking, due to the correlation between the different interactions, the sum of the interaction intensities for all the nucleotides does not add up to the total interaction energy or free energy of the system. However, given the Turner parameters for the different types of base stacks in a helix, the above pseudo-energy parameters may provide a crude estimate for the relative interaction strengths of the different noncanonical base pairs. For a loop, the different interactions may result in different nucleotide flexibilities. In contrast, for a helix, the structure is relatively rigid, so the different interaction strengths of the base pairs would not cause notable differences in nucleotide flexibility. Accounting for this, we suppressed the effect of the pseudo-energy parameters for helices in our model (see factor BP (n) in Eq. 6 below).

To quantify the energy of the stacked base conformation, we measured the distance and plane angle between the bases for each pair of stacked nucleotides. The base plane is defined as the triad of C2, C4, and C6 atoms. The center of each base is set as the center of the C2-C4-C6 triad. For nucleotides to meet the base-stacking criteria, the distance between the centers of the bases must be less than 9.5Å, and the base angle must be less than 30o.

To account for the effect of nucleotide interaction strength, we propose the following interaction function to characterize the interaction intensity for nucleotide n:

$$II(n)=\sum _m[a\cdot E_{\text{bp}}^{(t)}(n,m)+b]+\sum _m{E}_{st}(n,m).$$ (3)

The terms on the right hand side account for the base pairing and stacking interactions between n and its interacting partner m. The base pairing interaction $E_{\text{bp}}^{(t)}(n,m)$ between nucleotide n and m is sequence and base pairing type, t, dependent. Because helix stacking is accounted for in the BP (n) term (see Eq. 6 below), the base stacking interaction energy, E_st, for a pair of stacked bases, n and m, primarily considers loop stacking and is assumed to be sequence independent. Consecutive base pairs tend to form base stacks, so base pairing and base stacking can be coupled. The prefactor a introduced in Eq. 3 is a weighting factor to account for the correlation between base pairing and base stacking, while b is the minimum energy for base-pairing.

Ligand accessibility calculation

The ligand (SHAPE reagent) accessibility is another important factor to the SHAPE reaction. If a nucleotide 2’-OH is buried inside the RNA structure, SHAPE reagents cannot react with that site, which reduces the SHAPE reactivity. Ligand accessibility is expected to be a necessary condition for SHAPE to react.

The free SHAPE ligand, usually 1M7 or NMIA, has an effective radius between 2.0 and 2.5 Å (see Fig. S1 in the Supporting Material (SM) for more details). The accessible surface of 2’-OH is calculated using VMD.⁴⁸ The overall ligand accessibility result is found to be insensitive to different probe sizes within this range because different probe sizes generally induce insignificant changes in the ligand accessible surface area.

All-atom molecular dynamics sampling of near-native structure

Starting from the experimentally determined 3D structure, we estimated the nucleotide flexibility using all-atom molecular dynamics (MD) simulations. The MD simulations were carried out using the NAMD 2.10 package⁴⁹ with CHARMM27 and Amber16⁵⁰ with the Amber force fields for nucleic acids to verify that our results were force field independent. The methods and results presented here are based on Amber16 with the ff99bsc0 force field, but similar results were also obtained using NAMD with the CHARMM27 force field. The RNA molecule was embedded in a TIP3P⁵¹ truncated octahedral water box with a water shell of 15 Å Sodium and chloride ions were used as counterions in order to neutralize the RNA molecule and to keep 1M sodium concentration of the system. Sodium ions were manually added according to N_Na = 6.022 * 10⁻⁴ * V, where the number of sodium ions (N_Na) depends on the volume in ų (V) automatically output by tleap upon creation of the water box. Subsequently, chloride ions were added to neutralize the overall charge. The temperature was kept constant at 300 K by coupling the system to a Langevin heat bath. During the MD simulations, the backbone phosphate (P) atom positions and two nucleotide atom positions in base pairing atoms (C2, C6) were strongly constrained with a restraint weight of 500 kcal* Ų/mol to maintain the global folding and helical base pairing structure of each RNA molecule. Using the ff99bsc0 force field, we sampled the conformations of each nucleotide under the structural constraints such as base pairing and stacking. We used four simulation steps. The first step held the RNA fixed and minimized the energy of the surrounding ions and water. The second step minimized the entire system energy. The third step warmed the system to 300 K. The fourth step was the production step. With the crystalline PDB structure as the initial state for each RNA in the training set, the coordinates of all the atoms were written to the NAMD DCD (Amber MDCRD) file every 5 ps, which yielded 1000 snapshots of each case over 5 ns.

Training the parameters in the 3DSSR function

We constrained the backbone and base paired nucleotides during the MD simulations for each of our test cases, so the nucleotides were constrained to remain near their crystalline position. Dynamical analysis with relaxed constraints showed poor agreement with experimental SHAPE data, so we chose constraints that held the global crystal structure but allowed loop nucleotides to sample local conformational space. For each of our 12 cases, we assumed that each of the 1000 near-native structures could feasibly represent the native structure found in a solution environment, which is consistent with how SHAPE experiments are performed. Thus, we were able to grow our training set a thousand-fold. The parameters a, b, E_st, and S₀ in the 3DSSR function of Eq. 6 were optimized by randomly choosing these values, finding the average correlation of all thousand near-native MD generations for each case, and maximizing the average correlations for all of the cases.

To cross validate, the parameters were also optimized using the leave-one-out procedure. For the 12 RNA models we tested (see “RNA structures used for validation” section below), we defined each set of 1000 solution-native MD structures as the test set and obtained twelve training sets consisting of all the other (11,000) MD structures. We optimized the parameters by maximizing the average Pearson correlation coefficient between the experimental SHAPE data and our predicted SHAPE profiles in each training set.

To further test our parameters, we trained using a genetic algorithm, wherein we calculated the correlations for a population of 100 sets of parameters. For each iteration, the top 10 percent of parameters were maintained and the bottom 90 percent were mated using evolutionary principals. Then, we ranked the sets of parameters based on their respective correlations.

Non-native 3D sampling using coarse grained simulations

To test the ability of our algorithm to discriminate between near-native and non-native 3D structures, we sampled non-native 3D structures using a newly developed coarse grained (CG) model. We tested our ability to exclude non-native 3D structures by using both the native 2D structure and non-native 2D structures that were generated by Mfold⁵² (see Tables S3-S6 in SM). The non-native 2D structures were often very similar to their native counterparts, so this test allowed us to establish that 3DSSR meets a minimum secondary structure sensitivity benchmark.

Starting decoy 3D structures were generated from the non-native 2D structures using Vfold3D.⁵³ Maintaining the initial 2D structure, the CG simulations were performed. To enhance conformational sampling, we used Replica-Exchange MD (REMD) with 8 replicas for temperatures from 125 to 300 K. The total simulation time per replica was set to t = 5 ns with integration time-step ∆t = 0.5 fs. For each case, we collected about 7400 snapshots from these simulations with all heavy-atom, global RMSD from the native structure ranging from 0.5 to 14–40 Å depending on the size of the RNA.

Interaction Network Fidelity value calculation

To distinguish between SHAPE-compatible and SHAPE-incompatible structures, we utilized the Interaction Network Fidelity (INF) value to quantify the similarity of interaction pattern between decoy structures and near-native structures. The INF is calculated as

$$\text{INF}=\sqrt{\left(\frac{TP}{TP+FP}\right)\times \left(\frac{TP}{TP+FN}\right)},$$ (4)

where TP is the number of correctly predicted base-base interactions (BBI), FP is the number of predicted BBI in the test model with no corresponding interaction in the accepted model, and FN is the number of BBI in the native model not present in the test model. To find these interactions, we utilized the RNAview⁹ and the stacking calculations mentioned earlier.

The INF value is more useful than the global RMSD in distinguishing between these structures because SHAPE reactivity is determined by the ability of individual nucleotides to sample a variety of configurations. While two structures may have relatively high RMSD between them, the INF between these structures may be similar, and our predicted SHAPE profile may also be similar. In addition, two structures may have low RMSD from the native structure but have very different predicted SHAPE profiles, whereas if the INF for a structure is high, the correlation of its predicted profile with experimental SHAPE data should also be high.

RNA structures used for validation.

We analyzed the SHAPE profiles for twelve RNAs: the (174-nt) lysine riboswitch from T. maritima, the (79-nt) TPP riboswitch from E. coli, the (71-nt) adenine riboswitch from V. vulnificus, the (117-nt) SAM-I riboswitch from B. subtilis, the (154-nt) specificity domain of Ribonuclease P RNA, the (93-nt) cyclic-di-GMP riboswitch from V. cholera, the (29-nt) TAR RNA from HIV-1, the (30-nt) U1A protein binding site RNA from H. sapiens, the (76-nt) aspartate tRNA from Yeast, the (75-nt) preQ1 riboswitch aptamer from B. subtilis, the (36-nt) M-box riboswitch from B. subtilis, and the (154-nt) M-box riboswitch from B. subtilis. The crystallographic PDB IDs are 3DIG, 2GDI, 1Y26, 4KQY, 1NBS, 3IWN, 2L8H, 1AUD, 1EHZ, 1VTQ, 2L1V, and 3PDR, respectively. For RNA structures with multiple PDB entries in the database, we chose the one with the highest resolution. The SHAPE profiles for these RNAs are from the published experimental data^{30, 36, 37} (see Table S2 in SM for the experimental conditions).

RESULTS

The inter-nucleotide contacts of the folded 3D structure determine the local nucleotide dynamics of an RNA. For example, the nucleotides in helices, which involve strong base-base pairing and stacking interactions, can have only small fluctuations around their equilibrium positions, while nucleotides that do not interact with other nucleotides usually have larger fluctuations. Therefore, local nucleotide dynamics is correlated with the interaction strength as well as the 3D structure. Information from experiments,^23–26 such as SHAPE,^39–41 relating structure and dynamics can facilitate our understanding of the interaction energetics and structural features in RNA.

RNA 3D structure and SHAPE reactivity

There is a strong general tendency for flexible RNA nucleotides to be SHAPE-reactive. Based on SHAPE discrimination between helix and loop regions, SHAPE-assisted RNA secondary structure prediction algorithms have been developed and have led to many successful applications.^33–37 However, the relationship between RNA secondary structure and SHAPE reactivity can be complex, in significant part because not all loops and junctions are conformationally flexible. For example, some loop regions consistently show low SHAPE reactivities.^{33–37, 54} The nucleotides in such loops usually engage in constraining (non-canonical) interactions including irregular base pairs, base stacking, base triplets, and other higher-order interactions.

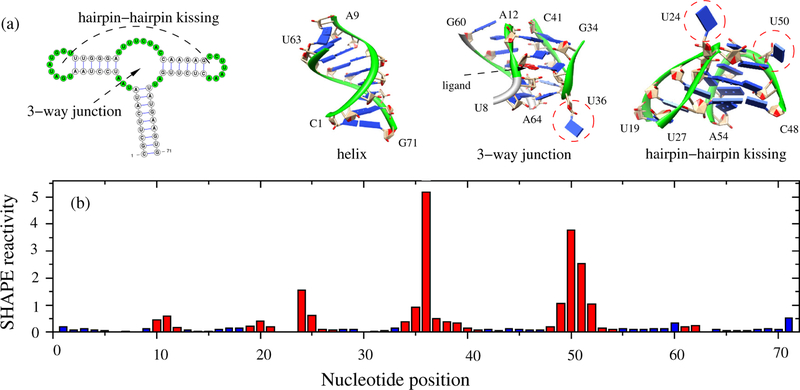
As shown in Fig. 1 for the Adenine riboswitch (PDB: 1Y26), nucleotides with high SHAPE reactivity come from flexible loops, and no significant interactions are involved because these nucleotides have their bases pointing to solvent. For example, nucleotide U36−a 3-way junction nucleotide− and nucleotides U24 and U50−hairpin-hairpin kissing motif nucleotides−display very high SHAPE reactivity because they engage in no significant interactions with other nucleotides. However, when compared to SHAPE values for nucleotides within helix regions, not all nucleotides in loop regions, colored red, have high SHAPE reactivity. In most cases, the low SHAPE reactivity in these loop regions can be explained by non-canonical, constraining interactions. While SHAPE-reactivity in loops depends on the flexibility of the specific loop, almost all the nucleotides in helix regions, colored blue, exhibit low SHAPE reactivity. Therefore, for nucleotides with low SHAPE reactivity, discerning whether nucleotides are in highly structured loops or rigid helices is a challenge. SHAPE probing for a nucleotide cannot provide details about what specific interactions are involved. On the other hand, for a given RNA 3D structure, all the existing interactions may provide significant information about the rigidity/flexibility of each nucleotide and convey to us the ability to predict the SHAPE profile for a given 3D structure.

Figure 1:

(a) The secondary structure of the Adenine riboswitch (PDB: 1Y26), the 3D structures of the helix, the 3-way junction and the hairpin-hairpin kissing motif. (b) Histogram of SHAPE reactivity³⁷ as a function of nucleotide position for 1Y26. The blue and red bars are for the nucleotides in helices and in loops/junctions, respectively. Not all the nucleotides in loops/junctions have high SHAPE reactivity, due to the constraints by other nucleotides and/or other molecules.

SHAPE reactivity vs. nucleotide flexibility

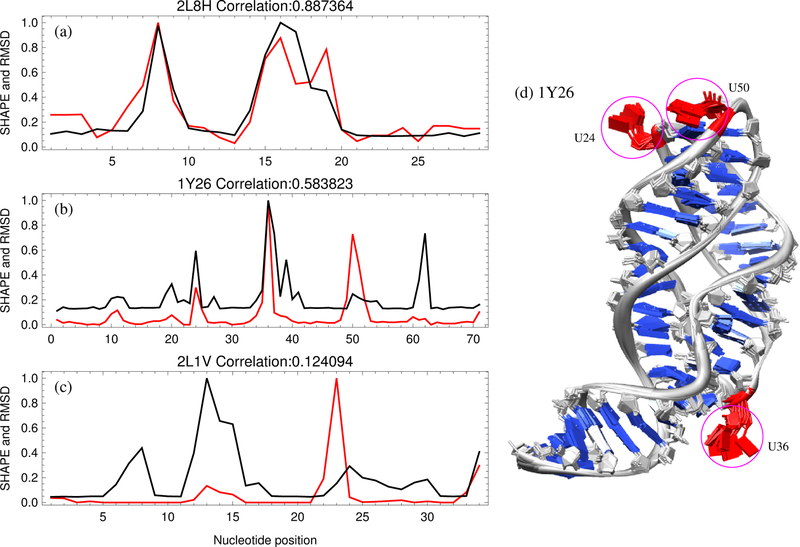
We characterized the nucleotide flexibility using conformational fluctuations in MD simulations. As shown in Figs. 2b,d, nucleotides within the helices have very small fluctuations due to the strong constraints of canonical base pairing and base stacking. However, nucleotides in loop/junction regions may undergo large fluctuations due to weak interactions from other nucleotides. As highlighted in Fig. 2d, for example, nucleotides U24, U36, and U50 sample more conformations than other nucleotides since their bases point outward into the solvent, making them prone to large conformational fluctuations around the equilibrium states. However, not all nucleotides in loops/junctions have large fluctuations since some may engage in non-canonical base pairing and other high-order non-canonical interactions.

Figure 2:

Experimental SHAPE data is generally correlated with nucleotide dynamics. The scaled SHAPE reactivities^{30, 36, 37} (shown in red) as a function of nucleotide position compared with the MD-estimated nucleotide flexibilities (scaled RMSD shown in black) for the highest correlated case (a) 2L8H, the example case (b) 1Y26, and the lowest correlated case (c) 2L1V, respectively. (d) Ten snapshots of an MD simulation for 1Y26, with backbone phosphate (P) atoms position-constrained. The global fold of the RNA molecule is conserved, while each nucleotide has different fluctuations around its equilibrium state due to the constraints provided by other nucleotides. Highlighted in red are three nucleotides (U24, U36 and U50) that have large fluctuations and the highest SHAPE reactivity. The ligand molecules are not included during MD simulations.

To depict the correspondence between SHAPE and nucleotide flexibility, we extracted the sampled conformations from MD trajectories and calculated the pairwise root-mean-square deviation (RMSD) for each pair of nucleotide conformations. The MD-estimated flexibility for each nucleotide (i) is defined as the average of the pairwise structural distance RMSD_p for the nucleotide i:

$$\text{RMSD}(i)=\frac{1}{N}\sum _{p=1}^N{\text{RMSD}}_p(i)\cdot$$ (5)

Here, the summation is over all the possible (N ) pairs of conformations. Because we strongly constrained the global structure, the RMSD for each nucleotide could be independently calculated.

For each case, we compared SHAPE reactivity with nucleotide RMSD (Figs.2 a,b,c and SM Fig. S3). For visualization purposes, the SHAPE reactivities and RMSD (see Eq. 5) values for each case shown in Fig. 2 have been scaled by their respective maximum values to range from 0 to 1. For reference, the RMSDs for nucleotides in helices are around 0.25Å, while the RMSDs for nucleotides within loops/junctions depend on the constraining interactions with other nucleotides. The comparison shows positive correlation as established by the average Pearson correlation coefficient of 0.51 for all cases. An exception to this is the smaller M-box riboswitch from B. subtilis (2L1V), whose dynamic correlation to SHAPE was low (Fig. 2c). However, the ligand accessibility was especially important for this compact structure as seen in Table 1, and multiple MD simulations may help attenuate overestimated parts of the dynamic profile and improve the correlation to SHAPE.

Table 1:

Pearson correlations between the experimental SHAPE data and the 3DSSR-predicted SHAPE profiles using the different combinations of the three factors: interaction intensity (II), base pairing pattern (BP ), and ligand accessible surface (sas = SAS+S₀). Although the correlations generally decrease as sequences get longer, the log-scaled p-values, representing the statistical significance of our results, are displayed to show that our method retains significance.

PDB	Length (nt)	1/|II − 1|	BP (n)	sas	BP /|II − 1|	BP ·sas	sas/|II − 1|	Prediction	Log(p-value)
2L8H	29	0.83	0.82	0.10	0.89	0.93	0.88	0.96	−16
1AUD	30	0.83	0.75	−0.04	0.90	0.83	0.83	0.92	−13
2L1V	36	0.49	0.20	0.56	0.51	0.53	0.92	0.83	−10
1Y26	71	0.78	0.38	0.26	0.76	0.60	0.88	0.88	−24
1VTQ	75	0.57	0.51	0.18	0.68	0.59	0.67	0.71	−12
1EHZ	76	0.70	0.46	0.40	0.69	0.65	0.80	0.80	−18
2GDI	79	0.84	0.53	0.43	0.80	0.75	0.88	0.89	−28
3IWN	93	0.67	0.53	0.32	0.73	0.67	0.68	0.74	−17
4KQY	117	0.64	0.54	0.17	0.69	0.65	0.67	0.75	−22
1NBS	154	0.49	0.46	0.18	0.57	0.57	0.52	0.61	−16
3PDR	154	0.50	0.31	0.16	0.59	0.46	0.61	0.61	−18
3DIG	174	0.57	0.43	0.21	0.58	0.59	0.66	0.70	−26
Average	92	0.66	0.49	0.24	0.70	0.65	0.75	0.78	−18

The RMSDs for nucleotides U24, U36, and U50 highlighted in Fig.2sgd, are 1.05, 1.77, and 0.44 Å, respectively. This indicates that SHAPE chemistry can reflect local structure fluctuation at single nucleotide resolution. While SHAPE chemistry is also likely to be influenced by dynamics on the timescale of seconds or longer, the results here, based on nano-second motions, suggest that the SHAPE reaction might also be sensitive to relative, local nucleotide dynamics on timescales much shorter than seconds.³⁰ However, to more thoroughly sample the available conformational space, combining multiple simulations may be helpful to account for the full SHAPE profile.

The three-Dimensional Structure-SHAPE Relationship (3DSSR) function: Prediction of SHAPE profiles from 3D structure and energetics

The above results show the positive correlation between SHAPE reactivity and the MD-estimated nucleotide flexibility. However, it is computationally inefficient to estimate nucleotide flexibilities for RNAs by MD simulations,⁵⁵ especially for large RNAs. Therefore, we propose an analytical function, namely the “3D Structure-SHAPE Relationship” (3DSSR) function:

$$P(n)=BP(n)\cdot \frac{SAS(n)+S_0}{\left|II(n)-1.0\right|}$$ (6)

to estimate the nucleotide stability. Here, P (n) is the predicted SHAPE reactivity of the nucleotide n; II(n) and SAS(n) are the aforementioned interaction intensity value (see Eq. 3) and ligand accessible 2’-OH surface area of the nucleotide n, respectively. S₀ is a constant, accounting for the dynamics of each nucleotide in solution during SHAPE probing and the possibility of a nucleotide becoming solvent accessible during the experiment.

Unlike II(n), which represents the effect of interaction, BP (n), the base-pairing factor, represents the effect of structure. Specifically, BP (n) is assigned a lower constant value of 0.01 for nucleotides in helix regions and a higher constant value of 1.0 for nucleotides in the flexible (loop and junction) regions. The values assigned in helix regions are much lower, which guarantees the SHAPE-profile prediction will be low. The relatively high values assigned to loops and junctions are modulated by the other factors to differentiate between flexible loops and rigid loops. According to our calculation, modifying the constant value in the denominator of P (n) (0.01 or 1.0) makes little difference to the final result, as it simply sets the upper limit on the score we assign to the nucleotide. Furthermore, the small value of BP (n) assigned to the nucleotides in helices silences the effect of the interaction intensity for the different base pairs/stacks. Consistent with the SHAPE experimental data, predicted SHAPE values for helix nucleotides have little variation.

The ligand accessibility value describes the probability that a given nucleotide is exposed to the SHAPE reagent. The base-pairing pattern distinguishes helix and loop regions. The interaction intensity value describes the local rigidity of the nucleotide and can distinguish rigid nucleotides from flexible nucleotides in loop regions. As predicted by the above 3DSSR function, any helix nucleotides with low ligand accessibility would be highly unlikely to reach a high SHAPE value. For the ligand accessible loop or junction nucleotides, the interaction intensity can modulate the predicted SHAPE value to describe its local flexibility and distinguish rigid and flexible loops. Since the information about local nucleotide stability and dynamics is embedded in the 3D structure and energetics, the 3DSSR function, combined with the effects of the interaction intensity (II(n)), ligand accessibility of 2’-OH (SAS(n)), and base pairing pattern (BP (n)), accounts for both the structural environment and the interaction energetics of the nucleotides.

Training the parameters

As shown in Table S1 in SM, the parameters that optimize the total correlation in the leave-one-out random search method are consistent for all twelve training sets. Additionally, the average parameters of the twelve training sets are consistent with the parameters found using random search training and the genetic algorithm for all structures. The consistency of the parameters for the different RNAs under different experimental conditions suggest that the above 3DSSR function might not be very sensitive to the solution conditions, such as ion concentrations, provided that the RNA can fold into the stable native structure (see also Table S2 in SM for the experimental conditions). However, it is important to note that for a given native structure, the solution condition can influence the global folding stability.

Using the parameters that maximize the correlation for all of the MD cases, we found an average correlation of 0.78 for the best cases. Because we found good agreement between our different training methods, we finally set the values of parameters as the optimal parameters that maximize the average correlation for all MD cases: a = 0.03, b = −0.49 kcal/mol, E_st = −0.24 kcal/mol, and S₀ = 15 Ų.

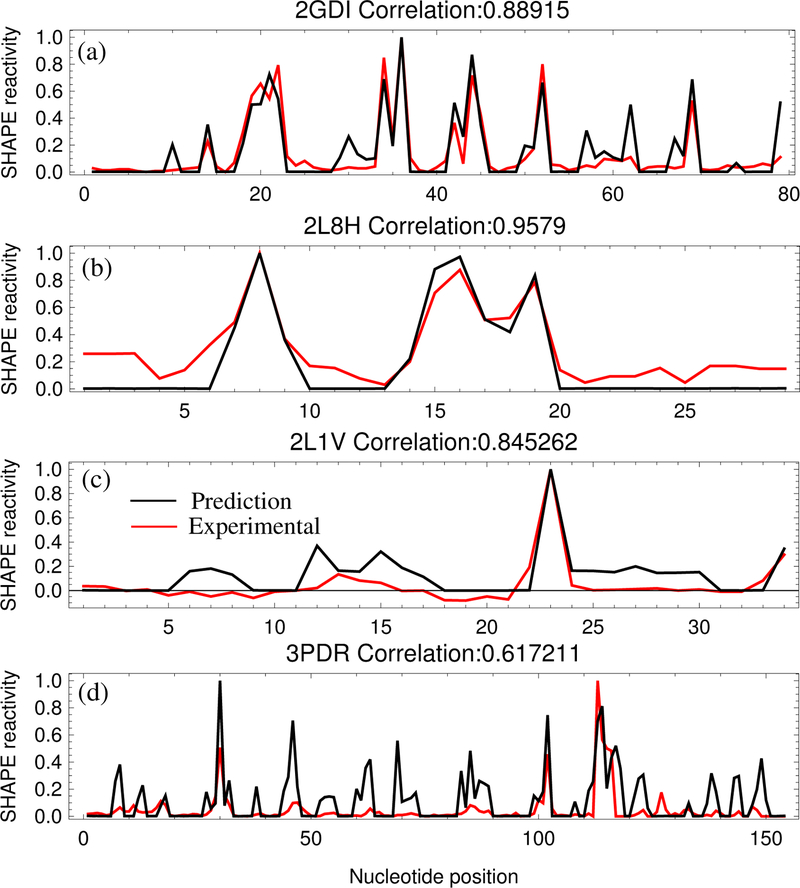
As listed in Table 1, the correlation between the experimentally determined SHAPE data and the 3DSSR-predicted SHAPE profile ranges from 0.61 to 0.96 and averages 0.78. As shown in Fig. 3, the 3DSSR function predicts most high SHAPE peaks, even for the worst predictions, 3PDR and 2L1V. As expected, for the low SHAPE reactivity of the helix nucleotides, 3DSSR shows good agreement with the experimental data. However, for nucleotides within structured loops/junctions of low SHAPE reactivity, the interaction intensity II(n) combined with the ligand accessibility SAS(n) can distinguish a rigid, structured-loop nucleotide from a flexible, unstructured-loop nucleotide of high SHAPE reactivity. While the 3DSSR function can discriminate most unstructured nucleotides from structured ones, the 3DSSR cannot predict the exact SHAPE reactivity profile for each nucleotide without specific information about SHAPE-reactive and inert conformations. Therefore, direct comparison for the absolute SHAPE reactivity values is not possible with our model. Because of this limitation, using the Pearson correlation coefficient to compare the predicted SHAPE profile (shape of the curve) to the experimental SHAPE profile provides a more effective test for the theory.

Figure 3:

(a) Comparison between the predicted (black) and the experimental (red) SHAPE profiles for the TPP riboswitch (2GDI),³⁶ the case with the smallest p-value. (b) Comparison of SHAPE profiles for the TAR RNA (2L8H),³⁰ the case with the highest correlation. (c) Comparison of SHAPE profiles for the (small) M-Box Riboswitch (2L1V),³⁶ the case with the largest p-value. (d) Comparison of SHAPE profiles for the (large) M-Box Riboswitch (3PDR),³⁶ the case with the lowest correlation.

Testing the 3DSSR function

Our tests consistently show correlation between the 3DSSR function and the experimental SHAPE data for each of the 12 RNA molecules, as listed in Table 1. The SHAPE reactivity function contains three parts: interaction intensity, ligand accessibility, and base pairing pattern. As listed in Table 1, no individual component of the 3DSSR function is as highly correlated with the experimental SHAPE profile as the 3DSSR function taken in its entirety, which indicates that the mechanism of SHAPE depends on multiple factors. The average correlations of individual components in 3DSSR to SHAPE data are 0.66, 0.49, and 0.24 for interaction intensity, base pairing pattern, and ligand accessibility, respectively. Therefore, the interaction intensity makes the major contribution to the SHAPE pattern. The base pairing pattern (secondary structure) has the second largest correlation to SHAPE data. BP (n) alone can reach 0.49 average correlation, which is why SHAPE technology can be used to improve the accuracy of RNA secondary structure prediction. Although the SHAPE reagent molecule directly binds to the 2’-OH on the nucleotides, the ligand accessible surface of 2’-OH group of each nucleotide alone shows the weakest correlation, which is consistent with the previous study.³⁰

Furthermore, the combinations of any two factors (shown in Table 1) show improvements over individual factors but failed to show better correlation than the complete function. These calculations again show that interaction intensity is the main contribution to SHAPE reactivity. Nucleotides with weaker and fewer interactions generally have a greater ability to sample SHAPE-reactive conformations. However, the modulation of this component is necessary to optimize the algorithm. The predicted profile successfully rebuilt the majority of SHAPE peaks (Fig. 3 and Fig. S2 in SM). The correlation of the 3DSSR function is better than the correlation of any isolated 3DSSR function component.

Excluding SHAPE-incompatible 3D structures

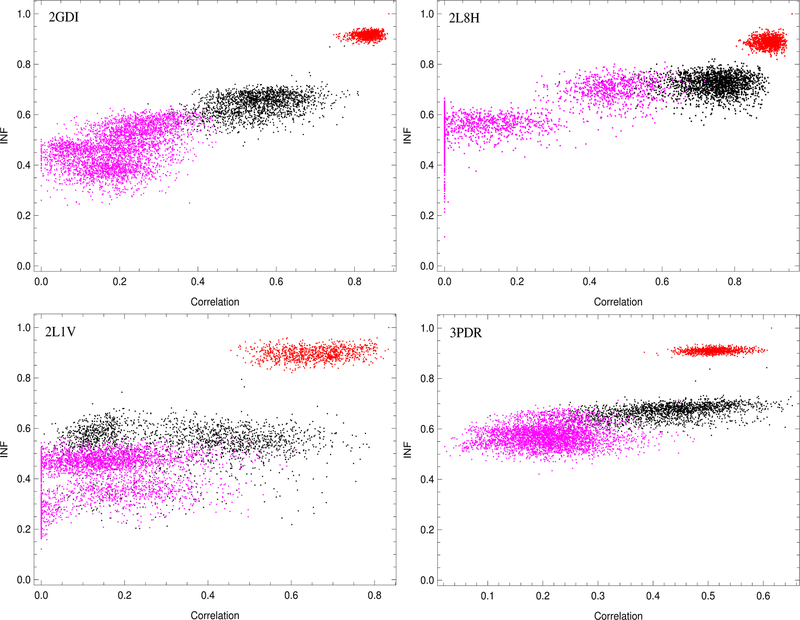
To support the idea that we can use our algorithm to exclude SHAPE-incompatible 3D structures, we plotted the INF for our models as a function of correlation between our predicted profile and SHAPE experimental data for each case (Figs. 6 and S4, S5 in SM). Our findings support the idea that the local interaction pattern may be used to predict SHAPE reactivity. After finding the model in our near-native MD simulations that yielded the highest predicted correlation to SHAPE for each case, we plotted the INF values from the preferred near-native model for all the cases as a function of correlation. Choosing the highest correlated case was a matter of convenience because we attained similar results regardless of which near-native MD case we picked. The 3D structures with lower INF trend toward lower correlations than structures with higher INF. This is especially true for the non-native 2D decoy structures. While the native 2D, non-native 3D structures sometimes attain higher correlations than our preferred MD model, the invariable benefit of this calculation is that structures with low INF did not have high SHAPE correlation and structures with high INF did not have low correlation. Because native 2D, non-native 3D structures sometimes attained strong correlations even with high RMSD (Figs. S6 and S7 in SM) and marginally lower INF, our algorithm cannot be used to select the native or even near-native 3D structure. However, our algorithm can be used to sieve structures and determine whether they are compatible with SHAPE. In addition, we found that our algorithm can use SHAPE data to distinguish between near-native and most 3D structures with non-native 2D structure.

Figure 6:

Comparison of INF and correlation for the best (top) and worst (bottom) cases that were shown in Fig. 3. All the near-native MD cases (red), native 2D, non-native 3D cases (black), and 3D structures with non-native 2D structure (magenta) are displayed for each case. These results show that exclusion of most non-native 2D structures and many non-native 3D structures is possible using the 3DSSR model.

DISCUSSION

The essence of this method is to capture some key parameters that best describe the mechanism of SHAPE reaction. The correlation between experimental SHAPE data and the predicted SHAPE profile from RNA crystal structure indicates that the nucleotide dynamical ability is the major factor in the SHAPE mechanism. In spite of many successful applications of SHAPE-directed RNA secondary structure prediction,^33–37 the application of SHAPE technique to 3D structure modeling is far more complicated. This is partly because the SHAPE mechanism is not fully understood. We found that for the same secondary structure, different 3D structures could have similar predicted SHAPE profiles. As a result, the current 3DSSR function may not be used to predict the native, crystalline structure from the near-native conformational ensemble. This is expected because SHAPE is a chemical probe utilized in a solution environment, therefore, many near-native structures can be considered native. However, our algorithm can be used to exclude many 3D structures that are not compatible with SHAPE, which could be useful, especially when combined with other methods to sieve the pool of low energy structures. More accurate evaluations for the interaction energies are required in order to improve the reliability of distinguishing structured loops from helices (both have low SHAPE reactivities). Furthermore, investigating the change of the SHAPE profile as a function of solution conditions will require more detailed modeling of effects such as temperature and ion concentrations. Nevertheless, large structural changes, caused by ligand-binding, site-mutations, temperature-jumps, etc., can be captured by the change of SHAPE profiles.⁵⁶ In such cases, SHAPE probing can provide significant insights into the structure and dynamics.

Interaction search

Local flexibility and some specific conformations facilitate SHAPE reaction. Information about a single static structure may not be sufficient to give strong correlation with the SHAPE reactivity. The SHAPE reaction mechanism is clearly quite complicated and requires detailed analysis for the dynamics, stability and structure of RNA with a large conformational ensemble. Our 3DSSR-based calculations indicate that flexibility contributes the most to the SHAPE mechanism. Interactions among the nucleotides stabilize the local structure and restrict local sampling ability and this results in lower SHAPE reactivity. Capturing all the interaction types is critical in rebuilding the SHAPE profile from a given RNA 3D structure.

Identifying the various interactions and assigning correct energy intensities are two primary issues in this calculation. We apply the RNAview plugin⁹ to capture base pair interactions and assign the interaction intensity based on the frequency of specific conformations among known RNA structures. Our current interaction intensity function for stacked bases is only dependent on angle and distance between the bases and is sequence-independent. Further improvements of the energy function will require a more detailed investigation based on the known RNA structures to extract parameters that are dependent on local sequence and structural motif.

In our calculation, several nucleotides yield false predictions. The interaction intensities at these positions are altered by base-backbone hydrogen bonding or other types of interactions that are not included in the algorithm. Further development of this algorithm should include more types of interactions.

Crystal structure vs. SHAPE reagent-involved solution structure

Our calculations are based on RNA crystal structures. The premise that solution structures in SHAPE experiments are identical or very close to the crystal structures obtained in the PDB database is inherent in this method. This presumption is not always correct. RNA molecules are quite dynamic in solution because of thermal fluctuations, the presence of possible alternative folds, and the interaction with other solution molecules, such as water and ions. Another issue concerns the ligand: our calculation shows the size of the SHAPE reagent molecule is significantly larger than water molecules. SHAPE-ligand binding may perturb the local RNA structure, but this remains for further investigation.

Our calculation shows that including the ligand accessibility term generally improves the correlation, especially for compact structures such as pseudoknot structures like the M-box riboswitch from B. subtilis (2L1V). However, analysis for several nucleotide positions showed that this calculation may also introduce some error. For some nucleotides, the crystal structure buries the 2’-OH and makes it inaccessible for the ligand binding. However, experimental SHAPE data showed some reactivities for these nucleotides. The RNA molecule probably displays large-scale structural motion in solution. This structure alteration results in higher ligand accessibility and makes nucleotide-ligand binding more probable. The constant S₀ in the 3DSSR function accounts for the dynamic effect of RNA molecules in solution. Although our results indicate ligand accessibility is not a generally negligible effect, we did find that ligand accessibility is the smallest contributor to the SHAPE mechanism, which is consistent with previous work.³²

SHAPE reactive and inert conformations

The SHAPE reaction may be exquisitely sensitive to the nucleotide conformation;³² thus, the SHAPE reactivity for a nucleotide is correlated to the probability of the nucleotide to adopt SHAPE-reactive conformations. The flexibility of each nucleotide corresponds to the potential for the nucleotide to access the reactive conformations. The flexibility per se does not provide the actual frequency (probability) for the nucleotide to reach the specific reactive conformations. In an attempt to search for SHAPE-reactive conformations,³² based on the SHAPE profile of the 16S rRNA in crystallized E. coli ribosome ( 1500 nucleotides), McGinnis et al. suggested the existence of several key factors for highly reactive conformations. The study mainly focused on 35 highly reactive nucleotides, and these highly reactive nucleotides are postulated to reveal a portion of the whole SHAPE chemistry.

As shown in Fig. 2c, nucleotides U24, U36, and U50 have comparable flexibilities (1.05, 1.77, and 0.44 Å) but differ significantly in SHAPE reactivity. For example, nucleotide U24 has a much lower SHAPE value than U36 (1.55 to 5.17). We also found that the flexible nucleotide A61 is nearly inert with SHAPE value of 0.2. We propose that conformations adopted by nucleotides U36 and U50 may be close to the respective SHAPE-reactive conformations and are, thus, SHAPE-reactive. In contrast, conformations adopted by nucleotides U24 and A61 may be away from the SHAPE-reactive conformations and are less SHAPE-reactive even though they are flexible. Systematic comparisons between SHAPE profile and nucleotide flexibility for a broad range of diverse RNAs may facilitate the search for SHAPE-reactive and inert conformations.

Investigating electrostatic potential energy

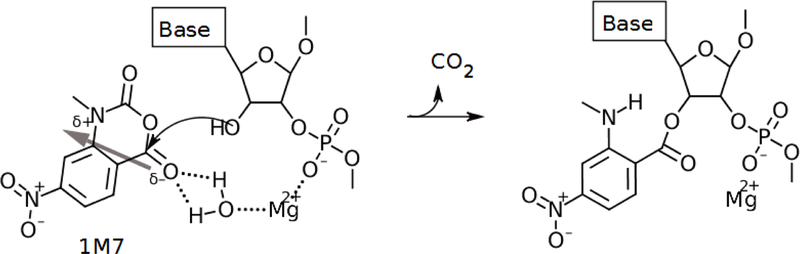
While the focus of this project is to develop a general sieving method to distinguish SHAPE-compatible structures from SHAPE-incompatible structures, we also attempted to determine the reason for the phenomenon of highly reactive nucleotides. From our search, several factors may potentially contribute to anomalously high SHAPE signals for select nucleotides. As previously explained, an absence of constraining forces and high ligand accessibility in tandem with a favorable propensity to sample SHAPE-reactive conformations may lead to a high SHAPE reactivity for some nucleotides. Additionally, the 1M7 molecule is polarized with a partially anionic oxygen covalently bound to the reactive ring carbon. As shown in Fig. 7, local neutralization of the anionic backbone charge by cationic factors, such as magnesium ions, might increase the frequency of 1M7 reactions with 2’-hydroxyl groups in regions with higher (less negative) electrostatic potential.

Figure 7:

In this reaction mechanism, a magnesium ion quenches the negatively charged backbone phosphate group and simultaneously coordinates the reaction of the 1M7 ligand with the nucleotide through a bridging water molecule. A thick grey arrow shows the dipole moment going through the 1M7 molecule, which points from the partially anionic oxygen bound to the reacting carbon toward the partially cationic ring nitrogen. If bound to an ideally positioned magnesium ion, a coordinating water molecule may weakly hydrogen bond to the partially anionic oxygen on the 1M7 molecule and facilitate increased sampling of SHAPE-reactive space. The magnesium ion may anchor 1M7 in a reactive orientation so that the reactive carbon collides with the 2’-hydroxyl oxygen until the reaction occurs. If the negatively charged phosphodiester backbone is not quenched, the polarized 1M7 molecule would be more likely to sample the reactive space in an unfavorable (nonreactive) orientation. An arced arrow shows the movement of electrons from the 2’-hydroxyl oxygen to form a bond with the reactive carbon. In this picture, the magnesium ion behaves as a kinetic catalyst by providing a means for SHAPE ligands to more frequently sample the reactive space in a favorable orientation, and it acts as a weak chemical catalyst by pulling electrons from the partially negative oxygen through the hydrogen bond with water and increasing the reactivity of the carbon.

In an idealized scenario, a magnesium ion could kinetically catalyze the SHAPE reaction by neutralizing the negatively charged phosphodiester backbone. This neutralization would allow polarized 1M7 molecules in reactive orientations to more frequently sample the reactive space around the 2’-hydroxyl group because repulsion by the phosphodiester group of the partially negative polar side of the 1M7 molecule would be lessened. Additionally, a water molecule could act as a bridge between a magnesium ion and the partially anionic oxygen bound to the reactive carbon of 1M7. If the magnesium ion were appropriately positioned, this coordinating water molecule could anchor the 1M7 ligand in a favorable orientation by exposing the reactive carbon to the 2’-hydroxyl group and encourage more frequent sampling of the reactive space around the 2’-hydroxyl group. Interaction between a bridging water molecule and the partially anionic oxygen of 1M7 would reduce the activation energy of the reactive carbon and provide chemical catalysis for the reaction (see Fig. 7). This conjectured effect may contribute to the hyper-reactivity for nucleotides in the E. coli ribosome (PDB ID: 3i1m),³² where nucleotides 530–532 are all found to be highly SHAPE-reactive and near a magnesium ion.

Using a tiered calculation to compare the electrostatic potential energy to the SHAPE profile, we found that the 2’-hydroxyl group of many highly reactive SHAPE nucleotides have higher average electrostatic potential energy. In contrast to our other metrics that take into account the dynamic propensity of each nucleotide, this measure corresponds to the ability of a nucleotide to attract the reactive part of the SHAPE reagent to the 2’-hydroxyl reaction site.

However, the local electrostatic potential energy is not immediately viable to be included in the 3DSSR function because it is highly sensitive to small conformational changes, so calculating the electrostatic potential energy profile for near-native MD structures can give wildly different results from one structure to the next. In our calculation, we utilized MD structures to find the average electrostatic potential energy profile for each RNA molecule. Although we averaged the electrostatic potential energy, several regions of high electrostatic potential energy correspond to helix regions, which are generally SHAPE inert. Furthermore, the electrostatic potential energy is generally higher on the surface of the RNA molecule, where the concentration of negatively charged, phosphate backbone atoms is lower, which means that the electrostatic potential energy may be correlated with both solvent accessibility and constraining interactions considered in the 3DSSR.

It is important to note that our calculations could not discern whether the electrostatic potential energy is an effect contributing to the physical SHAPE mechanism or if this trend is an artifact of the correlation between the electro-static potential energy, the solvent accessibility, and the number of constraining interactions for a given nucleotide. Therefore, this measure is not robust enough to account for the full SHAPE mechanism, and we consider nucleotide dynamics to be the primary driving force behind SHAPE reactivity. However, our search leads us to suggest that if the 2’-hydroxyl site on a flexible nucleotide is in a region of high electrostatic potential energy, the nucleotide may react more strongly to SHAPE than flexible nucleotides in regions with low electrostatic potential energy.

Future improvements to the 3DSSR function

Our interaction intensity function constitutes a lowest order approach at scoring the energy. Because we do not calculate the global free energy of the RNA to build a predicted SHAPE profile, we can use this approximation for individual RNA nucleotides to roughly measure the relative strength of their constraints. In the helix regions, the SHAPE reactivity is consistently low and accounted for by known secondary structure information (the BP (n) function). As shown in Table 1, our algorithm might be able to consider, to the lowest order approximation, tertiary interaction effects and predicts relative loop region reactivity. For the BP (n) function alone, the average correlation is only 0.49, while the entire 3DSSR prediction yields an average correlation of 0.78; without including the BP (n) function, we reach a slightly lower average correlation of 0.75. The improvement of the 3DSSR function, which accounts for tertiary effects, over the BP (n) function is mainly from the predictions for loop nucleotides. The 3DSSR algorithm would benefit from a more rigorous energy function in the future, but our results indicate that we can currently distinguish SHAPE-compatible structures from SHAPE-incompatible structures to a useful degree.

The predicted profile using 3DSSR strongly correlates to the experimental SHAPE data, as shown in Fig. 3, indicating that the three factors (interaction intensity, base pairing pattern and ligand accessible surface) in 3DSSR are the major contributors to SHAPE reactivity. The current algorithm for interaction intensity calculations contains the major interactions involved in RNA: base pairing and base stacking. However, several false predictions of major peaks are shown in Figs. 4 and 5. The results could be improved if the following interactions are considered.

Figure 4:

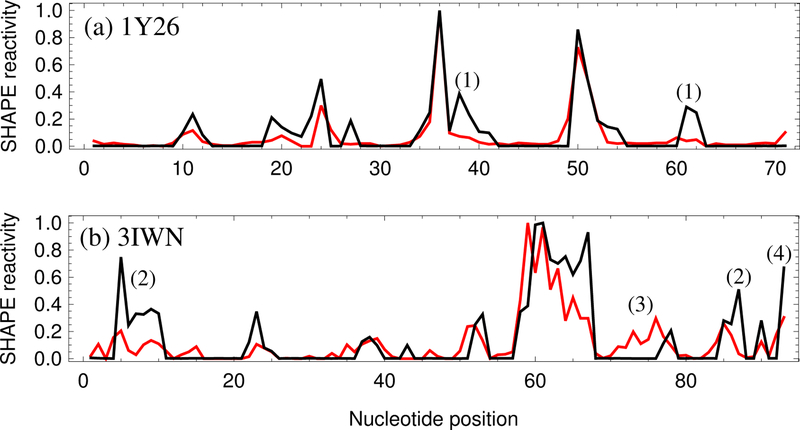
(a) Comparison between the 3DSSR-predicted (black) and experimental (red) SHAPE profile for the adenine riboswitch (1Y26),³⁷ which has a Pearson correlation of 0.88. (b) Comparison between the predicted (black) and experimental (red) SHAPE profile for the cyclic-di-GMP riboswitch from V. cholera (3IWN),³⁶ which has a Pearson correlation of 0.74. Nucleotides marked (1) and (2) have high predicted SHAPE reactivity due to the base-ligand interactions that are not considered in the 3DSSR model. Nucleotides marked (3) are in helix region but have medium SHAPE reactivity. The false prediction for the nucleotide marked (4) is likely due to the effect of the tail not considered in the current 3DSSR function.

Figure 5:

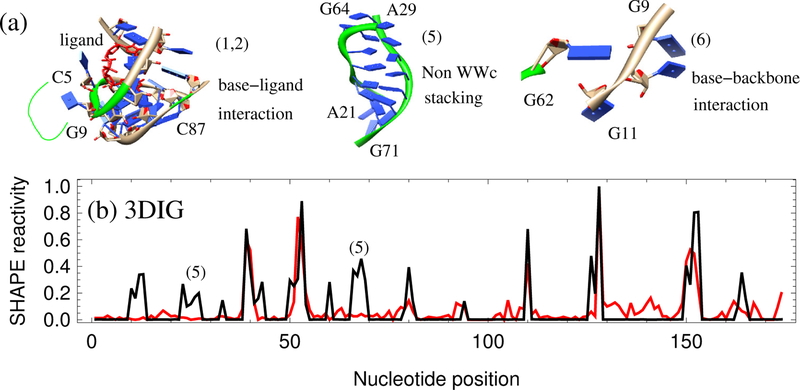
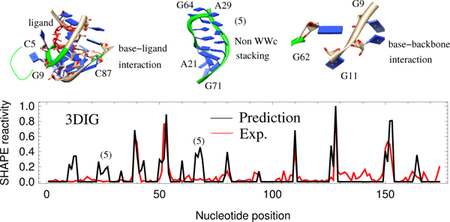
(a) 3D structures for some of the interactions not considered in the 3DSSR function: base-ligand interactions for (1) and (2) in Fig. 4; non-WWc stacking for (5) in Fig. 5b and base-backbone interactions between the nucleotide G62 and nucleotides G9-G11 (6) in the TPP riboswitch from E. coli (2GDI). (b) Comparison of the predicted (black) and experimental (red) SHAPE profile for the lysine riboswitch from T. maritime (3DIG),³⁶ which has a Pearson correlation of 0.70. The false prediction for the nucleotides marked (5) is likely caused by the under-estimation of the interaction intensity within the non-WWc stacking region shown in (a).

Base-ligand interactions:

While many molecules strongly interact with RNA, ligand binding is not considered in this model. For the adenine riboswitch (1Y26) shown in Fig. 4a, the 3DSSR function falsely predicts high SHAPE reactivities for nucleotides 38–40, 61, and 62. In Fig. 1a, we see that these nucleotides are interacting with a ligand molecule in the 3-way junction of 1Y26. Similarly, the Cyclic-di-GMP riboswitch from V. cholera (3IWN) has ligand interactions at nucleotides 5–9 and 87 in Fig. 4b. In all of these cases, the 3DSSR function predicts higher relative SHAPE reactivities than is experimentally observed. Lack of detailed base-ligand interactions in 3DSSR may be a factor contributing to the over-estimation. In the future, we must take into account the constraining effects of other molecules on the nucleotide flexibility. If the base-ligand and base-ion interactions can be accurately estimated, the 3DSSR-based prediction is expected to better correlate with experimental SHAPE data.

Non-WWc stacking:

As shown in Fig. 5b of the lysine riboswitch T.maritima (3DIG), nucleotides 21–29 and 65– 72 have much higher predicted relative SHAPE reactivities than is experimentally observed. These nucleotides are constrained by the non-WWc base stacking shown in Fig. 5a. Like A-form helices, this type of base stacking may also effectively constrain nucleotides. However, our current algorithm underestimates the interaction intensity of the non-WWc stacking and overestimates relative SHAPE reactivities when compared to experimental SHAPE data.

Base-backbone interaction:

Currently, the interaction intensity calculation contains base-base interactions only. Base-backbone and backbone-backbone interactions are not considered. As shown in Fig. 5a, the base group of nucleotide G62 forms a hydrogen bond with the backbone of nucleotide 10U in the TPP riboswitch from E. coli (2GDI). Because this stabilizing interaction is not included in the current 3DSSR model, we predicted higher relative SHAPE reactivities for G62 and 10U than are experimentally observed (see Fig. 3).

Tail effects:

During SHAPE probing, additional sequences at 5’ and 3’ ends are added to the RNA of study. These elongating sequences could possibly form interactions with terminal RNA nucleotides and attenuate their experimental SHAPE reactivity. Non-helical nucleotides are especially susceptible to this effect, and the current 3DSSR function does not account for additional tail sequences. In Fig. 4b, the last nucleotide of the Cyclic-di-GMP riboswitch from V. cholera (3IWN) is predicted to have a higher relative SHAPE reactivity than is indicated by the experimental data. Future development of the 3DSSR function should account for the tail effects.

CONCLUSIONS

Chemical structure mapping methods, such as SHAPE, provide useful insight into the structure and dynamics of RNA molecules. Using MD simulations, we first verified that SHAPE reactivity is correlated with nucleotide position and local nucleotide mobility by being unreactive in rigid helices and reactive in flexible loops (Figs. 1 and 2). Next, we used structural information—the aforementioned interaction intensity, base pairing pattern, and solvent accessibility—to build the 3D Structure-SHAPE Relationship model (3DSSR) that can predict SHAPE profiles from individual RNA structures (Figs. 3, 4, and 5). Then, we tested the 3DSSR on near-native 3D structures, non-native 3D structures with correct 2D structures, and non-native 3D structures with incorrect 2D structures to show that we can use the 3DSSR to separate structures that are incompatible with SHAPE data from SHAPE-compatible structures (Fig. 6). While our approach cannot determine the native crystal structure from SHAPE data, we can use SHAPE data to exclude incompatible structures from consideration, which may contribute towards using chemical mapping methods for RNA 3D structure analysis and prediction.

Abbreviations:

SHAPE

Selective 2’-hydroxyl acylation analyzed by primer extension

WWc

Canonical cis Watson-Crick/Watson-Crick conformation