The Stabilizing Properties of Foot Yaw in Human Walking

Abstract

Humans perform a variety of feedback adjustments to maintain balance during walking. These include lateral footfall placement, and center of pressure adjustment under the stance foot, to stabilize lateral balance. A less appreciated possibility would be to steer for balance like a bicycle, whose front wheel may be turned toward the direction of a lean to capture the center of mass. Humans could potentially combine steering with other strategies to distribute balance adjustments across multiple degrees of freedom. We tested whether human balance can theoretically benefit from steering, and experimentally tested for evidence of steering for balance. We first developed a simple dynamic walking model, which shows that bipedal walking may indeed be stabilized through steering—externally rotating the foot about vertical toward the direction of lateral lean for each footfall—governed by linear feedback control. Moreover, least effort (mean-square control torque) is required if steering is combined with lateral foot placement. If humans use such control, footfall variability should show a statistical coupling between external rotation with lateral placement. We therefore examined the spontaneous fluctuations of hundreds of strides of normal overground walking in healthy adults (N = 26). We found significant coupling (P = 9·10⁻⁸), of 0.54 rad of external rotation per meter of lateral foot deviation. Successive footfalls showed a weaker, negative correlation with each other, similar to how a bicycle’s steering adjustment made for balance must be followed by gradual corrections to resume the original travel direction. Steering may be one of multiple strategies to stabilize balance during walking.

1. Introduction

Humans maintain their lateral balance during walking in a variety of ways. Two of the best recognized are to make discrete adjustments to footfall location [1] or to apply continuous torque by the stance foot against ground, both of which alter the center of pressure (COP) location underfoot [6]. But given the body’s many degrees of freedom, there may well be other strategies, which the central nervous system (CNS) might use in combination to maintain stable and economical walking. One possibility would be to steer the body about the vertical axis for balance, similar to how a bicycle can be stabilized by turning toward the direction of leaning [9, 15]. It is, however, unknown whether steering of the foot could actually stabilize balance during walking, and whether humans actually employ such a strategy. We therefore examine the potential of steering as a means to maintain balance during human walking.

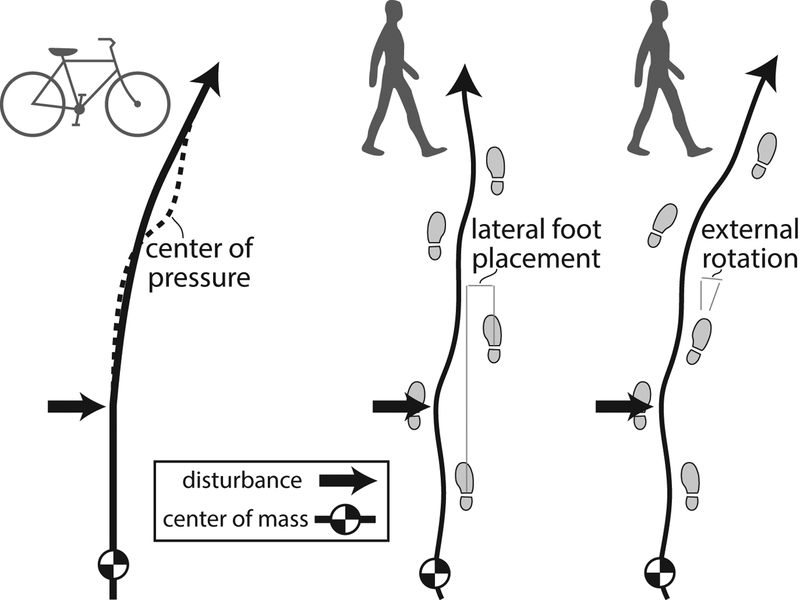
The utility of steering for balance may be explained intuitively (Figure 1). For both bicycle and human in steady motion, the COP must, on average, remain under the center of mass (COM). A lateral perturbation to the bicycle will cause the COM to lean sideways about the forward (roll) axis, and steering toward the direction it was pushed (e.g. steering to the right if pushed to the right) will allow the COP to capture the COM. Not only can such steering stabilize against falling, but it can even be achieved passively for appropriate bicycle geometry and speed [9]. Of course, human walking is quite different from bicycle motion, because the successive footsteps create two alternating centers of pressure. However, intuition suggests there may yet be opportunity to steer for balance, in addition to using the foot placement and ankle torque strategies [8]. This is demonstrated by a dynamic walking robot that stabilizes itself automatically with an ankle joint that kinematically couples steering with leaning [15, 16]. In humans, the leg is not kinematically constrained as such, but the CNS might actively steer for similar stability.

Figure 1:

Conceptual model of lateral stabilizing with lateral foot placement and foot rotation. A bicycle perturbed to the right can recover by steering the wheel to the right. A human perturbed to the right is shown recovering by stepping out and/or rotating the foot to the right. We propose that walking humans use both strategies to maintain lateral stability.

There are potential advantages to steering for stabilization. One is that steering allows for relatively gentle and compliant control, where the perturbation can temporarily redefine the direction of travel (e.g. if pushed to the right, turning to the right). In contrast, foot placement and COP control react more actively to a perturbation and attempt to restore motion to the original, nominal trajectory. That response could potentially be costly to perform, because the swing leg must be actively accelerated and because, for humans, steps either narrower or wider than the preferred step width, require more energy [4, 10]. Of course, in the case of steering, a perturbed direction of travel also requires a correction, but that could potentially be performed gradually and over longer duration compared to the more immediate need for fall prevention. Thus, steering could be considered a means to extend the duration of response to a perturbation across multiple steps. It is also possible that steering could be combined with foot placement control, and allow for smaller adjustments when used in combination than either strategy alone.

It is unknown whether the intuition above is correct, nor whether humans actually employ steering for balance. It is quite possible that the bicycle analogy would fail when applied to active control of walking. And even if feasible, it is not necessarily comparable to the other strategies in effectiveness. Steering control would presumably require the CNS to sense motion of the body in three-dimensional space, determine deviations from the nominal gait, and apply corrections to the body heading, for example by externally or internally rotating the leg. In the present study, we therefore use a simple model of bipedal walking to demonstrate the feasibility of using steering to stabilize balance. If humans steer for balance as demonstrated by the model, we would expect their footfalls to show correlations between foot yaw (angle about the vertical) and lateral placement. We therefore examine the spontaneous deviations that humans actually produce during overground walking, and test whether they exhibit trends that agree with coupled steering and foot placement.

2. Model

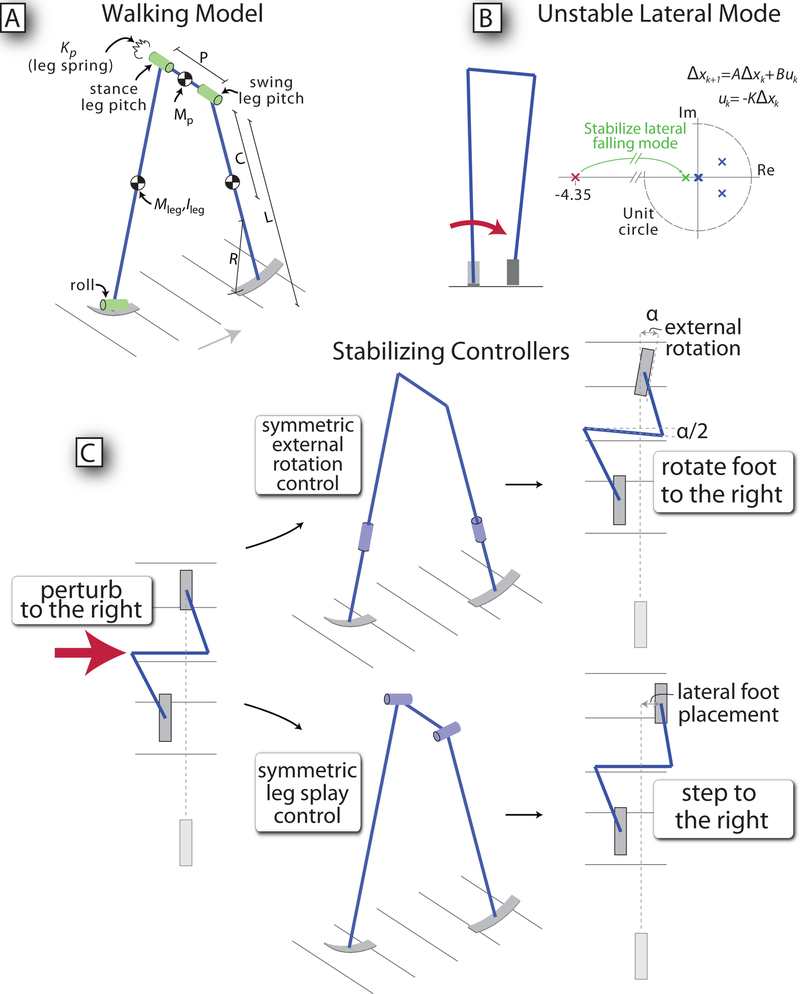
We developed a simple dynamic walking model, in which pendulum-like leg dynamics produce much of the walking motion passively (Figure 2A). Similar to a previous 3D model [8], it has three unactuated degrees of freedom, for swinging the two legs at the hip in the sagittal plane, and for roll. Although the forward walking motion is passively stable, the lateral degree of freedom renders the system laterally unstable (Figure 2B). The model also has two actively-controlled, kinematic degrees of freedom, one to perform lateral foot placement [8], and another added here to adjust the foot’s heading (Figure 2C). This model was used to compute stabilizing controllers to maintain balance through combinations of lateral foot placement and external rotation.

Figure 2:

Dynamic walking model with controlled lateral foot placement and external foot rotation. (A) The model has three unactuated degrees of freedom, roll motion about the stance ankle, and one for each leg rotation in the sagittal plane. (B) The model is passively stable in the forward direction, but has one unstable mode in the lateral direction, shown with pole locations of the linearized step-to-step dynamics, relative to the unit circle. (C) The model also has active control over external rotation of the leg to alter heading, and splaying of the legs for lateral foot placement, both applied symmetrically to both legs. Linear controllers can stabilize the system, using only lateral foot placement, only external rotation, or both methods together. When perturbed to the right, the model may be stabilized by stepping out to the right, or externally rotating toward the right, or both.

The model geometry resembles the previous model [8] and is therefore only summarized briefly here. Each foot is modeled as a portion of a cylinder that can roll forward on the ground. The stance foot yaw is therefore constrained by the line contact with the ground. A freely rotating hinge joint at the base of each leg acts as an ankle joint allowing the model to fall to the side in the frontal plane. The legs also swing freely about hinge joints at the hips, with a pitch axis passing through the pelvis. The model has roughly human-like anthropometric parameters [14, 8], summarized in Table 1. An addition to the previous model was a torsional spring at the hip, acting between the two legs, as a means to modulate step frequency [8]. The present model has two controlled degrees of freedom: hip abduction to control lateral foot placement, and external rotation of the leg to control foot angle. Both of these degrees of freedom are explicitly position-controlled, having no passive dynamics. A control command drives each mode symmetrically, with for example a single external rotation command causing both feet to rotate outward. This differs from humans, where many degrees of freedom are available to change the body’s heading or to adjust the relative angles of body and legs. The symmetry simplification lumps these degrees of freedom into one for heading (external rotation, yaw), and one for step width adjustment (abduction). Walking is powered by descending a gentle slope, but with active control over lateral foot placement and external rotation. To further simplify the analysis of the controlled degrees of freedom, we split the controller into two parts, a discrete feedback controller which chooses a desired rotation angle or foot placement based on state error, and a feedforward continuous controller, which constrains the controllable joints throughout the swing phase to smoothly attain the desired rotation angle or foot placement before the following footfall. For example, the control input for external rotation is a desired outward rotation angle for each leg at footfall. This is chosen at the beginning of each swing phase, and implemented continuously throughout the step by tracking a smooth trajectory defined as one half period of a cosine wave starting at the initial external rotation angle (0) and ending at the final desired angle, after which it was held fixed. The duration of the half sinusoid was specified to be brief enough (1.0 dimensionless time) to ensure completion within a swing phase. We constrain the external rotation acceleration throughout the swing phase to be a segment of a cosine which, when integrated twice, yields the desired cosine trajectory for external rotation position. Hip abduction is controlled in a similar manner. The passive dynamics are described by a total of six states, with the state vector x defined as the roll angle, stance leg angle, swing leg angle, followed by angular velocities for the same angles. The control vector u has two entries, defined as the commanded lateral foot placement and external rotation angle, chosen at the beginning of the swing phase.

Table 1:

Walking model parameters. All parameters are dimensionless, treating as base units total mass M, leg length L, and gravitational acceleration g.

Parameter	C	R	P	MP	Mleg	Ileg	Kp
Value	0.645	0.3	0.3	0.68	0.16	0.017	0.1

Stability analysis reveals the model to be laterally unstable. We integrated the equations of motion numerically (Matlab, “ode45”, Mathworks Inc. Natick, MA) and found a limit cycle for a human-like walking speed (about 1.25 m/s), using the nonlinear dynamic equations, and linearized the step-to-step return map in terms of state deviations Δx_k = x_k − x* from the limit cycle, where k refers to discrete steps, each defined at the instant following heelstrike:

$$\Delta x_{k+1}=A\Delta x_k+B{u}_k$$ (1)

where u_k refers to the control command at step k. The limit cycle of interest x* is passive (x* = F(x*,u = 0)), where F(x_k,u) is the integration of the continuous dynamics starting at the post-heelstrike state x_k, ending just after the subsequent heelstrike, with inputs u. As found previously [8], this system is passively stable (in the local asymptotic sense) in the forward walking direction, but highly unstable in one mode, representing falling laterally (see Figure 2B for eigenvalues of the linearized return map). The linearized A and B matrices found (for more computational details see [8]) are

$$\text{A}=\left[\begin{array}{cccccc}-2.5126& -0.1896& 0.0291& -2.4402& -0.2706& 0.0004\\ 0.9136& -0.6188& -0.4257& 0.9258& -0.5239& -0.0358\\ -0.3419& 1.3611& 0.8410& -0.4099& 1.2182& 0.0719\\ -1.8849& -0.2850& -0.0169& -2.2054& -0.3842& 0.0032\\ 0.4792& 0.4663& 0.0355& 0.4359& 0.8708& -0.0131\\ 0.2215& -0.6103& -0.4019& 0.3309& -0.6474& -0.0205\end{array}\right],B_{fp}=\left[\begin{array}{c}1.9766\\ -0.3110\\ 0.1121\\ 0.1501\\ -0.0551\\ 0.0792\end{array}\right],\text{\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}}{B}_{rot}=\left[\begin{array}{c}-0.0037\\ -0.2504\\ 0.0579\\ 0.9315\\ -0.0867\\ -0.0795\end{array}\right],$$

where B_fp and Brot correspond to foot placement and external rotation, respectively.

We designed linear controllers for lateral foot placement and external foot rotation. Pole placement was used to stabilize the unstable lateral falling mode, reflecting the unstable pole over the unit circle, to stabilize with minimal control effort according to the symmetric root locus design for a linear quadratic regulator [2]. In our case, we choose pole locations to be the same as the passive poles, except the pole at (−4.35, 0), which is replaced with its reflection over the unit circle, (−1/4.35, 0). This was verified to give substantially the same results as calculating LQR gains with no cost on state errors (therefore only considering control cost). The controller was implemented as a discrete adjustment u = −KΔx, which was then executed in continuous time as the sinusoidal trajectory above, with simulation of full nonlinear dynamics. Stabilizing controllers may thus be obtained for lateral foot placement alone, external rotation alone, and both simultaneously in a multi-input controller (Figure 2C). Examination of control gains K (Table 2) reveals that, for all three controllers, the most substantial gains are for roll angle and roll velocity. The gains are such that falling laterally (e.g. to the right during left foot stance) yields a lateral foot placement and external foot rotation (both to the right). The combined, multi-input controller allows the gains to be distributed and thus reduced in magnitude, to roughly half that of the individual controllers for the roll angle and velocity (Table 2). In other words, this shows that the control effort for either foot (external) rotation or (lateral) placement can be reduced by allowing the two controls to act together rather than alone. We did not assume a particular relative weighting between control costs, but mean-square control effort for a linear system is minimized with a combination of controls rather than any single control alone [2]. We therefore expect humans to combine strategies for walking stability, similar to the combined controller.

Table 2:

Control gains to stabilize walking model with minimal control effort. At heelstrike, the deviation of the state from the limit cycle in all 6 dimensions represents the state of the discrete system. Each row of the table shows the gains using a given control mechanism: using lateral foot placement only, external foot rotation only, or both lateral foot placement and external foot rotation in a multi-input controller.

	gains, K =
Controller	$[K_{\Delta q_{\text{roll}}}$	$K_{\Delta q_{\text{stance }}}$	$K_{\Delta q_{\text{swing}}}$	$K_{\Delta {\dot{q}}_{\text{roll}}}$	$K_{\Delta {\dot{q}}_{\text{stance}}}$	$K_{\Delta {\dot{q}}_{\text{swing}}}{]}^T$
Lateral placement	−1.9664	−0.2210	−0.0121	−2.0901	−0.2753	−0.0007
Foot rotation	−4.3512	−0.4891	−0.0267	−4.6248	−0.6091	−0.0016
Lateral placement	−0.9757	0.2182	0.0500	−1.1258	0.3720	−0.0086
and Foot rotation	−2.0726	0.0694	0.4961	−2.1707	−0.8156	0.0612

3. Experiment

To test the model, we examined the variability of foot placement and rotation during normal human walking. If humans use both lateral foot placement and external rotation for control, we would expect a positive correlation between the two. For example, if a foot placement deviates laterally from nominal, we expect it should also be externally rotated, on average. In contrast, the fore-aft stability of the model suggests less need for fore-aft foot placement. We therefore expect little correlation between fore-aft placement and either lateral foot placement or external rotation. In addition to these spatial expectations, we also examined temporal relationships between the measures, as summarized below.

We measured many contiguous strides of human walking in a hallway, using foot-mounted inertial measurement units [11, 13] to estimate foot placement deviations. A total of 26 healthy adult subjects participated. Although age-related effects were not a primary focus of this study, our subjects were of a range of ages, and were therefore categorized into Young (N = 15, age 23.1 ± 4.3 years, mean ± s.d.; 7 male and 8 female) and Elderly (N = 11, age 68.8 ± 5.6 years, 2 male and 9 female) groups. Subjects walked in a straight hallway (roughly 90 contiguous footfalls) at self-selected speed. The inertial measurement units were affixed to the instep of each foot, a location selected to avoid kinematic coupling between lateral placement and external rotation, as might occur with a location on the toe. Subjects consented to participation pursuant to institutional review board procedures.

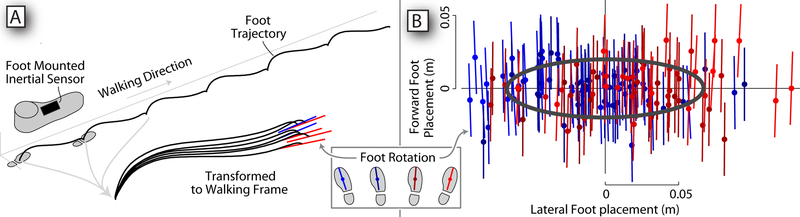
Inertial data were processed to estimate the position and orientation trajectories of the foot, using a zero velocity update at each footfall to reduce drift (Figure 3) [11, 13]. From these trajectories we estimated external foot rotation (heading about vertical), lateral foot placement and forward foot placement. To disregard slow path deviations and sensor drift unrelated to balance, each stride was examined relative to a local forward direction, defined by a moving average window of seven consecutive footfalls. Foot displacement was measured from the preceding footfall, and decomposed into forward (stride length; forward direction positive) and lateral (stride width; lateral direction positive) coordinates in this local frame. External foot rotation deviation was defined as rotation of the foot from its initial heading about vertical, relative to the local frame. Left and right foot strides were measured separately but then combined in these coordinates for each bout of walking.

Figure 3:

Measurement of human stride parameters during walking. (A.) Data from an inertial measurement unit on each shoe were processed to estimate the position and orientation of the foot. Individual strides were demarcated within a locally defined walking reference frame and aligned to begin at the origin, so that the endpoints represented the stride variations. (B.) Stride variability for a representative subject is shown as viewed from above, including foot placements (and their covariance ellipse, solid line) and external rotation. External foot rotation or heading is represented by lines for each footfall, colored from blue (pointing to the left) to red (pointing to the right).

We expected a positive correlation between lateral foot placement and external foot rotation. For each subject, the covariance matrix for forward foot placement, lateral foot placement, and external foot rotation was calculated based on all strides. We first tested for significant covariance between lateral foot placement and external foot rotation, using a t-test across subjects. We then quantified the coupling with the angle (or slope) of the covariance axis, using a total least squares linear fit of external foot rotation versus lateral foot placement, again evaluated with t-test. Based on the model, a positive rotation/lateral slope was expected, meaning that lateral foot placement deviations would be accompanied by external rotation deviations. Statistical tests were conducted with α = 0.01 as the criterion for significance. All values are non-dimensionalized using leg length, body mass, and gravitational acceleration as base units.

We did not expect a significant relationship between forward foot placement and external foot rotation, nor between forward and lateral foot placement, again evaluated with t-tests. In terms of individual left-to-right steps and vice versa, lateral and forward foot placement do exhibit weak coupling [1], but this was not expected to be the case for strides that combine two steps, which therefore negate that effect.

While both control methods can stabilize balance, they also entail a deviation from the original line of travel. A corrective footfall would displace the line of travel in that direction, and an external rotation would leave the body heading deviated in that direction. But in hallway walking, we would expect humans to gradually return toward the original line of travel. This would mean that an actively placed footfall made for balance would be followed by a series of smaller, corrective footfalls in the opposite direction to restore forward walking. We tested for this effect by computing cross-correlations in foot placement as a function of a lag in strides, for all combinations of stride measures. We expected that forward vs. lateral cross-correlations would be small and negative for nonzero lags.

4. Results

Human subjects generally exhibited quite typical gait, in terms of self-selected walking speed and stride length (Table 3). Our particular interest is in the stride variabilities, as illustrated by covariance ellipses for deviations (from the mean) of forward placement, lateral placement, and external rotation. Consistent with model predictions, the main results were a positive correlation between lateral foot placement and external foot heading, and a smaller and negative cross-correlation between successive steps.

Table 3:

Stride parameters and variabilities by subject group. Variabilities reported as root-mean-square foot placements, covariances between parameters, and as the angle of the best fit line between parameters, mean ± standard deviation, for All subjects, Young subjects, and Elderly subjects. Significant differences are indicated by symbols: ‘*’ for difference from zero for All subjects, ‘†’ for difference between Young and Elderly (Y vs E), both p < 0.01. All reported values are non-dimensionalized using leg length, body mass, and gravitational acceleration as base units.

Parameter	All	p	Young	Elderly	Y vs. E p
Speed	0.530 ±0.0864	1.46e–21 *	0.529 ± 0.0851	0.532 ± 0.0923	0.927
Speed variability	0.0224 ± 0.011	1.49e–10 *	0.020 ± 0.005	0.0256 ± 0.0157	0.213
Stride length	1.60 ± 0.166	2.13e–26 *	1.64 ± 0.122	1.55 ± 0.207	0.176
Forward foot placement RMS	0.0436 ± 0.0169	9.49e–13 *	0.0408 ± 0.00824	0.0475 ± 0.0243	0.328
Lateral foot placement RMS	0.0495 ± 0.0195	1.42e–12 *	0.0392 ± 0.00705	0.0635 ± 0.0225	0.001 †
External foot rotation RMS	0.0354 ± 0.0100	7.73e–16 *	0.0332 ± 0.00798	0.0383 ± 0.0120	0.203
Slope angle Frw/Ltr	0.0390 ± 0.862	0.819	0.130 ± 1.11	−0.0849 ± 0.3	0.541
Slope angle Rot/Ltr	0.492 ± 0.338	9.02e–08 *	0.558 ± 0.411	0.401 ± 0.182	0.252
Slope angle Rot/Frw	−0.00506 ± 0.755	0.973	−0.0363 ± 0.807	0.0375 ± 0.715	0.811
Covariance Frw-Lat	−7.50e–5 ± 4.77e–3	0.430	9.24e– 6 ± 8.84e–5	−1.90e–4 ± 7.30e–4	0.302
Covariance Rot-Lat	7.60e–4 ± 9.69e–4	4.93e–04 *	3.66e–4 ± 3.04e–4	1.30e–3 ± 1.29e–3	0.012
Covariance Rot-Frw	1.15e–5 ± 8.58e–5	0.502	−1.34e–6 ± 8.46e–5	2.89e–5 ± 8.84e–5	0.385

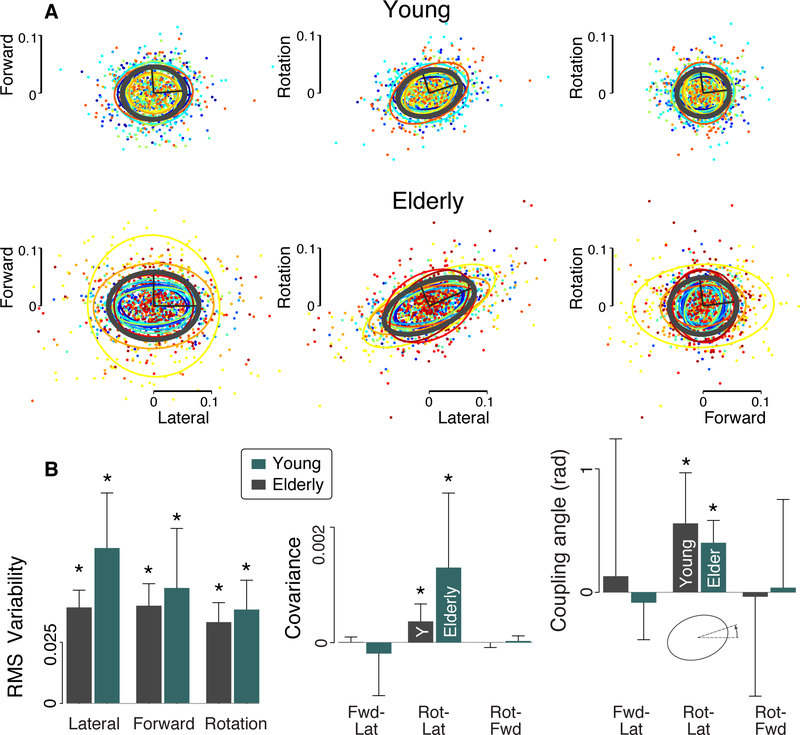
We first summarize the stride variabilities (see Figure 4 and Table 3). As expected, these revealed significant covariance between lateral foot placement and external foot rotation, also quantified by the angle of the covariance ellipse axis, which revealed a small but significant mean angle of 0.492 (rad) for external rotation vs. lateral foot placement (P = 9 · 10⁻⁸). This corresponds to a slope of 0.535 (nondimensional), which means that, for a subject of leg length 1 m, for each 1 cm lateral deviation of foot placement, subjects also externally rotated the foot by 0.3° further than normal. The other covariances and angles– rotation vs. forward placement and forward vs. lateral placement–were not significantly different from zero.

Figure 4:

Stride variabilities and covariances. (A.) Individual stride deviations (dots, colors denote different subjects) and associated covariances ellipses for forward placement, lateral placement, external rotation, and combinations thereof, for each subject (thin ellipses) and for all subjects and strides together (thick ellipse), for both Young (N =15) and Elderly (N =11)subjects. (B.) Significance of covariances, (left to right:) Root-mean-square (RMS) variability for each measure (square root of each diagonal of covariance matrix); Covariance for off-diagonal terms; Coupling angle between measures, defined as angle of covariance axis. Data are shown for Young (N =15) and Elderly (N =11)subjects, with error bars denoting standard deviations across subjects. Significant covariances (differing from zero, p < 0.01) are denoted with asterisks. Significant covariance was observed between external foot rotation and lateral foot placement for both subject groups.

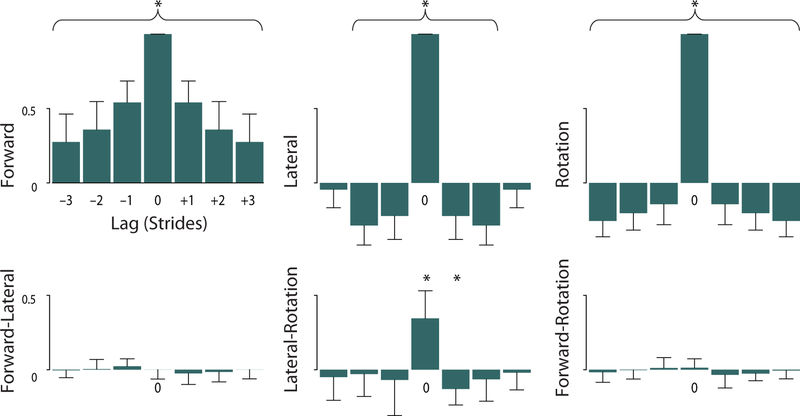
Deviations in lateral foot placement and foot heading were also temporally different than for forward deviations. Auto-correlations show that lateral foot placement was either negatively correlated or uncorrelated with that for preceding and succeeding strides (Figure 5, top-middle). This was also the case for foot heading and for the cross-correlation between the two, as well as their coupling (Figure 6). If one footfall was placed laterally and rotated externally, the following footfall of the same foot would also typically deviate in the opposite direction (placed medially and rotated internally) but by a smaller amount. In contrast, forward deviations were positively correlated with preceding or succeeding strides, which would not be expected for instantaneous corrections made for balance.

Figure 5:

Cross-correlations of stride measures across neighboring strides. All combinations of Forward, Lateral, and Rotation (about vertical) are cross-correlated with each other. These are computed with lags ranging from −3 to 3 strides, so that zero lag corresponds to covariance (Figure 4B) with diagonals normalized to unity. Bars represent mean cross-correlations across subjects (asterisks denote significant difference from zero with P < 0.01), and error bars denote standard deviations.

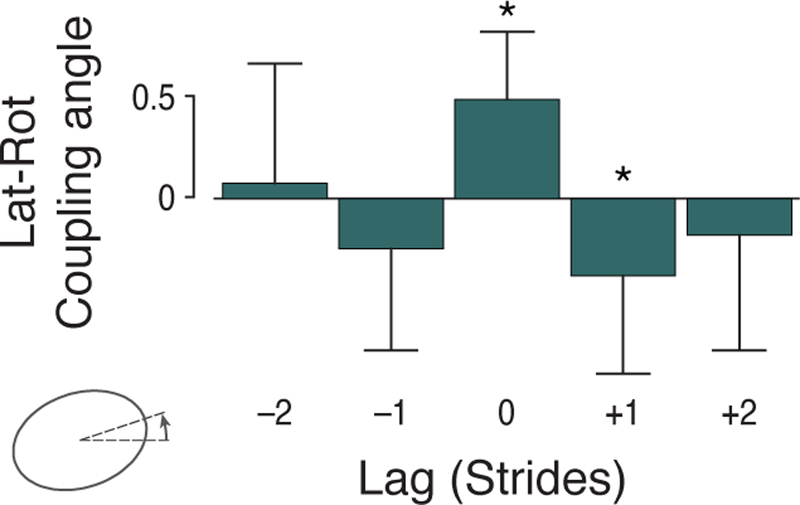
Figure 6:

Coupling between lateral foot placement at one footfall and the external rotation at a lag of a number of strides later (or earlier). Coupling is defined as angle of covariance axis between lateral placement and rotation (mean ± S.D. across all strides and subjects). Coupling was significant (P < 0.01) for lag of 0 (current stride), and for lag +1(succeeding stride) which was smaller and negative. This may indicate a balance correction at stride 0, with a subsequent overall heading correction back towards a forward walking direction at stride 1.

There were few notable differences related to age. Elderly subjects generally walked with covariances similar to Young. The exception was lateral foot placement variability, which increased significantly (Table 3). Relationships between measures (slopes and covariances) for Elderly subjects exhibited similar relationships as Young subjects, both spatially and temporally. An example is the covariance between lateral foot placement and external rotation, which was positive for both groups but greater in Elderly (insignificantly, p > 0.01).

5. Discussion

We had sought to determine whether foot rotation can contribute to lateral balance during walking. A simple walking model demonstrates highly unstable dynamics in the lateral direction, which may be stabilized with foot rotation, analogously to how a bicycle may be steered for balance. Moreover, control effort may be reduced by combining external rotation with lateral foot placement. We interpret the observed spatial and temporal characteristics of human foot placement as consistent with both strategies being used to actively control balance. For example, the significantly non-zero (p = 9.02 · 10⁻⁸) positive slope angle for foot rotation and lateral foot placement shows a lateral foot placement to external foot ratio of 2.11-to-1. To compare to the model prediction, we consider the gains of the control matrix (Table 2) between the lateral placement and foot rotation controllers, which represent the amount of each actuation required to correct for a given lateral disturbance. The ratio of gains for Lateral Placement to those for Foot Rotation range from 0.469 – 0.539. While the magnitudes of these ratios differ from human walking, the sign of the relationship is predicted, and they are on the same order of magnitude. The cross-correlations suggest that this relationship could be a corrective action for balance (Figure 5), because each coupled footfall deviation was also succeeded by smaller, negative corrections. This would be expected if a fast adjustment for balance were followed by a slower correction toward the original direction of travel over multiple subsequent strides. Both the balance adjustments and subsequent corrections made by humans might initiate from active, integrative control by the CNS.

Forward foot placement was quite different. Fore-aft deviations were spatially and temporally uncorrelated with lateral placement and foot heading. We had previously hypothesized that walking may benefit from inherent dynamic stability in the sagittal plane [1, 8], which may be achievable with spinal feedback, as opposed to the integrative control needed for lateral balance [10]. We did observe positive temporal relationships between successive forward foot placements, which may result from relatively slow fluctuations in walking speed [3] rather than step-by-step balance adjustments.

There may be additional contributions to balance not examined here. Other compensations might include movements of the torso and arms, modulation of the swing leg [8], or trailing leg push-off [7]. Steering for balance might be an effective contribution, particularly where space allows. But when task constraints limit freedom, the strategy might change to accommodate those constraints. Examples include walking on a narrow treadmill or hallway or on stepping stones or a balance beam, where steering would be challenging. Task constraints may limit the feasible balance strategies and favor differing combinations of movements. It may be advantageous for the CNS to combine multiple control strategies to reduce effort when unconstrained, and to exploit particular strategies when task demands dictate.

There are a number of limitations to this study. We used a very simple model of walking with relatively few parameters for our theoretical exploration. There may be alternative parameter values than those selected here, for example the closed-loop control behavior. There are also other ways to mechanically implement the control mechanisms studied, such as using asymmetric control, potentially decoupling foot angle control from center of mass movement. Our model certainly does not replicate the human’s many degrees of freedom, but rather attempts to qualitatively predict the overall actions helpful for balance. We therefore cannot predict the particular combination of lateral foot placement and external rotation used by humans, but rather only the expectation that some combination might be beneficial. Another limitation is that we have only examined correlations between steps in our experiment. Causal relationships might be better revealed through physical or sensory perturbations. Further modeling and experimentation are necessary to establish causality and to probe the trade-offs between multiple stability mechanisms.

Our findings may have implications for pathologic gait. We examined only healthy subjects here, but we did observe greater variability in lateral foot placement in the Elderly subject group, and particularly in the covariance between lateral placement and rotation (Table 3). This might be indicative of reduced sensory precision and greater motor variability with age [12]. These effects might be still greater in pathologic cases. Other populations might experience other limitations on balance. For example, lower limb amputees cannot easily exert active torque to generate pushoff with the prosthetic foot [5], and might also be limited in the ability to steer that foot. Whereas healthy gait may incorporate steering and other balance strategies, various pathologies may limit the ability or efficacy of some degrees of freedom, and thereby increase reliance on other compensations to maintain balance. A multimodal perspective might be helpful for understanding such compensations.