Visualizing and interpreting single-cell gene expression datasets with Similarity Weighted Nonnegative Embedding

Summary

High throughput single-cell gene expression profiling has enabled the definition of new cell types and developmental trajectories. Visualizing these datasets is crucial to biological interpretation, and a popular method is t-Stochastic Neighbor embedding (t-SNE), which visualizes local patterns well, but distorts global structure, such as distances between clusters. We developed Similarity Weighted Nonnegative Embedding (SWNE), which enhances interpretation of datasets by embedding the genes and factors that separate cell states on the visualization alongside the cells, and maintains fidelity when visualizing local and global structure for both developmental trajectories and discrete cell types. SWNE uses nonnegative matrix factorization to decompose the gene expression matrix into biologically relevant factors, embeds the cells, genes and factors in a 2D visualization, and uses a similarity matrix to smooth the embeddings. We demonstrate SWNE on single cell RNA-seq data from hematopoietic progenitors and human brain cells. SWNE is available as an R package at github.com/yanwu2014/swne.

eTOC Blurb

Visualizing high dimensional single cell datasets is critical to interpretation. Existing methods, such as t-SNE and UMAP, can distort the datasets, especially for developmental trajectories. Here, we developed SWNE, which uses NMF to decompose the data into latent biological factors, embeds the factors, cells, and genes in a 2D visualization, and uses a similarity network to smooth the cell embeddings. SWNE faithfully visualizes both trajectories and discrete cell types, while adding biological context via embedded genes and factors.

Graphical Abstract

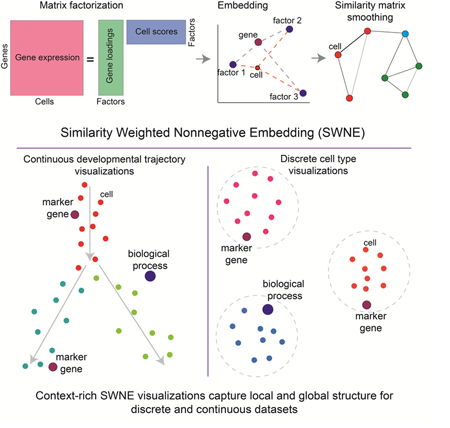
Introduction

Single cell gene expression profiling has enabled the quantitative analysis of many different cell types and states, including human brain cell types (Lake et al. 2016; Lake et al. 2017) and cancer cell states (Puram et al., 2017; Tirosh et al., 2016), while also enabling the reconstruction of cell state trajectories during reprogramming and development (Qiu et al., 2017; Setty et al., 2016; Trapnell et al., 2014). Recent advances in droplet based single cell RNA-seq technology (Macosko et al. 2015; Lake et al. 2017) as well as combinatorial indexing techniques (Cao et al., 2017; Rosenberg et al., 2017) have improved throughput to the point where tens of thousands or even millions of single cells can be sequenced in a single experiment, creating an influx of single cell gene expression datasets. In response to this influx of data, computational methods have been developed for latent factor identification (Buettner et al., 2017), clustering (Wang et al., 2017), cell trajectory reconstruction (Qiu et al., 2017; Setty et al., 2016), and differential expression (Kharchenko et al., 2014). However, visualization of these high dimensional datasets is critical to their interpretation, and existing visualization methods often distort properties of the data, while lacking in biological context.

A common visualization method is t-Stochastic Neighbor Embedding (t-SNE), a nonlinear visualization method that tries to minimize the Kullback-Leibler (KL) divergence between the probability distribution defined in the high dimensional space and the distribution in the low dimensional space (Maaten and Hinton, 2008; van der Maaten, 2014). This property enables t- SNE to find local patterns in the data that other methods, such as Principal Component Analysis (PCA) (Abdi and Williams, 2010) and Multidimensional Scaling (MDS) (Kruskal, 1964), cannot (Maaten and Hinton, 2008). However, t-SNE often fails to accurately capture global structure in the data, such as distances between clusters, making interpreting higher order features of t- SNE plots difficult. While a recent method, UMAP, addresses the issue of capturing global structure in discrete datasets, it seems to still distort single cell gene expression trajectories (McInnes and Healy, 2018).

Additionally, visualizations such as t-SNE and UMAP lack biological context, such as which genes are expressed in which cell types, requiring additional plots or tables for interpretation. Dual-tSNE creatively addressed this issue by plotting genes and samples in parallel tSNE plots, which enabled users to link gene expression in one plot to specific samples in the partner plot, and vice versa (Huisman et al., 2017). Genetically Weighted Connectivity Analysis linked gene sets to the physical connectome using spatial transcriptomics (Ganglberger et al., 2018), and Onco-GPS enabled users to embed biologically interpretable factors alongside samples (Kim et al., 2017). However, to our knowledge, there are still no methods that allow for features and samples to be embedded onto the same plot.

Here, we developed a method for visualizing high dimensional single cell gene expression datasets, Similarity Weighted Nonnegative Embedding (SWNE), which captures both local and global structure in the data, while enabling the genes and biological factors that separate the cell types and trajectories to be embedded directly onto the visualization. SWNE adapts the Onco-GPS NMF embedding framework (Kim et al., 2017) to decompose the gene expression matrix into latent factors, embeds both factors and cells in two dimensions, and smooths both the cell and factor embeddings by using a similarity matrix to ensure that cells which are close in the high dimensional space are also close in the visualization. In this way, SWNE maintains fidelity when visualizing the global and local structure of the data for both developmental trajectories and discrete cell types.

Results

SWNE overview and methodology

SWNE combines Nonnegative Matrix Factorization (NMF) and Shared Nearest Neighbors (SNN) networks to generate a two dimensional visualization of both genes and cells. First, SWNE uses NMF (Franc et al., 2005; Lee and Seung, 1999) to create a parts based factor decomposition of the data (Figure 1a). The number of factors (k) is chosen by selecting the highest k that results in a decrease in reconstruction error above the decrease in reconstruction error for a randomized matrix (Frigyesi and Höglund, 2008) (Methods). With NMF, the gene expression matrix (A) is decomposed into: (1) a genes by factors matrix (W), and (2) a factors by cells matrix (H) (Figure 1a). SWNE then uses the similarity matrix, specifically an SNN network (Houle et al., 2010), to smooth the H matrix, resulting in a new matrix H_smooth. SWNE calculates the pairwise distances between the rows of the H_smooth matrix, and uses Sammon mapping (Sammon, 1969) to project the distance matrix onto two dimensions (Figure 1a). Next, SWNE embeds cells relative to the factors using the cell scores in the unsmoothed H matrix, and embeds genes relative to the factors using the gene loadings W matrix. Finally, SWNE uses the SNN network to smooth the cell coordinates so that cells which are close in the high dimensional space are close in the visualization (Figure 1a).

Figure 1: SWNE overview and ability to capture local and global structure in simulated datasets.

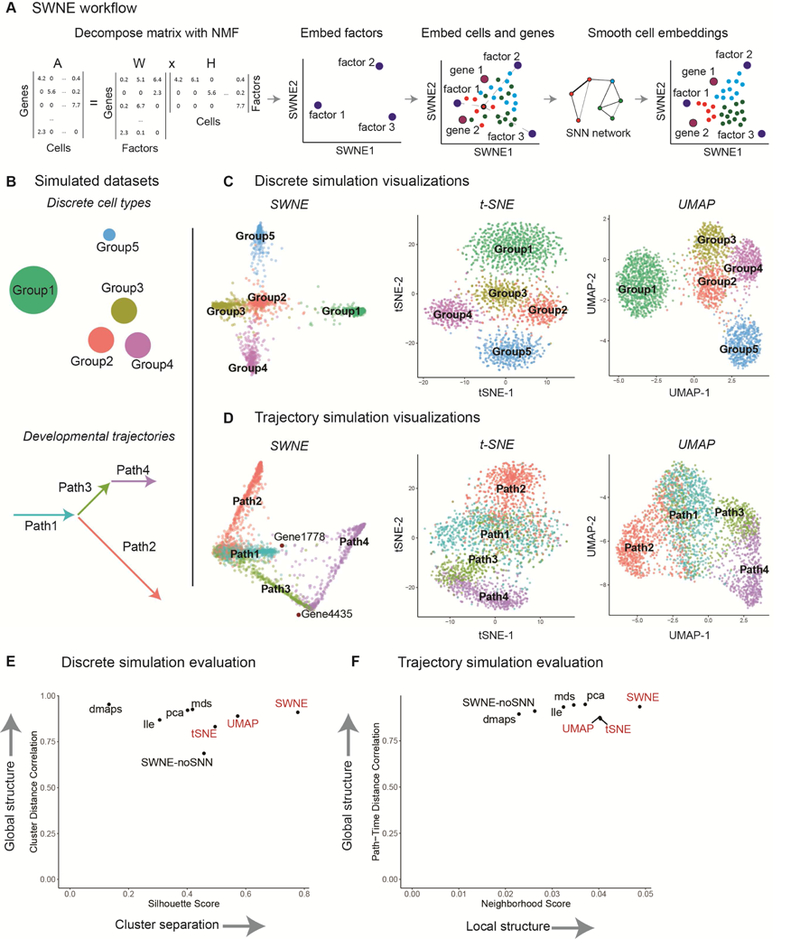
(a) The gene expression matrix (A) is decomposed into a gene loadings matrix (W) and a factor matrix (H) using NMF, selecting the number of factors by taking the highest number of factors that still results in a reduction in reconstruction error above noise (Frigyesi and Höglund, 2008) (Methods). The factor matrix (H) is smoothed using the SNN network, and factors (rows of H) are embedded in 2 dimensions via Sammon mapping of their pairwise distances. Cells are embedded relative to the factors using the cell scores matrix (H), and selected genes are embedded relative to the factors using the gene loadings matrix (W). Finally, the cell embeddings are refined using the SNN network, (b) Simulating a discrete dataset with five clusters, and a branching trajectory dataset with four paths, (c) SWNE, t-SNE, and UMAP plots of the simulated discrete dataset (see Figure S1e for additional plots), (d) SWNE, t-SNE, and UMAP plots of the simulated trajectory dataset (see Figure S1f for additional plots), (e) Quantitative evaluation of SWNE and existing visualization methods on the discrete simulation. Global structure is evaluated by correlating pairwise cluster distances in the embedding with distances in the gene expression space. Cluster separation is evaluated with the Silhouette score, (f) Quantitative evaluation of SWNE and existing visualization methods on the trajectory simulation. Global structure is evaluated by dividing each path up into time steps, and correlating pairwise path-time-step distances in the embedding with distances in the gene expression space. Local structure is evaluated by taking the Jaccard similarity of the nearest neighbors in the embeddings with the true nearest neighbors.

SWNE faithfully captures local and global structure in simulated datasets

To benchmark SWNE against t-SNE, UMAP, and other visualization methods, we used the Splatter single-cell RNA-seq simulation method (Zappia et al., 2017) to generate two synthetic datasets. We generated a 2700 cell dataset with five discrete groups, where Groups 2–4 were relatively close and Groups 1 & 5 were further apart (Figure 1b). We also generated a simulated branching trajectory dataset with 2730 cells and four different paths, where Path 1 branches into Paths 2 & 3, and Path 4 continues from Path 3 (Figure 1b).

For the discrete simulation, the t-SNE plot qualitatively distorts the cluster distances, making Groups 1 & 5 closer than they should be to Groups 2–4 (Figure 1c). The SWNE and UMAP plots both accurately show that Groups 1 & 5 are far from each other and Groups 2–4, while still separating Groups 2–4 (Figure 1c). PCA, LLE, and MDS do a better job of accurately visualizing cluster distances, but have trouble visually separating Groups 2–4 (Figure S1a). For the branching trajectory simulation, the t-SNE and UMAP plots incorrectly expand the background variance of the paths, while the SWNE plot does a better job of capturing the important axes of variance, resulting in more clearly defined paths (Figure 1d). PCA, LLE, and MDS again do a better job of capturing the trajectory-like structure of the data, but still expand the background variance more than SWNE (Figure S1b).

To quantitatively benchmark the visualizations, we developed metrics to quantify how well each embedding captures both the global and local structure of the original dataset. For the discrete simulation, we calculated the pairwise distances between the group centroids in the original gene expression space, and then correlated those distances with the pairwise distances in the 2D embedding space to evaluate the embeddings’ ability to capture global structure (Methods). To evaluate local structure, we calculated the average Silhouette score (Rousseeuw, 1987), a measure of how well the groups are separated, for each embedding (Methods). For maintaining global structure, SWNE outperforms t-SNE, performs similarly to UMAP, and performs about as well as PCA, MDS, and Diffusion Maps (Figure 1e). SWNE also outperforms every other method, including t-SNE and UMAP, in cluster separation (Figure 1e).

For the trajectory simulation, since we know the simulated pseudotime for each cell, we divide each path into groups of cells that are temporally close (Methods). We then evaluate global structure by calculating pairwise distances between each path-time-group in the original gene expression space and the 2D embedding space, and then correlating those distances (Methods). We can evaluate local structure by constructing a ground truth neighbor network by connecting cells from adjacent pseudotimes, and then computing the Jaccard similarity between each cell’s ground truth neighborhood matches and its 2D embedding neighborhood (Methods). SWNE outperforms t-SNE and UMAP in capturing global structure, and performs about as well as PCA, MDS, and LLE (Figure 1f). For capturing neighborhood structure, SWNE again outperforms every other embedding, including t-SNE and UMAP (Figure 1f). Finally, both the qualitative and quantitative benchmarks show that SNN smoothing of the cell and factor embeddings is critical to SWNE’s performance, especially for capturing local structure in the data (Figure 1e,2b, 1f, Figure S1a, S1b).

Figure 2: Illuminating the branching structure of hematopoiesis.

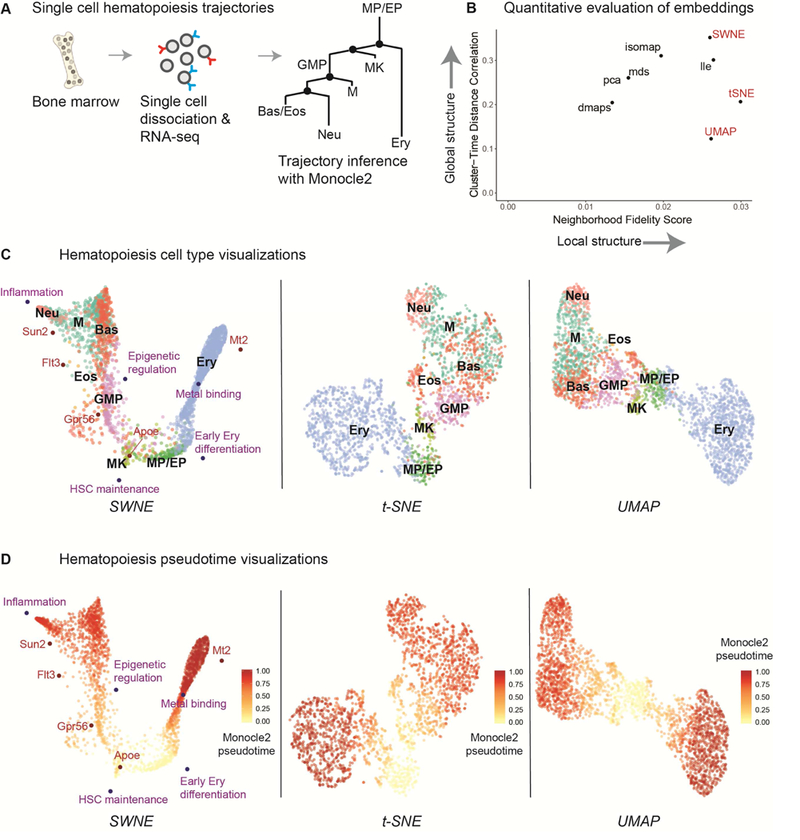
(a) Paul et al sorted single hematopoietic cells from bone marrow, sequenced them with single cell RNA-seq (Mars-Seq), and identified the relevant cell types. The hematopoiesis trajectories were reconstructed using Monocle2, and the cells were ordered according to their Monocle2 differentiation pseudotime. (b) Quantitative evaluation of SWNE and other embeddings on the hematopoiesis dataset. Global structure is evaluated by dividing cell type clusters into groups of cells with similar pseudotime, and correlating pairwise cluster-pseudotime-group distances in the embedding with distances in the gene expression space. Local structure is evaluated by taking the Jaccard similarity of the nearest neighbors in the embeddings with the nearest neighbors in the gene expression space. (c) SWNE plot of the hematopoiesis dataset, with selected genes and biological factors displayed (see Figure 4a, 4c, Table S1 for gene and factor annotations), alongside the t-SNE and UMAP plots. (d) SWNE, t-SNE, and UMAP plots of the hematopoiesis dataset, with developmental pseudotime calculated using Monocle2 overlaid onto the plot.

We assessed how changing the number of factors affects both the quantitative of qualitative performance of SWNE on the trajectory and discrete simulated datasets. Visually, using too few factors results in sub-optimal cluster separation, while using too many factors results in only a minor decrease in visualization quality (Figure S1c, S1d). The quantitative performance of SWNE is fairly robust across the number of factors used, although again there is more of a penalty for using too few factors than too many (Figure S1e, S1f).

Additionally, we assessed SWNE’s runtime alongside UMAP and t-SNE on simulated datasets. It seems like SWNE scales linearly with the number of samples, and visualizes 50,000 cells using the top 3,000 over-dispersed genes in about 8 minutes (Table S2). In comparison, t- SNE and UMAP visualize the same dataset, using the top 40 principal components as input, in about 8 minutes and 2 minutes respectively (Table S2).

Illuminating the branching structure of hematopoiesis

We then applied SWNE to analyze the single cell gene expression profiles of hematopoietic cells at various stages of differentiation (Paul et al., 2015). Briefly, single cells were sorted from bone marrow and their mRNA was sequenced with single cell RNA-seq (Paul et al., 2015) (Figure 2a). The differentiation trajectories of these cells were reconstructed using Monocle2 (Qiu et al., 2017), a method built to identify branching trajectories and order cells according to their differentiation status, or “pseudotime” (Figure 2a). The branched differentiation trajectories are shown in the tree in Figure 2a, starting from the monocyte and erythrocyte progenitors (MP/EP) and either moving to the erythrocyte (Ery) branch on the right, or the various monocyte cell types on the left (Qiu et al., 2017). We selected the number of factors for SWNE using our error reduction above noise selection method (Figure S2a, S2b, Methods).

We benchmarked SWNE performance on the hematopoiesis dataset using the same metrics we applied to the simulated trajectory dataset. To evaluate global structure, we divided the cell type clusters into groups that are temporally close according to their Monocle2 pseudotime, and then correlated pairwise distances between each cluster-pseudotime-group in the original gene expression space with distances in the 2D embedding space (Methods). We evaluated local structure by computing the Jaccard similarity between each cell’s neighborhood in the gene expression space and its neighborhood in the embedding space (Methods). SWNE outperforms t-SNE and UMAP, as well as other embedding methods, when it comes to maintaining global structure in the dataset (Figure 2b). SWNE performs about as well as UMAP in capturing neighborhood structure, and is slightly out-performed by t-SNE (Figure 2b).

Qualitatively, the SWNE plot does a better job of capturing the two dominant branches: erythrocyte and the monocyte, and shows that those two branches are the primary axes of variation in this dataset (Figure 2c). While the t-SNE plot captures the correct orientation of the cell types, it disproportionately expands the more differentiated cell types, obfuscating the branch-like structure of the data (Figure 2c). The UMAP plot also disproportionately expands the mature cell types, while placing the monocyte and erythrocyte branches too far apart. Qualitatively, SWNE, t-SNE and UMAP seem to all visually separate the cell types well. However, none of the methods accurately orient the different monocyte cell types in the monocyte branch, most likely because the variance is dominated by the erythrocyte - monocyte split, and the extent of differentiation.

We also used Monocle2 to calculate differentiation pseudotime for the dataset, which is a metric that orders cells by how far along the differentiation trajectory they are (Qiu et al., 2017). We then overlaid the pseudotime score on the SWNE, t-SNE, and UMAP plots (Figure 2d, 2e). In the SWNE plot, there is a clear gradient of cells at different stages of differentiation along the two main branches (Figure 2d). The gradient in the t-SNE and UMAP plots is not as visible, most likely because t-SNE and UMAP obscure the branching structure by expanding the more differentiated cell types (Figure 2e).

Additionally, we compared the SWNE visualization with the two types of trajectory plots generated by Monocle2, which uses reversed graph embedding (RGE) to learn the underlying graph that best represents the data (Qiu et al., 2017). The Monocle2 plot of two RGE components is able to resolve the main erythrocyte and monocyte branches, but cannot visually separate the monocyte cell types (Figure S2c). With ten RGE components, Monocle2’s tree- based visualization can resolve the different monocyte branches (Figure S2d). Nevertheless, SWNE is able to both capture the two main branches of the data while still visually separating the monocyte cell types (Figure 3c). Additionally, the Monocle2 visualizations assume the data is continuous, and are specific to the Monocle2 analysis framework, while SWNE makes no such assumptions and is meant to be used for both discrete cell types/states and continuous cellular trajectories (Qiu et al., 2017).

Figure 3: Creating an interpretable map of the human visual cortex and cerebellum.

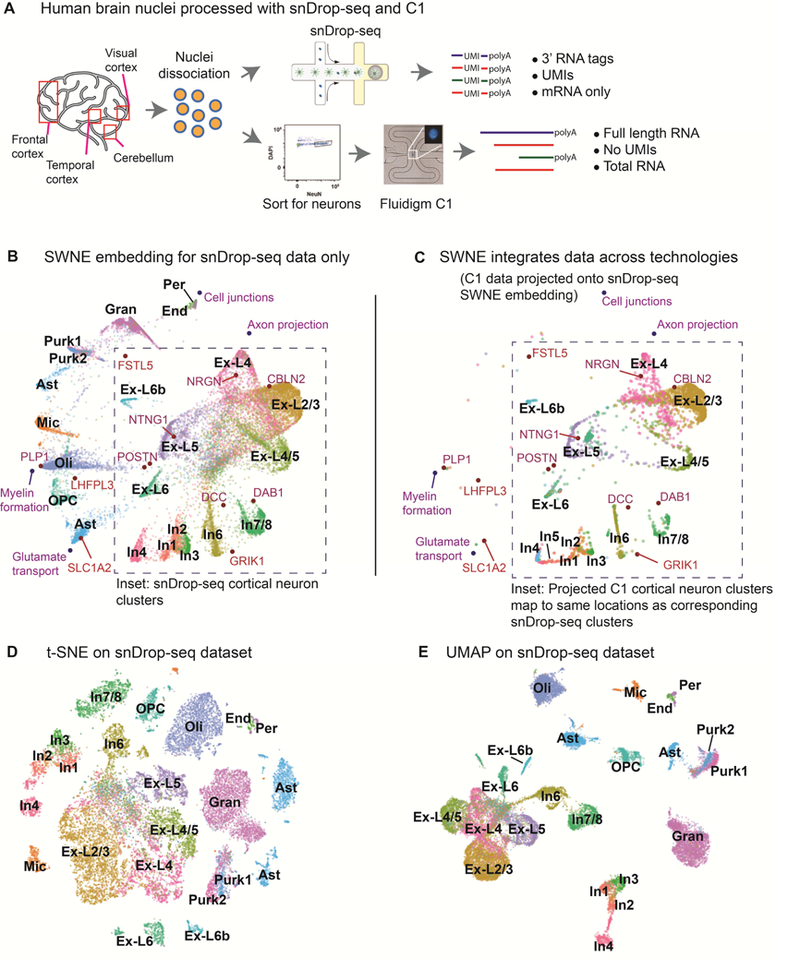
(a) Single nuclei were dissociated from the human cortex and cerebellum, and sequenced using both single nucleus Drop-Seq (snDrop-Seq) and the Fluidigm C1 platform (Lake et al. 2016; Lake et al. 2017). snDrop-Seq uses unique molecular indexes (UMIs), and only captures the 3’ end of mRNA transcripts. The C1 method does not use UMIs and captures full length total RNA. (b) SWNE plot of cells from the visual cortex and cerebellum generated using snDrop-Seq, with selected genes and factors displayed (see Figure 4b, 4d, Table S1 for gene and factor annotations). (c) C1 data projected onto the snDrop-Seq SWNE embedding. The grey inset outlines the region where cortical neurons are embedded. (d) t-SNE plot of cells from the visual cortex and cerebellum generated using snDrop-Seq. (e) UMAP plot of cells from the visual cortex and cerebellum generated using snDrop-Seq.

Furthermore, SWNE provides an intuitive framework to show how specific genes and biological factors contribute to the visual separation of cell types or trajectories by embedding factors and genes onto the visualization. We used the gene loadings matrix (W) to identify the top genes associated with each factor, as well as the top marker genes for each cell type, defined using Seurat (Butler et al., 2018; Satija et al., 2018) (Methods, Table S1). We chose five factors and five genes that we found biologically relevant (Figure 4a, 4c, Table S1). The genes are: Apoe, Flt3, Mt2, Sun2, and Gpr56. The factors are: Inflammation, Epigenetic regulation, Metal binding, HSC maintenance, and Early erythrocyte differentiation, and factor names were determined from the top genes associated with each factor (Table S1). These factors and genes enable the association of biological processes and genes with the cell types and trajectories shown in the data visualization. For example, erythrocytes (Ery) are associated with metal binding and express Mt2, a key metal binding protein, while neutrophils (Neu) are associated with inflammation (Figure 2c). Additionally, the embedded factors and genes allow for interpretation of the overall differentiation process (Figure 2d). Undifferentiated progenitors (MP/EP) express Apoe, granulocyte-monocyte progenitors (GMP) express Flt3, while more differentiated neutrophils (Neu) express Sun2 (Figure 2d).

Figure 4: Identifying and validating gene embeddings.

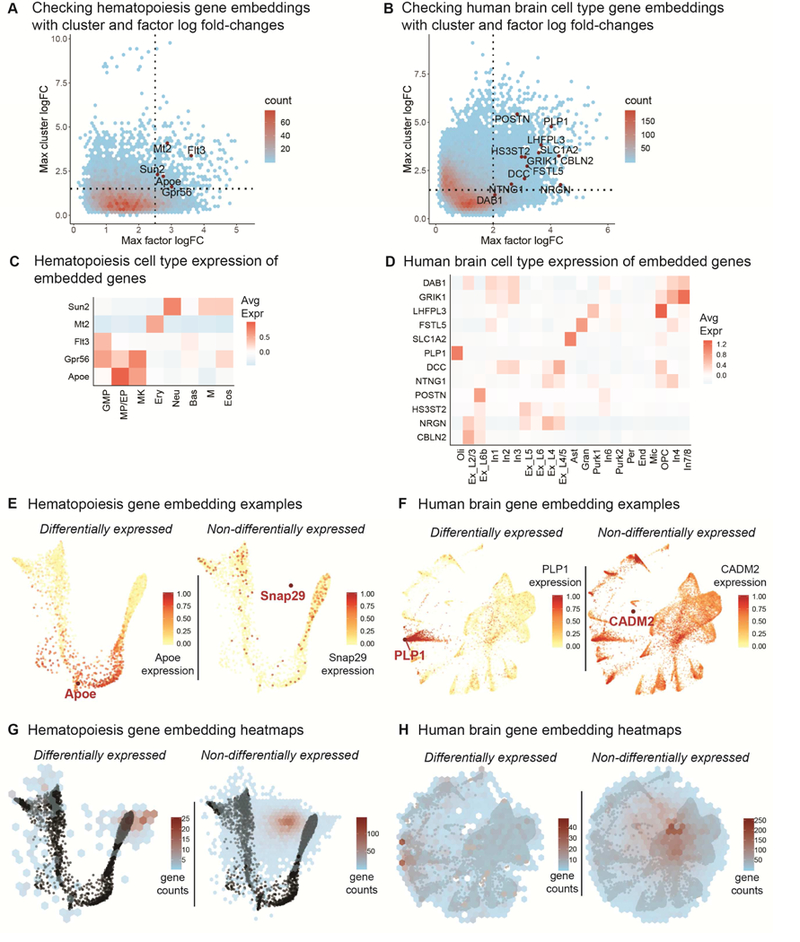
(a - b) Top cluster expression log fold-changes vs top factor loading log-fold changes for genes in the hematopoiesis (a) (Figure 2) and human brain (b) (Figure 3) datasets, with genes chosen for embedding labeled. Genes with both high cell type and factor log fold-changes are high quality candidates for embedding (top right quandrant). (c - d) Cell type specific gene expression for embedded genes in the hematopoiesis (c) (Figure 2) and human brain (d) (Figure 3) datasets. (e) An example of a differentially expressed gene (Apoe) and a non-differentially expressed gene (Snap29) embedded onto the hematopoiesis SWNE plot with corresponding expression overlaid (Figure 2). (f) An example of a differentially expressed gene (PLP1) and a non-differentially expressed gene (CADM2) embedded onto the human brain SWNE plot with corresponding expression overlaid (Figure 3). (g) Heatmap showing the locations of embedded differentially expressed and non-differentially expressed genes on the hematopoiesis SWNE embedding. (h) Heatmap showing the locations of embedded differentially expressed and non-differentially expressed genes on the human brain SWNE embedding.

Creating an interpretable map of the human visual cortex and cerebellum

We also applied SWNE to a single nucleus RNA-seq (snDrop-Seq) human brain dataset (Lake et al. 2017) from the visual cortex (13,232 cells) and the cerebellum (9,921 cells) (Figure 3a). Briefly, single nuclei were dissociated from the visual cortex and cerebellum of a single donor and sequenced using snDrop-Seq (Figure 3a) (Lake et al. 2017). Again, the number of factors for SWNE was selected using the error reduction above noise method (Figure S2e, S2f).

As with the hematopoiesis dataset, SWNE is able to visually separate cell types while providing an intuitive framework to visualize the contributions of specific genes and factors to that visual separation (Figure 3b). We selected four factors (Myelin formation, Cell Junctions, Glutamate transport and Axon projection) and ten genes (PLP1, GRIK1, SLC1A2, LHFPL3, CBLN2, NRGN, FSTL5, POSTN, DCC, DAB1, NTNG1) to embed onto the SWNE plot using cell type markers and gene loadings (Figure 4b, 4d, Table S1), adding biological context to the spatial placement of the cell types (Figure 3b). CBLN2, a gene known to be expressed in excitatory neuron types (Seigneur and Sudhof, 2017), is visually close to Layer 2/3 excitatory neurons (Ex_L2/3) and GRIK1, a key glutamate receptor (Sander, 1997), is close to inhibitory neurons (Figure 3b, Figure 4d). Additionally, the Myelin formation biological factor is near Oligodendrocytes (Oli), consistent with their function in creating the myelin sheath (Bunge, 1968) (Figure 3b). The Cell junction biological factor is very close to Pericytes (Per) and Endothelial cells (End), reinforcing their functions as the linings of blood vessels, while the Axon projection factor is close to the excitatory neuron clusters, reflecting their role in transmitting action potentials (Figure 3b).

We also demonstrate that SWNE is able to project data across technologies by projecting a 3000-cell cortical neuron dataset, generated from a different individual, using Smart-seq+ on a Fluidigm C1 microfluidic system onto the snDrop-Seq SWNE embedding (Figure 3a) (Lake et al., 2016). The Smart-seq+ protocol generates full length, total RNA without UMIs while the snDrop-Seq system generates 3’ mRNA tags with UMIs (Figure 3a) (Lake et al. 2016; Lake et al. 2017). Despite the major differences in technologies, the cortical neuron cell types in the C1 data project onto the same locations where the corresponding cell types in the snDrop-Seq data were embedded (Figure 3c). Plotting the C1 and snDrop-Seq data together shows that the technology specific batch effects are minimal (Figure S2g). Thus, SWNE’s ability to project new data onto existing embeddings can be used to integrate datasets across technologies and individuals.

t-SNE (Figure 3d) and UMAP (Figure 3e) are also able to visually separate the various brain cell types. Again, t-SNE seems to distort distances between cell types. For example, the Inhibitory neuron 7/8 (In7/8) cluster is equidistant from both the In6 cluster and Oligodendrocyte Progenitors (OPCs) (Figure 3d). Based off of their biological functions, In7/8 and In6 should be close and both clusters should be far from OPCs. Both SWNE and UMAP are able to more accurately visualize cluster distances (Figure 3b, 3e). UMAP in particular seems to generate the qualitatively cleanest visual separation between cell type clusters, while also maintaining the global structure of the data (Figure 3e).

Validating and assessing gene embeddings

To check if the embedded genes in the hematopoiesis and human brain datasets are indeed informative, we plotted the top cluster log fold-change vs top factor loading log fold-change for each gene (Figure 4a-b). Genes with high cluster specific expression are more likely to be biologically relevant, and genes that have high factor loading specificity are more likely to be visually informative. The genes we chose to embed for both datasets fell above the cluster and factor log fold-change cutoffs (Figure 4a-b). Additionally, we generated cell type expression heatmaps for the embedded genes to show in which cell type(s) each embedded gene is expressed (Figure 4c-d).

We also evaluated where differentially expressed (DE) genes and non-differentially expressed (non-DE) genes would be embedded. To start we looked at examples of where DE and non-DE genes would embed. We picked the DE genes and non-DE genes by ranking genes in each dataset by the average of the cluster log fold-change and the factor log fold- change, and picking genes from the top and bottom of the list. For the hematopoiesis dataset, we chose Apoe as the DE gene, specific to monocotyte and erythrocyte progenitors (MP/EP), and Snap29 as the non-DE gene, overlaying their respective expression levels onto the SWNE plot (Figure 4e). Apoe is visually close to MP/EP cell type, while Snap29 seems to be equidistant from all cells (Figure 4e). For the human brain dataset, we chose PLP1, an oligodendrocyte (Oli) marker, as the DE gene, and CADM2 as the non-DE gene. Again, PLP1 embeds close to the cluster that expresses it, while CADM2 embeds near the middle of the plot (Figure 4f). For a more systematic evaluation of gene embedding locations, we generated heatmaps of gene embedding locations. For the hematopoiesis dataset, DE genes tend to embed near the edges of the plot, while non-DE genes mostly embed towards the center (Figure 4g). For the human brain dataset, the DE genes are slightly more spread out but the non-DE genes still mostly embed near the center (Figure 4h).

Discussion

SWNE improves visualization fidelity for both continuous and discrete datasets

Interpretation and analysis of high dimensional single cell gene expression datasets often involves summarizing the expression patterns of tens of thousands of genes in two dimensions, creating a map that shows viewers properties of the data such as the number of cell states or trajectories, and how distinct cell states are from each other. However, while t-SNE, the most popular visualization method, can visualize subtle local patterns of expression that other methods cannot, it often distorts global properties of the dataset such as cluster distances and sizes (Figure 1e, 1f). This is especially apparent in t-SNE visualizations of developmental datasets, as t-SNE tends to exaggerate the size of cell types instead of visualizing the axes of differentiation (Figure 2c, 2d). While UMAP, a more recent visualization method, addresses these issues for discrete datasets (Figure 3e), it also has limitations when visualizing continuous time-series data with developmental trajectories, and actually performs worse than t- SNE in capturing the trajectories in some cases (Figure 2b, 2c, 2d).

Here, we integrated NMF with a Nearest Neighbors smoothing method to create SWNE, a visualization method that preserves global and local properties of the data for both continuous and discrete datasets. A key factor in SWNE’s performance is the Shared Nearest Neighbors (SNN) network weighting. Without SNN weighting, the quantitative and qualitative performance of SWNE drops off (Figure 1e, 1f, S1a, S1b). We believe SNN weighting reduces the effect of biological or technical noise, collapsing the data onto the biologically relevant components of heterogeneity. Surprisingly, this ability to minimize noise enables SWNE to capture local structure in the data better than t-SNE, and in some cases, UMAP (Figure 1e, 1f). This ability to capture local structure enables SWNE to be effective at illuminating the branch-like structure in developmental trajectory datasets (Figure 1f, 2c, 2d).

SWNE adds biological context to visualizations and projects data across technologies

Additionally, t-SNE, UMAP, and other existing methods only display cells, forcing important biological context, such as cell type marker genes, to be shown in separate plots. One of SWNE’s key advantages is that the nonnegative factor embedding framework allows for embedding of genes and cells on the same visualization. The factors act as a skeleton for the data, as both cells and genes are embedded relative to these factors. The closer a group of cells is to a gene or a factor on the visualization, the more of that gene or factor the cells express (Figure 4e, 4g). If one thinks of visualizations as maps, these embedded genes and factors act as landmarks, adding key biological waypoints to features of the visualization. Embedding genes and factors also streamlines the presentation of the data, eliminating the need for separate plots of marker genes or gene sets.

Batch effects in single cell RNA-seq are a well-known issue, and multiple methods have recently been developed for dataset integration (Butler et al., 2018; Haghverdi et al., 2018). SWNE’s framework enables new data to be projected onto an existing SWNE embedding, which we demonstrated by projecting data generated using the Fluidigm C1 microfluidic system onto an embedding generated from snDrop-Seq (Figure 3c). Despite the differences between the Fluidigm C1 and snDrop-Seq technologies, the C1 cortical neuron cell clusters map closely to the corresponding snDrop-Seq cell clusters in the embedding. Thus, SWNE’s ability to project data onto existing embeddings can be used to analyze datasets across technologies or individual patient samples.

SWNE limitations and future work

SWNE’s runtime is currently dominated by the NMF decomposition, so future work could focus on improving NMF speed, or substituting NMF with a faster matrix decomposition method such as f-scLVM or Pagoda/Pagoda2 (Buettner et al., 2017; Fan et al., 2016). Additionally, SNN weighting occurs sequentially after embedding the cells, factors, and genes. This causes the genes and factors to sometimes be further from cell clusters than they should be, although they are still generally closest to the most relevant cell cluster. Future work could involve developing a more elegant method that allows factor embeddings to shift relative to the cell embeddings.

Overall, we developed a projection and visualization method, SWNE, which captures both the local and global structure of the data for continuous and discrete datasets, and enables relevant biological factors and genes to be embedded directly onto the visualization. Capturing global structure enables SWNE to address issues of distortion that occurs with t-SNE and in some cases, UMAP, creating a more accurate map of the data. Capturing local structure with the SNN network smoothing enables SWNE to accurately visualize the key axes of variation. This enables SWNE to illuminate differentiation trajectories that are not apparent in other visualizations, such as t-SNE or UMAP. Finally, embedding key marker genes and relevant biological factors adds important biological context to the SWNE visualization. As single cell gene expression datasets increase in size and scope, we believe that SWNE’s ability to create an accurate, context-rich map of the datasets will enable more complete and meaningful biological interpretation.

STAR Methods

Contact for Reagent and Resource Sharing

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Kun Zhang (kzhang@bioeng.ucsd.edu).

Method Details

Normalization, variance adjustment, and scaling

We normalize the gene expression matrix by dividing each column (sample) by the column sum and multiplying by a scaling factor. Batch effects were normalized by a simple model, adapted from Pagoda2 (Barkas et al., 2018; Fan et al., 2016), that subtracts any batch specific expression from each gene. We used the variance adjustment method from Pagoda (Fan et al., 2016) to adjust the variance of features, an important step when dealing with RNA-seq data. Briefly, a mean-variance relationship for each feature is fit using a generalized additive model (GAM) and each feature is multiplied by a variance scaling factor calculated from the GAM fit. Feature scaling is also performed using either a log-transform, or the Freeman-Tukey transform.

Feature Selection

We recommend using feature selection to identify biologically relevant features/genes before running SWNE, as the NMF algorithm scales poorly with the number of features. Both Pagoda2 and Seurat offer feature selection methods that select overdispersed, and we have included an SWNE function for feature selection based off of the Pagoda2 method.

Nonnegative Matrix Factorization

We use the NNLM package (Lin and Paul C Boutros, 2016) to run the Nonnegative Matrix Factorization (NMF). Equation 1 shows the NMF decomposition:

$$A=\mathrm{WH}$$ (1)

Where A is the (features × samples) data matrix, W is the (features × factors) feature loading matrix, and H is the (factors × samples) low dimensional representation of the data. The NMF initialization method can affect the embedding, and we offer an Independent Component Analysis (ICA) initialization, a Nonnegative-SVD (NNSVD) initialization, and a purely random initialization. We have found that ICA initialization works well with most datasets, and is set as the default option. For datasets with a large number of features, ICA can be fairly slow so we use SVD as a pre-processing step for the ICA initialization.

Model Selection

To select the number of factors for NMF, we use the method developed by Frigyesi et al where we compare the decrease in reconstruction error for the input matrix with the decrease in reconstruction error for a randomized matrix. We take the highest number of factors such that the decrease in reconstruction error for the input matrix is still higher than the decrease in error for the randomized matrix (Frigyesi and Höglund, 2008). Specifically, we calculate the reconstruction error for both the input matrix and the randomized input matrix for a range of factors. We then compute decrease in reconstruction error with an increasing number of factors (k) for both matrices, and subtract the decrease in error for the randomized matrix from the decrease in error for the input matrix to create an error reduction above noise metric. We select the maximum number of factors before this error reduction above noise falls below zero (Figure S2a-b, S2e-f).

Generating the SNN matrix

In order to ensure that samples which are close to each other in the high dimensional space are close in the 2d embedding, we smooth the NMF embeddings with a Shared Nearest-Neighbors (SNN) matrix, calculated using code adapted from the Seurat package (Butler et al., 2018; Satija et al., 2018). Briefly, we calculate the approximate k-nearest neighbors for each sample using the Euclidean distance metric (in the Principal Component space. We then calculate the fraction of shared nearest neighbors between that sample and its neighbors. We can then raise the SNN matrix, denoted here as S, to the exponent $\beta :S^{\prime }=S^{\beta }.$ If $\beta >1$ , then the effects of neighbors on the cell embedding coordinates will be decreased, and if β < 1, then the effects will be increased. Finally we normalize the SNN matrix so that each row sums up to one.

Weighted Factor Projection

We adapt the Onco-GPS (Kim et al., 2017) methodology to embed the NMF factors onto a two dimensional visualization. First, we smooth the H matrix with the SNN matrix using Equation 2:

$$H_{\mathrm{smooth}}=H*S$$ (2)

We then calculate the pairwise similarities between the factors (rows of the H_smooth matrix) using either cosine similarity, or mutual information (Kim et al., 2016). The similarity is convertec into a distance with equation 3:

$$D=\sqrt{2(1-R)}$$ (3)

Here, R is the pairwise similarity. We use Sammon mapping(Sammon, 1969) to project the distance matrix into two dimensions, which represent the x and y coordinates for each factor. The factor coordinates are rescaled to be within the range zero to one.

Weighted Sample Embedding

Let $F_{ix}$ , $F_{iy}$ represent the x and y coordinates for factor i.To embed the samples, we use the sample loadings from the unsmoothed H matrix via equations 4 & 5:

$$L_{jx}=\frac{\sum _i{\left(H_{ij}{F}_{ix}\right)}^{\alpha }}{\sum _i{H_{ij}}^{\alpha }}$$ (4)

$$L_{jy}=\frac{\sum _i{\left(H_{ij}{F}_{iy}\right)}^{\alpha }}{\sum _i{H_{ij}}^{\alpha }}$$ (5)

Here, j is the sample index and i is iterating over the number of factors in the decomposition (number of rows in the H matrix). The exponent α can be used to increase the “pull” of the NMF components to improve separation between sample clusters, at the cost of distorting the data. Additionally, we can choose to sum over a subset of the top factors by magnitude for a given sample, which can sometimes help reduce noise. We end up with a 2 x N matrix of sample coordinates, L.

To weight the effects of the SNN matrix on the samples, the sample coordinates L are smoothed using equation 6:

$$L_{smooth}=S*L$$ (6)

The smoothed sample coordinates (L_smooth) are then visualized. While we have found that an SNN matrix works well in improving the local accuracy of the embedding, other similarity matrices, such as those generated by scRNA-seq specific methods like SIMLR, could also work. In general, you should use whichever similarity or distance matrix you used for clustering.

Embedding features

In addition to embedding factors directly on the SWNE visualization, we can also use the gene loadings matrix (W) to embed genes onto the visualization. We simply use the W matrix to embed a gene relative to each factor, using the same method we used to embed the cells in the H matrix. If a gene has a high loading for a factor, then it will be very close to that factor in the plot, and far from factors for which the gene has zero loadings. To ensure that embedded features have both cluster specificity and contain relevant spatial information in the SWNE embedding, we plot the top cluster log fold-change against the top factor loading log fold- change for each feature, highlighting the embedded features (Figure 4a-b). Any features that fall below the cluster log fold-change cutoff or the factor loading log fold-change cutoff may not be good candidates for embedding, and SWNE will warn users if they attempt to embed those features.

Constructing the SNN matrix from different dimensional reductions

The SNN matrix can be constructed from either the original gene expression matrix (A), or on some type of dimensional reduction. We have found that constructing the SNN matrix from a PCA reduction tends to work well, especially in datasets where that follow a trajectory or trajectories. We believe this is due to PCA’s ability to capture the axes of maximum variance, while NMF looks for a parts-based representation (Abdi and Williams, 2010; Lee and Seung, 1999). For datasets where there are discrete cell types, constructing the SNN matrix from the NMF factors is often similar to constructing the SNN matrix from PCA components. Thus, we default to building the SNN matrix from principal components.

Interpreting NMF components

In order to interpret the low dimensional factors, we look at the gene loadings matrix (W). We can find the top genes associated with each factor, in a manner similar to finding marker genes for cell clusters. Since we oftentimes only run the NMF decomposition on a subset of the overdispersed features, we can use a nonnegative linear model to project the all the genes onto the low dimensional factor matrix. One can also run Geneset Enrichment Analysis (Subramanian et al., 2005) on the gene loadings for each factor to find the top genesets associated with that factor.

Projecting New Data

To project new data onto an existing SWNE embedding, we first have to project the new gene expression matrix onto an existing NMF decomposition, which we can do using a simple nonnegative linear model. The new decomposition looks like equation 7:

$$A^{\prime }=W{H}^{\prime }$$ (7)

Here, A’ is the new gene expression matrix, and W is the original gene loadings matrix, which are both known. Thus, we can simply solve for H’. The next step is to project the new samples onto the existing SNN matrix. We project the new samples onto the existing principal components, and then for each test sample, we calculate the k closest training samples. Since we already have the kNN graph for the training samples, we can calculate, for each test sample, the fraction of Shared Nearest Neighbors between the test sample and every training sample. With the test factor matrix H’, and the test SNN matrix, we can run the SWNE embedding as previously described to project the new samples onto the existing SWNE visualization.

Generating Simulated Datasets

We used the Splatter (Zappia et al., 2017) R package to generate a discrete dataset with five different clusters, estimating parameters from the 3k PBMC dataset published by 10X genomics. We generated five distinct clusters (groups), where Groups 1 and 5 had a differential expressed gene (DEG) probability of 0.3, while Groups 2–4 had a DEG probability of 0.15. Group 5 contains 1215 cells, Groups 2–4 contain 405 cells each, and Group 1 contains 270 cells. Thus, Groups 1 & 5 should be relatively distant and Groups 2–4 should be relatively close. To simulate a branching trajectory dataset, we estimated parameters from the hematopoiesis dataset from Paul et al. We generated four paths, where each path is parameterized by the number of cells in that path and the number of “time-steps”, which essentially controls how long the path is. Path 1 branches into Paths 2 and Paths 3, and Path 3 continues onto Path 4. Paths 1 & 2 contained 819 cells each, and Paths 3 & 4 contained 546 cells each. Path 1 had 100 steps, Path 2 was the “longest” path with 200 steps, and Paths 3 & 4 had 50 steps each. Each cell is assigned to a path, and a time-step. For example, Cell2522 might belong to Pathl and time-step 68.

Evaluating Embedding Performance

To evaluate how well each embedding maintained the global structure of the discrete simulation, we correlated the pairwise cluster distances in the 2D embedding with the pairwise cluster distances in the original gene expression space. We then calculated the average Silhouette score for each embedding, evaluating how well the visualization separates the clusters. For the trajectory simulation, we divided each path into “chunks” of five time-steps. We correlated the pairwise distances of each “path-time-chunk” in the embedding space with the pairwise distances in the gene expression space to evaluate how well the embeddings maintained the global structure. To evaluate the local structure, we constructed a “ground-truth” neighborhood graph by adding an edge between every cell in each path-time-step, and every cell in each neighboring path-time-step. For example, we would connect all the cells in Pathl at time-step 23, with all the cells in Pathl and time-step 24. We then created a nearest neighbor graph for each embedding, and took the Jaccard similarity between each cell’s neighborhood in the embedding and the true neighborhood. We used the average Jaccard similarity as our “neighborhood score”.

We adopted a similar approach to evaluate the hematopoiesis dataset. To quantitatively evaluate how well each embedding captured the global structure, we divided each annotated cluster into “chunks” of 50 cells by pseudotime calculated using Monocle2. We then correlated the pairwise distances of each cluster-time-chunk in the embedding space with the pairwise distances in the gene expression space. To evaluate the local structure, we compute the overlap in the 30 nearest neighbors for each cell in the embedding space with the nearest neighbors in the gene expression space using the Jaccard similarity. We average the Jaccard similarities across all cells as our “neighborhood fidelity score”.

Running UMAP, t-SNE and other dimensional reduction methods

UMAP and t-SNE were run through the Seurat R package (Butler et al., 2018). We first reduced the dimensionality of the gene expression matrix with PCA, and used a variance explained elbow plot to select the number of principal components to keep. The principal components were used as inputs to UMAP and t-SNE.

Diffusion maps, Isomap, Locally Linear Embedding (LLE), and Multidimensional Scaling (MDS) were run directly on the normalized gene expression matrix. Diffusion maps was run using the Destiny R package (Angerer et al., 2015), Isomap and LLE were run with the RDRToolbox R package, while MDS was run using the cmdscale function in R. Default parameters were used in all cases unless otherwise specified.

Quantification and Statistical Analysis

To ensure that the single cell RNA-seq data was approximately Gaussian with zero inflation, we used histogram plots to assess the distributions of each dataset with and without zeros.

Data and Software Availability

The SWNE package is available at https://github.com/yanwu2014/swne. The scripts used for this manuscript are under the Scripts directory. The data needed to recreate the figures can be found here:

• http://genome-tech.ucsd.edu/public/SWNE/hemato_data.tar.gz (Hematopoiesis data)

• http://genome-tech.ucsd.edu/public/SWNE/neuronal_data.tar.gz (Neuronal data)

The raw data for the hematopoietic and neuronal cells can be found at the GEO accessions GSE72857 and GSE97930, respectively. The PBMC dataset can be found at the 10X genomics website: https://support.10xgenomics.com/single-cell-gene-expression/datasets/1.1.0/pbmc3k. The simulated datasets can be found at: http://genome-tech.ucsd.edu/public/SWNE/splatter_simulated_data.tar.gz

Supplementary Material

Table S1:

Cell type and biological factor annotation for the hematopoiesis and human brain datasets. Related to Figures 2 and 3.

Table S2:

Runtime analysis for SWNE, t-SNE, and UMAP. Related to Figure 1.

Figure S1: SWNE model selection stability and additional visualizations of simulated datasets. Related to Figure 1.

(a) Additional visualizations for the discrete simulation: SWNE without SNN weighting, PCA, locally linear embedding (LLE), multidimensional scaling (MDS). (b) Additional visualizations for the trajectory simulation: SWNE without SNN weighting, PCA, locally linear embedding (LLE), multidimensional scaling (MDS). (c) SWNE visualizations of the discrete simulation across a range of k. (d) SWNE visualizations of the trajectory simulation across a range of k. (e) Quantitative evaluation of SWNE performance across a range of k for the discrete simulation, (f) Quantitative evaluation of SWNE performance across a range of k for the trajectory simulation.

Figure S2:

Factor selection plots and additional visualizations of the hematopoiesis and human brain datasets. Related to Figures 2 and 3.

(a) Factor selection for the hematopoiesis dataset (Figure 2). The optimal number of factors is when the decrease in reconstruction error above noise falls below zero (Methods) (b) Hematopoiesis factor selection plot across five randomizations to demonstrate stability (Figure 2). (c) Monocle2 reversed graph embedding (RGE) plots of two RGE components with cells labeled by cell types and pseudotime (Figure 2). (d) Monocle2 reversed graph embedding complex tree plots generated from ten RGE components with cells labeled by cell types and pseudotime (Figure 2). (e) Factor selection for the human brain dataset (Figure 3, Methods), (f) Hematopoiesis factor selection plot across five randomizations to demonstrate stability (Figure 3). (g) Cortical neurons generated using the Fluidigm C1 system projected onto human brain data generated from single nucleus Drop-Seq (snDropSeq), labeled by the technology used to generate the cells (Figure 3).

Highlights.

• SWNE visualizes high dimensional single cell genomics datasets

• SWNE creates 2D cell and gene embedding with NMF and similarity weighting

• Visualization captures local/global structure in continuous/discrete datasets

• Embedded genes and factors add key biological context to visualization