Abstract
The ability to separate RBCs from the other components of whole blood has a number of useful clinical and research applications ranging from removing RBCs from typical clinical blood draw, bone marrow transplants to transfusions of these RBCs to patients after significant blood loss. Viewed from a mechanistic/process perspective, there are three primary methodologies to remove RBCs: 1) RBCs lysis, 2) separation of the RBCs from the nucleated cells (i.e., stem cells) based on density differences typically facilitated through centrifugation or sedimentation agents, and 3) antibody based separation in which a targeted RBC is bound with an affinity ligand that facilitates its removal. More recently, several microfluidic based techniques have also been reported. In this report, we describe the performance of continuous RBC separation achieved by the deflection of intrinsically magnetic, deoxygenated RBCs as they flow through a magnetic energy gradient created by quadrupole magnet. This quadrupole magnetic, with aperture of 9.65 mm, has a maximum field of B0 = 1.36 T at the pole tips and a constant field gradient of B0/r0 = 286 T/m. The annular flow channel, contained within this quadrupole magnet, is 203 mm long, has an inner radius of 3.98 mm, and an inner, outer radius of 4.36 mm, which corresponds to an annulus radius of 380 micron. At the entrance and exit to this annular channel, a manifold was designed which allows a cell suspension and sheath fluid to be injected, and a RBC enriched exit flow (containing the magnetically deflected RBCs) and a RBC depleted exit flow to be collected. Guided by theoretical models previously published, a limited number of operating parameters; total flow rate, flow rate ratios of flows in and flow out, and ratios of RBC to polystyrene control beads was tested. The overall performance of this system is consistent with our previously presented, theoretical models and our intuition. As expected, the normalized recovery of RBCs in the RBC exit fraction ranged from approximately 95% down to 60%, as the total flow rate through the system increased from 0.1 to 0.6 ml/min. At the cell concentrations studied, this corresponds to a cell flow rate of 1.5 × 106 to 9 × 106 cells/min. While the throughput of these pilot scale studies are slow for practical applications, the general agreement with theory, and the small cross-sectional area in which the actual separation is achieved, 77 mm2 (annulus radius times the length), and corresponding volume of approximately 2 mls, suggests the potential to scale-up a system for practical applications exists and is actively being pursued.
Keywords: red blood cells, magnetophoresis, continuous separation, quadrupole magnetic separator
Introduction
Very significant improvements in the safety of the blood supply have been made over the past few years, especially with respect to minimizing the risk of transfusing units that are contaminated with infectious agents. However, opportunities still exist to reduce the modifiable risk factors that are inherent in the red blood cell (RBC) unit itself. For example, an RBC unit contains approximately 300 mL of RBCs and saline-based preservative solutions. This volume is injected directly into the recipient’s circulation and, in at-risk recipients, can lead to congestive heart failure, a condition known as transfusion associated circulatory overload (TACO). TACO has been estimated to occur following approximately 1:100-1:50 transfusions and is a leading cause of transfusion related mortality.(Narick, Triulzi et al. 2012, Alam, Lin et al. 2013, Lieberman, Maskens et al. 2013) It is known that, depending on the storage duration of the RBC unit, up to 25% of the RBCs that are transfused are cleared from the recipient’s circulation within 24 hours.(Luten, Roerdinkholder-Stoelwinder et al. 2008) These rapidly removed RBCs are likely of little benefit to the recipient and in fact their rapid clearance might be harmful as it has been speculated that the iron burden caused by these cleared RBCs might lead to oxidative stress, inflammatory cytokine release, and an increased amount of non-transferrin bound iron in the circulation that might predispose the recipient to infection and other adverse events.(Hod, Zhang et al. 2010) If these soon to be cleared RBCs can be removed from the RBC unit before they are transfused, the recipient will be exposed to a smaller volume of RBCs, hence a lower rate of TACO would be expected, and they would be spared the potential adverse effects of the cytokine storm and iron release that occurs when they are destroyed. In addition, the RBCs that are transfused would be expected to have a longer life span in circulation.
Similarly, it is known that repeated blood donation leads to iron deficiency in the donor.(Rieben, Frauenfelder et al. 1992, DeAndrade, Waters et al. 2016) Since the blood donor is doing so of their own altruistic volition, it is important that their health status be respected and optimized during the donation process. By removing the oldest RBCs that are not expected to survive for 24 hours when they are transfused from the donated unit and returning them to the donor (perhaps in an in-line process during the donation process itself), the donor would be less likely to become iron deficient and could perhaps donate more frequently since a smaller volume of RBCs (and hence iron) is being removed during each donation. The ability to separate RBCs from the other components of whole blood has other useful clinical applications outside of preparing RBC units for transfusion. When stem cells are collected either from the bone marrow or from peripheral blood, the stem cells have to be separated from the RBCs that are also collected during the harvest. Traditionally this is performed by adding an agent that enhances the RBC sedimentation rate relative to the stem cells thereby affecting a crude separation. This process can take hours to complete. A labeless method of separating RBCs from stem cells that does not require the addition of sedimentation agents, that would not harm the stem cells, and that would be more rapid than the current method would be highly desirable.(Basford 2010, Markus 2012)
It is thus clear that the removal of RBCs from a blood or bone marrow sample for diagnostic or therapeutic applications would be a very desirable laboratory practice/procedure. In terms of therapeutic use, approximately 14 million units of human red blood cells were transfused in the US in 2011, and more than 18,000 bone marrow or umbilical cord blood transplants were performed in the US in 2013. With respect to diagnostic use, the number of blood samples in which the RBCs must be removed before testing is on the order of tens of thousands per day in hospitals throughout the USA, in particular in chemistry and coagulation laboratories.
Viewed from a mechanistic/process perspective, there are three primary methodologies to remove RBCs: 1) RBCs lysis, 2) separation of the RBCs from the nucleated cells (i.e., stem cells) based on density differences typically facilitated through centrifugation or sedimentation agents, 3) antibody based separation in which a targeted RBC is bound with an affinity ligand that facilitates its removal, and 4) recently presented microfluidic based techniques that exploit hydrodynamic lift forces or deterministic lateral displacement, both of which exploit differences in cell sizes. (Huang 2004, Mutlu 2017) Of these methods, the two most commonly used methods are the density difference method and the RBC lysis. Having a method of separating RBCs from whole blood for diagnostic or therapeutic use that is labeless, does not damage the RBCs during the separation, and quite whose equipment does not occupy a large footprint in the laboratory would have significant value in a variety of applications. Not damaging the RBCs in the process of separation would be an improvement on current separation methods because if hemolysis occurs during separation, the contents of the RBCs, such as potassium and bilirubin, will enter the plasma and can artificially inflate the concentration of these analytes in the plasma thereby confounding the accurate determination of the patient’s actual plasma concentrations.
We have previously reported on the characterization, both theoretically and experimentally, of the magnetically induced velocity, magnetophoretic mobility, m, of oxygenated, deoxygenated, and the met-hemoglobin state of RBC (Figure 1).(Zborowski, Ostera et al. 2003) Mathematically, magnetophoretic mobility is defined by:
| (1) |
where Vm is the magnetically induced velocity, Sm is the magnetic energy gradient, B is the magnetic flux, and μ0 is the permeability of free space. The magnetic properties of the heme molecule in RBCs was first characterized by Pauling and Coryell (1936a, b)(Pauling and Coryell 1936).(Pauling and Coryell 1936) Fundamentally, when the iron in a functioning hemoglobin molecule in RBCs is bound to oxygen, the chemical bond has a covalent nature; conversely, when the hemoglobin is deoxygenated, the iron has an ionic nature with corresponding unpaired electrons which impart a paramagnetic nature to the hemoglobin. An analogous paramagnetic characteristic of hemoglobin can be created when hemoglobin is chemically oxidized, metHb, with a chemical such as sodium dithionite.
Figure 1.
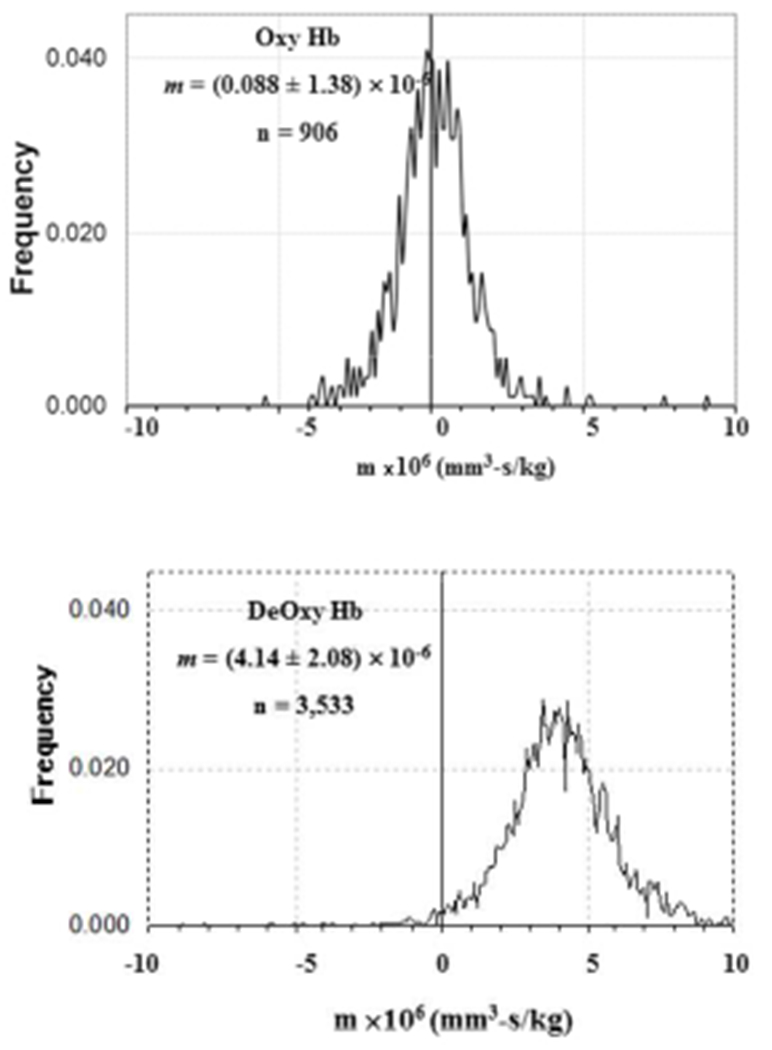
Magnetophoretic mobility histograms of oxygenated and deoxygenated human red blood cells. From Zborowski et al. [10]
Initial demonstrations of the exploitation of this paramagnetic characteristic of RBCs for separation was conducted by Melville, and co-workers, using what has come to be called a high gradient magnetic field (HGMF). In their application, they created the HGMF using a wire mesh placed within the cell suspension, facilitating close proximity of the HGMF to the RBCs. This HGMF was induced by a magnetic field external to the cell suspension containing the HGMF.(Melville 1975) Such a structure with a wire mesh coming in contact with the cell suspension, while relatively easy to create a HGMF, present the possibility of plugging.(Jin, Abbot et al. 2012) Further, accurate modeling of the magnetic field and the flow field that RBCs experience through the HGMF is nearly impossible.
In contrast, alternative designs have been developed in which a high gradient magnetic field is imposed on a “zone” through which the cells are flowing; an “open gradient” separation system. In this approach, the primary mechanism of separation is the movement, or magnetophoretic mobility, of the targeted cells across different flow stream in the separation “zone” with the targeted cells either depositing on a surface in this “zone”, or actually leaving the separator; i.e. a continuous magnetic separator. This is in contrast to the traditional HGMS (i.e. a MACS column, Miltenyi Biotec) in which the primary mechanisms of separation is the holding and/or retention of the targeted cells to the HGMF matrix within the separator.
A number of reports exist of different types of “open gradient” cell separators that utilize magnetophoretic mobility with either subsequent deposition/retention of the targeted cells on a surface within the device, or the flow of the cells into multiple exit flow streams, based on the cells magnetically induced velocity which is typically perpendicular to the flow direction (Zborowski 1995, Toner 2005, Han 2006, Xia 2006, Jung 2010, Schneider 2010, Moore 1998, Sun 1998, Lara 2004). As indicated in Equation 1, this magnetically induced velocity is the product of the cells magnetophoretic mobility and the magnetic energy gradient imparted on the cell:
| (2) |
To maximize this magnetic velocity, either the cells magnetophoretic mobility must be maximized, typically through bound antibody magnetic particle conjugates, or in the case of cells with intrinsic magnetism, such as deoxygentated RBCs, a high value of Sm and/or long residence time in the Sm zone is needed to achieve an effective separation.
With respect to RBC separations based on intrinsic magnetization using an “open gradient” architecture, a high performance system (i.e. reasonable throughput, high purity and recovery) requires well characterized flow fields and as high as possible values of Sm (Nath 2008, Jung 2010, Moore, Nehl et al. 2013, Rahman 2016, Sun submitted). In our laboratory we have been developing a magnetic separation approach based on the use of a quadrupole magnetic field surrounding an annular flow channel, QMS(Sun 1998, Lara 2004). While originally designed for the separation of cells labeled with antibodies conjugated to magnetic nanoparticles, we have extended the design to included separating RBCs based solely on the intrinsic magnetization of the deoxy and met form of hemoglobin. The latest reports using the QMS system were focused on batch, capture and release of RBCs (Moore, Nehl et al. 2013, Moore, Williams et al. 2014). In this report, we wish to describe the performance, and the scale up potential, for using the QMS to separate RBCs in a continuous mode of operation which includes an in-line deoxygenation step.
Materials and methods.
Magnet design.
An open gradient magnetic separator, QMS, was assembled using permanent magnet blocks arranged in a special configuration that we call a “windmill”, producing a centrifugal force on paramagnetic molecules inside its air bore. Permanent magnet blocks (neodymium-iron-boron, maximum energy product 42 and 52 MGOe, Applied Magnetics, Plano, TX) and suitably-shaped, 1018 C steel pole pieces generated quadrupole field with a maximum field of B0 = 1.36 T at the pole tips and a constant field gradient of B0/r0 = 286 T/m. The magnet assembly’s aperture (9.65 mm) accommodated a cylindrical flow channel of 9.52 mm outer diameter and 203 mm length. The volume near the center of the channel, where the magnetic centrifugal force was the lowest, was excluded by insertion of a co-axial solid 316 stainless steel rod of 3.98 mm (Figure 2).
Figure 2.

Cross sectional field heat map calculated midway down the length of the QMS magnet, left, and 3-D perspective view of the QMS magnet, right.
Flow channel.
Figure 3 presents cross sectional view of the flow channel contained within the QMS magnet. The region of the channel surrounded by the QMS magnet, the rod and cylinder, are made of type 316 stainless steel which has very low relative magnetic permeability (1.002-1.005). The entrance and exit manifolds were constructed by a high-resolution 3D printer by Spectrum Plastics Group (Westminster, CO) of resin Watershed 11122XC, a material that is optically clear, and that has low water uptake and negligible magnetic interaction. The actual computer design of the manifolds used the software, SolidWorks™.
Figure 3.

Cross sectional diagram of the separation column contained within the magnet assembly.
An add-on module for the SolidWorks™, FloWorks™, conducts computation fluid dynamics, CFD, simulation of SolidWorks assemblies. Figure 4 presents two axial cross-sectional views, front and rotated axially 45 degrees of these entrance and exit manifolds. The component flow rates (Qa’, Qb’, Qa and Qb, corresponding to inlet inner, inlet outer, outlet inner and outlet outer) presented in Figure 4 are for flow rates of 0.2, 0.8, 0.2 and 0.8 ml/min, which when compared to the actual values used and presented below, are higher than experimental operation. Further analysis, and subsequent calculations not presented, indicate that the flow is fully developed, with no dead spaces, instabilities or boundary layer separation. The estimated shear stresses are well below the 50 dynes/cm2 reported to exist in arteriole circulation (RL 1968). The highest shear stress occurs in the short ducts that connect external tubing to the annular flow. The smallest of these is 0.021”, while the connecting tubing ID is 0.020” (0.51 mm). For the case of Qb’ = 0.8 ml/min (1 ml/min total flow rate and a flow rate ratio of 0.8) the wall shear stress for fluid of 1 cP viscosity is 1.04 N/m2 or 10.4 dyne/cm2.
Figure 4.
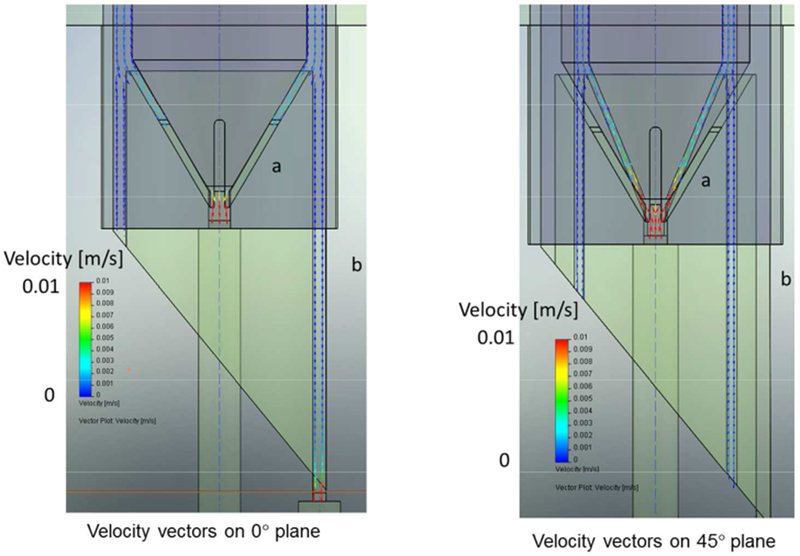
FloWorks™ simulations of the fluid flow profiles through the exit manifold. The difference between the two images is a rotation of 45 degrees.
Figure 5 presents an overview diagram of the system/apparatus used in this report. Specific points of interest is the Liqui-Cell Micromodule™ hollow fiber module used to deoxygenate the cell-free carrier. Unfortunately, we observed that hollow fiber module non-specifically entraps RBCs; subsequently, we deoxygenated the RBCs in a batch process prior to entrance into the magnetic separation system using a 3D printed, stirred tank. This stirred tank has a pure nitrogen inlet port and an outlet exhaust port, as well as an outlet cell suspension port. Further, there is an opening in the lid to allow a probe that is connected to a dissolved oxygen meter (Oakton DO 110), which sends data via RS-232C output to a laptop. The nitrogen gas flow rate was monitored and adjusted to be in the range of 50-60 ml/min.
Figure 5.

Schematic of the RBC sorting apparatus. Direction of the flow is specified by arrows.
Three of the four inlet/outlet flows to the QMS were controlled by two Harvard syringe pumps. The sample inlet flow rate was controlled by application of a relative vacuum due to mass conservation. PEEK tubing, shown in orange was used throughout liquid flow compartments due to its low oxygen permeability. The online UV detector was used to determine when a steady operation of the separation was achieved, and to judge when sufficient cell free carrier was flushed through at the end of the sort to stop the process.
Model cell mixtures.
Two different types of cell suspensions were used in this study: 1) RBC suspension obtained by a 1:100 dilution of whole blood, obtained from healthy volunteer donors (providing a signed consent form, approved by the Cleveland Clinic Institutional Review Board, IRB), and 2) Dilute whole blood in various number ratios with 12 μm polystyrene microbeads, PS (diameter CV <= 18%, #7510B, Thermo Scientific). These PS beads are sufficiently distinct in diameter compared to RBCs to allow separate enumeration in a particle counter, Coulter Z2 (Beckman-Coulter, Hialeah, FL, USA). In both cases, the final concentration was approximately 3e07 cells or cells and particles per ml. The diluent was Ca- and Mg-free PBS with 2 mM EDTA and 0.5 % (w/v) BSA. This diluent was also the cell-free “carrier” fed into the b’ inlet.
Concentration analysis.
From concentrations of RBC and PS evaluated by the Z2, the recovery F, normalized recovery NF, purity P, and enrichment rate E, were determined by the equations below. The subscript j refers to the outlet (a or b – or when explicitly stated - the feed f). Each equation applies to either species (RBC or PS).
| (3) |
| (4) |
| (5) |
| (6) |
Model separation predictions.
An advantage of an “open gradient” system is that since the fluid flow is sufficiently low (laminar flow regime) and at steady state, and the magnetic flux density is accurately known/predictable, the performance of the QMS can be simulated in a straight forward manner. For a number of years we have been designing, theoretically analyzing, and simulating, “open gradient” magnetic cell separation systems (Zborowski 1995, Williams PS 1999, Jing 2007, Schneider 2010, Moore 1998). For example, Jing et al. (Jing 2007) used the following relationship:
| (7) |
to predict the change in dimensionless radial position, ρ, from ρ1 to ρ2, as the cell moves axially along down the QMS channel (Figures 2 and 3). The range of z from 0 to L defines the boundaries of the permanent magnet. A1 is a constant defined by the geometry, ρ is dimensionless radius r/r0, m is cell magnetophoretic mobility, Q is the total flow rate and Smo is the force field strength, equal to Bo2/μoro). The trajectory is either from (ρ1, z=0) to (ρ2, z=L), the case of the cell exiting without reaching the cylinder wall; or from (ρ1, z=0) to (ρ=1.0, z<L), the case of the cell reaching the cylinder wall before exiting the channel. See table of nomenclature for a complete description of the various variables and symbols used.
Equations 1–7, along with several more presented in Jing et al. were applied to a computer program written in MAPLE (Waterloo Maple, Canada), and subsequently converted to MATLAB to predict the performance of the QMS system. In addition to various constants associated with the channel and the magnets, this program requires an input of the mobility distribution of the cells – in the form of mobility increment versus frequency – obtained from CTV measurements (Figure 1 for this current study). Each mobility increment-frequency pair is processed by use of equation 7 to obtain recovery in exit flows a and b. Additionally a wall w retention is assigned for those trajectories that reach the wall at r=r0 or ρ=1 and z < L. The recovery increments are weighted by frequency in the sample and summed to obtain overall recovery in a, b, and w: F(a), F(b), and F(w).
Assumptions in the simulation include: 1) the flow is fully developed in the channel, 2) cells are uniformly distributed before acted upon by the magnetic field, 3) cells are point masses, 4) interparticle effects are negligible, and, 5) when cells reach the cylinder wall there is no further motion.
Results
Positive control.
Guided by computer simulations using the algorithm outlined above, initial studies were conducted with 1:100 diluted whole blood, which corresponds to a cell concentration of approximately 3 × 107 cells/ml. Using constant inlet and outlet flow rate ratios Qa’/Q and Qa/Q, of 0.5 and 0.55, respectively (See Figure 3 for locations of these flows), and a total flow rate ranging from 0.05 to 0.75 ml/min, the recovery of RBCs in outlet b was determined and is presented in Figure 6. Each flow rate condition was repeated 4 times, and the error bars correspond to 1 standard deviation.
Figure 6.

Experimental and theoretical results of a positive control study using RBCs. Fb, Fw, and Fb + Fw as a function of total flow rate through the system. While it initially appears that Fb alone shows poor agreement between theoretical and experimental data, but when Fb and Fw have been added together, similar trend could be observed.
As can be observed, the recovery of the RBCs in the enriched outlet flow b decreases with increasing flow rate, since a higher flow rate results in a shorter time for the RBCs to move into the flow streams going to outlet b. An initial comparison of the experimental and theoretical data would seem to show poor agreement. However, if we add the theoretical wall fraction to the b fraction (green line), we find a similar trend to the experimental curve. The computer simulation assumes that when a cell reaches the cylinder wall of the annular channel, the cells are retained; but in reality, some RBCs roll down the wall or are driven by the flow to outlet b. The Fb+Fw curve surpasses the experimental curve, perhaps because not all of the wall-bound cells are recovered, or there is particle holdup elsewhere, such as in the connecting tubing.
Effect of presence of non-magnetic PS beads.
As described above, it is often desirable to deplete RBCs to recover the WBC fraction that might contain CTCs, stem cells, etc. Thus, we are concerned not just with quantitative removal of RBCs, but a high recovery of the remaining cell types. 12 μm PS particles are used as stand-ins for these, as they are completely distinguishable by Coulter Counter. This study makes no attempt to account for the native WBCs that overlap the RBCs in diameter, and whose number concentration is approximately 0.1% that of RBCs. To investigate the recovery of non-RBCs in the non-magnetic exit stream, Fa, flow conditions that gave a high recovery of RBCs in Fb, (Q=0.1 mL/min, Qa’/Q =0.50, and Qa/Q = 0.55), Fig. 6, were selected and held constant. With this constant flow rate, the feed composition, expressed as the number ratio of RBC:PS, was varied from 90:10 to 50:50. The results are presented in Figure 7. The recovery of PS beads in outlet a is roughly independent of feed composition, and is >= 80% in all cases, satisfying a desirable separation criterion. However, there is a decrease in RBC recovery in the magnetically enriched outlet b with increasing PS concentration. We suggest this is the result of increasing interference of the radially magnetically-driven RBCs by the PS, acting as obstacles. This is analogous to the hindered settling phenomenon, where a higher concentration of slow- or non-settling particles increases the settling time of faster settlers, through the mechanism of higher effective viscosity (McCabe 1985).
Figure 7.
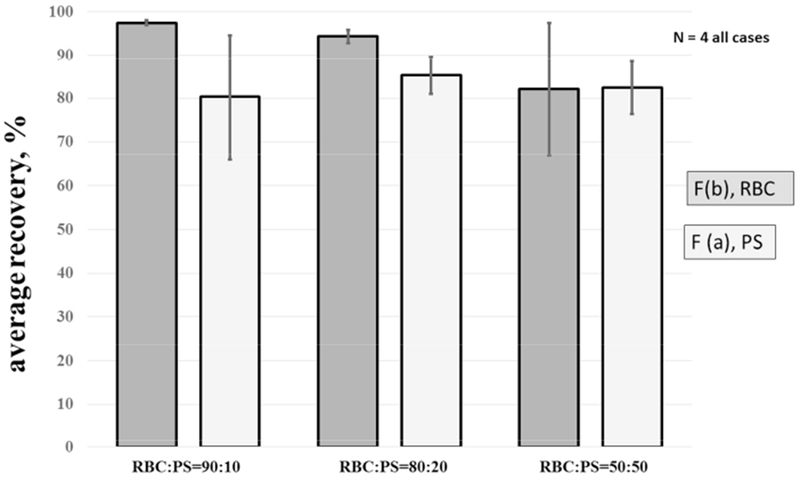
Experimental and theoretical results of a 1:100 diluted blood sample spiked with polystyrene, PS beads. Comparison of the recovery of RBC and PS using various RBC:PS ratio. Total flow rate, Q = 0.1 mL/min, Q′a/Q = 0.55, Qa/Q = 0.55.
Effect of total flow rate on recoveries.
To investigate the recovery of both RBCs and non-RBCs in their respective exit flows as a function of total flow rate, Q was varied from 0.1 to 0.6 ml/min, while Qa’/Q and Qa/Q were held constant at 0.5 and 0.55, respectively. The feed composition was maintained at RBC:PS = 90:10. Figure 8 presents the results of this study. The normalized recovery of RBCs in outlet b increases with lower total flow rates, consistent with the view that longer residence time correlates with higher Fb. However, the recovery of the PS beads in outlet a appears to be only weakly affected by total flow rate.
Figure 8.
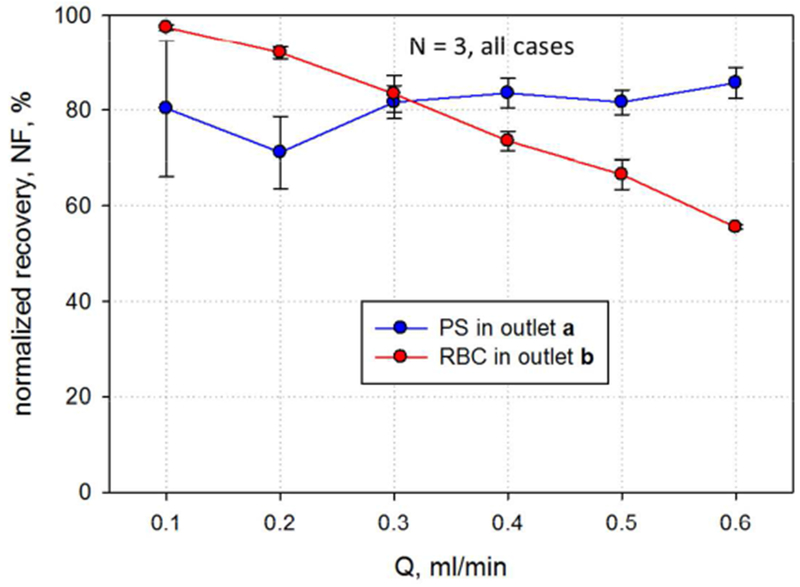
Comparison of the RBC and PS normalized recovery as a function of total flow rate. As illustrated in the text, only the RBC recovery rate decreases with increasing flow rate. RBC:PS of 90:10, Q′a/Q = 0.5, Qa/Q = 0.55.
Figure 9 shows that the purity of the RBCs in outlet b does not change with total flow rate. This is predicted by the results of Figure 8; the recovery of PS in outlet a is high and consistent, few of them cross over and contaminate the b outlet which would lower the purity of the RBCs in b outlet. However, the purity of PS in outlet a increases with decreased flow rate. The longer residence time allows removal of more RBC, whose superior number fraction will have a pronounced effect on purity.
Figure 9.

Comparison of the RBC and PS purity as a function of total flow rate. RBC:PS of 90:10, Q′a/Q = 0.5, Qa/Q = 0.55.
Using the definition of enrichment rate, E, Equation 6, a plot was made of the enrichment as a function of total flow rate for the RBCs and the PS, Figure 10. Since E is just the ratio of purity of the outlet to the purity of the feed, the theoretical maximum of RBC E is 100/90 = 1.11, and that for PS is 100/10 = 10. We see that RBC E, ranging between 1.06 and 1.10, with no clear trend, is quite close to this limit. However, PS E approaches the theoretical limit only in the case of the lowest flow rate.
Figure 10.

Comparison of the RBC and PS enrichment rate as a function of total flow rate. RBC:PS of 90:10, Q′a/Q = 0.5, Qa/Q = 0.55.
Discussion
The overall performance of this system is consistent with our theoretical models and our intuition. Specifically, the most obvious observation is that the longer the residence time of the magnetic RBCs in the region of high Sm, the higher the recovery of the RBCs in the magnetic fraction. Further, at the concentrations studied, the PS beads were unaffected by the magnetic migration of the RBCs; however high PS concentration did appear to impede the magnetic migration of the RBCs. While the presence of PS adversely affected the recovery of RBCs in outlet b, it did not affect their purity – which always exceeded 96%.
The best results were found at Q = 0.1 ml/min; the flow rate of the cell feed was half this: Qa = 0.05 ml/min. This corresponds to a cell throughput of approximately 1.5 × 106 cells/min, or since the blood sample was diluted 1:100, the equivalent flow rate of whole blood becomes 5 × 10−7 L/min. As a point of comparison, Han and Frasier (Han 2006) reported similar performance, at rate of 8.3 × 10-8 L/min of blood in a three stage cascading, intrinsic magnetization, micro separating system.
While the recovery of RBCs was high at the lowest flow rates, it still was not 100%. As with virtually all biological systems, the presence of a specific property is not “binary”, but instead is characterized by a distribution around a mean value. Figure 1 presents such a distribution with respect to magnetophoretic mobility. Further, we have recently demonstrated that this mean mobility decreases with RBC storage, which we claim is the result of hemoglobin loss as the RBCs are stored. During this storage period there is a time in which this distribution is significantly larger around the mean than is presented in Figure 1(Chalmers 2017).
Final radial position of a RBC in the QMS at the exit depends on initial position and magnetophoretic mobility. The initial position could vary over the inner half of the annulus, because the inlet flow rate ratio was 0.5. While this confounds the assumption that distinctly different mobility increments exist at each radial position, the general assumption that the most mobile cells reach the wall, while the least exit outlet a, is still valid. If the QMS were operated with less regard for throughput, sharp cutoff motilities could be achieved by reducing the inlet flow rate ratio, placing the RBCs in a tighter radial band at the start of separation. In this mode, the QMS would be operated as a “fractionator” yielding up to three fractions where the wall fraction would subsequently be recovered by a high flow rate “flush” step. Further, the outlet manifold could be modified by the inclusion of additional concentric splitters to increase the number of distinct fractions. In fact, a dual splitter, 3-outlet flow manifold has been built by 3D printing, but not yet tested. If sufficient numbers of RBCs with high and low magnetophoretic mobility are able to be fractionated into multiple fractions, animal models exist to test the hypothesis that these different fractions, presumably with different levels of hemoglobin, have different biological properties.
These initial results provide further motivation to improve the performance of continuous separation of RBCs. While the current throughputs are not practical, a number of approaches can be taken to improve it. While probably not directly scalable, if whole blood were able to perform in this system in an equivalent manner, the throughput, on a per cell basis, would be 100 times higher, which means 1 ml of blood in 10 to 20 minutes. In addition, while it might seem intuitive to increase the radius of the channel, theoretical calculations which have been experimentally validated, indicate that unless the magnetic gradient is held constant as the radius is increased, no gain is made. It should be noted that we are near the maximum value of B possible without resorting to superconducting electromagnets which are not practical for this application. Alternatively, we are actively investigating other geometries which allow us to increase the flow volume in which a well-designed/controlled, high value of Sm can be subjected. In the current QMS system, approximately 2 ml of flowing cell suspension is subjected to a perpendicular average value of Sm of 343 T2/m. Other geometries suggest that this volume can be significantly scaled up with a higher values of Sm. By combining a higher cell suspension concentration, with large volumes and higher values of Sm, it is possible to make magnetic separation of RBCs competitive with other methods of RBC removal, and if we can fractionate RBCs into high a low hemoglobin fractions, a separation approach not current available could be created.
Acknowledgements
We thankfully acknowledge the funding of this work by grants NIH CA62349, NHLB 1R01HL131720-01A1, and DARPA BAA07-21.
Footnotes
Nomenclature.
| A1 | dimensionless constant A1 = 1 + ρi2 − (1 − ρi2)/ln(1/ρi), Eq. 7 |
| B | magnetic flux |
| E | enrichment rate |
| F | recovered fraction |
| I | integral solution, Eq. 7 |
| L | total radial height of the annular channel |
| m | magnetophoretic mobility |
| N | number of red blood cells |
| NF | normalized recovered fraction |
| P | purity |
| Q | flow rate |
| Sm | magnetic energy gradient |
| v | velocity |
| z, r | radial coordinates |
Greek Characters.
| μ0 | magnetic permeability of free space, 4π × 10−7 T/m*A |
| ρ | dimensionless radial position (r/r0) |
References
- Alam A, Lin Y, Lima A, Hansen M and Callum JL (2013). “The prevention of transfusion-associated circulatory overload.” Transfusion medicine reviews 27(2): 105–112. [DOI] [PubMed] [Google Scholar]
- Basford C, Forraz N, Habibollah S, Hanger1 K, McGuckin C. (2010). “ The Cord Blood Separation League Table: a Comparison of the Major Clinical Grade Harvesting Techniques for Cord Blood Stem Cells.” International Journal of Stem Cells 3(1): 32–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chalmers JJ, Jin X, Palmer A, Yazer M, Moore L, Pan J, Park J Zborowski M (2017). “ Femtogram resolution of iron content per cell: storage of red blood cells leads to loss of hemoglobin..” Analytical Chemistry 89(6): 3702–3709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAndrade D, Waters JH, Triulzi DJ, Alarcon L, Wisniewski MK, Dyga R and Yazer MH (2016).”Very low rate of patient-related adverse events associated with the use of intraoperative cell salvage.” Transfusion. [DOI] [PubMed] [Google Scholar]
- Han KH, Frazier AB (2006). “Paramagnetic capture mode magnetophoretic microseparator for high efficiency blood cell separations.” Lab Chip 8: 1079–1086. [DOI] [PubMed] [Google Scholar]
- Hod EA, Zhang N, Sokol SA, Wojczyk BS, Francis RO, Ansaldi D, Francis KP, Della-Latta P, Whittier S, Sheth S, Hendrickson JE, Zimring JC, Brittenham GM and Spitalnik SL (2010). “Transfusion of red blood cells after prolonged storage produces harmful effects that are mediated by iron and inflammation.” Blood 115(21): 4284–4292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang L, Rchard SJC (2004). “Continuous Particle Separation Through Deterministic Laterial Displacement.” Science 304: 987–990. [DOI] [PubMed] [Google Scholar]
- Jin X, Abbot S, Zhang X, Kang L, Voskinarian-Berse V, Zhao R, Kameneva MV, Moore LR, Chalmers JJ and Zborowski M (2012). “Erythrocyte enrichment in hematopoietic progenitor cell cultures based on magnetic susceptibility of the hemoglobin.” PLoS One 7(8): e39491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jing Y, Moore LR, Schneider T, Williams PS, Chalmers JJ., Farag SS, Bolwell B, Zborowski M. (2007). “Blood progenitor cell separation from clinical leukapheresis product by magnetic nanoparticle binding and magnetophoresis “ Biotechnol Bioeng 96(6): 1139–1154. [DOI] [PubMed] [Google Scholar]
- Jung Y, Choi, Yoonsu, Han, Ki Ho, Frazier A. Bruno (2010). “Six-stage cascade paramagnetic mode magnetophoretic separation system for human blood samples.” Biomed Microdevices 12: 637–645. [DOI] [PubMed] [Google Scholar]
- Lara O, Tong X, Zborowski M, Chalmers JJ ( 2004). “Enrichment of Rare Cancer Cells through Depletion of Normal Cells Using Density and Flow-Through, Immunomagnetic Cell Separation.” Experimental Hematology 32(10): 891–904. [DOI] [PubMed] [Google Scholar]
- Lieberman L, Maskens C, Cserti-Gazdewich C, Hansen M, Lin Y, Pendergrast J, Yi QL and Callum J (2013). “A retrospective review of patient factors, transfusion practices, and outcomes in patients with transfusion-associated circulatory overload.” Transfusion medicine reviews 27(4): 206–212. [DOI] [PubMed] [Google Scholar]
- Luten M, Roerdinkholder-Stoelwinder B, Schaap NP, de Grip WJ, Bos HJ and Bosman GJ (2008). “Survival of red blood cells after transfusion: a comparison between red cells concentrates of different storage periods.” Transfusion 48(7): 1478–1485. [DOI] [PubMed] [Google Scholar]
- Markus D, Gerda, Leitner, Christoph W, Kopp, Ying, Chen, Mariann, Gyongyosi, Irene, Lang, (2012). “Processing of autologous bone marrow cells by apheresis technology for cell-based cardiovascular regeneration.” Cytotherapy 14: 1005–1010. [DOI] [PubMed] [Google Scholar]
- McCabe S, Harriott P ( 1985). “Unit Operations in Chemical Engineering, 4th Eddition.” 4th Edition. McGraw-Hill Book Company,: 144–145. [Google Scholar]
- Melville D, Paul F, Roath S (1975). “Direct magnetic separation or red cells from whole blood.” Nature 225: 706. [DOI] [PubMed] [Google Scholar]
- Moore LR, Nehl F, Dorn J, Chalmers JJ and Zborowski M (2013). “Open Gradient Magnetic Red Blood Cell Sorter Evaluation on Model Cell Mixtures.” IEEE Trans Magn 49(1): 309–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore LR, Williams PS, Nehl F, Abe K, Chalmers JJ and Zborowski M (2014). “Feasibility study of red blood cell debulking by magnetic field-flow fractionation with step-programmed flow.” Anal Bioanal Chem 406(6): 1661–1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore LR, Zborowski M, Sun L Chalmers JJ ( 1998). “Lymphocyte fractionation using immunomagnetic colloid and dipole magnet flow cell sorter.” J. Biochemical and Biophysical Methods 37: 11–33. [DOI] [PubMed] [Google Scholar]
- Mutlu B, R. Smith, Kyle C, Edd, Jon F, Nadar, Priyanka, Dlamini, Mcolisi, Kapur, Ravi, Toner, Mehmet (2017). “Non-equalibrium Intertial Separation Array for High-throughput, Large-volume Blood Fractionation.” Scientific Reports 7: 9915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narick C, Triulzi DJ and Yazer MH (2012). “Transfusion-associated circulatory overload after plasma transfusion.” Transfusion 52(1): 160–165. [DOI] [PubMed] [Google Scholar]
- Nath P, Strelnik J, Vasanji A, Moore LR, Williams PS, Zborowski M, Roy S, Fleischman AJ (2008). “Development of Multistage Magnetic Deposition Microscopy.” Analytical Chemistry 81(1): 43–49. [DOI] [PubMed] [Google Scholar]
- Pauling L and Coryell CD (1936). “The Magnetic Properties and Structure of Hemoglobin, Oxyhemoglobin and Carbonmonoxyhemoglobin.” Proc Natl Acad Sci U S A 22(4): 210–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pauling L and Coryell CD (1936). “The Magnetic Properties and Structure of the Hemochromogens and Related Substances.” Proc Natl Acad Sci U S A 22(3): 159–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahman A, Fattah A, Ghosh S, Puri I (2016). “High gradient magnetic field microstructures for magnetophoreticcell separation.” Journal of Chromatography B 1027: 194–199. [DOI] [PubMed] [Google Scholar]
- Rieben R, Frauenfelder A and Nydegger UE (1992). “Naturally occurring ABO antibodies: long-term stable, individually distinct anti-A IgG spectrotypes.” Eur J Immunol 22(8): 2129–2133. [DOI] [PubMed] [Google Scholar]
- RL W (1968). “Rheology of the circulation.” [Google Scholar]
- Schneider T, Karl S, Moore LR, Chalmers JJ, Williams PS, Zborowski M (2010. ). “Sequential CD34 cell fractionation by magnetophoresis in a magnetic dipole flow sorter.” The Analyst 135(1): 62–70 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Moore L, Xie, Wei, Kim J, Zborowski M, Chalmers JJ (submitted). “The potential to separate intrinsically magnetic biological entities in a very high, well defined, microfluidic magnetic deposition system.” Biotechnol Bioeng. [Google Scholar]
- Sun L, Zborowski M, Moore L, Chalmers JJ ( 1998). “Continuous, Flow-Through Immunomagnetic Cell Separation in a Quadrupole Field.” Cytometry 33: 469–475. [DOI] [PubMed] [Google Scholar]
- Toner M, Irimia D (2005). “Blood-on-a-chip.” Annu. Rev. Biomed. Eng. 7: 77–2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams PS ZM, Chalmers JJ (1999. ). “Flow Rate for the Quadrupole Magnetic Cell Sorter.” Anal Chem 71: 3799–3807. [DOI] [PubMed] [Google Scholar]
- Xia N, Hunt TP, Mayers BT, Alsberg E, Whitesides GM, Westervelt RM, Ingber DE (2006). “Combined microfluidic-micromagnetic separation of living cells in continuous flow.” Biomed Microdevices 8: 299–308. [DOI] [PubMed] [Google Scholar]
- Zborowski M, Fuh CB, Green R, Sun L, Chalmers JJ, (1995). “ Analytical Magnetopheresis of Ferritin-labeled Lymphocytes,.” Analytical Chemistry 67(20): 3702–3712. [DOI] [PubMed] [Google Scholar]
- Zborowski M, Ostera GR, Moore LR, Milliron S, Chalmers JJ and Schechter AN (2003). “Red blood cell magnetophoresis.” Biophys J 84(4): 2638–2645. [DOI] [PMC free article] [PubMed] [Google Scholar]


