Abstract
Background and Aims
Dispersal is crucial due to its direct impact on dynamics of a species’ distribution as well as having a role in shaping adaptive potential through gene flow. In plants forming scarce and small populations, knowledge about the dispersal process is required to assess the potential for colonizing new habitats and connectivity of present and future populations. This study aimed to assess dispersal potential in Taxus baccata, a dioecious gymnosperm tree with a wide but highly fragmented distribution.
Methods
Seed and pollen dispersal kernels were estimated directly in the framework of the spatially explicit mating model, where genealogies of naturally established seedlings were reconstructed with the help of microsatellite markers. In this way, six differently shaped dispersal functions were compared.
Key Results
Seed dispersal followed a leptokurtic distribution, with the Exponential-Power, the Power-law and Weibull being almost equally best-fitting models. The pollen dispersal kernel appeared to be more fat-tailed than the seed dispersal kernel, and the Lognormal and the Exponential-Power function showed the best fit. The rate of seed immigration from the background sources was not significantly different from the rate of pollen immigration (13.1 % vs. 19.7 %) and immigration rates were in agreement with or below maximum predictions based on the estimated dispersal kernels. Based on the multimodel approach, 95 % of seeds travel <109 m, while 95 % of pollen travels <704 m from the source.
Conclusions
The results showed that, at a local spatial scale, yew seeds travel shorter distances than pollen, facilitating a rapid development of a kinship structure. At the landscape level, however, although yew exhibits some potential to colonize new habitats through seed dispersal, genetic connectivity between different yew remnants is strongly limited. Taking into account strong population fragmentation, the study suggests that gene dispersal may be a limiting factor of the adaptability of the species.
Keywords: Population fragmentation, dispersal, pollen, seed, dispersal kernel, gene flow, neighborhood model, microsatellite, dioecy, Taxus baccata
INTRODUCTION
Gene flow between populations has a significant impact on genetic diversity for several reasons. Generally, gene exchange compensates for the loss of genetic variation due to such processes as genetic drift and directional selection (Ellstrand, 2014). Migrant pollen gametes increase heterozygosity (Ismail et al., 2012; Rymer et al., 2015) and counterbalance the effect of inbreeding in a population. Importantly, gene flow can alter linkage disequilibrium through the mixing of locally fixed (e.g. through adaptation or genetic drift) gene combinations. Hence, gene flow can have either a positive or negative impact on the process of local adaptation. All these consequences make gene flow an important driver of plant species’ ecology and evolution (Krutovsky et al., 2012). In species having scattered distribution, in particular, genetic connectivity between populations can be a major limiting factor of their viability, persistence and adaptability (Young et al., 1996; Aguilar et al., 2008).
Habitat fragmentation makes local populations spatially disconnected in a landscape. However, numerous studies show that genetic connectivity needs to be considered in relative rather than absolute terms, taking into account the dispersal potential of a given species relative to spatial discontinuity due to fragmentation. Interestingly, studies on pollen dispersal in a fragmented habitat routinely show that population fragmentation does not lead to the complete isolation of remnants (e.g. White et al., 2002; Robledo-Arnuncio and Gil, 2005; Craft and Ashley, 2010; Buschbom et al., 2011; Moracho et al., 2016). For example, in an extremely isolated (≥30 km) population of anemophilous Pinus sylvestris in Spain, 35 out of 813 pollen gametes captured in genotyped seeds had an unknown origin (Robledo-Arnuncio and Gil, 2005). In addition, the assay of paternally inherited chloroplast DNA showed that these 35 immigrant pollen gametes came from at least 30 different trees, excluding the possibility that a single unsampled isolated tree was a source of immigrant pollen. Thus, although pollination occurred mostly within the fragment, the non-negligible proportion of immigrant pollen ensured genetic connectivity despite spatial isolation.
Most plants disperse their genes through pollen and seeds. In the context of population fragmentation, in particular, it is worth trying to disentangle these two components of gene flow. Usually, pollen-mediated gene flow is believed to occur more efficiently. This is not only because pollen often disperse longer distances than seeds (Ennos, 1994; Kremer et al., 2012). An equally important reason is that, thanks to pollen flow, plants from different populations can instantly form a common pool of gametes (gene pool). Consequently, pollen immigration has an immediate and positive impact on the current effective population size (or the effective number of mating individuals). For example, inbreeding in the next generation is immediately reduced as a consequence of pollen flow due to the decreased relatedness between parents. On the other hand, although successful seed gene flow is potentially twice as effective as pollen gene flow per propagule unit (Crawford, 1984), seed gene flow requires seed immigrants to germinate and survive until the reproductive stage in order to affect a local effective population size (and related parameters, e.g. inbreeding). Such a delayed seed gene flow becomes particularly important in long-living organisms, having slow generation turnover, such as many tree species.
Gene exchange between plant populations relies upon the long-distance dispersal (LDD) capability of a species. LDD is not a unified term, however, and the definition depends upon the context (e.g. genetic vs. ecological; Jordano, 2017). Moreover, different requirements may define seed and pollen LDD. In seeds, LDD is related to two functions: gene flow and colonization (Cain et al., 2000; Nathan, 2006). Therefore, even if dispersed seeds fail to reach another population, they still may be effective in gene flow in the process leading to population establishment. In this case, acting as a stepping-stone, LDD events may open up the possibility of gene flow between otherwise disconnected populations (Lobo Segura and Vargas, 2014; Davies et al., 2015). On the contrary, pollen LDD events are strictly related to successful pollination and are, therefore, required to reach another population. Otherwise, pollen is lost and LDD is not effective. In plants occupying fragmented habitats, both seed and pollen LDD may be important for gene flow. However, in the case of newly colonized (through seed LDD) habitats, being at risk of pollen limitation, pollen LDD is crucial for maintaining sexual reproduction and population growth. Pollen LDD plays an important role as the driver of the fast spread of adaptive variation. Hence, for long-living plants (such as trees), pollen LDD may be necessary to face rapid (compared with generation turnover) enviromental or climate changes, (Aguilée et al., 2016) because it increases the chance of progeny surviving to adulthood.
The assessment of the importance of dispersal in the functioning of a population requires a quantitative characterization of the dispersal process (Jeltsch et al., 2008; Kramer et al., 2008; McConkey et al., 2012; Aguilée et al., 2016). Various mathematical functions, known as dispersal kernels (Nathan et al., 2012), are typically utilized for this purpose. However, although data on dispersal distances in plants have accumulated over many years (e.g. Levin and Kerster, 1974; Dow and Ashley, 1996; Streiff et al., 1999), dispersal kernels suitable for predictive ecological models are not readily available for many plant species (for a recent summary, see Bullock et al. 2017). Due to methodological difficulties (Lavigne et al., 1996), related to the need to use molecular markers (Smouse and Sork, 2004), pollen dispersal kernels are particularly lacking for many plants. Examination of different pollen dispersal kernel functions is also not very common (but see, for example, Austerlitz et al., 2004; Ottwell et al., 2012; Saro et al., 2014). Due to gaps in knowledge regarding dispersal kernels, conservation biologists are often unable to assess quantitatively current and predict future responses of remnant populations to global changes, building their forecasts on qualitative information on dispersal potential (e.g. Thomas and Garcia-Martí, 2015).
Taxus baccata L. (yew) can be considered as a model plant to study the impact of fragmentation on gene flow and, in a broader perspective, on adaptation. Yew has a wide but scattered natural distribution across Europe (Thomas and Polwart, 2003). The maximum presence of yew occurred during the Sub-boreal period (5000–2500 years BP) when it was relatively abundant (Deforce and Bastiaens, 2007). After then, yew started declining and now it is recognized as a rare species along the natural range, although it may show occasional expansions under favourable conditions (Svenning and Magård, 1999; Dobrowolska et al., 2012). In the southern range margin, in particular, local populations are at high risk of extinction due to increased drought and fragmentation of suitable habitats (Thomas and Garcia-Martí, 2015). As a threatened species, yew is under protection in many European countries. However, genetic connectivity of remnant yew populations remains poorly studied, especially with regard to pollen dispersal. Yew reveals mixed seed dispersal syndrome, i.e. seeds are often dispersed through birds (thrushes) (Jordano et al., 2007; Martínez et al., 2008; Lavabre et al., 2016), although they also fall and germinate beneath maternal trees without any vector-mediated dispersal. Consequently, seeds are frequently dispersed on a local spatial scale (Martínez et al., 2008; Martínez and González-Taboada, 2009; Lavabre et al., 2016). Whether locally produced seeds result from local or non-local pollination, however, remains largely unknown. High levels of genetic differentiation among populations and elevated inbreeding despite obligatory outcrossing due to dioecy (Myking et al., 2009; Dubreuil et al., 2010; González-Martínez et al., 2010; Burgarella et al., 2012; Chybicki et al., 2012; Litkowiec et al., 2018) suggest that pollen gene flow is limited in this species. On the other hand, yew is characterized by wind pollination which is known to be a very efficient dispersal mechanism, especially in trees (Petit and Hampe, 2006).
The aim of this study was to estimate seed and pollen dispersal kernels, and consequently to quantify the potential of yew for dispersal and gene flow. First, based on spatially explicit parentage modelling using data on genotypes at nuclear and (effectively) paternally transmitted mitochondrial markers as well as tree gender and spatial location, we attempted to select the best-fitting dispersal models for seeds and pollen. To assess the potential for gene flow, we estimated selected quantiles of seed and pollen dispersal kernels as well as cumulative dispersal distance distributions for seeds and pollen and compared them with the observed immigration rates. In this way, we performed an indirect test for agreement between inferred dispersal kernels and the observed overall pattern of seed and pollen dispersal.
MATERIALS AND METHODS
Study site and sampling design
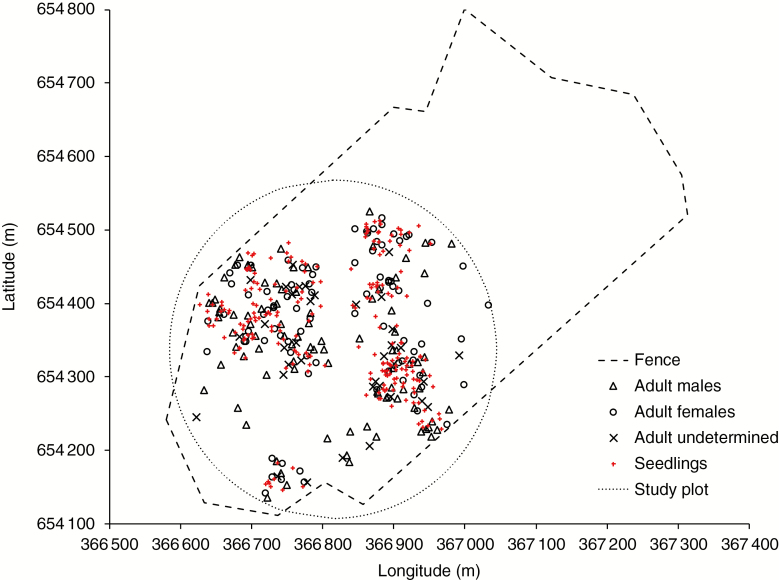
This study site, ‘Cisy w Czarnem’, is located in northern Poland, where yew is a natural component of the flora. Cisy w Czarnem is a nature reserve established in 1957 to protect a remnant population of English yew. Currently, the population consists of 439 adult yew trees (100–350 years old) scattered throughout the 26 ha mixed forest patch (Fig. 1). Together with black alder [Alnus glutinosa (L.) Gaertn.] and young Norway spruce [Picea abies (L.) H. Karst], English yew forms the understorey layer. The canopy is formed by common European trees, including European beech (Fagus sylvatica L.), pedunculate oak (Quercus robur L.), Scots pine (Pinus sylvestris L.) and hornbeam (Carpinus betulus L.), all at an age of up to 200 years. The reserve is fenced in order to lower browsing intensity and mortality of yew seedlings. The closest yew remnant is located 48 km due north-west (‘Cisy Tychowskie’ reserve; 70 adult trees; Janyszek et al., 2002). In addition, there are single trees located in the proximity of the study population (>4–5 km; data from Czarne Człuchowskie Forest District). Thus, the reserve is quite well isolated from the other pollen and seed sources. Our previous studies showed that the yew population exhibits a relatively high level of genetic variation compared with the other yew remnants (Chybicki et al., 2012) as well as a significant positive spatial autocorrelation of genes (Chybicki et al., 2011, 2016). The latter supports the origin of the adult population from natural regeneration.
Fig. 1.
Map of the distribution of sampled yew trees and seedlings within the ‘Cisy w Czarnem’ nature reserve. Co-ordinates are given in the ETRS89 reference system.
In April 2008, 216 adult trees within a plot of radius of approx. 230 m were mapped using a GPS device and sampled for short twigs, which were used to extract DNA. In addition, for every tree, the trunk diameter was measured and the sex was determined based on male and female flowers as well as fruit remains (cupule) attached to trees. In this way, we unambiguously classified 90 female and 89 male individuals. For 37 individuals, no signatures of sex expression were found at the time of collection of the materials, and these individuals were classified as not sexed. In addition, we sampled and mapped a cohort of 220 young seedlings at the (estimated) age of 5–15 years.
Genotyping
DNA was extracted using the cetyltrimethylammonium bromide (CTAB) protocol (Doyle and Doyle, 1990) in the same year that plants were sampled, and stored in –80 °C. In March 2016, DNA was used to genotype adult trees and seedlings using a set of eight nuclear expressed sequence tag-simple sequence repeat markers (nSSRs), developed based on transcriptome sequence data (Ueno et al., 2015). In addition, all individuals were assayed for the mitochondrial microsatellite marker TB01 (Miao et al., 2008) which reveals paternal inheritance in the study species (Chybicki et al., 2016). nSSRs were amplified in a single multiplex PCR using the QIAGEN Multiplex PCR Kit (Qiagen, Hilden, Germany) following the manufacturer’s protocol. PCR was conducted using a PTC200 thermal cycler (Bio-Rad, Hercules, CA, USA). PCR products were resolved using a capillary genetic analyser ABI3130XL (Applied Biosystems, Carlsbad, CA, USA) and Gene Mapper 4.0 software delivered with the analyser. Information about genetic variation is given in Supplementary Data Table S1.
Data analysis
Dispersal modelling.
To model a gene dispersal process, we used an approach of spatially explicit modelling of seedling parentage, implemented in the framework of the ‘seedling neighborhood model’ (SNM; Burczyk et al., 2006). The SNM uses spatial locations of seedlings and candidate parents as well as their genotypes simultaneously to estimate seedling genealogies and parameters of pollen and seed forward dispersal kernels. An accurate estimation of dispersal kernels benefits much from the incorporation of individual fecundities or their covariates, and SNM allows the inclusion of either data type (Burczyk et al., 2006).
In the SNM, data are represented by the multilocus genotypes of J progeny individuals O = {O1,O2, …, OJ} and K candidate parents within the sample plot T = {T1,T2, …, TK}. Each term in the vector O and T is a multilocus genotype at L unlinked loci. A population outside a sample plot is represented by allele frequencies at L loci F = {F1,F2, …, FL}. Note that FL is a vector of allele frequencies at a given locus. In this study, following the suggestion of Burczyk and Chybicki (2004), F was assumed to be equal to local allele frequencies. Also, spatial positions X = {x1,x2,…} of all individuals are known, so that interindividual Euclidean distances are readily available. In addition, trunk diameters of candidate parents Z = {z1,z2,…} were incorporated as a surrogate of individual fecundity.
In the SNM, the seedling may result either from seed immigration (with the probability ms) or from seed dispersal within the sample plot (with the probability 1 – ms. In the latter case, the maternal plant of a seedling is within the sample plot. Under dioecy, two alternative scenarios of seed origin are taken into account, i.e. with the probability 1 – mp, seed originated from local pollen movement (i.e. the father is inside the sample plot) or, with the probability mp, from pollen immigration (i.e. the unknown father is outside the sample plot). The j-th adult plant is assigned the probability ψij of being a seed parent for the i-th seedling. Similarly, the k-th adult tree is assigned the probability ϕjk of being a pollen donor for the j-th tree. Thus, the probability of observing the multilocus genotype of the i-th offspring Oi in the spatial location (xi) is equal to
| (1) |
where Pr(Oi|F) is the transition probability that the genotype Oi originated outside the sample plot, Pr(Oi|Tj,F) is the transition probability that the genotype Oi originated from a local mother of genotype Tj (i.e. a seed parent) and an unknown father (i.e. a pollen parent) outside the sample plot, Pr(Oi|Tj,Tk) is the transition probability that the genotype Oi originated from a local mother of genotype Tj and a local father of genotype Tk. All transition probabilities were computed assuming a possibility of random genotyping errors, with error rates ε = {ε1,ε2,…εL} (each element is the probability of erroneous scoring of a random allele at a given locus) being unknown parameters to estimate during the analysis. Also, because the probability of maternal transmission of the cytoplasmic (mtDNA) genome (r; see equations A5–A7 in Chybicki, 2018) is close to zero but remains uncertain to some degree (see Chybicki et al., 2016), we set this quantity as an estimable parameter together with the remaining parameters of the model. We should stress here that treating r as an estimable parameter was reasonable because we are dealing with a dioecious species.
In this study, the relative probabilities ψij and ϕjk were assumed to be a function of gender (g), seed or pollen production (fs or fp) and seed or pollen dispersal kernel (πs or πp). Under dioecy, gender determines whether the j-th tree can be a mother or a father, so that we used a discrete function of form
| (2) |
Because individual fecundities (seed or pollen production) were unknown, we used a diameter of the tree as a proxy (Clark et al., 1999; Younginger et al., 2017). We assumed that individual amounts of seed and pollen production are an exponential function of tree diameter, i.e.
| (3a) |
and
| (3b) |
where z is a standardized diameter of a tree, and βs and βp are the coefficients proportional to the effect of tree diameter on a logarithm of female and male fecundity, respectively. The exponential function can result from the assumption that fs or fp (fecundity) is inversely proportional to the probability of a null contribution of female or male gametes (Chybicki, 2018).
Seed or pollen dispersal kernels (qs or qp) were the focal functions of the model. In this study, we used several dispersal (location; see Nathan et al., 2012) kernel functions in order to infer the best predictive dispersal model. As a null model, we used the uniform distribution
| (4) |
where d is a dispersal distance computed as a Euclidean distance based on individual co-ordinates and c is a normalizing constant. Six alternative non-uniform dispersal kernels were considered, i.e.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
where θ is a parameter a or a vector of parameters a and b, with a and b representing the scale and the shape parameter of the function, respectively. Except for the Tufto model (Tufto et al., 1997), dispersal kernels were summarized in Nathan et al. (2012). Generally, selected dispersal kernels cover a wide range of dispersal models.
Taking all the factors into account, the relative probabilities ψij and ϕjk were computed as
| (11a) |
| (11b) |
Note that, due to the construct of the relative probabilities ψij and ϕjk, normalizing constants appearing in dispersal kernel functions [eqns (4–8)] eventually cancel out in ψij and ϕjk.
In the model, ε, ms, mp, r, βs and βp as well as θs and θp were set as estimable. Estimation was performed using the Maximum Likelihood (ML) method using the log-likelihood function
| (12) |
Because the ML estimation of the set of parameters was analytically intractable based on ℓ, the ML estimates were obtained numerically using the Newton method (Brandt, 1998). Standard errors of estimates were extracted from the diagonal of the inversed Hessian matrix. In the case of dispersal kernel parameter(s), in place of a scale parameter (a) the inverse of the forward average dispersal distancen (1/δ) was estimated. This approach allowed us to avoid problems with convergence occurring in the case of a two-parameter dispersal function (see Oddou-Muratorio et al., 2005). In addition, unlike a and δ, 1/δ is expected to have a symmetric (normal) probability distribution. Therefore, confidence bounds can be computed using the normal approximation (and not the time-consuming profile likelihood approach). The analysis was conducted using the NMπ computer program (Chybicki, 2018), updated to incorporate six dispersal kernels and the option to estimate the probability of maternal transmission of a cytoplasmic marker.
The six dispersal kernel functions yielded 6 × 6 = 36 combinations of non-random seed and pollen dispersal scenarios. In addition, we analysed the null model (random dispersal). Because alternative dispersal models represented generally non-nested models, we could not perform the standard likelihood ratio tests for model comparisons, while a simulation-based unified version of the test proposed by Lewis et al. (2011) was beyond computational capacities. Therefore, to compare competing dispersal models, we used the Akaike information criterion (AIC) computed for the m-th model as AICm = 2km – 2ℓm, where km is the number of parameters in the m-th model and ℓm is the maximum value of log-likelihood of the m-th model (Burnham and Anderson, 2002). The best model was that with the lowest value of AIC (AICMIN). In addition, for each model, we computed Δm = AICm – AICMIN. Following a suggestion of Burnham and Anderson (2002), if Δm is <2, the m-th model was treated as being indistinguishably worse in fit than the best model. Also, for each model, the relative support was estimated as the Akaike weight . Akaike weights were then used to estimate the overall relative support of each of the six dispersal models [eqns (5–10)]. Values of wm were also used to provide multimodel estimates of the parameters following the method in Burnham and Anderson (2002). In this way, the estimates (and their standard errors) account for dispersal model uncertainty. In the case of ms, mp, α, γ, β and mistyping error rates (ε1, …ε8, εmt), multimodel averages were computed across all 36 dispersal models. For seed dispersal parameters, multimodel averages were estimated for a specific-seed dispersal kernel across six alternative pollen dispersal kernels. For pollen dispersal parameters, we averaged across six alternative seed dispersal kernels. In this way, we attempted to take dispersal model uncertainty into consideration.
Post-modelling inferences.
Based on the fitted dispersal parameters, we estimated the average distance of dispersal as well as quantiles of dispersal kernels. In the case of quantiles, we focused specifically on the median (q50 %) as well two right-end quantiles: q95 % and q99 %. These quantiles provide information about the upper limit of dispersal distance of 50, 95 and 99 % propagules (either seeds or pollen). The quantiles were computed numerically via solving the equation for qc, where c is the cumulative probability of observing dispersal at a distance up to qc m from a source.
Finally, we tested whether empirical immigration rates fit the immigration rates expected based on the best-fitting dispersal kernels. The expected immigration rate, as a function of dispersal kernel, is difficult to assess (Goto et al., 2006). This is because it requires several assumptions to be made a priori regarding potential sources of immigrant propagules (Goto et al., 2006; Moran and Clark, 2011). Such sources, however, are routinely unknown. The only method currently in use that the authors are aware of assumes that a study plot is a fragment of a continuous population and that the background population is characterized by the same effective density of trees (Goto et al., 2006; Chybicki and Burczyk, 2010). In addition, it requires a cohort of sampled progeny (seedlings) to be located in the centre of the plot, so that every seedling has an approximately equal probability of being an immigrant if its true parent(s) is(are) located beyond a threshold distance L, with L = distance from the sub-plot of seedlings to the edge of the study plot. Under such conditions, the expected immigration can be estimated as . Nonetheless, when seedlings are distributed over the whole study plot, as in our case, this equation provides an inaccurate estimate of the expected immigration, because it does not take into account high variation in distances to plot edges of both parents and progeny. Therefore, in this study, we employed Monte Carlo simulation which does not have these limitations. Details of the simulation are given in Supplementary Data Fig. S1. Here, we only underline that the simulation is designed in a way that allows prediction of the maximum expected immigration rate. The significance of the difference between the observed immigration and Em was assessed using the Z-test, with standard errors for ms and mp computed based on the Hessian matrix (given in the standard output of NMπ software).
RESULTS
Dispersal modelling
Model selection.
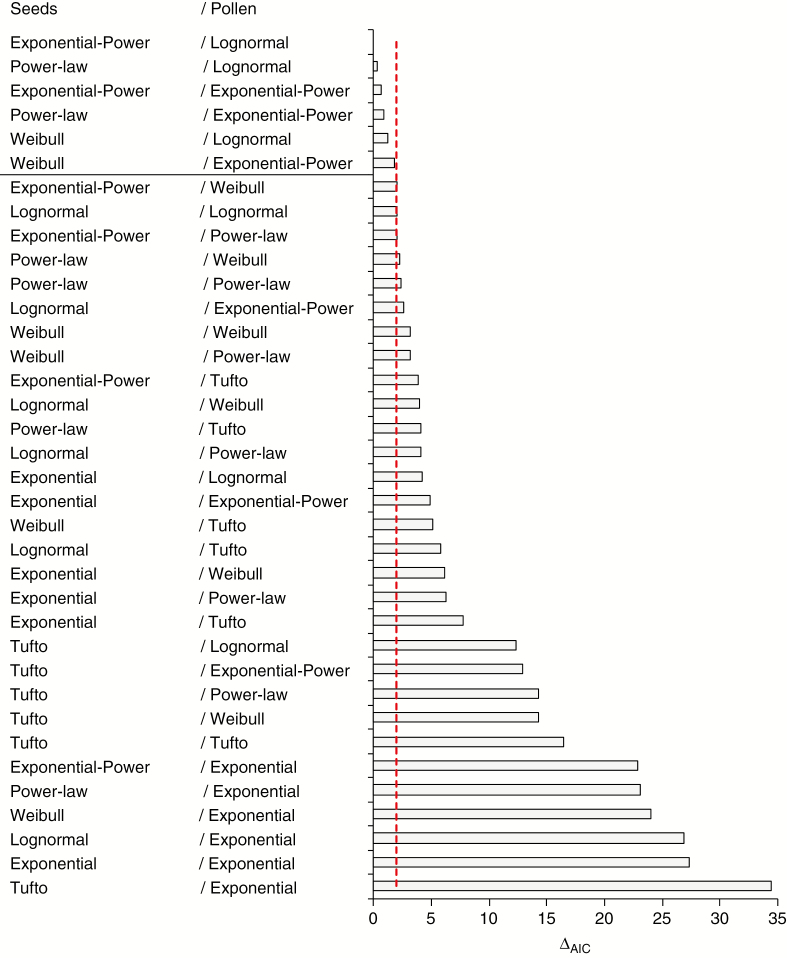
Based on the AIC, the null dispersal model (AIC = 7319.86) had an apparently worse fit than the worst-fitting non-random dispersal model (i.e. Tufto/exponential for seed/pollen dispersal, AIC = 6628.50). Using the likelihood ratio test, we rejected the null model as a model explaining the observed patterns of seed and pollen dispersal (χ2 = 695, d.f. = 2, P-value approx. 0). Among 36 alternative dispersal models, AIC ranged between 6628.50 (Tufto/Exponential) and 6594.02 (Exponential-Power/Lognormal) (Fig. 2). Based on the threshold value for Δm, the Exponential-Power, Power-law and Weibull models had the comparably best fit as seed dispersal kernels. For pollen dispersal, only the Lognormal and the Exponential-Power were credible models.
Fig. 2.
Relative fit of dispersal models expressed as the difference of the AIC value for a given model and the best model (ΔAIC). The dashed vertical line shows the threshold used to select models having comparable fit.
According to the sums of Akaike weights, which take into account uncertainty about a dispersal model for the opposite sex propagule (seeds vs. pollen), the Exponential-Power and Power-law models worked distinguishably better (i.e. above the average = 1/6) than the Weibull model as the seed dispersal kernel, with the relative probability of 0.346 and 0.303 vs. 0.119, respectively (Table 1). In the case of pollen dispersal kernels, the sum of weights confirmed the results based on Δm. Interestingly, with an overall average relative probability of 0.314, the Exponential-Power model showed the best overall fit as a model for seed and pollen dispersal.
Table 1.
Estimates of seed and pollen dispersal kernel parameters
| Dispersal kernel | 1/δ | s.e | b | s.e. | Σwm |
|---|---|---|---|---|---|
| Seeds | |||||
| Exponential | 0.0334 | 0.0029 | 0.042 | ||
| Tufto | 0.0297 | 0.0071 | 0.001 | ||
| Exponential-Power | 0.0285 | 0.0043 | 0.6004 | 0.1348 | 0.346 |
| Weibull | 0.0308 | 0.0037 | 1.1810 | 0.1292 | 0.189 |
| Lognormal | 0.0214 | 0.0050 | 1.0574 | 0.1148 | 0.119 |
| Power-law | 0.0246 | 0.0076 | 5.0743 | 1.9135 | 0.303 |
| Multimodel mean | 0.0271 | 0.0064 | |||
| Pollen | |||||
| Exponential | 0.0184 | 0.0021 | 0.000 | ||
| Tufto | 0.0064 | 0.0040 | 0.051 | ||
| Exponential-Power | 0.0065 | 0.0044 | 0.2727 | 0.1053 | 0.283 |
| Weibull | 0.0104 | 0.0037 | 0.8967 | 0.1421 | 0.142 |
| Lognormal | 0.0039 | 0.0031 | 1.5019 | 0.2626 | 0.386 |
| Power-law | 0.0006 | 0.0004 | 3.0299 | 0.0246 | 0.137 |
| Multimodel mean | 0.0052 | 0.0045 | |||
Note that estimates were obtained as multimodel averages.
δ, mean dispersal distance; b, shape parameter; s.e., standard error (computed taking into account both the within- and between-models uncertainty); Σwm, relative probability of the model estimated as a sum of Akaike weights for a given dispersal model across all competing dispersal models of the opposite-sex propagule (i.e. seeds vs. pollen).
Parameter estimates.
Generally, except for dispersal kernel parameters, estimates showed little variation across all 36 dispersal models (Supplementary Data Table S2). Therefore, we focus here on multimodel averages only. Seed and pollen immigration rates were equal to 0.131 (s.e. = 0.041) and 0.200 (s.e. = 0.049), and both estimates differed significantly from zero (Table 2). Selection gradients for the effect of trunk diameter on female and male reproductive success were 0.240 and 0.278, respectively. Because their confidence intervals did not include zero, the effects of trunk diameter were statistically significant (α = 0.05). Modelling also involved the estimation of the probability of maternal transmission of mtDNA, r. However, r showed little variation across all tested models. The average estimate of r equalled 0.041 with an s.e. of 0.024 and the 95 % confidence interval between –0.006 and 0.088. Thus, r did not differ significantly from zero, meaning that the transmission of mtDNA can be treated as effectively paternal.
Table 2.
Multimodel estimates of parameters of the neighborhood model, excluding dispersal kernel parameters
| Parameter | Parameter | Estimate | s.e. | 95 % CI |
|---|---|---|---|---|
| Probability of seed immigration | m s | 0.131 | 0.041 | 0.050, 0.212 |
| Probability of pollen immigration | m p | 0.200 | 0.049 | 0.103, 0.296 |
| Effect of tree size* on female reproductive success | γ | 0.240 | 0.095 | 0.055, 0.425 |
| Effect of tree size on male reproductive success | β | 0.278 | 0.103 | 0.077, 0.479 |
| Probability of maternal transmission of mtDNA | α | 0.041 | 0.024 | –0.006, 0.087 |
| Mistyping error rates: | ||||
| B-26615-282A | ε 1 | 0.026 | 0.009 | 0.009, 0.044 |
| B-20918-231C | ε 2 | 0.009 | 0.008 | –0.007, 0.025 |
| Ma-722-463C | ε 3 | 0 | ||
| Ma-2571-171A | ε 4 | 0.118 | 0.018 | 0.084, 0.153 |
| Ma-6281-999D | ε 5 | 0.006 | 0.004 | –0.003, 0.014 |
| Me-998-304A | ε 6 | 0.019 | 0.010 | 0.000, 0.037 |
| Me-25598-508C | ε 7 | 0 | ||
| Me-30893-225A | ε 8 | 0 | ||
| TB01 (mtDNA) | ε mt | 0 |
Parameter estimates were obtained as weighted averages across all alternative dispersal models with weight equal to Akaike information criterion weights.
*Tree size was quantified as trunk diameter at the height of 100 cm from the ground.
While the estimates of genotyping error rates showed little variation across different models, they showed some variation among loci. The estimates of error rates ranged from zero to 0.118, with an average of 0.020 (Table 2). Only two loci showed a mistyping error rate significantly greater than zero, as their 95 % confidence intervals did not include zero. In contrast, with the invariant estimate of zero, five loci (including the mtDNA marker) did not show any signal of genotyping errors.
In order to keep partial specificity of dispersal kernel parameters (due to a specific shape parameter), their estimates were characterized separately for each kernel function (Table 1). Nonetheless, 1/δ can be compared across different dispersal models. The analysis revealed that for seeds 1/δs was quite similar across dispersal kernels and ranged from 0.0214 (Lognormal) to 0.0334 (Exponential). By comparison, 1/δp was strongly dependent on dispersal function, spanning between 0.0006 (Power-law) and 0.0184 (Exponential). Based on the multimodel averages, 1/δp was one order of magnitude lower than 1/δs and the difference 1/δs – 1/δp for the multimodel estimates was statistically significant (P-value = 0.005; based on the Z-test).
Post-modelling inferences.
Given the estimates of dispersal parameters, we obtained several summary statistics of the predictive dispersal model, including the average dispersal distances and quantiles of dispersal distributions.
Estimates of the average seed dispersal distance (δs) ranged from 29.7 to 47.8 m, depending on the model (Supplementary Data Table S2). Under the best fitting Exponential-Power and Power-law models δs equalled 35.1 and 40.7 m, respectively. For comparison, the median seed dispersal distance (i.e. the distance limit for dispersal of 50 % of seeds) under these two models equalled 25.4 and 25.8 m, respectively. Estimates of the average distance of pollen dispersal (δp) spanned between 53.7 and 1818.2 m, depending on the dispersal kernel. For the best-fitting Lognormal kernel, the value of δp was 256.7 m. The median distance of pollen dispersal predicted under the Lognormal model (q50 %) was 83.2 m. For the second-best fitting model (Exponential-Power), the estimates were generally lower, with the average and median distance δp = 153.8 m and q50 % = 72.3 m. According to the best-fitting model, 5 % of seeds travel further than 99 m, whereas 1 % of seeds disperse further than 157.3 m. Under the best pollen dispersal model, 5 and 1 % of pollen travel further than 983.7 and 2733.4 m, respectively.
The multimodel average dispersal distance was 37.4 and 418.1 m for seeds and pollen, respectively. Multimodel estimates of quantiles q50 %, q95 % and q99 % of the ‘average’ seed dispersal kernel were 25.6, 108.9 and 193.5 m, respectively. The quantiles q50 %, q95 % and q99 % of the ‘average’ pollen dispersal kernel were 73.6, 704.3 and 2167.9 m, respectively.
Monte Carlo simulations showed that the expected immigration of seeds and pollen was 0.106 (s.e. ±0.002) and 0.357 (s.e. ±0.004), respectively. Consequently, as revealed by the Z-test, we observed only a slight and non-significant excess of seed immigration (P-value = 0.538) and a significant deficiency of pollen immigration (P-value = 0.001), compared with predictions based on the inferred dispersal kernels.
DISCUSSION
Robustness of estimated dispersal models
This study focused on modelling gene dispersal based on the seedling parentages in the frame of the spatially explicit mating model. We attempted to capture the main factors that can be critical for the outcome models. For example, we allowed molecular data to contain errors. As recently shown (Chybicki, 2018), this approach allows the estimation procedure to be robust to mismatches between parents and progeny. Also, we incorporated the effect of tree size (a proxy for fecundity). Although the neighborhood model is generally not influenced by differences in seed and pollen fecundities (Robledo-Arnuncio and Garcia, 2007), if the number of seed/pollen parents decreases below 100 the bias in dispersal kernel parameters can be substantial when individual fecundities exhibit a high variation (Robledo-Arnuncio, 2008). In our case, the number of candidate parents of each gender is very close to the suggested threshold (Robledo-Arnuncio, 2008). Therefore, incorporation of the effect of fecundity, even if indirectly through the selection gradient on a trunk diameter (Clark et al., 1999), should improve the accuracy of the resulting models. Finally, we explicitly treated gender as well as the uniparentally inherited mitochondrial marker. In this way, we eliminated the ambiguity of parentage analysis based on nuclear markers (Dow and Ashley, 1996) with respect to sexual roles of assigned parents as well as distances of propagule movement.
However, our approach was not free from limitations. The dimensions of the study plot put obvious spatial constraints on the observed distribution of dispersal events (Saro et al., 2014). In fact, the observed distribution of dispersal distances can be considered as the distribution truncated at the spatial limits of the plot. The truncated distribution provides little, if any, information about the right-hand tail of the dispersal kernel so that the shape of the dispersal kernel was inferred based on the central part of the distribution, excluding the right-hand tail. Consequently, our approach to predict LDD is an extrapolation performed under quite a restrictive assumption that the dispersal process follows a single probability function within the entire domain (theoretically going from zero to infinity). We attempted to address this problem at least partially, comparing a number of differently shaped dispersal kernels for their relative goodness of fit. In addition, we showed that the observed proportion of immigrant seeds is in good agreement with predictions based on the inferred dispersal kernels, while the observed proportion of immigrant pollen is lower than predicted. The latter observation will be discussed in greater detail later.
Although our approach was shown to be quite robust to mistyping errors, one consequence of treating mistyping errors explicitly in the model is that markers prone to errors provide less information than markers without mistyping problems. Molecular markers that differ in their discrimination power have different weights in the total information used in order to assess the relative support for competing models. In this context, it still remains an open question as to which strategy works better: include all markers, regardless of their genotyping quality, and control for mistyping errors vs. include only good-quality markers at the cost of reduced information for parentage modelling. Because we had only nine nuclear markers (including mtDNA), we followed the former approach. However, additional study is needed to resolve this dilemma.
Seed dispersal
Yew is a typical bird-dispersed plant, producing fleshy ‘fruits’ with their intensive red cover (arils) that attract birds, especially thrushes (Turdus spp.). Generally, thrushes are considered to be efficient dispersal vectors (Jordano et al., 2007; Martínez et al., 2008; Morales et al., 2013). Direct observations of foraging behaviour of thrushes within yew stands revealed that the distribution of post-foraging distances shows two peaks, one at the distance of several metres from a female yew tree and the second between 100 and 200 m from a female yew tree (Martínez et al., 2008). However, a non-negligible proportion (up to 15 %) of flights were beyond 200 m. These observations were generally confirmed by the empirical distributions of seed dispersal distances (Lavabre et al., 2016). Using genotyped endocarps and female trees, Lavabre et al. (2016) identified maternal individuals for seeds collected in seed traps. For seeds having their mother trees within the study site (69 %), a majority of mother trees were found in the close vicinity of traps. On the other hand, 31 % of dispersal events from unidentified sources represented distances beyond 300 m. These observations suggested that seed dispersal in yew generally follows a fat-tailed dispersal kernel.
To our knowledge, only one study attempted to estimate seed dispersal kernel for T. baccata (Martínez and González-Taboada, 2009). Using the inverse modelling approach, they showed that observed seed densities are best explained by the log-normal dispersal kernel, which can be considered as a fat-tailed dispersal kernel (Nathan et al., 2012). Interestingly, a log-normal dispersal kernel has a peak at a non-zero distance, so it might be better suited for a pattern of seedling establishment created under the Janzen–Connell effect (Janzen, 1970) rather than for seed dispersal. In this study, on the other hand, based on established seedlings, we selected a group of three alternative models as best-fitting seed dispersal kernels, namely the Exponential-Power, Power-law and Weibull, all representing fat-tailed distributions with the maximum at zero. The two studies show that the dispersal kernel may reveal site to site variation related to habitat characteristics. Such a variation in zoochorous plants may be related to the variation in communities of dispersers (Moran and Clark, 2012).
Martínez and González-Taboada (2009) also showed that dispersal kernel parameters for two successive years differed significantly, emphasizing that year to year variation in the process of seed dispersal in yew can be very high. Consequently, dispersal kernels estimated based on a sample taken during a single season may not be representative for the dispersal process in the long run. For this reason, we believe that a sample of seedlings of different ages used in our study is advantageous for the analysis of dispersal potential because the estimates reflect a multiseasonal average and should, therefore, be relatively robust to temporal variation.
Based on the multimodel inferences, median seed dispersal was 26 m. Nonetheless, our estimate is at least one order of magnitude shorter than the previous estimates based on the inverse modelling of seed shadows (264–1370 m; Martínez and González-Taboada, 2009). We found this discrepancy interesting. Even if we take into account that 13 % of seeds came from outside the study plot, the median should still not be altered, because we showed that the observed seed immigration rate is in agreement with the estimated dispersal kernels. On the other hand, our results are in good agreement with the empirical distribution of seed dispersal distances obtained recently after exact identification of seed sources based on molecular markers (Lavabre et al., 2016). The inflated variance of dispersal estimates obtained based on the inverse modelling (Jones and Muller-Landau 2008) can be a possible explanation of the differences between genetic and non-genetic estimates.
Molecular markers enable the identification of immigrants, which may be good indicators of LDD events. The immigration rate depends on dimensions of the study site, the distance to background seed sources as well as less apparent factors such as relative fecundities of internal vs. external sources. Our study plot is quite well isolated from the other yew remnants, except for trees growing within the reserve outside the study plot. Because thrushes disperse yew seeds mostly within yew stands (Martínez et al., 2008), we believe that the 13 % of seed immigrants estimated in this study came from the remaining yew trees growing in the close neighbourhood of the study plot. Nonetheless, we cannot exclude that some immigrant seedlings originated from seeds after LDD (Lavabre et al., 2016).
Pollen dispersal
Unlike many other conifers, yew pollen does not have sacci or any similar structures decreasing the terminal velocity (Dyakowska, 1959). As a medium-size tree, it often forms the understorey layer and experiences reduced wind speed as compared with the canopy. Pollen trapping revealed that the density of pollen decreases rapidly with the distance from male trees (Noryśkiewicz, 2006). Thus, pollen dispersal is expected to be rather spatially restricted compared with seed dispersal. However, the magnitude of pollen dispersal has not been studied. In this study, we provided direct estimates of pollen dispersal kernels.
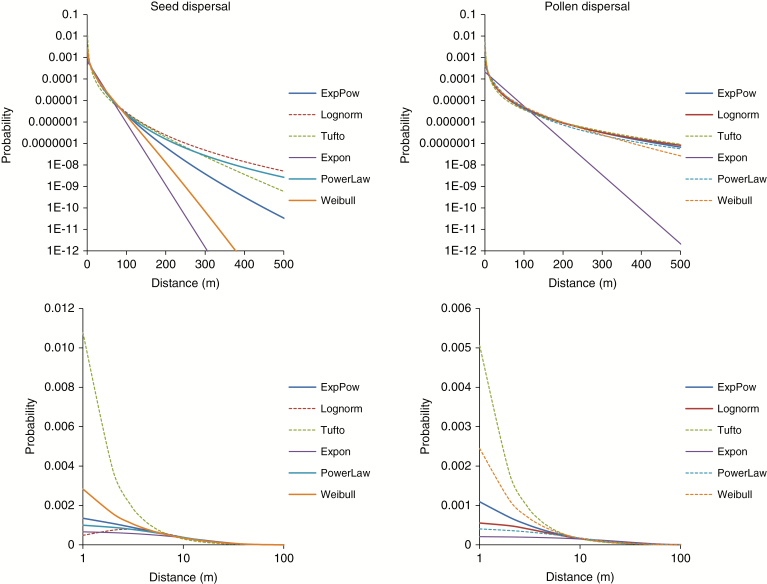
Among six dispersal models tested in this study, the Lognormal model appeared to work the best. On the other hand, the exponential model and the Tufto wind threshold model showed the worst fit. These two models were not equivalent, however. Inspection of the plots (Fig. 3) shows that the exponential model had a much thinner tail while the Tufto model was characterized by the elevated density within the range 0–10 m. Under the best-fitting Lognormal dispersal kernel, the average distance of pollen dispersal in yew was about 250 m. However, the mean of a fat-tailed kernel is somewhat hard to interpret because it is strongly affected by relatively rare LDD events. This argument can explain apparent differences (approx. 100 m) between mean distances predicted based on the Lognormal and Exponential-Power kernel, which otherwise were very similar in terms of their fit to data. For example, median pollen dispersal distances predicted based on these two kernels were very close to each other, allowing us to conclude that 50 % of pollen released by a male tree disperses within a radius of 70–80 m. The slightly better fit of the ‘zero-at-zero’ Lognormal model over the ‘maximum-at-zero’ Exponential-Power model might be related to the fact that dioecy generates a deficiency of short mating distances, especially when gender reveals spatial clustering (Supplementary Data Fig. S2).
Fig. 3.
Estimated dispersal kernel functions for seeds (left) and pollen (right). Functions showing comparable best fit are plotted using solid bold lines. In order to show details of left and right tails, functions were plotted using linear (upper) and logarithmic (lower) distance scales.
Interestingly, despite the fact that pollen dispersal quantiles were larger than seed dispersal quantiles, the estimated pollen immigration rate of 20 % was not significantly higher than the seed immigration rate (13 %). Moreover, we noted a significant deficiency of pollen immigration as compared with the (maximum) prediction based on the estimated dispersal kernels. In other words, according to estimated dispersal kernels, pollen dispersal is more extensive than seed dispersal. However, disagreement between the immigration rate and dispersal kernel suggests that the tail of the pollen dispersal kernel may be overestimated, and/or the background pollen donors were not as fertile (or abundant) as assumed in the simulation. In particular, the latter explanation seems to be concordant with the absence of yew in the neighbourhood of the nature reserve (see the Materials and Methods). As an alternative avenue of explanation, we need to underline that, unlike the estimated dispersal kernels (Klein et al., 2013), the estimated immigration rates are not robust to selection. Hence, the difference between mp and the maximum predicted value can be a result of a negative selection against maladapted pollen immigrants. Nonetheless, we have no information indicating that this could be the case.
The study population is characterized by a significant spatial genetic structure (SGS) (Chybicki et al., 2011), that makes biparental inbreeding a likely phenomenon. Inbreeding may lead to early-stage inbreeding depression in terms of seed abortion or poor seed/seedling performance relative to outbred progeny (Kärkkäinen and Savolainen, 1993). Unfortunately, information on inbreeding depression is not available for the study species. However, dioecy is generally believed to facilitate the maintenance of lethal factors in a species’ genome (Willi et al., 2006). Unless there is strong selection towards inbred lines (such as in breeding programmes) or a strong genetic drift (such as in small populations), lethal factors are slowly eliminated from the gene pool of a population. Therefore, we cannot exclude that the observed pollination pattern may be confounded by inbreeding depression, and pollen dispersal may be even more restricted than shown in this study. Our current project focuses on the magnitude and factors of inbreeding depression in T. baccata based on samples of seeds. Hopefully, in the near future, we will be able to verify whether inbreeding can influence the pollination pattern observed in this study.
Implications for gene flow
In plants, gene flow occurs due to the dispersal of seeds and pollen. Their relative contribution to the total gene flow depends on the balance between the effectiveness (seeds carry twice as many genes per locus as pollen) and potential of the dispersal of seeds vs. pollen. Gene flow through pollen expressed as immigration conditional on pollen migration (m|mp) is half that through seeds (m|ms) (Hamilton and Miller, 2002), i.e. m|mp = mp/2 and (assuming that seed immigration implies pollen immigration) m|ms = ms. Our approach allowed us to estimate ms and mp at the level of the study plot. We can then predict that the rate of gene flow into the study plot through pollen and seeds is m|mp = 0.100 (s.e. = 0.025) and m|ms = 0.131 (s.e. = 0.041), respectively. Here, the s.e. for m|mp was approximated using the property of variance Var(cX) = c2Var(X). Thus, seed immigration contributed slightly more to the total gene flow than pollen immigration, but the difference was not statistically significant (P-value = 0.516; based on the Z-test). Therefore, based on the estimates of seed and pollen immigration rates, we can conclude that both propagule types are equally important for gene flow in the study species. Our results seem to reflect specific circumstances of pollen and seed dispersal in yew, including the lack of sacci and low height at the release point in the case of pollen and partial zoochory in the case of seeds. However, we believe that high isolation due to population fragmentation is the main factor that limits effective gene dispersal through pollen despite greater potential compared with seeds indicated by the estimated dispersal kernels.
A separate question is whether m|mp and m|ms are high or low from the long-term perspective. The answer, however, depends on unknown information about the source of immigrants. The estimates of dispersal kernels suggest that sources are located very close to the study plot, especially in the case of seeds. In the case of pollen, we predicted that only 1 % of pollen disperse further than 2.2 km. The closest group of candidate pollen sources is located in the unsampled part of the reserve. Outside the reserve, the closest groups are located about 4–5 km from the reserve, while the closest yew remnant population is located 48 km due north-west. Although we cannot exclude the possibility that the immigrant pollen came from the outside of the reserve, we are fairly sceptical about pollen exchange between neighbouring remnants. However, taking into account all the limitations of the neighborhood model discussed earlier, the genetic assignment-based approach (Robledo-Arnuncio, 2011) would be a valuable alternative tool to cross-check our results. Nonetheless, because its requirements regarding the sampling design go beyond our current capabilities, a separate study is needed.
Our results also shed light on the difference in gene flow between nuclear (nuDNA) and mitochondrial genes. Because mtDNA in the study species is effectively paternally transmitted, gene immigration at the level of mtDNA can be computed as mp + ms = 0.331 (s.e. =0.064; s.e. approximated under the assumption of independence of mp and ms). For comparison, gene immigration for nuDNA is mp/2 + ms = 0.231 (s.e. = 0.048). Thus, gene flow for mtDNA is greater than for nuDNA, but the difference is not statistically significant (P-value = 0.210; based on the Z-test). However, mtDNA has a lower effective population size (equal to the effective number of males) compared with the nuclear genome. Therefore, except for female-biased populations, we can expect that the rate of divergence for mtDNA is higher than that for nuDNA in the study species (see also Chybicki et al.2016).
Fecundity
We found that the diameter of a tree is positively associated with both maternal and paternal reproductive success. The results are in line with our expectations based on the very general assumption that larger individuals produce more flowers so that they can contribute more gametes to the next generation. The recent survey showed that, with some exceptions, trunk diameter is a good predictor of fecundity (Younginger et al., 2017). However, the diameter is a compound effect of individual ability to acquire resources (genotype), resource availability, individual age and random factors. Because the study site represents a natural population, we cannot assume that the age structure is uniform. In addition, we have no detailed knowledge about microsite quality at the resolution of single trees. Consequently, although positive selection cannot be ruled out, whether it occurs within the population remains an open question. However, regardless of whether positive selection does or does not occur, differences in fecundity result in non-random mating patterns and, together with spatially restricted propagule dispersal, contribute to the process of genetic drift (Wilson and Levin, 1986) routinely observed within natural yew stands (Myking et al., 2009; Dubreuil et al., 2010; González-Martínez et al., 2010; Chybicki et al., 2012; Litkowiec et al., 2018).
Conclusions
Seed dispersal in yew is extensive enough for colonization of nearby sites (Martínez et al., 2008; Lavabre et al., 2016; this study). However, according to our predictive model, such colonization events are extremely rare as compared with the frequency of dispersal within the vicinity of mother trees. Interestingly, the results allow us to predict that 95 % of pollen can travel distances up to 700 km from a male tree. Therefore, pollen dispersal is sufficient to maintain genetic connectivity between distant trees within the same remnant, although local mating patterns are far from random. In contrast, pollen dispersal alone does not seem to guarantee gene exchange between different remnants in the fragmented landscape. In this respect, seed and pollen dispersal may be equally important for gene flow in yew. The strong fragmentation of the species’ distribution lasting over many generations (approx. 3000 years; Deforce and Bastiaens, 2007) provided the opportunity for some adaptation to negative consequences of isolation, e.g. through genetic purging (Glémin, 2003). Therefore, we cannot exclude that the genetic isolation between remnants may have no negative consequences in stable environments. However, the question remains whether the predicted dispersal potential is a limiting factor of adaptability of the study species in the face of global change.
SUPPLEMENTARY DATA
Supplementary data are available online at https://academic.oup.com/aob and consist of the following. A short paragraph describes details of the simulation algorithm used to estimate the expected immigration rates. A short paragraph describes the observed genetic structure. Table S1: genetic structure parameters estimated for the study population. Table S2: estimates of parameters of the neighborhood model for 36 combinations of dispersal kernel functions. Figure S1: map showing the distribution of adult trees and the border used to delimitate dispersal within and outside the plot. Figure S2: spatial correlogram for tree gender.
ACKNOWLEDGEMENTS
We thank Katarzyna Meyza and Ewa Sztupecka for their assistance in the field and in laboratory work. We also thank John Sved as well as two anonymous reviewers for their suggestions on the manuscript. This work was supported by the National Science Center, Poland (grant no. UMO-2014/15/B/NZ9/04404 to I.J.C.).
LITERATURE CITED
- Aguilar R, Quesada M, Ashworth L, Herrerias-Diego Y, Lobo J. 2008. Genetic consequences of habitat fragmentation in plant populations: susceptible signals in plant traits and methodological approaches. Molecular Ecology 17: 5177–5188. [DOI] [PubMed] [Google Scholar]
- Aguilée R, Raoul G, Rousset F, Ronce O. 2016. Pollen dispersal slows geographical range shift and accelerates ecological niche shift under climate change. Proceedings of the National Academy of Sciences, USA 113: E5741–E5748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Austerlitz F, Dick CW, Dutech C, et al. 2004. Using genetic markers to estimate the pollen dispersal curve. Molecular Ecology 13: 937–954. [DOI] [PubMed] [Google Scholar]
- Brandt S. 1998. Data analysis. Statistical and computational methods for scientists and engineers. Berlin: Springer-Verlag. [Google Scholar]
- Bullock JM, Mallada González L, Tamme R, et al. 2017. A synthesis of empirical plant dispersal kernels. Journal of Ecology 105: 6–19. [Google Scholar]
- Burczyk J, Chybicki IJ. 2004. Cautions on direct gene flow estimation in plant populations. Evolution 58: 956–963. [DOI] [PubMed] [Google Scholar]
- Burczyk J, Adams WT, Birkes DS, Chybicki IJ. 2006. Using genetic markers to directly estimate gene flow and reproductive success parameters in plants based on naturally regenerated seedlings. Genetics 173: 363–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgarella C, Navascués M, Zabal-Aguirre M, et al. 2012. Recent population decline and selection shape diversity of taxol-related genes. Molecular Ecology 21: 3006–3021. [DOI] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. 2002. Model selection and multimodel inference: a practical information-theoretic approach, 2nd edn Berlin: Springer-Verlag. [Google Scholar]
- Buschbom J, Yanbaev Y, Degen B. 2011. Efficient long-distance gene flow into an isolated relict oak stand. Journal of Heredity 102: 464–472 [DOI] [PubMed] [Google Scholar]
- Cain ML, Milligan BG, Strand AE. 2000. Long-distance seed dispersal in plant populations. American Journal of Botany 87: 1217–1227. [PubMed] [Google Scholar]
- Chybicki IJ. 2018. NMπ – improved re-implementation of NM+, a software for estimating gene dispersal and mating patterns. Molecular Ecology Resources 18: 159–168. [DOI] [PubMed] [Google Scholar]
- Chybicki IJ, Burczyk J. 2010. Realized gene flow within mixed stands of Quercus robur L. and Q. petraea (Matt.) L. revealed at the stage of naturally established seedling. Molecular Ecology 19: 2137–2151. [DOI] [PubMed] [Google Scholar]
- Chybicki IJ, Oleksa A, Burczyk J. 2011. Increased inbreeding and strong kinship structure in Taxus baccata estimated from both AFLP and SSR data. Heredity 107: 589–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chybicki IJ, Oleksa A, Kowalkowska K. 2012. Variable rates of random genetic drift in protected populations of English yew: implications for gene pool conservation. Conservation Genetics 13: 899–911. [Google Scholar]
- Chybicki IJ, Dering M, Iszkuło G, Meyza K, Suszka J. 2016. Relative strength of fine-scale spatial genetic structure in paternally vs. biparentally inherited DNA in a dioecious plant depends on both sex proportions and pollen-to-seed dispersal ratio. Heredity 117: 449–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark JS, Silman M, Kern R, Macklin E, Hillerislambers J. 1999. Seed dispersal near and far: patterns across temperate and tropical forests. Ecology 80: 1475–1494. [Google Scholar]
- Craft KJ, Ashley MV. 2010. Pollen-mediated gene flow in isolated and continuous stands of bur oak, Quercus macrocarpa (Fagaceae). American Journal of Botany 97: 1999–2006. [DOI] [PubMed] [Google Scholar]
- Crawford TJ. 1984. The estimation of neighbourhood parameters for plant populations. Heredity 52: 273–283. [Google Scholar]
- Davies SJ, Cavers S, Finegan B, White A, Breed MF, Lowe AJ. 2015. Pollen flow in fragmented landscapes maintains genetic diversity following stand-replacing disturbance in a neotropical pioneer tree, Vochysia ferruginea Mart. Heredity 115: 125–129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deforce K, Bastiaens J. 2007. The holocene history of Taxus baccata (yew) in Belgium and neighbouring regions. Belgian Journal of Botany 140: 222–237. [Google Scholar]
- Dobrowolska D, Olszowska G, Niemczyk M. 2012. Stand structure and populations of yew (Taxus baccata L.) in the Cisy Rokickie and Bogdanieckie Cisy reserves. Leśne Prace Badawcze 73: 313–322 [in Polish, English summary]. [Google Scholar]
- Dow BD, Ashley MV. 1996. Microsatellite analysis of seed dispersal and parentage of saplings in bur oak, Quercus macrocarpa. Molecular Ecology 5: 120–132. [Google Scholar]
- Doyle JJ, Doyle JL. 1990. Isolation of plant DNA from fresh tissue. Focus 12: 13–15. [Google Scholar]
- Dubreuil M, Riba M, Gonzalez-Martinez SC, Vendramin GG, Sebastiani F, Mayol M. 2010. Genetic effects of chronic habitat fragmentation revisited: strong genetic structure in a temperate tree, Taxus baccata (Taxaceae), with great dispersal capability. American Journal of Botany 97: 303–310. [DOI] [PubMed] [Google Scholar]
- Dyakowska J. 1959. Podręcznik palinologii. Warszawa: Wydawnictwa Geograficzne. [Google Scholar]
- Ellstrand NC. 2014. Is gene flow the most important evolutionary force in plants?American Journal of Botany 101: 737–753. [DOI] [PubMed] [Google Scholar]
- Ennos RA. 1994. Estimating the relative rates of pollen and seed migration among plant populations. Heredity 72: 250–259. [Google Scholar]
- Glémin S. 2003. How are deleterious mutations purged? Drift versus nonrandom mating. Evolution 57: 2678–2687. [DOI] [PubMed] [Google Scholar]
- González-Martínez SC, Dubreuil M, Riba M, Vendramin GG, Sebastiani F, Mayol M. 2010. Spatial genetic structure of Taxus baccata L. in the western Mediterranean Basin: past and present limits to gene movement over a broad geographic scale. Molecular Phylogenetics and Evolution 55: 805–815. [DOI] [PubMed] [Google Scholar]
- Goto S, Shimatani K, Yoshimaru H, Takahashi Y. 2006. Fat-tailed gene flow in the dioecious canopy tree species Fraxinus mandshurica var. japonica revealed by microsatellites. Molecular Ecology 15: 2985–2996. [DOI] [PubMed] [Google Scholar]
- Hamilton MB, Miller JR. 2002. Comparing relative rates of pollen and seed gene flow in the island model using nuclear and organelle measures of population structure. Genetics 162: 1897–1909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ismail SA, Ghazoul J, Ravikanth G, Shaanker RU, Kushalappa CG, Kettle CJ. 2012. Does long-distance pollen dispersal preclude inbreeding in tropical trees? Fragmentation genetics of Dysoxylum malabaricum in an agro-forest landscape. Molecular Ecology 21: 5484–5496. [DOI] [PubMed] [Google Scholar]
- Janyszek S, Szczepanik-Janyszek M, Król S. 2002. Walory botaniczne rezerwatu przyrody ‘Cisy Tychowskie’. Roczniki Akademii Rolniczej w Poznaniu 5: 79–88 [in Polish with English summary]. [Google Scholar]
- Janzen DH. 1970. Herbivores and the number of tree species in tropical forests. American Naturalist 104: 501–528. [Google Scholar]
- Jeltsch F, Moloney KA, Schurr FM, Köchy M, Schwager M. 2008. The state of plant population modelling in light of environmental change. Perspectives in Plant Ecology, Evolution and Systematics 9: 171–189. [Google Scholar]
- Jones FA, Muller-Landau HC. 2008. Measuring long-distance seed dispersal in complex natural environments: an evaluation and integration of classical and genetic methods. Journal of Ecology 96: 642–652. [Google Scholar]
- Jordano P. 2017. What is long-distance dispersal? And a taxonomy of dispersal events. Journal of Ecology 105: 75–84. [Google Scholar]
- Jordano P, García C, Godoy JA, García-Castaño JL. 2007. Differential contribution of frugivores to complex seed dispersal patterns. Proceedings of the National Academy of Sciences, USA 104: 3278–3282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kärkkäinen K, Savolainen O. 1993. The degree of early inbreeding depression determines the selfing rate at the seed stage: model and results from Pinus sylvestris (Scots pine). Heredity 71: 160–166. [Google Scholar]
- Klein EK, Bontemps A, Oddou-Muratorio S. 2013. Seed dispersal kernels estimated from genotypes of established seedlings: does density‐dependent mortality matter? Methods in Ecology and Evolution 4: 1059–1069.
- Kramer K, Buiteveld J, Forstreuter M, et al. 2008. Bridging the gap between ecophysiological and genetic knowledge to assess the adaptive potential of European beech. Ecological Modelling 216: 333–353. [Google Scholar]
- Kremer A, Ronce O, Robledo-Arnuncio JJ, et al. 2012. Long-distance gene flow and adaptation of forest trees to rapid climate change. Ecology Letters 15: 378–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krutovsky KV, Burczyk J, Chybicki IJ, Finkeldey R, Pyhajarvi T, Robledo-Arnuncio JJ. 2012. Gene flow, spatial structure, local adaptation, assisted migration in trees. In: Schnell RJ, Priyadarshan PM, eds. Genomics of tree crops. New York: Springer, 71–116. [Google Scholar]
- Lavabre JE, Gilarranz LJ, Fortuna MA, Bascompte J. 2016. How does the functional diversity of frugivorous birds shape the spatial pattern of seed dispersal? A case study in a relict plant species. Philosophical Transactions of the Royal Society B: Bological Sciences 371: 20150280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavigne C, Godelle B, Reboud X, Gouyon PH. 1996. A method to determine the mean pollen dispersal of individual plants growing within a large pollen source. Theoretical and Applied Genetics 93: 1319–1326. [DOI] [PubMed] [Google Scholar]
- Levin DA, Kerster HW. 1974. Gene flow in seed plants. Evolutionary Biology 7: 139–220. [Google Scholar]
- Lewis F, Butler A, Gilbert L. 2011. A unified approach to model selection using the likelihood ratio test. Methods in Ecology and Evolution 2: 155–162. [Google Scholar]
- Litkowiec M, Lewandowski A, Wachowiak W. 2018. Genetic variation in Taxus baccata L.: a case study supporting Poland’s protection and restoration program. Forest Ecology and Management 409: 148–160. [Google Scholar]
- Lobo Segura J, Vargas DJ. 2014. Pollen dispersal patterns in a fragmented population of Carapa nicaraguensis (Meliaceae). International Journal of Plant Sciences 175: 176–185. [Google Scholar]
- Martínez I, González-Taboada F. 2009. Seed dispersal patterns in a temperate forest during a mast event: performance of alternative dispersal kernels. Oecologia 159: 389–400. [DOI] [PubMed] [Google Scholar]
- Martínez I, García D, Obeso JR. 2008. Differential seed dispersal patterns generated by a common assemblage of vertebrate frugivores in three fleshy-fruited trees. Ecoscience 15: 189–199. [Google Scholar]
- McConkey KR, Prasad S, Corlett RT, et al. 2012. Seed dispersal in changing landscapes. Biological Conservation 146: 1–13. [Google Scholar]
- Miao Y-C, Su J-R, Zhang Z-J, Li H, Luo J, Zhang Y-P. 2008. Isolation and characterization of microsatellite markers for the endangered Taxus yunnanensis. Conservation Genetics 9: 1683–1685. [Google Scholar]
- Moracho E, Moreno G, Jordano P, Hampe A. 2016. Unusually limited pollen dispersal and connectivity of Pedunculate oak (Quercus robur) refugial populations at the species’ southern range margin. Molecular Ecology 25: 3319–3331. [DOI] [PubMed] [Google Scholar]
- Morales JM, García D, Martínez D, Rodriguez-Pérez J, Herrera JM. 2013. Frugivore behavioural details matter for seed dispersal: a multi-species model for Cantabrian thrushes and trees. PLoS One 8: e65216. doi:10.1371/journal.pone.0065216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran EV, Clark JS. 2011. Estimating seed and pollen movement in a monoecious plant: a hierarchical Bayesian approach integrating genetic and ecological data. Molecular Ecology 20: 1248–1262. [DOI] [PubMed] [Google Scholar]
- Moran EV, Clark JS. 2012. Between-site differences in the scale of dispersal and gene flow in red oak. PLoS One 7: e36492. doi:10.1371/journal.pone.0036492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myking T, Vakkari P, Skrøppa T. 2009. Genetic variation in northern marginal Taxus baccata L. populations. Implications for conservation. Forestry 82: 529–539. [Google Scholar]
- Nathan R, Klein EK, Robledo-Arnuncio JJ, Revilla E. 2012. Dispersal kernels. In: Clobert J, Baguette M, Benton T, Bullock J, eds. Dispersal ecology and evolution. Oxford: Oxford University Press, 187–210. [Google Scholar]
- Nathan R. 2006. Long-distance dispersal of plants. Science 313: 786–788. [DOI] [PubMed] [Google Scholar]
- Noryśkiewicz M. 2006. Historia cisa w okolicy Wierzchlasu w świetle analizy pyłkowej. Toruń: Wydawnictwo Uniwersytetu Mikołaja Kopernika w Toruniu. [Google Scholar]
- Oddou-Muratorio S, Klein EK, Austerlitz F. 2005. Pollen flow in the wildservice tree, Sorbus torminalis (L.) Crantz. II. Pollen dispersal and heterogeneity in mating success inferred from parent–offspring analysis. Molecular Ecology 14: 4441–4452. [DOI] [PubMed] [Google Scholar]
- Ottewell K, Grey E, Castillo F, Karubian J. 2012. The pollen dispersal kernel and mating system of an insect-pollinated tropical palm, Oenocarpus bataua. Heredity 109: 332–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petit RJ, Hampe A. 2006. Some evolutionary consequences of being a tree. Annual Review of Ecology, Evolution and Systematics 37: 187–214. [Google Scholar]
- Robledo-Arnuncio JJ. 2008. Seed dispersal estimation without fecundities: a reply to Ralph. Molecular Ecology 17: 1883–1884. [DOI] [PubMed] [Google Scholar]
- Robledo-Arnuncio JJ. 2011. Wind pollination over mesoscale distances: an investigation with Scots pine. New Phytologist 190: 222–233. [DOI] [PubMed] [Google Scholar]
- Robledo-Arnuncio JJ, García C. 2007. Estimation of the seed dispersal kernel from exact identification of source plants. Molecular Ecology 16: 5098–5109. [DOI] [PubMed] [Google Scholar]
- Robledo-Arnuncio JJ, Gil L. 2005. Patterns of pollen dispersal in a small population of Pinus sylvestris L. revealed by total exclusion paternity analysis. Heredity 94: 13–22. [DOI] [PubMed] [Google Scholar]
- Rymer PD, Sandiford M, Harris SA, Billingham MR, Boshier DH. 2015. Remnant Pachira quinata pasture trees have greater opportunities to self and suffer reduced reproductive success due to inbreeding depression. Heredity 115: 115–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saro I, Robledo-Arnuncio JJ, González-Pérez MA, Sosa PA. 2014. Patterns of pollen dispersal in a small population of the Canarian endemic palm (Phoenix canariensis). Heredity 113: 215–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smouse PE, Sork VL. 2004. Measuring pollen flow in forest trees: an exposition of alternative approaches. Forest Ecology and Management 197: 21–38. [Google Scholar]
- Streiff R, Ducousso A, Lexer C, Steinkellner H, Gloessl J, Kremer A. 1999. Pollen dispersal inferred from paternity analysis in a mixed oak stand of Quercus robur L and Q. petraea (Matt.) Liebl. Molecular Ecology 8: 831–841. [Google Scholar]
- Svenning J-C, Magård E. 1999. Population ecology and conservation status of the last natural population of English yew Taxus baccata in Denmark. Biological Conservation 88: 173–182. [Google Scholar]
- Thomas PA, Garcia-Martí X. 2015. Response of European yews to climate change: a review. Forest Systems 24: eR01 http://dx.doi.org/10.5424/fs/2015243–07465. [Google Scholar]
- Thomas PA, Polwart A. 2003. Taxus baccata L. Journal of Ecology 91: 489–524. [Google Scholar]
- Tufto J, Engen S, Hindar K. 1997. Stochastic dispersal processes in plant populations. Theoretical Population Biology 52: 16–26. [DOI] [PubMed] [Google Scholar]
- Ueno S, Wen Y, Tsumura Y. 2015. Development of EST–SSR markers for Taxus cuspidata from publicly available transcriptome sequences. Biochemical Systematics and Ecology 63: 20–26. [Google Scholar]
- White GM, Boshier DH, Powell W. 2002. Increased pollen flow counteracts fragmentation in a tropical dry forest: an example from Swietenia humilis Zuccarini. Proceeding of the National Academy of Sciences, USA 99: 2038–2042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willi Y, Van Buskirk J, Hoffmann AA. 2006. Limits to the adaptive potential of small populations. Annual Review of Ecology, Evolution and Systematics 37: 433–458. [Google Scholar]
- Wilson JB, Levin DA. 1986. Some genetic consequences of skewed fecundity distributions in plants. Theoretical and Applied Genetics 73: 113–121. [DOI] [PubMed] [Google Scholar]
- Young A, Boyle T, Brown T. 1996. The population genetic consequences of habitat fragmentation for plants. Trends in Ecology and Evolution 11: 413–418. [DOI] [PubMed] [Google Scholar]
- Younginger BS, Sirová D, Cruzan MB, Ballhorn DJ. 2017. Is biomass a reliable estimate of plant fitness?Applications in Plant Sciences 5: apps.1600094. doi:10.3732/apps.1600094. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.